棱柱、棱锥和棱台的结构特征
1.1 棱柱、棱锥、棱台的结构特征(第1课时)

有两个面互相平行,其余各面都是四边形,
并且每相邻两个四边形的公共边都互相平行,
这些面所围成的多面体叫做棱柱. E1 D1
底面:两个互相平行的面.
F1 A1 B1 C1
简称底.
侧面:其余各面. 侧棱:相邻侧面的公共边.
侧棱
底 ED 面
顶点:侧面与底面的公共顶点.
F
C
AB 侧面
顶点
棱柱的分类
按底面多边形的边数来分
A' D
侧棱:相邻侧面的公共边.
上底面
C' B' C
顶点:侧面与上(下)底面的 A
B
公共顶点
下底面
棱台的分类
由三棱锥、四棱锥、五棱锥……截得的棱台 分别叫做三棱台、四棱台、五棱台……
棱台的表示:用各底面顶点的字母表示
三棱台 四棱台
五棱台
棱台ABCD—A ' B ' C ' D '
1.判断下列说法是否正确,正确的在后面的 括号内打“√”,错误的打“×”. (1)棱柱的侧面可以不是平行四边形.( ) (2)三棱锥的四个面都可以作为底面.( ) (3)四棱台有8个顶点,6个面,4条侧棱.( ) • 答案:(1)× (2)√ (3)√
2.试判断下列说法正确与否: ①由六个面围成的封闭图形只能是五棱锥;
②两个底面平行且相似,其余各面都是梯形的 多面体是棱台.
• 解:①不正确,由六个面围成的封闭图形有 可能是四棱柱;
• ②不正确,两个底面平行且相似,其余各面 都是梯形的多面体,侧棱不一定相交于一
多面体的表面展开图
•
如图是三个几何体的表面展开图,请
B.2 个 D.4 个
2.下面图形所表示的几何体中,不是棱锥的为( )
第1节 棱柱、棱锥、棱台的结构特征

平移 (1)
平移 (2)
棱柱的特点
1.有两个互相平行且全等的面 2.夹在两个平行平面间的每相邻的两个面的交线都互相平行且 且相等.
棱柱的相关概念
棱柱的两个互相平行的面叫做棱柱的底面。其余各面叫做棱
柱的侧面,两个侧面的公共边叫做棱柱的侧棱。
棱柱的两个底面之间的距离叫做棱柱的高。
棱柱的符号表示:棱柱 ABCDEF A' B 'C ' D' E ' F '
(2)棱锥的侧面是有公共顶点的三角形,但是各侧棱不一定相等,故①②不
正确;棱台是由平行于棱锥底面的平面截棱锥底面得到的,故各个侧棱的延长
线一定交于一点,③正确;棱台的各条侧棱必须交于一点故④错误.
[答案] (1)B (2)C
练习:下列关于四棱柱的说法:①四条侧棱互相平行且相等;②两对相对的侧面互相平行;
(3)图(3)中的几何体叫做________,它是由棱锥________被平行于底面 ABCD 的平面________截得的 AA′,BB′叫它的__________,平面 BCC′B′、平面 DAA′D′叫它的________.
[答案] (1)棱柱 侧棱 顶点 (2)棱锥 侧棱 侧面 底面 (3)棱同学们仔细观察下面的几何体,它们有哪些共同的特点?
(1)
(2)
这些多面体是棱柱
(3)
(4)
棱柱的形成
从运动的观点来观察,棱柱可以看成一个多边形(包括围 成的平面部分)上各点都沿着同一个方向移动相同的距离所形 成的几何体。
图(1) 和 (2) 中的几何体分别由平行四边形和五边形沿某一方 向平移得来的。
正棱台:由正棱锥截得的棱台
下底面
上底面 D'
教学设计1:1.1.2 棱柱、棱锥和棱台的结构特征
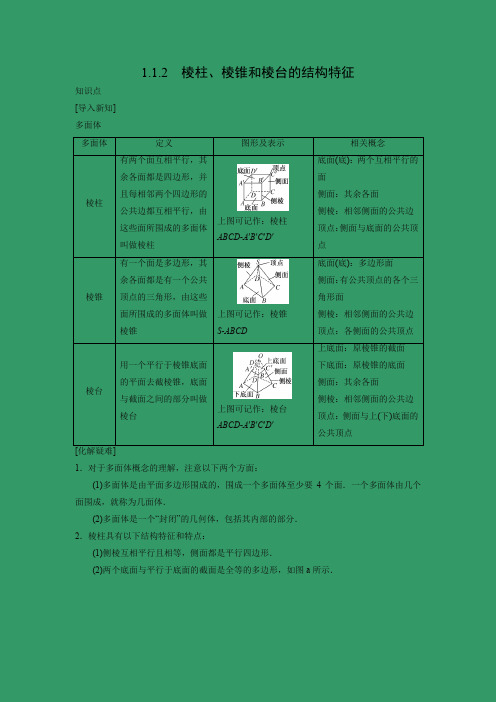
1.1.2棱柱、棱锥和棱台的结构特征知识点[导入新知]多面体多面体定义图形及表示相关概念棱柱有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱上图可记作:棱柱ABCDA′B′C′D′底面(底):两个互相平行的面侧面:其余各面侧棱:相邻侧面的公共边顶点:侧面与底面的公共顶点棱锥有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥上图可记作:棱锥SABCD底面(底):多边形面侧面:有公共顶点的各个三角形面侧棱:相邻侧面的公共边顶点:各侧面的公共顶点棱台用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分叫做棱台上图可记作:棱台ABCDA′B′C′D′上底面:原棱锥的截面下底面:原棱锥的底面侧面:其余各面侧棱:相邻侧面的公共边顶点:侧面与上(下)底面的公共顶点[化解疑难]1.对于多面体概念的理解,注意以下两个方面:(1)多面体是由平面多边形围成的,围成一个多面体至少要4个面.一个多面体由几个面围成,就称为几面体.(2)多面体是一个“封闭”的几何体,包括其内部的部分.2.棱柱具有以下结构特征和特点:(1)侧棱互相平行且相等,侧面都是平行四边形.(2)两个底面与平行于底面的截面是全等的多边形,如图a所示.(3)过不相邻的两条侧棱的截面是平行四边形,如图b所示.(4)有两个面平行,其余各面都是平行四边形的几何体不一定是棱柱,如图c所示.3.对于棱锥要注意有一个面是多边形,其余各面都是三角形的几何体不一定是棱锥,必须强调其余各面是共顶点的三角形,如图d所示.4.棱台中各侧棱延长后必相交于一点,否则不是棱台.题型一棱柱的结构特征[例1]下列关于棱柱的说法:(1)所有的面都是平行四边形;(2)每一个面都不会是三角形;(3)两底面平行,并且各侧棱也平行;(4)被平面截成的两部分可以都是棱柱.其中正确说法的序号是________.【答案】(3)(4)[类题通法]有关棱柱的结构特征问题的解题策略(1)紧扣棱柱的结构特征进行有关概念辨析.①两个面互相平行;②其余各面是四边形;③相邻两个四边形的公共边互相平行.求解时,首先看是否有两个平行的面作为底面,再看是否满足其他特征.(2)多注意观察一些实物模型和图片便于反例排除.[活学活用]下列说法正确的是()A.有两个面平行,其余各面都是四边形的几何体叫棱柱B.有两个面平行,其余各面都是平行四边形的几何体叫棱柱C.各个侧面都是正方形的四棱柱一定是正方体D.九棱柱有9条侧棱,9个侧面,侧面均为平行四边形【答案】D题型二棱锥、棱台的结构特征[例2]下列关于棱锥、棱台的说法:(1)用一个平面去截棱锥,底面和截面之间的部分组成的几何体叫棱台;(2)棱台的侧面一定不会是平行四边形;(3)棱锥的侧面只能是三角形;(4)由4个面围成的封闭图形只能是三棱锥;(5)棱锥被平面截成的两部分不可能都是棱锥.其中说法正确的序号是________.【答案】(2)(3)(4)[类题通法]判断棱锥、棱台形状的两个方法(1)举反例法:结合棱锥、棱台的定义举反例直接判断关于棱锥、棱台结构特征的某些说法不正确.(2)直接法:判定方法棱锥棱台定底面只有一个面是多边形,此面即为底面两个互相平行的面,即为底面看侧棱相交于一点延长后相交于一点[活学活用]下列说法正确的有()①由5个面围成的多面体只能是四棱锥;②仅有两个面互相平行的五面体是棱台;③两个底面平行且相似,其余各面都是梯形的多面体是棱台;④有两个面互相平行,其余4个面都是等腰梯形的六面体是棱台.A.0个B.1个C.2个D.3个【答案】A题型三多面体的平面展开图[例3]如下图是三个几何体的侧面展开图,请问各是什么几何体?解由几何体的侧面展开图的特点,结合棱柱,棱锥,棱台的定义,可把侧面展开图还原为原几何体,如图所示:所以①为五棱柱,②为五棱锥,③为三棱台.[类题通法]1.解答此类问题要结合多面体的结构特征发挥空间想象能力和动手能力.2.若给出多面体画其展开图时,常常给多面体的顶点标上字母,先把多面体的底面画出来,然后依次画出各侧面.3.若是给出表面展开图,则可把上述程序逆推.[活学活用]水平放置的正方体的6个面分别用“前面、后面、上面、下面、左面、右面”表示,如图是一个正方体的表面展开图(图中数字写在正方体的外表面上),若图中“0”上方的“2”在正方体的上面,则这个正方体的下面是()A.1B.5C.快D.乐【答案】B易错易误辨析1.柱、锥、台结构特征判断中的误区[典例]如下图所示,下列关于这个几何体的正确说法的序号为________.①这是一个六面体;②这是一个四棱台;③这是一个四棱柱;④此几何体可由三棱柱截去一个三棱柱得到;⑤此几何体可由四棱柱截去一个三棱柱得到.【解析】①正确,因为有6个面,属于六面体的范围;②错误,因为侧棱的延长线不能交于一点,所以不正确;③正确,如果把几何体放倒就会发现是一个四棱柱;④⑤都正确,如下图所示.【答案】①③④⑤[易错防范]1.解答过程中易忽视侧棱的延长线不能交于一点,直观感觉是棱台,而不注意逻辑推理.2.解答空间几何体概念的判断题时,要注意紧扣定义,切忌只凭图形主观臆断.[成功破障]如图所示,将装有水的长方体水槽固定底面一边后倾斜一个小角度,则倾斜后水槽中的水形成的几何体是()A.棱柱B.棱台C.棱柱与棱锥的组合体D.不能确定【答案】A当堂检测1.下列图形中,不是三棱柱的展开图的是()【答案】C2.如图所示,在三棱台ABCA′B′C′中,截去三棱锥A′ABC,则剩余部分是()A.三棱锥B.四棱锥C.三棱柱D.组合体【答案】B3.面数最少的棱柱为________棱柱,共有________个面围成.【答案】三54.如图所示,M是棱长为2 cm的正方体ABCDA1B1C1D1的棱CC1的中点,沿正方体表面从点A到点M的最短路程是________ cm.【答案】135.如图所示,长方体ABCD A1B1C1D1.(1)这个长方体是棱柱吗?如果是,是几棱柱?为什么?(2)用平面BCNM把这个长方体分成两部分,各部分形成的几何体还是棱柱吗?如果是,是几棱柱,并用符号表示;如果不是,请说明理由.解:(1)是棱柱,并且是四棱柱,因为长方体相对的两个面是互相平行的四边形(作底面),其余各面都是矩形(作侧面),且相邻侧面的公共边互相平行,符合棱柱的定义.(2)截面BCNM的上方部分是三棱柱BB1MCC1N,下方部分是四棱柱ABMA1DCND1.。
【课件】棱柱、棱锥、棱台的结构特征

棱柱的表示:
用表示底面各顶点的字母表示 棱柱ABC- A'B'C'
C'
A'
B'
D' A'
C' B'
D'
E'
C'
A' B'
A
C
D
BA
C B
三棱柱
四棱柱
E DC
A五棱柱B
棱柱的结构特征
思考:对于棱柱,
1.侧棱长相等吗? 相等
侧面是什么四边形?
平行四边形
E' F'
A'
D' C'
B'
2.两个底面多边形是什么关系? E D
C’ B’
有两个面互相平行,
其余各面都是四边形,
底
并且每相邻两个四边形
面
的公共边都互相平行。
ED
侧棱 F
C
A
B
侧面
顶点
棱柱的结构特征
1.棱柱的概念:
棱柱的底面:两个互相平行的面. 底面
简称底.
E' D'
F'
C'
棱柱的侧面:其余各面.
A'
B' 侧
棱柱的侧棱:
侧
面
棱 ED
相邻侧面的公共边. F
棱柱的顶点:
【解析】面最少的棱柱是三棱柱,它有 5 个面;顶点最少的一个棱台 是三棱台,它有 3 条侧棱.
5.画一个三棱台,再把它分成: (1)一个三棱柱和另一个多面体; (2)三个三棱锥,并用字母表示.
【解析】画三棱台一定要利用三棱锥. (1)如图①所示,三棱柱是棱柱 A′B′C′-AB″C″,另一个多
课件11:§1.1 第1课时 棱柱、棱锥、棱台的结构特征

公共点
新知预习
知识点二 多面体
多面体 定义
图形及表示
有两个面互相平
行,其余各面都是
四边形,并且每相
棱柱 邻两个四边形的公 共边都互相平行, 如图可记作:棱柱 由这些面所围成的 ABCDEF- 多面体叫作棱柱 A′B′C′D′E′F′
相关概念 底面(底):两个互 相平行的面;侧 面:其余各面; 侧棱:相邻侧面 的公共边;顶点: 侧面与底面的公 共顶点
当有4个顶点时,可围成4个面,所以一个多面体至少应 有4个面,而且这样的面必是三角形,故C也是真命题; 对于D,只有当截面与底面平行时才对. 【答案】(1)C (2)D
课堂探究 类型二 简单几何体的判定 例2 如图所示,长方体ABCD-A1B1C1D1.
(1)这个长方体是棱柱吗?如果是,是几棱柱?为什么?
新知预习
棱锥
有一个面是多
边形,其余各面
底面(底):多边形面;
都是有一个公 共顶点的三角
侧面:有公共顶点的 各个三角形面;侧棱: 相邻侧面的公共边;
形,由这些面所 如图可记作:棱 顶点:各侧面的公共
围 成 的 多 面 体 锥 S-ABCD 顶点
叫作棱锥
新知预习
棱台
用一个平行于 棱锥底面的平 面去截棱锥,底 面与截面之间 的部分叫作棱 台
新知预习
2.空间几何体的分类
多面体
旋转体
定义
由若干个平面多边形围成的 几何体
由一个平面图形绕它所在 平面内的一条定直线旋转 所形成的封闭几何体
图形
新知预习
2.空间几何体的分类 多面体
旋转体
面:围成多面体的各个多
相 关 边形;棱:相邻两个面的 轴:形成旋转体所绕的
高一数学棱柱、棱锥和棱台的结构特征2

三棱锥 (四面体)
四棱锥
五棱锥
(2)正棱锥:如果棱锥的底面是正多边 形,并且水平放置, 它的顶点又在过正 多边形中心的铅垂线上,则这个棱锥叫做 S 正棱锥!
D
E
A
O
B
C
5.正棱锥的性质: (1)正棱锥的各侧面都是全等的等腰三 角形; (2)等腰三角形底边上的高都相等,叫 做棱锥的斜高! 6.棱锥的表示: (1)用顶点和底面各顶点的字母表示棱 锥:如三棱锥P-ABC,四棱锥S-ABCD. (2)用对角面表示:如四棱锥可以用P- AC表示.
2 2
即正四棱锥的高为6,斜高为 2 10
练习题:
1.能保证棱锥是正棱锥的一个条件是
( C ) (A)底面为正多边形 (B)各侧棱都相等 (C)各侧面与底面都是全等的正三角形 (D)各侧面都是等腰三角形
2.若正棱锥的底面边长与侧棱长相等, 则该棱锥一定不是( D ) (A)三棱锥 (B)四棱锥
(C)五棱锥 (D)六棱锥
因为底面正方形ABCD的面积是16,所以 BC=4,MB=OM=2,
OB BM OM 2 2
2 2
又因为VB= 2 11 ,在Rt△VOB 中,由勾股定理得
VO VB OB
2 2
2 2
(2 11) (2 2) 6
在Rt△VOM中,由勾股定理得
VM 6 2 2 10
四.棱台及相关概念
1.定义:棱锥被平行于底面的平面所截, 截面和底面间的部分叫做棱台.
上底面 侧棱 侧面 高 顶点 下底面
2.相关概念: (1)棱台的下底面、上底面:原棱锥的底 面和截面分别叫做棱台的下底面、上底面; (2)棱台的侧面:棱台中除上、下底面以 外的面叫做棱台的侧面; (3)棱台的侧棱:相邻两侧面的公共边叫 做棱台的侧棱; (4)棱台的高:当棱台的底面水平放置时, 铅垂线与两底面交点间的线段或距离叫做棱 台的高。
棱柱、棱锥、棱台的结构特征说课稿 教案 教学设计
棱柱、棱锥、棱台的结构特征一、教学目标1.知识与技能(1)通过实物操作,增强学生的直观感知。
(2)会用语言概述棱柱、棱锥、棱台的结构特征。
(3)会表示有关于几何体以及棱柱、棱锥、棱台的分类。
2.过程与方法(1)让学生通过直观感受,从实物中概括出棱柱、棱锥、棱台的几何结构特征。
(2)让学生观察、讨论、归纳、概括所学的知识。
3.情感态度与价值观(1)使学生感受空间几何体存在于现实生活周围,增强学生学习的积极性,同时提高学生的观察能力。
(2)培养学生的空间想象能力和抽象括能力。
二、教学重点、难点重点:让学生感受大量空间实物及模型、概括出棱柱、棱锥、棱台的结构特征。
难点:棱柱、棱锥、棱台的结构特征的概括。
三、教学用具(1)学法:观察、思考、交流、讨论、概括。
(2)实物模型、投影仪四、教学过程(一)复习巩固:回顾几个概念①、如果我们只考虑这些物体的形状和大小,而不考虑其他因素,那么由这些物体抽象出来的空间图形叫做空间几何体。
②、由若干个平面多边形围成的空间几何体叫做多面体;围成多面体的各个多边形叫做多面体的面;相邻两个面的公共边叫做多面体的棱;棱与棱的公共点叫做多面体的顶点。
(二)E`D`C`B`A`A B CDE 、探究新知 D'C'B'CA B D A`棱柱:1、观察这些图形有什么共同特征?(学生观察思考后,师生共同完成)①有两个面互相平行;②其余各面都是四边形;③相邻两个四边形的公共边互相平行;小结:满足这三个特征的多面体叫做棱柱。
(哪位同学能给棱柱下个定义)六、棱柱的结构特征棱柱:一般地,有两个面相互平行,期于各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面组成的多面体;棱柱的面:棱柱中两个相互平行的面叫做棱柱的底面,简称底;其余各面叫做棱柱的侧面;C'棱柱的侧棱:相邻侧面的公共边;棱柱的顶点:侧面与地面的公共顶点.七、棱柱的性质(1)有两个面互相平行且全等;(2)其余各面都是四边形;(3)每相邻两个四边形的公共边都互相平行;(4)侧面是平行四边形;3、理解棱柱的定义问2:可不可以把棱柱的定义改为:有两个面互相平行,其余各面都是平行四边形。
棱柱、棱锥、棱台的结构特征 课件
规律方法 判断棱锥、棱台形状的两个方法 (1)举反例法: 结合棱锥、棱台的定义举反例直接判断关于棱锥、棱台结构 特征的某些说法不正确. (2)直接法:
棱锥
棱台
定底 只有一个面是多边形,此 两个互 相 平行的 面 ,
面 面即为底面
看侧 棱
相交于一点
即为底面 延长后相交于一点
类型三 多面体的表面展开图(互动探究) 【例3】 画出如图所示的几何体的表面展开图.
[课堂小结] 1.棱柱、棱锥、棱台的关系 在运动变化的观点下,棱柱、棱锥、棱台之间的关系可以用 下图表示出来(以三棱柱、三棱锥、三棱台为例).
2.(1)各种棱柱之间的关系 ①棱柱的分类
棱柱直棱柱正 一棱 般柱 的直棱柱 斜棱柱
②常见的几种四棱柱之间的转化关系
(2)棱柱、棱锥、棱台在结构上既有区别又有联系,具体见下表:
规律方法 棱柱的结构特征: (1)两个面互相平行; (2)其余各面是四边形; (3)相邻两个四边形的公共边互相平行.求解时,首先看是否有 两个平行的面作为底面,再看是否满足其他特征.
类型二 棱锥、棱台的结构特征 【例2】 下列关于棱锥、棱台的说法:
(1)用一个平面去截棱锥,底面和截面之间的部分组成的几何 体叫棱台; (2)棱台的侧面一定不会是平行四边形; (3)棱锥的侧面只能是三角形; (4)由四个面围成的封闭图形只能是三棱锥; (5)棱锥被平面截成的两部分不可能都是棱锥. 其中正确说法的序号是________.
解析 (1)错误,若平面不与棱锥底面平行,用这个平面去截 棱锥,棱锥底面和截面之间的部分不是棱台; (2)正确,棱台的侧面一定是梯形,而不是平行四边形; (3)正确,由棱锥的定义知棱锥的侧面只能是三角形; (4)正确,由四个面围成的封闭图形只能是三棱锥; (5)错误,如图所示四棱锥被平面截成的两部分都是棱锥.
必修四棱柱、棱锥、棱台的结构特征(附答案)
棱柱、棱锥、棱台的结构特征[学习目标] 1.通过对实物模型的观察,归纳认知简单多面体——棱柱、棱锥、棱台的结构特征.2.能运用棱柱、棱锥、棱台的结构特征来判断、描述现实生活中的实物模型.知识点一空间几何体1.概念:如果只考虑物体的形状和大小,而不考虑其他因素,那么由这些物体抽象出来的空间图形叫做空间几何体.2.多面体与旋转体由一个平面图形绕它所在平面内的一条定直线旋转所形知识点二棱柱、棱锥、棱台的结构特征平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的如图可记作:棱柱ABCDEF-A′B′C′D′E′F′底面的面侧面:其余各面侧棱:顶点:顶点边形,其余各面都是有一个公共顶点的底面侧面:三角形面用一个平行于棱锥底面的平面去截棱锥,底面与截面之.如图可记作:棱台ABCD-A′B′C′D′上底面:原棱锥的截面下底面:原棱锥的底面侧面:其余各面侧棱:顶点:侧面与上的公共顶点思考(1)棱柱的侧面一定是平行四边形吗?(2)棱台的上下底面互相平行,各侧棱延长线一定相交于一点吗?答(1)根据棱柱的概念侧棱平行、底面平行可知,棱柱的侧面一定是平行四边形.(2)根据棱台的定义可知其侧棱延长线一定交于一点.题型一棱柱的结构特征例1下列说法中,正确的是()A.棱柱中所有的侧棱都相交于一点B.棱柱中互相平行的两个面叫做棱柱的底面C.棱柱的侧面是平行四边形,而底面不是平行四边形D.棱柱的侧棱相等,侧面是平行四边形答案 D解析A选项不符合棱柱的特点;B选项中,如图①,构造四棱柱ABCD-A1B1C1D1,令四边形ABCD是梯形,可知平面ABB1A1∥平面DCC1D1,但这两个面不能作为棱柱的底面;C 选项中,如图②,底面ABCD可以是平行四边形;D选项是棱柱的特点.故选D.跟踪训练1下列关于棱柱的说法错误..的是()A.所有的棱柱两个底面都平行B.所有的棱柱一定有两个面互相平行,其余各面每相邻面的公共边互相平行C.有两个面互相平行,其余各面都是四边形的几何体一定是棱柱D.棱柱至少有五个面答案 C解析对于A、B、D,显然是正确的;对于C,棱柱的定义是这样的:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面围成的几何体叫做棱柱,显然题中漏掉了“并且每相邻两个四边形的公共边都互相平行”这一条件,因此所围成的几何体不一定是棱柱.如图所示的几何体就不是棱柱,所以C错误.题型二棱锥、棱台的结构特征例2下列关于棱锥、棱台的说法:①棱台的侧面一定不会是平行四边形;②由四个平面围成的封闭图形只能是三棱锥;③棱锥被平面截成的两部分不可能都是棱锥.其中正确说法的序号是________.答案①②解析①正确,棱台的侧面一定是梯形,而不是平行四边形;②正确,由四个平面围成的封闭图形只能是三棱锥;③错误,如图所示四棱锥被平面截成的两部分都是棱锥.跟踪训练2下列说法中,正确的是()①棱锥的各个侧面都是三角形;②有一个面是多边形,其余各面都是三角形,由这些面围成的几何体是棱锥;③四面体的任何一个面都可以作为棱锥的底面;④棱锥的各侧棱长相等.A.①②B.①③C.②③D.②④答案 B解析由棱锥的定义,知棱锥的各侧面都是三角形,故①正确;有一个面是多边形,其余各面都是三角形,如果这些三角形没有一个公共顶点,那么这个几何体就不是棱锥,故②错;四面体就是由四个三角形所围成的几何体,因此四面体的任何一个面作底面的几何体都是三棱锥,故③正确;棱锥的侧棱长可以相等,也可以不相等,故④错.题型三多面体的表面展开图例3画出如图所示的几何体的表面展开图.解表面展开图如图所示:跟踪训练3如图是三个几何体的侧面展开图,请问各是什么几何体?解由几何体的侧面展开图的特点,结合棱柱、棱锥、棱台的定义,可把侧面展开图还原为原几何体,如图所示:所以(1)为五棱柱;(2)为五棱锥;(3)为三棱台.截面周长最小问题例4 如图所示,在侧棱长为23的正三棱锥V -ABC 中,∠AVB =∠BVC =∠CVA =40°,过点A 作截面AEF 分别交VB ,VC 于点E ,F ,求截面△AEF 周长的最小值.分析 将正三棱锥沿侧棱VA 展开→求截面周长转化为求线段长→ 利用正三棱锥的性质求解解 将三棱锥V -ABC 沿侧棱VA 剪开,将其侧面展开图平铺在一个平面上,如图所示,则△AEF 的周长=AE +EF +F A 1. 因为AE +EF +F A 1≥AA 1,所以线段AA 1(即A ,E ,F ,A 1四点共线时)的长即为所求△AEF 周长的最小值.作VD ⊥AA 1,垂足为点D . 由VA =VA 1,知D 为AA 1的中点. 由已知∠AVB =∠BVC =∠CVA 1=40°, 得∠AVD =60°.在Rt △AVD 中,AD =VA sin 60°=23×32=3, 即AA 1=2AD =6.所以截面△AEF 周长的最小值是6.1.下列命题中,真命题是( )A.顶点在底面上的投影到底面各顶点的距离相等的三棱锥是正三棱锥B.底面是正三角形,各侧面是等腰三角形的三棱锥是正三棱锥C.顶点在底面上的投影为底面三角形的垂心的三棱锥是正三棱锥D.底面是正三角形,并且侧棱都相等的三棱锥是正三棱锥2.下列三个命题:①用一个平面去截棱锥,棱锥底面和截面之间的部分是棱台;②两个底面平行且相似,其余各面都是菱形的多面体是棱台;③有两个面互相平行,其余四个面都是等腰梯形的六面体是棱台.其中,正确的有()A.0个B.1个C.2个D.3个3.如图所示,不是正四面体(各棱长都相等的三棱锥)的展开图的是()A.①③B.②④C.③④D.①②4.下列几何体中,_______是棱柱,_______是棱锥,_______是棱台(仅填相应序号).5.如图,将装有水的长方体水槽固定底面一边后将水槽倾斜一个小角度,则倾斜后水槽中的水形成的几何体的形状是.一、选择题1.下列四个命题中,真命题有()①底面是平行四边形的四棱柱是平行六面体;②底面是矩形的直平行六面体是长方体;③直四棱柱是直平行六面体;④直平行六面体是长方体.A.1个B.2个C.3个D.4个2.一般棱台不具有的性质是()A.两底面相似B.侧面都是梯形C.侧棱都相等D.侧棱延长后都交于一点3.在正五棱柱中,不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线,那么一个正五棱柱对角线的条数为()A.20B.15C.12D.104.某棱台的上、下底面对应边之比为1∶2,则上、下底面面积之比是()A.1∶2B.1∶4C.2∶1D.4∶15.用一个平行于棱锥底面的平面去截这个棱锥,截得的棱台上、下底面的面积比为1∶4,且截去的棱锥的高是3 m,则棱台的高是()A.12 cmB.9 cmC.6 cmD.3 cm6.某同学制作了一个对面图案相同的正方体礼品盒(如图),则这个正方体礼品盒的表面展开图应该为()7.如图,往透明塑料制成的长方体ABCD-A1B1C1D1容器内灌进一些水,将容器底面一边BC固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列三个说法:①水的部分始终呈棱柱状;②水面四边形EFGH的面积不改变;③当E∈AA1时,AE+BF是定值.其中,正确的说法是()A.①②B.①C.①②③D.①③8.如图,M是棱长为2 cm的正方体ABCD-A1B1C1D1的棱CC1的中点,沿正方体表面从点A 到点M的最短路程是________cm.9.下列叙述正确的是________.(只填序号)①四棱锥的四个侧面都可以是直角三角形;②三棱锥的四个面都可以是直角三角形;③用一个平面去截棱锥,棱锥底面和截面之间的部分是棱台;④两个底面平行且相似,其余各面都是梯形的多面体是棱台.10.在正方体上任意选择4个顶点,它们可能是如下各种几何体的4个顶点,这些几何体是________.(写出所有正确结论的编号)①矩形;②不是矩形的平行四边形;③有三个面为等腰直角三角形,有一个面为等边三角形的四面体;④每个面都是等边三角形的四面体;⑤每个面都是直角三角形的四面体.11.如图所示,在三棱锥S-ABC中,SA=SB=SC=1,∠ASB=∠ASC=∠BSC=30°,一只蚂蚁从点A出发沿三棱锥的表面爬行一周后又回到A点,则蚂蚁爬过的最短路程为______.12.如图,在边长为2a的正方形ABCD中,E,F分别为AB,BC的中点,沿图中虚线将3个三角形折起,使点A、B、C重合,重合后记为点P.问:(1)折起后形成的几何体是什么几何体?(2)这个几何体共有几个面,每个面的三角形有何特点?(3)每个面的三角形面积为多少?13.长方体ABCD-A1B1C1D1(如图所示)中,AB=3,BC=4,A1A=5,现有一甲壳虫从A出发沿长方体表面爬行到C1来获取食物,试画出它的最短爬行路线,并求其路程的最小值.当堂检测答案1.答案 D解析对于选项A,到三角形各顶点距离相等的点为三角形外心,该三角形不一定为正三角形,故该命题是假命题;对于选项B,如图所示,△ABC为正三角形,若P A=PB=AB=BC=AC≠PC,△P AB,△PBC,△P AC都是等腰三角形,但它不是正三棱锥,故该命题是假命题;对于选项C,顶点在底面上的投影为底面三角形的垂心,底面为任意三角形皆可,故该命题是假命题;对于选项D,顶点在底面上的正投影是底面三角形的外心,又因为底面三角形为正三角形,所以外心即为中心,故该命题是真命题.2.答案 A解析①中的平面不一定平行于底面,故①错;②中侧面是菱形,所以侧棱互相平行,延长后无交点,故②错;③用反例验证(如图),故③错.3.答案 C解析可选择阴影三角形作为底面进行折叠,发现①②可折成正四面体,③④不论选哪一个三角形作底面折叠都不能折成正四面体.4.答案①③④⑥⑤解析结合棱柱、棱锥和棱台的定义可知①③④是棱柱,⑥是棱锥,⑤是棱台.5.答案四棱柱解析由于倾斜角度较小,所以倾斜后水槽中水形成的几何体的形状应为四棱柱.课时精练答案一、选择题1.答案 B解析根据平行六面体的定义,知①为真命题;根据长方体的定义,知②为真命题;直平行六面体是侧棱与底面垂直的平行六面体,所以其底面必是平行四边形,而直四棱柱的底面不一定是平行四边形,所以③为假命题;同理,长方体是底面为矩形的直平行六面体,所以④为假命题.2.答案 C解析当棱台是斜棱台时其侧棱不全相等.3.答案 D解析正五棱柱任意不相邻的两条侧棱可确定一个平面,每个平面可得到正五棱柱的两条对角线,5个平面共可得到10条对角线,故选D.4.答案 B解析因为棱台的上下底面相似,所以上下底面面积之比等于边长比的平方.5.答案 D解析由棱锥、棱台的性质可知,棱台的上、下底面相似.又因为上、下底面的面积比为1∶4,所以上、下底面的边长比为1∶2,所以截去的小棱锥与原大棱锥的高之比为1∶2,则棱台的高是3 cm.6.答案 A解析两个☆不能并列相邻,B、D错误;两个※不能并列相邻,C错误,故选A.也可通过实物制作检验来判定.7.答案 D解析显然水的部分呈三棱柱或四棱柱状,故①正确;容器倾斜度越大,水面四边形EFGH 的面积越大,故②不正确;由于水的体积不变,四棱柱ABFE-DCGH的高不变,所以梯形ABFE的面积不变,所以AE+BF是定值,故③正确.所以四个命题中①③正确.故选D.二、填空题8.答案13解析由题意,若以BC为轴展开,则A,M两点连成的线段所在的直角三角形的两直角边的长度分别为2 cm,3 cm,故两点之间的距离是13 cm.若以BB1为轴展开,则A,M两点连成的线段所在的直角三角形的两直角边的长度分别为1,4,故两点之间的距离是17 cm.故沿正方体表面从点A到点M的最短路程是13 cm.9.答案①②解析如图,当四棱锥的底面是一个矩形,并且一条侧棱垂直于底面时,四棱锥的四个侧面就可以都是直角三角形,所以①是正确的;如图,当三棱锥满足侧棱AD⊥底面DCB(其中△BCD中,∠BCD是直角)时,三棱锥的四个面就都是直角三角形,所以②是正确的;③中的平面不一定平行于底面,所以③是错误的;若④中多面体的侧棱延长后不能交于一点,则相应的多面体就不是棱台,所以④是错误的.10.答案①③④⑤解析在正方体ABCD-A1B1C1D1上任意选择4个顶点,它们可能是如下各种几何体的4个顶点,这些几何体是:①矩形,如四边形ACC1A1;③有三个面为等腰直角三角形,有一个面为等边三角形的四面体,如A-A1BD;④每个面都是等边三角形的四面体,如A-CB1D1;⑤每个面都是直角三角形的四面体,如A-A1DC,所以填①③④⑤.11.答案 2解析如图所示,将三棱锥S-ABC沿SA剪开,连接AA′,则AA′为最短距离,∠ASA′=90°,SA=SA′=1,∴AA′= 2.三、解答题12.解(1)如图,折起后的几何体是三棱锥.(2)这个几何体共有4个面,其中△DEF为等腰三角形,△PEF为等腰直角三角形,△DPE 和△DPF均为直角三角形.(3)S△PEF=12a2,S△DPF=S△DPE=12×2a×a=a2,S△DEF=S正方形ABCD-S△PEF-S△DPF-S△DPE=(2a)2-12a2-a2-a2=32a2.13.解把长方体的部分面展开,如图所示.再在长方形DCC1D1内由F到C1,其最短路程为74.。
1.1.1棱柱、棱锥、棱台的结构特征
(二)棱柱,棱锥,棱台 棱柱,棱锥,
1.棱柱:有两个面互相平行,其余各面都是四 .棱柱:有两个面互相平行, 边形, 边形,并且每相邻两个四边形的公共边都互相 平行, 平行,由这些面所围成的几何体叫做棱柱.
顶点 侧面 底面
用表示底面各顶点表示棱柱. 用表示底面各顶点表示棱柱.
侧棱 按底面多边形的边数分为三棱柱,四棱柱,五棱柱… 按底面多边形的边数分为三棱柱,四棱柱,五棱柱
3.棱台:用一个平行于棱锥底面的平面去截棱锥, 棱台:用一个平行于棱锥底面的平面去截棱锥, 底面与截面之间的部分叫做棱台. 底面与截面之间的部分叫做棱台.
上底面
棱台用表示底 面各顶点的字 母表示. 母表示.
按底面多边形的边 数为三棱台, 数为三棱台,四棱 五棱台…. 台,五棱台
下底面
棱柱,棱锥, 棱柱,棱锥,棱台的结构特征比较
上底面
下底面Biblioteka 棱台和圆台统称为台体. 棱台和圆台统称为台体. 台体
球的结构特征
球:以半圆的直径所在的直线为旋转轴,半圆 以半圆的直径所在的直线为旋转轴, 面旋转一周形成的几何体叫做球体 球体. 面旋转一周形成的几何体叫做球体.
球心
A
直径
O
C
大圆
B
圆柱,圆锥,圆台, 圆柱,圆锥,圆台,球的结构特征比较
问题2 与其他多面体相比,图片中的多面体 问题2:与其他多面体相比,图片中的多面体(14), , (15)有什么样的共同特征? 有什么样的共同特征? 有什么样的共同特征
思考:长方体被截去一部分, 思考:长方体被截去一部分,剩下的部分 是棱柱吗? 是棱柱吗?
A D E H G C F B
2.棱锥:有一个面是多边形,其余各面都 .棱锥:有一个面是多边形, 是有一个公共顶点的三角形, 是有一个公共顶点的三角形,由这些面所围 成的几何体叫做棱锥.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
棱柱、棱锥和棱台的结构特征.
教案
主编:林鹤审核人:备课人:林鹤
备课时间:使用时间:
知基础 2 / 11
堂导学、激励环节设计、随堂练习、课多面体及多面体的有关概探究点一堂检测念或课后巩固)1.多面体多面体是由若干个平面多边形所(1) 围成的几何体.把一个多面体的任意一个面延展(2)为平面,如果其余的各面都在这个平面的同一侧,则这样的多面体就叫做凸多面体.棱柱的结构特征探究点二
3 / 11
2.棱柱
侧棱与底面不垂直的棱柱叫做斜(4)棱柱,侧棱与底面垂直的棱柱叫做直棱柱,底面是
正多边形的直棱柱叫做正棱柱.底面是平行四边形的棱柱叫做平(5)行六面体,侧棱与底面垂直的平行六面体叫做直平行六面体,底面是矩形的直平行六面体是长方体,棱长都相等的长方体是正方体.)
下列命题中正确的是1例(
4 / 11
棱锥的结构特征探究点三我们把下面的
多面体取名为思考1棱锥,据此你能给棱锥下一个定义吗?棱锥的底面、侧面、侧棱、顶点分别是什么含义?你能作图加以说明吗? 5 / 11
(1)棱锥的主要结构特征:
边形……分别叫做三棱锥、四棱锥、五棱锥……三个棱锥从左到右可分别-PABCDABC表示为S-,S-,用一个平行
于棱锥底面的平ABCDE.面去截棱锥,截面与底面的形状是相似多边形.如果棱锥的底面是正多边形,且它(4)的顶点在过底面中心且与底面垂直的直线上,则这个棱锥叫做正棱锥.正棱锥各侧面都是全等的等腰三角形,这些等腰三角形底边上的高都相等, 6 / 11
若三棱锥的底面为正三角形,侧面为,底面周长2等腰三角形,侧棱长为为9,求棱锥的高.
,底面面积ABCD已知正四棱锥V—,计算它11216为,一条侧棱长为的高和斜高. 7 / 11
的高为ABCDS-13.已知正四棱锥7. 3,侧棱长为(1)求侧面上的斜高;求一个侧面的面积;(2) 求底面的面积.(3)
.
.棱台4棱锥被平行于底面的平面所截,
截(1)面和底面间的部分叫做棱台.原棱锥的底面和截面分别叫做棱台的下底面、上底面;其他各面叫做棱台的侧 8 / 11
9 / 11
堂练几何体的形状.课习、2.(1)各种棱柱之间的关系堂检测或棱柱的分类①课后巩固)?正棱柱???直棱柱?一般的直棱柱棱柱???斜棱柱②常见的几种四棱柱之间的转化关
系
10 / 11
得:课后失:反思纠: 11 / 11。
