立体几何大题训练及答案
高三精选立体几何大题30题(含详细解答)
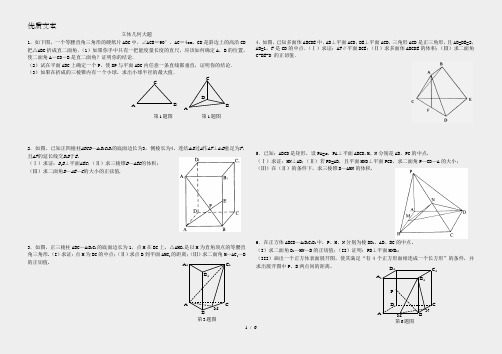
A BC第1题图ABCD第1题图立体几何大题1．如下图，一个等腰直角三角形的硬纸片ABC中，∠ACB＝90°，AC＝4cm，CD是斜边上的高沿CD 把△ABC折成直二面角．（1）如果你手中只有一把能度量长度的直尺，应该如何确定A，B的位置，使二面角A－CD－B是直二面角？证明你的结论．（2）试在平面ABC上确定一个P，使DP与平面ABC内任意一条直线都垂直，证明你的结论．（3）如果在折成的三棱锥内有一个小球，求出小球半径的最大值．2．如图，已知正四棱柱ABCD—A1B1C1D1的底面边长为3，侧棱长为4，连结A1B过A作AF⊥A1B垂足为F，且AF的延长线交B1B于E。
（Ⅰ）求证：D1B⊥平面AEC；（Ⅱ）求三棱锥B—AEC的体积；（Ⅲ）求二面角B—AE—C的大小的正弦值.3．如图，正三棱柱ABC—A1B1C1的底面边长为1，点M在BC上，△AMC1是以M为直角顶点的等腰直角三角形.（I）求证：点M为BC的中点；（Ⅱ）求点B到平面AMC1的距离；（Ⅲ）求二面角M—AC1—B 的正切值. 4．如图，已知多面体ABCDE中，AB⊥平面ACD，DE⊥平面ACD，三角形ACD是正三角形，且AD=DE=2，AB=1，F是CD的中点．（Ⅰ）求证：AF∥平面BCE；（Ⅱ）求多面体ABCDE的体积；（Ⅲ）求二面角C-BE-D 的正切值．5．已知：ABCD是矩形，设PA=a，PA⊥平面ABCD.M、N分别是AB、PC的中点.（Ⅰ）求证：MN⊥AB；（Ⅱ）若PD=AB，且平面MND⊥平面PCD，求二面角P—CD—A的大小；（Ⅲ）在（Ⅱ）的条件下，求三棱锥D—AMN的体积.6．在正方体ABCD—A1B1C1D1中，P、M、N分别为棱DD1、AB、BC的中点。
（I）求二面角B1—MN—B的正切值；（II）证明：PB⊥平面MNB1；（III）画出一个正方体表面展开图，使其满足“有4个正方形面相连成一个长方形”的条件，并求出展开图中P、B两点间的距离。
高中数学立体几何专项练习题及答案
高中数学立体几何专项练习题及答案一、选择题1. 下面哪个选项不是描述柱体的特点？A. 体积恒定B. 底面形状不限C. 侧面是矩形D. 顶面和底面平行答案：A2. 如果一个四面体的一个顶点的对边垂直于底面，那么这个四面体是什么类型？A. 正方形四面体B. 倒立四面体C. 锥体D. 正方锥体答案：C3. 以下哪个选项正确描述了一个正方体的特点？A. 全部面都是正方形B. 12 条棱长度相同C. 8 个顶点D. 6 个面都是正方形答案：D4. 若长方体的高度是 6cm，底面积是 5cm²，底面对角线长为 a cm，那么 a 的值为多少？A. √11B. √29C. √31D. √41答案：C二、填空题1. 一个正方体的棱长为 4cm，它的体积是多少？答案：64cm³2. 一个球的表面积是100π cm²，那么它的半径是多少？答案：5cm3. 一个圆柱体的底面半径为 3cm，高度为 8cm，它的体积是多少？答案：72π cm³4. 一个圆锥的底面半径为 6cm，高度为 10cm，它的体积是多少？答案：120π cm³三、计算题1. 一个四棱锥的底面是边长为 5cm 的正方形，高度为 8cm，它的体积是多少？答案：单位为 cm³，计算过程如下：首先计算底面积：5cm * 5cm = 25cm²再计算体积：25cm² * 8cm / 3 = 200cm³2. 一个圆柱体的底面直径为 12cm，高度为 15cm，它的体积是多少？答案：单位为 cm³，计算过程如下：首先计算底面半径：12cm / 2 = 6cm再计算底面积：π * 6cm * 6cm = 36π cm²最后计算体积：36π cm² * 15cm = 540π cm³3. 一个球的直径为 8cm，它的体积是多少？答案：单位为 cm³，计算过程如下：首先计算半径：8cm / 2 = 4cm再计算体积：4/3 * π * 4cm * 4cm * 4cm = 268.08π cm³4. 一个圆锥的底面半径为 10cm，高度为 20cm，它的体积是多少？答案：单位为 cm³，计算过程如下：首先计算底面积：π * 10cm * 10cm = 100π cm²最后计算体积：100π cm² * 20cm / 3 = 2000π cm³四、解答题1. 若一个长方体的长度、宽度、高度分别为 a、b、c，它的表面积为多少？答案：单位为 cm²，计算过程如下：首先计算侧面积：2 * (a * b + a * c + b * c)再计算底面积：a * b最后计算表面积：2 * (a * b + a * c + b * c) + a * b2. 一个四棱锥的底面为边长为 a 的正三角形，高度为 h，求这个四棱锥的体积。
高中数学立体几何大题训练题含答案
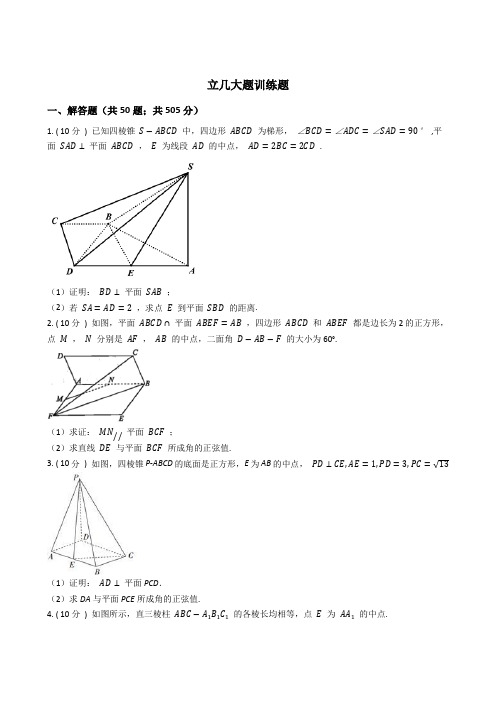
立几大题训练题一、解答题（共50题；共505分）1. ( 10分) 已知四棱锥S−ABCD中，四边形ABCD为梯形，∠BCD=∠ADC=∠SAD=90°,平面SAD⊥平面ABCD，E为线段AD的中点，AD=2BC=2CD.（1）证明：BD⊥平面SAB；（2）若SA=AD=2，求点E到平面SBD的距离.2. ( 10分) 如图，平面ABCD∩平面ABEF=AB，四边形ABCD和ABEF都是边长为2的正方形，点M，N分别是AF，AB的中点，二面角D−AB−F的大小为60°.（1）求证：MN//平面BCF；（2）求直线DE与平面BCF所成角的正弦值.3. ( 10分) 如图，四棱锥P-ABCD的底面是正方形，E为AB的中点，PD⊥CE,AE=1,PD=3,PC=√13（1）证明：AD⊥平面PCD．（2）求DA与平面PCE所成角的正弦值.4. ( 10分) 如图所示，直三棱柱ABC−A1B1C1的各棱长均相等，点E为AA1的中点.（1）证明：EB1⊥BC1；（2）求二面角C1−EB1−C的余弦值.AD，G是PB的中点，5. ( 10分) 已知在四棱锥P−ABCD中，AD//BC，AB=BC=CD=12ΔPAD是等边三角形，平面PAD⊥平面ABCD.（1）求证：CD⊥平面GAC；（2）求二面角P−AG−C的余弦值.6. ( 10分) 如图，多面体ABCE中，平面AEC⊥平面ABC，AC⊥BC，AE⊥CD四边形BCDE 为平行四边形.（1）证明：AE⊥EC；（2）若AE=EC=CB=√2，求二面角D−AC−E的余弦值.7. ( 10分) 如图,在三棱锥A−BCD中, △ABC是等边三角形, ∠BAD=∠BCD=90°,点P是AC 的中点,连接BP,DP．（1）证明:平面ACD⊥平面BDP;（2）若BD=√6,且二面角A−BD−C为120°,求直线AD与平面BCD所成角的正弦值．8. ( 10分) 如图，在四棱锥P−ABCD中，AP⊥平面PCD，AD//BC，AB⊥BC，AP=AB=AD，E为AD的中点，AC与BE相交于点O.BC=12（1）证明：PO⊥平面ABCD.（2）若OB=1，求点C到平面PAB的距离.9. ( 10分) 如图，在斜三棱柱ABC−A1B1C1中，平面ABC⊥平面A1ACC1，CC1=2，△ABC，△ACC1，均为正三角形，E为AB的中点.（1）证明: AC1//平面B1CE，（2）求直线AC1与平面B1BAA1所成角的正弦值.10. ( 10分) 如图，四棱锥P−ABCD中，底面ABCD是边长为2的正方形，平面PAB⊥平面ABCD，AP=PB，AP⊥PB，E为CP的中点.（1）求证：AP//平面BDE；（2）求点D到平面ACP的距离.11. ( 10分) 在三棱柱ABC−A1B1C1中，已知AB=AC=AA1=√5，BC=4，O为BC的中点，A1O⊥平面ABC（1）证明四边形BB1C1C为矩形；（2）求直线AA1与平面A1B1C所成角的余弦值.12. ( 10分) 如图，四棱锥P−ABCD的底面是正方形，PA⊥平面ABCD，AE⊥PD.（1）证明：AE⊥平面PCD；（2）若AP=AB，求二面角B−PC−D的余弦值.13. ( 10分) 在直角梯形ABCD（如图1），∠ABC=90°，BC//AD，AD=8，AB=BC=4，M为线段AD中点.将△ABC沿AC折起，使平面ABC⊥平面ACD，得到几何体B−ACD（如图2）.（1）求证：CD⊥平面ABC；（2）求AB与平面BCM所成角θ的正弦值.14. ( 15分) 如图，四棱锥S−ABCD的底面是边长为1的正方形，SD垂直于底面ABCD，SD=1.（1）求证BC⊥SC；（2）求平面SBC与平面ABCD所成二面角的大小；（3）设棱SA的中点为M，求异面直线DM与SB所成角的大小.15. ( 10分) 已知菱形ABCD的边长为4, AC∩BD=O, ∠ABC=60°,将菱形ABCD沿对角线BD折起,使AC=a,得到三棱锥A−BCD,如图所示.⇒（1）当a=2√2时,求证: AO⊥平面BCD;（2）当二面角A−BD−C的大小为120°时,求直线AD与平面ABC所成的正切值.16. ( 10分) 在四棱锥P–ABCD中，AB//CD，CD=2AB．⇀=mAP⇀(m>0)，且MN//平面PCD，求实数m的值；（1）设AC与BD相交于点M，AN（2）若AB=AD=DP，∠BAD=60°，PB=√2AD，且PD⊥AD，求二面角A−PC−B的余弦值．17. ( 10分) 如图，在四棱锥P−ABCD中，PA⊥平面ABCD，ABCD是正方形，E是CD中点，点F在BC上，且BF=3FC.（1）证明：EF⊥平面PAE；（2）若PA=AB=4，求点C到平面PEF的距离.18. ( 10分) 如图，在四棱锥P−ABCD中，PA⊥平面ABCD，ABCD是正方形，E是CD中点，点F在BC上，且BF=3FC.（1）证明EF⊥平面PAE；AB，求平面PAB与平面PEF所成二面角的正弦值.（2）若PA=5419. ( 10分) 如图（1），在平面五边形EADCB中，已知四边形ABCD为正方形，ΔEAB为正三角形.沿着AB将四边形ABCD折起得到四棱锥E−ABCD，使得平面ABCD⊥平面EAB，设F在线段AD上且满足DF=2AF，G在线段CF上且满足FG=CG，O为ΔECD的重心，如图（2）.（1）求证：GO//平面ABE；（2）求直线CF与平面BCE所成角的正弦值.20. ( 10分) 如图所示，在矩形ABCD中，AB=4，AD=2，E是CD的中点，O为AE的中点，以AE为折痕将ΔADE向上折起，使D点折到P点，且PC=PB.（1）求证: PO⊥面ABCE；（2）求AC与面PAB所成角θ的正弦值.21. ( 10分) 如图，在以A，B，C，D，E，F为顶点的多面体中，四边形ACDF是菱形，∠FAC=600,AB//DE,BC//EF,AB=BC=3,AF=2√3,BF=√15（1）求证：平面ABC⊥平面ACDF（2）求平面AEF与平面ACE所成的锐二面角的余弦值22. ( 10分) 已知四棱锥E−ABCD，AB=3，BC=4，CD=12，AD=13，cos∠ADC= 12，EC⊥平面ABCD.13（1）求证：平面ABE⊥平面EBC；（2）当CE=60时，求直线AC和平面ADE所成角的正弦值.23. ( 10分) 如图，在四棱锥P−ABCD中，四边形ABCD是直角梯形，AB⊥AD，AB//CD，PC⊥底面ABCD，AB=2AD=2CD=4，PC=2a，E是PB的中点.（1）求证：AC⊥平面PBC；，求直线PA与平面EAC所成角的正弦值.（2）若二面角P−AC−E的余弦值为√6324. ( 10分) 如图1，在等腰梯形ABF1F2中，两腰AF2=BF1=2，底边AB=6，F1F2=4，D，C是AB的三等分点，E是F1F2的中点.分别沿CE，DE将四边形BCEF1和ADEF2折起，使F1，F2重合于点F，得到如图2所示的几何体.在图2中，M，N分别为CD，EF的中点.（1）证明：MN⊥平面ABCD.（2）求直线CN与平面ABF所成角的正弦值.25. ( 15分) 如图，在四棱锥P一ABCD中，已知AB=BC=√5,AC=4,AD=DC=2√2，点Q为AC中点，PO⊥底面ABCD, PO=2，点M为PC的中点.（1）求直线PB与平面ADM所成角的正弦值；（2）求二面角D-AM-C的正弦值；（3）记棱PD的中点为N，若点Q在线段OP上，且NQ//平面ADM，求线段OQ的长.26. ( 10分) 如图，已知ΔABC为等边三角形，ΔABD为等腰直角三角形，AB⊥BD，平面ABC⊥平面ABD，点E与点D在平面ABC的同侧，且CE//BD，BD=2CE.点F为AD中点，连接EF.（1）求证：EF//平面ABC；（2）求二面角C−AE−D的余弦值.27. ( 10分) 如图，在四棱锥S−ABCD中，底面ABCD是直角梯形，AD//BC，AB⊥BC，ΔSAB 是等边三角形，侧面SAB⊥底面ABCD，AB=2√3，BC=3，AD=1，点M、点N分别在棱SB、棱CB上，BM=2MS，BN=2NC，点P是线段MN上的任意一点.（1）求证：AP//平面SCD；（2）求二面角S−CD−B的大小.28. ( 15分) 如图，四棱锥P−ABCD的底面是正方形，PA⊥底面ABCD，PA=AD=2，点M,N分别在棱PD,PC上，且PC⊥平面AMN.（1）求证：AM⊥PD；（2）求直线CD与平面AMN所成角的正弦值.（3）求二面角C−AM−N的余弦值29. ( 10分) 如图,四棱锥P−ABCD中, PD⊥底面ABCD,且底面ABCD为平行四边形,若∠DAB= 60°, AB=2, AD=1.（1）求证: PA⊥BD;（2）若∠PCD=45°,求点D到平面PBC的距离ℎ.30. ( 10分) 在长方体ABCD−A1B1C1D1中，底面ABCD是边长为2的正方形，E是AB的中点，F是BC的中点.（1）求证：EF//平面A1DC1；（2）若AA1=2√3，求平面A1DC1与平面B1EF所成二面角的正弦值.31. ( 10分) 如图，在四棱锥P−ABCD中，底面ABCD是矩形，侧棱PD⊥底面ABCD，且PD= CD=1，过棱PC的中点E，作EF⊥PB交PB于点F.（1）证明：PA//平面EDB；，求PA与面ABCD所成角的正弦值．（2）若面DEF与面ABCD所成二面角的大小为π332. ( 5分) 如图，在三棱柱ABC−A1B1C1中，AA1⊥平面ABC，D是AB的中点，BC=AC，AB=2DC=2√2，AA1=4.（Ⅰ）求证：BC1//平面A1CD；（Ⅱ）求平面BCC1B1与平面A1CD所成锐二面角的平面角的余弦值.33. ( 10分) 如图，在三棱柱ABC−A1B1C1中，AA1⊥平面ABC，点D是AB的中点，BC= AC，AB=2DC=2，AA1=√3.（1）求证：平面A1DC⊥平面ABB1A1；（2）求点A到平面A1DC的距离.34. ( 10分) 如图，在平行六面体ABCD﹣A1B1C1D1中，AA1＝A1D，AB＝BC，∠ABC＝120°.（1）证明：AD⊥BA1；（2）若平面ADD1A1⊥平面ABCD，且A1D＝AB，求直线BA1与平面A1B1CD所成角的正弦值.35. ( 10分) 如图,在四棱锥P−ABCD中, PA⊥平面ABCD,∠ABC=∠BAD=90°,AD=AP= 4,AB=BC=2, M,N为线段PC,AD上一点不在端点.AD，求证：MN∥面PBA（1）当M为中点时，AN=14，若存在（2）当N为AD中点时，是否存在M，使得直线MN与平面PBC所成角的正弦值为2√55求出M的坐标，若不存在，说明理由.36. ( 10分) 如图，正方体ABCD−A1B1C1D1的棱长为2，E为棱CC1的中点.（1）求 AD 1 与 DB 所成角的大小；（2）求 AE 与平面 ABCD 所成角的正弦值.37. ( 20分 ) 如图， E 是以 AB 为直径的半圆 O 上异于 A,B 的点，矩形 ABCD 所在的平面垂直于半圆 O 所在的平面，且 AB =2 ， AD =3（1）求证：平面 EAD ⊥ 平面 EBC ；（2）若 EB ⌢ 的长度为 π3，求二面角 A −DE −C 的正弦值． 38. ( 5分 ) 如图1，在直角梯形 ABCD 中，AB ∥CD ， AB ⊥AD ，且 AB =AD =12CD =1 ．现以 为一边向梯形外作正方形 ADEF ，然后沿边 AD 将正方形 ADEF 翻折，使平面 ADEF 与平面 ABCD 垂直，如图2．（Ⅰ）求证：BC ⊥平面DBE ；（Ⅱ）求点D 到平面BEC 的距离.39. ( 10分 ) 如图，扇形 AOB 的半径为 2 ，圆心角 ∠AOB =120∘ ，点 C 为弧 AB 上一点， PO ⊥ 平面 AOB 且 PO =√5 ，点 M ∈PB 且 BM =2MP ， PA ∥平面 MOC ．（1）求证：平面MOC⊥平面POB；（2）求平面POA和平面MOC所成二面角的正弦值的大小.40. ( 10分) 如图，已知四边形ABCD为等腰梯形，BDEF为正方形，平面BDEF⊥平面ABCD，AD//BC,AD=AB=1，∠ABC=60°.（1）求证:平面CDE⊥平面BDEF；（2）点M为线段EF上一动点，求BD与平面BCM所成角正弦值的取值范围.41. ( 10分) 如图，在四棱锥P-ABCD中，AD=2√3,AB=3,AP=√3,AD//BC，AD⊥平面PAB，∠APB=90°，点E满足PE⇀=23PA⇀+13PB⇀.（1）证明：PE⊥DC；（2）求二面角A-PD-E的余弦值.42. ( 10分) 在斜三棱柱ABC−A1B1C1中，侧面AC1⊥平面ABC，AA1=√2a，A1C=CA=AB=a，AB⊥AC，D是AA1的中点．（1）求证：CD⊥平面AB1；（2）在侧棱BB1上确定一点E，使得二面角E−A1C1−A的大小为π．343. ( 10分) 如图,在四棱锥P−ABCD中,侧面PAD⊥底面ABCD,底面ABCD为梯形，AB//CD,=2.∠ABC=∠BCD=90°,BC=CD=AB2（1）证明: BD⊥PD;（2）若△PAD为正三角形,求二面角A−PB−C的余弦值.44. ( 10分) 如图，已知四棱锥P−ABCD的底面为直角梯形，∠ADC为直角，AP⊥平面ABCD，BC:AD:CD=5:4:2，且CD=1.（1）求证：BP⊥AC；（2）若AP=CD，求二面角D−PC−B的余弦值.45. ( 10分) 如图，在四棱锥P−ABCD中，底面ABCD是矩形，PA⊥平面ABCD,PA=AD=2,AB=1, AM⊥PD于点M，连接BM.（1）求证：PD⊥BM；（2）求直线CD与平面ACM所成角的正弦值.BC=1，E是BC的中46. ( 10分) 如图所示1，已知四边形ABCD满足AD//BC，BA=AD=DC=12点.将△BAE沿着AE翻折成△B1AE，使平面B1AE⊥平面AECD，F为CD的中点，如图所示2.（1）求证：EF⊥平面AB1E；（2）求AE到平面CB1D的距离.47. ( 10分) 如图,四棱锥P﹣ABCD的底面ABCD是平行四边形,∠BCD=135°,PA⊥平面ABCD,AB=AC=PA=2,E,F,M分别为线段BC,AD,PD的中点.（1）求证:直线EF⊥平面PAC;（2）求平面MEF与平面PBC所成二面角的正弦值.48. ( 5分) 如图，三棱柱A1B1C1−ABC中，BB1⊥平面ABC，AB⊥BC，AB=2，BC= 1，BB1=3，D是CC1的中点，E是AB的中点.（Ⅰ）证明：DE//平面C1BA1；（Ⅱ）F是线段CC1上一点，且直线AF与平面ABB1A1所成角的正弦值为1，求二面角F−3BA1−A的余弦值.49. ( 5分) 如图,在四棱锥P−ABCD中, PA⊥平面ABCD, AD⊥CD,AD//BC,BC=4,PA= AD=CD=2,点E为PC的中点.(I) 证明：DE//平面PAB;(II)求直线PB与平面PCD所成角的正弦值.50. ( 10分) 如图，AB是圆的直径，PA垂直圆所在的平面，C是圆上的一点.（1）求证：平面PAC⊥平面PBC；（2）若AB=2 , AC=PA=1，求直线PA与平面PBC所成角的正弦值.答案解析部分一、解答题1.【答案】（1）解：由题意知∠BCD=∠ADC=90°，BC//ED,且BC=CD=12AD=DE，所以四边形BCDE是正方形，连接CE，所以BD⊥CE，又因为BC//AE，BC=AE，所以四边形ABCE是平行四边形，所以CE//AB，则BD⊥AB.因为平面SAD⊥平面ABCD，∠SAD=90°，平面SAD∩平面ABCD=AD，故SA⊥平面ABCD.所以SA∩AB=A，所以SA⊥BD，又因为SA∩AB=A，则BD⊥平面SAB.（2）解：∵SA=AD=2，BE=DE=1，∴△BDE的面积为12，又由（1）知SA⊥平面ABCD，∴V S−BDE=13×12×2=13，又在RtΔSAB中，SA=2，AB=DB=√2，∴SB=√6，由（1）知BD⊥SB，∴ΔSBD的面积为12×√2×√6=√3，设点E到平面SBD的距离为ℎ，则13S△BDS⋅ℎ=13，即ℎ=√33.【考点】直线与平面垂直的判定，点、线、面间的距离计算【解析】【分析】（1)利用线面垂直的判定定理，即可证得BD⊥平面SAB.（2）由（1）知SA⊥平面ABCD，求得V S−BDE=13，再根据等体积法，即可求解点点E到平面SBD的距离.2.【答案】（1）证明：∵M，N分别是AF，AB的中点，∴MN∥BF.∵MN⊄平面BCF，BF⊂平面BCF，∴MN//平面BCF.（2）解：∵四边形ABCD和ABEF都是边长为2的正方形，∴DA⊥AB，FA⊥AB，∴∠DAF就是二面角D−AB−F的平面角，∴∠DAF=60°.连接DM，在△DAM中，DA=2，AM=1，∠DAM=60°，∴DM2=AM2+AD2−2AM⋅AD⋅cos60°=3，∴DM=√3.∴DM2+AM2=AD2，∴DM⊥AM.∵DA⊥AB，FA⊥AB，FA∩DA=A，∴AB ⊥ 平面 ADM ， ∴AB ⊥DM .∴DM ⊥ 平面 ABEF .以点 M 为原点， MF ， MG （ G 是 BE 中点）， MD 所在直线分别为 x 轴， y 轴， z 轴建立如图空间直角坐标系，如图所示：则 D(0,0,√3) ， E(1,2,0) ， B(−1,2,0) ， F(1,0,0) ， A(−1,0,0) ，DE ⃗⃗⃗⃗⃗ =(1,2,−√3) ， BF ⃗⃗⃗⃗⃗ =(2,−2,0) ， BC ⃗⃗⃗⃗⃗ =AD ⃗⃗⃗⃗⃗ =(1,0,√3) .设平面 BCF 的法向量为 m⃗⃗ =(x,y,z) ， 则 {m ⇀⋅BF ⇀=2x −2y =0m ⇀⋅BC⇀=x +√3z =0 ，取 m ⃗⃗ =(√3,√3,−1) . 设直线 DE 与平面 BCF 所成角为 θ ，则 sinθ=|m⃗⃗⃗ ⋅DE ⃗⃗⃗⃗⃗⃗ ||m ⃗⃗⃗ ||DE ⃗⃗⃗⃗⃗⃗ |=√427 ，∴ 直线 DE 与平面 BCF 所成角的正弦值为 √427. 【考点】直线与平面平行的判定，用空间向量求直线与平面的夹角【解析】【分析】（1）根据三角形的中位线，有 MN ∥BF ，再利用线面平行的判定定理证明.（2）根据点 M ， N 分别是 AF ， AB 的中点，二面角 D −AB −F 的大小为60°，证明 DM ⊥ 平面 ABEF ，然后以点 M 为原点， MF ， MG （ G 是 BE 中点）， MD 所在直线分别为 x 轴， y 轴， z 轴建立如图空间直角坐标系，再求得平面 BCF 的一个法向量，利用线面角的向量求法求解.3.【答案】 （1）证明：因为E 为AB 的中点， AE =1 ，所以 CD =AB =2 ，所以 CD 2+PD 2=PC 2 ，从而 PD ⊥CD .又 PD ⊥CE ， CD ∩CE =C ，所以 PD ⊥ 底面ABCD ， 所以 PD ⊥AD .因为四边形ABCD 是正方形，所以 AD ⊥CD .又 CD ∩PD =D ，所以 AD ⊥ 平面PCD.（2）解：以D 为坐标原点，建立空间直角坐标系 D −xyz ，如图所示，则 A(2,0,0) ， P(0,0,3) ， E(2,1,0) ， C(0,2,0) ，所以 PE ⃗⃗⃗⃗⃗ =(2,1,−3) ， EC ⃗⃗⃗⃗⃗ =(−2,1,0) ， DA ⃗⃗⃗⃗⃗ =(2,0,0) .设平面PCE 的法向量为 n⃗ =(x,y,z) ， 则 PE ⃗⃗⃗⃗⃗ ⋅n ⃗ =EC ⃗⃗⃗⃗⃗ ⋅n ⃗ =0 ，即 {2x +y −3z =0−2x +y =0 ，令 x =3 ，得 n ⃗ =(3,6,4) . cos〈n ⃗ ,DA ⃗⃗⃗⃗⃗ 〉=n ⃗ ⋅DA ⃗⃗⃗⃗⃗⃗ |n ⃗ ||DA ⃗⃗⃗⃗⃗⃗ |=3√6161 ， 故DA 与平面PCE 所成角的正弦值为 3√6161 .【考点】直线与平面垂直的判定，用空间向量求直线与平面的夹角【解析】【分析】（1）通过证明 PD ⊥AD ， AD ⊥CD 即可证明线面垂直；（2）建立空间直角坐标系，利用向量方法求解线面角的正弦值.4.【答案】 （1）证明：设 BC 1 与 CB 1 交点为 O ，连接 OE ， BE .由题可知四边形 BCC 1B 1 为正方形，所以 BC 1⊥CB 1 ，且 O 为 BC 1 中点.又因 BE 2=AB 2+AE 2 ， C 1E 2=A 1E 2+A 1C 12 ，所以 BE =C 1E ，所以 BC 1⊥OE .又因为 OE ∩CB 1=O ，所以 BC 1⊥ 平面 EB 1C .因为 EB 1⊂ 平面 EB 1C ，所以 BC 1⊥EB 1 .（2）解：取 AB 的中点 O ′ ，连接 O ′C ， O ′C ⊥AB ，在平面 ABB 1A 1 过点 O ′ 内作 AB 的垂线，如图所示，建立空间直角坐标系 O ′−xyz .设 AB =2 ，则 E(0,−1,1) ， B 1(0,1,2) ， B(0,1,0) ， C 1(−√3,0,2) .所以 EB 1⃗⃗⃗⃗⃗⃗⃗ =(0,2,1) ， EC 1⃗⃗⃗⃗⃗⃗⃗ =(−√3,1,1) .设平面 C 1EB 1 的一个法向量为 n ⃗ =(x,y,z) ，则 {n ⇀⋅EB1⇀=2y +z =0n ⇀⋅EC 1⇀=−√3x +y +z =0 ，令 y =√3 ，则 n ⃗ =(−1,√3,−2√3) . 由（1）可知平面 CEB 1 的一个法向量为 BC 1⃗⃗⃗⃗⃗⃗⃗ =(−√3,−1,2) ， 则 |cos〈BC 1⃗⃗⃗⃗⃗⃗⃗ ,n⃗ 〉|=|n ⃗ ⋅BC 1⃗⃗⃗⃗⃗⃗⃗⃗ ||n ⃗ |⋅|BC 1⃗⃗⃗⃗⃗⃗⃗⃗ |=√3√3+1+4⋅√1+3+12=√64.由图可知二面角 C 1−EB 1−C 为锐角，所以其余弦值为 √64.【考点】空间中直线与直线之间的位置关系，用空间向量求平面间的夹角【解析】【分析】（1）通过证明 BC 1⊥ 平面 EB 1C 即可证得；（2）建立空间直角坐标系，利用向量求解.5.【答案】 （1）证明：取 AD 的中点为 O ，连结 OP ， OC ， OB ，设 OB 交 AC 于 H ，连结 GH . 因为 AD//BC ， AB =BC =CD =12AD ， 四边形 ABCO 与四边形 OBCD 均为菱形， ∴OB ⊥AC ， OB//CD ， CD ⊥AC ， 因为 △PAD 为等边三角形， O 为 AD 中点， ∴PO ⊥AD ，因为平面 PAD ⊥ 平面 ABCD ，且平面 PAD ∩ 平面 ABCD =AD .PO ⊂ 平面 PAD 且 PO ⊥AD ， ∴PO ⊥ 平面 ABCD 因为 CD ⊂ 平面 ABCD ， ∴PO ⊥CD ，因为H ， G 分别为 OB ， PB 的中点， ∴GH//PO ， ∴GH ⊥CD .又因为 GH ∩AC =H ， AC,GH ⊂ 平面 GAC ， ∴CD ⊥ 平面 GAC .（2）解：取 BC 的中点为 E ，以 O 为空间坐标原点，分别以 OE ⇀,OD ⇀,OP ⇀ 的方向为 x 轴、 y 轴、 z 轴的正方向，建立如图所示的空间直角坐标系 O −xyz .设 AD =4 ，则 P(0,0,2√3) ， A(0,−2,0) ， C(√3,1,0) ， D(0,2,0) ， G(√32,−12,√3)AP ⃗⃗⃗⃗⃗ =(0,2,2√3) ， AG ⇀=(√32,32,√3) ， 设平面 PAG 的一法向量 n →=(x,y,z) .由 {n ⇀⋅AP⇀=0n ⇀⋅AG ⇀=0 ⇒{2y +2√3z =0√32x +32y +√3z =0⇒{y =−√3z x =z .令 z =1 ，则 n ⃗ =(1,−√3,1) . 由（1）可知，平面 AGC 的一个法向量 CD ⃗⃗⃗⃗⃗ =(−√3,1,0) ， cos〈n ⇀,CD⇀〉=n ⇀⋅CD ⇀|n⇀||CD ⇀|=−√155∴ 二面角 P −AG −C 的平面角的余弦值为 −√155.【考点】直线与平面垂直的判定，用空间向量求平面间的夹角【解析】【分析】（1）取 AD 的中点为 O ，连结 OP ， OC ， OB ，设 OB 交 AC 于 H ，连结 GH .证明 AC ⊥CD ， GH ⊥CD ，即可证 CD ⊥ 平面 GAC ；（2）取 BC 的中点为 E ，以 O 为空间坐标原点，分别以 OE⇀,OD ⇀,OP ⇀ 的方向为 x 轴、 y 轴、 z 轴的正方向，建立如图所示的空间直角坐标系 O −xyz .设 AD =4 ，利用向量法求二面角 P −AG −C 的余弦值.6.【答案】 （1）解：因为平面 AEC ⊥ 平面 ABC ，交线为 AC ，又 AC ⊥BC ， 所以 BC ⊥ 平面 AEC ， ∴BC ⊥AE ，又 AE ⊥CD ， CD ∩BC =C ， 则 AE ⊥ 平面 BCDE ， EC ⊂ 平面 BCDE ， 所以， AE ⊥EC ；（2）解：取 AC 的中点 O ， AB 的中点 F ，连接 OE ， OF ，则 OE ⊥ 平面 ABC ， OF ⊥ 平面 AEC ；以点 O 为坐标原点，分别以 OA ， OF ， OE 为 x 轴， y 轴， z 轴建立空间直角坐标系如图所示，已知 AE =EC =CB =√2 ，则 AC =2 ， OE =1 ， O(0,0,0) ， A(1,0,0) ， C(−1,0,0) ， D(0,−√2,1) ， 则 AC⃗⃗⃗⃗⃗ =(−2,0,0) ， AD ⃗⃗⃗⃗⃗ =(−1,−√2,1) ， 设平面 DAC 的一个法向量 m⃗⃗ =(x,y,z) ， 由 {m ⇀⋅AC⇀=0,m ⇀⋅AD ⇀=0 得 {−2x =0,−x −√2y +z =0令 y =√2 ，则 x =0 ， z =2 ，即 m ⃗⃗ =(0,√2,2) ；平面 ECA 的一个法向量为 n ⃗ =(0,1,0) ； cos〈m ⃗⃗ ,n ⃗ 〉=m⃗⃗⃗ ⋅n ⃗ |m ⃗⃗⃗ ||n ⃗ |=√2√2+4=√33.所以二面角 D −AC −E 的余弦值为 √33.【考点】空间中直线与直线之间的位置关系，用空间向量求平面间的夹角【解析】【分析】（1）先通过平面 AEC ⊥ 平面 ABC 得到 BC ⊥AE ，再结合 AE ⊥CD ，可得 AE ⊥ 平面 BCDE ，进而可得结论；（2）取 AC 的中点 O ， AB 的中点 F ，连接 OE ， OF ，以点 O 为坐标原点，分别以 OA ， OF ， OE 为 x 轴， y 轴， z 轴建立空间直角坐标系，求出平面 DAC 的一个法向量以及平面 ECA 的一个法向量，求这两个法向量的夹角即可得结果. 7.【答案】 （1）证明:因为 △ABC 是等边三角形, ∠BAD =∠BCD =90° , 所以 Rt △ABD ≅Rt △CBD ,可得 AD =CD ． 因为点 P 是 AC 的中点,则 PD ⊥AC , PB ⊥AC , 因为 PD ∩PB =P , PD ⊂ 平面PBD, PB ⊂ 平面 PBD , 所以 AC ⊥ 平面 PBD ,因为 AC ⊂ 平面 ACD , 所以平面 ACD ⊥ 平面 BDP ．（2）解：如图,作 CE ⊥BD ,垂足为 E 连接 AE ．因为 Rt △ABD ⊆Rt △CBD ,所以 AE ⊥BD, AE =CE, ∠AEC 为二面角A-BD-C 的平面角． 由已知二面角 A −BD −C 为 120° ,知 ∠AEC =120° ． 在等腰三角形 AEC 中,由余弦定理可得 AC =√3AE ． 因为 △ABC 是等边三角形,则 AC =AB ,所以 AB =√3AE ． 在 Rt △ABD 中,有 12AE ⋅BD =12AB ⋅AD ,得 BD =√3AD , 因为 BD =√6 ,所以 AD =√2 ． 又 BD 2=AB 2+AD 2 ,所以 AB =2 ． 则 AE =2√33, ED =√63．以 E 为坐标原点,以向量 EC ⃗⃗⃗⃗⃗ , ED ⃗⃗⃗⃗⃗ 的方向分别为 x 轴, y 轴的正方向, 以过点 E 垂直于平面 BCD 的直线为 z 轴,建立空间直角坐标系 E −xyz ,则 D(0,√63,0) , A(−√33,0,1) ,向量 AD ⃗⃗⃗⃗⃗ =(√33,√63,−1) ,平面 BCD 的一个法向量为 m⃗⃗ =(0,0,1) , 设直线 AD 与平面 BCD 所成的角为 θ , 则 cos〈m ⃗⃗ ,AD ⃗⃗⃗⃗⃗ 〉=m⃗⃗⃗ ⋅AD ⃗⃗⃗⃗⃗⃗ |m⃗⃗⃗ ||AD ⃗⃗⃗⃗⃗⃗ |=√2×1=−√22, sinθ=|cos〈m ⃗⃗ ,AD⃗⃗⃗⃗⃗ 〉|=√22所以直线 AD 与平面 BCD 所成角的正弦值为 √22．【考点】平面与平面垂直的判定，直线与平面所成的角，二面角的平面角及求法【解析】【分析】（1）由 △ABC 是等边三角形, ∠BAD =∠BCD =90° ,得 AD =CD ．再证明 PD ⊥AC , PB ⊥AC ,从而和证明 AC ⊥ 平面 PBD ,故平面 ACD ⊥ 平面 BDP 得证．（2）作 CE ⊥BD ,垂足为 E 连接 AE ．由 Rt △ABD ⊆Rt △CBD ,证得 AE ⊥BD, AE =CE, 结合二面角 A −BD −C 为 120° ,可得 AB =2 , AE =2√33, ED =√63 .建立空间直角坐标系,求出点的坐标则 D(0,√63,0) , A(−√33,0,1) ,向量AD ⃗⃗⃗⃗⃗ =(√33,√63,−1) ,即平面 BCD 的一个法向量 m ⃗⃗ =(0,0,1) ,运用公式 cos〈m ⃗⃗ ,AD ⇀〉=m ⃗⃗⃗ ⋅AD ⇀|m⃗⃗⃗ ||AD ⇀| 和 sinθ=|cos〈m ⃗⃗ ,AD ⇀〉| ,即可得出直线 AD 与平面 BCD 所成角的正弦值． 8.【答案】 （1）证明：∵ AP ⊥ 平面 PCD ，∴ AP ⊥CD . ∵ AD//BC ， BC =12AD ，∴四边形 BCDE 为平行四边形， ∴ BE//CD ， ∴ AP ⊥BE .又∵ AB ⊥BC ， AB =BC =12AD ，且 E 为 AD 的中点， ∴四边形 ABCE 为正方形，∴ BE ⊥AC .又 AP ∩AC =A ，∴ BE ⊥ 平面 APC ，则 BE ⊥PO . ∵ AP ⊥ 平面 PCD ，∴ AP ⊥PC ，又 AC =√2AB =√2AP ， ∴ ΔPAC 为等腰直角三角形， O 为斜边 AC 上的中点， ∴ PO ⊥AC 且 AC ∩BE =O ，∴ PO ⊥ 平面 ABCD .（2）解：∵ OB =1 ，∴ PA =PB =AB =√2 . 设 C 到平面 PAB 的距离为 d ， 由 V C−PAB =V P−ABC ，得 13×√34×(√2)2×d =13×12×(√2)2×1 ，解得 d =2√33.【考点】直线与平面垂直的判定，点、线、面间的距离计算【解析】【分析】（1）首项通过证明 AP ⊥CD,CD//BE ，证得 AP ⊥BE ，然后通过证明四边形 ABCE 是正方形证得 BE ⊥AC ，由此证得 BE ⊥ 平面 APC ，所以 BE ⊥PO .通过证明 ΔPAC 为等腰直角三角形证得 PO ⊥AC ，由此证得 PO ⊥ 平面 ABCD .（2）利用等体积法，由 V C−PAB =V P−ABC 列方程，解方程求得点 C 到平面 PAB 的距离.9.【答案】 （1）解：如图，连接 BC 1 ，交 B 1C 于点M ，连接ME ，则 ME//AC 1 . 因为 AC 1⊄ 平面 B 1CE ， ME ⊂ 平面 B 1CE ，所以 AC 1// 平面 B 1CE .（2）解：设O 是AC 的中点，连接 OC 1 ，OB.因为 △ACC 1 为正三角形， 所以 OC 1⊥AC ，又平面 ABC ⊥ 平面 A 1ACC 1 ，平面 ABC ∩ 平面 A 1ACC 1=AC ， 所以 OC 1⊥ 平面ABC.由已知得 AC =2 .如图，分别以射线OB ，OA ， OC 1 的方向为x ，y ，z 轴的正方向，建立空间直角坐标系，则有 A(0,1,0) ， B(√3,0,0) ， C 1(0,0,√3) ， A 1(0,2,√3) ， 故 AC 1⃗⃗⃗⃗⃗⃗⃗ =(0,−1,√3) ， AB ⃗⃗⃗⃗⃗ =(√3,−1,0) ， AA 1⃗⃗⃗⃗⃗⃗⃗ =(0,1,√3) ， 设平面 B 1BAA 1 的一个法向量为 m⃗⃗ =(x,y,z) ，则 {AB ⇀⋅m ⇀=0AA 1⇀⋅m ⇀=0 ， 所以 {√3x −y =0y +√3z =0 令 x =1 ，则 m ⃗⃗ =(1,√3,−1) .设直线 AC 1 与平面 B 1BAA 1 所成的角为 θ ， 则 sinθ=|AC⃗⃗⃗⃗⃗ ⋅m ⃗⃗⃗ ||AC⃗⃗⃗⃗⃗1|⋅|m⃗⃗⃗ |=√32×5=√155，故直线 AC 1 与平面 B 1BAA 1 所成角的正弦值为 √155.【考点】直线与平面平行的判定，直线与平面所成的角【解析】【分析】（1）如图，连接 BC 1 ，交 B 1C 于点M ，连接ME ，则 ME//AC 1 ，再利用线面平行的判定定理，即可证明线面平行；（2）设O 是AC 的中点，连接 OC 1 ，OB ，分别以射线OB ，OA ， OC 1 的方向为x ，y ，z 轴的正方向，建立空间直角坐标系，求出平面 B 1BAA 1 的一个法向量为 m ⃗⃗ =(1,√3,−1) ，设直线 AC 1 与平面 B 1BAA 1 所成的角为 θ ，代入公式 sinθ=|AC ⃗⃗⃗⃗⃗ ⋅m ⃗⃗⃗ ||AC ⃗⃗⃗⃗⃗ 1|⋅|m⃗⃗⃗ | 运算，即可得答案.10.【答案】 （1）解：如图，连接 AC 交 BD 于 O ，连接 OE ，则 O 为 AC 的中点.又E为CP上的中点，所以OE//PA.又AP⊄平面BDE，OE⊂平面BDE，所以AP//平面BDE（2）解：如图，取AB的中点M，连接PM，因为AP⊥PB，AP=PB，所以PM⊥AB，PM=12AB=1，AP=PB=√2，又平面PAB⊥平面ABCD，平面PAB∩平面ABCD=AB，PM⊂平面PAB，所以PM⊥平面ABCD.同理可得BC⊥平面PAB，∵AP、BP⊂平面PAB，∴BC⊥AP，BC⊥BP. 又因为AP⊥BP，BC∩BP=B，所以AP⊥平面BCP，∵PC⊂平面BCP，则AP⊥PC，所以PC=√PB2+BC2=√6，所以SΔAPC=12AP⋅PC=12×√2×√6=√3，又SΔACD=12×2×2=2，设点D到平面ACP的距离为ℎ，由V D−APC=V P−ACD，得13⋅SΔAPC⋅ℎ=13⋅PM⋅SΔACD，所以ℎ=3=2√33，即点D到平面ACP的距离为2√33.【考点】直线与平面平行的判定，点、线、面间的距离计算【解析】【分析】（1）连接AC交BD于O，则O为AC的中点，利用中位线的性质可得出OE//PA，然后利用直线与平面平行的判定定理可证明出AP//平面BDE；（2）取AB的中点M，连接PM，利用面面垂直的性质定理可得出PM⊥平面ABCD，由此可计算出三棱锥P−ACD的体积，并计算出ΔAPC的面积，并设点D到平面ACP的距离为ℎ，由V P−ACD=13SΔACP⋅ℎ可计算出点D到平面ACP的距离的值.11.【答案】（1）解：连接AO，因为O为BC的中点，可得BC⊥AO，∵ A 1O ⊥ 平面 ABC ， BC ⊂ 平面 ABC ，∴ A 1O ⊥BC ， 又∵ AO ∩A 1O =O ，∴ BC ⊥ 平面 AA 1O ，∴ BC ⊥AA 1 ， ∵ BB 1//AA 1 ， ∴ BC ⊥BB 1 ， 又∵四边形 BB 1C 1C 为平行四边形， ∴四边形 BB 1C 1C 为矩形；（2）解：如图，分别以 OA,OB,OA 1 所在直线为 x,y,z 轴，建立空间直角坐标系，则 A(1,0,0),B(0,2,0),C(0,−2,0),Rt △AOB 中， AO =√AB 2−BO 2=1 ， Rt △AA 1O 中， A 1O =√AA 12−AO 2=2 ，A 1(0,0,2) ，∴ AA 1⃗⃗⃗⃗⃗⃗⃗ =(−1,0,2) ， A 1C ⃗⃗⃗⃗⃗⃗⃗ =(0,−2,−2) ， A 1B 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ =(−1,2,0) ，设平面 A 1B 1C 的法向量是 n⃗ =(x,y,z) ， 由 {n ⇀⋅AB⇀=0,n ⇀⋅A 1C ⇀=0, 得 {−x +2y =0,−2y −2z =0, 即 {x =2y,z =−y, ，可取 n ⃗ =(2,1,−1) ， 设直线 AA 1 与平面 A 1B 1C 所成角为 θ ，则 θ∈[0,π2] ，sinθ=|cos <AA 1⃗⃗⃗⃗⃗⃗⃗ ,n ⃗ >| =|AA 1⃗⃗⃗⃗⃗⃗⃗⃗ ⋅n ⃗ ||AA 1⃗⃗⃗⃗⃗⃗⃗⃗ |⋅|n ⃗ |=√5⋅√6=215√30 ， ∵ θ∈[0,π2] ，∴ cosθ=√1−sin 2θ=√10515，即直线 AA 1 与平面 A 1B 1C 所成角的余弦值为 √10515．【考点】直线与平面所成的角【解析】【分析】（1）连接 AO ，可得 BC ⊥AO ，易证 A 1O ⊥BC ，则 BC ⊥ 平面 AA 1O ，从而可证 BC ⊥BB 1 ，由此即可得出结论；（2）以 OA,OB,OA 1 所在直线分别为 x,y,z 轴建立空间直角坐标系，利用法向量解决问题．12.【答案】 （1）证明:因为 PA ⊥ 平面 ABCD , CD ⊂ 平面 ABCD , 所以 PA ⊥CD ,因为底面 ABCD 是正方形,所以 AD ⊥CD , 又 PA ∩AD =A ,所以 CD ⊥ 平面 PAD , 因为 AE ⊂ 平面 PAD ,所以 CD ⊥AE ,又因为 AE ⊥PD,CD ∩PD =D , CD,PD ⊂ 平面 PCD , 所以 AE ⊥ 平面 PCD（2）解：因为 PA ⊥ 平面 ABCD ,底面 ABCD 为正方形,所以 PA ⊥AB,PA ⊥AD,AB ⊥AD ,以 A 为原点,分别以 AB 、AD 、AP 所在的直线为x 轴、y 轴、z 轴建立空间直角坐标系 A −xyz （如图所示）,设 PA =AB =1 ,则 A(0,0,0),B(1,0,0),C(1,1,0),D(0,1,0),P(0,0,1) , 因为 AE ⊥PD ,所以 E 为 PD 中点,所以 E(0,12,12) , 所以 PB ⃗⃗⃗⃗⃗ =(1,0,−1),PC ⃗⃗⃗⃗⃗ =(1,1,−1),AE ⃗⃗⃗⃗⃗ =(0,12,12) , 由（1）得 AE ⃗⃗⃗⃗⃗ =(0,12,12) 为平面 PCD 的一个法向量, 设平面 PBC 的一个法向量为 m⃗⃗ =(x,y,z) , 由 {PB ⇀⋅m ⃗⃗ =0PC ⇀⋅m ⃗⃗ =0 ,即 {x −z =0x +y −z =0 ,令 x =1 ,则 z =1,y =0 ,所以 m ⃗⃗ =(1,0,1) , 因此 cos〈m⃗⃗ ,AE ⃗⃗⃗⃗⃗ 〉=m⃗⃗⃗ ⋅AE ⃗⃗⃗⃗⃗ |m⃗⃗⃗ |⋅|AE ⃗⃗⃗⃗⃗ |=12√2×√12=12, 由图可知二面角 B −PC −D 的大小为钝角, 故二面角 B −PC −D 的余弦值为 −12【考点】直线与平面垂直的判定，用空间向量求平面间的夹角【解析】【分析】（1）由 PA ⊥ 平面 ABCD 及底面 ABCD 是正方形可证得 CD ⊥ 平面 PAD ,则 CD ⊥AE ,又由 AE ⊥PD ,即可求证；（2）以 A 为原点,分别以 AB 、AD 、AP 所在的直线为x 轴、y 轴、z 轴建立空间直角坐标系 A −xyz ,由（1）可知 AE ⃗⃗⃗⃗⃗ 为平面 PCD 的一个法向量,求得平面 PBC 的一个法向量 m ⃗⃗ ,进而利用数量积求解即可13.【答案】 （1）解：由题设可知 AC =4√2 ， CD =4√2 ， AD =8 ∴ AD 2=CD 2+AC 2 ∴ CD ⊥AC又∵平面 ABC ⊥ 平面 ACD ，平面 ABC ∩ 平面 ACD =AC ∴ CD ⊥ 面 ABC .（2）解：法一、等体积法取 AC 的中点 O 连接 OB ，由题设可知 △ABC 为等腰直角三角形，所以 OB ⊥ 面 ACM ∵ V B−ACM =V A−BCM 且 V B−ACM =13S ACM ⋅BO =16√23而 S ΔBCM =4√3∴ A 到面 BCM 的距离 ℎ=4√63，所以 sinθ=ℎAB =√63.法二、向量法取 AC 的中点 O 连接 OB ，由题设可知 △ABC 为等腰直角三角形，所以 OB ⊥ 面 ACM ，连接 OM ，因为 M 、O 分别为 AB 和 AC 的中点，所以 OM//CD ，由（1）可知 OM ⊥AC ，故以 OM 、OC 、OB 所在直线为 x 轴、 y 轴、 z 轴建立空间直角坐标系，如图所示. 则 A(0,−2√2,0) ， B(0,0,2√2) ， C(0,2√2,0) ， M(2√2,0,0) ∴ CB⃗⃗⃗⃗⃗ =(0,−2√2,2√2) CM ⃗⃗⃗⃗⃗⃗ =(2√2,−2√2,0) BA ⃗⃗⃗⃗⃗ =(0,−2√2,−2√2) ∴面 BCM 的一个法向量 n ⃗ =(1,1,1) ∴ sinθ=|BA⃗⃗⃗⃗⃗ ⋅n ⃗ ||BA ⃗⃗⃗⃗⃗ ||n⃗ |=√63【考点】直线与平面垂直的判定，直线与平面所成的角【解析】【分析】（1）通过计算结合勾股定理的逆定理可以证明 CD ⊥AC ，再根据面面垂直的性质定理进行证明即可；（2）法一、取 AC 的中点 O 连接 OB ，根据 V B−ACM =V A−BCM ，结合三棱锥的体积公式进行求解即可；法二、取 AC 的中点 O 连接 OB ，由题设可知 △ABC 为等腰直角三角形，所以 OB ⊥ 面 ACM ，连接 OM ，因为 M 、O 分别为 AB 和 AC 的中点，所以 OM//CD ，由（1）可知 OM ⊥AC ，故以 OM 、OC 、OB 所在直线为 x 轴、 y 轴、 z 轴建立空间直角坐标系，如图所示.运用向量法求解即可.14.【答案】 （1）证明：∵底面 ABCD 是正方形， ∴ BC ⊥CD ，∵ SD ⊥ 底面 ABCD ， BC ⊂ 底面 ABCD ，∴ SD ⊥BC ，又 DC ∩SD =D ， ∴ BC ⊥ 平面 SDC ，∵ SC ⊂ 平面 SDC ，∴ BC ⊥SC .（2）解：由（1）知 BC ⊥SC ，又 CD ⊥BC ，∴ ∠SCD 为所求二面角的平面角， 在 RtΔDSC 中，∵ SD =DC =1 ，∴ ∠SCD =45° .（3）解：取AB中点P，连结MP,DP，在ΔABS，由中位线定理得MP//SB，∴∠DMP或其补角是异面直线DM与SB所成角，∵MP=12SB=√32，DM=√22,DP=√1+14=√52，所以ΔDMP中，有DP2=MP2+DM2，∴∠DMP=90°.【考点】直线与平面垂直的判定，二面角的平面角及求法【解析】【分析】（1）根据题意，由线面垂直证线线垂直，再根据线面垂直的判定定理，证明线面垂直，再证线线垂直.（2）由（1）中线面垂直，可知所求二面角的平面角为∠SCD，根据题意可求角度.（3）利用中位线将异面直线平移，则∠DMP或其补角是异面直线DM与SB所成角，根据勾股定理，即可求解.15.【答案】（1）解：在△AOC中, OA=OC=2,AC=a=2√2,∴OA2+OC2=AC2∴∠AOC=90°,即AO⊥OC,∵AO⊥BD,且AO∩BD=O,∴AO⊥平面BCD（2）解：由(1)知, OC⊥OD,以O为原点, OC,OD所在的直线分别为x轴, y轴建立如图的空间直角坐标系O−xyz:则 Q(0,0,0), B(0,−2√3,0), C(2,0,0), D(0,2√3,0) . ∵AO ⊥BD,CO ⊥BD∴∠AOC 为二面角 A −BD −C 的平面角, ∴∠AOC =120° ∴ 点 A(−1,0,√3)AD⃗⃗⃗⃗⃗ =(1,2√3,−√3) , BA ⃗⃗⃗⃗⃗ =(−1,2√3,√3) , BC ⃗⃗⃗⃗⃗ =(2,2√3,0) 设平面 ABC 的法向量为 n⃗ =(x,y,z) ,则 ∴ {n ⃗ ⋅BC ⇀=0n ⃗ ⋅BA ⇀=0 故 {2x +2√3y =0x +2√3y +√3z =0 取 x =1 ,则 y =−√33,z =√3∴ n ⃗ =(1,−√33,√3)设直线 AD 与平面 ABC 所成的角为 θ , sinθ=|AD⃗⃗⃗⃗⃗⃗ ⋅n ⃗ ||AD ⃗⃗⃗⃗⃗⃗ ||n ⃗ |=4√133=√313 ∴cosθ=√1−sin 2θ=√1013 ∴tanθ=sinθcosθ=√310=√3010∴ 直线 AD 与平面 ABC 所成的正切值: √3010【考点】直线与平面垂直的判定，用空间向量求直线与平面的夹角，用空间向量求平面间的夹角 【解析】【分析】(1)根据线面垂直定义,即可求得答案.(2)由于平面 ABC 不是特殊的平面,故建系用法向量求解,以 O 为原点建系, OC,OD 所在的直线分别为 x 轴, y 轴,求出平面 ABC 的法向量 n ⃗ ,求解 AD ⃗⃗⃗⃗⃗ 和 n⃗ 的夹角,即可求得答案. 16.【答案】 （1）解：因为 AB//CD ，所以 AMMC =ABCD =12 ，即AM AC=13.因为 MN// 平面PCD ， MN ⊂ 平面PAC ，平面 PAC ∩ 平面 PCD =PC ， 所以 MN//PC ． 所以 ANAP =AM AC=13 ，即 m =13（2）解：因为 AB =AD ， ∠BAD =60° ，可知 △ABD 为等边三角形， 所以 BD =AD =PD ，又 BP =√2AD ， 故 BP 2=PD 2+DB 2 ，所以 PD ⊥DB ．由已知 PD ⊥AD ， AD ∩BD =D ，所以 PD ⊥ 平面ABCD ，如图，以D 为坐标原点， DA ⃗⃗⃗⃗⃗ ,DP⃗⃗⃗⃗⃗ 的方向为x ， y 轴的正方向建立空间直角坐标系，设 AB =1 ，则 AB =AD =DP =1 ， CD =2 ， 所以 A(1,0,0) ， B(12,0,√32) ， P(0,1,0) ， C(−1,0,√3) ，则 PB ⃗⃗⃗⃗⃗ =(12,−1,√32) ， PC ⃗⃗⃗⃗⃗ =(−1,−1,√3) ， PA ⃗⃗⃗⃗⃗ =(1,−1,0) 设平面PBC 的一个法向量为 n 1⃗⃗⃗⃗ =(x 1,y 1,z 1) ，则有 {n 1⇀⋅PB⇀=0n 1⇀⋅PC ⇀=0 即 {x 1−2y 1+√3z 1=0x 1+y 1−√3z 1=0. 令 x 1=1 ，则 y 1=2,z 1=√3 ，即 n 1⃗⃗⃗⃗ =(1,2,√3) ， 设平面APC 的一个法向量为 n 2⃗⃗⃗⃗ =(x 2,y 2,z 2) ，则有{n 2⇀⋅PA ⇀=0n 2⇀⋅PC ⇀=0，即 {x 2−y 2=0−x 2−y 2+√3z 2=0 令 x 2=y 2=√3 ，则 z 2=2 ，即 n 2⃗⃗⃗⃗ =(√3,√3,2) ． 所以 cos <n 1⃗⃗⃗⃗ ,n 2⃗⃗⃗⃗ >=n 1⃗⃗⃗⃗⃗ ⋅n 2⃗⃗⃗⃗⃗ |n 1⃗⃗⃗⃗⃗ |⋅|n 2⃗⃗⃗⃗⃗ |=√32√2×√10=√154设二面角 A −PC −B 的平面角为 θ ，则 cosθ=√154【考点】向量的共线定理，直线与平面平行的性质，用空间向量求平面间的夹角 【解析】【分析】（1）由AB ∥CD ， 得到AM AC=13 ，由MN ∥平面PCD ， 得MN ∥PC ， 从而 ANAP =AM AC=13，由此能实数m 的值；（2）由AB ＝AD ， ∠BAD ＝60°，知△ABD 为等边三角形，推导出PD ⊥DB ， PD ⊥AD ， 从而PD ⊥平面ABCD ， 以D 为坐标原点， DA ⃗⃗⃗⃗⃗ ，DP ⃗⃗⃗⃗⃗ 的方向为x ， y 轴的正方向建立空间直角坐标系，由此能求出二面角B ﹣PC ﹣B 的余弦值．17.【答案】 （1）证明：因为 PA ⊥ 平面 ABCD ， EF ⊂ 平面 ABCD ，故可得 EF ⊥PA ； 设底面正方形的边长为4，故可得 AE =√AD 2+DE 2=√16+4=2√5 ， EF =√FC 2+CE 2=√1+4=√5 ， AF =√AB 2+BF 2=√16+9=5 ， 故在 △AFE 中，满足 AE 2+EF 2=AF 2 ，故可得 AE ⊥EF ； 又 PA,AE ⊂ 平面 PAE ，且 PA ∩AE =A ， 则 EF ⊥ 平面 PAE ，即证.（2）解：因为 PA ⊥ 平面 ABCD ，故 PA 为三棱锥 P −EFC 底面上的高线.故可得V P−EFC=13S∆EFC×PA=13×12×1×2×4=43.在△PEF中，因为PE=√PA2+AE2=6，EF=√5，由（1）可知EF⊥平面PAE，又PE⊂平面PAE，故可得EF⊥PE，则S△PEF=12×EF×PE=3√5，设点C到平面PEF的距离为ℎ，故可得V P−EFC=V C−PEF=13×S∆PEF×ℎ=43，解得ℎ=4√515.即点C到平面PEF的距离为：4√515.【考点】直线与平面垂直的判定，点、线、面间的距离计算【解析】【分析】（1）根据PA⊥平面ABCD，可得EF⊥PN，再证EF⊥AE，即可由线线垂直推证线面垂直；（2）转换三棱锥顶点，用等体积法求点面距离即可.18.【答案】（1）证明：因为PA⊥平面ABCD，EF⊂平面ABCD，故可得EF⊥PA；设底面正方形的边长为4，故可得AE=√AD2+DE2=√16+4=2√5，EF=√FC2+CE2=√1+4=√5，AF=√AB2+BF2=√16+9=5，故在△AFE中，满足AE2+EF2=AF2，故可得AE⊥EF；又PA,AE⊂平面PAE，且PA∩AE=A，则EF⊥平面PAE，即证.（2）解：因为PA⊥平面ABCD, AB,AD⊂平面ABCD，故可得PA⊥AB,PA⊥AD，又底面ABCD为正方形，故可得AB⊥AD，故以A为坐标原点，以AB,AD,AP所在直线为x,y,z轴建立空间直角坐标系如下图所示：设AB=4，故可得A(0,0,0),P(0,0,5),B(4,0,0),E(2,4,0),F(4,3,0)设平面PEF的法向量为m⃗⃗ =(x,y,z)，则{m⃗⃗ ⋅EF⇀=0m⃗⃗ ⋅PE⇀=0，则{2x−y=02x+4y−5z=0取y=2，则m⃗⃗ =(1,2,2).不妨取平面PAB的法向量n⃗=(0,1,0).则cos〈m⃗⃗ ,n⃗ 〉=m⃗⃗⃗ ⋅n⃗|m⃗⃗⃗ ||n⃗ |=√9×1=23.。
立体几何大题综合(含答案)
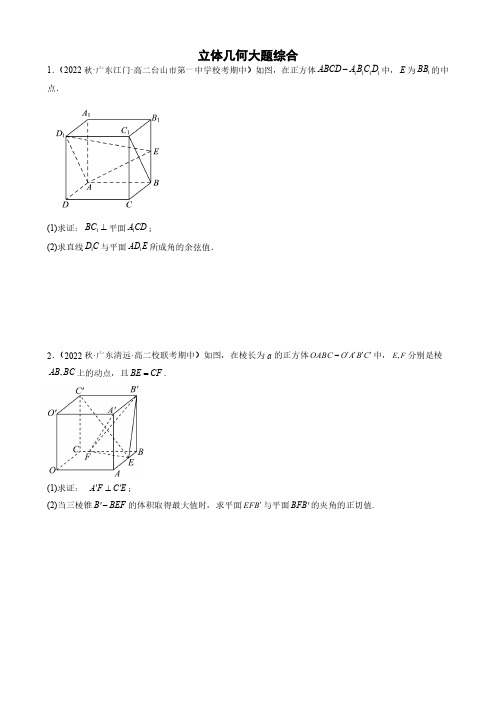
立体几何大题综合1．（2022秋·广东江门·高二台山市第一中学校考期中）如图，在正方体1111ABCD A B C D -中，E 为1BB 的中点．(1)求证：1BC ⊥平面1ACD ；(2)求直线1D C 与平面1AD E 所成角的余弦值．2．（2022秋·广东清远·高二校联考期中）如图，在棱长为a 的正方体OABC O A B C ''''-中，,E F 分别是棱,AB BC 上的动点，且BE CF =.(1)求证：A F C E ''⊥；(2)当三棱锥B BEF '-的体积取得最大值时，求平面EFB '与平面BFB '的夹角的正切值.3．（2022秋·广东肇庆·高二校考期中）如图在棱长为1的正方体1111ABCD A B C D -中，E 为11A B 的中点，F 为AB 的中点，H 为1DD 的中点，K 为1BB 的中点.(1)求直线1A H 到直线KC 的距离；(2)求直线FC 到平面1AEC 的距离.4．（2022秋·广东江门·高二校考期中）如图，在四棱锥P －ABCD 中，PD ⊥底面ABCD ，底面ABCD 是边长为2的正方形，PD CD =，F ，G 分别是PB ，AD 的中点．(1)求证：FG //平面PCD ；(2)求点C 到平面PGB 的距离．5．（2022秋·广东清远·高二校联考期中）如图，在四棱锥P ABCD -中，底面ABCD 为矩形，AB ⊥平面PAD ，E 是AD 的中点，PAD 为等腰直角三角形，DP AP ⊥，2PA AB ==2(1)求证：PE BD ⊥；(2)求点A 到平面PBE 的距离．6．（2022秋·广东江门·高二新会陈经纶中学校考期中）如图，在直角梯形ABCD 中，,=90,AD BC ADC AE ∠︒⊥∥平面ABCD ，EF CD ∥，112BC CD AE EF AD =====．(1)求证：BE AF ⊥；(2)在线段BC 上是否存在点M ，使平面EMD 与平面AMD 的夹角的大小为π3若存在，求出CM 的长；若不存在，请说明理由．7．（2022秋·广东江门·高二台山市第一中学校考期中）如图，边长为1的正方形ABCD 所在平面与正方形ABEF 所在平面互相垂直，动点M 、N 分别在正方形对角线AC 和BF 上移动，且(0CM BN a a ==<<．(1)求证MN 与平面BCE 平行；(2)当a =A MN B --的余弦值．8．（2022秋·广东肇庆·高二肇庆市端州中学校考期中）如图在四棱锥P ABCD －中，侧面PAD ⊥底面ABCD ，侧棱PA PD ==ABCD 为直角梯形，其中BC AD ∥，AB AD ⊥，222AD AB BC ===，O 为AD 的中点．(1)求证：PO ⊥平面ABCD ；(2)求二面角C PD A --的正弦值．9．（2022秋·广东江门·高二江门市第二中学校考期中）如图，已知PA ⊥平面ABCD ，底面ABCD 为矩形，2,,PA AD AB M N ===分别为,AB PC 的中点.(1)求证：MN 平面PAD ；(2)求平面PMC 与平面PAD 的夹角的余弦值.10．（2022秋·广东阳江·高二校联考期中）图1是直角梯形ABCD ，//AB DC ，90,2,3,2D AB DC AD CE ED ︒∠====.以BE 为折痕将BCE 折起，使点C 到达C 1的位置，且1AC = 2.(1)证明：平面1BC E ⊥平面ABED ；(2)求直线1BC 与平面1AC D 所成角的正弦值.11．（2022秋·广东深圳·高二深圳外国语学校校考期中）如图所示，在四棱锥P ABCD -中，底面ABCD 为正方形，E 为侧棱PC的中点．(1)设经过A 、B 、E 三点的平面交PD 于F ，证明：F 为PD 的中点；(2)若PA ⊥底面ABCD ，且2PA AD ==，求点P 到平面ABE 的距离．12．（2022秋·广东阳江·高二校联考期中）如图，在四棱柱ABCD -A 1B 1C 1D 1中，四边形ABCD 是一个边长为2的菱形，∠DAB ＝60°.侧棱DD 1⊥平面ABCD ，DD 1＝3.(1)求二面角B -D 1C -D 的平面角的余弦值；(2)设E 是D 1B 的中点，在线段D 1C 上是否存在一点P ，使得AE ∥平面PDB ？若存在，请求出11D P D C的值；若不存在，请说明理由.13．（2022秋·广东茂名·高二统考期中）在直四棱柱1111ABCD A B C D -中，四边形ABCD 为平行四边形，M为1AA 的中点，1BC BD ==，1AB AA ==(1)求证：DM ⊥平面1BDC ；(2)求平面1MBC 与平面1D B C 夹角的余弦值.14．（2022秋·广东揭阳·高二惠来县第一中学校考期中）已知四棱锥P ABCD -中，底面ABCD 是矩形，且2=AD AB ，PAD 是正三角形，CD ⊥平面PAD ，E 、F 、G 、O 分别是PC 、PD 、BC 、AD 的中点．(1)求平面EFG 与平面ABCD 所成角的大小；(2)线段PA 上是否存在点M ，使得直线GM 与平面EFG 所成角的大小为π6，若存在，求出PM PA的值；若不存在，说明理由．15．（2022秋·广东佛山·高二顺德一中校考期中）如图，在直棱柱1111ABCD A B C D -中，底面ABCD 是边长为4的菱形，60BAD ∠= ，14AA =，P 是1AD 上的动点（不含端点）.(1)当P 为1AD 的中点时，求直线AD 到平面PBC 的距离；(2)求直线1AD 和平面BCP 所成角的正弦值的取值范围.16．（2022秋·广东佛山·高二顺德一中校考期中）如图，在直角梯形ABED 中，//BE AD ，DE AD ⊥，BC AD ⊥，4AB =，BC =BE =.将矩形BEDC 沿BC 翻折，使得平面ABC ⊥平面BCDE .(1)求DB 与平面ADE 所成角的正弦值.(2)求平面ADE 与平面ABC 所成的锐二面角的余弦值.17．（2022秋·广东珠海·高二珠海市第二中学校考期中）如图1，在MBC 中，24BM BC BM BC ==⊥，，,A D 分别为棱,BM MC 的中点，将△MAD 沿AD 折起到PAD 的位置，使90PAB ∠=︒，如图2，连接,PB PC .(1)求证：平面PAD ⊥平面ABCD ；(2)若E 为PC 中点，求直线DE 与平面PBD 所成角的正弦值；(3)线段PC 上是否存在一点G ，使二面角G AD P --求出PG PC 的值；若不存在，请说明理由.18．（2022秋·广东广州·高二广州市第八十九中学校考期中）如图，已知梯形ABCD ，AB //CD ，,120AD DC BC ADC ︒==∠=，四边形ACFE 为正方形，且平面ACFE ⊥平面ABCD ．(1)求证：BC ⊥平面ACFE ；(2)点M 在线段EF 上运动，求平面MAB 与平面ADE 夹角余弦值的取值范围．19．（2022秋·广东东莞·高二校考期中）如图，在长方体ABCD-A 1B 1C 1D 1中，E ，M 分别是BC ，AE 的中点，AD=AA 1=1，AB=2.(1)试问在线段CD 1上是否存在一点N ，使MN ∥平面ADD 1A 1?若存在，确定N 的位置；若不存在，请说明理由；(2)在（1）中，当MN ∥平面ADD 1A 1时，试确定直线BB 1与平面DMN 的交点F 的位置，并求BF 的长.20．（2022秋·广东湛江·高二湛江二十一中校考期中）如图，在长方体1111ABCD A B C D -中，11AD AA ==，2AB =，点E 在棱AB 上移动．(1)证明：11D E A D ⊥；(2)求平面1ACD 的法向量.(3)当E 为AB 的中点时，求点E 到面1ACD 的距离.21．（2022秋·广东广州·高二统考期中）如图，在四棱锥P —ABCD 中，PA ⊥平面ABCD ，底面ABCD 是边长为2的正方形，PA =，G 为CD 的中点，E ，F 是棱PD 上两点（F 在E 的上方），且2EF =．(1)若BF //平面AEG ，求DE ；(2)当点F 到平面AEC 的距离取得最大值时，求直线AG 与平面AEC 所成角的正弦值．22．（2022秋·广东广州·高二校联考期中）在多面体ABCDEF 中，平面ABCD 为正方形，2AB =，3AE =，DE =E AD C --//EF BD .(1)证明：平面ABCD ⊥平面DCE ；(2)若()0EF DB λλ=> ，求平面ABF 与平面CEF 所成锐二面角的余弦值的取值范围.23．（2022秋·广东佛山·高二佛山市顺德区容山中学校考期中）如图，圆柱的轴截面ABCD 为正方形，点E 在底面圆周上，且,BE CE M =为AE 上的一点，且,BM AC N ⊥为线段AC 上一动点（不与,A C 重合）(1)若2AN NC =，设平面BMN ⋂面BEC l =，求证：//MN l ；(2)当平面BMN 与平面DEC 夹角为π3，试确定N 点的位置.24．（2022秋·广东肇庆·高二肇庆市端州中学校考期中）如图，四棱锥P ABCD -的底面为菱形，,23ABC AB AP π∠===，PA ⊥底面ABCD ，,E F 分别是线段,PB PD 的中点，G 是线段PC 上的一点.(1)若G 是直线PC 与平面AEF 的交点，试确定PG CG的值；(2)若直线AG 与平面AEF 所成角的正弦值为35，求三棱锥P EFG -体积.25．（2022秋·广东江门·高二校考期中）如图甲，在矩形ABCD 中，2AB AD E ==为线段DC 的中点，ADE V 沿直线AE 折起，使得DC .(1)求证：BE ⊥平面ADE ；(2)线段AB 上是否存在一点H ，使得平面ADE 与平面DHC 所成的角为π4若不存在，说明理由；若存在，求出H 点的位置.26．（2022秋·广东惠州·高二统考期中）如图，在四棱锥P ABMN -中，PNM △是边长为2的正三角形，AN NP ⊥，AN BM ∥，3AN =，1BM =，AB =C ，D 分别是线段AB ，NP 的中点.(1)求证：平面ANMB ⊥平面NMP ；(2)求直线CD 与平面ABP 所成角的正弦值.27．（2022秋·广东广州·高二校联考期中）如图，在四棱锥P ABCD -中，平面PAD ⊥平面,2,4,ABCD PA AD BD AB ====，BD 是ADC ∠的平分线，且BD BC ⊥.(1)若点E 为棱PC 的中点，证明：BE 平面PAD ；(2)已知二面角P AB D --的大小为60 ，求平面PBD 和平面PCD 的夹角的余弦值.28．（2022秋·广东珠海·高二珠海市斗门区第一中学校考期中）如图，等腰直角△ACD 的斜边AC 为直角△ABC 的直角边，E 是AC 的中点，F 在BC 上．将三角形ACD 沿AC 翻折，分别连接DE ，DF ，EF ，使得平面DEF ⊥平面ABC ．已知2AC =，30B ∠=︒，(1)证明：EF ∥平面ABD ；(2)若DF =A BC D --的余弦值．29．（2022秋·广东阳江·高二统考期中）如图，在四面体ABCD 中，ABC 是正三角形，ACD 是直角三角形，ABD CBD ∠=∠，AB =BD ．(1)求证：平面ACD ⊥平面ABC ；(2)若DE mDB = ，二面角D AE C --的余弦值为17，求m ．30．（2022春·广东广州·高二执信中学校考期中）已知△ABC 是边长为6的等边三角形，点M ，N 分别是边AB ，AC 的三等分点，且13AM AB =，13CN CA =，沿MN 将△AMN 折起到A MN '△的位置，使90A MB '∠=︒．(1)求证：A M '⊥平面MBCN ；(2)在线段BC 上是否存在点D ，使平面A ND '与平面A MB '所成锐二面角的余弦值为13若存在，设()0BD BC λλ=> ，求λ的值；若不存在，说明理由．立体几何大题综合答案1．（2022秋·广东江门·高二台山市第一中学校考期中）如图，在正方体1111ABCD A B C D -中，E 为1BB 的中点．(1)求证：1BC ⊥平面1ACD ；(2)求直线1D C 与平面1AD E 所成角的余弦值．（2）以AD 方向为x 轴正方向，妨设正方体边长为1，则()0,0,0A 面1AD E 的法向量为(),,n x y z = ，则设直线1D C 与平面1AD E 所成角为2．（2022秋·广东清远·高二校联考期中）如图，在棱长为a 的正方体OABC O A B C ''''-中，,E F 分别是棱,AB BC 上的动点，且BE CF =.(1)求证：A F C E ''⊥；(2)当三棱锥B BEF '-的体积取得最大值时，求平面EFB '与平面BFB '的夹角的正切值.则()()()0,0,0,1,0,0,0,1,0,C O B B (,1,0),(0,,0)E m F m ，(1,A F '=- 则(1)(1)11A F C E m m ''⋅=-+-⨯+ ∴A F C E ''⊥ ，故A F C E ''⊥.（2）由（1）知1BB '=,而B BEF V '-故当S 取到最大值时，三棱锥111111的中点，F 为AB的中点，H为1DD的中点，K为1BB的中点.(1)求直线1A H到直线KC的距离；(2)求直线FC到平面1AEC的距离.【详解】（1）长为2的正方形，PD CD =，F ，G 分别是PB ，AD 的中点．(1)求证：FG //平面PCD ；(2)求点C 到平面PGB 的距离．【详解】（1）以D 为原点，DA ，DC ，DP 所在直线分别为x 轴，y 轴，z 轴建立空间直角坐标系，则(1,0,0),(0,0,2),(2,0,0),(2,2,0),(0,2,0),(1,1,1),G P A B C F 明显面PCD 的一个法向量为()1,0,0n =r ，又()0,1,1GF = ，()()1,0,00,1,10n GF ∴⋅=⋅= ，GF n ∴⊥ ，又GF ⊄面PCD ，//GF ∴面PCD ；（2）(1,0,2),(2,2,2)PG PB =-=- ，设平面PGB 的一个法向量为(,,)m a b c = ，00m PB m PG ⎧⋅=⎪∴⎨⋅=⎪⎩ ，即222020a b c a c +-=⎧⎨-=⎩，令1c =，则2,1a b ==-所以平面PGB 的一个法向量为(2,1,1)m =- ，又()2,0,0CB = ，所以点C 到平面PGB 的距离4263||411CB m d m ⋅===++ 5．（2022秋·广东清远·高二校联考期中）如图，在四棱锥P ABCD -中，底面ABCD 为矩形，AB ⊥平面PAD ，E 是AD 的中点，PAD 为等腰直角三角形，DP AP ⊥，2PA AB ==2(1)求证：PE BD ⊥；(2)求点A 到平面PBE 的距离．【详解】（1）∵AB ⊥平面PAD ，PE ⊂平面PAD ，∴PE AB ⊥，又∵PAD 是等腰直角三角形，E 是斜边AD 的中点，∴PE AD ⊥，又∵AD ⊂平面ABCD ，AB ⊂平面ABCD ，AB AD A ⋂=，∴PE ⊥平面ABCD又∵BD ⊂平面ABCD ，∴PE BD ⊥；因为22PA AB ==，则()000E ，，，(0,1,1)B ，()010A ，，则(0,1,1)EB = ，(1,0,0)EP = ，PA 设平面PBE 的一个法向量为(n = 00EB n y z EP n x ⎧⋅=+=⎪⎨⋅==⎪⎩ ，取1y =，则z 设点A 到平面PBE 的距离为h ，则∴点A 到平面PBE 的距离为226．（2022秋·广东江门·高二新会陈经纶中学校考期中）如图，在直角梯形,=90,AD BC ADC AE ∠︒⊥∥平面ABCD ，EF CD ∥，112BC CD AE EF AD =====．(1)求证：BE AF ⊥；(2)在线段BC 上是否存在点M ，使平面EMD 与平面AMD 的夹角的大小为π3若存在，求出CM 的长；若不存在，请说明理由．【详解】（1）如图，作,FG EA AG EF ，连接EG ，AF ，BG ，∵EF CD ∥且EF AG ∥，AG CD ∴ ，即点G 在平面ABCD 内，所以四边形CDAG 为平行四边形，四边形AEFG 为平行四边形.又90ADC ∠=︒，BG AG ∴⊥，因为⊥AE 平面ABCD ，BG ⊂平面ABCD ，所以AE BG ⊥，又因为AG AE A = ，,AG AE ⊂平面AEFG ，∴BG ⊥平面AEFG ，因为AF ⊂平面AEFG ，BG AF ∴⊥．AE AG ⊥ ，所以平行四边形AEFG 为矩形，又因为AE EF =，所以矩形AEFG 为正方形，所以AF EG ⊥，又因为BG EG G = ，,BG EG ⊂平面BGE ，所以AF ⊥平面BGE ，因为BE ⊂平面BGE ，所以AF BE ⊥.（2）由（1）知AG ，AD ，AE 为三条两两互相垂直的直线，所以以A 为原点，AG 为x 轴，AD 为y 轴，AE 为z 轴建立空间直角坐标系A xyz -，如图，则(0,0,0),(1,0,0),(0,0,1),(0,2,0)A G E D ，设()001,,0,[1,2]M y y ∈，∴(0,2,1)ED =- ，()01,2,0DM y =- ，设平面EMD 的法向量为(,,)n x y z = ，则00n ED n DM ⎧⋅=⎪⎨⋅=⎪⎩，即()02020y z x y y -=⎧⎨+-=⎩，令1y =，得02,2z x y ==-，所以平面EMD 的法向量为()02,1,2n y =- ，又⊥AE 平面ABCD ，即⊥AE 平面AMD ，ABEF 所在平面互相垂直，动点M 、N 分别在正方形对角线AC 和BF 上移动，且(0CM BN a a ==<<．(1)求证MN 与平面BCE 平行；(2)当a =A MN B --的余弦值．8．（2022秋·广东肇庆·高二肇庆市端州中学校考期中）侧棱2PA PD ==，底面ABCD 为直角梯形，其中BC AD ∥，AB AD ⊥，222AD AB BC ===，O 为AD 的中点．(1)求证：PO ⊥平面ABCD ；(2)求二面角C PD A --的正弦值．【详解】（1）PA PD = ，O 为AD 的中点，PO AD ∴⊥，侧面PAD ⊥底面ABCD ，侧面PAD ⋂底面ABCD AD =，PO ⊂平面PAD ，PO ∴⊥平面ABCD ；（2） 底面ABCD 为直角梯形，其中BC AD ∥，AB AD ⊥，222AD AB BC ===，OC AD ∴⊥，又PO ⊥平面ABCD ，∴以O 为原点，OC 所在直线为x 轴，OD 所在直线为y 轴，OP 所在直线为z 轴，建立空间直角坐标系，易得平面PAD 的法向量(1,0,0m =设平面PCD 的法向量(,,n x y z = 设二面角C PD A --夹角为θ，则1cos 3m n m n θ⋅==⋅ ，则sin θ2,,PA AD AB M N ===分别为,AB PC 的中点.(1)求证：MN 平面PAD ；(2)求平面PMC 与平面PAD 的夹角的余弦值.（2）由题意，可构建如下图示的空间直角坐标系，令2x =，故(2,1,1)m =- ，又(1,0,0)n = 是面PAD 的一个法向量，所以26cos ,3||||6m n m n m n ⋅<>=== 故平面PMC 与平面PAD 的夹角的余弦值10．（2022秋·广东阳江·高二校联考期中）图90,2,3,2D AB DCAD CE ED ︒∠====.以BE 为折痕将BCE 折起，使点C 到达C 1的位置，且1AC = 2.(1)证明：平面1BC E ⊥平面ABED ；(2)求直线1BC 与平面1AC D 所成角的正弦值.（2）如图②，以D 为坐标原点，DA ，DE 的方向分别为空间直角坐标系.D xyz -则(0,0,0),(3,0,0),(3,2,0),(0,1,0)D A BE ，F 33(,,0)22，133(,,3)22C ，31(,,3)BC =-- ()3,0,0DA = ,DC = 正方形，E 为侧棱PC 的中点．(1)设经过A 、B 、E 三点的平面交PD 于F ，证明：F 为PD 的中点；(2)若PA ⊥底面ABCD ，且2PA AD ==，求点P 到平面ABE 的距离．【详解】（1）因为底面ABCD 为矩形，所以//AB CD .又AB ⊄平面PCD ，且CD ⊂平面PCD ，所以//AB 平面PCD .又AB ⊂平面ABE ，且平面ABE ⋂平面PCD EF =，所以//AB EF .又因为//AB CD ，所以//CD EF因为E 为PC 的中点，所以F 为PD 的中点.（2）如图所示，以A 为原点，,,AB AD AP 所在的直线分别为x 轴、y 轴、z 轴，建立如图所示的空间直角坐标系.则(2,0,0),(2,2,0),(0,0,2),(1,1,1)B C P E ，设(,,)n x y z = 是平面ABE 的法向量，则0,0n AE n AB ⋅=⋅= ，即200x x y z =⎧⎨++=⎩令1y =，则平面ABE 的一个法向量为(0,1,1)n =- 又因为(0,0,2)AP = ，所以点P 到平面ABE 的距离为222|||00+01+21|2||011AP n n ⋅⨯⨯⨯==++ （-），即点P 到平面ABE 的距离为2．12．（2022秋·广东阳江·高二校联考期中）如图，在四棱柱ABCD -A 1B 1C 1D 1中，四边形ABCD 是一个边长为2的菱形，∠DAB ＝60°.侧棱DD 1⊥平面ABCD ，DD 1＝3.(1)求二面角B -D 1C -D 的平面角的余弦值；(2)设E 是D 1B 的中点，在线段D 1C 上是否存在一点P ，使得AE ∥平面PDB ？若存在，请求出11D P D C 的值；若不存在，请说明理由.【详解】（1）如图1，连接BD ，由题意，△ADB 是正三角形，设M 是AB 的中点，则DM ⊥AB ，所以DM ⊥DC ，又DD 1⊥平面ABCD ，所以DM ⊥平面DD 1C 1C.以D 为原点，建立如图所示的空间直角坐标系，则D (0,0,0)，D 1(0,0,3)，C (0,2,0)，B (3,1,0)，则BC ＝(－3,1,0)，1BD ＝(－3,－1,3).显然，平面D 1CD 的一个法向量是()1,0,0m = ，设平面BD 1C 的法向量为n = (x ,y ,z )，则1=30,330,n BC x y n BD x y z ⎧⋅-+=⎪⎨⋅=--+=⎪⎩ 令x ＝3，得n = (3,3,2)，设二面角B -D 1C -D 的平面角为θ，由几何体的特征可知θ为锐角，则cos ||||m n m n θ⋅=⋅＝33941++⨯＝34.故二面角B -D 1C -D 的平面角的余弦值为34.（2）设11D P D C＝λ，即有11λD P D C ＝，其中01λ≤≤由（1）知D 1(0,0,3)，C (0,2,0)，则()10,2,3D C =- ，所以P (0,2,33)λλ-+，又D (0,0,0)，B (3,1,0)，1111为1AA的中点，1BC BD==，1AB AA==(1)求证：DM⊥平面1BDC；(2)求平面1MBC与平面1D B C夹角的余弦值.则()0,0,0D，21,0,2M⎛⎫⎪⎪⎝⎭，2=AD AB ，PAD 是正三角形，CD ⊥平面PAD ，E 、F 、G 、O 分别是PC 、PD 、BC 、AD 的中点．(1)求平面EFG 与平面ABCD 所成角的大小；(2)线段PA 上是否存在点M ，使得直线GM 与平面EFG 所成角的大小为π6，若存在，求出PMPA的值；若不存在，说明理由．【详解】（1）解：因为PAD 是正三角形，O 为AD 的中点，所以PO AD ⊥，因为CD ⊥平面PAD ，PO ⊂平面PAD ，PO CD ∴⊥，,,AD CD D AD CD Q Ç=Ì平面ABCD ，PO ∴⊥平面ABCD ，因为AD BC ∥且AD BC =，O 、G 分别为AD 、BC 的中点，所以AO BG ∥且AO BG =，所以四边形ABGO 为平行四边形，15．（2022秋·广东佛山·高二顺德一中校考期中）如图，在直棱柱1111为4的菱形，60BAD ∠= ，14AA =，P 是1AD 上的动点（不含端点）.(1)当P 为1AD 的中点时，求直线AD 到平面PBC 的距离；(2)求直线1AD 和平面BCP 所成角的正弦值的取值范围.则()0,0,0O ，()23,0,0A ，()10,2,4D -，()1123,2,0B C =-∴- ，AB P 为1AD 的中点，则(P()3,3,2BP =∴- ，(BC =- 则33202320n BP x y z n BC x y ⎧⋅=-+=⎪⎨⋅=--=⎪⎩4AB =，BC =BE =.将矩形BEDC 沿BC 翻折，使得平面ABC ⊥平面BCDE .(1)求DB 与平面ADE 所成角的正弦值.(2)求平面ADE 与平面ABC 所成的锐二面角的余弦值.【详解】（1） 平面ABC ⊥平面BCDE ，平面ABC ⋂平面BCDE BC =，CD BC ⊥，BE ⊂平面BCDE ，CD \^平面ABC ，则以C 为原点，,,CA CB CD正方向为,,x y z 轴，可建立如图所示的空间直角坐标系，则()0,0,0C ，()22,0,0A()22,0,23AD ∴=- ，DE设平面ADE 的法向量为n =则2223220AD n x z DE n y ⎧⋅=-+=⎪⎨⋅==⎪⎩DB n ⋅ ,A D 分别为棱,BM MC 的中点，将△MAD 沿AD 折起到PAD 的位置，使90PAB ∠=︒，如图2，连接,PB PC .(1)求证：平面PAD ⊥平面ABCD ；(2)若E 为PC 中点，求直线DE 与平面PBD 所成角的正弦值；(3)线段PC 上是否存在一点G ，使二面角G AD P --的余弦值为10若存在，求出PG PC 的值；若不存在，请说明理由.由题意得(0,1,0),(0,0,2),(2,0,0),(2,2,0),D P B C 所以(1,0,1)DE = ，(2,0,2),PB PD =-=设平面PBD 的法向量(,,)n x y z =，则22020PB n x z PD n y z ⎧⋅=-=⎪⎨⋅=-=⎪⎩ ，解得(1,2,1)n = 设直线DE 与平面PBD 所成角为θ，n DE ⋅,120AD DC BC ADC ︒==∠=，四边形ACFE 为正方形，且平面ACFE ⊥平面ABCD ．(1)求证：BC ⊥平面ACFE ；(2)点M 在线段EF 上运动，求平面MAB 与平面ADE 夹角余弦值的取值范围．令(03)FM λλ=≤≤，则(3,0,0),(0,1,0),(,0,3),(3,0,A B M E λ1111AD=AA 1=1，AB=2.(1)试问在线段CD 1上是否存在一点N ，使MN ∥平面ADD 1A 1?若存在，确定N 的位置；若不存在，请说明理由；(2)在（1）中，当MN ∥平面ADD 1A 1时，试确定直线BB 1与平面DMN 的交点F 的位置，并求BF 的长.延长DM交AB于点G，可证点G是线段再过点G作GF//AB1与线段BB1交于点20．（2022秋·广东湛江·高二湛江二十一中校考期中）如图，在长方体11111 AB=，点E在棱AB上移动．2(1)证明：11D E A D ⊥；(2)求平面1ACD 的法向量.(3)当E 为AB 的中点时，求点E 到面1ACD 的距离.【详解】（1）以D 为坐标原点，分别以1DA DC DD ､､所在直线为x y z ､､轴，建立如图的坐标系，则()()()()()110,0,0,1,0,1,0,0,1,1,0,00,2,0D A D A C ，，所以()11,0,1DA = ，设()1,,0E t ，所以()11,,1D E t =- ，所以11110DA D E ⋅=-= ，故11DA D E ⊥ 所以11D E A D ⊥；（2）设平面1ACD 的法向量为(),,n x y z =r，则()()11,0,1,1,2,0AD AC =-=-，由10,0n AD n AC ⋅=⋅=，得020x z x y -+=⎧⎨-+=⎩，令1x =得11,,12n ⎛⎫= ⎪⎝⎭；（3）当E 为AB 的中点时，()1,1,0E ，则()11,1,1D E =-，由点到平面的距离公式，得()12221111111231112n D E d n ⨯+⨯+⨯-⋅===⎛⎫++ ⎪⎝⎭，边长为2的正方形，PA=，G为CD的中点，E，F是棱PD上两点（F在E的上方），且2EF=．(1)若BF//平面AEG，求DE；(2)当点F到平面AEC的距离取得最大值时，求直线AG与平面AEC所成角的正弦值．则()0,0,0A ，()2,2,0C ，()1,2,0G ，因为2EF =，所以EFC 的面积为定值，又点A 到平面EFC 的距离为定值，所以三棱锥A -EFC 的体积为定值，即三棱锥所以要使点F 到平面AEC的距离最大，则AEC △即E 到AC 的距离最小时，点F 到平面AEC 的距离最大，设()0,2,3E t t -，则()0,2,3AE t t =- ，AC22AE AC⎛⎫⋅ DE =E AD C --//EF BD .(1)证明：平面ABCD ⊥平面DCE ；(2)若()0EF DB λλ=>，求平面ABF 与平面CEF 所成锐二面角的余弦值的取值范围.【详解】（1）∵2AB AD ==，3AE =，5DE =，∴222AD DE AE +=，即AD DE ⊥，又∵在正方形ABCD 中，AD DC ⊥，且DE DC D ⋂=，DE ⊂平面EDC ，DC ⊂平面EDC ，∴AD ⊥平面EDC ，又AD ⊂平面ABCD ，∴平面ABCD ⊥平面EDC ；（2）由（1）知，EDC ∠是二面角E AD C --的平面角，作OE CD ⊥于点O ，则cos 1OD DE EDC =⋅∠=，2OE =，且平面ABCD ⊥平面EDC ，平面ABCD ⋂平面EDC CD =，OE ⊂平面EDC ，∴OE ⊥平面ABCD ，取AB 中点M ，连接OM ，则OM CD ⊥，如图，建立空间直角坐标系，则()2,1,0A -，()2,1,0B ，()0,1,0D -，()0,1,0C ，()0,0,2E ，()2,2,0DB = ，()2,2,0EF λλ=，()0,1,2EC =- ，设平面CEF 的一个法向量为(),,m x y z=，则20220m EC y z m EF x y λλ⎧⋅=-=⎪⎨⋅=+=⎪⎩ ，取11,1,2m ⎛⎫=-- ⎪⎝⎭ ，()22,21,2BF λλ=--，()0,2,0AB = ，设平面ABF 的一个法向量为(),,n a b c =，在底面圆周上，且,BE CE M =为AE 上的一点，且,BM AC N ⊥为线段AC 上一动点（不与,A C 重合）(1)若2AN NC =，设平面BMN ⋂面BEC l =，求证：//MN l ；(2)当平面BMN 与平面DEC 夹角为π3，试确定N 点的位置.【详解】（1）由题知AB ⊥面,BEC EC ⊂面BEC ，则AB EC ⊥，由BC 为底面圆的直径，则EC BE ⊥，由BE AB B =I ，,BE AB ⊂面ABE ，则(220,,,1,33BM CA ⎛⎫=-=-+ ⎪ ⎪⎝⎭设()(,,2,CN CA λλλλλ==-∈设面BMN 的法向量为(,,n x y z =r 13λ-⎛⎫,23ABC AB AP π∠===，PA ⊥底面ABCD ，,E F 分别是线段,PB PD 的中点，G 是线段PC 上的一点.(1)若G 是直线PC 与平面AEF 的交点，试确定PGCG的值；(2)若直线AG 与平面AEF 所成角的正弦值为35，求三棱锥P EFG -体积.则()()(0,0,0,3,1,0,3,1,0A BC-()31,,1,0,1,122AE AF ⎛⎫=-= ⎪ ⎪⎝⎭ (0,0,AG AP PG AP PC λ=+=+=设平面AEF 的法向量(,,m a b =ADE V 沿直线AE 折起，使得DC .(1)求证：BE ⊥平面ADE ；(2)线段AB 上是否存在一点H ，使得平面ADE 与平面DHC 所成的角为π4若不存在，说明理由；若存在，求出H 点的位置.【详解】（1）证明：连接BE ，取线段AE 的中点O ，连接,DO OC ，在Rt ADE V 中，DA DE ==,1DO AE DO ∴⊥=，在OEC △中，11,2OE AE ==()()()1,0,1,1,1,0,2,0,0,D C A B -平面ADE 的法向量()10,1,0n =，在平面直角坐标系xOy 中，直线设H 的坐标为(),2,0t t -，()(。
立体几何大题训练及答案
1、如图，正方形所在平面与平面四边形所在平面互相垂直，△是等腰直角三角形，（1）线段的中点为，线段的中点为，求证：；（2）求直线与平面所成角的正切值.解：（1）取的中点为，连,,则,面/面, .............. 分5（2）先证出面，.............. 分8为直线与平面所成角，................ 分11................ 分142、己知多面体ABCDE中，DE平面ACD,, AC=AD=CD=DE=2 AB =1, O 为CD 的中点.（1）求证：AO平面CDE（2）求直线BD与平面CBE所成角的正弦值3、如图，在△中，，，点在上，交于，交于•沿将△翻折成△，使平面平面；沿将△翻折成△ ，使平面平面．（ 1 ）求证：平面；（2 ）若，求二面角的平面角的正切值.解：（1）因为，平面，所以平面.因为平面平面，且，所以平面. …2分同理，平面，所以，从而平面. …4分所以平面平面，从而平面.2)因为，，所以，，，．过E作，垂足为M，连结.由( 1)知，可得，所以，所以.所以即为所求二面角的平面角，可记为.在Rt△中，求得，所以. …4、如图，平面ABC,平面BCD, DE=DA=AB=AC,. M(1) 求直线EM与平面BCD所成角的正弦值；(2) P为线段DM上一点，且DM，求证：AP//DE. (12)分15 分为BC中点.解：(1) 平面,为在平面上的射影,为与平面所成角. …分2平面,, 设,又,. 在△中，，，又为中点，， ,.…5分在△中，，．……………………分 (7)2),为中点, ．又平面, ,平面．又平面,,分11 …分9又，平面. .............. 分13又平面，. .............. 分145、如图，已知ABCD是边长为1的正方形，AF丄平面ABCD, CE// AF,(1)证明：BD丄EF;(2)若AF= 1，且直线BE与平面ACE所成角的正弦值为,求的值.解：(1)连结BD、AC,交点为O. •/ ABCD是正方形/• BD丄AC ……2分•/ AF丄平面ABCD A AF丄BD ……4分••• BD丄平面ACEF (6)A BD丄EF ……7分(2)连结0E,由(1)知，BD丄平面ACEF所以/ BEO即为直线BE与平面ACE所成的角. ……10分•/ AF丄平面ABCD, CE// AF , • CE丄平面ABCD, CE1 BC,•/ BC =1 , AF= 1 ,贝U CE= , BE= , B0=,• RtA BEO 中，，…1盼因为解得. …… 15分6、如图在几何体中平面ABC分别是的中点.(1) 求证：平面CDE；(2) 求二面角的平面角的正切值.解：(1)连接ACR1R交EC于点F ,由题意知四边形ACCR1RE是矩形,贝U F是ACR1R的中连接DF, •/ D是AB的中点，•ABCR1R勺中位线，a BCR1R//DF， 4 分•/ BCR1RF面EDC DF平面EDC,• BCR1R//平面CDE. 7 分(2)作AH丄直线CD,垂足为H ,连接HE,•/ AAR1R丄平面ABC, • AAR1RL DC,CD丄平面AHE,CD丄EH ,••• AHE是二面角E -CD -A的平面角. 11分•/ D是AB的中点，• AH等于点B到CD的距离，在厶BCD中，求得：AH=, 在厶AEH中，即所求二面角的正切值为.7、如图，已知平面与直线均垂直于所在平面，且,( 1 )求证：平面；(2)若，求与平面所成角的正弦值.解：(1)证明：过点作于点，•••平面丄平面，•平面……2分又•••丄平面•- 〃 , ......... 分又•••平面• 〃平面 ......... 分(2) •••平面•,又•/••………………分8•点是的中点，连结，则•平面•//,•四边形是矩形………………分10设得：，又•••，•，从而，过作于点，则：•是与平面所成角…………………………………………分…… •，• 与平面所成角的正弦值为…………………………分14&如图，在直三棱柱中，是等腰直角三角形，，侧棱AA仁2, D, E分别为点，点E在平面ABD上的射影是的重心.(1) 求证：DE// 平面ACB；(2) 求A1B与平面ABD所成角的正弦值.12CC1 与A1B 的中9、如图，在侧棱垂直于底面的三棱柱ABC-A1B1中，底面△ ABC为等腰直角三角形，/ B=90°D为棱BB1的中点。
高考数学理数立体几何大题训练(含答案)
高考数学理数立体几何大题训练(含答案)1.（2020·新课标Ⅲ·理）在长方体中，点P、Q分别在棱AB、CD上，且AP=CQ.（1）证明：点PQ平分长方体的体对角线；（2）若PQ在平面BCFE内，求二面角的正弦值．2.（2020·新课标Ⅱ·理）如图，已知三棱柱ABC-A1B1C1的底面是正三角形，侧面BB1C1C是矩形，M、N分别为BC、B1C1的中点，P为AM上一点，过B1C1和P的平面交AB于E，交AC于F.（1）证明：AA1∥MN，且平面A1AMN⊥EB1C1F；（2）设O为△A1B1C1的中心，若AO∥平面EB1C1F，且AO=AB，求直线B1E与平面A1AMN 所成角的正弦值.3.（2020·新课标Ⅰ·理）如图，D为圆锥的顶点，O是圆锥底面的圆心，底面是内接正三角形ABC，P为上一点，AP为底面直径，DP⊥底面．（1）证明：DP平分∠ADC；（2）求二面角平面APD与平面ABC的余弦值．4.（2020·新高考Ⅰ）如图，四棱锥P-ABCD的底面为正方形，PD⊥底面ABCD．设平面PAD与平面PBC的交线为l．（1）证明：l⊥平面PDC；（2）已知PD=AD=1，Q为l上的点，求PB与平面QCD所成角的正弦值的最大值．5.（2020·天津）如图，在三棱柱ABC-A1B1C1中，点P、Q分别在棱AB、A1B1上，且AP=A1Q，平面PQC1为棱BC1的中垂面，M为棱AC的中点．（Ⅰ）求证：PM∥B1Q，且PM=B1Q；（Ⅱ）求二面角平面PQC1与直线PM所成角的正弦值；（Ⅲ）求直线B1Q与平面PQC1所成角的正弦值．6.（2020·江苏）在三棱锥ABCD中，已知CB=CD=1，AC=2，BD=2，O为BD的中点，AO⊥平面BCD，AO=2，E为AC上一点，DE⊥平面BCD，DE=1.（1）求直线AB与DE所成角的余弦值；（2）若点F在BC上，满足BF=BC，设二面角F-DE-C的大小为θ，求sinθ的值．7.（2020·北京）如图，正方体ABCD-EFGH中，E为AD的中点，P为BF上一点．（Ⅰ）求证：PE∥CG；（Ⅱ）求直线PE与平面CGH所成角的正弦值．8.（2020·浙江）如图，三棱台DEF-ABC中，面ADFC⊥面ABC，∠ACB=∠ACD=45°，XXX．（Ⅰ）证明：EF⊥DB；（Ⅱ）求DF与面DBC所成角的正弦值．9.（2020·扬州模拟）如图，在等边三角形ABC的三棱锥ABCD中，D为底面的中点，E为线段AD上一动点，记DE=λAD.（1）当λ=1时，求证：DE与平面ABC垂直；（2）当λ=2时，求直线BE与平面ACD所成角的正弦值．求证：直线AD与平面BCD垂直；2）若平面ABD与平面ACD所成二面角为，求二面角ABC与平面BCD所成二面角的正弦值。
立体几何大题练习(附答案)
1.(本小题总分值14分)如图,在四棱锥 P ABCD 中,底面ABCD 是正方形,侧棱PD 底面ABCD, PD DC 1, E 是PC 的中点,作EF PB 交PB 于点F.(I)证实： PA //平面EDB; (II)证实：PB ,平面EFD; (III)求三棱锥P DEF 的体积.2 .(本小题总分值(m)求三棱锥(I )求证：B 118.(本小题总分值14分)如右图,在直角梯形ABCD中, B=90 °,1DC//AB,BC=CD= -AB=2 , G 为线段AB 的中点,将VADG 沿GD 2折起,使平面ADG 平面BCDG,得到几何体A-BCDG.(1)假设E,F分别为线段AC,AD的中点,求证：EF//平面ABG;(2)求证：AG 平面BCDG;(3)求V C-ABD 的值.4、(本小题总分值14分)如图4, AA是圆柱的母线, AB是圆柱底面圆的直径,C是底面圆周上异于A,B的任意一点, AA AB 2.(1)求证：BC 平面A〔AC ；(2)求三棱锥A ABC的体积的最大值.图4C (n ) 求证：EF 面PAC;〔出〕求三棱锥B-PAC的体积.6 .〔本小题总分值14分〕如图,平行四边形ABCD中,CD 1, BCD 60,且BD CD ,正方形ADEF 和平面ABCD成直二面角,G, H是DF , BE的中点.〔I〕求证：BD 平面CDE ;〔n〕求证：GH 〃平面CDE；〔出〕求三棱锥D CEF的体积.7.〔本小题总分值14分〕右图是一个直三棱柱〔以A i B i C i为底面〕被一平面所截得到的几何体,截面为ABC.A i B i = B i C i = l, ZAi B i C i = 90 ,AA i = 4,BB i=2, CC i=3.(I)设点O是AB的中点,证实：OC//平面A i B i C i;(II)求此几何体的体积.8 .(本小题总分值i4分)如图,在正方体ABCD—A i B i C i D i中,E、F为棱AD、AB的中点.(i )求证：EF//平面CB i D i；(2)求证：平面CAA i C■平面CB i D i.9 .(本小题总分值i4分)如图i ,在直角梯形ABEF中(图中数字表示线段的长度),将直角梯形DCEF沿CD折起,使平面DCEF 平面ABCD,连结局部线段后围成一个空间几何体,如图2.(I)求证：BE〃平面ADF ;(n)求三棱锥F BCE的体积.图图-10 .(本小题总分值14分)在直三棱柱ABC ABG中,AD 平面ABC,其垂足D落在直线A〔B上.(I )求证：BC A1B ；(n)假设AD J3, AB BC 2, P为AC的中点,求三棱锥P ABC的体积.B1…1 .解：(1)证实：连结AC, AC交BD于O,连结EO••・底面ABCD是正方形,,点O是AC的中点在PAC中,EO是中位线,,PA // EO而EO 平面EDB且PA 平面EDB,所以,PA //平面EDB.(2)证实：PD,底面ABCD 且DC 底面ABCD,,PD DCPD=DC,可知PDC是等腰直角三角形,而DE是斜边PC的中线,.DE PC ①同样由PD,底面ABCD,得PDXBC•••底面ABCD是正方形,有DCXBC,,BC,平面PDC 而DE 平面PDC, BC DE ②由①和②推得DE 平面PBC而PB 平面PBC, . DE PB又EF PB 且DE EF E,所以PB ,平面EFD................................ 8分(3) . PD DC 1,由 PD ,平面 ABCD,PDXBC,又.BCXCD, PDACD = D,BC± PC.-CL 2f在Z^BDE 中,DE -------- , BD22221 DE2 BE 2 BD 2 — 2 而由(2), PB,平面EFD,••.BC,平面 PCD,3 c-一 2 0,即 DEL BE.2PBXDE,因而 DEL 平面 BEF,2在 RtABPD 中,BF BP BD , BF1 1 . V DE EF PF 32 2.解：(I)证实：连结 BD ,那么 BD // B 1D 1,ABCD 是正方形,,AC BD. CE 面 ABCD,,CE BD .又 A .CE C, BD 面 ACE. . AE 面 ACE, . . BD AE ,• .B 1D 1 AE .(n)证实：作BB 1的中点F,连结AF 、CF 、EF.• •・E 、F 是 CC 、BB 1 的中点,,CE?B 1F , • •・四边形B 〔FCE 是平行四边形,, CF// B 1E .E,F 是 CC 、BB 1 的中点,,EF//BC ,又 BC//AD , EF //AD ...............14分136；Rt 革EFEF. AF I CF C , B 1EI ED E ,,平面 ACF 〃面 B 1DE .又 AC 平面 ACF , . . AC 〃面 B 1DE .4证实：二.是底面圆周上异于 A, B 的任意 柱底面圆的直径, •••BCXAC,……2 分,.AA1,平面 ABC , BC i 平面 ABC, . AAiXBC,…… 4 分•.AA i AAC=A , AA 1 i 平面 AA i C, AC i 平面 AA1 C, . EC ,平面AA1C.……6分 (2)解法 1 :设 AC=x ,在 RtMBC 中,BC = J AB 2 AC 2 h x 2(o<x<2),……7 分....1 一 … 1 11 -~~2故 V ARABC = —S VABC AA 1— — AC BC AA 1 _x \ 4x (0<x<2),13 3 23即 V A 「ABC =4“ x 2 1 \/x 2 (4 x 2)：J (x 2~2)2~4 . ……11 分 23 33,-0<x<2 , 0<x 2<4 ,「.当 x 2=2,即 x = 五时, 三棱锥A 1-ABC 的体积的最大值为 -.……14分35(1)证实：在三角形 PBC 中,E 是PC 中点.F 为PB 中点所以 EF//BC , BC 面ABC, EF 面ABC, 所以 EF 〃面ABC ……4分,四边形ADEF 是平行四边形,AF // ED ,(3)S ABD - AB AD 2 •2VA BDE VE ABD1S ~ SABDCE1S3 SABDCE2 3又AB 是.O 的直径,所以BC AC …… ⑵ ……7分 由(1) (2)得 BC 面PAC 因EF//BC BC 面PAC ,所以EF 面PAC ……9分(出)因PA OO 所在的平面,AC 是PC 在面ABC 内的射影,1V B PACV P ABC S ABC PA37 . (1)证实：作OD //.交片81于口,连C 1D .那么 OD // BB 1 // CC 1 .作BH(n) PA BC面ABC 面ABCBC PA所成角 PCA 450,PA=AC11分在Rt ABC 中,E 是PC 中点,BAC -, AC BC 2412分Q O 是AB 的中点,OD1-(AA 1 BB 1) 3 CC 1 .2那么ODCQ 是平行四边形,OC // C 1D .……4分Q C 1D 平面 C 1B 1A 且 OC 平面C1B1A ,OC // 面 A 1B 1C 1.(2)如图,过B 作截面BA 2c 2CC 1 于 A 2,//面ABG,分别交AA1,Q CC 1 面 BA 2c 2, CC 1BH ,那么BH 平面AC .又Q A 2B AB 1 1 , BC 2B 1c l 1 , BH --, 2V B AA 2C 2C1 S A A 2c 2c3BH 1 1 厂J.21 (1 2) '2 -3 2 22PCA 即为PC 与面ABC'.2----- …14分3所求几何体体积为：V V B AACC . 八八 2 J 2 J8 .〔本小题总分值14分〕折叠之后平行关系不变. BC 平面ADF , AD 平面 • .BC//平面 ADF ,V AB|C 1 A2BC 21八, SA A 1B 1C 1BB 1 - 2 1〔1〕证实：连结 BD .在长方体AC i 中, 对角线BD//B 1D 1. 又Q E 、F 为棱AD 、AB 的中点, ・.EF //BD . . .EF //BD 1. 又 B 1D 1 平面 CBD 1, EF 平面 CB 1D 1,,EF//平面 CB 1D 1. (2) Q 在长方体 AC ［中,AA 1,平面 A 1B 1C 1D 1,而 B 1D 1 平面 A 1B 1C 1D 1, . AA iX B i D i . 又Q 在正方形 A 1B 1C 1D 1 中,A 1C 1 XB 1D 1, .. B 1D 1,平面 CAA 1C 1. 又Q B 1D 1 平面 CB 1D 1,,平面 CAA 1C 1,平面 CB 〔D 1. 14分9 .〔本小题总分值14分〕 证实：〔I 〕证法一：取 DF 中点为G,连结AG, EG 中, 八 1一 八 一八.CE — DF ,,EG 〃CD 且 EG CD 2 又•••AB 〃CD 且AB CD,,EG 〃AB 且 EG AB四边形ABEG 为平行四边形,,BE//AG. BE 平面ADF , AG 平面 ADF,. ・BE 〃平面 ADF ,证法二：由图1可知BC // AD , CE//DFV A 1B 1C 1 A 2BC 2同理CE〃平面ADF ................... 4分. BCI CE C , BC , CE 平面BCE ,,平面BCE 〃平面ADF ......... 6分. BE 平面BCE ,,BE 〃平面ADF ......... 7 分(II)解法1：V F BCE V B CEF .................... 8分由图1可知BC CD.平面DCEF 平面ABCD ,平面DCEF I平面ABCD CDBC 平面ABCD,..BC 平面DCEF ,1 1由图 1 可知DC CE 1 S CEF -CE DC .................. ........... 12 分2 2V F BCE V B CEF 3 BC S CEF解法2：由图1可知CD BC , CD CEBCI CE C. .CD 平面BCE ,. DF //DC点F到平面BCE的距离等于点D到平面BCE的距离为1 ,由图1可知BC CE 1 S BCE 1-BC CE 2BCE 1 … c 13 CD S BCE 6解法3:过E作EH FC ,垂足为H , ....................... 8分由图1可知BC CD•••平面DCEF 平面ABCD,平面DCEFI 平面ABCD CD11分A B11分BC 平面 ABCD,. BC 平面 DCEF ,EH 平面 DCEF.BC EH,EH 平面BCF 1 、5S BCF -BC DF —, .......... 12 分 2 2又 BD CD. .BD ¥® CDE(n )证实：连结 EA ,那么G 是AE 的中点••• EAB 中,GH // AB又 AB//CD . GH //CD . .GH 〃平面CDE 11分 由 BC FC , FC .DC 2 DF 2 5, 在 CEF 中,由等面积法可得 EHV F BCE V E BCF EH S BCF13分 14分 6.(本小题总分值14分)(I )证实：平面 ADEF 平面ABCD ,交线为ADED AD• .ED 平面ABCDED BD2〔出〕解：设Rt BCD中BC边上的高为h1 1 -依题意：一2 h 1 32 23• • h —2_ ___ _____ .. 一、. .3即：点C到平面DEF的距离为- ---------------- 10•V D CEF V C DEF .32,33分------- 14 分。
高中《立体几何》大题(附答案解析)
《立体几何》大题及答案解析1.（2009全国卷Ⅰ）如图，四棱锥S ABCD −中，底面ABCD 为矩形，SD ⊥底面ABCD，AD =，2DC SD ==，点M 在侧棱SC 上，∠ABM=60。
（I ）证明：M 是侧棱SC 的中点；()ΙΙ求二面角S AM B −−的大小。
2.（2009全国卷Ⅱ）如图，直三棱柱ABC-A 1B 1C 1中，AB ⊥AC,D 、E 分别为AA 1、B 1C 的中点，DE ⊥平面BCC 1（Ⅰ）证明：AB=AC（Ⅱ）设二面角A-BD-C 为60°,求B 1C 与平面BCD 所成的角的大小ACBA 1B 1C 1DE3.（2009浙江卷）如图，DC ⊥平面ABC ，//EB DC ，22AC BC EB DC ====，120ACB ∠=，,P Q 分别为,AE AB 的中点．（I ）证明：//PQ 平面ACD ；（II ）求AD 与平面ABE 所成角的正弦值．4.（2009北京卷）如图，四棱锥P ABCD −的底面是正方形，PD ABCD ⊥底面，点E 在棱PB 上.（Ⅰ）求证：平面AEC PDB ⊥平面；（Ⅱ）当PD =且E 为PB 的中点时，求AE 与平面PDB 所成的角的大小.5.（2009江西卷）如图，在四棱锥P ABCD −中，底面ABCD 是矩形，PA ⊥平面ABCD ，4PA AD ==，2AB =．以BD 的中点O 为球心、BD 为直径的球面交PD 于点M ． （1）求证：平面ABM ⊥平面PCD ； （2）求直线PC 与平面ABM 所成的角； （3）求点O 到平面ABM 的距离．6.（2009四川卷）如图，正方形ABCD 所在平面与平面四边形ABEF 所在平面互相垂直，△ABE 是等腰直角三角形，,,45AB AE FA FE AEF °==∠= （I ）求证：EF BCE ⊥平面；（II ）设线段CD 、AE 的中点分别为P 、M ，求证： PM ∥BCE 平面 （III ）求二面角F BD A −−的大小。
立体几何大题训练题(含答案)
立体几何大题训练题一、解答题（共17题；共150分）1.如图，在四棱锥P-ABCD中，PA⊥平面ABCD，在四边形ABCD中，∠ABC= ，AB=4，BC=3，CD= ，AD=2 ，PA=4.（1）证明：CD⊥平面PAD；（2）求二面角B-PC-D的余弦值..2.如图，在四棱锥中，平面，在四边形中，，，，，，.（1）证明：平面；（2）求B点到平面的距离3.如图，在四棱锥中，底面为长方形，底面，，，为的中点，F 为线段上靠近B 点的三等分点.（1）求证：平面；（2）求平面与平面所成二面角的正弦值.4.如图，四边形为正方形，分别为的中点，以为折痕把折起，使点到达点的位置，且.（1）证明：平面平面;（2）求与平面所成角的正弦值.5.如图，在三角锥中，, , 为的中点.（1）证明：平面;（2）若点在棱上，且MC=2MB，求点C到平面POM的距离.6.如图，在三角锥中，, , 为的中点.（1）证明：平面;（2）若点在棱上，且二面角为，求与平面所成角的正弦值. 7.如图，在四棱锥P﹣ABCD中，AB∥CD，且∠BAP=∠CDP=90°．（12分）（1）证明：平面PAB⊥平面PAD；（2）若PA=PD=AB=DC，∠APD=90°，求二面角A﹣PB﹣C的余弦值．8.如图，长方体ABCD–A1B1C1D1的底面ABCD是正方形，点E在棱AA1上，BE⊥EC1.（1）证明：BE⊥平面EB1C1；（2）若AE=A1E，求二面角B–EC–C1的正弦值.9.如图，直四棱柱ABCD-A1B1C1D1的底面是菱形，AA1=4，AB=2，BAD=60°，E，M，N分别是BC，BB1，A1D的中点（1）证明：MN∥平面C1DE；（2）求二面角A-MA1-N的正弦值。
10.已知三棱柱，底面三角形为正三角形，侧棱底面，，为的中点，为中点.（1）求证：直线平面；（2）求平面和平面所成的锐二面角的余弦值.11.如图，已知三棱柱ABC-A1B1C1，平面A1AC1C⊥平面ABC，∠ABC=90°.∠BAC=30°，A1A=A1C=AC，E，F 分别是AC，A1B1的中点（1）证明：EF⊥BC（2）求直线EF与平面A1BC所成角的余弦值.12.如图，四面体ABCD中，△ABC是正三角形，△ACD是直角三角形，∠ABD=∠CBD，AB=BD．（Ⅰ）证明：平面ACD⊥平面ABC；（Ⅱ）过AC的平面交BD于点E，若平面AEC把四面体ABCD分成体积相等的两部分，求二面角D﹣AE﹣C 的余弦值．13.如图，四棱锥P﹣ABCD中，侧面PAD为等边三角形且垂直于底面ABCD，AB=BC= AD，∠BAD=∠ABC=90°，E是PD的中点．（Ⅰ）证明：直线CE∥平面PAB；（Ⅱ）点M在棱PC 上，且直线BM与底面ABCD所成角为45°，求二面角M﹣AB﹣D的余弦值．14.如图，已知多面体ABCA1B1C1，A1A，B1B，C1C均垂直于平面ABC，∠ABC=120°，A1A=4，C1C=1，AB=BC=B1B=2．（Ⅰ）证明：AB1⊥平面A1B1C1；（Ⅱ）求直线AC1与平面ABB1所成的角的正弦值．15.如图所示多面体中，AD⊥平面PDC，四边形ABCD为平行四边形，点E，F分别为AD，BP的中点，AD ＝3，AP＝3 ，PC ．（1）求证：EF//平面PDC；（2）若∠CDP＝120°，求二面角E﹣CP﹣D的平面角的余弦值．16.如图，四棱锥中，侧棱垂直于底面，，，为的中点，平行于，平行于面，.（1）求的长；（2）求二面角的余弦值.17.如图，在斜三棱柱中，侧面，，，，．（Ⅰ）求证：平面平面；（Ⅱ）若为中点，求二面角的正切值．答案解析部分一、解答题1.【答案】（1）解：连接，由∠ABC= ，AB=4，BC=3，则，又因为CD= ，AD=2 ，所以，即，因为PA⊥平面ABCD，平面ABCD，所以，因为，所以CD⊥平面PAD；（2）解：以点D为坐标原点，的延长线为x，为y轴，过点D与平行线为z轴，建立空间直角坐标系，如图：作交与点G，，即，所以，，所以，所以，，，，则，，，设平面的一个法向量为，则，即，令，则，，即，设平面的一个法向量为，则，即，令，则，，即，由，所以二面角B-PC-D的余弦值为.【解析】【分析】（1）连接，证出，利用线面垂直的性质定理可得，再利用线面垂直的判定定理即可证出.（2）以点D为坐标原点，的延长线为x，为y轴，过点D与平行线为轴，建立空间直角坐标系，分别求出平面的一个法向量与平面的一个法向量，利用向量的数量积即可求解.2.【答案】（1）解：在平面中，，，，则，又，∴，即，又平面，则，又，∴平面.（2）解：在平面中，过A作BC的平行线交CD的延长线于M，因为，，，则,又因为，,所以.所以又，则，所以,在中，.因为,则面,所以由可知：，,所以，则，因此P点到平面的距离为.【解析】【分析】(1)在三角形中，由勾股定理可证得，由平面，可得，根据线面垂直的判定定理即可证得结论；(2) 在平面中，过A作BC的平行线交CD 的延长线于M，因为利用等体积转换即可求得距离.3.【答案】（1）证明：，为线段中点，.平面，平面，.又底面是长方形，.又，平面.平面，. 又，平面.（2）解：由题意，以为轴建立空间直角坐标系，则，，，，，.所以, ，，，设平面的法向量，则，即，令，则，，，同理可求平面的法向量，，，即平面与平面所成角的正弦值为.【解析】【分析】（1）通过，可证明平面，进而可得，结合证明线面垂直.（2）以为轴建立空间直角坐标系，可求出平面的法向量，平面的法向量，则可求出两向量夹角的余弦值，从而可求二面角的正弦值.4.【答案】（1）解：由已知可得，BF⊥PF，BF⊥EF，又，∴BF⊥平面PEF.∴又平面ABFD，平面PEF⊥平面ABFD.（2）解：作PH⊥EF，垂足为H.由（1）得，PH⊥平面ABFD.以H为坐标原点，的方向为y轴正方向，为单位长，建立如图所示的空间直角坐标系H−xyz.由（1）可得，DE⊥PE.又DP=2，DE=1，所以PE= .又PF=1，EF=2，故PE⊥PF.可得.则为平面ABFD的法向量. 设DP与平面ABFD所成角为，则.∴DP与平面ABFD所成角的正弦值为.【解析】【分析】(1)在翻折过程中,作于H,由得到,从而得到面面垂直;(2)DP与平面所成的角就是,在三角形中求其正弦值.5.【答案】（1）∵PA=PC=AC=4 且O是AC的中点∴PO⊥AC∵AB=BC=2 ，AC=4,∴∴∠ABC=90°连接BO则OB=OC∴PO2+BO2=PB2PO⊥OB，PO⊥OCOB∩OC=O∴PO⊥平面ABC（2）过点C作CH⊥OM交OM于点H又∵PO⊥平面ABC∴∴CH的长度为点C到平面POM的距离在△COM中，CM= ，OC=2，∠OCM=45°∴∴OM=∴【解析】【分析】（1）由线面垂直的判定定理易得；（2）由线面垂直可得面面垂直，易找点面距，可求.6.【答案】（1）PA=PC=AC=4 且O是AC的中点PO⊥AC∵AB=BC=2 ，AC=4,∴∴∠ABC=90°连接BO则OB=OC∴PO2+BO2=PB2PO⊥OB，PO⊥OCOB∩OC=O∴PO⊥平面ABC（2）∵PO⊥平面ABC，∴PO⊥OB∴AB=BC=2 O是AC的中点∴OB⊥AC OB⊥平面PAC如图所示以O为坐标原点，为x轴正方向建立如图所示的直角坐标系O-xyz则P（0,0，）A（,0，-2,0），C（0,2,0），B（2,0,0）平面PAC法向量为=（1,0,0）设M（x，2-x，0）平面PAC法向量为=（1，λ，μ），=（0，2，）, = （x，4-x，0）则即即得到，∴x=-4（舍），x=即M∴PAM的法向量记PC与平面PAM所成的角为θ∴即PC与平面PAM所成的角为的正弦值为.【解析】【分析】（1）由线面垂直的判定定理易得；（2）先由条件建系，找到点M的位置，再用公式求线面角.7.【答案】（1）证明：∵∠BAP=∠CDP=90°，∴PA⊥AB，PD⊥CD，∵AB∥CD，∴AB⊥PD，又∵PA∩PD=P，且PA⊂平面PAD，PD⊂平面PAD，∴AB⊥平面PAD，又AB⊂平面PAB，∴平面PAB⊥平面PAD；（2）解：∵AB∥CD，AB=CD，∴四边形ABCD为平行四边形，由（1）知AB⊥平面PAD，∴AB⊥AD，则四边形ABCD为矩形，在△APD中，由PA=PD，∠APD=90°，可得△PAD为等腰直角三角形，设PA=AB=2a，则AD= ．取AD中点O，BC中点E，连接PO、OE，以O为坐标原点，分别以OA、OE、OP所在直线为x、y、z轴建立空间直角坐标系，则：D（），B（），P（0，0，），C（）．，，．设平面PBC的一个法向量为，由，得，取y=1，得．∵AB⊥平面PAD，AD⊂平面PAD，∴AB⊥AD，又PD⊥PA，PA∩AB=A，∴PD⊥平面PAB，则为平面PAB的一个法向量，．∴cos＜＞= = ．由图可知，二面角A﹣PB﹣C为钝角，∴二面角A﹣PB﹣C的余弦值为．【解析】【分析】（1.）由已知可得PA⊥AB，PD⊥CD，再由AB∥CD，得AB⊥PD，利用线面垂直的判定可得AB⊥平面PAD，进一步得到平面PAB⊥平面PAD；（2.）由已知可得四边形ABCD为平行四边形，由（1）知AB⊥平面PAD，得到AB⊥AD，则四边形ABCD 为矩形，设PA=AB=2a，则AD= ．取AD中点O，BC中点E，连接PO、OE，以O为坐标原点，分别以OA、OE、OP所在直线为x、y、z轴建立空间直角坐标系，求出平面PBC的一个法向量，再证明PD⊥平面PAB，得为平面PAB的一个法向量，由两法向量所成角的余弦值可得二面角A﹣PB﹣C的余弦值．8.【答案】（1）解：由已知得，平面，平面，故．又，所以平面．（2）由（1）知．由题设知，所以，故，．以为坐标原点，的方向为x轴正方向，为单位长，建立如图所示的空间直角坐标系D-xyz，则C（0，1，0），B（1，1，0），（0，1，2），E（1，0，1），，．设平面EBC的法向量为=（x，y，x），则即所以可取= .设平面的法向量为=（x，y，z），则即所以可取=（1，1，0）．于是．所以，二面角的正弦值为．【解析】【分析】（1）根据题意由线面垂直的性质得出线线垂直，再由线线垂直的判定定理出线面垂直。
立体几何大题训练及答案
1、如图，正方形 ABCD 所在平面与平面四边形 ABEF 所在平面互相垂直，△ ABE 是等腰E(1) 线段CD 的中点为P ,线段AE 的中点为M ，求证：PM Zz 平面BCE ；(2) 求直线CF 与平面BCE 所成角的正切值•D解：（1）取 AB 的中点为 N ,连 MN , P N 则MN/∕EB ,PN∕∕BC P.面 PMN //面 EBC ,. PM // 平面 BCE⑵先证出FE _面EBC ，■ Z FCE 为直线CF 与平面BCE 所成角，FE _ 6^~6~2、己知多面体 ABCDE 中，DE _ 平面 ACD , AB//DE , AC=AD=CD=DE=2 , AB =1 , O 为CD 的中点.⑴求证：AO-平面CDE ;(2)求直线BD 与平面CBE 所成角的正弦值解：(I)证明；THC =才D, O 为QD 的中点I ^AO 丄C D. 又 DE 丄平面 ACD. Ad^ACD t AOLDE, :、AO 丄平面CDE ・ 一(in E Φ 点F,连接 A 尸、DF t山已知可得，ABHDE 且用月=丄DE,2在 ∖CDE 中.OF //DE 且OF=ZD £』2Λ四边形ABFO 是平行四边形..∖ BF f/ AO f 宙(I)知.BF 丄平面 CDE. TCD = D E ,二 DF 丄 CE. :、DF 丄平面 CBE . ：.Z r DBF 就是直线BD 与平面CBE 所成角• …・直角三角形， AB =AE =2,FA =FE,. AEF =45 tan . FCE(第19题)12分MC 分BE7分E即口线BD与平面CBE所咸角的正弦值为零.*<(此题证ZQBF为所求角，方法较多，酌情给分)3、如图，在厶ABC 中，.C =90 , AC=BC=3a ,点P 在AB 上，PE//BC 交AC 于E , PF // AC交BC于F •沿PE将厶APE翻折成△ A' PE ,使平面A' PE _平面ABC ；沿PF将厶BPF翻折成△ B'PF ,使平面B'PF _平面ABC •(1)求证：B'C//平面A'PE ;(2)若AP =2PB ,求二面角A'-PC -E的平面角的正切值.解：（1）因为FC // PE , FC二平面A' PE ,所以FC //平面A PE •因为平面A'PE _平面PEC ,且A'E _ PE ,所以A'E _平面ABC . 同理，B'F —平面ABC ,所以B'F //A'E ,从而B'F //平面A' PE . 所以平面B'CF //平面A'PE ,从而B'C//平面A'PE .（2）因为AC=BC= 3a , AP=2BP ,所以CE =a , EA =2a , PE =2a , PC= 5a .过E作EM _ PC ,垂足为M ,连结A M .在ΛBDF中.DF = √2 J5D = √5由(1)知A' E _平面ABC ,可得A E _ PC , 所以PC _面AEM ,所以AM _ PC .所以.A'ME即为所求二面角A'-PC - E的平面角，可记为二. …12分在Rt△ PCE 中，求得EM =^-5aAC EB- P（第20 题）5............. 9分又 AP 平面 DAM , BC _ AP ,又 AP _ DM , AP _ 平面 BCD .又 ED _ 平面 BCD ,AP//DE .5、如图，已知ABCD 是边长为1的正方形，AF 丄平面ABCD (1) 证明：BD 丄EF;(2) 若AF = 1,且直线BE 与平面ACE 所成角的正弦值所以 ta ^ =EMr…15分DA _平面 .EMD 为 EM ,DA _ 平面 ABC , DA _ AB,DA _ AC ,设 AB = a ,又.DA = AB= AC , DC = DB 在厶 ABC 中， BAC =120， BC = 又.M 为BC 中点，.DM _ BC ，35a, DM a .…5 分 2 21 BM BC =2在 Rt △ EDM 中，EM=.DE 2 DM 2Si n EMD(2) AB=AC ,BC _ DA ,=匹_EM 3a 2M 为BC 中点，.BC _ AM .又.BC _ 平面 DAM .DA _ 平面 ABC ,11分 13分 14分,CE // AF , C^ AFC 1).C与平面BCD 所成角.2分4、如图, 中占I 八、、ABC ， ED _ 平面 BCD ，DE=DA=AB=AC. . BAC =120°，M 为 BC CMD为302 ,求•的值∙解：(1)连结BD、AC,交点为O.∙∙∙ ABCD是正方形∕∙ BD丄AC ……2分∙∙∙ AF丄平面 ABCD ∙∙∙ AF丄BD ……4分∙∙∙ BD丄平面 ACEF ……6分∙ BD丄EF ……7分(2)连结OE,由(1)知，BD丄平面ACEF ,所以∠ BEO即为直线BE与平面ACE所成的角. ……10分∙∙∙ AF 丄平面 ABCD , CE // AF , ∙ CE 丄平面ABCD , CE⊥ BC,∙∙∙ BC =1 , AF = 1,贝U CE = . , BE =、1 ∙2 , BO = -2 ,2∙Rt△ BEO 中，Sin. BEO=B O -—2一二3^2 , …13 分BE 2胡丘104因为■ ∙1 ,解得，. ……15分36、如图，在几何体中,AA1 _ 平面 ABC , AB _ BC,CC1 // AA1, AB = BC = AA1 = 2, CC1 =1,D,E分别是AB, AA1的中点.(1) 求证：BC1 // 平面 CDE ;(2) 求二面角E -DC-A的平面角的正切值解：(1)连接ACR 1R交EC于点F ,由题意知四边形 ACCR I RE是矩形，则F是ACR 1R 的中点，连接DF ,∙∙∙ D是AB的中点，∙ DF是厶ABCR I R的中位线，∙ BCR I RzzDF , 4 分∙∙∙ BCR 1R 二平面 EDC , DF 平面 EDC , ∙ BCR I RZZ平面 CDE.⑵作AH 丄直线CD ,垂足为H ,连接HE ,∙∙∙ AAR ιR⊥平面 ABC ,∙'∙ AAR i R 丄 DC, ∙∙∙ CD 丄平面AHE ,∙ CD 丄 EH ,又∙.∙ PA 丄平面ABC∙ QD // PA,......... 2 分又∙∙∙ QD 平面QBC ∙ PA //平面 QBC......... 6 分(2)∙∙∙ PQ _ 平面 QBC∙ PQB =∕PQC =90 ,又∙.∙ PB= PC ) PQ= PQ∙ PQB = PQC ∙ BQ =CQ .......................... 8 分 ∙点D 是BC 的中点，连结AD ,则AD — BC ∙ AD —平面 QBC ∙ PQ // AD , AD _ QD ∙四边形PADQ 是矩形 ........... 10分设 PA = AB = AC= 2a 得：PQ=AD = .2a , PD= 6a又∙∙∙ BC — PA l BC — PQ ,∙ BC —平面 PADQ ,ZAHE 是二面角 E -CD -A 的平面角. 11分D 是AB 的中点，AH 等于点B 到CD 的距离， 在厶BCD 中，求得:AH = 2^5AE J5 在厶 AEH 中，tan EAHE =AH 27、如图，已知平面 QBC 与直线PA 均垂直于Rt ABC 所在平面，且 PA=AB = AC ,(1)求证：PA //平面QBC ;即所求二面角的正切值为A从而 平面PBC _平面PADQ ,过Q 作QH _ PD 于点H ,则：QH _平面PBC ∙ . QCH 是CQ 与平面PBC 所成角2、2a 2 "3• ∙ QHa , CQ= BQ胚 3QH 2.3 12 sinQCHCQ 3 ^/63&如图，在直三棱柱 ABC-AB iG 中，UBC 是等腰直角三角形，∙ ACB = 90° ,侧棱 AA ι=2，D ，E 分别为CC i 与A l B 的中点，点E 在平面ABD 上的射影是 ABD 的重心.⑴求证：DE//平面ACB ；(2)求A i B 与平面ABD 所成角的正弦值.＜【)取中点d 普EF 、FU 、曲已知可得 EF 汙2^DC //A i A r 所以购边形DEFC 为平打凹边形 则EDHCF冈为EDU 平面虫BC. FC ⊂ T ：面ABC,ClD 过E 作£H 丄QF 于∕Λ连结HR.12=.6a∙∙∙ CQ 与平面PBC 所成角的正弦值为14分CC I 丄平面di?LABCL VnS ABC卜n CG 丄AB^2分AC = BC …—F n AB丄CF tAF —κCF∩CD = C,CΛCD⊂平^DEFC∖所^AB丄平面DEFC∖ EH U 平^DEFC所以丄EH t义EH丄DF,DFn Ali = FM/DF U T所⅛E/7 1 平［ii∖A BD t为州B与平面』EQ所成角的平面角，.......... Ii分H为Zvl j8D的巫心,在E∆DEFΨ EF2= FH FDJFDj所以^ro = √3,∕∕r -= √2ψFB= √2t£2? = Λ铤血ZEBH二醫=冬所ft J1/?与ip UiMBD所成饬的iE弦值为辱........... 诂分9、如图，在侧棱垂直于底面的三棱柱ABC — A i B i C i中，底面△ ABC为等腰直角三角形,∠ B=90° ,D为棱BB i的中点。
高三精选立体几何大题30题(含详细解答)
1．如下图，一个等腰直角三角形的硬纸片ABC中，∠ACB＝90°，AC＝4cm，CD是斜边上的高沿CD把△ABC折成直二面角．
（1）如果你手中只有一把能度量长度的直尺，应该如何确定A，B的位置，使二面角A－CD－B是直二面角？证明你的结论．
（2）试在平面ABC上确定一个P，使DP与平面ABC内任意一条直线都垂直，证明你的结论．
∴ ，∴ ．
∴ ．
5．已知：ABCD是矩形，设PA=a，PA⊥平面ABCD.M、N分别是AB、PC的中点.
（Ⅰ）求证：MN⊥AB；
（Ⅱ）若PD=AB，且平面MND⊥平面PCD，求二面角P—CD—A的大小；
（Ⅲ）在（Ⅱ）的条件下，求三棱锥D—AMN的体积.
（Ⅰ）连结AC，AN.由BC⊥AB，AB是PB在
.
6．如图，正方体ABCD—A1B1C1D1中，P、M、N
分别为棱DD1、AB、BC的中点。
（I）求二面角B1—MN—B的正切值；
（II）证明：PB⊥平面MNB1；
（III）画出一个正方体表面展开图，使其满足
“有4个正方形面相连成一个长方形”的条件，
（Ⅲ）求二面角C-BE-D的正切值．
证：（Ⅰ）取CE中点M，连结FM，BM，则有 ．
∴四边形AFMB是平行四边形．
∴AF//BM，
∵ 平面BCE，
平面BCE，
∴AF//平面BCE．
（Ⅱ）由于DE⊥平面ACD，
则DE⊥AF．
又△ACD是等边三角形，则AF⊥CD．而CD∩DE=D，因此AF⊥平面CDE．
= × ×3×3×
= （10分）
解（Ⅲ）连CF，
∵CB⊥平面A1B1BA，又BF⊥AE，
由三垂线定理知，CF⊥AE.
2024届新高考数学大题精选30题--立体几何含答案
大题立体几何1(2024·黑龙江·二模)如图，已知正三棱柱ABC-A1B1C1的侧棱长和底面边长均为2，M是BC的中点，N是AB1的中点，P是B1C1的中点．(1)证明：MN⎳平面A1CP；(2)求点P到直线MN 的距离．2(2024·安徽合肥·二模)如图，在四棱锥P-ABCD中，底面ABCD是边长为2的菱形，∠BAD=60°,M是侧棱PC的中点，侧面PAD为正三角形，侧面PAD⊥底面ABCD．(1)求三棱锥M-ABC的体积；(2)求AM与平面PBC所成角的正弦值．2024届新高考数学大题精选30题--立体几何3(2023·福建福州·模拟预测)如图，在三棱柱ABC-A1B1C1中，平面AA1C1C⊥平面ABC,AB= AC=BC=AA1=2，A1B=6．(1)设D为AC中点，证明：AC⊥平面A1DB；(2)求平面A1AB1与平面ACC1A1夹角的余弦值．4(2024·山西晋中·三模)如图，在六面体ABCDE中，BC=BD=6，EC⊥ED，且EC=ED= 2，AB平行于平面CDE，AE平行于平面BCD，AE⊥CD.(1)证明：平面ABE⊥平面CDE；(2)若点A到直线CD的距离为22，F为棱AE的中点，求平面BDF与平面BCD夹角的余弦值．5(2024·辽宁·二模)棱长均为2的斜三棱柱ABC-A1B1C1中，A1在平面ABC内的射影O在棱AC的中点处，P为棱A1B1(包含端点)上的动点．(1)求点P到平面ABC1的距离；(2)若AP⊥平面α，求直线BC1与平面α所成角的正弦值的取值范围．6(2024·重庆·模拟预测)在如图所示的四棱锥P-ABCD中，已知AB∥CD，∠BAD=90°，CD= 2AB，△PAB是正三角形，点M在侧棱PB上且使得PD⎳平面AMC．(1)证明：PM=2BM；(2)若侧面PAB⊥底面ABCD，CM与底面ABCD所成角的正切值为311，求二面角P-AC-B的余弦值．7(2024·安徽·模拟预测)2023年12月19日至20日，中央农村工作会议在北京召开，习近平主席对“三农”工作作出指示．某地区为响应习近平主席的号召，积极发展特色农业，建设蔬菜大棚．如图所示的七面体ABG-CDEHF是一个放置在地面上的蔬菜大棚钢架，四边形ABCD是矩形，AB=8m，AD=4m，ED=CF=1m，且ED，CF都垂直于平面ABCD，GA=GB=5m，HE=HF，平面ABG⊥平面ABCD．(1)求点H到平面ABCD的距离；(2)求平面BFHG与平面AGHE所成锐二面角的余弦值．8(2024·重庆·模拟预测)如图，ACDE为菱形，AC=BC=2，∠ACB=120°，平面ACDE⊥平面ABC，点F在AB上，且AF=2FB，M，N分别在直线CD，AB上．(1)求证：CF⊥平面ACDE；(2)把与两条异面直线都垂直且相交的直线叫做这两条异面直线的公垂线，若∠EAC=60°，MN为直线CD，AB的公垂线，求ANAF的值；(3)记直线BE与平面ABC所成角为α，若tanα>217，求平面BCD与平面CFD所成角余弦值的范围．9(2024·安徽·二模)将正方形ABCD 绕直线AB 逆时针旋转90°，使得CD 到EF 的位置，得到如图所示的几何体．(1)求证：平面ACF ⊥平面BDE ；(2)点M 为DF 上一点，若二面角C -AM -E 的余弦值为13，求∠MAD ．10(2024·安徽黄山·二模)如图，已知AB 为圆台下底面圆O 1的直径，C 是圆O 1上异于A ,B 的点，D 是圆台上底面圆O 2上的点，且平面DAC ⊥平面ABC ，DA =DC =AC =2，BC =4，E 是CD 的中点，BF =2FD ．(1)证明：DO 2⎳BC ；(2)求直线DB 与平面AEF 所成角的正弦值.11(2024·黑龙江哈尔滨·一模)正四棱台ABCD -A 1B 1C 1D 1的下底面边长为22，A 1B 1=12AB ，M 为BC 中点，已知点P 满足AP =1-λ AB +12λ⋅AD +λAA 1 ，其中λ∈0,1 ．(1)求证D 1P ⊥AC ；(2)已知平面AMC 1与平面ABCD 所成角的余弦值为37，当λ=23时，求直线DP 与平面AMC 1所成角的正弦值．12(2024·辽宁·三模)如图，在三棱柱ABC -A 1B 1C 1中，侧面ACC 1A 1⊥底面ABC ,AC =AA 1=2，AB =1,BC =3，点E 为线段AC 的中点.(1)求证：AB 1∥平面BEC 1；(2)若∠A 1AC =π3，求二面角A -BE -C 1的余弦值.13(2024·广东广州·一模)如图，在四棱锥P-ABCD中，底面ABCD是边长为2的菱形，△DCP是等边三角形，∠DCB=∠PCB=π4，点M，N分别为DP和AB的中点.(1)求证：MN⎳平面PBC；(2)求证：平面PBC⊥平面ABCD；(3)求CM与平面PAD所成角的正弦值.14(2024·广东梅州·二模)如图，在四棱锥P-ABCD中，平面PAD⊥平面ABCD，底面ABCD 为直角梯形，△PAD为等边三角形，AD⎳BC，AD⊥AB，AD=AB=2BC=2．(1)求证：AD⊥PC；(2)点N在棱PC上运动，求△ADN面积的最小值；(3)点M为PB的中点，在棱PC上找一点Q，使得AM⎳平面BDQ，求PQQC的值．15(2024·广东广州·模拟预测)如图所示，圆台O1O2的轴截面A1ACC1为等腰梯形，AC=2AA1= 2A1C1=4,B为底面圆周上异于A,C的点，且AB=BC,P是线段BC的中点.(1)求证：C1P⎳平面A1AB.(2)求平面A1AB与平面C1CB夹角的余弦值.16(2024·广东深圳·二模)如图，三棱柱ABC-A1B1C1中，侧面BB1C1C⊥底面ABC，且AB= AC，A1B=A1C．(1)证明：AA1⊥平面ABC；(2)若AA1=BC=2，∠BAC=90°，求平面A1BC与平面A1BC1夹角的余弦值．17(2024·河北保定·二模)如图，在四棱锥P -ABCD 中，平面PCD 内存在一条直线EF 与AB 平行，PA ⊥平面ABCD ，直线PC 与平面ABCD 所成的角的正切值为32，PA =BC =23，CD =2AB =4.(1)证明：四边形ABCD 是直角梯形.(2)若点E 满足PE =2ED ，求二面角P -EF -B 的正弦值.18(2024·湖南衡阳·模拟预测)如图，在圆锥PO 中，P 是圆锥的顶点，O 是圆锥底面圆的圆心，AC 是圆锥底面圆的直径，等边三角形ABD 是圆锥底面圆O 的内接三角形，E 是圆锥母线PC 的中点，PO =6,AC =4.(1)求证：平面BED ⊥平面ABD ；(2)设点M 在线段PO 上，且OM =2，求直线DM 与平面ABE 所成角的正弦值.19(2024·湖南岳阳·三模)已知四棱锥P -ABCD 的底面ABCD 是边长为4的菱形，∠DAB =60°，PA =PC ，PB =PD =210，M 是线段PC 上的点，且PC =4MC ．(1)证明：PC ⊥平面BDM ；(2)点E 在直线DM 上，求BE 与平面ABCD 所成角的最大值．20(2024·湖南·二模)如图，直四棱柱ABCD -A 1B 1C 1D 1的底面是边长为2的菱形，∠ABC =60°,BD 1⊥平面A 1C 1D .(1)求四棱柱ABCD -A 1B 1C 1D 1的体积；(2)设点D 1关于平面A 1C 1D 的对称点为E ，点E 和点C 1关于平面α对称(E 和α未在图中标出)，求平面A 1C 1D 与平面α所成锐二面角的大小.21(2024·山东济南·二模)如图，在四棱锥P-ABCD中，四边形ABCD为直角梯形，AB∥CD，∠DAB=∠PCB=60°,CD=1,AB=3,PC=23，平面PCB⊥平面ABCD，F为线段BC的中点，E为线段PF上一点.(1)证明：PF⊥AD；(2)当EF为何值时，直线BE与平面PAD夹角的正弦值为74.22(2024·山东潍坊·二模)如图1，在平行四边形ABCD中，AB=2BC=4，∠ABC=60°，E为CD 的中点，将△ADE沿AE折起，连结BD，CD，且BD=4，如图2．(1)求证：图2中的平面ADE⊥平面ABCE；(2)在图2中，若点F在棱BD上，直线AF与平面ABCE所成的角的正弦值为3010，求点F到平面DEC 的距离．23(2024·福建·模拟预测)如图，在三棱锥P-ABC中，PA⊥PB,AB⊥BC,AB=3,BC=6，已知二面角P-AB-C的大小为θ，∠PAB=θ.(1)求点P到平面ABC的距离；(2)当三棱锥P-ABC的体积取得最大值时，求：(Ⅰ)二面角P-AB-C的余弦值；(Ⅱ)直线PC与平面PAB所成角.24(2024·浙江杭州·二模)如图，在多面体ABCDPQ中，底面ABCD是平行四边形，∠DAB=60°, BC=2PQ=4AB=4,M为BC的中点，PQ∥BC,PD⊥DC,QB⊥MD．(1)证明：∠ABQ=90°；(2)若多面体ABCDPQ的体积为152，求平面PCD与平面QAB夹角的余弦值．25(2024·浙江嘉兴·二模)在如图所示的几何体中，四边形ABCD为平行四边形，PA⊥平面ABCD,PA∥QD，BC=2AB=2PA=2,∠ABC=60°.(1)证明：平面PCD⊥平面PAC；(2)若PQ=22，求平面PCQ与平面DCQ夹角的余弦值.26(2024·浙江绍兴·二模)如图，在三棱锥P-ABC中，AB=4，AC=2，∠CAB=60°，BC⊥AP.(1)证明：平面ACP⊥平面ABC；(2)若PA=2，PB=4，求二面角P-AB-C的平面角的正切值.27(2024·河北沧州·一模)如图，在正三棱锥A -BCD 中，BC =CD =BD =4，点P 满足AP=λAC ，λ∈(0,1)，过点P 作平面α分别与棱AB ，BD ，CD 交于Q ，S ，T 三点，且AD ⎳α，BC ⎳α.(1)证明：∀λ∈(0,1)，四边形PQST 总是矩形；(2)若AC =4，求四棱锥C -PQST 体积的最大值.28(2024·湖北·二模)如图1．在菱形ABCD 中，∠ABC =120°，AB =4，AE =λAD ，AF =λAB(0<λ<1)，沿EF 将△AEF 向上折起得到棱锥P -BCDEP ．如图2所示，设二面角P -EF -B 的平面角为θ．(1)当λ为何值时，三棱锥P -BCD 和四棱锥P -BDEF 的体积之比为95(2)当θ为何值时，∀λ∈0,1 ，平面PEF 与平面PFB 的夹角φ的余弦值为5529(2024·湖北·模拟预测)空间中有一个平面α和两条直线m ，n ，其中m ，n 与α的交点分别为A ，B ，AB =1，设直线m 与n 之间的夹角为π3，(1)如图1，若直线m ，n 交于点C ，求点C 到平面α距离的最大值；(2)如图2，若直线m ，n 互为异面直线，直线m 上一点P 和直线n 上一点Q 满足PQ ⎳α，PQ ⊥n 且PQ ⊥m ，(i )求直线m ，n 与平面α的夹角之和；(ii )设PQ =d 0<d <1 ，求点P 到平面α距离的最大值关于d 的函数f d ．30(2024·浙江绍兴·模拟预测)如图所示，四棱台ABCD -A 1B 1C 1D 1，底面ABCD 为一个菱形，且∠BAD =120°. 底面与顶面的对角线交点分别为O ，O 1. AB =2A 1B 1=2，BB 1=DD 1=392，AA 1与底面夹角余弦值为3737.(1)证明：OO 1⊥平面ABCD ；(2)现将顶面绕OO 1旋转θ角，旋转方向为自上而下看的逆时针方向. 此时使得底面与DC 1的夹角正弦值为64343，此时求θ的值(θ<90°)；(3)求旋转后AA 1与BB 1的夹角余弦值.大题 立体几何1(2024·黑龙江·二模)如图，已知正三棱柱ABC -A 1B 1C 1的侧棱长和底面边长均为2，M 是BC 的中点，N 是AB 1的中点，P 是B 1C 1的中点．(1)证明：MN ⎳平面A 1CP ；(2)求点P 到直线MN 的距离．【答案】(1)证明见解析(2)3【分析】(1)建立如图空间直角坐标系A -xyz ，设平面A 1CP 的一个法向量为n=(x ,y ,z )，利用空间向量法证明MN ⋅n=0即可；(2)利用空间向量法即可求解点线距.【详解】(1)由题意知，AA 1⊥平面ABC ，∠BAC =60°，而AB ⊂平面ABC ，所以AA 1⊥AB ，在平面ABC 内过点A 作y 轴，使得AB ⊥y 轴，建立如图空间直角坐标系A -xyz ，则A (0,0,0),B (2,0,0),C (1,3,0),A 1(0,0,2),B 1(2,0,2)，得M 32,32,0,N (1,0,1),P 32,32,2，所以A 1C =(1,3,-2),A 1P =32,32,0 ,MN =-12,-32,1 ，设平面A1CP 的一个法向量为n=(x ,y ,z )，则n ⋅A 1C=x +3y -2z =0n ⋅A 1P =32x +32y =0，令x =1，得y =-3,z =-1，所以n=(1,-3,-1)，所以MN ⋅n =-12×1+-32×(-3)+1×(-1)=0，又MN 不在平面A 1CP 内即MN ⎳平面A 1CP ；(2)如图，连接PM ，由(1)得PM =(0,0,-2)，则MN ⋅PM =-2，MN =2,PM =2，所以点P 到直线MN 的距离为d =PM 2-MN ⋅PMPM2= 3.2(2024·安徽合肥·二模)如图，在四棱锥P -ABCD 中，底面ABCD 是边长为2的菱形，∠BAD =60°,M 是侧棱PC 的中点，侧面PAD 为正三角形，侧面PAD ⊥底面ABCD ．(1)求三棱锥M -ABC 的体积；(2)求AM 与平面PBC 所成角的正弦值．【答案】(1)12(2)3311．【分析】(1)作出辅助线，得到线线垂直，进而得到线面垂直，由中位线得到M 到平面ABCD 的距离为32，进而由锥体体积公式求出答案；(2)证明出BO ⊥AD ，建立空间直角坐标系，求出平面的法向量，进而由法向量的夹角余弦值的绝对值求出线面角的正弦值.【详解】(1)如图所示，取AD 的中点O ，连接PO ．因为△PAD 是正三角形，所以PO ⊥AD ．又因为平面PAD ⊥底面ABCD ,PO ⊂平面PAD ，平面PAD ∩平面ABCD =AD ，所以PO ⊥平面ABCD ，且PO =3．又因为M 是PC 的中点，M 到平面ABCD 的距离为32，S △ABC =12×2×2×sin 2π3=3，所以三棱锥M -ABC 的体积为13×3×32=12．(2)连接BO ,BD ，因为∠BAD =π3，所以△ABD 为等边三角形，所以BO ⊥AD ，以O 为原点，OA ,OB ,OP 所在直线分别为x 轴，y 轴，z 轴，建立如图所示的空间直角坐标系，则P 0,0,3 ,A 1,0,0 ,B 0,3,0 ,C -2,3,0 ，所以M -1,32,32 ,AM =-2,32,32,PB =0,3,-3 ,BC =-2,0,0 ．设平面PBC 的法向量为n=x ,y ,z ，则PB ⋅n =0BC ⋅n =0，即3y -3z =0-2x =0 ，解得x =0，取z =1，则y =1，所以n=0,1,1 ．设AM 与平面PBC 所成角为θ，则sin θ=cos AM ,n =AM ⋅nAM ⋅n=-2,32,32 ⋅0,1,14+34+34×1+1=3311．即AM 与平面PBC 所成角的正弦值为3311．3(2023·福建福州·模拟预测)如图，在三棱柱ABC -A 1B 1C 1中，平面AA 1C 1C ⊥平面ABC ,AB =AC =BC =AA 1=2，A 1B =6．(1)设D 为AC 中点，证明：AC ⊥平面A 1DB ；(2)求平面A 1AB 1与平面ACC 1A 1夹角的余弦值．【答案】(1)证明见解析；(2)55【分析】(1)根据等边三角形的性质得出BD ⊥AC ，根据平面ACC 1A 1⊥平面ABC 得出BD ⊥平面ACC 1A 1，BD ⊥A 1D ，利用勾股定理得出AC ⊥A 1D ，从而证明AC ⊥平面A 1DB ；(2)建立空间直角坐标系，利用坐标表示向量，求出平面A 1AB 1的法向量和平面ACC 1A 1的一个法向量，利用向量求平面A 1AB 1与平面ACC 1A 1的夹角余弦值．【详解】(1)证明：因为D 为AC 中点，且AB =AC =BC =2，所以在△ABC 中，有BD ⊥AC ，且BD =3，又平面ACC 1A 1⊥平面ABC ，且平面ACC 1A 1∩平面ABC =AC ，BD ⊂平面ABC ,所以BD ⊥平面ACC 1A 1，又A 1D ⊂平面ACC 1A 1，则BD ⊥A 1D ，由A 1B =6，BD =3，得A 1D =3，因为AD =1，AA 1=2，A 1D =3，所以由勾股定理，得AC ⊥A 1D ，又AC ⊥BD ，A 1D ∩BD =D ,A 1D ,BD ⊂平面A 1DB ，所以AC ⊥平面A 1DB ；(2)如图所示，以D 为原点，建立空间直角坐标系D -xyz ，可得A (1,0,0),A 1(0,0,3),B (0,3,0)，则AA 1 =-1,0,3 ,AB=-1,3,0 ，设平面A 1AB 1的法向量为n=(x ,y ,z )，由n ⋅AA 1=-x +3z =0n ⋅AB=-x +3y =0，令x =3，得y =1，z =1，所以n=3,1,1 ,由(1)知，BD ⊥平面ACC 1A 1，所以平面ACC 1A 1的一个法向量为BD=(0,-3,0)，记平面A 1AB 1与平面ACC 1A 1的夹角为α，则cos α=|n ⋅BD ||n ||BD |=35×3=55，所以平面A 1AB 1与平面ACC 1A 1夹角的余弦值为55．4(2024·山西晋中·三模)如图，在六面体ABCDE 中，BC =BD =6，EC ⊥ED ，且EC =ED =2，AB 平行于平面CDE ，AE 平行于平面BCD ，AE ⊥CD .(1)证明：平面ABE ⊥平面CDE ；(2)若点A 到直线CD 的距离为22，F 为棱AE 的中点，求平面BDF 与平面BCD 夹角的余弦值．【答案】(1)证明见解析(2)10535【分析】(1)设平面ABE 与直线CD 交于点M ，使用线面平行的性质，然后用面面垂直的判定定理即可；(2)证明BE ⊥平面CDE ，然后构造空间直角坐标系，直接用空间向量方法即可得出结果.【详解】(1)设平面ABE 与直线CD 交于点M ，连接ME ,MB ，则平面ABE 与平面CDE 的交线为ME ，平面ABE 与平面BCD 的交线为MB ，因为AB 平行于平面CDE ，AB ⊂平面ABE ，平面ABE 和平面CDE 的交线为ME ，所以AB ∥ME ．同理AE ∥MB ，所以四边形ABME 是平行四边形，故AE ∥MB ，AB ∥ME .因为CD ⊥AE ，AE ∥MB ，所以CD ⊥MB ，又BC =BD =6，所以M 为棱CD 的中点在△CDE 中，EC =ED ，MC =MD ，所以CD ⊥ME ，由于AB ∥ME ，故CD ⊥AB .而CD ⊥AE ，AB ∩AE =A ，AB ,AE ⊂平面ABE ，所以CD ⊥平面ABE ，又CD ⊂平面CDE ，所以平面ABE ⊥平面CDE .(2)由(1)可知，CD ⊥平面ABME ，又AM ⊂平面ABME ，所以CD ⊥AM .而点A 到直线CD 的距离为22，故AM =2 2.在等腰直角三角形CDE 中，由EC =ED =2,得CD =2,MC =MD =ME =1.在等腰三角形BCD 中，由MC =MD =1，BC =BD =6，得BM = 5.在平行四边形ABME 中，AE =BM =5，AB =EM =1，AM =22，由余弦定理得cos ∠MEA =EM 2+AE 2-AM 22EM ·AE=-55，所以cos ∠BME =55，所以BE =BM 2+EM 2-2BM ·EM cos ∠BME =2.因为BE 2+ME 2=22+12=5 2=BM 2，所以BE ⊥ME .因为平面ABME ⊥平面CDE ，平面ABME 和平面CDE 的交线为ME ，BE 在平面ABME 内.所以BE ⊥平面CDE .如图，以E 为坐标原点，EC ,ED ,EB 分别为x ,y ,z 轴正方向，建立空间直角坐标系.则E 0,0,0 ,C 2,0,0 ,D 0,2,0 ,B 0,0,2 ,A -22,-22,2 ,F -24,-24,1.所以CD =-2,2,0 ,DB =0,-2,2 ,FB =24,24,1 .设平面BCD 的法向量为m=x 1,y 1,z 1 ，则m ⋅CD=0m ⋅DB =0，即-2x 1+2y 1=0-2y 1+2z 1=0 .则可取x 1=2，得m=2,2,2 .设平面BDF 的法向量为n =x 2,y 2,z 2 ，则n ⋅FB =0n ⋅DB=0，即24x 2+24y 2+z 2=0-2y 2+2z 2=0.取z 2=1，则n=-32,2,1 ．设平面BDF 与平面BCD 的夹角为θ，则cos θ=m ⋅n m ⋅n =-3210×21=10535.所以平面BDF 与平面BCD 夹角的余弦值为10535.5(2024·辽宁·二模)棱长均为2的斜三棱柱ABC -A 1B 1C 1中，A 1在平面ABC 内的射影O 在棱AC 的中点处，P 为棱A 1B 1(包含端点)上的动点．(1)求点P 到平面ABC 1的距离；(2)若AP ⊥平面α，求直线BC 1与平面α所成角的正弦值的取值范围．【答案】(1)23913；(2)25,104.【分析】(1)以O 为原点建立空间直角坐标系，求出平面ABC 1的法向量，再利用点到平面距离的向量求法求解即得.(2)由向量共线求出向量AP的坐标，再利用线面角的向量求法列出函数关系，并求出函数的值域即可.【详解】(1)依题意，A 1O ⊥平面ABC ，OB ⊥AC (底面为正三角形)，且A 1O =OB =3，以O 为原点，OB ,OC ,OA 1的方向分别为x ,y ,z 轴的正方向，建立空间直角坐标系，如图，则O (0,0,0),A (0,-1,0),B (3,0,0),C (0,1,0),A 1(0,0,3),C 1(0,2,3)，AC 1 =(0,3,3)，BC 1 =(-3,2,3)，AA 1 =(0,1,3)，由A 1B 1⎳AB ，A 1B 1⊄平面ABC 1，AB ⊂平面ABC 1，则A 1B 1⎳平面ABC 1，即点P 到平面ABC 1的距离等于点A 1到平面ABC 1的距离，设n =(x ,y ,z )为平面ABC 1的一个法向量，由n ⋅AC 1=3y +3z =0n ⋅BC 1=-3x +2y +3z =0，取z =3，得n=(1,-3,3)，因此点A 1到平面ABC 1的距离d =|AA 1 ⋅n||n |=2313=23913，所以点P 到平面ABC 1的距离为23913．(2)设A 1P =λA 1B 1 ，λ∈[0,1]，则AP =AA 1 +A 1P =AA 1 +λAB=(0,1,3)+λ(3,1,0)=(3λ,1+λ,3)，由AP ⊥α，得AP为平面α的一个法向量，设直线BC 1与平面α所成角为θ，则sin θ=|cos ‹BC 1 ,AP ›|=|BC 1 ⋅AP||BC 1 ||AP |=|5-λ|10⋅3λ2+(1+λ)2+3=5-λ25⋅2λ2+λ+2，令t =5-λ，则λ=5-t ，t ∈[4,5]，则sin θ=t 25⋅2(5-t )2+(5-t )+2=t25⋅2t 2-21t +57=125⋅2-21t+57t 2=125571t-7382+576，由t ∈[4,5]，得1t ∈15,14 ，于是571t -738 2+576∈225,516，25⋅571t -738 2+576∈2105,52 ，则sin θ∈25,104，所以直线BC 1与平面α所成角的正弦值的取值范围是25,104.6(2024·重庆·模拟预测)在如图所示的四棱锥P -ABCD 中，已知AB ∥CD ，∠BAD =90°，CD =2AB ，△PAB 是正三角形，点M 在侧棱PB 上且使得PD ⎳平面AMC ．(1)证明：PM =2BM ；(2)若侧面PAB ⊥底面ABCD ，CM 与底面ABCD 所成角的正切值为311，求二面角P -AC -B 的余弦值．【答案】(1)证明见解析；(2)1010．【分析】(1)连接BD 与AC 交于点E ，连接EM ，由已知得AB CD=EBED ，由线面平行的性质得PD ∥EM ，根据三角形相似可得EB ED =BM PM=12，即PM =2BM(2)设AB 的中点O ，首先由已知得PO ⊥底面ABCD ，在△PAB 中过点M 作MF ∥PO 交AB 于点F ，得MF ⊥底面ABCD ，则∠MCF 为CM 与底面ABCD 所成角，在底面ABCD 上过点O 作OG ⊥AC 于点G ，则∠PGO 是二面角P -AC -B 的平面角，根据条件求解即可【详解】(1)证明：连接BD 与AC 交于点E ，连接EM ，在△EAB 与△ECD 中，∵AB ∥CD ，∴AB CD=EBED ，由CD =2AB ，得ED =2EB ，又∵PD ⎳平面AMC ，而平面PBD ∩平面AMC =ME ，PD ⊂平面PBD ，∴PD ∥EM ，∴在△PBD 中，EB ED =BM PM=12，∴PM =2BM ；(2)设AB 的中点O ，在正△PAB 中，PO ⊥AB ，而侧面PAB ⊥底面ABCD ，侧面PAB ∩底面ABCD =AB ，且PO ⊂平面PAB ，∴PO ⊥底面ABCD ，在△PAB 中过点M 作MF ⎳PO 交AB 于点F ，∴MF ⊥底面ABCD ，∴∠MCF 为CM 与底面ABCD 所成角，∴MF CF=311，设AB =6a ，则MF=3a，∴CF=11a，BF=MF3=a，则在直角梯形ABCD中，AF=5a，而CD=12a，则AD=11a2-12a-5a2=62a，在底面ABCD上过点O作OG⊥AC于点G，则∠PGO是二面角P-AC-B的平面角，易得OA=3a，AC=66a，在梯形ABCD中，由OAOG=ACAD⇒3aOG=66a62a，得OG=3a，在Rt△POG中，PG=30a，∴cos∠PGO=OGPG=1010．7(2024·安徽·模拟预测)2023年12月19日至20日，中央农村工作会议在北京召开，习近平主席对“三农”工作作出指示．某地区为响应习近平主席的号召，积极发展特色农业，建设蔬菜大棚．如图所示的七面体ABG-CDEHF是一个放置在地面上的蔬菜大棚钢架，四边形ABCD是矩形，AB=8m，AD=4m，ED=CF=1m，且ED，CF都垂直于平面ABCD，GA=GB=5m，HE=HF，平面ABG⊥平面ABCD．(1)求点H到平面ABCD的距离；(2)求平面BFHG与平面AGHE所成锐二面角的余弦值．【答案】(1)4(2)413【分析】(1)取AB,CD的中点M,N，证得平面ADE⎳平面MNHG，得到AE⎳GH，再由平面ABG⎳平面CDEHG，证得AG⎳EH，得到平行四边形AGHE，得到GH=AE，求得HN=4，结合HN⊥平面ABCD，即可求解；(2)以点N为原点，建立空间直角坐标系，分别求得平面BFHG和平面AGHE的法向量n =(1,3,4)和m =(1,-3,4)，结合向量的夹角公式，即可求解.【详解】(1)如图所示，取AB,CD的中点M,N，连接GM,MN,HN，因为GA=GB，可得GM⊥AB，又因为平面ABG⊥平面ABCD，且平面ABG∩平面ABCD=AB，GM⊂平面ABG，所以GM⊥平面ABCD，同理可得：HN⊥平面ABCD，因为ED⊥平面ABCD，所以ED⎳HN，又因为ED⊄平面MNHG，HN⊂平面MNHG，所以ED⎳平面MNHG，因为MN⎳AD，且AD⊄平面MNHG，MN⊂平面MNHG，所以AD⎳平面MNHG，又因为AD∩DE=D，且AD,DE⊂平面ADE，所以平面ADE⎳平面MNHG，因为平面AEHG与平面ADE和平面MNHG于AE,GH，可得AE⎳GH，又由GM⎳HN，AB⎳CD，且AB∩GM=M和CD∩HN=N，所以平面ABG⎳平面CDEHG，因为平面AEHG与平面ABG和平面CDEHF于AG,EH，所以AG⎳EH，可得四边形AGHE 为平行四边形，所以GH =AE ，因为AE =AD 2+DE 2=42+12=17，所以GH =17，在直角△AMG ，可得GM =GB 2-AB 22=52-42=3，在直角梯形GMNH 中，可得HN =3+17-42=4，因为HN ⊥平面ABCD ，所以点H 到平面ABCD 的距离为4.(2)解：以点N 为原点，以NM ,NC ,NH 所在的直线分别为x ,y ,z 轴，建立空间直角坐标系，如图所示，则E (0,-4,1),F (0,4,1),G (4,0,3),H (0,0,4)，可得HE =(0,-4,-3),HF =(0,4,-3),HG=(4,0,-1)，设平面BFHG 的法向量为n=(x ,y ,z )，则n ⋅HG=4x -z =0n ⋅HF=4y -3z =0，取z =4，可得x =1,y =3，所以n=(1,3,4)，设平面AGHE 的法向量为m=(a ,b ,c )，则m ⋅HG=4a -c =0m ⋅HE=-4b -3c =0，取c =4，可得a =1,b =-3，所以m=(1,-3,4)，则cos m ,n =m ⋅n m n=1-9+161+9+16⋅1+9+16=413，即平面BFHG 与平面AGHE 所成锐二面角的余弦值413.8(2024·重庆·模拟预测)如图，ACDE 为菱形，AC =BC =2，∠ACB =120°，平面ACDE ⊥平面ABC ，点F 在AB 上，且AF =2FB ，M ，N 分别在直线CD ，AB 上．(1)求证：CF ⊥平面ACDE ；(2)把与两条异面直线都垂直且相交的直线叫做这两条异面直线的公垂线，若∠EAC =60°，MN 为直线CD ，AB 的公垂线，求ANAF的值；(3)记直线BE 与平面ABC 所成角为α，若tan α>217，求平面BCD 与平面CFD 所成角余弦值的范围．【答案】(1)证明见解析(2)AN AF=913(3)528,255 【分析】(1)先通过余弦定理及勾股定理得到CF ⊥AC ，再根据面面垂直的性质证明；(2)以C 为原点，CA 的方向为x 轴正方向，建立如图所示空间直角坐标系C -xyz ，利用向量的坐标运算根据MN ⋅CD =0MN ⋅AF =0，列方程求解即可；(3)利用向量法求面面角，然后根据tan α>217列不等式求解.【详解】(1)AB 2=AC 2+BC 2-2AC ⋅BC ⋅cos ∠ACB =12，AB =23，AF =2FB ，所以AF =433，CF=13CA +23CB ，CF 2=19CA 2+49CB 2+49CA ⋅CB =43，AC 2+CF 2=4+43=163=AF 2，则CF ⊥AC ，又因为平面ACDE ⊥平面ABC ，平面ACDE ∩平面ABC =AC ，CF ⊂面ABC ，故CF ⊥平面ACDE ；(2)以C 为原点，CA 的方向为x 轴正方向，建立如图所示空间直角坐标系C -xyz ，由∠EAC =60°，可得∠DCA =120°，DC =2，所以C 0,0,0 ,D -1,0,3 ,A 2,0,0 ,F 0,233,0 所以AF =-2,233,0 ，CD =-1,0,3 ，设AN =λAF =-2λ,233λ,0 ，则N 2-2λ,233λ,0 ，设CM =μCD ，则M -μ,0,3μ ，MN =2-2λ+μ,233λ,-3μ ，由题知，MN ⋅CD=0MN ⋅AF =0 ⇒2λ-2-μ-3μ=04λ-4-2μ+43λ=0 ，解得λ=913，μ=-213，故AN AF=913；(3)B -1,3,0 ，设∠EAC =θ，则E 2-2cos θ,0,2sin θ ，BE=3-2cos θ,-3,2sin θ ，可取平面ABC 的法向量n=0,0,1 ，则sin α=cos n ,BE=n ⋅BEn ⋅BE =2sin θ 3-2cos θ 2+3+4sin 2θ=sin θ4-3cos θ，cos α=4-3cos θ-sin 2θ4-3cos θ，则tan α=sin θ4-3cos θ-sin 2θ>217，整理得10cos 2θ-9cos θ+2<0，故cos θ∈25,12，CF =0,23,0，CD =-2cos θ,0,2sin θ ，CB =-1,3,0 ，记平面CDF 的法向量为n 1 =x ,y ,z ，则有n 1 ⋅CD =0n 1 ⋅CF =0 ⇒-2x cos θ+2z sin θ=023y =0，可得n 1=sin θ,0,cos θ ，记平面CBD 的法向量为n 2 =a ,b ,c ，则有n 2 ⋅CD=0n 2 ⋅CB =0 ⇒-2a cos θ+2c sin θ=0-a +3b =0，可得n 2=3sin θ,sin θ,3cos θ ，记平面BCD 与平面CFD 所成角为γ，则cos γ=cos n 1 ,n 2 =33+sin 2θ，cos θ∈25,12 ，所以sin 2θ∈34,2125 ，3+sin 2θ∈152,465 ，故cos γ=33+sin 2θ∈528,255 ．9(2024·安徽·二模)将正方形ABCD 绕直线AB 逆时针旋转90°，使得CD 到EF 的位置，得到如图所示的几何体．(1)求证：平面ACF ⊥平面BDE ；(2)点M 为DF上一点，若二面角C -AM -E 的余弦值为13，求∠MAD ．【答案】(1)证明见解析(2)∠MAD =45°【分析】(1)根据面面与线面垂直的性质可得BD ⊥AF ，结合线面、面面垂直的判定定理即可证明；(2)建立如图空间直角坐标系，设∠MAD =α，AB =1，利用空间向量法求出二面角C -AM -E 的余弦值，建立方程1-sin αcos α1+sin 2α1+cos 2α=13，结合三角恒等变换求出α即可.【详解】(1)由已知得平面ABCD ⊥平面ABEF ，AF ⊥AB ，平面ABCD ∩平面ABEF =AB ，AF ⊂平面ABEF ，所以AF ⊥平面ABCD ，又BD ⊂平面ABCD ，故BD ⊥AF ，因为ABCD 是正方形，所以BD ⊥AC ，AC ，AF ⊂平面ACF ，AC ∩AF =A ，所以BD ⊥平面ACF ，又BD ⊂平面BDE ，所以平面ACF ⊥平面BDE .(2)由(1)知AD ，AF ，AB 两两垂直，以AD ，AF ，AB 所在直线分别为x ，y ，z 轴，建立空间直角坐标系，如图.设∠MAD =α，AB =1，则A 0,0,0 ，M cos α,sin α,0 ，C 1,0,1 ，E 0,1,1 ，故AM =cos α,sin α,0 ，AC =1,0,1 ，AE =0,1,1设平面AMC 的法向量为m =x 1,y 1,z 1 ，则m ⋅AC =0，m ⋅AM=0故x 1+z 1=0x 1cos α+y 1sin α=0，取x 1=sin α，则y 1=-cos α，z 1=-sin α所以m=sin α,-cos α,-sin α设平面AME 的法向量为n =x 2,y 2,z 2 ，n ⋅AE =0，n ⋅AM=0故y 2+z 2=0x 2cos α+y 2sin α=0，取x 2=sin α，则y 2=-cos α，z 2=cos α所以n=sin α,-cos α,cos α ，所以cos m ,n =1-sin αcos α1+sin 2α1+cos 2α，由已知得1-sin αcos α1+sin 2α1+cos 2α=13，化简得：2sin 22α-9sin2α+7=0，解得sin2α=1或sin2α=72(舍去)故α=45°，即∠MAD =45°.10(2024·安徽黄山·二模)如图，已知AB 为圆台下底面圆O 1的直径，C 是圆O 1上异于A ,B 的点，D 是圆台上底面圆O 2上的点，且平面DAC ⊥平面ABC ，DA =DC =AC =2，BC =4，E 是CD 的中点，BF =2FD ．(1)证明：DO 2⎳BC ；(2)求直线DB 与平面AEF 所成角的正弦值.【答案】(1)证明见解析(2)68585【分析】(1)取AC 的中点O ，根据面面垂直的性质定理，可得DO ⊥平面ABC ，即可求证DO 2⎳OO 1，进而可证矩形，即可根据线线平行以及平行的传递性求解.(2)建系，利用向量法，求解法向量n =1,-12,3 与方向向量DB =(-1,4,-3)的夹角，即可求解．【详解】(1)证明：取AC 的中点为O ，连接DO ，OO 1，O 1O 2，∵DA =DC ，O 为AC 中点，∴DO ⊥AC ，又平面DAC ⊥平面ABC ，且平面DAC ∩平面ABC =AC ，DO ⊂平面DAC ,∴DO ⊥平面ABC ，∴DO ⎳O 1O 2，DO =O 1O 2，故四边形DOO 1O 2为矩形，∴DO 2⎳OO 1，又O ，O 1分别是AC ，AB 的中点，∴OO 1⎳BC ，∴DO 2⎳BC ；(2)∵C 是圆O 1上异于A ，B 的点，且AB 为圆O 1的直径，∴BC ⊥AC ，∴OO 1⊥AC ，∴如图以O 为原点建立空间直角坐标系，由条件知DO =3，∴A (1,0,0),B (-1,4,0),C (-1,0,0),D (0,0,3)，∴E -12,0,32 ，设F (x ,y ,z )，∴BF =(x +1,y -4,z )，FD=(-x ,-y ,3-z )，由BF =2FD ，得F -13,43,233 ，∴AF =-43,43,233 ，∴DB =(-1,4,-3)，AE =-32,0,32 ，设平面AEF 法向量为n=(x 1,y 1,z 1)，则n ⋅AE=-32x 1+32z 1=0n ⋅AF =-43x 1+43y 1+233z 1=0，取n =1,-12,3 ，设直线BD 与平面AEF 所成角为θ，则sin θ=|cos <n ,DB>|=625⋅172=68585∴直线BD 与平面AEF 所成角的正弦值为68585．11(2024·黑龙江哈尔滨·一模)正四棱台ABCD -A 1B 1C 1D 1的下底面边长为22，A 1B 1=12AB ，M 为BC 中点，已知点P 满足AP =1-λ AB +12λ⋅AD +λAA 1，其中λ∈0,1 ．(1)求证D 1P ⊥AC ；(2)已知平面AMC 1与平面ABCD 所成角的余弦值为37，当λ=23时，求直线DP 与平面AMC 1所成角的正弦值．【答案】(1)证明见解析(2)241391【分析】(1)方法一运用空间向量的线性运算，进行空间位置关系的向量证明即可.方法二：建立空间直角坐标系，进行空间位置关系的向量证明即可.(2)建立空间直角坐标系，利用线面角的向量求法求解即可.【详解】(1)方法一：∵A 1B 1=12AB ，∴AA 1 ⋅AB =AA 1 ⋅AD =22×22=2．∵D 1A =-12AD-AA 1∴D 1P =D 1A +AP =1-λ AB +12λ-12AD+λ-1 AA 1∴D 1P ⋅AC =1-λ AB +12λ-12AD +λ-1 AA 1 ⋅AB +AD =1-λ AB 2+12λ-12 AD2+λ-1 AB ⋅AA 1 +λ-1 AD ⋅AA 1=81-λ +812λ-12+4λ-1 =0．∴D 1P ⊥AC ，即D 1P ⊥AC ．方法二：以底面ABCD 的中心O 为原点，以OM 方向为y 轴，过O 点平行于AD 向前方向为x 轴，以过点O 垂直平面ABCD 向上方向为z 轴，建立如图所示空间直角坐标系，设正四棱台的高度为h ，则有 A 2,-2,0 ，B 2,2,0 ，C -2,2,0 ，D -2,-2,0 ，A 122,-22,h ，C 1-22,22,h ，D 1-22,-22,h ，M 0,2,0 ，AC =-22,22,0AP =1-λ 0,22,0 +12λ-22,0,0 +λ-22,22,0 =-322λ,22-322λ,λhD 1A =322,-22,-h ，D 1P =D 1A +AP =-322λ+322,-322λ+322,λh -h ．故AC ⋅D 1P=0，所以D 1P ⊥AC ．(2)设平面ABCD 的法向量为n=0,0,1 ，设平面AMC 1的法向量为m =x ,y ,z ，AM =-2,22,0 ，AC 1 =-322,322,h ，则有AM ⋅m=0AC 1 ⋅m=0 ，即-2x +22y =0-322x +322y +hz =0，令x =22h ，则m=22h ,2h ,3 ．又题意可得cos m ,n =38h 2+2h 2+9=37，可得h =2．因为λ=23，经过计算可得P 0,0,43 ，D 1-22,-22,2 ，D 1P =2,2,43．将h =2代入，可得平面AMC 1的法向量m=42,22,3 ．设直线DP 与平面AMC 1所成角的为θsin θ=cos DP ,m =8+4+42+2+16932+8+9=241391．12(2024·辽宁·三模)如图，在三棱柱ABC -A 1B 1C 1中，侧面ACC 1A 1⊥底面ABC ,AC =AA 1=2，AB =1,BC =3，点E 为线段AC 的中点.(1)求证：AB 1∥平面BEC 1；(2)若∠A 1AC =π3，求二面角A -BE -C 1的余弦值.【答案】(1)证明见详解(2)-22【分析】(1)连接BC 1，交B 1C 于点N ，连接NE ，利用线面平行的判定定理证明；(2)由已知可知，△AA 1C 为等边三角形，故A 1E ⊥AC ，利用面面垂直的性质定理可证得A 1E ⊥底面ABC ，进而建立空间直角坐标系，利用向量法即可求二面角余弦值.【详解】(1)连接BC 1，交B 1C 于点N ，连接NE ，因为侧面BCC 1B 1是平行四边形，所以N 为B 1C 的中点，又因为点E 为线段AC 的中点，所以NE ⎳AB 1，因为AB 1⊄面BEC 1，NE ⊂面BEC 1，所以AB 1⎳面BEC 1.(2)连接A 1C ，A 1E ，因为∠A 1AC =π3，AC =AA 1=2，所以△AA 1C 为等边三角形，A 1C =2，因为点E 为线段AC 的中点，所以A 1E ⊥AC ，因为侧面ACC 1A 1⊥底面ABC ，平面ACC 1A 1∩平面ABC =AC ，A 1E ⊂平面ACC 1A 1，所以A 1E ⊥底面ABC ，过点E 在底面ABC 内作EF ⊥AC ，如图以E 为坐标原点，分布以EF ，EC ，EA 1 的方向为x ,y ,z 轴正方向建立空间直角坐标系，则E 0,0,0 ，B 32,-12,0 ，C 10,2,3 ，所以EB =32,-12,0 ，EC 1 =0,2,3 ，设平面BEC 1的法向量为m=x ,y ,z ，则m ⋅EB =32x -12y =0m ⋅EC 1=2y +3z =0，令x =1，则y =3,z =-2，所以平面BEC 1的法向量为m=1,3,-2 ，又因为平面ABE 的法向量为n=0,0,1 ，则cos m ,n =-21+3+4=-22，经观察，二面角A -BE -C 1的平面角为钝角，所以二面角A -BE -C 1的余弦值为-22.13(2024·广东广州·一模)如图，在四棱锥P -ABCD 中，底面ABCD 是边长为2的菱形，△DCP 是等边三角形，∠DCB =∠PCB =π4，点M ，N 分别为DP 和AB 的中点.(1)求证：MN ⎳平面PBC ；(2)求证：平面PBC ⊥平面ABCD ；(3)求CM 与平面PAD 所成角的正弦值.【答案】(1)证明见解析；(2)证明见解析；(3)33.【分析】(1)取PC 中点E ，由已知条件，结合线面平行的判断推理即得.(2)过P 作PQ ⊥BC 于点Q ，借助三角形全等，及线面垂直的判定、面面垂直的判定推理即得.(3)建立空间直角坐标系，利用线面角的向量求法求解即得.【详解】(1)取PC 中点E ，连接ME ,BE ，由M 为DP 中点，N 为AB 中点，得ME ⎳DC ,ME =12DC ，又BN ⎳CD ,BN =12CD ，则ME ⎳BN ,ME =BN ，因此四边形BEMN 为平行四边形，于是MN ⎳BE ，而MN ⊄平面PBC ,BE ⊂平面PBC ，所以MN ⎳平面PBC .(2)过P 作PQ ⊥BC 于点Q ，连接DQ ，由∠DCB =∠PCB =π4,CD =PC ,QC =QC ，得△QCD ≌△QCP ，则∠DQC =∠PQC =π2，即DQ ⊥BC ，而PQ =DQ =2,PQ 2+DQ 2=4=PD 2，因此PQ ⊥DQ ，又DQ ∩BC =Q ,DQ ,BC ⊂平面ABCD ，则PQ ⊥平面ABCD ，PQ ⊂平面PBC ，所以平面PBC ⊥平面ABCD .(3)由(2)知，直线QC ,QD ,QP 两两垂直，以点Q 为原点，直线QC ,QD ,QP 分别为x ,y ,z 轴建立空间直角坐标系，则C (2,0,0),P (0,0,2),D (0,2,0),M 0,22,22,A (-2,2,0)，CM =-2,22,22,AD =(2,0,0),DP =(0,-2,2)，设平面PAD 的一个法向量n =(x ,y ,z )，则n ⋅AD=2x =0n ⋅DP=-2y +2z =0，令y =1，得n=(0,1,1)，设CM 与平面PAD 所成角为θ，sin θ=|cos ‹CM ,n ›|=|CM ⋅n||CM ||n |=23⋅2=33，所以CM 与平面PAD 所成角的正弦值是33.14(2024·广东梅州·二模)如图，在四棱锥P -ABCD 中，平面PAD ⊥平面ABCD ，底面ABCD 为直角梯形，△PAD 为等边三角形，AD ⎳BC ，AD ⊥AB ，AD =AB =2BC =2．(1)求证：AD ⊥PC ；(2)点N 在棱PC 上运动，求△ADN 面积的最小值；(3)点M 为PB 的中点，在棱PC 上找一点Q ，使得AM ⎳平面BDQ ，求PQQC的值．【答案】(1)证明见解析(2)2217(3)4【分析】(1)取AD 的中点H ，连接PH ，CH ，依题意可得四边形ABCH 为矩形，即可证明CH ⊥AD ，再由PH ⊥AD ，即可证明AD ⊥平面PHC ，从而得证；(2)连接AC 交BD 于点G ，连接MC 交BQ 于点F ，连接FG ，即可得到CG AG=12，再根据线面平行的性质得到CF FM =12，在△PBC 中，过点M 作MK ⎳PC ，即可得到MKCQ=2，最后由PQ =2MK 即可得解.【详解】(1)取AD 的中点H ，连接PH ，CH ，则AH ⎳BC 且AH =BC ，又AD ⊥AB ，所以四边形ABCH 为矩形，所以CH ⊥AD ，又△PAD 为等边三角形，所以PH ⊥AD ，PH ∩CH =H ，PH ,CH ⊂平面PHC ，所以AD ⊥平面PHC ，又PC ⊂平面PHC ，所以AD ⊥PC .(2)连接HN ，由AD ⊥平面PHC ，又HN ⊂平面PHC ，所以AD ⊥HN ，所以S △ADH =12AD ⋅HN =HN ，要使△ADN 的面积最小，即要使HN 最小，当且仅当HN ⊥PC 时HN 取最小值，因为平面PAD ⊥平面ABCD ，平面PAD ∩平面ABCD =AD ，PH ⊂平面PAD ，所以PH ⊥平面ABCD ，又HC ⊂平面ABCD ，所以PH ⊥HC ，在Rt △HPC 中，CH =2，PH =3，所以PC =CH 2+PH 2=7，当HN ⊥PC 时HN =PH ⋅CH PC =237=2217，所以△ADN 面积的最小值为2217.(3)连接AC 交BD 于点G ，连接MC 交BQ 于点F ，连接FG ，因为AD ⎳BC 且AD =2BC =2，所以△CGB ∽△AGD ，所以CG AG =BC AD=12，因为AM ⎳平面BDQ ，又AM ⊂平面ACM ，平面BDQ ∩平面ACM =GF ，所以GF ⎳AM ，所以CF FM =CG AG=12，在△PBC 中，过点M 作MK ⎳PC ，则有MK CQ =MF CF=2，所以PQ =2MK ，所以PQ =2MK =4CQ ，即PQQC=415(2024·广东广州·模拟预测)如图所示，圆台O 1O 2的轴截面A 1ACC 1为等腰梯形，AC =2AA 1=2A 1C 1=4,B 为底面圆周上异于A ,C 的点，且AB =BC ,P 是线段BC 的中点.(1)求证：C 1P ⎳平面A 1AB .(2)求平面A 1AB 与平面C 1CB 夹角的余弦值.【答案】(1)证明见解析(2)17【分析】(1)取AB 的中点H ，连接A 1H ,PH ，证明四边形A 1C 1PH 为平行四边形，进而得C 1P ⎳A 1H ，即可证明；(2)建立空间直角坐标系，求两平面的法向量，利用平面夹角公式求解.【详解】(1)取AB 的中点H ，连接A1H ,PH ，如图所示，因为P 为BC 的中点，所以PH ⎳AC ,PH =12AC .在等腰梯形A 1ACC 1中，A 1C 1⎳AC ,A 1C 1=12AC ，所以HP ⎳A 1C 1,HP =A 1C 1，所以四边形A 1C 1PH 为平行四边形，所以C 1P ⎳A 1H ，又A 1H ⊂平面A 1AB ,C 1P ⊄平面A 1AB ，所以C 1P ⎳平面A 1AB .(2)因为AB =BC ,故O 2B ⊥AC ，以直线O 2A ,O 2B ，O 2O 1分别为x ,y ,z 轴，建立空间直角坐标系，如图所示，在等腰梯形A 1ACC 1中，AC =2AA 1=2A 1C 1=4，此梯形的高为h =AA 21-AC -A 1C 122= 3.因为A 1C 1=12AC ,A 1C 1⎳AC ，。
(完整版)高中数学立体几何大题(有答案)
1．(2014•山东）如图,四棱锥P﹣ABCD中，AP⊥平面PCD，AD∥BC，AB=BC=AD,E,F分别为线段AD,PC的中点．(Ⅰ）求证:AP∥平面BEF；（Ⅱ）求证:BE⊥平面PAC．解答：证明：（Ⅰ）连接CE,则∵AD∥BC，BC=AD,E为线段AD的中点，∴四边形ABCE是平行四边形,BCDE是平行四边形,设AC∩BE=O，连接OF，则O是AC的中点，∵F为线段PC的中点，∴PA∥OF，∵PA⊄平面BEF，OF⊂平面BEF，∴AP∥平面BEF;(Ⅱ）∵BCDE是平行四边形，∴BE∥CD,∵AP⊥平面PCD,CD⊂平面PCD，∴AP⊥CD，∴BE⊥AP，∵AB=BC，四边形ABCE是平行四边形，∴四边形ABCE是菱形，∴BE⊥AC，∵AP∩AC=A，∴BE⊥平面PAC．3．（2014•湖北）在四棱锥P﹣ABCD中，侧面PCD⊥底面ABCD，PD⊥CD，E为PC中点，底面ABCD是直角梯形，AB∥CD，∠ADC=90°，AB=AD=PD=1，CD=2．（Ⅰ）求证：BE∥平面PAD；（Ⅱ）求证：BC⊥平面PBD;（Ⅲ)设Q为侧棱PC上一点，，试确定λ的值，使得二面角Q﹣BD﹣P为45°．解答：解：(Ⅰ)取PD的中点F，连接EF，AF,∵E为PC中点，∴EF∥CD，且，在梯形ABCD中，AB∥CD,AB=1，∴EF∥AB，EF=AB,∴四边形ABEF为平行四边形,∴BE∥AF，∵BE⊄平面PAD，AF⊂平面PAD，∴BE∥平面PAD．（4分）（Ⅱ）∵平面PCD⊥底面ABCD，PD⊥CD，∴PD⊥平面ABCD,∴PD⊥AD．（5分)如图，以D为原点建立空间直角坐标系D﹣xyz．则A(1，0，0），B（1,1，0)，C（0，2，0)，P(0，0，1）．（6分），,∴，BC⊥DB,（8分）又由PD⊥平面ABCD,可得PD⊥BC，∴BC⊥平面PBD．(9分）(Ⅲ）由（Ⅱ）知,平面PBD的法向量为,（10分）∵，，且λ∈(0,1）∴Q(0,2λ,1﹣λ），（11分）设平面QBD的法向量为=(a，b，c），,，由，，得，∴，（12分）∴，(13分)因λ∈（0，1），解得．（14分）4．（2014•江苏)如图，在三棱锥P﹣ABC中，D，E,F分别为棱PC，AC，AB的中点，已知PA⊥AC，PA=6,BC=8，DF=5．求证：（1)直线PA∥平面DEF；（2)平面BDE⊥平面ABC．解答：证明：（1）∵D、E为PC、AC的中点,∴DE∥PA,又∵PA⊄平面DEF，DE⊂平面DEF，∴PA∥平面DEF;（2）∵D、E为PC、AC的中点，∴DE=PA=3;又∵E、F为AC、AB的中点,∴EF=BC=4;∴DE2+EF2=DF2，∴∠DEF=90°，∴DE⊥EF；∵DE∥PA,PA⊥AC,∴DE⊥AC；∵AC∩EF=E，∴DE⊥平面ABC;∵DE⊂平面BDE，∴平面BDE⊥平面ABC．13．(2012•江苏）如图，在直三棱柱ABC﹣A1B1C1中,A1B1=A1C1，D，E分别是棱BC,CC1上的点（点D 不同于点C）,且AD⊥DE，F为B1C1的中点．求证：（1）平面ADE⊥平面BCC1B1；（2)直线A1F∥平面ADE．解答：解：（1）∵三棱柱ABC﹣A1B1C1是直三棱柱，∴CC1⊥平面ABC，∵AD⊂平面ABC,∴AD⊥CC1又∵AD⊥DE，DE、CC1是平面BCC1B1内的相交直线∴AD⊥平面BCC1B1，∵AD⊂平面ADE∴平面ADE⊥平面BCC1B1；（2）∵△A1B1C1中，A1B1=A1C1，F为B1C1的中点∴A1F⊥B1C1，∵CC1⊥平面A1B1C1,A1F⊂平面A1B1C1，∴A1F⊥CC1又∵B1C1、CC1是平面BCC1B1内的相交直线∴A1F⊥平面BCC1B1又∵AD⊥平面BCC1B1，∴A1F∥AD∵A1F⊄平面ADE，AD⊂平面ADE，∴直线A1F∥平面ADE．16．(2010•深圳模拟）如图，在四棱锥S﹣ABCD中,底面ABCD为正方形，侧棱S D⊥底面ABCD，E、F分别是AB、SC的中点（1）求证：EF∥平面SAD(2)设SD=2CD，求二面角A﹣EF﹣D的大小．解答：（1）如图，建立空间直角坐标系D﹣xyz．设A（a，0,0)，S（0，0,b）,则B(a，a，0），C(0,a,0）,，．取SD的中点,则．平面SAD，EF⊄平面SAD，所以EF∥平面SAD．（2)不妨设A（1,0，0），则B（1，1，0），C(0，1,0)，S(0，0,2），，．EF 中点，，,又，，所以向量和的夹角等于二面角A﹣EF﹣D的平面角．．所以二面角A﹣EF﹣D的大小为．。
(完整word版)高中立体几何大量习题及答案
立体几何一、选择题1. 给出下列四个命题①垂直于同一直线的两条直线互相平行；②垂直于同一平面的两个 平面互相平行；③若直线4与同一平面所成的角相等，则4互相平行；④若直线 /|仏是异面直线，则与都相交的两条直线是异面直线。
其中假命题的个数是（）A. 1B. 2 C ・ 3 D. 42. 将正方形ABCD 沿对角线〃£）折成一个120。
的二面角，点C 到达点G ，这时异面直 线AD 与BCi 所成角的余弦值是（）A. —B. -C.逅D.- 2 2 4 43. —个长方体一顶点的三个面的面积分别是血、巧、后，这个长方体对角线的长为（）6. 正方体A ,B ,C ,D ,—ABCD 的棱长为a, EF 在AB 上滑动，且|EF|=b （b<a=9 Q 点在DC 上滑动，则四面体N —EFQ 的体积（）A ・与E 、尸位置有关 B.与Q 位置有关C.与E 、F 、0位置都有关D.与E 、F 、0位買均无关，是定值 7. 三个两两垂直的平面，它们的三条交线交于一点O,点P 到三个平面的距离比为1 ：2 ： 3, PO=2V14 ,则P 到这三个平面的距离分别是（）4. A. 2^3 B. 3^2 C. 6 如图，在正三角形ABC 中，D 、E 、尸分别为各边的中点，G 、H 、I 、丿分别为AF 、AD. BE 、DE 的中点.将△ ABC 沿QE 、EF 、Q 尸折成三棱锥以后，与〃所成角的度数为（A. 90° B ・ 60° C. 45。
5.两相同的正四棱锥组成如图所示的几何体，可放棱 长为1的正方体内，使正四棱锥的底面ABCD 与正 方体的某一个平面平行，且各顶点均在正方体的面 上，则这样的几何体体积的可能值有（）A ・I 个B. 2个C. 3个 D0°D.A. 1, 2, 3 B・ 2, 4, 6 C・ 1, 4, 6 D・ 3, 6, 98. 如图，在四而体ABCD 中，截rfij AEF 经过四面 体的内切球（与四个面都相切的球）球心O,且 与BC, DC 分别截于E 、F,如果截面将四面体 分成体积相等的两部分，设四棱锥A —BEFD 与 三棱锥A-EFC 的表面积分别是Si ，52,则必有 （）A. S\<S2B. Si>S2C. S I =52D. 5I ，S2的大小关系不能确定 9. 条件甲：四棱锥的所有侧面都是全等三角形，条件乙：这个四棱锥是正四棱锥，则条 件甲是条件乙的（）A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件10. 已知棱锥的顶点为P, P 在底面上的射影为O, PO=a,现用平行于底面的平面去截 这个棱锥，截面交PO 于点M,并使截得的两部分侧面积相等，设OM=b ，则a 与b 的关系是（） B ・ h= （ V2 +1） aD.后土色 2 —♦ f11. 已知向量d=（2, 4, x ）, 〃=（2, y, 2）,若f |=6, “ 丄〃，则 x+y 的值是（）12. 一个长方体共一顶点的三个面的面积分别是迈,JI 亦，这个长方体它的八个顶点都在同一个球面上，这个球的表面积是（）A.1271B. 1871C.3671D. 6兀 13. 己知某个几何体的三视图如下，图中标出的尺寸（单位:cm ）,则这个几何体的体积是（）已知圆锥的全面积是底面积的3倍，那么该圆锥的侧tfri 展开图扇形的圆心角为（ A.12O 0 B.15O 0 C.180° D.24O 0A ・ b= ( 5/2 —l)a A. 4000 14. A8000 正视图 俯视图20. 15.在一个倒置的正三棱锥容器内，放入一个钢球，钢球恰好与棱锥的四个而都接触，经 过棱锥的一条侧棱和高作截面，正确的截面图形是（）“（-1,0,2）,且几+》与必―》互相垂直，贝IJR 值是（） 厂3 “7 C. — D.— 5516. 正四棱柱 ABCD-AiBiCiDi 中，AB=3, BBi=4.长为 1 的线段PQ 在棱AAi 上移动，长为3的线段MN 在棱 CCi±移动，点R 在棱BBi 上移动，则四棱锥R- PQMN 的体积是（）A. 6B. 10 C ・12 D ・不确定17. 已知三棱锥0—ABC 中，OA 、OB 、OC 两两互相垂直，若x+y=4,则已知三棱锥O —ABC 体积的最大值是（）1 2 >/3 B. — C. — D. 3 3 3 A.l18. 如图，在正四面体A-BCD 中，E 、F 、G 分别是三角形ADC 、ABD 、BCD 的中心, 则AEFG 在该正四面体各个面上的射影所有可能的序号是（）A.①③B.②®® c.③④D.②④ A/ \ /◎、L ________ \ ① MB — — —②19. 如來底而直径和高相等的圆柱的侧面积是s •那么圆柱的体积等于A.-VSB.-J-C.-VSD.- 2 2V K 44 vn 已知直线AB. CD 是异面直线，AC 丄AB, AC 丄CD, BD 丄CD, 则异面直线AB 与CD 所成角的大小为（）A. 30°B. 45° 且 AB=2, CD=1,C. 60°D. 75°已知向量”m°）,B.- 5 A. 1 OC=1, OA=x, OB=y,22. 在四棱锥的四个侧面中，直角三角形最参可有（）A.4个B.2个C.3个D.1个23. 三棱锥A-BCD 中，AC 丄BD, E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点，则四边形EFGH 是（）A.菱形B.矩形C.梯形D.正方形24. 在正四面体P —ABC 中，D 、E 、F 分别是AB 、BC 、CA 的中点，下面四个结论中不 成立的是（）25. 一棱锥被平行于底面的平面所截，若截面1何积与底面面积的比为1： 3,则此截面把一条侧棱分成的两线段之比为（）A.1： 3B.1： 2C.1：羽D.1：羽一 1 26. 正四面体P —ABC 中，M 为棱AB 的中点，则PA 与CM 所成角的余弦值为（）A 並B 並C 返D 迴 A. 2 B. § C. 4 D. 327. —个三棱锥S —ABC 的三条侧棱SA 、SB 、SC 两两互相垂直，且长度分别为1, & ,3 已知该三棱锥的四个顶点都在一个球而上，则这个球的表面积为（）A.16nB.32 兀C.36 兀D.64 兀28. 在棱长为。
立体几何专题专练100题(含详解)
1.（本题满分15分）如图，在三棱锥D -ABC 中，DA =DB =DC ,D 在底面ABC 上的射影为E ，AB ⊥BC ，DF ⊥AB 于F ．（Ⅰ）求证：平面ABD ⊥平面DEF ；（Ⅱ）若AD ⊥DC ，AC =4，∠BAC =60°，求直线BE 与平面DAB 所成的角的正弦值.答案及解析：1.（Ⅰ）如图，由题意知⊥DE 平面ABC所以DE AB ⊥，又DFAB ⊥所以⊥AB 平面DEF ，………………3分又⊂AB 平面ABD 所以平面⊥ABD 平面DEF…………………6分（Ⅱ）解法一：由DC DB DA ==知ECEB EA ==所以E 是ABC ∆的外心又BC AB ⊥所以E 为AC 的中点…………………………………9分过E 作DF EH ⊥于H ，则由（Ⅰ）知⊥EH 平面DAB所以EBH ∠即为BE 与平面DAB 所成的角…………………………………12分由4=AC ， 60=∠BAC 得2=DE ，3=EF 所以7=DF ，732=EH 所以721sin ==∠BE EH EBH …………………………………15分解法二：如图建系，则)0,2,0(-A ，)2,0,0(D ，)0,1,3(-B 所以)2,2,0(--=DA ，)2,1,3(--=DB ……………………………………9分设平面DAB 的法向量为),,(z y x n =由⎪⎩⎪⎨⎧=⋅=⋅00DB n DA n 得⎩⎨⎧=--=--023022z y x z y ，取)1,1,33(-=n ………………12分设EB 与n 的夹角为θ所以7213722||||cos ==⋅=n EB nEB θ所以BE 与平面DAB 所成的角的正弦值为721………………………………15分2.如图，在直三棱柱ABC ﹣A 1B 1C 1中，AA 1=AC=2AB=2，且BC 1⊥A 1C ．（1）求证：平面ABC 1⊥平面A 1ACC 1；（2）设D是线段BB1的中点，求三棱锥D﹣ABC1的体积．答案及解析：2.【考点】棱柱、棱锥、棱台的体积；平面与平面垂直的判定．【专题】综合题；转化思想；综合法；立体几何．【分析】（1）证明A1C⊥面ABC1，即可证明：平面ABC1⊥平面A1ACC1；（2）证明AC⊥面ABB1A1，利用等体积转换，即可求三棱锥D﹣ABC1的体积．【解答】（1）证明：在直三棱锥ABC﹣A1B1C1中，有A1A⊥面ABC，而AB⊂面ABC，∴A1A⊥AB，∵A1A=AC，∴A1C⊥AC1，又BC1⊥A1C，BC1⊂面ABC1，AC1⊂面ABC1，BC1∩AC1=C1∴A1C⊥面ABC1，而A1C⊂面A1ACC1，则面ABC1⊥面A1ACC1…（2）解：由（1）知A1A⊥AB，A1C⊥面ABC1，A1C⊥AB，故AB⊥面A1ACC1，∴AB⊥AC，则有AC⊥面ABB1A1，∵D是线段BB1的中点，∴．…【点评】本题考查线面垂直、平面与平面垂直的判定，考查三棱锥D﹣ABC1的体积，考查学生分析解决问题的能力，正确运用定理是关键．3.如图所示，在四棱锥P﹣ABCD中，底面ABCD是矩形，侧棱PA垂直于底面，E、F分别是AB、PC的中点．（1）求证：CD⊥PD；（2）求证：EF∥平面PAD．答案及解析：3.【考点】空间中直线与直线之间的位置关系；直线与平面平行的判定．【分析】本题是高考的重要内容，几乎年年考，次次有：（1）的关键是找出直角三角形，也就是找出图中的线线垂直．（2）的关键是找出平面PAD中可能与EF平行的直线．【解答】解：（1）证明：∵PA⊥平面ABCD，而CD⊂平面ABCD，∴PA⊥CD，又CD⊥AD，AD∩PA=A，∴CD⊥平面PAD，∴CD⊥PD、（2）取CD的中点G，连接EG、FG．∵E、F分别是AB、PC的中点，∴EG∥AD，FG∥PD，∴平面EFG∥平面PAD，又∵EF⊂平面EFG，∴EF∥平面PAD．【点评】线线垂直可由线面垂直的性质推得，直线和平面垂直，这条直线就垂直于平面内所有直线，这是寻找线线垂直的重要依据．判断或证明线面平行的常用方法有：①利用线面平行的定义（无公共点）；②利用线面平行的判定定理（a∥α，b⊂α，a∥b⇒a∥α）；③利用面面平行的性质定理（α∥β，a⊂α⇒a∥β）；④利用面面平行的性质（α∥β，a⊄β，a∥α⇒a∥β）．4.如图，在直三棱柱ABC﹣A1B1C1中，AC=3，BC=4，AB=5，点D是AB的中点．（1）求证：AC⊥BC1；（2）求证：AC1∥平面CDB1．答案及解析：4.【考点】直线与平面垂直的性质；直线与平面平行的判定．【专题】综合题；空间位置关系与距离．【分析】（1）利用勾股定理的逆定理可得AC⊥BC．利用线面垂直的性质定理可得CC1⊥AC，再利用线面垂直的判定定理即可证明结论；（2）利用直三棱柱的性质、正方形的性质、三角形的中位线定理即可得出ED∥AC1，再利用线面平行的判定定理即可证明结论【解答】证明：（1）因为三棱柱ABC﹣A1B1C1为直三棱柱，所以C1C⊥平面ABC，所以C1C⊥AC．又因为AC=3，BC=4，AB=5，所以AC2+BC2=AB2，所以AC⊥BC．又C1C∩BC=C，所以AC⊥平面CC1B1B，所以AC⊥BC1．（2）连结C1B交CB1于E，再连结DE，由已知可得E为C1B的中点，又∵D为AB的中点，∴DE为△BAC1的中位线．∴AC1∥DE又∵DE⊂平面CDB1，AC1⊄平面CDB1∴AC1∥平面CDB1．【点评】熟练掌握勾股定理的逆定理、线面垂直的判定和性质定理、直三棱柱的性质、正方形的性质、三角形的中位线定理、线面平行的判定定理是解题的关键．5.已知在三棱锥S﹣ABC中，∠ACB=90°，又SA⊥平面ABC，AD⊥SC于D，求证：AD⊥平面SBC．答案及解析：5.【考点】直线与平面垂直的判定．【专题】证明题．【分析】要证明AD⊥平面SBC，只要证明AD⊥SC（已知），AD⊥BC，而结合已知∠ACB=90°，又SA⊥平面ABC，及线面垂直的判定定理及性质即可证明【解答】证明：∵SA⊥面ABC，∴BC⊥SA；∵∠ACB=90°，即AC⊥BC，且AC、SA是面SAC内的两相交线，∴BC⊥面SAC；又AD⊂面SAC，∴BC⊥AD，又∵SC⊥AD，且BC、SC是面SBC内两相交线，∴AD⊥面SBC．【点评】本题主要考查了直线与平面垂直，平面与平面垂直的相互转化，线面垂直的判定定理的应用，属于基础试题6.如图，在四棱锥P﹣ABCD中，底面ABCD为矩形，PA⊥底面ABCD，AP=AB=，点E 是棱PB的中点．（Ⅰ）证明：AE⊥平面PBC；（Ⅱ）若AD=1，求二面角B﹣EC﹣D的平面角的余弦值．答案及解析：6.【考点】二面角的平面角及求法；直线与平面垂直的判定．【专题】空间位置关系与距离；空间角．【分析】（Ⅰ）由PA⊥底面ABCD，得PA⊥AB．又PA=AB，从而AE⊥PB．由三垂线定理得BC⊥PB，从而BC⊥平面PAB，由此能证明AE⊥平面PBC．（Ⅱ）由BC⊥平面PAB，AD⊥AE．取CE的中点F，连结DF，连结BF，则∠BFD为所求的二面角的平面角，由此能求出二面角B﹣EC﹣D的平面角的余弦值．【解答】（Ⅰ）证明：如图1，由PA⊥底面ABCD，得PA⊥AB．又PA=AB，故△PAB为等腰直角三角形，而点E是棱PB的中点，所以AE⊥PB．由题意知BC⊥AB，又AB是PB在面ABCD内的射影，由三垂线定理得BC⊥PB，从而BC⊥平面PAB，故BC⊥AE．因为AE⊥PB，AE⊥BC，所以AE⊥平面PBC．（Ⅱ）解：由（Ⅰ）知BC⊥平面PAB，又AD∥BC，得AD⊥平面PAB，故AD⊥AE．在Rt△PAB中，PA=AB=，AE=PB==1．从而在Rt△DAE中，DE==．在Rt△CBE中，CE==，又CD=，所以△CED为等边三角形，取CE的中点F，连结DF，则DF⊥CE，∵BE=BC=1，且BC⊥BE，则△EBC为等腰直角三角形，连结BF，则BF⊥CE，所以∠BFD为所求的二面角的平面角，连结BD，在△BFD中，DF=CD=，BF=，BD==，所以cos∠BFD==﹣，∴二面角B﹣EC﹣D的平面角的余弦值为﹣．【点评】本题考查直线与平面垂直的证明，考查二面角的余弦值的求法，解题时要认真审题，注意向量法的合理运用．7.如图所示，四棱锥P ABCD的底面ABCD是平行四边形，BA=BD=，AD=2，PA=PD=，E，F分别是棱AD，PC的中点，二面角PADB为60°．（1）证明：平面PBC⊥平面ABCD；（2）求直线EF与平面PBC所成角的正弦值．答案及解析：7.证明：（1）连接PE，BE，∵PA=PD，BA=BD，而E为AD中点，∴PE⊥AD，BE⊥AD，∴∠PEB为二面角P﹣AD﹣B的平面角．在△PAD中，由PA=PD=，AD=2，解得PE=2．在△ABD中，由BA=BD=，AD=2，解得BE=1．在△PEB中，PE=2，BE=1，∠PEB=60˚，由余弦定理，解得PB==，∴∠PBE=90˚，即BE⊥PB．又BC∥AD，BE⊥AD，∴BE⊥BC，∴BE⊥平面PBC．又BE⊂平面ABCD，∴平面PBC⊥平面ABCD．解：（2）连接BF，由（1）知，BE⊥平面PBC，∴∠EFB为直线EF与平面PBC所成的角．∵PB=，∠ABP为直角，MB=PB=，∴AM=，∴EF=．又BE=1，∴在直角三角形EBF中，sin∠EFB==．∴直线EF与平面PBC所成角的正弦值为．考点：直线与平面所成的角；平面与平面垂直的判定．专题：证明题；转化思想；综合法；空间位置关系与距离；空间角．分析：（1）连接PE，BE，由已知推导出∠PEB为二面角P﹣AD﹣B的平面角，推导出BE⊥PB，BE⊥BC，由此能证明平面PBC⊥平面ABCD．（2）连接BF，由BE⊥平面PBC，得∠EFB为直线EF与平面PBC所成的角，由此能求出直线EF与平面PBC所成角的正弦值．解答：证明：（1）连接PE，BE，∵PA=PD，BA=BD，而E为AD中点，∴PE⊥AD，BE⊥AD，∴∠PEB为二面角P﹣AD﹣B的平面角．在△PAD中，由PA=PD=，AD=2，解得PE=2．在△ABD中，由BA=BD=，AD=2，解得BE=1．在△PEB中，PE=2，BE=1，∠PEB=60˚，由余弦定理，解得PB==，∴∠PBE=90˚，即BE⊥PB．又BC∥AD，BE⊥AD，∴BE⊥BC，∴BE⊥平面PBC．又BE⊂平面ABCD，∴平面PBC⊥平面ABCD．解：（2）连接BF，由（1）知，BE⊥平面PBC，∴∠EFB为直线EF与平面PBC所成的角．∵PB=，∠ABP为直角，MB=PB=，∴AM=，∴EF=．又BE=1，∴在直角三角形EBF中，sin∠EFB==．∴直线EF与平面PBC所成角的正弦值为．点评：本题考查面面垂直的证明，考查线面角的正弦值的求法，是中档题，解题时要认真审题，注意空间思维能力的培养8.（15分）（2010秋•杭州校级期末）如图，已知△BCD中，∠BCD=90°，AB⊥平面BCD，BC=CD=1，分别为AC、AD的中点．（1）求证：平面BEF⊥平面ABC；（2）求直线AD与平面BEF所成角的正弦值．答案及解析：8.【考点】平面与平面垂直的判定；直线与平面所成的角．【专题】计算题；证明题．【分析】（1）通过证明CD⊥平面ABC，CD∥EF，说明EF⊂平面BEF，即可证明平面BEF⊥平面ABC；（2）过A作AH⊥BE于H，连接HF，可得AH⊥平面BEF，推出∠AFH为直线AD与平面BEF所成角．在Rt△AFH中，求直线AD与平面BEF所成角的正弦值．【解答】解：（1）证明：∵AB⊥平面BCD，∴AB⊥CD．又∵CD⊥BC，∴CD⊥平面ABC．∵E、F分别为AC、AD的中点，∴EF∥CD．∴EF⊥平面ABC，∵EF⊂平面BEF，∴平面BEF⊥平面ABC．（2）过A作AH⊥BE于H，连接HF，由（1）可得AH⊥平面BEF，∴∠AFH为直线AD与平面BEF所成角．在Rt△ABC中，为AC中点，∴∠ABE=30°，∴．在Rt△BCD中，BC=CD=1，∴．∴在Rt△ABD中，∴．∴在Rt△AFH中，，∴AD与平面BEF所成角的正弦值为．【点评】证明两个平面垂直，关键在一个面内找到一条直线和另一个平面垂直；利用三垂线定理找出二面角的平面角，解三角形求出此角，是常用方法．9.答案及解析：9.10.（12分）（2015秋•拉萨校级期末）如图，边长为2的正方形ABCD中，（1）点E是AB的中点，点F是BC的中点，将△AED，△DCF分别沿DE，DF折起，使A，C两点重合于点A′．求证：A′D⊥EF（2）当BE=BF=BC时，求三棱锥A′﹣EFD的体积．答案及解析：10.【考点】直线与平面垂直的性质；棱柱、棱锥、棱台的体积．【专题】空间位置关系与距离．【分析】（1）由正方形ABCD知∠DCF=∠DAE=90°，得A'D⊥A'F且A'D⊥A'E，所以A'D⊥平面A'EF．结合EF⊂平面A'EF，得A'D⊥EF；（2）由勾股定理的逆定理，得△A'EF是以EF为斜边的直角三角形，而A'D是三棱锥D﹣A'EF的高线，可以算出三棱锥D﹣A'EF的体积，即为三棱锥A'﹣DEF的体积．【解答】解：（1）由正方形ABCD知，∠DCF=∠DAE=90°，∴A'D⊥A'F，A'D⊥A'E，∵A'E∩A'F=A'，A'E、A'F⊆平面A'EF．∴A'D⊥平面A'EF．又∵EF⊂平面A'EF，∴A'D⊥EF．（2）由四边形ABCD为边长为2的正方形故折叠后A′D=2，A′E=A′F=，EF=则cos∠EA′F==则sin∠EA′F==•A′E•A′F•sin∠EA′F=故△EA′F的面积S△EA′F由（1）中A′D⊥平面A′EF可得三棱锥A'﹣EFD的体积V=××2=．【点评】本题以正方形的翻折为载体，证明两直线异面垂直并且求三棱锥的体积，着重考查空间垂直关系的证明和锥体体积公式等知识，属于中档题．11.（12分）（2015秋•沧州月考）如图，在△ABC中，AO⊥BC于O，OB=2OA=2OC=4，点D，E，F分别为OA，OB，OC的中点，BD与AE相交于H，CD与AF相交于G，将△ABO 沿OA折起，使二面角B﹣OA﹣C为直二面角．（Ⅰ）在底面△BOC的边BC上是否存在一点P，使得OP⊥GH，若存在，请计算BP的长度；若不存在，请说明理由；（Ⅱ）求二面角A﹣GH﹣D的余弦值．答案及解析：11.【考点】用空间向量求平面间的夹角；直线与平面垂直的性质；二面角的平面角及求法．【专题】数形结合；向量法；空间位置关系与距离；空间角；空间向量及应用．【分析】（Ⅰ）根据条件便知H，G分别为△AOB，△AOC的重心，从而有GH∥EF∥BC，并可说明∠BOC为直角，过O作OP⊥BC，从而有OP⊥GH，而根据摄影定理便有，这样即可求出BP的长度；（Ⅱ）根据上面知OB，OC，OA三直线两两垂直，分别以这三直线为x，y，z轴，建立空间直角坐标系，从而可以根据条件求出图形上一些点的坐标，从而可以得到向量的坐标，可设平面AGH的法向量为，而根据即可求出，同样的方法可以求出平面DGH的一个法向量，根据cos=即可得出二面角A﹣GH﹣D的余弦值．【解答】解：（Ⅰ）H，G分别为△AOB和△AOC的重心；∴；连接EF，则GH∥EF；由已知，EF∥BC，∴GH∥BC；∵OA⊥OB，OA⊥OC，二面角B﹣OA﹣C为直二面角；∴∠BOC为直角；∴在Rt△BOC中，过O作BC的垂线，垂足为P，OP⊥BC，又BC∥GH；∴OP⊥GH，则由摄影定理得：OB2=BP•BC；∴；（Ⅱ）分别以OB，OC，OA为x，y，z轴，建立如图所示空间直角坐标系，则：O（0，0，0），A（0，0，2），D（0，0，1），B（4，0，0），C（0，2，0），H（），；∴，；设为平面AGH的法向量，则：；取x1=1，则y1=2，z1=1，∴；设为平面DGH的法向量，则：；取x2=1，则；∴；∴由图可知二面角A﹣GH﹣D为锐角，∴该二面角的余弦值为．【点评】考查三角形重心的概念及其性质，平行线分线段成比例，三角形中位线的性质，以及二面角的平面角的定义，直角三角形的摄影定理的内容，建立空间直角坐标系，利用空间向量解决二面角问题的方法，平面的法向量的概念及求法，能求空间点的坐标，根据点的坐标求向量的坐标，向量垂直的充要条件，以及向量夹角的余弦公式，清楚两平面所成二面角的大小和两平面的法向量夹角的关系．12.（12分）（2014•芜湖模拟）如图，E是以AB为直径的半圆上异于A、B的点，矩形ABCD 所在的平面垂直于该半圆所在的平面，且AB=2AD=2．（1）求证：EA⊥EC；（2）设平面ECD与半圆弧的另一个交点为F．①试证：EF∥AB；②若EF=1，求三棱锥E﹣ADF的体积．答案及解析：12.【考点】直线与平面垂直的性质；棱柱、棱锥、棱台的体积；直线与平面平行的性质．【专题】空间位置关系与距离．【分析】（1）利用面面垂直的性质，可得BC⊥平面ABE，再利用线面垂直的判定证明AE⊥面BCE，即可证得结论；（2）①先证明AB∥面CED，再利用线面平行的性质，即可证得结论；②取AB中点O，EF的中点O′，证明AD⊥平面ABE，利用等体积，即可得到结论．【解答】（1）证明：∵平面ABCD⊥平面ABE，平面ABCD∩平面ABE=AB，BC⊥AB，BC⊂平面ABCD∴BC⊥平面ABE∵AE⊂平面ABE，∴BC⊥AE∵E在以AB为直径的半圆上，∴AE⊥BE∵BE∩BC=B，BC，BE⊂面BCE∴AE⊥面BCE∵CE⊂面BCE，∴EA⊥EC；（2）①证明：设面ABE∩面CED=EF∵AB∥CD，AB⊄面CED，CD⊂面CED，∴AB∥面CED，∵AB⊂面ABE，面ABE∩面CED=EF∴AB∥EF；②取AB中点O，EF的中点O′，在Rt△OO′F中，OF=1，O′F=，∴OO′=∵BC⊥面ABE，AD∥BC∴AD⊥平面ABE∴V E﹣ADF =V D﹣AEF===【点评】本题考查面面垂直的性质，线面垂直的判定与性质，考查线面垂直，考查三棱锥体积的计算，考查学生分析解决问题的能力，属于中档题．13.（12分）（2014•浙江模拟）如图，在直三棱柱ABC﹣A1B1C1中，AC=3，BC=4，AB=5，点D是AB的中点．（1）求证：AC⊥BC1；（2）求证：AC1∥平面CDB1．答案及解析：13.【考点】直线与平面垂直的性质；直线与平面平行的判定．【专题】综合题；空间位置关系与距离．【分析】（1）利用勾股定理的逆定理可得AC⊥BC．利用线面垂直的性质定理可得CC1⊥AC，再利用线面垂直的判定定理即可证明结论；（2）利用直三棱柱的性质、正方形的性质、三角形的中位线定理即可得出ED∥AC1，再利用线面平行的判定定理即可证明结论【解答】证明：（1）因为三棱柱ABC﹣A1B1C1为直三棱柱，所以C1C⊥平面ABC，所以C1C⊥AC．又因为AC=3，BC=4，AB=5，所以AC2+BC2=AB2，所以AC⊥BC．又C1C∩BC=C，所以AC⊥平面CC1B1B，所以AC⊥BC1．（2）连结C1B交CB1于E，再连结DE，由已知可得E为C1B的中点，又∵D为AB的中点，∴DE为△BAC1的中位线．∴AC1∥DE又∵DE⊂平面CDB1，AC1⊄平面CDB1∴AC1∥平面CDB1．【点评】熟练掌握勾股定理的逆定理、线面垂直的判定和性质定理、直三棱柱的性质、正方形的性质、三角形的中位线定理、线面平行的判定定理是解题的关键．14.如图，在三棱锥S﹣ABC中，SB⊥底面ABC，且SB=AB=2，BC=，D、E 分别是SA、SC的中点．（I）求证：平面ACD⊥平面BCD；（II）求二面角S﹣BD﹣E的平面角的大小．答案及解析：14.【考点】用空间向量求平面间的夹角；平面与平面垂直的判定．【专题】空间位置关系与距离；空间角．【分析】（Ⅰ）根据面面垂直的判定定理证明AD⊥平面BCD即可证明平面ACD⊥平面BCD．（Ⅱ）建立空间直角坐标系，利用向量法即可求二面角S﹣BD﹣E的余弦值．【解答】证明：（I）∵∠ABC=，∴BA⊥BC，建立如图所示的坐标系，则C（0，，0），A（2，0，0），D（1，0，1），E（0，，1），S（0，0，2），则=（﹣1，0，1），=（0，，0），=（1，0，1），则•=（﹣1，0，1）•（0，，0）=0，•=（﹣1，0，1）•（1，0，1）=﹣1+1=0，则⊥，⊥，即AD⊥BC，AD⊥BD，∵BC∩BD=B，∴AD⊥平面BCD；∵AD⊂平面BCD；∴平面ACD⊥平面BCD；（II）=（0，，1），则设平面BDE的法向量=（x，y，1），则，即，解得x=﹣1，y=，即=（﹣1，，1），又平面SBD的法向量=（0，，0），∴cos＜，＞==，则＜，＞=，即二面角S﹣BD﹣E的平面角的大小为．【点评】本题主要考查空间面面垂直的判定，以及二面角的求解，利用向量法是解决二面角的常用方法．15.如图，在四棱锥P﹣ABCD中，AD∥BC，AB⊥AD，AB⊥PA，BC=2AB=2AD=4BE，平面PAB⊥平面ABCD，（Ⅰ）求证：平面PED⊥平面PAC；（Ⅱ）若直线PE与平面PAC所成的角的正弦值为，求二面角A﹣PC﹣D的平面角的余弦值．答案及解析：15.【考点】用空间向量求平面间的夹角；平面与平面垂直的判定；二面角的平面角及求法．【专题】计算题；空间位置关系与距离；空间角．【分析】（I）由面面垂直的性质定理证出PA⊥平面ABCD，从而得到AB、AD、AP两两垂直，因此以AB、AD、AP为x轴、y轴、z轴，建立坐标系o﹣xyz，得A、D、E、C、P的坐标，进而得到、、的坐标．由数量积的坐标运算公式算出且，从而证出DE⊥AC且DE⊥AP，结合线面垂直判定定理证出ED⊥平面PAC，从而得到平面PED⊥平面PAC；（II）由（Ⅰ）得平面PAC的一个法向量是，算出、夹角的余弦，即可得到直线PE与平面PAC所成的角θ的正弦值，由此建立关于θ的方程并解之即可得到λ=2．利用垂直向量数量积为零的方法，建立方程组算出=（1，﹣1，﹣1）是平面平面PCD的一个法向量，结合平面PAC的法向量，算出、的夹角余弦，再结合图形加以观察即可得到二面角A﹣PC﹣D的平面角的余弦值．【解答】解：（Ⅰ）∵平面PAB⊥平面ABCD，平面PAB∩平面ABCD=AB，AB⊥PA∴PA⊥平面ABCD结合AB⊥AD，可得分别以AB、AD、AP为x轴、y轴、z轴，建立空间直角坐标系o﹣xyz，如图所示…（2分）可得A（0，0，0）D（0，2，0），E（2，1，0），C（2，4，0），P（0，0，λ）（λ＞0）∴，，得，，∴DE⊥AC且DE⊥AP，∵AC、AP是平面PAC内的相交直线，∴ED⊥平面PAC．（4分）∵ED⊂平面PED∴平面PED⊥平面PAC（6分）（Ⅱ）由（Ⅰ）得平面PAC的一个法向量是，设直线PE与平面PAC所成的角为θ，则，解之得λ=±2∵λ＞0，∴λ=2，可得P的坐标为（0，0，2）（8分）设平面PCD的一个法向量为=（x0，y0，z0），，由，，得到，令x0=1，可得y0=z0=﹣1，得=（1，﹣1，﹣1）（10分）∴cos＜，（11分）由图形可得二面角A﹣PC﹣D的平面角是锐角，∴二面角A﹣PC﹣D的平面角的余弦值为．（12分）【点评】本题在四棱锥中证明面面垂直，并且在线面所成角的正弦情况下求二面角A﹣PC ﹣D的余弦值．着重考查了线面垂直、面面垂直的判定定理和利用空间向量研究直线与平面所成角和二面角大小的方法，属于中档题．16.如图，四棱锥P﹣ABCD中，底面ABCD为平行四边形，∠DAB=60°，AB=2AD，PD⊥底面ABCD．（Ⅰ）证明：PA⊥BD；（Ⅱ）若PD=AD，求二面角A﹣PB﹣C的余弦值．答案及解析：16.（Ⅰ）证明：因为∠DAB=60°，AB=2AD，由余弦定理得BD=，从而BD2+AD2=AB2，故BD⊥AD又PD⊥底面ABCD，可得BD⊥PD所以BD⊥平面PAD．故PA⊥BD（Ⅱ）如图，以D为坐标原点，AD的长为单位长，射线DA为x轴的正半轴建立空间直角坐标系D﹣xyz，则A（1，0，0），B（0，，0），C（﹣1，，0），P（0，0，1）．=（﹣1，，0），=（0，，﹣1），=（﹣1，0，0），设平面PAB的法向量为=（x，y，z），则即，因此可取=（，1，）设平面PBC的法向量为=（x，y，z），则，即：可取=（0，1，），cos＜＞==故二面角A﹣PB﹣C的余弦值为：﹣．考点：直线与平面垂直的性质；用空间向量求平面间的夹角．专题：计算题；证明题；综合题；数形结合；转化思想．分析：（Ⅰ）因为∠DAB=60°，AB=2AD，由余弦定理得BD=，利用勾股定理证明BD⊥AD，根据PD⊥底面ABCD，易证BD⊥PD，根据线面垂直的判定定理和性质定理，可证PA⊥BD；（Ⅱ）建立空间直角坐标系，写出点A，B，C，P的坐标，求出向量，和平面PAB的法向量，平面PBC的法向量，求出这两个向量的夹角的余弦值即可．解答：（Ⅰ）证明：因为∠DAB=60°，AB=2AD，由余弦定理得BD=，从而BD2+AD2=AB2，故BD⊥AD又PD⊥底面ABCD，可得BD⊥PD所以BD⊥平面PAD．故PA⊥BD（Ⅱ）如图，以D为坐标原点，AD的长为单位长，射线DA为x轴的正半轴建立空间直角坐标系D﹣xyz，则A（1，0，0），B（0，，0），C（﹣1，，0），P（0，0，1）．=（﹣1，，0），=（0，，﹣1），=（﹣1，0，0），设平面PAB的法向量为=（x，y，z），则即，因此可取=（，1，）设平面PBC的法向量为=（x，y，z），则，即：可取=（0，1，），cos＜＞==故二面角A﹣PB﹣C的余弦值为：﹣．点评：此题是个中档题．考查线面垂直的性质定理和判定定理，以及应用空间向量求空间角问题，查了同学们观察、推理以及创造性地分析问题、解决问题能力．17.如图，在三棱锥P﹣ABC中，∠ABC=90°，PA⊥平面ABC，E，F分别为PB，PC的中点．（1）求证：EF∥平面ABC；（2）求证：平面AEF⊥平面PAB．答案及解析：17.【考点】平面与平面垂直的判定；直线与平面平行的判定．【专题】空间位置关系与距离．【分析】（1）根据三角形中位线定理可得EF∥BC，进而根据线面平行的判定定理可得EF∥平面ABC；（2）根据PA⊥平面ABC，可得PA⊥BC，结合∠ABC=90°，及线面垂直的判定定理可得BC⊥平面PAB，进而由线面垂直的第二判定定理可得EF平面PAB，最后由面面垂直的判定定理可得平面AEF⊥平面PAB．【解答】证明：（1）∵E，F分别为PB，PC的中点．∴EF∥BC，又∵BC⊂平面ABC，EF⊄平面ABC，∴EF∥平面ABC；（2）∵PA⊥平面ABC，BC⊂平面ABC，∴PA⊥BC，又∵∠ABC=90°，∴AB⊥BC，又∵PA∩AB=A，PA，AB⊂平面PAB，∴BC⊥平面PAB，由（1）中EF∥BC，∴EF⊥平面PAB，又∵EF⊂平面AEF，∴平面AEF⊥平面PAB．【点评】本题考查的知识点是线面平行的判定定理，线面垂直的判定定理，面面垂直的判定定理，是空间线面关系的简单综合应用，难度中档．18.（14分）如图，已知AF⊥平面ABCD，四边形ABEF为矩形，四边形ABCD为直角梯形，∠DAB=90°，AB∥CD，AD=AF=CD=2，AB=4．（Ⅰ）求证：AC⊥平面BCE；（Ⅱ）求三棱锥A﹣CDE的体积；（Ⅲ）线段EF上是否存在一点M，使得BM⊥CE？若存在，确定M点的位置；若不存在，请说明理由．答案及解析：18.【考点】棱柱、棱锥、棱台的体积；直线与平面垂直的判定．【专题】空间位置关系与距离．【分析】（I）如图所示，取AB的中点N，连接CN，可得四边形ADCN是正方形，可得NA=NB=NC，可得AC⊥CB，利用AF⊥平面ABCD，AF∥BE，可得BE⊥平面ABCD，即可证明．=V三棱锥E﹣ACD=即可得出．（II）利用V三棱锥A﹣CDE（III）线段EF上存在一点M为线段EF的中点，使得BM⊥CE．连接MN，BM，EN，则四边形BEMN为正方形，可得BM⊥EN，利用线面面面垂直的判定与性质定理可得：CN⊥平面ABEF，可得CN⊥BM，又BM⊥CE．即可证明BM⊥平面CEN．【解答】（I）证明：如图所示，取AB的中点N，连接CN，则四边形ADCN是正方形，可得NA=NB=NC，∴AC⊥CB，∵AF⊥平面ABCD，AF∥BE，∴BE⊥平面ABCD，∴BE⊥AC，又BE∩BC=B，∴AC⊥平面BCE．=V三棱锥E﹣ACD===．（II）解：V三棱锥A﹣CDE（III）解：线段EF上存在一点M为线段EF的中点，使得BM⊥CE．连接MN，BM，EN，则四边形BEMN为正方形，∴BM⊥EN，∵CN⊥AB，平面ABEF⊥平面ABCD，平面ABEF∩平面ABCD=AB，∴CN⊥平面ABEF，∴CN⊥BM，又CN∩EN=N，∴BM⊥平面CEN，∴BM⊥CE．【点评】本题考查了线面面面垂直的判定与性质定理、正方形的判定与性质定理、三棱锥的体积计算公式，考查了推理能力与计算能力，属于中档题．19.（13分）如图，在正方体A1B1C1D1﹣ABCD中，（1）在正方体的12条棱中，与棱AA1是异面直线的有几条（只要写出结果）（2）证明：AC∥平面A1BC1；（3）证明：AC⊥平面BDD1B1．答案及解析：19.【考点】直线与平面垂直的判定；直线与平面平行的判定．【专题】证明题；数形结合；数形结合法；空间位置关系与距离．【分析】（1）画出正方体ABCD﹣A1B1C1D1，根据异面直线的概念即可找出与棱AA1异面的棱．（2）连接AC，A1C1，则A1C1∥AC，利用线面平行的判定定理即可证明；（3）由DD1⊥面AC，知DD1⊥AC，由DD1⊥BD，能够证明AC⊥平面BDD1B1．【解答】解：（1）与棱AA1异面的棱为：CD，C1D1，BC，B1C1，共4条．（2）证明：连接AC，A1C1，则A1C1∥AC，∵AC⊄平面A1BC1，A1C1⊂平面A1BC1，∴AC∥平面A1BC1；（3）证明：∵DD1⊥面AC，AC⊂平面AC，∴DD1⊥AC，∵AC⊥BD，DD1∩BD=D，BD⊂平面BDD1B1，DD1⊂平面BDD1B1∴AC⊥平面BDD1B1．【点评】考查异面直线的概念，直线与平面垂直的证明，直线与平面平行的判定，解题时要认真审题，仔细解答，注意合理地进行等价转化，属于中档题．20.如图，在正方体ABCD﹣A1B1C1D1中，（1）证明：BC1⊥面A1B1CD；（2）求直线A1B和平面A1B1CD所成的角．答案及解析：20.【考点】直线与平面所成的角；直线与平面垂直的判定．【分析】（1）要证BC1⊥面A1B1CD；应通过证明A1B1⊥BC1．BC1⊥B1C两个关系来实现，两关系容易证明．（2）因为BC1⊥平面A1B1CD，所以A1O为斜线A1B在平面A1B1CD内的射影，所以∠BA1O 为A1B与平面A1B1CD所成的角．在RT△A1BO中求解即可．【解答】解：（1）连接B1C交BC1于点O，连接A1O．在正方体ABCD﹣A1B1C1D1中因为A1B1⊥平面BCC1B1．所以A1B1⊥BC1．又∵BC1⊥B1C，又BC1∩B1C=O∴BC1⊥平面A1B1CD（2）因为BC1⊥平面A1B1CD，所以A1O为斜线A1B在平面A1B1CD内的射影，所以∠BA1O 为A1B与平面A1B1CD所成的角．设正方体的棱长为a在RT△A1BO中，A1B=a，BO=a，所以BO=A1B，∠BA1O=30°，即直线A1B和平面A1B1CD所成的角为30°．【点评】本题考查空间直线与平面垂直关系的判断，线面角大小求解，考查空间想象能力、推理论证、计算、转化能力．21.如图，在四棱锥P﹣ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，E是PC的中点．（1）证明：PA∥平面EDB；（2）证明：平面PAC⊥平面PDB．答案及解析：21.【考点】平面与平面垂直的判定；直线与平面平行的判定．【专题】证明题；转化思想；综合法；空间位置关系与距离．【分析】（1）欲证PA∥平面EDB，根据直线与平面平行的判定定理可知只需证PA与平面EDB内一直线平行，连接AC，交BD于O，连接EO，根据中位线定理可知EO∥PA，PA⊄平面EDB，EO⊂平面EDB，满足定理所需条件；（2）证明AC⊥平面PBD，即可证明平面PAC⊥平面PDB．【解答】证明：（1）设AC与BD相交于点O，则O为AC的中点．∵E是P的中点，∴EO∥PA又∵EO⊂平面EDB，PA⊄平面EDB，∴PA∥平面EDB；（2）∵PO⊥平面ABCD，∴PD⊥AC又∵四边形ABCD为正方形，∴AC⊥BD从而AC⊥平面PBD，∴平面PAC⊥平面PBD．【点评】本题考查直线与平面平行的判定，以及平面与平面垂直的判定，考查空间想象能力，逻辑思维能力，计算能力，是中档题．22.如图，在直三棱柱ABC=A1B1C1中，AD⊥平面A1BC，其垂足D落在直线A1B上．（1）求证：BC⊥A1B；（2）若AD=，AB=BC=2，P为AC的中点，求二面角P﹣A1B﹣C的平面角的余弦值．答案及解析：22.【考点】用空间向量求平面间的夹角；空间中直线与直线之间的位置关系．【专题】空间位置关系与距离；空间角．【分析】（Ⅰ）由已知得A1A⊥平面ABC，A1A⊥BC，AD⊥BC．由此能证明BC⊥A1B．（Ⅱ）由（Ⅰ）知BC⊥平面A1AB，从而BC⊥AB，以B为原点建立空间直角坐标系B﹣xyz，利用向量法能求出二面角P﹣A1B﹣C的平面角的余弦值．【解答】（Ⅰ）证明：∵三棱柱ABC﹣A1B1C1为直三棱柱，∴A1A⊥平面ABC，又BC⊂平面ABC，∴A1A⊥BC，∵AD⊥平面A1BC，且BC⊂平面A1BC，∴AD⊥BC．又AA1⊂平面A1AB，AD⊂平面A1AB，A1A∩AD=A，∴BC⊥平面A1AB，又A1B⊂平面A1BC，∴BC⊥A1B．（Ⅱ）解：由（Ⅰ）知BC⊥平面A1AB，AB⊂平面A1AB，从而BC⊥AB，如图，以B为原点建立空间直角坐标系B﹣xyz∵AD⊥平面A1BC，其垂足D落在直线A1B上，∴AD⊥A1B．在Rt△ABD中，AD=，AB=2，sin∠ABD==，∠ABD=60°，在直三棱柱ABC﹣A1B1C1中，A1A⊥AB．在Rt△ABA1中，AA1=AB•tan60°=2，则B（0，0，0），A（0，2，0），C（2，0，0），P（1，1，0），A 1（0，2，2），，=（0，2，2），，设平面PA1B的一个法向量，则，即，得，设平面CA1B的一个法向量，则，即，得，，∴二面角P﹣A1B﹣C平面角的余弦值是．…【点评】本题考查异面直线垂直的证明，考查二面角的余弦值的求法，解题时要认真审题，注意空间思维能力的培养．23.（16分）如图，在正方体ABCD﹣A1B1C1D1的棱长为a，E为棱AB上的一动点．（1）若E为棱AB的中点，①求四棱锥B1﹣BCDE的体积②求证：面B1DC⊥面B1DE（2）若BC1∥面B1DE，求证：E为棱AB的中点．答案及解析：23.【考点】棱柱、棱锥、棱台的体积；直线与平面平行的判定；平面与平面垂直的判定．【专题】数形结合；数形结合法；空间位置关系与距离．【分析】（1）①四棱锥B1﹣BCDE的底面为直角梯形BEDC，棱锥的高为B1B，代入体积公式即可；②面B1DC∩面B1DE=B1D，故只需在平面B1DE找到垂直于交线B1D的直线即可，由DE=B1E=a可易知所找直线为等腰△EB1D底边中线；（2）辅助线同上，由中位线定理可得OF∥DC，且OF=DC，从而得出OF∥EB，由BC1∥面B1DE可得EO∥B1C，故四边形OEBF是平行四边形，得出结论．【解答】证明：（1）①∵正方体ABCD﹣A1B1C1D1∴B1B平面BEDC，•B1B=•（a+）•a•a=．∴V=•S梯形BCDE②取B1D的中点O，设BC1∩B1C=F，连接OF，∵O，F分别是B1D与B1C的中点，∴OF∥DC，且OF=DC，又∵E为AB中点，∴EB∥DC，且EB=DC，∴OF∥EB，OF=EB，即四边形OEBF是平行四边形，∴OE∥BF，∵DC⊥平面BCC1B1，BC1⊂平面BCC1B1，∴BC1⊥DC，∴OE⊥DC．又BC1⊥B1C，∴OE⊥B1C，又∵DC⊂平面B1DC，B1C⊂平面B1DC，DC∩B1C=C，∴OE⊥平面B1DC，。
立体几何经典试题（含答案）
1. 如图，三棱柱ABC －A 1B 1C 1中，侧棱垂直底面，∠ACB=90°，AC=BC=12AA 1，D 是棱AA 1的中点的中点(Ｉ)证明：平面BDC 1⊥平面BDC（Ⅱ）平面BDC 1分此棱柱为两部分，求这两部分体积的比. 【解析】（Ⅰ）由题设知BC BC⊥⊥1CC ,BC ,BC⊥⊥AC AC，，1CC AC C Ç=,∴BC ^面11ACC A , , 又又∵1DC Ì面11ACC A ，∴1DC BC ^,由题设知01145A DC ADC Ð=Ð=,∴1CDC Ð=090,即1DC DC ^, 又∵DC BC C Ç=, , ∴∴1DC ⊥面BDC , , ∵∵1DC Ì面1BDC ， ∴面BDC ⊥面1BDC ；（Ⅱ）设棱锥1B DACC -的体积为1V ，AC =1，由题意得，1V =1121132+´´´=12，由三棱柱111ABC A B C -的体积V =1，∴11():V V V -=1:1， ∴平面1BDC 分此棱柱为两部分体积之比为1:1. 2. 如图5所示，在四棱锥P ABCD -中，AB ^平面PAD ，//AB CD ，PD AD =，E 是PB 的中点，F 是CD 上的点且12DF AB =，PH 为△PAD 中AD 边上的高. （1）证明：PH ^平面ABCD ；（2）若1PH =，2AD =，1FC =，求三棱锥E BCF -的体积；的体积；（3）证明：EF ^平面PAB . B 1C B A D C 1A 1【解析】（1）证明：因为AB ^平面PAD ，所以PH AB ^。
因为PH 为△PAD 中AD 边上的高，边上的高， 所以PH AD ^。
因为AB AD A = ，所以PH ^平面ABCD 。
（2）连结BH ，取BH 中点G ，连结EG 。
立体几何大题(解析版)
立体几何大题1.空间中的平行关系（1）线线平行（2）线面平行的判定定理：平面外一直线与平面内一直线平行，则线面平行（3）线面平行的性质定理若线面平行，经过直线的平面与该平面相交，则直线与交线平行（4）面面平行的判定定理判定定理1：一个平面内有两条相交直线分别平行于另一个平面，则面面平行判定定理2：一个平面内有两条相交直线分别于另一个平面内两条相交直线平行，则面面平行（5）面面平行的性质定理性质定理1：两平面互相平行，一个平面内任意一条直线平行于另一个平面性质定理2：两平面互相平行，一平面与两平面相交，则交线互相平行6.空间中的垂直关系（1）线线垂直（2）线面垂直的判定定理一直线与平面内两条相交直线垂直，则线面垂直（3）线面垂直的性质定理性质定理1：一直线与平面垂直，则这条直线垂直于平面内的任意一条直线性质定理2：垂直于同一个平面的两条直线平行（4）面面垂直的判定定理一个平面内有一条直线垂直于另一个平面，则两个平面垂直(或：一个平面经过另一个平面的垂线，则面面垂直)（5）面面垂直的性质定理两平面垂直，其中一个平面内有一条直线与交线垂直，则这条直线垂直于另一个平面6.异面直线所成角cos θ=cos a ,b =|a ⋅b ||a |⋅|b |=|x 1x 2+y 1y 2+z 1z 2|x 12+y 12+z 12⋅x 22+y 22+z 22(其中θ(0°<θ≤90°)为异面直线a ,b 所成角，a ,b 分别表示异面直线a ,b 的方向向量)7.直线AB 与平面所成角，sin β=AB ⋅m |AB ||m |(m 为平面α的法向量).8.二面角α-l -β的平面角cos θ=m ⋅n |m ||n |(m ，n 为平面α，β的法向量).9.点B 到平面α的距离d =|AB ⋅n | |n |(n 为平面α的法向量，AB 是经过面α的一条斜线，A ∈α).模拟训练一、解答题1(22·23下·湖南·二模)如图，在直三棱柱ABC -A B C 中，∠ABC =120°,AB =BC =2,AC =BB ，点D 为棱BB 的中点，AE =13AC ．(1)求DE 的长度；(2)求平面CDE 与平面BDE 夹角的余弦值．【答案】(1)393(2)34【分析】(1)在△ABC 中，用余弦定理可得到AC =23，在△ABE 中，用余弦定理可得BE =233，即可求得DE =DB 2+BE 2=393；(2)以B 为原点，分别以BE ,BC ,BB 所在的直线为x ,y ,z 轴建立空间直角坐标系，求出平面CDE 与平面BDE 的法向量，即可求解【详解】(1)因为在直三棱柱ABC -A B C 中，∠ABC =120°,AB =BC =2，在△ABC 中，由余弦定理得cos ∠ABC =AB 2+BC 2-AC 22AB ⋅BC=22+22-AC 22×2×2=-12，解得AC =23，则AE =13AC =233，在△ABE 中，由余弦定理得cos ∠BAE =AB 2+AE 2-BE 22AB ⋅AE =22+233 2-BE 22×2×233=32，解得BE =233，又AC =BB =23，所以BD =12BB =3，因为BB ⊥平面ABC ，BE ⊂平面ABC ，所以BB ⊥BE ，在直角三角形DBE 中，DE =DB 2+BE 2=(3)2+233 2=393；(2)因为AE =BE =233，所以∠ABE =∠BAE =30°，则∠CBE =∠ABC -∠ABE =120°-30°=90°，则BE ,BC ,BB 两两互相垂直，以B 为原点，分别以BE ,BC ,BB 所在的直线为x ,y ,z 轴建立如下图所示的空间直角坐标系：则点C 0,2,0 ,D 0,0,3 ,E 233,0,0 ，则CD =0,-2,3 ,CE =233,-2,0 ，设平面CDE 的法向量为n =x ,y ,z ，由n ⋅CD =x ,y ,z ⋅0,-2,3 =-2y +3z =0n ⋅CE =x ,y ,z ⋅233,-2,0 =233x -2y =0 ，得z =233y x =3y，令y =3，得平面CDE 的一个法向量为n =3,3,2 ；平面BDE 的一个法向量为m =0,1,0 ．设平面CDE 与平面BDE 夹角的大小为θ，则cos θ=m ⋅n m n =0,1,0 ⋅3,3,2 1×4=34，故平面CDE 与平面BDE 夹角的余弦值为34．2(22·23下·绍兴·二模)如图，在多面体ABCDE 中，DE ⊥平面BCD ,△ABC 为正三角形，△BCD 为等腰Rt △,∠BDC =90°,AB =2,DE =2.(1)求证：AE ⊥BC ；(2)若AE ⎳平面BCD ，求直线BE 与平面ABC 所成的线面角的正弦值.【答案】(1)证明见解析(2)63【分析】(1)由线面垂直的性质定理和判定定理即可证明；(2)法一：由分析可知，∠EBH 就是直线BE 与平面ABC 所成的线面角，设∠AFD =α，当α<90°时，O 与D 重合，可得A ,E 两点重合，不符合题意，当α>90°时，求出EH ,BE ，即可得出答案；法二：建立空间直角坐标系，求出直线BE 的方向向量与平面ABC 的法向量，由线面角的向量公式代入即可得出答案.【详解】(1)设F 为BC 中点，连接AF ,EF ，则由△ABC 为正三角形，得AF ⊥BC ；DE ⊥平面BCD ，且△BCD 为等腰直角三角形，计算可得：BE =CE =2,∴EF ⊥BC .EF ∩AF =F ,EF ,AF ⊂面AEF ，于是BC ⊥面AEF ，AE ⊂面AEF ，从而BC ⊥AE .(2)法一：由(1)可知，过点E 作EH ⊥AF ，垂足为H ，则∠EBH 就是直线BE 与平面ABC 所成的线面角.当AE ⎳平面BCD 时，可得A 到平面BCD 的距离为 2.设∠AFD =α，所以AF ⋅sin α=2，可得sin α=63，当α<90°时，cos α=33，不妨设A 在底面BCD 射影为O ，则FO =1，此时O 与D 重合，可得A ,E 两点重合，不符合题意，舍去；当α>90°时，FO =1，此时O 在DF 的延长线上，作EH ⊥AF ，由于AODE 为矩形，可得AE =DO =2,AE ∥OD ，可得sin ∠EAH =63，可得EH =263.于是sin ∠EBH =EH BE=63.法二：建立如图坐标系，可得F 0,0,0 ,B 1,0,0 ，C -1,0,0 ,D 0,1,0 ,E 0,1,2 ,A 0,a ,b由AF =3，解得a 2+b 2=3，又∵AE ⎳平面BCD ，令n =0,0,1 ，可得AB ⋅n =0，解得b =2,a =±1.当a =1时A ,E 重合，所以a =-1，此时A 0,-1,2 .不妨设平面ABC 的法向量为m =x ,y ,z ，则CB ⋅m =0CA ⋅m =0代入得x -y +2z =02x =0 ，令z =1，则y =2，所以m =0,2,1 .由于BE =-1,1,2 ，不妨设所成角为θ，则sin θ=∣cos BE ,m |=63.3(22·23·张家口·三模)如图，在三棱柱ABC -A 1B 1C 1中，侧面BB 1C 1C 为菱形，∠CBB 1=60°，AB =BC =2，AC =AB 1=2.(1)证明：平面ACB 1⊥平面BB 1C 1C ；(2)求平面ACC 1A 1与平面A 1B 1C 1夹角的余弦值.【答案】(1)证明见解析；(2)57.【分析】(1)利用面面垂直的判定定理进行证明；(2)利用垂直关系建立空间直角坐标系，用向量法进行求解.【详解】(1)如图，连接BC 1，交B 1C 于O ，连接AO .因为侧面BB 1C 1C 为菱形，所以B 1C ⊥BC 1，且O 为BC 1的中点.又AC =AB 1=2，故AO ⊥B 1C .又AB =BC =2，且∠CBB 1=60°，所以CO =1,BO =3，所以AO =AC 2-CO 2=1.又AB =2，所以AB 2=BO 2+AO 2，所以AO ⊥BO .因为BO ,CB 1⊂平面BB 1C 1C ，BO ∩CB 1=O ，所以AO ⊥平面BB 1C 1C .又AO ⊂平面ACB 1，所以平面ACB 1⊥平面BB 1C 1C .(2)由(1)知，OA ,OB ,OB 1两两互相垂直，因此以O 为坐标原点，OB ,OB 1,OA 所在直线分别为x 轴，y 轴，z 轴，建立如图所示的空间直角坐标系O -xyz ，则A (0,0,1)，B (3,0,0)，C (0,-1,0)，C 1(-3,0,0).故CC 1 =(-3,1,0)，CA =(0,1,1)，CB =(3,1,0).设n =(x 1,y 1,z 1)为平面ACC 1A 1的一个法向量，则有n ⋅CC 1 =0n ⋅CA =0 ，即-3x 1+y 1=0y 1+z 1=0 ，令x 1=1，则n =(1,3,-3).设m =(x 2,y 2,z 2)为平面ABC 的一个法向量，则有m ⋅CA =0m ⋅CB =0，即y 2+z 2=03x 2+y 2=0 ，令x 2=1，则m =(1,-3,3).因为平面A 1B 1C 1∥平面ABC ，所以m =(1,-3,3)也是平面A 1B 1C 1的一个法向量.所以cos <n ,m > =n ⋅m n m=1-3-3 7×7=57.所以平面ACC 1A 1与平面A 1B 1C 1夹角的余弦值57. 4(22·23·湛江·二模)如图1，在五边形ABCDE 中，四边形ABCE 为正方形，CD ⊥DE ，CD =DE ，如图2，将△ABE 沿BE 折起，使得A 至A 1处，且A 1B ⊥A 1D ．(1)证明：DE ⊥平面A 1BE ；(2)求二面角C -A 1E -D 的余弦值．【答案】(1)证明见解析(2)63【分析】(1)由已知易得DE ⊥BE ，即可证明线面垂直；(2)建立空间直角坐标系，用坐标公式法求解即可．【详解】(1)由题意得∠BEC =∠CED =π4，∠BED =π2，DE ⊥BE ，因为AB ⊥AE ，则A 1B ⊥A 1E ，又A 1B ⊥A 1D ，A 1E ∩A 1D =A 1,A 1E ,A 1D ⊂面A 1ED ，所以A 1B ⊥面A 1ED ，又DE ⊂面A 1ED ，则DE ⊥A 1B ，又DE ⊥BE ，A 1B ∩BE =B ，A 1B ⊂平面A 1BE ，BE ⊂平面A 1BE ，所以DE ⊥平面A 1BE ．(2)取BE 的中点O ，可知BE =2CD ,OE =CD ，由DE ⊥BE ，且CD ⊥DE 可得OE ⎳CD ，所以四边形OCDE 是平行四边形，所以CO ∥DE ，则CO ⊥平面A 1BE ，设BE =2，以点O 为坐标原点，OB ,OC ,OA 1所在直线为坐标轴建立空间直角坐标系，如图，则A 1(0,0,1),E (-1,0,0),B (1,0,0),C (0,1,0),D (-1,1,0)，EA 1 =(1,0,1),EC =(1,1,0),ED =(0,1,0)，设平面A 1EC 的一个法向量为n 1 =(x 1,y 1,z 1)，则n 1 ⋅EA 1 =0n 1 ⋅EC =0 ，即x 1+z 1=0x 1+y 1=0 ，取x 1=1，则n 1 =(1,-1,-1)，设平面A 1ED 的一个法向量为n 2 =(x 2,y 2,z 2)，则n 2 ⋅E 1A =0n 2 ⋅ED =0 ，即x 2+z 2=0y 2=0 ，取x 2=1，则n 2 =(1,0,-1)，所以cos n 1 ,n 2 =n 1 ⋅n 2 n 1 n 2=63，由图可知，二面角C -A 1E -D 为锐角，所以面角C -A 1E -D 的余弦值为63．5(22·23下·长沙·三模)如图，在多面体ABCDE 中，平面ACD ⊥平面ABC ，BE ⊥平面ABC ，△ABC 和△ACD 均为正三角形，AC =4，BE =3，点F 在AC 上.(1)若BF ⎳平面CDE ，求CF ；(2)若F 是AC 的中点，求二面角F -DE -C 的正弦值.【答案】(1)CF =1(2)8517【分析】(1)记AC 中点为M ，连接DM 、BM ，依题意可得DM ⊥AC ，根据面面垂直的性质得到DM ⊥平面ABC ，如图建立空间直角坐标系，求出平面CDE 的法向量，设F a ,0,0 ，a ∈2,-2 ，依题意可得BF ⋅n =0求出a 的值，即可得解；(2)依题意点F 与点M 重合，利用空间向量法计算可得.【详解】(1)记AC 中点为M ，连接DM 、BM ，△ACD 为正三角形，AC =4，则DM ⊥AC ，且DM =2 3.因为平面ACD ⊥平面ABC ，平面ACD ∩平面ABC =AC ，DM ⊂平面ACD ，所以DM ⊥平面ABC ，又△ABC 为正三角形，所以BM ⊥AC ，所以BM =23，如图建立空间直角坐标系，则B 0,23,0 ，C -2,0,0 ，D 0,0,23 ，E 0,23,3 ，所以CD =2,0,23 ，CE =2,23,3 ，设平面CDE 的法向量为n =x ,y ,z ，则n ⋅CD =2x +23z =0n ⋅CE =2x +23y +3z =0，令x =3，则z =-3，y =-32，则n =3,-32,-3 ，设F a ,0,0 ，a ∈-2,2 ，则BF =a ,-23,0 ，因为BF ⎳平面CDE ，所以BF ⋅n =3a +-23 ×-32+0×-3 =0，解得a =-1，所以F 为CM 的中点，此时CF =1.(2)若F 是AC 的中点，则点F 与点M 重合，则平面FDE 的一个法向量可以为m =1,0,0 ，设二面角F -DE -C 为θ，显然二面角为锐角，则cos θ=m ⋅n m ⋅n=332+-32 2+-3 2=651，所以sin θ=1-cos 2θ=1-651 2=8517，所以二面角F -DE -C 的正弦值为8517.6(22·23下·湖北·二模)如图，S 为圆锥的顶点，O 是圆锥底面的圆心，△ABC 内接于⊙O ,AC ⊥BC ,AC =BC =322，AM =2MS ,AS =3,PQ 为⊙O 的一条弦，且SB ⎳平面PMQ .(1)求PQ 的最小值；(2)若SA ⊥PQ ，求直线PQ 与平面BCM 所成角的正弦值.【答案】(1)22(2)3010【分析】(1)作出辅助线，找到符合要求的PQ ，并利用垂径定理得到最小值；(2)在第一问基础上，得到当PQ 取得最小值时，SA ⊥PQ ，并建立空间直角坐标系，利用空间向量求解线面角.【详解】(1)过点M 作MH ⎳SB 交AB 于点H ，过点H 作PQ ⊥AB ，此时满足SB ⎳平面PMQ ，由平面几何知识易知，PQ =2r 2-d 2，当弦心距d 最大时，d =OH ，弦长最短，即PQ 取得最小值，因为AM =2MS ,AS =3，所以AH =2HB ，因为AC ⊥BC ,AC =BC =322，由勾股定理得AB =322⋅2=3，故AH =2,HB =1，连接OQ ，则OQ =32，由勾股定理得HQ =OQ 2-OH 2=94-14=2，所以PQ =2HQ =22；(2)连接OS ，则OS ⊥平面ACB ，因为PQ ⊂平面ACB ，故OS ⊥PQ ，而SA ⊥PQ ，OS ∩SA =S ，所以PQ ⊥平面AOS ，即有PQ ⊥AB .以O 为坐标原点，过点O 且平行PQ 的直线为x 轴，OB 所在直线为y 轴，OS 所在直线为z 轴，建立空间直角坐标系，则P -2,12,0 ,Q 2,12,0 ,B 0,32,0 ,C 32,0,0 ,M 0,-12,3 ，设平面BCM 的法向量为m =x ,y ,z ，则m ⋅CB =x ,y ,z ⋅-32,32,0 =-32x +32y =0m ⋅MB =x ,y ,z ⋅0,2,-3 =2y -3z =0，令x =1，则y =1,z =233，故m =1,1,233，设直线PQ 与平面BCM 所成角的大小为θ，则sin θ=cos PQ ,m =PQ ⋅m PQ ⋅m =22,0,0 ⋅1,1,233 22×1+1+43=3010.故直线PQ与平面BCM所成角的正弦值为30 10.7(22·23·深圳·二模)如图，在四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD,PA= AD=2AB，点M是PD的中点.(1)证明：AM⊥PC；(2)设AC的中点为O，点N在棱PC上(异于点P，C)，且ON=OA，求直线AN与平面ACM所成角的正弦值.【答案】(1)证明见解析(2)1510【分析】(1)由等腰三角形的性质可得AM⊥PD，由面面垂直的性质可得CD⊥平面PAD，则CD⊥AM，所以由线面垂直的判定可得AM⊥平面PCD，从而可得结论；(2)以AB,AD,AP所在直线分别为x,y,z轴建立空间直角坐标系，利用空间向量求解即可.【详解】(1)证明：因为PA=AD，点M是PD的中点，所以AM⊥PD.因为PA⊥平面ABCD,PA⊂平面PAD，所以平面PAD⊥平面ABCD，因为四边形ABCD为矩形，所以CD⊥AD，因为平面PAD∩平面ABCD=AD，CD⊂平面ABCD，所以CD⊥平面PAD，所以CD⊥AM，因为PD∩CD=D，PD,CD⊂平面PCD，所以AM⊥平面PCD，因为PC⊂平面PCD，所以AM⊥PC.(2)解：由题意可得AB,AD,AP两两垂直，设AB=1，如图，以AB,AD,AP所在直线分别为x,y,z轴建立空间直角坐标系，则A(0,0,0),B(1,0,0),C(1,2,0),D(0,2,0),P(0,0,2)，因为点M是PD的中点，所以M0,22,22，所以AM =0,22,22 ,AC =1,2,0 ，设平面ACM 的法向量为n =x ,y ,z ，则AM ⋅n =22y +22z =0AC ⋅n =x +2y =0，令y =-1可得x =2,z =1，所以平面ACM 的一个法向量n =2,-1,1 .PC =1,2,-2 ，设N x N ,y N ,z N ,PN =λPC =λ,2λ,-2λ (0<λ<1)，即x N ,y N ,z N -2 =λ,2λ,-2λ ，所以N λ,2λ,2-2λ .又O 12,22,0 ,ON =OA =32，所以λ-12 2+2λ-22 2+(2-2λ)2=34，化简得5λ2-7λ+2=0，解得λ=25或λ=1(舍去).所以AN =25,225,325，设直线AN 与平面ACM 所成的角为θ，则sin θ=n ⋅AN n ⋅AN=3252+1+1×425+825+1825=1510，所以直线AN 与平面ACM 所成角的正弦值为1510.8(22·23下·温州·二模)已知三棱锥D -ABC 中，△BCD 是边长为3的正三角形，AB =AC =AD ,AD 与平面BCD 所成角的余弦值为33．(1)求证：AD ⊥BC ；(2)求二面角D -AC -B 的平面角的正弦值．【答案】(1)证明见解析(2)223【分析】(1)取BC 的中点E ，连接AE ,DE ，证明BC ⊥平面ADE ，即可得证；(2)取正三角形BCD 的中心O ，连接OA ，从而可得OA ⊥平面BCD ，则∠ODA 即为AD 与平面BCD 所成角的平面角，进而可得AB =AC =AD =3，取AC 中点为H ，连接DH ,BH ，则DH ⊥AC ,BH ⊥AC ，故∠BHD 即为二面角D -AC -B 的平面角，解△BDH 即可得解.【详解】(1)取BC 的中点E ，连接AE ,DE ，因为AB =AC ，所以AE ⊥BC ，因为△BCD 是边长为3的正三角形，所以DE ⊥BC ，又AE ∩DE =E ,AE ,DE ⊂平面ADE ，所以BC ⊥平面ADE ，因为AD ⊂平面ADE ，所以AD ⊥BC ；(2)取正三角形BCD 的中心O ，连接OA ，则点O 在DE 上，且OD =23DE ，由AB =AC =AD ，△BCD 是正三角形，得三棱锥A -BCD 为正三棱锥，则OA ⊥平面BCD ，故∠ODA 即为AD 与平面BCD 所成角的平面角，又AD 与平面BCD 所成角的余弦值为33，所以OD AD =3×32×23AD=33，即AB =AC =AD =3，即三棱锥A -BCD 是正四面体，取AC 中点为H ，连接DH ,BH ，则DH ⊥AC ,BH ⊥AC ，故∠BHD 即为二面角D -AC -B 的平面角，在△BDH 中，BH =DH =332,BD =3，则cos ∠BHD =BH 2+DH 2-BD 22⋅BH ⋅DH =274+274-92×332×332=13，所以sin ∠BHD =1-cos 2∠BHD =223，所以二面角D -AC -B 的平面角的正弦值223．9(22·23下·浙江·二模)如图，四面体ABCD ,AD ⊥CD ,AD =CD ,AC =2,AB =3,∠CAB =60°，E 为AB 上的点，且AC ⊥DE ,DE 与平面ABC 所成角为30°，(1)求三棱锥D -BCE 的体积；(2)求二面角B -CD -E 的余弦值.【答案】(1)答案见解析；(2)答案见解析．【分析】(1)取AC 中点F ，可证明AC ⊥平面DEF ，得平面ABC ⊥平面DEF ，DE 在平面ABC 内的射影就是直线EF ，∠DEF 是DE 与平面ABC 所成的角，即∠DEF =30°，由正弦定理求得∠FDE ，有两个解，在∠FDE =60°时可证DF ⊥平面ABC ，在∠FDE =120°时，取FE 中点H 证明DH ⊥平面ABC ，然后由棱锥体积公式计算体积；(2)建立如图所示的空间直角坐标系，用空间向量法求二面角．【详解】(1)取AC 中点F ，连接FE ,FD ，因为AD =CD ，所以DF ⊥AC ，又AC ⊥DE ，DE ∩DF =D ，DE ,DF ⊂平面DEF ，所以AC ⊥平面DEF ，而FE ⊂平面DEF ，所以AC ⊥FE ，由已知AF =1，∠BAC =60°，所以EF =3，AE =2，BE =1，由AC ⊥平面DEF ，AC ⊂平面ABC 得平面ABC ⊥平面DEF ，因此DE 在平面ABC 内的射影就是直线EF ，所以∠DEF 是DE 与平面ABC 所成的角，即∠DEF =30°，AD =CD ,AC =2，因此DF =12AC =1，在△DEF 中，由正弦定理EF sin ∠FDE =DF sin ∠DEF 得1sin30°=3sin ∠FDE ，sin ∠FDE =32，∠FDE 为△DEF 内角，所以∠FDE =60°或120°，S △ABC =12AB ×AC ×sin ∠BAC =12×3×2×sin60°=333，S △CBE =BE BAS △ABC =3-23×332=32，若∠FDE =60°，则∠DFE =90°，即DF ⊥FE ，AC ∩FE =F ，AC ,FE ⊂平面ABC ，所以DF ⊥平面ABC ，V D -BCE =13S △BCE ⋅DF =13×32×1=36；若∠FDE =120°，则∠DFE =30°，DF =DE =1，取EF 中点H ，连接DH ，则DH ⊥EF ，因为平面ABC ⊥平面DEF ，平面ABC ∩平面DEF =EF ，而DH ⊂平面DEF ，所以DH ⊥平面ABC ，DH =DF sin ∠DFE =1×sin30°=12，所以V D -BCE =13S △BCE ⋅DF =13×32×12=312；(2)若∠FDE =60°，以FA ,FE ,FD 为x ,y ,z 轴建立如图所示的空间直角坐标系F -xyz ，则D (0,0,1)，C (-1,0,0)，A (1,0,0)，E (0,3,0)，AE =(-1,3,0)，EB =12AE =-12,32,0 ，所以B 点坐标为-12,332,0 ，CD =(1,0,1)，CB =12,332,0 ，CE =(1,3,0)，设平面DBC 的一个法向量是m =(x 1,y 1,z 1)，则m ⋅CD =x 1+z 1=0m ⋅CB =12x 1+332y 1=0，取y 1=-1，则x 1=33，z 1=-33，即m =(33,-1,-33)，设平面DEC 的一个法向量是n =(x 2,y 2,z 2)，则n ⋅CD =x 2+z 2=0n ⋅CE =x 2+3y 2=0，取y 2=-1，则x 2=3，z 2=-3，即m =(3,-1,-3)，cos m ,n =m ⋅n m n =9+1+955×7=19385385，所以二面角B -CD -E 的余弦值是19385385；若∠FDE =120°，以FA 为x 轴，FE 为y 轴，过F 且平行于HD 的直线为z 轴建立如图所示的空间直角坐标系F -xyz ，FH =12FE =32，则D 0,32,12 ，C (-1,0,0)，A (1,0,0)，E (0,3,0)，AE =(-1,3,0)，EB =12AE =-12,32,0 ，所以B 点坐标为-12,332,0 ，CD =1,32,12 ，CB =12,332,0 ，CE =(1,3,0)，设平面DBC 的一个法向量是m =(x 1,y 1,z 1)，则m ⋅CD =x 1+32y 1+12z 1=0m ⋅CB =12x 1+332y 1=0，取y 1=-1，则x 1=33，z 1=-53，即m =(33,-1,-53)，设平面DEC 的一个法向量是n =(x 2,y 2,z 2)，则n ⋅CD =x 2+32y 2+12z 2=0n ⋅CE =x 2+3y 2=0，取y 2=-1，则x 2=3，z 2=-3，即m =(3,-1,-3)，cos m ,n =m ⋅n m n =9+1+15103×7=25721721，所以二面角B -CD -E 的余弦值是25721721．10(22·23下·襄阳·三模)如图，在三棱柱ABC -A 1B 1C 1中，侧面BB 1C 1C 为矩形，∠BAC =90°，AB =AC =2，AA 1=4，A 1在底面ABC 的射影为BC 的中点N ，M 为B 1C 1的中点.(1)求证：平面A 1MNA ⊥平面A 1BC ；(2)求平面A 1B 1BA 与平面BB 1C 1C 夹角的余弦值.【答案】(1)证明见解析(2)23015【分析】(1)利用线面垂直和面面垂直的判定定理证明；(2)利用空间向量的坐标运算求面面夹角的余弦值.【详解】(1)如图，∵A 1N ⊥面ABC ，连AN ，则AN ⊥A 1N ，又AB =AC =2，∴AN ⊥BC ，又AN ∩BC =N ，A 1N ⊂面A 1BC ，BC ⊂面A 1BC ，于是AN ⊥面A 1BC ，又AN ⊂面A 1MN ，，所以面A 1BC ⊥面A 1MNA .(2)由(1)可得，以NA ,NB ,NA 1 为x ,y ,z 轴，建系如图，∠BAC =90°，AB =AC =2，BC =22则A (2,0,0),B (0,2,0),C (0,-2,0),因为AA 1=4,AN =2,所以A 1N =14,则A 1(0,0,14),因为NB 1 =NB +BB 1 =NB +AA 1 =0,2,0 +-2,0,14 =-2,2,14 ,所以B 1-2,2,14 ,设平面A 1BB 1的一个法向量为m =(x ,y ,z )，因为A 1B =(0,2,-14),B 1B =(2,0,-14),所以A 1B ⋅m =2y -14z =0B 1B ⋅m =2x -14z =0 ，令y =7，则x =7,z =1，所以m =(7,7,1)，设平面BCC 1B 1的一个法向量为n =(a ,b ,c )，因为BC =(0,-22,0),BB 1 =(-2,0,14),所以BC ⋅n =-22b =0BB 1 ⋅n =-2a +14c =0，令a =7，则b =0,c =1，所以n =(7,0,1)，设平面A 1BB 1与平面BCC 1B 1夹角为θ，则cos θ=cos <m ,n >=m ⋅n m n=7+0+17+7+1×7+0+1=23015，所以平面A 1BB 1与平面BCC 1B 1夹角的余弦值为23015.11(22·23·唐山·二模)如图，在三棱柱ABC -A 1B 1C 1中，△ABC 是等边三角形，侧面ACC 1A 1⊥底面ABC ，且AA 1=AC ，∠AA 1C 1=120°，M 是CC 1的中点．(1)证明：A 1C ⊥BM ．(2)求二面角A 1-BC -M 的正弦值．【答案】(1)证明见解析(2)45【分析】(1)根据菱形的性质、结合面面垂直的性质，线面垂直的判定定理进行证明即可；(2)建立空间直角坐标系，运用空间向量夹角公式进行求解即sk .【详解】(1)取AC 的中点O ，连接OM ，OB ，AC 1．在三棱柱ABC -A 1B 1C 1中，由AA 1=AC ，得四边形ACC 1A 1为菱形，所以A 1C ⊥AC 1，易知OM ∥AC 1，则A 1C ⊥OM ．由△ABC 是等边三角形，知OB ⊥AC ，又平面ACC 1A 1⊥平面ABC ，平面ACC 1A 1∩平面ABC =AC ，OB ⊂平面ABC ，知OB ⊥平面ACC 1A 1，则OB ⊥A 1C ，又OB ∩OM =O ,OB ,OM ⊂平面OBM ，得A 1C ⊥平面OBM ，又BM ⊂平面OBM ，故A 1C ⊥BM ．.(2)连接OA 1，因为侧面ACC 1A 1为菱形，∠AA 1C 1=120°，则∠A 1AC =60°，则△A 1AC 为等边三角形，所以A 1O ⊥AC ，又由(1)易知OA 1，OB ，AC 两两垂直，故以O 为坐标原点，分别以OB ，OC ，OA 1 的方向为x 轴、y 轴、z 轴的正方向，建立空间直角坐标系．不妨设AB =2，则O 0,0,0 ，B 3,0,0 ，C 0,1,0 ，A 10,0,3 ，C 10,2,3 ，BA 1 =-3,0,3 ，BC =-3,1,0 ，CC 1 =0,1,3 ，设平面A 1BC 的法向量为n =x ,y ,z ，则n ⋅BC =-3x +y =0n ⋅BA 1 =-3x +3z =0 ，令x =1，得n =1,3,1 ，设平面BCC 1的法向量为m =a ,b ,c ，则m ⋅BC =-3a +b =0m ⋅CC 1 =b +3c =0，令a =1，得m =1,3,-1 ，所以cos n ,m =n ⋅m n ⋅m=35⋅5=35，即二面角A 1-BC -M 的正弦值为45．12(22·23下·盐城·三模)如图，该几何体是由等高的半个圆柱和14个圆柱拼接而成，点G 为弧CD 的中点，且C ，E ，D ，G 四点共面.(1)证明：平面BDF ⊥平面BCG ；(2)若平面BDF 与平面ABG 所成二面角的余弦值为155，且线段AB 长度为2，求点G 到直线DF 的距离.【答案】(1)证明见解析(2)62【分析】(1)过G 作GH ⎳CB ，交底面弧于H ，连接HB ，有HBCG 为平行四边形，根据题设可得FB ⊥HB ，即FB ⊥CG ，再由线面垂直的性质可得CB ⊥FB ，最后根据线面、面面垂直的判定即可证结论.(2)构建如下图示空间直角坐标系A -xyz ，令半圆柱半径为r ，高为h ，确定相关点坐标，进而求平面BDF 、平面ABG 的法向量，利用空间向量夹角的坐标表示及已知条件可得h =2r ，即可求出点G 到直线DF 的距离.【详解】(1)过G 作GH ⎳CB ，交底面弧于H ，连接HB ，易知：HBCG 为平行四边形，所以HB ⎳CG ，又G 为弧CD 的中点，则H 是弧AB 的中点，所以∠HBA =45°，而由题设知：∠ABF =45°，则∠HBF =∠HBA +∠ABF =90°，所以FB ⊥HB ，即FB ⊥CG ，由CB ⊥底面ABF ，FB ⊂平面ABF ，则CB ⊥FB ，又CB ∩CG =C ，CB ,CG ⊂平面BCG ，所以FB ⊥平面BCG ，又FB ⊂平面BDF ，所以平面BDF ⊥平面BCG .(2)由题意，构建如下图示空间直角坐标系A -xyz ，令半圆柱半径为r ，高为h ，则B 0,2r ,0 ，F 2r ,0,0 ，D 0,0,h ，G -r ,r ,h ，所以FD =-2r ,0,h ，BD =0,-2r ,h ，AB =0,2r ,0 ，AG =-r ,r ,h ，若m =x ,y ,z 是面BDF 的一个法向量，则m ⋅FD =-2rx +hz =0m ⋅BD =-2ry +hz =0 ，令z =2r ，则m =h ,h ,2r ，若n =a ,b ,c 是面ABG 的一个法向量，则n ⋅AB =2rb =0n ⋅AG =-ra +rb +hc =0 ，令c =r ，则n =h ,0,r ，所以cos m ,n =m ⋅n m n=h 2+2r 22h 2+4r 2×h 2+r 2=155，整理可得h 2-4r 2 h 2+2r 2 =0，则h =2r ，又AB =2，由题设可知，此时点G -1,1,2 ，D 0,0,2 ，F 2,0,0 ，则DF =2,0,-2 ，DG =-1,1,0 ，所以点G 到直线DF 的距离d =DG 2-DG ⋅DF 2DF2=62.13(22·23下·江苏·三模)如图，圆锥DO 中，AE 为底面圆O 的直径，AE =AD ，△ABC 为底面圆O 的内接正三角形，圆锥的高DO =18，点P 为线段DO 上一个动点.(1)当PO =36时，证明：PA ⊥平面PBC ；(2)当P 点在什么位置时，直线PE 和平面PBC 所成角的正弦值最大.【答案】(1)证明见解析；(2)P 点在距离O 点36处【分析】(1)利用勾股定理证明出AP ⊥BP 和AP ⊥CP ，再用线面垂直的判定定理证明出PA ⊥平面PBC ；(2)建立空间直角坐标系，利用向量法求解.【详解】(1)因为AE =AD ，AD =DE ，所以△ADE 是正三角形，则∠DAO =π3，又DO ⊥底面圆O ，AE ⊂底面圆O ，所以DO ⊥AE ，在Rt △AOD 中，DO =18，所以AO =DO 3=63，因为△ABC 是正三角形，所以AB =AO ×32×2=63×3=18，AP =AO 2+PO 2=92，BP =AP ，所以AP 2+BP 2=AB 2，AP ⊥BP ，同理可证AP ⊥CP ，又BP ∩PC =P ，BP ，PC ⊂平面PBC ，所以PA ⊥平面PBC .(2)如图，建立以O 为原点的空间直角坐标系O -xyz .设PO =x ，(0≤x ≤18)，所以P 0,0,x ，E -33,9,0 ，B 33,9,0 ，C -63,0,0 ，所以EP =33,-9,x ，PB =33,9,-x ，PC =-63,0,-x ，设平面PBC 的法向量为n =a ,b ,c ，则n ⋅PB =33a +9b -cx =0n ⋅PC =-63a -cx =0，令a =x ，则b =-3x ，c =-63，故n =x ,-3x ,-63 ，设直线PE 和平面PBC 所成的角为θ，则sin θ=cos EP ,n =33x +93x -63x 108+x 2⋅x 2+3x 2+108=63x 108+x 2⋅4x 2+108=634x 2+1082x 2+540≤6324x 2⋅1082x 2+540=13，当且仅当4x 2=1082x 2，即PO =x =36时，直线PE 和平面PBC 所成角的正弦值最大，故P 点在距离O 点36处.14(22·23下·镇江·三模)如图，四边形ABCD 是边长为2的菱形，∠ABC =60°，四边形PACQ 为矩形，PA =1，从下列三个条件中任选一个作为已知条件，并解答问题(如果选择多个条件分别解答，按第一个解答计分).①BP ,DP 与平面ABCD 所成角相等；②三棱锥P -ABD 体积为33；③cos ∠BPA =55(1)平面PACQ ⊥平面ABCD ；(2)求二面角B -PQ -D 的大小；(3)求点C 到平面BPQ 的距离.【答案】(1)证明见解析(2)2π3(3)32【分析】(1)若选①，则作PA ⊥面ABCD ，证明A 和A 重合从而得到PA ⊥面ABCD ，从而得到面面垂直；若选②，计算得到P 到面ABD 的距离h =1=PA ，得到PA ⊥面ABCD ，从而得到面面垂直；若选③，通过余弦定理计算得到PA ⊥AB ，再通过PA ⊥面ABCD ，从而得到面面垂直；(2)通过建立空间直角坐标系，求出两个平面的法向量，结合二面角计算公式计算即可；(3)通过点面距离的计算公式直接计算即可.【详解】(1)选①，连接BD ，作PA ⊥面ABCD ，垂足为A .∵BP ,DP 与平面ABCD 所成角相等，∴A B =A D ，∴A 在BD 的中垂线AC 上，∵在平面PACQ 内，PA ⊥AC ,PA ⊥AC ,∴A 和A 重合，∴PA ⊥面ABCD ，又PA ⊂面PACQ ，∴面PACQ ⊥面ABCD若选②，设P 到面ABD 的距离为h ，∵V P -ABD =13S △ABD ⋅h =13×3⋅h =33，得h =1=PA ，∴PA 即为P 到面ABD 的距离，即PA ⊥面ABCD ，又PA ⊂面PACQ ，∴面PACQ ⊥面ABCD .若选③，由余弦定理得，cos ∠BPA =PB 2+PA 2-AB 22PB ⋅PA =55，∴BP =5,∴BP 2=AP 2+AB 2∴PA ⊥AB ，又PA ⊥AC ,AC ∩AB =A ,AC ,AB ⊂面ABCD∴PA ⊥面ABCD ，又PA ⊂面PACQ∴面PACQ ⊥面ABCD(2)因为PA ⊥面ABCD ，OB ,OC ⊂面ABCD ，所以PA ⊥OB ,PA ⊥OC ，取PQ 中点G ，则OG ⎳PA ，所以OG ⊥OB ,OG ⊥OC ，又因为OB ⊥OC ，所以建立如下图所示空间直角坐标系，∵B 3,0,0 ,P 0,-1,1 ,D -3,0,0 ,Q 0,1,1 ，∴BQ =-3,1,1 ,DQ =3,1,1 ,DP =3,-1,1 ，设平面BPQ 的一个法向量为m =x ,y ,z ，则m⋅BP =0m ⋅BQ =0 ，即-3x -y +z =0-3x +y +z =0 ，令x =3，则y =0,z =3,∴m =3,0,3 ，设平面DPQ 的一个法向量为n =x 1,y1,z 1 ，则n ⋅DP=0n ⋅DQ =0 ，即3x 1-y 1+z 1=3x 1+y 1+z 1=0，令x1=3，则y 1=0,z 1=-3,∴n =3,0,-3 ，∴cos m ,n =m ⋅n m ⋅ n =-623×23=-12，∵m ,n ∈0,π ,∴m ,n =2π3，由图可知二面角B -PQ -D 是钝角，所以二面角B -PQ -D 的大小为2π3.(3)∵C 0,1,0 ,Q 0,1,1 ，∴CQ =0,0,1 ,∵平面BPQ 的一个法向量为m =3,0,3 ，∴点C 到平面BPQ 的距离d =CQ ⋅m m=323=32.15(22·23下·江苏·一模)在三棱柱ABC -A 1B 1C 1中，平面A 1B 1BA ⊥平面ABC ，侧面A 1B 1BA 为菱形，∠ABB 1=π3，AB 1⊥AC ，AB =AC =2，E 是AC 的中点.(1)求证：A 1B ⊥平面AB 1C ；(2)点P 在线段A 1E 上(异于点A 1，E )，AP 与平面A 1BE 所成角为π4，求EP EA 1的值.【答案】(1)证明见解析(2)EP EA 1=25【分析】(1)作B 1O ⊥AB 交AB 于O 点，由面面垂直的性质可得B 1O ⊥平面ABC ，可得B 1O ⊥AC ，再由线面垂直的判定定理得AC ⊥平面A 1B 1BA ，从而得到AC ⊥A 1B ，再由线面垂直的判定定理可得答案；(2)以A 为原点，AB 、AC 、AO 1所在的直线分别为x 、y 、z 轴，建立空间直角坐标系，设EP =λEA 1 ，可得AP =-λ,1-λ,3λ ，求出平面A 1BE 的一个法向量，由线面角的向量求法可得答案.【详解】(1)因为侧面A 1B 1BA 为菱形，∠ABB 1=π3，AB =AC =2，所以△ABB 1、△AA 1B 1为边长为2的等边三角形，作B 1O ⊥AB 交AB 于O 点，则O 点为AB 的中点，因为平面A 1B 1BA ⊥平面ABC ，平面A 1B 1BA ∩平面ABC =AB ，B 1O ⊂平面A 1B 1BA ，所以B 1O ⊥平面ABC ，AC ⊂平面ABC ，可得B 1O ⊥AC ，又AB 1⊥AC ，B 1O ∩AB 1=B 1，B 1O 、AB 1⊂平面A 1B 1BA ，可得AC ⊥平面A 1B 1BA ，因为A 1B ⊂平面A 1B 1BA ，所以AC ⊥A 1B ，因为侧面A 1B 1BA 为菱形，所以B 1A ⊥A 1B ，AB 1∩AC =A ，AB 1、AC ⊂平面AB 1C ，所以A 1B ⊥平面AB 1C ；(2)由(1)知，AC ⊥平面A 1B 1BA ，∠BAC =π2，取做A 1B 1的中点O 1，连接AO 1，则B1O ⎳AO 1，所以AO 1⊥平面ABC ，以A 为原点，AB 、AC 、AO 1所在的直线分别为x 、y 、z 轴，建立空间直角坐标系，则A 0,0,0 ，A 1-1,0,3 ，B 2,0,0 ，E 0,1,0 ，A 1B =3,0,-3 ，EA 1 =-1,-1,3 ，设EP =λEA 1 ，可得P -λ,1-λ,3λ ，所以AP =-λ,1-λ,3λ ，设平面A 1BE 的一个法向量为n=x ,y ,z ，则A 1B ⋅n=0EA 1 ⋅n =0，即3x -3z =0-x -y +3z =0 ，令z =3，可得n =1,2,3 ，可得sin π4=cos n ,AP =n ⋅AP n AP=-λ+2-2λ+3λ 1+4+3λ2+1-λ 2+3λ2，解得λ=0舍去，或λ=25，所以EP EA 1=25.16(22·23下·河北·三模)如图，四棱锥P -ABCD 的底面ABCD 是菱形，其对角线AC ,BD 交于点O ，且PO ⊥平面ABCD ,OC =1,OD =OP =2,M 是PD 的中点，N 是线段CD 上一动点．(1)当平面OMN ⎳平面PBC 时，试确定点N 的位置，并说明理由；(2)在(1)的前提下，点Q 在直线MN 上，以PQ 为直径的球的表面积为214π．以O 为原点，OC ,OD ,OP 的方向分别为x 轴、y 轴、z 轴的正方向建立空间直角坐标系O -xyz ，求点Q 的坐标．【答案】(1)N 是CD 的中点(2)12,1,0 ，-1310,1,185 【分析】(1)根据面面平行的性质证明MN ⎳PC ，即可得解；(2)先根据球的体积求出PQ ，然后根据空间中两点间的距离公式即可得解.【详解】(1)因为平面OMN ⎳平面PBC ，平面OMN ∩平面PCD =MN ，平面PBC ∩平面PCD =PC ，所以MN ⎳PC ，因为M 是PD 的中点，所以N 是CD 的中点；(2)由题意4π×PQ 22=214π，解得PQ =212，设MQ =λMN,λ∈R ，由题意，P 0,0,2 ,M 0,1,1 ,N 12,1,0 ，则PM =0,1,-1 ,MN =12,0,-1 ，则PQ =PM +MQ =0,1,-1 +λ12,0,-1 =λ2,1,-λ-1 ，则λ24+1+-λ-1 2=212，解得λ=1或λ=-135，当λ=1时，MQ =MN ，则Q 12,1,0 ，当λ=-135时，MQ =-135MN =-1310,0,135，设Q x ,y ,z ，则MQ =x ,y -1,z -1 =-1310,0,135，所以x =-1310y -1=0z -1=135 ，解得x =-1310y =1z =185 ，则Q -1310,1,185 ，综上所述点Q 的坐标为12,1,0，-1310,1,185 .17(22·23·汕头·三模)如图，圆台O 1O 2的轴截面为等腰梯形A 1ACC 1，AC =2AA 1=2A 1C 1=4,B 为底面圆周上异于A ,C 的点.(1)在平面BCC 1内，过C 1作一条直线与平面A 1AB 平行，并说明理由；(2)若四棱锥B -A 1ACC 1的体积为23，设平面A 1AB ∩平面C 1CB =l ,Q ∈l ，求CQ 的最小值.【答案】(1)作图见解析，理由见解析(2)7【分析】(1)根据线面平行的判定和中位线定理即可求解;(2)根据几何关系或空间向量方法即可求解.【详解】(1)取BC 中点P ，作直线C 1P 即为所求，取AB 中点H ，连接A 2H ,PH ，则有PH ∥AC ,PH =12AC ，如图，在等腰梯形A 1ACC 1中，A 1C 1=12AC ，有HP ∥A 1C 1,HP =A 1C 1，则四边形A 1C 1PH 为平行四边形，即有C 1P ∥A 1H ，又A 1H ⊂平面A 1AB ,C 1P⊄平面A 1AB ，所以C 1P ∥平面A 1AB .(2)法一：延长AA 1,CC 1交于点O ，故O ∈AA 1⊂平面ABA 1,O ∈CC 1⊂平面CC 1B故平面A 1AB ∩平面C 1CB =BO ,BO 即l ,在△OBC 中，OC ,OB 均为圆锥母线.过点B 作BO ⊥AC 于O .在等腰梯形A 1ACC 1中，AC =2AA 1=2A 1C 1=4，此梯形的高h =AA 21-AC -A 1C 122=3,∴等腰梯形A 1ACC 1的面积为S =122+4 3=33，所以四棱锥B -A 1ACC 1的体积V =13S ×BO =13×33×BO =23，解得BO =2，故点O 与O 2重合，BC =22由AC =2AA 1=2A 1C 1，得OC =2CC 1，且∠C 1CA =60°，故OC =AC =4=OB .△OBC 中，O 到BC 距离h 1=OB 2-BC 22=14.则△OBC 面积=12OB ⋅CQ min =12BC ⋅h 1,得：CQ 的最小值为：CQ min =22⋅144=7.法二：同法一求出B 的位置.以O 2为原点，OB ,OC ,O 2O 1方向为x ,y ,z 轴正向建立空间直角坐标系，C 0,2,0 ,B 2,0,0 ,AA 1 =0,1,3 ,AB =2,2,0 ,CC 1 =0,-1,3 ,BC=-2,2,0设面A 1AB 的法向量为a=x 1,y 1,z 1a ⋅AA 1=y 1+3z 1=0a ⋅AB=2x 1+2y 1=0，取z 1=1，有a=3,-3,1 ；同理可得面C 1CB 的法向量为β=3,3,1 ,由l =面C 1CB ∩面A 1AB ，可知B ∈l ，设l 的方向向量为l=x ,y ,z ，故l ⋅a =3x -3y +z =0,l ⋅β=3x +3y +z =0取l=1,0,3 ,下面分2个方法求|CQ |min求|CQ |min 方法1：BQ =l=t ,0,3t ,，∵B 2,0,0 ,∴Q t -2,0,3t∴CQ =(t -2)2+22+(3t )2=4t 2-4t +8，当t =12时，CQ 取最小值为7.求CQ min 方法2：BC 在l 上的投影向量的模为BC ⋅l l =-2×1+2×0+0×32=1故CQ 的最小值即C 到l 的距离为BC 2-12=7.法三:在三角形△BCO 中，BO =CO =4,BC =22,cos ∠CBO =42+(22)2-422×4×22=122⋅sin ∠CBO =1-1222=722,所以CQ ≥CB sin ∠CBO =722×22=7.18(19·20下·临沂·二模)如图①，在Rt △ABC 中，B 为直角，AB =BC =6，EF ∥BC ，AE =2，沿EF 将△AEF 折起，使∠AEB =π3，得到如图②的几何体，点D 在线段AC 上．(1)求证：平面AEF ⊥平面ABC ；(2)若AE ⎳平面BDF ，求直线AF 与平面BDF 所成角的正弦值．【答案】(1)证明见解析；(2)64.【分析】(1)由余弦定理计算证明EA ⊥AB ，再利用线面垂直的判定、性质，面面垂直的判定推理作答.(2)以A 为原点，建立空间直角坐标系，利用空间向量求线面角的正弦作答.【详解】(1)在△ABE 中，AE =2,BE =4，∠AEB =π3，由余弦定理得：AB 2=AE 2+BE 2-2AE ⋅BE cos ∠AEB =4+16-2×2×4×12=12，则AB =23，有EB 2=EA 2+AB 2，于是∠EAB =π2，即有EA ⊥AB ，又EF ⊥EB ,EF ⊥EA ,EA ∩EB =E ,EA ,EB ⊂平面ABE ，因此EF ⊥平面ABE ，而AB ⊂平面ABE ，则EF ⊥AB ，又因为EA ∩EF =E ,EA ,EF ⊂平面AEF ，从而AB ⊥平面AEF ，而AB ⊂平面ABC ，所以平面AEF ⊥平面ABC .(2)以A 为原点，以AB ,AE 分别为x ,y 轴，过点A 垂直于平面ABE 的直线为z 轴，建立空间直角坐标系，如图，由(1)知，EF ⊥平面ABE ，而EF ⎳BC ，则有BC ⊥平面ABE ，则A (0,0,0),B (23,0,0),E (0,2,0),F (0,2,2),C (23,0,6)，AF =(0,2,2),FB =(23,-2,-2),AC=(23,0,6)，连接EC 与FB 交于点G ，连接DG ，因为AE ⎳平面BDF ，AE ⊂平面AEC ，平面AEC ∩平面BDF =DG ，则AE ⎳GD ，有GC GE =DCDA，在四边形BCFE 中，由EF ⎳BC ，得GC GE =BC EF =3，即DC DA=3，AD =14AC =32,0,32 ，FD =AD -AF =32,-2,-12，设平面BDF 的法向量为n =(x ,y ,z )，则n ⋅FD =32x -2y -12z =0n ⋅FB =23x -2y -2z =0，令x =1，得n =(1,0,3)，设直线AF 与平面BDF 所成角为θ，于是sin θ=|cos ‹n ,AF ›|=|n ⋅AF ||n ||AF |=2322×2=64，所以直线AF 与平面BDF 所成角的正弦值为64.19(22·23下·广州·三模)如图，四棱锥P -ABCD 的底面为正方形，AB =AP =2，PA ⊥平面ABCD ，E ,F 分别是线段PB ,PD 的中点，G 是线段PC 上的一点.(1)求证：平面EFG ⊥平面PAC ；(2)若直线AG 与平面AEF 所成角的正弦值为13，且G 点不是线段PC 的中点，求三棱锥E -ABG 体积.【答案】(1)证明见解析(2)19【分析】(1)由线面垂直判定可证得BD ⊥平面PAC ，由中位线性质知EF ⎳BD ，从而得到EF ⊥平面PAC ，由面面垂直判定可得结论；(2)以A 为坐标原点可建立空间直角坐标系，设PG =λPC ，λ∈0,12 ∪12,1 ，由线面角的向量求法可构造方程求得λ，结合垂直关系可得G 平面PAB 的距离为16BC =13，利用棱锥体积公式可求得结果.【详解】(1)连接BD ，∵E ,F 分别是线段PB ,PD 的中点，∴EF ⎳BD ，∵底面四边形ABCD 为正方形，∴BD ⊥AC ，∵PA ⊥平面ABCD ，BD ⊂平面ABCD ，∴PA ⊥BD ，又PA ∩AC =A ，PA ,AC ⊂平面PAC ，∴BD ⊥平面PAC ，∵EF ⎳BD ，∴EF ⊥平面PAC ，又EF ⊂平面EFG ，∴平面EFG ⊥平面PAC .(2)以A 为坐标原点，分别以AB ,AD ,AP 所在直线为x ,y ,z 轴建立空间直角坐标系，则A 0,0,0 ，E 1,0,1 ，F 0,1,1 ，P 0,0,2 ，C 2,2,0 ，设PG =λPC ，λ∈0,12 ∪12,1 ，则AG =AP +PG =0,0,2 +2λ,2λ,-2λ =2λ,2λ,2-2λ ，AE =1,0,1 ，AF =0,1,1 ，设平面AEF 的一个法向量为n=x ,y ,z ，则n ⋅AE=x +z =0n ⋅AF=y +z =0，令z =-1，解得：x =1，y =1，∴n =1,1,-1 ；设直线AG 与平面AEF 所成角为θ，sin θ=cos n ,AG =n ⋅AGn ⋅AG=6λ-2 3⋅4λ2+4λ2+2-2λ 2=13，解得：λ=16或λ=12(舍)，∴PG =16PC ，∵PA ⊥平面ABCD ，BC ⊂平面ABCD ，∴PA ⊥BC ；∵BC ⊥AB ，PA ∩AB =A ，PA ,AB ⊂平面PAB ，∴BC ⊥平面PAB ，∴G 到平面PAB 的距离为16BC =13，∴V E -ABG =V G -ABE =13S △ABE ⋅16BC =13×12×12×2×2×13=19.20(22·23下·长沙·一模)斜三棱柱ABC -A 1B 1C 1的各棱长都为2，∠A 1AB =60°，点A 1在下底面ABC 的投影为AB 的中点O ．(1)在棱BB 1(含端点)上是否存在一点D 使A 1D ⊥AC 1若存在，求出BD 的长；若不存在，请说明理由；(2)求点A 1到平面BCC 1B 1的距离．【答案】(1)存在，BD =25(2)2155【分析】(1)连接OC ，以O 点为原点，如图建立空间直角坐标系，设BD =tBB 1 ,t ∈0,1 ，根据AC 1 ⋅A 1D=0，求出t 即可；(2)利用向量法求解即可.【详解】(1)连接OC ，因为AC =BC ，O 为AB 的中点，所以OC ⊥AB ，由题意知A 1O ⊥平面ABC ，又AA 1=2，∠A 1AO =60°，所以A 1O =3，以O 点为原点，如图建立空间直角坐标系，则A 10,0,3 ，A 1,0,0 ，B -1,0,0 ，C 0,3,0 ，由AB =A 1B 1得B 1-2,0,3 ，同理得C 1-1,3,3 ，设BD =tBB 1,t ∈0,1 ，得D -1-t ,0,3t ，又AC 1 =-2,3,3 ，A 1D =-1-t ,0,3t -3 ，由AC 1 ⋅A 1D=0，得-2-1-t +33t -3 =0，得t =15，又BB 1=2，∴BD =25，∴存在点D 且BD =25满足条件；(2)设平面BCC 1B 1的法向量为n=x ,y ,z ，BC =1,3,0 ，CC 1 =-1,0,3 ，则有n ⋅BC=x +3y =0n ⋅CC 1=-x +3z =0，可取n =3,-1,1 ，又BA 1=1,0,3 ，∴点A 1到平面BCC 1B 1的距离为d =BA 1 cos BA 1 ,n =BA 1 ×3+0+3BA 1×5=2155，∴所求距离为2155.21(22·23下·长沙·三模)如图，三棱台ABC -A 1B 1C 1，AB ⊥BC ，AC ⊥BB 1，平面ABB 1A 1⊥平面ABC ，AB =6,BC =4，BB 1=2，AC 1与A 1C 相交于点D ，AE =2EB，且DE ∥平面BCC 1B 1.(1)求三棱锥C -A 1B 1C 1的体积；(2)平面A 1B 1C 与平面ABC 所成角为α，CC 1与平面A 1B 1C 所成角为β，求证：α+β=π4.【答案】(1)2(2)证明见解析【分析】(1)通过证明线线和线面垂直，并结合已知条件即可得出三棱锥C -A 1B 1C 1的体积；(2)建立空间直角坐标系，表达出各点的坐标，求出所成角为α与β的正余弦值，即可证明结论.【详解】(1)由题意，∵平面ABB 1A 1⊥平面ABC ，且平面ABB 1A 1∩平面ABC =AB ，AB ⊥BC ，BC ⊂平面ABC ∴BC ⊥平面ABB 1A 1，∵BB 1⊂平面ABB 1A 1，∴BC ⊥BB 1，又AC ⊥BB 1，BC ∩AC =C ，BC ,AC ⊂平面ABC ∴BB 1⊥平面ABC ，连接C 1B ，∵DE ⎳平面BCC 1B 1，DE ⊂平面ABC 1，平面ABC 1∩平面BCC 1B 1=C 1B ，∴DE ∥C 1B ，∵AE =2EB ，∴AD =2DC 1 ，∴A 1C 1=12AC .∴三棱锥C -A 1B 1C 1底面A 1B 1C 1的面积S 1=12×2×3=3，高h =BB 1=2，。
立体几何练习题(含答案)精选全文完整版
可编辑修改精选全文完整版《立体几何 》练习题一、 选择题1、一条直线和三角形的两边同时垂直，则这条直线和三角形的第三边的位置关系是（ ）A 、垂直B 、平行C 、相交不垂直D 、不确定2. 在正方体1111ABCD A B C D -中, 与1A C 垂直的是（ ）A. BDB. CDC. BCD. 1CC3、线n m ,和平面βα、，能得出βα⊥的一个条件是( )A.βα//n ,//m ,n m ⊥B.m ⊥n ,α∩β=m ,n ⊂αC.αβ⊆⊥m n n m ,,//D.βα⊥⊥n m n m ,,//4、平面α与平面β平行的条件可以是（ ）A.α内有无穷多条直线与β平行；B.直线a//α,a//βC.直线a α⊂,直线b β⊂,且a//β,b//αD.α内的任何直线都与β平行5、设m 、n 是两条不同的直线，,,αβγ是三个不同的平面，给出下列四个命题：①若m ⊥α，n //α，则m n ⊥ ②若αβ//，βγ//，m ⊥α，则m ⊥γ③若m //α，n //α，则m n // ④若αγ⊥，βγ⊥，则//αβ其中正确命题的序号是( )A.①和②B.②和③C.③和④D.①和④6.点P 为ΔABC 所在平面外一点，PO ⊥平面ABC ，垂足为O,若PA=PB=PC ，则点O 是ΔABC 的（ ）A.内心B.外心C.重心D.垂心7. 若l 、m 、n 是互不相同的空间直线，α、β是不重合的平面，则下列命题中为真命题的是（ ）A ．若//,,l n αβαβ⊂⊂，则//l nB ．若,l αβα⊥⊂，则l β⊥C. 若,//l l αβ⊥，则αβ⊥ D ．若,l n m n ⊥⊥，则//l m8. 已知两个平面垂直，下列命题中正确的个数是（ ）①一个平面内的已知直线必垂直于另一个平面的任意一条直线；②一个平面内的已知直线必垂直于另一个平面的无数条直线；③一个平面内的任一条直线必垂直于另一个平面；④过一个平面内任意一点作交线的垂线，则垂线必垂直于另一个平面.A.3B.2C.1D.09． 设m.n 是两条不同的直线,α.β是两个不同的平面,（ ） A ．若m ∥α,n ∥α,则m ∥n B ．若m ∥α,m ∥β,则α∥βC ．若m ∥n,m ⊥α,则n ⊥αD ．若m ∥α,α⊥β,则m ⊥β10． 设l 为直线,,αβ是两个不同的平面,下列命题中正确的是（ ）A ．若//l α,//l β,则//αβB ．若l α⊥,l β⊥,则//αβC ．若l α⊥,//l β,则//αβD ．若αβ⊥,//l α,则l β⊥ 二、填空题11、在棱长为2的正方体ABCD —A 1B 1C 1D 1中，E ，F 分别是棱AB ，BC 中点，则三棱锥B —B 1EF 的体积为 .12．对于空间四边形ABCD ，给出下列四个命题：①若AB=AC ，BD=CD 则BC ⊥AD ；②若AB=CD ，AC=BD 则BC ⊥AD ；③若AB ⊥AC ，BD ⊥CD 则BC ⊥AD ；④若AB ⊥CD ， BD ⊥AC 则BC ⊥AD ；其中真命题序号是 ．13. 已知直线b//平面α，平面α//平面β，则直线b 与β的位置关系为 .14. 如图，△ABC 是直角三角形，∠ACB=︒90，PA ⊥平面ABC ，此图形中有 个直角三角形参考答案 选择题：AACDA,BCCCB填空题：11、1312、①④ 13、//b b ββ⊂或 14、4A B C P欢迎您的下载，资料仅供参考！致力为企业和个人提供合同协议，策划案计划书，学习资料等等打造全网一站式需求。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1、如图，正方形所在平面与平面四边形所在平面互相垂直，△是等腰直角三角形，（1）线段的中点为，线段的中点为，求证：；（2）求直线与平面所成角的正切值.解：（1）取AB 的中点为N ，连MN ,PN ,则//MN EB ,//PN BC∴PMN EBC ∴//PM BCE 平面FE ⊥EBC FCE ∴∠⊥//AB DE (1)求证：AO ⊥平面CDE ；(2)求直线BD 与平面CBE 所成角的正弦值3、如图，在△ABC 中，︒=∠90C ，a BC AC 3==，点P 在AB 上，BC PE //交AC 于E ，AC PF //交BC 于F ．沿PE 将△APE 翻折成△PE A '，使平面⊥PE A '平面ABC ；沿PF 将△BPF 翻折成△PF B '，使平面⊥PF B '平面ABC ． （1）求证：//'C B 平面PE A '；（2）若PB AP 2=，求二面角E PC A --'的平面角的正切值．解：（1）因为PE FC //，⊄FC 平面PE A '，所以//FC 平面PE A '．因为平面⊥PE A '平面PEC ，且PE E A ⊥'，所以⊥E A '平面ABC ． …2分 同理，⊥F B '平面ABC ，所以E A F B '//'，从而//'F B 平面PE A '． …4分 所以平面//'CF B 平面PE A '，从而//'C B 平面PE A '．…6分（2）因为a BC AC 3==，BP AP 2=，所以a CE =，a A E 2='，a PE 2=，a PC 5=．…8分ABCDE FM .. C BF PAF C'B 'A EABCDEP M过E 作PC EM ⊥，垂足为M ，连结M A '．由（1）知ABC E A 平面⊥'，可得PC E A ⊥'， 所以EM A PC '⊥面，所以PC M A ⊥'．所以ME A '∠即为所求二面角E PC A --'的平面角，可记为θ． …12分在Rt △PCE 中，求得a EM 552=， 所以55522tan =='=a aEM E A θ． …15分4、如图，⊥DA 平面ABC ，⊥ED 平面BCD ，DE=DA=AB=AC.0120=∠BAC ，M 为BC 中点. (1)求直线EM 与平面BCD 所成角的正弦值； (2)P 为线段DM 上一点，且⊥AP DM ，求证：AP解：(1) ED ⊥平面BCD ，为在平面上的射影， 为与平面所成角．……………………2分 DA ⊥Q 平面ABC ，， 设，又=Q DA AB =AC ，． 在△ABC 中，Q ，， 又Q 为中点，∴⊥DM BC ，12==BM BC ，∴．…5分 在Rt △EDM中，EM =32a =， PABF C'B 'A E（第20题）MA BCDE A 1C 1sin EMD ∠=32DE a EM a =23=． ………………………7分 （2）=AB AC ，M 为BC 中点，∴⊥BC AM ．又⊥DA 平面ABC ， ∴⊥BC DA ，平面． ……………………9分又平面，， ……………………11分 又，平面． ……………………13分 又ED ⊥平面BCD ，． ……………………14分5、如图，已知ABCD 是边长为1的正方形，AF⊥平面ABCD ，CE∥AF，)1(>=λλAF CE ．（1）证明：BD⊥EF；（2）若AF ＝1，且直线BE 与平面ACE 所成角的正弦值为1023，求λ的值．解：（1）连结BD 、AC ，交点为Ｏ．∵ABCD 是正方形∵AF⊥平面ABCD ∴AF⊥BD ……4分 ∴BD⊥平面ACEF ……6分 ∴BD⊥EF ……7分（2）连结OE ，由（1）知，BD⊥平面ACEF ，所以∠BEO 即为直线BE 与平面ACE 所成的角． ……10分 ∵AF⊥平面ABCD ，CE∥AF ，∴CE⊥平面ABCD ，CE⊥BC， ∵BC =1，AF ＝1，则CE ＝λ，BE ＝21λ+，BO ＝22， ∴Rt△BEO 中， 1023122sin 2=λ+==∠BE BO BEO ， …13分 因为1>λ，解得34=λ． ……15分6、如图，在几何体中，⊥1AA 平面ABC ，,2,//,111===⊥AA BC AB AA CC BC AB E D CC ,,11=分别是1,AA AB 的中点. (1)求证：//1BC 平面CDE ；(2)求二面角A DC E --的平面角的正切值.解：（1）连接ACR 1R 交EC 于点F ，由题意知四边形ACCR 1RE 是矩形，则F 是ACR 1R 的中点，连接DF ，∵D 是AB 的中点，∴DF 是△ABCR 1R 的中位线，∴ BCR 1R ⊄⊂ 7分 (2) 作AH ⊥直线CD ，垂足为H ，连接HE ， ∵ AAR 1R ⊥平面ABC ，∴ AAR 1R ⊥DC ，∴ CD ⊥平面AHE ， ∴ CD ⊥EH ，∴ ∠AHE 是二面角E – CD – A 的平面角. 11分 ∵ D 是AB 的中点，∴ AH 等于点B 到CD 的距离，在△BCD 中，求得：AH ＝552， 在△AEH 中， 25tan ==∠AH AE AHE 即所求二面角的正切值为25.7、如图，已知平面与直线均垂直于所在平面，且, （1）求证：平面；（2）若，求与平面所成角的正弦值.解：（1）证明：过点作于点，∵平面⊥平面，∴平面……2分 又∵⊥平面∴∥, ………………2分 又∵平面∴∥平面 ………………6分（2）∵平面 ∴，又∵∴ ∴ ………………8分 ∴点是的中点，连结，则 ∴平面 ∴∥，∴四边形是矩形 ………………10分 设QPABCABCA 1B 1C 1DE 得：， 又∵，∴，从而，过作于点，则：∴是与平面所成角 ………………………………………………12分 ∴，∴与平面所成角的正弦值为…………………………14分8、如图，在直三棱柱111C B A ABC -中，ABC ∆是等腰直角三角形，090=∠ACB ，侧棱AA 1=2，D ，E 分别为CC 1与A 1B 的中点，点E 在平面ABD 上的射影是ABD ∆的重心. (1)求证：DE9、如图，在侧棱垂直于底面的三棱柱ABC —A 1B 1C 1中，底面△ABC 为等腰直角三角形，∠B=90°,D 为棱BB 1的中点。
（1）求证：面DA 1C⊥面AA 1C 1C ； （2）若1AA AB=A —A 1D —C 的大小。
10、如图，在四棱锥P-ABCD中，PA ⊥平面ABCD ，AB ABCD DC AB //E F AB AB DE ⊥AB CF ⊥2,3===FB EF CF G FBt AE =BCF ADE ∆∆,CF DE ,A B P PEFCD （1）求证：//PD 平面EGC ；（2）当⊥EG 面PFC 时,求DG 与平面A BCA 1B 1C 1D PAC DMCD EFC DPED 所成角的正切值.（1）证明：连接DF 交EC 于点M ，连接MGG M ,Θ为中点 MG PD //∴ 又EGC PD 面⊄ΘEGC MG 面⊂ ∴//PD 平面EGC ———5分（2）当⊥EG 面PFC 时, PF EG ⊥ 又ΘG 为FB 的中点，2==∴EP EF ，2=∴t —————7分过点G 在平面PEF 中作EP 的垂线，垂足为N ，连接DN . ⊥DE Θ面PEF ∴面⊥PED 面PEF ⊥∴GN 面PED GDN ∠∴即为DG 与平面PED 所成角.——————11分易求得221,23==DN GN ,所以DG 与平面PED 所成角的正切值为77.——14分12、如图，在四边形ABCD 中，4==AD AB ，7==CD BC ，点为线段上的一点.现将DCE ∆沿线段EC 翻折到PAC ，使得平面PAC ⊥平面ABCE ，连接PA ，PB .(1)证明：⊥BD 平面PAC ；(2)若︒=∠60BAD ，且点E 为线段的中点，求直线PE 与平面ABCE 所成角的正弦值.解：(1)连接AC ，BD 交于点O ,在四边形ABCD 中， ∵4==AD AB ，7==CD BC∴ADC ABC ∆≅∆，∴BAC DAC ∠=∠,∴BD AC ⊥ 又∵平面PAC ⊥平面ABCE ，且平面PAC I 平面ABCE =AC ∴⊥BD 平面PAC ………… 6分(2)如图，过点P 作AC 的垂线，垂足为H ，连接EH ，EC并取AO 中点F ，连接EF ，∵平面PAC ⊥平面ABCE ，且平面PAC I 平面ABCE =AC ，AC PH ⊥ ∴⊥PH 平面ABCE ，∴PEH ∠即为直线PE 与平面ABCE 的所成角， 由(Ⅰ)可知，BD AC ⊥，且32=AO ，3=CO ，又2=PE ，7=PC ，设x CH =，则有27x PH -=，3222-=-=x PH PE EHBA CDEPABCA 11C 1OPPP 1AA BBCCM又∵F 为AO 的中点，在EFH Rt ∆中，x FH -=32，1=EF由勾股定理得，31)32(22-=+-x x ，解得334=x ， ∴332=EH ，335=PH ∴直线PE 与平面ABCE 的所成角的正弦值即33sin ==∠PE EH PEH .13、在三棱柱ABC —A 1B 1C 1中，AB=AC=AA 1 =2，平面ABC 1⊥平面AA 1C 1C ，∠AA 1C 1=∠BAC 1=60°，设AC 1与AC 相交于点O ，如图． （1）求证：BO⊥平面AA 1C 1C ； （2）求二面角B 1—AC 1—A 1的大小。
14、如图1，四面体PABC 中，BC=BP=1，AC=AP=3，AB=2，将PAB ∆沿直线AB 翻折至AB P 1∆，使点C B P A ,,,1在同一平面内(如图2)，点M 为PC 中点. (1)求证：直线//1PP 平面MAB ； (2) 求证：AB PC ⊥；(3)求直线PA 与平面P 1PC 所成角的大小.答案：（3）、3π。