自己整理的必修二直线方程的几种形式
直线方程的四种形式
y y1 y2 y1
x x1 x2 x1
, x1
x2 ,
y1
y2
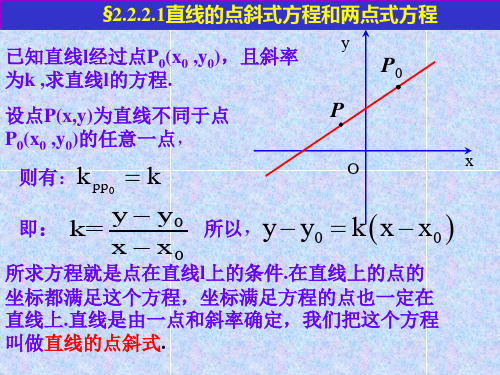
§2.2.2.1直线的点斜式方程和两点式方程
1.已知直线在x轴上的截距是a,在y轴
上的截距是b,且a≠0,b≠0,
y
求证直线的方程可写为 x y 1 ab
(这种形式的直线方程,
叫做直线的截距式方程)
b
a
O
x
§2.2.2.1直线的点斜式方程和两点式方程
例二 根据下列直线方程,分别写出各直线经过的 一点和直线斜率
1 y 2 x 1 2 y 4 3x 2;
3 y 4x 3
点评:
4 y 2 x 3
5
逆用直线方程,即由方程可看出经过的点和 直线的斜率.
§2.2.2.1直线的点斜式方程和两点式方程
§2.2.2.1直线的点斜式方程和两点式方程
总结与反思
点斜式y y0 k x x 0
1.四种直线方程: 斜截式y kx+b
体会形与数之间
两点式 y y1 x x1
的转化. 2.四种直线方程的应
截距式yx2
yy1
x2
1
x1
ab
用及其注意事项和适
用条件.
3.方程的思想;数形结合的思想;分 类讨论的思想;求动点轨迹的方法和 思路.
§2.2.2.1直线的点斜式方程和两点式方程
课后作业
1. 通读教材内容,熟记所学四种方程,完 成课后练习.
2. 基训.
3. 学案.
方程.
x-y+1=0
2.求经过点A(1,2)与点B(3,2)的直
线方程.
y=2
3.求经过点A(1,2)与点B(1,4) 的直线方程. x=1
解析几何直线方程的五种形式

解析几何直线方程的五种形式一、点斜式方程点斜式方程是解析几何中直线方程的一种形式,它由直线上已知一点的坐标和直线的斜率决定。
点斜式方程的一般形式为y - y1 = k(x - x1),其中(x1, y1)为直线上已知的一点的坐标,k为直线的斜率。
例如,给定直线上的一点A(2, 3)和斜率k = 2,我们可以得到该直线的点斜式方程为y - 3 = 2(x - 2)。
二、斜截式方程斜截式方程是解析几何中直线方程的另一种常见形式,它由直线上的截距和直线的斜率决定。
斜截式方程的一般形式为y = kx + b,其中k为直线的斜率,b为直线与y轴的截距。
例如,给定直线的斜率k = -3和截距b = 4,我们可以得到该直线的斜截式方程为y = -3x + 4。
三、一般式方程一般式方程是解析几何中直线方程的标准形式,它由直线的斜率和截距的比值决定。
一般式方程的一般形式为Ax + By + C = 0,其中A、B、C为常数,且A和B不同时为0。
例如,给定直线的斜率k = 1/2和截距 b = 3,我们可以得到该直线的一般式方程为2x - y - 6 = 0。
四、两点式方程两点式方程是解析几何中直线方程的一种形式,它由直线上的两个已知点的坐标决定。
两点式方程的一般形式为(x - x1)/(x2 - x1) = (y - y1)/(y2 - y1),其中(x1, y1)和(x2, y2)为直线上的两个已知点的坐标。
例如,给定直线上的两个点A(1, 2)和B(3, 4),我们可以得到该直线的两点式方程为(x - 1)/(3 - 1) = (y - 2)/(4 - 2)。
五、截距式方程截距式方程是解析几何中直线方程的一种形式,它由直线与x轴和y轴的截距决定。
截距式方程的一般形式为x/a + y/b = 1,其中a 和b分别为直线与x轴和y轴的截距。
例如,给定直线与x轴和y轴的截距分别为a = 2和b = 3,我们可以得到该直线的截距式方程为x/2 + y/3 = 1。
直线方程的五种形式

2 x 5 y 10 0
五.直线方程的一般式
在平面直角坐标系中 , 对于任何一条直线 , 都有一
个表示这条直线的关于 x, y的二元一次方程 形式为 证明: 关于x, y的二元一次方程的一般
Ax By C 0( A, B不同时为 0)
A C A 1)当B 0时, 有y x , 这 是 斜 率 为 , BC B B 在y轴 上 的 斜 距 为 的直线方程 . B C 2)当B 0时,因A, B不 同 时 为 0, 故A 0, x . A 它表示一条与 y轴平行或重合的直线 .
求这个三角形三边所在 的直线方程 .
解: 把A, B代入两点式 ,得
y0 x (5) 3 0 3 (5)
3x 8 y 15 0
把B, C代入两点式 ,得
y 3 x 3 23 03
5x 3 y 6 0
A(5,0), B(3,3), C (0,2) 例3三角形的顶点是
二
名称
直线方程的五种形式
方程 说明 不包括y轴和平行于y轴 的直线 不包括y轴和平行于y轴 的直线
已知条件
点斜式 点P1(x1,y1)和斜率 y-y1=k(x-x1) k 斜截式 斜率k和y轴上截 距 两点式 点P1(x1,y1)和点 P2(x2,y2) 截距式 在x轴上的截距a 在y轴上的截距b 一般式 A、B不同时为零 y=kx+b
已知直线 l的 斜 率 为 k , 与y轴 的 交 点 是 (0, b), 求直线的方程 . 解: 由直线的点斜式,得 y b k ( x 0)
即y kx b
y
l
方程 y kx b叫做直线方程的斜截式 .
直线方程的四种形式

03
然后,将斜率k代入一般 形式的直线方程 y=kx+b中,得到yy1=k*(x-x1)。
04
最后,将k的具体值代入 上式,得到两点式方程。
谢谢观看
04
法线式
法线式的定义
法线式方程是形如 (y - y_1 = m(x x_1)) 的直线方程,其中 (m) 是直线 的斜率,((x_1, y_1)) 是直线上的一 点。
VS
法线式方程表示的是通过点 ((x_1, y_1)) 且斜率为 (m) 的直线。
法线式的应用场景
当已知直线上的一点和斜率时,可以使用法线式方程来表示该直线。
进一步变形,得到 (y - y_1 = frac{A}{B}(x - x_1)),这就是法
线式方程。
05
点向式
点向式的定义
点向式是指通过直线上的一点和直线的方向 向量来表示直线方程的一种形式。具体地, 点向式方程可以表示为 (x - x_1 = m(y y_1)),其中 ((x_1, y_1)) 是直线上的一个点, (m) 是直线的方向向量。
详细描述
在几何问题中,如果已知直线上的一点和斜率,就可以使用点斜式来求解直线的方程。 例如,在解析几何、物理和工程领域中,点斜式被广泛应用于解决与直线相关的问题。
点斜式的推导过程
要点一
总结词
点斜式可以通过直线上两点的坐标来推导得出。
要点二
详细描述
设直线上的两点为 (x1, y1) 和 (x2, y2),其中 x1 ≠ x2。根据 两点式,直线的斜率 m = (y2 - y1) / (x2 - x1)。将这个斜率 和一点 (x1, y1) 代入点斜式方程,即可得到直线的方程为 y y1 = m(x - x1)。
17..2.2.2 直线方程的几种形式

②过点(0,2),斜率为-1;
③过点(-3,1),平行于x轴;
④经过点(-2,0)且垂直于x轴
⑤在y轴上的截距为2,且与x轴平行
⑥经过A(-1,8),B(4,-2)两点
⑦在x,y轴上的截距分别是4,-3
【小结】
探究二:直线 经过点P(2,3),且在x,y轴上的截距相等,试求该直线的方程。
A. y=kx+b B. y=k(x-b) C. y=k(x+b) D. y=kx-b
3.下列说法中不正确的是( )
A.点斜式 适用于不垂直于x轴的任何直线;
B.斜截式 适用于不垂直于x轴的任何直线
C.两点式 适用于不垂直于坐标轴的任何直线
D.截距式 适用于不过原点的任何直线
【我的疑惑】
探究案
探究一:写出满足下列条件的直线的方程。
【拓展】在直线y-1=k(x+1)中,k取遍所有的实数,可得无数条直线,这无数条直线都过定点_________
【小结】
【课堂小结】
1.知识方面
2.数学思想方法
课题:2.2.2直线方程的几种形式
【学习目标】
1.熟练掌握直线方程的几种形式(点斜式、斜截式、两点式、截距式),提高求直线方程的能力。
2.自主学习、合作探究,学会各种直线方程的运用方法。
3.激情投入,高效学习,体会数形结合的魅力。
【使用说明及学法指导】
1.先精读一遍教材必修二课本P77-81,用红色笔进行勾画;再针对预习自学二次阅读并回答;
2.推导过 ,且 的直线的两点式方程(提示:利用点斜式)
3.已知直线 在x轴上的截距为a,在y轴上截距为b,且 ,求证直线 的方程可写为 (这种形式的直线方程叫做直线的截距式方程)
高中数学必修二课件-2.2.2 直线方程的几种形式4-人教B版

(1)经过点(2, 1),且倾斜角是150 °; y - 1 = - 3 ( x - 2 ) 3
(2)经过点(3, 2), 且垂直于 y轴的直线; y = 2
(3)经过点(2,1), 且斜率是 -1的直线. y - 1 = -( x - 2)
6.已知直线的方程是y+7=-x-3,则( )C A.直线经过点(-3,7),斜率为-1;
:
(1)l1
// l2
kb11
k2 b2
(2)l1 ⊥l2 ⇔k1 • k2 = -1
2.已知直线y = ax - 2和y = - a x+1互相垂直,
2
则a =
. 2
3.若直线l1 :
2
y
=
-
2 a
x
-
1 a
与直线l2
:
y
=
3x
-1互相平行,
则a =
3
.
4.当a为何值时,直线l1 : y = -x+2a与直线 l2:y = (a2 - 2)x+2平行?
直线的点斜式方程 y - y0 = k(x - x0 )
:
2.直线的点斜式方程能否表示坐标平面 上所有的直线?
直线的点斜式y:- y0 = k(x - x0 )
点P0 (x0 , y0 )+斜率k
3.思考:过点P0(x0,y0) (1)平行于x轴或与x轴重合的直线方程是什么? (2)平行于y轴或与y轴重合的直线方程是什么?
直线的点斜式方程得:
y -b = k(x - 0)
即:y = kx+b 直线的斜
截距不是距离,
k:直线的斜率 b:直线在y轴上的截距
直线方程的五种形式之

2:一条直线经过点A(0,5),倾斜角为00, ),倾斜角为 例2:一条直线经过点A(0,5),倾斜角为00,求这直线 方程 y
解:这条直线经过点A(0,5) 斜率是k=tan00=0 代入点斜式,得 y - 5 = 0 O x 5
②直线的斜截式方程: 直线的斜截式方程:
已知直线l的斜率是 , 轴的交点是P( , ), ),求 已知直线 的斜率是k,与y轴的交点是 (0,b),求 的斜率是 轴的交点是 求这条直线的方程。 求这条直线的方程。 代入点斜式方程, 的直线方程 的直线方程: 代入点斜式方程,得l的直线方程:y - b =k ( x - 0) ) 即 y = kx + b。 (2)
3
BP95
㈣总结: ①直线的点斜式,斜截式方程在 直线斜率存在时才可以应用。 ②直线方程的最后形式应表示成 二元一次方程的一般形式。
③两种形式都有限制条件
直线方程的五种形式之: 直线方程的五种形式之: 点斜式方程和 斜截式方程
新课: 新课: 1、直线的点斜式方程:
已知直线l经过已知点 ),并且它的斜率是 并且它的斜率是k 已知直线l经过已知点P1(x1,y1),并且它的斜率是 求直线l的方程 的方程。 求直线 的方程。 设点P( , )是直线l上 设点 (x,y)是直线 上 不同于P 的任意一点。 不同于 1的任意一点。 l 根据经过两点的直线斜率 y P 公式, 公式,得
k
=
可化为
y y 1 = k (x x 1 )
y y1 x x1
. .
P1
O
x
由直线上一点和直线的斜率确定的直线方程,叫直 由直线上一点和直线的斜率确定的直线方程, 线的点斜式方程。 线的点斜式方程。
小结: 小结: 为直线上的任意一点, ⑴P为直线上的任意一点,它的 为直线上的任意一点 位置与方程无关 直线上任意一点P与这条直线上 直线上任意一点 与这条直线上 一个定点P 所确定的斜率都相等。 一个定点 1所确定的斜率都相等。
直线方程(直线方程完美总结 归纳)

直线方程(直线方程完美总结归纳)一、倾斜角与斜率直线的倾斜角是指直线与x轴正方向的夹角。
当直线与x 轴平行或重合时,其倾斜角规定为0度。
倾斜角的范围是小于等于α,且α小于180度。
直线的斜率是指直线倾斜角的正切值,记作k=tanα(α不等于90度)。
当直线与x轴平行或重合时,斜率为0;当直线与x轴垂直时,斜率不存在。
经过两点P的直线的斜率公式是k=(y2-y1)/(x2-x1)。
每条直线都有倾斜角,但并不是每条直线都有斜率。
求斜率的一般方法有两种:已知直线上两点,根据斜率公式k=(y2-y1)/(x2-x1)求斜率;已知直线的倾斜角α或α的某种三角函数,根据k=tanα来求斜率。
利用斜率证明三点共线的方法:已知A(x1,y1),B(x2,y2),C(x3,y3),若x1=x2=x3或kAB=kBC,则有A、B、C三点共线。
考点一:斜率与倾斜角。
例1.已知直线l的斜率的绝对值等于3,则直线的倾斜角为30度或150度。
例2.已知过两点A(m2+2,m2-3),B(3-m2-m,2m)的直线l的倾斜角为45度,求实数m的值。
考点二:三点共线。
已知三点A(a,2)、B(3,7)、C(-2,-9a)在一条直线上,求实数a的值。
考点三:斜率范围。
例1.已知两点A(-2,-3),B(3,0),过点P(-1,2)的直线l与线段AB始终有公共点,求直线l的斜率k的取值范围。
例2.已知实数x、y满足2x+y=8,当2≤x≤3时,求y的最大值与最小值。
二、直线方程直线方程有四种形式:点斜式、斜截式、两点式和截距式。
其中,点斜式的形式为y-y1=k(x-x1),斜截式的形式为y=kx+b,两点式的形式为(y-y1)/(x-x1)=(y2-y1)/(x2-x1),截距式的形式为xy+a+b=0.点斜式的局限性是不包括垂直于x轴的直线,斜率k为斜率。
斜截式的局限性是不包括垂直于x轴和y轴的直线,k为斜率,b是直线在y轴上的截距。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、下列命题中,所有真命题的序号为
①方程
k x x y y =--0
表示过点()000,y x P 且斜率为k 的直线方程;②经过定点()000,y x P 的直线,都可
以用()00x x k y y -=-来表示;③经过()b A ,0的直线都可以用方程b kx y +=来表示; ④不经过原点的直线都可用方程
1=+b
y
a x 来表示;⑤直线l 过点()11,y x P ,倾斜角为090,则其方程为1x x =;⑥直线l 过点()11,y x P ,斜率为0,则其方程为1y y =;⑦经过任意不同两点()111,y x P ,
()222,y x P 的直线都可以用方程()()()()121121y y x x x x y y --=--来表示;
2、若方程0=++C By Ax 表示直线,则B A ,应满足的条件为( )
A.0≠A
B.0≠B
C.0≠•B A
D. 02
2
≠+B A
例1:已知直线l 经过点()23-,
,且在两坐标轴上的截距相等,求直线l 的方程。
方法一:依题意,直线l 的斜率k 存在且不为0,设直线的方程为()32-=+x k y 令0=x ,得k y 32--=;令0=y ,得 32
+=
k
x ()03201=+=-+y x y x 或
方法二: 设直线l 在两坐标轴上的截距均为a .
若0=a ,则直线l 过原点,此时l 的方程为032=+y x ; 若0≠a ,则l 的方程可设为
1=+a
y
a x 变式:经过点()2,1A ,并且在两坐标轴上截距的绝对值相等的直线共有( )
A.1条
B. 2条
C. 3条
D. 4条
例2:已知直线过点()43,
-,且在两坐标轴上的截距之和为12,求直线l 的方程. 解:方法一:由题可知所求直线l 的斜率存在,设直线l 的方程为()()034≠+=-k x k y 当0=x 时,43+=k y ;当0=y 时,34
--=k
x 由题可知124334=++--
k k ()()0413041132=-+⇒=--⇒k k k k ,4=∴k 或3
1-=k ∴所求直线l 的方程为()344+=-x y 或()33
1
4+-=-x y ,即0164=+-y x 或093=-+y x
方法二:由题可知所求直线l 在两坐标轴上的截距存在且不为零
设直线l 的方程为1=+b y a x ,则12=+b a ①, 又直线过点()43,-,14
3=+-∴b
a ②
由①②得⎩⎨
⎧==39b a 或⎩⎨⎧=-=16
4b a ∴所求直线l 的方程为139=+y x 或
1164=+-y
x 例3:过点()1,0M 作直线l ,使它被两已知直线0103:1=+-y x l 和082:2=-+y x l 所截得的线段恰好被M 平分,求直线l 的一般式方程。
()044=-+y x
例4:已知直线l 的方程为(
)(
)
14322
2
-=-+-+m y m m x m m ,根据下列条件,分别确定m 的值: (1)直线l 的斜率为1;(2)直线l 在x 轴的截距为1;(3)直线l 在y 轴的截距为2
3
-
. 例5:直线l 过点()3,2-P ,它与两坐标轴围成的三角形面积等于4,求直线l 的一般式方程. 【直线过定点问题】 ()01229042=++=-+y x y x 或
例6:求证:不论m 取什么实数,直线()()047112=--+++m y m x m l :
恒过定点,并求出此定点坐标. 解:直线l 的方程变为:()4720472+--=-+⇒=--+++y x m y x m y my x mx 若不论m 取什么实数,方程恒成立,必须使⎩⎨
⎧==⇒⎩⎨
⎧=+--=-+1
3
04072y x y x y x ∴不论m 取什么实数,直线l 恒过定点,定点坐标为()1,3
变式1:直线031=++-k y kx 恒过定点( ) A.()13-,
B.()1,3-
C.()31-,
D.()3,1- 变式2:不论m 为何值,直线()0121=++--m y x m 恒过定点( ) A.⎪⎭
⎫
⎝⎛
-
21,1 B.()0,2- C.()3,2 D. ()3,2- 1、已知点()m P ,3,在过()1,2-M 和()4,3-N 的直线上,则m 的值是( )A.5B.2C 2-.D.6- 2、若点()00,y x P 在直线0=++C By Ax 上,则直线方程可以表示为( ) A.()()000=-+-y y B x x A B.()()000=---y y B x x A C.()()000=-+-y y A x x B D.()()000=---y y A x x B 3、如果0,0<>AC AB ,则直线0=++C By Ax 不通过( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限 4、如果直线0=++C By Ax 在坐标轴上的截距相等,那么C B A 、、满足( )
A.B A =
B.B A =
C.0==C B A 且
D.B A C =≠且0或0=C 5、已知三角形的三个顶点()()()2,0,3,3,0,5C B A --.
(1)求BC 边所在的直线方程; (2)求BC 边上中线所在的直线方程.。
