第四章 约束非线性优化的理论与方法讲解
非线性约束最优化
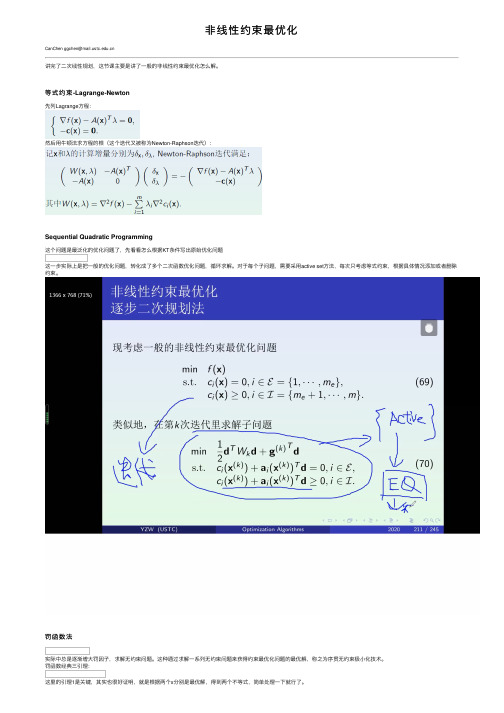
⾮线性约束最优化CanChen ggchen@讲完了⼆次线性规划,这节课主要是讲了⼀般的⾮线性约束最优化怎么解。
等式约束-Lagrange-Newton先列Lagrange⽅程:然后⽤⽜顿法求⽅程的根(这个迭代⼜被称为Newton-Raphson迭代):Sequential Quadratic Programming这个问题是最泛化的优化问题了,先看看怎么根据KT条件写出原始优化问题这⼀步实际上是把⼀般的优化问题,转化成了多个⼆次函数优化问题,循环求解。
对于每个⼦问题,需要采⽤active set⽅法,每次只考虑等式约束,根据具体情况添加或者删除约束。
罚函数法实际中总是逐渐增⼤罚因⼦,求解⽆约束问题。
这种通过求解⼀系列⽆约束问题来获得约束最优化问题的最优解,称之为序贯⽆约束极⼩化技术。
罚函数经典三引理:这⾥的引理1是关键,其实也很好证明,就是根据两个x分别是最优解,得到两个不等式,简单处理⼀下就⾏了。
三个引理刻画了罚函数法动态变化的过程。
其中,第三个引理就是说,我迭代到⼀步,不想迭代了,这个时候实际上得到的解是把定义域扩⼤了之后的解。
乘⼦罚函数这⾥实际上就是⽬标函数,加朗格朗⽇项,加罚项。
使⽤罚函数,必须要求罚因⼦趋于⽆穷⼤,然⽽这在实际中很难办到。
这⾥引⼊朗格朗⽇项,让罚因⼦不⽤趋于⽆穷,就能得到结果。
本质是就是将乘⼦罚函数在迭代中寻找和拉格朗⽇函数的关系,从⽽将带约束问题转化为⽆约束问题。
这⾥给出了带约束问题的⼆阶充分条件,⾮常⽜逼,之前只是必要条件。
障碍函数法这个实际上通过⽆限限制边界,将有约束问题转化为⽆约束问题。
内点法这个实际上是改变互补松弛条件,sz=u>0, 所以s>0,所以⼀定是内点。
本质上还是在求解KT系统,把不等式改造成等式,还在内部,这个⽐较野蛮。
后⾯凸优化就是⼲这个。
障碍函数法和内点法本质是⼀样的。
最优化方法-约束非线性最优化方法

充分条件: 如果 L( X *, ) 0 且行列式方程:
所有根Zj>0(j=1,2,…,n-l),则X*为局部极小点;反 之所有Zj<0,为局部极大点;有正有负非极值点
例题4-1用拉格朗日乘子算法求解:
max f ( X ) x12 , s.t. h1 ( x) 2x12 2x1x2 24 0
1)K-T条件:
考虑两种情况:
0 无解 2 * * x1 x2 / 5 0 x1 0; x2 0; * 2 2)局部最小判别:看课本
3.罚函数法(外点法)
序列无约束最优化方法SUMT ( Sequential Unconstrained Minimization Technique) 1.罚函数概念: min f ( x) f : Rn R ( fgh) s.t. g i ( x ) 0, i 1, 2,..., m h j ( x) 0 j 1, 2,..., l 构造外部罚函数: P ( X , M k ) f ( X ) ( M k , g ( X ), h( X )) f ( X ) M k { [min(0, g i ( X ))] [( h j ( X ))]2 }
L [m(uij ) m 1 dij2 ] 0; uij [ 2 ]1/( m 1) uij mdij
i 1 ij
i 1
m
2 dij
m
i1[
c
1 1/(m1) ] 1 2 dij
所以
uij
[ l 1
c
1 dij dlj
]2/( m2)
FCM的中心迭代过程
第四章 约束非线性优化的理论与方法

h( x) x1 x2 6 0.
f
解:
(
x
)
(2
x1,1)T ,g1(
2x1 1
x) (1,0)T
21 x2 1
, g2 0,
(
x
)
(
2
x1
,2
x2
)T
,
h1
(
x
)
(1,1)
;
K T条件为
1 22 x2 1 0,
x* (1,0)T 是 最 优 点 , 起 作 用 约 束I ( x*) {1,3},f ( x*) (1,0)T
g1( x*) (0,1)T , g3 ( x*) (0,1)T , 显 然 找 不 到1 , 3 0, 使 f ( x*) 1g1( x*) 5g3 ( x*)成 立 。
F(x0)= f (x0) + g (x0)=0.
若 F ( x0 , h) hT 2F ( x0 )h 0, h 0
gi ( x0; h) 0, i 1,2,, m
则x0是局部极小点。 二,具不等式约束的问题
1,下降方向和可行方向
考虑一般非线性约束优化问题:
满足:
f
(
x
)
m
i 1
1 ,m T ;
p
i gi ( x ) jhj ( x
j1
1 )
,,
0
ቤተ መጻሕፍቲ ባይዱ
p
T
i gi ( x ) 0, i 0, i 1,, m
称上式为K-T条件,满足上式的点称K-T点。
第四章约束问题的最优化方法

当limr(k) 0 k
则(x, r(k) ) f (x) , xk * x *
例: 用内点法求
min
f
(x)
x2 1
x2 2
s.t. g( x) 1 x1 0 的约束最优解。
解:
首先构造内点惩罚函数: (
x,
r)
x2 1
x2 2
rk
ln(x1
1)
用解析法求函数的极小值,运用极值条件:
二. 直接解法:
基本思想:合理选择初始点,确定搜索方向,以迭代公式 x(k+1)= x(k)+α(k)S(k)在可行域中寻优,经过若干次迭代,收敛至最优点。 适用范围:只能求解不等式约束优化问题的最优解。
基本要点:选取初始点、确定搜索方向及适当步长。
搜索原则:每次产生的迭代点必须满足可行性与适用性两个条件。 可行性:迭代点必须在约束条件所限制的可行域内,即满足
1
u1 gu (x)
② .(x, r(k) )
m
f (x) r(k)
1
u1 gu (x)
③ .(x, r (k) )
f (x)
m
r (k) u u 1
1 gu (x)
其中:gu (x) 0,u 1,2,...m
其中:gu (x) 0,u 1,2,...m
gu(x)0, u=1,2,…,p
适用性:当前迭代点的目标函数值较前一点是下降的,即满足 F(xk+1)<F(xk)
收敛条件:
• 边界点的收敛条件应该符合 K-T 条件;
• 内点的收敛条件为: xk1 xk 1
和
不等式约束的非线性优化问题

不等式约束的非线性优化问题非线性优化问题是当前研究领域中一个重要且复杂的研究方向,其中加入了不等式约束,则研究难度更大。
不等式约束可以帮助提供更多颜色的解决,从而丰富了非线性优化问题的研究内容,特别是在重要的科学技术领域,偏见较大的决策问题中。
例如,在金融行业,投资组合的构建问题依然是一个重要的研究难题,而有了不等式约束,就可以得到更加准确的优化结果,为投资者带来更多投资机会。
同时,不等式约束对于经济学研究领域也具有重要意义。
在计算机仿真中,不等式约束可以指导模拟结果如何随着市场环境的变化而变化。
而在关系分析的仿真建模中,不等式约束可以实质性地保证模型参数的稳定,从而让模型更具有可信度。
再者,由于不等式约束可以扩展多变量线性模型,因此可以解决复杂的决策问题,探索模型内部数据运动规律,有助于深入理解经济问题,特别是现代经济中复杂而多变的定量问题。
当然,由于非线性优化问题涉及到约束,数学模型的复杂性较大,因此算法的设计相对较困难。
传统的优化方法,例如随机搜索、梯度下降和牛顿法等,大多只能处理简单的线性约束,而在具有不等式约束的优化问题中,由于约束的复杂性,这些算法的效果可能不太理想。
为了克服这些问题,目前研究已经提出了一些新的算法,例如贪婪算法、自适应种群算法、可变群体算法等,这些都是针对不等式约束优化问题的有效算法。
除此之外,还有一些混合算法也非常有效,可以采用特定的算法组合,在多个算法之间进行灵活切换,来实现更加优秀的效果。
相比于传统的算法,这些新的算法性能更加稳定,可以在具有不等式约束的非线性优化问题中取得更优结果。
综上所述,不等式约束对于非线性优化问题具有重要作用,它不仅可以丰富研究问题,还可以为各个研究领域实现更准确和稳定的理论依据。
非线性优化与约束优化问题的求解方法

非线性优化与约束优化问题的求解方法非线性优化问题是在目标函数和约束条件中包含非线性项的优化问题。
约束优化问题是在目标函数中加入了一些约束条件的优化问题。
解决这些问题在实际应用中具有重要意义,因此研究非线性优化和约束优化问题的求解方法具有重要的理论和实际意义。
一、非线性优化问题的求解方法非线性优化问题的求解方法有很多,下面介绍几种常见的方法:1. 黄金分割法:黄金分割法是一种简单但有效的搜索方法,它通过不断缩小搜索范围来逼近最优解。
该方法适用于目标函数单峰且连续的情况。
2. 牛顿法:牛顿法利用目标函数的一阶和二阶导数信息来逼近最优解。
该方法收敛速度较快,但在计算高阶导数或者初始点选取不当时可能产生不稳定的结果。
3. 拟牛顿法:拟牛顿法是对牛顿法的改进,它通过逼近目标函数的Hessian矩阵来加快收敛速度。
拟牛顿法可以通过不同的更新策略来选择Broyden-Fletcher-Goldfarb-Shanno(BFGS)方法或者DFP方法。
4. 全局优化方法:全局优化方法适用于非凸优化问题,它通过遍历搜索空间来寻找全局最优解。
全局优化方法包括遗传算法、粒子群优化等。
二、约束优化问题的求解方法约束优化问题的求解方法也有很多,下面介绍几种常见的方法:1. 等式约束问题的拉格朗日乘子法:等式约束问题可以通过引入拉格朗日乘子来转化为无约束优化问题。
通过求解无约束优化问题的驻点,求得原始约束优化问题的解。
2. 不等式约束问题的罚函数法:不等式约束问题可以通过引入罚函数来转化为无约束优化问题。
罚函数法通过将违反约束条件的点处添加罚项,将约束优化问题转化为无约束问题。
3. 逐次二次规划法:逐次二次规划法是一种常用的求解约束优化问题的方法。
该方法通过依次处理逐个约束来逼近最优解,每次处理都会得到一个更小的问题,直至满足所有约束条件。
4. 内点法:内点法是一种有效的求解约束优化问题的方法。
该方法通过向可行域内部逼近,在整个迭代过程中都保持在可行域内部,从而避免了外点法需要不断向可行域逼近的过程。
第四章 约束非线性优化

m * 0 f ( x * ) i*ci ( x * ) 0, i 1 *c ( x * ) 0, * 0, i 1, 2, ..., m; * 0. i 0 i i
f ( x* d ) f ( x* ) 且 ci ( x * d ) 0
对于0 = 都成立,这与已知x*为局部极小矛盾.
最优化方法之约束非线性规划 怀化学院数学系
最优性条件
定理4.1( Fritz John一阶必要条件)
设x*为(1)的局部极小点且f ( x ), ci ( x )(1 i m )在点x*可微,
i 1 m
最优化方法之约束非线性规划
怀化学院数学系
最优性条件
Gordan引理的几何意义为:
不存在向量d 使aiT d 0( i 1, ..., m ),是指向量a1 , a2 , ..., am不同时
处于过原点的任何超平面的同一侧.
这时,总可以适当放大或缩小各向量的长度,使变化后 各向量的组合为零向量. 引理4.3(几何最优性条件) 在问题(1)中,假定x*为(1)的局部
% % 不等式约束ci ( x ) 0为x的有效约束;反之,若有ci ( x ) 0, % % 则称不等式约束ci ( x ) 0为x的非有效约束.称所有在x处的 有效约束的下标组成的集合
% % I ( x ) {i | ci ( x ) 0} {1, 2, ..., m}
% % 为x处的有效约束指标集, 简称x处的有效集. 在讨论两个重要引理前先给出凸锥的定义. 定义4.2 设非空集合C Rn , 某一点x C .对d Rn和t 0, 当x d C时,必有x td C , 则称C为以x为顶点的锥.当C
非线性优化的基本理论

非线性优化的基本理论引言非线性优化是数学和计算机科学领域的一个重要研究方向。
它研究的是在给定约束条件下,如何寻找某个目标函数的最优解。
与线性优化问题不同,非线性优化问题涉及非线性函数的优化,更具有挑战性。
基本概念1.目标函数(Objective Function):非线性优化问题中需要优化的目标函数,通常表示为f(x),其中x表示自变量。
2.约束条件(Constraints):非线性优化问题中限制目标函数的函数或等式,通常表示为g(x) <= 0和h(x) = 0。
3.最优解(Optimal Solution):非线性优化问题中使目标函数取得最小(或最大)值的自变量的取值。
4.局部最优解(Local Optimum):非线性优化问题中某个点附近的最优解,但不一定是全局最优解。
5.全局最优解(Global Optimum):非线性优化问题中使目标函数取得最小(或最大)值的自变量的取值,是优化问题的最优解。
基本原理非线性优化的基本原理是寻找目标函数在给定约束条件下的最优解。
常用的方法包括梯度下降法、牛顿法和拟牛顿法等。
1. 梯度下降法(Gradient Descent)梯度下降法是一种基于目标函数梯度信息的迭代优化方法。
它的基本思想是通过不断迭代调整自变量的取值,使目标函数逐渐收敛到最优解。
具体步骤如下:1. 初始化自变量的取值。
2. 计算目标函数在当前自变量取值下的梯度。
3. 根据梯度的方向和步长,更新自变量的取值。
4. 重复步骤2和步骤3,直到满足停止准则。
2. 牛顿法(Newton’s Method)牛顿法是一种基于目标函数二阶导数信息的迭代优化方法。
它的基本思想是通过将目标函数进行二阶泰勒展开,以二阶导数的倒数作为步长,调整自变量的取值。
具体步骤如下: 1.初始化自变量的取值。
2. 计算目标函数在当前自变量取值下的一阶导数和二阶导数。
3. 根据一阶导数和二阶导数,更新自变量的取值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1) 下降方向的选择 如果方向P在点x0处是下降方向,则P应与-f (x0)同侧, 即: T f ( x ) P 0
0
T F { P f ( x0 ) P 0} 为点x0处的下降方向集。 记 0
2) 可行方向的选择 在x0处的可行方向应满足:
gi ( x0 P ) 0, i 1,2,, m hj ( x0 P ) 0, j 1,2,, p
注1 注2
g1 ( x0 ),, gm ( x0 ) 是x0处法空间的一组基。
方程组
的一组线 g i ( x0 , h) 0, i 1,2, , m 性无关的解构成曲面S上x0处切空间的一组基。 min f (x,y) S.t. g (x,y)=0 0,则f (x0,y0)与g (x0,y0)
j
g i ( x 0 ) h j 0, i 1,2, , m x j g m ( x 0 ) x1 g1 ( x 0 ), g m ( x 0 ) g m ( x 0 ) x n
系数矩阵
满秩,则称x0为曲面S上的一个正规点。
m in f ( x ) S x g ( x ) 0, h ( x ) 0, i 1, , m; j 1, , p i j
n f ( x ) x1 x2 S x x1 x 2 1 0,1 x1 0,1 x 2 0
2,具等式约束问题的极值必要条件 考虑二维问题:
结论1:若在极小点(x0,y0)处,g (x0,y0)
线性相关,即f (x0,y0) + g (x0,y0)=0。
结论2:(Lagrange乘子规则)设(x0,y0)是局部极小点,且g (x0,y0)
0,则存在常数 ,对函数F (x0,y0)= f (x0,y0)+ g (x0,y0),满足 F(x0,y0)= f (x0,y0) + g (x0,y0)=0.
结论3(充分条件):设点x0满足必要条件: F(x0)= f (x0) + g (x0)=0. 若 F ( x0 , h) hT 2 F ( x0 )h 0, h 0 g i ( x 0 ; h) 0, i 1,2, , m 则x0是局部极小点。 二,具不等式约束的问题 1,下降方向和可行方向 考虑一般非线性约束优化问题:
g ( x i i ) 为Fritz-John 条件。其中 iI x
g1 ( x ),, gm ( x ) 线性无关。
在最优点x*处应满足 f ( x ) g ( x ), i 0 i i i g ( x ) 0, i 1,, m i i Farkas引理:给定向量a i(i =1,2,…,k)与b,不存在向量P同
m i n f ( x) 的最优解,则x*处 G0 F0 gi ( x ) 0, i 1,, m n x R
换言之,在x*处满足 gi ( x ) P 0, i I ( x )
T
的方向P必有 称 f ( x )
T
f ( x ) P 0
T x* ( 1, 0 ) 是最优点,起作用约束 I ( x*) {1,3},f ( x*) ( 1,0)T
g1 ( x*) (0,1)T , g 3 ( x*) (0,1)T , 显然找不到1 , 3 0, 使 f ( x*) 1g1 ( x*) 5g 3 ( x*)成立。
第四章 约束非线性优化的理论与方法
一,等式约束问题 1,切向量与正规性 定义1 设x0 是由方程组gi(x)=0, i=1,2, …,m,确定的曲面 S上的一点,若在S上存在曲线x(t),x(0)= x0,x’(0)=h, 则称向量是曲面S上点x0处的切向量。 定义2:如果关于h 的线性方程组:
g i ( x 0 , h) g1 ( x 0 ) x1 g1 ( x 0 ) x n
时满足条件 aiT P 0, i 1,2,, k 和 bT P 0 的充要
条件是 向量b 在ai 所张成的凸锥内,即满足
b
a
i 1 i
k
i
, i 0
定理1:设x*为问题
的一个可行点,并且前t个约束为起作用约束,则x*为最 优解的一个必要条件是下式成立:
f ( x*)
结论1:若 x 0 S 所有方向P都是可行的。
T x S P 0 结论2:若 当 gi ( x0 ) 0, i I ( x0 ) {i gi ( x0 ) 0} 时
0
则P为可行方向。 记 G0 { P T gi ( x0 ) P 0, i I ( x0 )} 为可行方 向集。 注:对等式约束而言,所有约束都是起作用约束。 2,最优性条件 定义1:若对xC和0,有 xC ,则称C为锥,如果C是 凸的,则称其为凸锥。 定义2:设是约束集,称 D { P P 0, x0 P S , 0, 为x0处的可行方向锥。 下面进一步讨论最优性条件。设x*是问题
m i n f ( x ), x R n n a ij x i bi , i 1, , m i 1
a
i 1 i
t
i
, i 0
例:考虑问题
min f ( x ) x1 , g ( x) 3 ( 1 x ) x2 0, 1 1 g ( x ) x 0, g ( x ) x 0 1 3 2 2
