信息论与编码理论基础王育民 ppt课件
观察到010之后不能断定是哪个消息出现了。但是由观察结 果计算出来的某个消息出现的后验概率大于1/2或小于1/2,使 我们可比未观察前较有把握地推断消息出现的可能性，因 而多少得到了一些有关出现的“信息”。
若p<1/2，则1-p>1/2，也即010是消息x1的输出可能性大。
2020/4/5
7
直观认识
互信息量的性质：
（1）I(xk; yj)=loga(rkj/(qkwj))。因此有对称性：
I(xk; yj)=I(yj; xk)。
（2）当rkj=qkwj时, I(xk; yj)=0。即当(rkj/qk)=wj时，I(xk; yj)=0。
又即当(rkj/wj)=qk时，I(xk; yj)=0。
换句话说，当“X=xk”与“Y= yj”这两个事件相互独立时，互信 息量为0）。
2020/4/5
12
非平均互信息量性质
（3）当rkj>qkwj时 I(xk; yj)>0，当rkj<qkwj时 I(xk; yj)<0。 当(rkj/qk) > wj时，I(xk; yj)>0； 当(rkj/qk) < wj时，I(xk; yj)<0。 换句话说，
当“X=xk”与“Y= yj”这两个事件相互肯定时，互信息量为 正值；
信息量和熵
§2.1 离散型随机变量的非平均信息量（事件的信息量）
§2.2 离散型随机变量的平均自信息量（熵）
§2.4 离散型随机变量的平均互信息量
§2.5 连续型随机变量的平均互信息量和微分熵
§2.6 凸函数与(离散型随机变量的)平均互信息量凸性
2020/4/5
1
§2.1 离散型随机变量的非平均信息量 （事件的信息量）
2020/4/5
15
非平均自信息量
定义2.1.3(非平均自信息量) 给定一个离散型随机变量{X, xk, qk, k=1~K}。 事件xk∈X的自信息量定义为 I(xk)=loga(1/qk)，
其中底数a是大于1的常数。
2020/4/5
2Hale Waihona Puke 非平均互信息量例2.1.1
输入 消息
码字 （输出）
p(xk)
X1 000
1/8
X2 001
1/8
X3 010
1/8
X4 011
1/8
X5 100
1/8
X6 101
1/8
X7 110
1/8
x8 111
1/8
2020/4/5
收到0
1/4 1/4 1/4 1/4
0 0 0 0
收到01 收到011
可以推广到任意有限多个空间情况
2020/4/5
14
互信息的可加性
u1
u2 u3
系统
u1
u2
系统
u3
I(u1;u2,u3)I(u1;u2)I(u1;u3|u2) I(u1;u3)I(u1;u2|u3)
意味着：（u2,u3）联合给出的关于u1的信息量等于u2给出的关 于u1的信息量与u2已知条件下u3给出的关于u1的信息量之和。
从上述两个系统可以看出，在一个系统中我们 所关心的输入是哪个消息的问题，只与事件出
现的先验概率和经过观察后事件出现的后验概
率有关。 信息应当是先验概率和后验概率的函数，即
I(xk;yj)=f [Q(xk),P(xk|yj)]
2020/4/5
8
研究表明
信息量就表示成为事件的后验概率与事件的先 验概率之比的对数函数!!!
I( xi ; yj )=[收到yj 前，收信者对信源发xi 的不确定性] -[收到yj 后，收信者对信源发xi仍然存在 的 不确定性]
=收信者收到yj 前后，收信者对信源发xi 的 不确定性的消除
2020/4/5
11
非平均互信息量性质
其中底数a是大于1的常数。常用a=2或a=e，当a=2时互信息量 的单位为“比特”。
事件xk∈X与事件yj∈Y的互信息量定义为
I(xk;yj)logaP(XP (X xk|Yxk )yj)logaP(YP (Y yj|X yj )xk) logaP P((X (X,Yx)k)P((xYk,yyj)j))logaqkrkw j j
2020/4/5
10
非平均互信息量直观认识
若信源发某符号xi, 由于信道中噪声的随机干扰，收信者收到 的是xi的某种变形yj，收信者收到yj后，从yj中获取xi的信息量 用I( xi ; yj )表示，则有
0
0
0
0
1/2
0
1/2
1
0
0
0
0
0
0
0
0
3
非平均互信息量
输入消息
X1 X2 X3 X4 X5 X6 X7 x8
码字
000 001 010 011 100 101 110 111
p(xk)
1/8 1/4 1/8 1/4 1/16 1/16 1/16 1/16
收到0
1/6 1/3 1/6 1/3
0 0 0 0
2020/4/5
9
非平均互信息量
（本章将给出各种信息量的定义和它们的性质。）
定义2.1.1(非平均互信息量) 给定一个二维离散型随机变量
{(X x k,,j)y Y ,k,j) rk 1 ,~(K 1 ~ ;Jj}
因此就给定了两个离散型随机变量 { X ,x k ,q k ,k 1 ~ K } 和 { Y ,y j,w j,j 1 ~ J }
5
非平均互信息量
例2.1.2
输入消息 码字
X1
000
X2 111
p(xk)
1/2 1/2
收到0
1-p p
收到01
1/2 1/2
收到010
1-p p
1-p
0
0
p
p
1
1
1-p
2020/4/5
6
直观认识
在接收010的过程中，消息出现的可能性，即后验概率也在 不断变化，但变化趋势不再像例2.1.1 那样单调地变化，而 是有起伏的，且最后并未达到1或0.
当“X=xk”与“Y= yj”这两个事件相互否定时，互信息量为 负值。
2020/4/5
13
条件互信息和联合事件互信息
三个事件集的条件互信息定义（定义2.1.2）为
I ( u 1 ;u 2 |u 3 ) lo g p ( u p 1 ( u |1 u 2 |， u 3 u )3 ) lo g p ( u p 1 ( u |u 1 ， 3 ) u p 2 ( u |u 2 3 |) u 3 )
收到01
0 0 1/3 2/3 0 0 0 0
收到011
0 0 0 1 0 0 0 0
2020/4/5
4
直观认识
对观察者来说，同样观察事件011，但输 入消息等概情况下“收获”要大些，即 得到的“信息”要多些。
越是不太可能发生的事件竟然发生了， 越是令人震惊。获得的“信息”要多些。
2020/4/5
合集下载
精品课课件信息论与编码(全套讲义)
拓展应用领域 信息论的应用领域将进一步拓展，如生物信息学、 量子信息论等新兴领域，以及与人工智能、大数 据等技术的结合。
跨学科交叉融合
信息论将与更多学科进行交叉融合，如物理学、 化学、社会学等，共同推动信息科学的发展。
编码技术的发展趋势
高效编码算法
随着计算能力的提升，更高效的编码算法将不断涌现，以提高数据 传输和存储的效率。
智能化编码
借助人工智能和机器学习技术，编码将实现智能化，自适应地调整 编码参数以优化性能。
跨平台兼容性
未来的编码技术将更加注重跨平台兼容性，以适应不同设备和网络环 境的多样性。
信息论与编码的交叉融合
理论与应用相互促进
信息论为编码技术提供理论支持， 而编码技术的发展又反过来推动 信息论的深入研究。
共同应对挑战
精品课课件信息论与编码(全套 讲义)
目
CONTENCT
录
• 信息论基础 • 编码理论 • 信道编码 • 信源编码 • 信息论与编码的应用 • 信息论与编码的发展趋势
01
信息论基础
信息论概述
信息论的研究对象
研究信息的传输、存储、处理和变换规律的科学。
信息论的发展历程
从通信领域起源，逐渐渗透到计算机科学、控制论、 统计学等多个学科。
卷积编码器将输入的信息序列按位输入到一个移位寄存器中，同时根据生成函数将移位寄存 器中的信息与编码器中的冲激响应进行卷积运算，生成输出序列。
卷积码的译码方法
卷积码的译码方法主要有代数译码和概率译码两种。代数译码方法基于最大似然译码准则， 通过寻找与接收序列汉明距离最小的合法码字进行译码。概率译码方法则基于贝叶斯准则， 通过计算每个合法码字的后验概率进行译码。
04
跨学科交叉融合
信息论将与更多学科进行交叉融合，如物理学、 化学、社会学等，共同推动信息科学的发展。
编码技术的发展趋势
高效编码算法
随着计算能力的提升，更高效的编码算法将不断涌现，以提高数据 传输和存储的效率。
智能化编码
借助人工智能和机器学习技术，编码将实现智能化，自适应地调整 编码参数以优化性能。
跨平台兼容性
未来的编码技术将更加注重跨平台兼容性，以适应不同设备和网络环 境的多样性。
信息论与编码的交叉融合
理论与应用相互促进
信息论为编码技术提供理论支持， 而编码技术的发展又反过来推动 信息论的深入研究。
共同应对挑战
精品课课件信息论与编码(全套 讲义)
目
CONTENCT
录
• 信息论基础 • 编码理论 • 信道编码 • 信源编码 • 信息论与编码的应用 • 信息论与编码的发展趋势
01
信息论基础
信息论概述
信息论的研究对象
研究信息的传输、存储、处理和变换规律的科学。
信息论的发展历程
从通信领域起源，逐渐渗透到计算机科学、控制论、 统计学等多个学科。
卷积编码器将输入的信息序列按位输入到一个移位寄存器中，同时根据生成函数将移位寄存 器中的信息与编码器中的冲激响应进行卷积运算，生成输出序列。
卷积码的译码方法
卷积码的译码方法主要有代数译码和概率译码两种。代数译码方法基于最大似然译码准则， 通过寻找与接收序列汉明距离最小的合法码字进行译码。概率译码方法则基于贝叶斯准则， 通过计算每个合法码字的后验概率进行译码。
04
信息论与编码基础_教学课件_1
绪论
Notable awards:
Alfred Noble Prize IEEE Medal of Honor
信息论与编码基础
一、信息概念
二、信息论的诞生
绪论
三、信息论研究的基本问题及内容
四、编码技术的发展
五、信息论与其它学科的交叉发展
信息论与编码基础
1、信息论研究的基本问题
绪论
2、信息论研究的内容
信息论与编码基础
Fields: Electronic engineer
and mathematician
绪论
Alma mater: MIT
University of Michigan
Institutions:
Bell Laboratories Massachusetts Institute of Technology Institute for Advanced Study
信息论与编码基础
全信息理论
信息 传递 信息处理—再生
绪论
信息 传递
信息 获取
外部世界 问题／环境
信息运动过程
信息 施用
思考题
一位朋友不赞同“消息中未知的成分才算是信息”的说法
他举例说：我多遍地欣赏梅兰芳大师的同一段表演，百看 不厌，大师正在唱的、正在表演的使我愉快，将要唱的和
表演的我都知道，照这种说法电视里没给我任何信息，怎
信息论与编码基础
例子
绪论
1、2021年9月11日上午9时，一颗小行星将和地球相撞。
2、2022年7月11日上午9时，将发生日食。
信息论与编码基础
一、信息概念
二、信息论的诞生
绪论
三、信息论研究的基本问题及内容
《信息论与编码》课件第1章 绪论
1.2 通信系统的模型
信源符号
信 源 编码 信 源
（序列）
编码器 信 道 译码器
x y yˆ
重建符号 （序列）
x
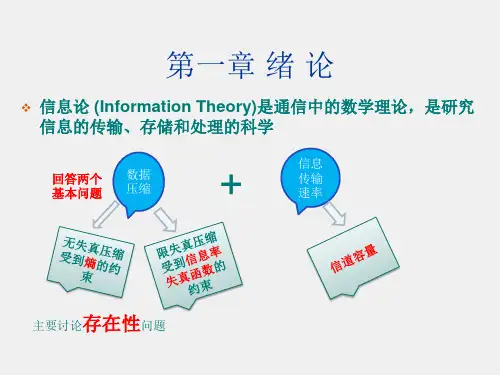
❖ 无失真编码： x xˆ
重建符号与信源发送符号一致， 即编码器输出码字序列与信源 发送序列一一映射；
限失真编码： x xˆ
总是成立的
y yˆ
分别是编码输出码字和接收到的码字
重建符号与信源发送符号不 完全一致；编码器输出码字 序列与信源输出符号序列之 间不是一一映射关系，出现 符号合并，使得重建符号的 熵减少了。
限失真、无失真是由于编译 码器形成的
信道编码
增加冗余
提高
对信道干 扰的抵抗 力
信息传输 的可靠性
❖ 由于信道中存在干扰， 数据传递过程中会出现 错误，信道编码可以检 测或者纠正数据传输的 错误，从而提高数据传 输的可靠性。
1.2 通信系统的模型
调制器
作用：
➢ 将信道编码的输出变换为适合信道传输的 要求的信号 ；
消息
信息的表现形 式；
文字，图像， 声音等；
信号
信号的变化描 述消息；
信息的基本特点
1.不确定性
受信者在接收到信息之前，不知道信源发送 的内容是什么，是未知的、不确定性事件；
2.受信者接收到信息后，可以减少或者消除不确定性；
3. 可以产生、消失、存储，还可以进行加工、处理；
4. 可以度量
1.2 通信系统的模型
冗 信源符号 余 变 相关性强 化 统计冗余强
信源编码器
码序列 相关性减弱 统计冗余弱
相关冗余 统计冗余 生理冗余
模型简化
信源输出前后符号之间存在一定相关性
信源输出符号不服从等概率分布
信息论与编码理论基础(第一章)
11:02
13
11:02
14
第一章：引论（简介）
一、通信系统模型 二、Shannon信息论的中心问题 三、Shannon信息的概念 四、概率复习内容
11:02
15
一、通信系统模型
信源、信道、信宿 信源是消息的来源， 信道是消息传送媒介， 信宿是消息的目的地。
信息是多样的，客观事物是多种多样的、五花 八门的，事物的状态和变化是多姿多彩、变幻 无穷的，属性不同就出现了不同的信息，需要 给出不同的信息定义，从而可创建不同的信息 理论。
比如说信息的不确定性，引出了概率信息，这 是我们讲的最多的。
再如信息的模糊性，引出了模糊信息和模糊信 息论，这个在70年代末提出来的。
信息论基础
11:02
1
教材
王育民、李晖， 信息论与编码理论 （第2版）， 高等教育出版社， 2013.
11:02
2
参考书
Thomas M. Cover, Joy A. Thomas, Elements of Information Theory，2nd ed, WILEY Press, 2006. 阮吉寿 张华 译 信息论基础，机械工业出版社，2007.
11:02
6
信息的度量
信息可以被感知，但是不是所有的信息 都可以定量计数，因此，我们要区分信 息和信息量 。
从数学上来说，关于信息量的定义，大 概有100多种。
如果将信息提升到科学进行研究，必须 要对信息进行定量，给出信息的科学测 度，但是这并不是一件很容易的事情。
11:02
7
信息与信息量
还如信息的量子属性，引出了量子信息和量子 信息论。
11:02
8
信息与信息量
信息论与编码理论基础 王育民(第二章 )
2020/4/5
9
非平均互信息量
（本章将给出各种信息量的定义和它们的性质。）
定义2.1.1(非平均互信息量) 给定一个二维离散型随机变量
{(Xx k,, j)y Y ,k,j)r k ,1 ~(K 1 ~ ; Jj}
因此就给定了两个离散型随机变量 { X ,x k ,q k ,k 1 ~ K } 和 { Y ,y j,w j,j 1 ~ J }
事件xk∈X与事件yj∈Y的互信息量定义为
I(xk;yj)loga
P(XP(Xxk|Yxk)yj)loga
P(Yyj |Xxk) P(Yyj)
logaP P((X (X,Yx)k)P((xYk,yyj)j))logaqkrkw j j
2020/4/5
10
非平均互信息量直观认识
若信源发某符号xi, 由于信道中噪声的随机干扰，收信者收到 的是xi的某种变形yj，收信者收到yj后，从yj中获取xi的信息量 用I( xi ; yj )表示，则有
2020/4/5
15
非平均自信息量
定义2.1.3(非平均自信息量) 给定一个离散型随机变量{X, xk, qk, k=1~K}。 事件xk∈X的自信息量定义为 I(xk)=loga(1/qk)，
其中底数a是大于1的常数。
从上述两个系统可以看出，在一个系统中我们 所关心的输入是哪个消息的问题，只与事件出
现的先验概率和经过观察后事件出现的后验概
率有关。 信息应当是先验概率和后验概率的函数，即
I(xk;yj)=f [Q(xk),P(xk|yj)]
2020/4/5
8
研究表明
信息量就表示成为事件的后验概率与事件的先 验概率之比的对数函数!!!
2020/4/5
《信息论与编码》课件
优点
可以快速计算出哈希值，常用于数据完整性验证和密码存储。
缺点
对于某些输入，哈希函数可能产生冲突，即不同的输入可能会产生相同的哈希值。
信息论的应用
05
数据压缩
数据压缩是信息论的一个重要应用，通过编码技术减少数据冗余，提高存储和传输效率。
压缩算法
常见的压缩算法包括哈夫曼编码、算术编码、LZ77和LZ78等，这些算法利用数据的统计特性进行压缩。
定义
RSA（Rivest-Shamir-Adleman）、ECC（椭圆曲线加密）等。
常见的非对称加密算法
密钥管理相对简单，安全性较高。
优点
加密速度较慢，通常比对称加密算法慢几个数量级。
缺点
定义
哈希函数是一种将任意长度的数据映射为固定长度哈希值的函数。
常见的哈希函数
MD5（Message Digest Algorithm 5）、SHA（Secure Hash Algorithm）等。
互信息定义
条件互信息表示一个随机变量在给定另一个随机变量的条件下与第三个随机变量之间的相关性。
条件互信息定义
信源编码
02
无损压缩编码是一种完全保留原始数据，没有任何信息损失的编码方式。
有损压缩编码是一种允许一定信息损失的编码方式，通常用于图像、音频和视频等连续媒体数据的压缩。有损压缩编码通过去除数据中的冗余信息和细节来减少存储空间或传输时间。解压缩时，虽然不能完全恢复原始数据，但人眼或耳朵通常无法察觉到损失的信息。因此，它常用于需要快速传输或低成本存储的场景，如数字电视广播、互联网流媒体等。有损压缩编码的优点是压缩率高，适合处理大量数据；缺点是原始数据的完整性和真实性可能受到损失。常见的有损压缩算法包括JPEG、MPEG、MP3等。这些算法通过离散余弦变换、小波变换等技术来减少数据量，同时采用量化等技术来控制信息损失的程度。
《信息论与编码全部》课件
添加副标题
信息论与编码全部PPT课件
汇报人：PPT
目录
CONTENTS
01 添加目录标题 03 信息度量与熵
02 信息论与编码的基 本概念
04 信源编码
05 信道编码
06 加密与解密技术
07 信息安全与认证技 术
添加章节标题
信息论与编码的基本概 念
信息论的发展历程
1948年，香农提出信 息论，奠定了信息论
提高安全性
优点：安全性 高，速度快，
易于实现
应用：广泛应 用于电子商务、 网络通信等领
域
发展趋势：随 着技术的发展， 混合加密技术 将更加成熟和
完善
信息安全与认证技术
数字签名技术
数字签名：一种用于验证信息来源和完整性的技术 数字签名算法：RSA、DSA、ECDSA等 数字证书：用于存储数字签名和公钥的文件 数字签名的应用：电子邮件、电子商务、网络银行等
汇报人：PPT
熵越小，表示信息量越小，不确 定性越小
熵是概率分布的函数，与概率分 布有关
信源编码
定义：无损信源编码是指在编码过 程中不丢失任何信息，保持原始信 息的完整性。
无损信源编码
应用：无损信源编码广泛应用于音 频、视频、图像等媒体数据的压缩 和传输。
添加标题
添加标题
添加标题
添加标题
特点：无损信源编码可以保证解码 后的信息与原始信息完全一致，但 编码和解码过程通常比较复杂。
古典密码学：公元前400年，古希腊人使用替换密码 近代密码学：19世纪，维吉尼亚密码和Playfair密码出现 现代密码学：20世纪，公钥密码体制和数字签名技术出现 当代密码学：21世纪，量子密码学和后量子密码学成为研究热点
信息论与编码全部PPT课件
汇报人：PPT
目录
CONTENTS
01 添加目录标题 03 信息度量与熵
02 信息论与编码的基 本概念
04 信源编码
05 信道编码
06 加密与解密技术
07 信息安全与认证技 术
添加章节标题
信息论与编码的基本概 念
信息论的发展历程
1948年，香农提出信 息论，奠定了信息论
提高安全性
优点：安全性 高，速度快，
易于实现
应用：广泛应 用于电子商务、 网络通信等领
域
发展趋势：随 着技术的发展， 混合加密技术 将更加成熟和
完善
信息安全与认证技术
数字签名技术
数字签名：一种用于验证信息来源和完整性的技术 数字签名算法：RSA、DSA、ECDSA等 数字证书：用于存储数字签名和公钥的文件 数字签名的应用：电子邮件、电子商务、网络银行等
汇报人：PPT
熵越小，表示信息量越小，不确 定性越小
熵是概率分布的函数，与概率分 布有关
信源编码
定义：无损信源编码是指在编码过 程中不丢失任何信息，保持原始信 息的完整性。
无损信源编码
应用：无损信源编码广泛应用于音 频、视频、图像等媒体数据的压缩 和传输。
添加标题
添加标题
添加标题
添加标题
特点：无损信源编码可以保证解码 后的信息与原始信息完全一致，但 编码和解码过程通常比较复杂。
古典密码学：公元前400年，古希腊人使用替换密码 近代密码学：19世纪，维吉尼亚密码和Playfair密码出现 现代密码学：20世纪，公钥密码体制和数字签名技术出现 当代密码学：21世纪，量子密码学和后量子密码学成为研究热点
信息论与编码理论基础王育民 ppt课件
[收到yj = xi 后，收信者对信源发xi仍然存在的不确定性]=0
I( xi ; xi )=[收到xi前，收信者对信源发xi 的不确定性] = I( xi )
2020/4/5
18
2020/4/5
19
2020/4/5
20
2020/4/5
21
条件的非平均自信息量
定义2.1.4(条件的非平均自信息量) 给定一个二维离散型随机变量
互信息量的性质：
（1）I(xk; yj)=loga(rkj/(qkwj))。因此有对称性：
I(xk; yj)=I(yj; xk)。
（2）当rkj=qkwj时, I(xk; yj)=0。即当(rkj/qk)=wj时，I(xk; yj)=0。
又即当(rkj/wj)=qk时，I(xk; yj)=0。
换句话说，当“X=xk”与“Y= yj”这两个事件相互独立时，互信 息量为0）。
0
2020/4/5
39
平均自信息量——熵
例2.2.1 离散型随机变量X有两个事件x1和x2， P(X=x1)=p，P(X=x2)=1-p
则X 的平均自信息量（熵）为 H(X)=ploga(1/p)+(1-p)loga(1/(1-p))
收到01
0 0 1/3 2/3 0 0 0 0
收到011
0 0 0 1 0 0 0 0
2020/4/5
4
直观认识
对观察者来说，同样观察事件011，但输 入消息等概情况下“收获”要大些，即 得到的“信息”要多些。
越是不太可能发生的事件竟然发生了， 越是令人震惊。获得的“信息”要多些。
2020/4/5
5
非平均互信息量
例2.1.2
输入消息 码字
I( xi ; xi )=[收到xi前，收信者对信源发xi 的不确定性] = I( xi )
2020/4/5
18
2020/4/5
19
2020/4/5
20
2020/4/5
21
条件的非平均自信息量
定义2.1.4(条件的非平均自信息量) 给定一个二维离散型随机变量
互信息量的性质：
（1）I(xk; yj)=loga(rkj/(qkwj))。因此有对称性：
I(xk; yj)=I(yj; xk)。
（2）当rkj=qkwj时, I(xk; yj)=0。即当(rkj/qk)=wj时，I(xk; yj)=0。
又即当(rkj/wj)=qk时，I(xk; yj)=0。
换句话说，当“X=xk”与“Y= yj”这两个事件相互独立时，互信 息量为0）。
0
2020/4/5
39
平均自信息量——熵
例2.2.1 离散型随机变量X有两个事件x1和x2， P(X=x1)=p，P(X=x2)=1-p
则X 的平均自信息量（熵）为 H(X)=ploga(1/p)+(1-p)loga(1/(1-p))
收到01
0 0 1/3 2/3 0 0 0 0
收到011
0 0 0 1 0 0 0 0
2020/4/5
4
直观认识
对观察者来说，同样观察事件011，但输 入消息等概情况下“收获”要大些，即 得到的“信息”要多些。
越是不太可能发生的事件竟然发生了， 越是令人震惊。获得的“信息”要多些。
2020/4/5
5
非平均互信息量
例2.1.2
输入消息 码字
信息论与编码教学课件(全)
信息论与编码教学课件(全)
目录
• 课程介绍与背景 • 信息论基础 • 编码理论基础 • 信道编码技术 • 数据压缩技术 • 多媒体信息编码技术 • 课程总结与展望
01
课程介绍与背景
Chapter
信息论与编码概述
信息论的基本概念
01
信息、信息量、信息熵等
编码的基本概念
02
信源编码、信道编码、加密编码等
02
极化码（Polar Codes）
一种新型信道编码方式，通过信道极化现象实现高效可靠的信息传输。
03
深度学习在信道编码中的应用
利用深度学习技术优化传统信道编码算法，提高编码性能和效率。
05
数据压缩技术
Chapter
数据压缩概述与分类
数据压缩定义
通过去除冗余信息或使用更高效的编码方式，减小数据表示所需存储空间的过 程。
线性分组码原理：线性分组码是一 种将信息序列划分为等长的组，然 后对每组信息进行线性变换得到相 应监督位的编码方式。
具有严谨的代数结构，易于分析和 设计；
具有一定的检错和纠错能力，适用 于各种通信和存储系统。
循环码原理及特点
循环码原理：循环码是一种特殊的线 性分组码，其任意两个码字循环移位
后仍为该码的码字。
03
编码理论基础
Chapter
编码的基本概念与分类
编码的基本概念
编码是将信息从一种形式或格式转换为另一种形式的过程，以 满足传输、存储或处理的需要。
编码的分类
根据编码的目的和原理，可分为信源编码、信道编码、加密编 码等。
线性分组码原理及特点
线性分组码特点
监督位与信息位之间呈线性关系， 编码和解码电路简单；
目录
• 课程介绍与背景 • 信息论基础 • 编码理论基础 • 信道编码技术 • 数据压缩技术 • 多媒体信息编码技术 • 课程总结与展望
01
课程介绍与背景
Chapter
信息论与编码概述
信息论的基本概念
01
信息、信息量、信息熵等
编码的基本概念
02
信源编码、信道编码、加密编码等
02
极化码（Polar Codes）
一种新型信道编码方式，通过信道极化现象实现高效可靠的信息传输。
03
深度学习在信道编码中的应用
利用深度学习技术优化传统信道编码算法，提高编码性能和效率。
05
数据压缩技术
Chapter
数据压缩概述与分类
数据压缩定义
通过去除冗余信息或使用更高效的编码方式，减小数据表示所需存储空间的过 程。
线性分组码原理：线性分组码是一 种将信息序列划分为等长的组，然 后对每组信息进行线性变换得到相 应监督位的编码方式。
具有严谨的代数结构，易于分析和 设计；
具有一定的检错和纠错能力，适用 于各种通信和存储系统。
循环码原理及特点
循环码原理：循环码是一种特殊的线 性分组码，其任意两个码字循环移位
后仍为该码的码字。
03
编码理论基础
Chapter
编码的基本概念与分类
编码的基本概念
编码是将信息从一种形式或格式转换为另一种形式的过程，以 满足传输、存储或处理的需要。
编码的分类
根据编码的目的和原理，可分为信源编码、信道编码、加密编 码等。
线性分组码原理及特点
线性分组码特点
监督位与信息位之间呈线性关系， 编码和解码电路简单；
《信息论与编码》课件
发展趋势与未来挑战
探讨信息论和编码学领域面临的未 来挑战。
介绍多媒体数字信号压缩和编码技术的发展和应用。
可靠的存储与传输控制技术
解释可靠存储和传输控制技术在信息论中的重要性。
生物信息学中的应用
探讨信息论在生物信息学领域的应用和突破。
总结与展望
信息论与编码的发展历程
回顾信息论和编码学的发展历程和 里程碑。
信息技术的应用前景
展望信息技术在未来的应用前景和 可能性。
介绍误码率和信噪比的定义和关系。
2
码率与修正码率的概念
解释码率和修正码率在信道编码中的重要性。
3
线性码的原理与性质
探讨线性码的原理、特点和应用。
4
编码与译码算法的实现
详细介绍信道编码和译码算法的实现方法。
第四章 信息论应用
无线通信中的信道编码应用
探索无线通信领域中信道编码的应用和进展。
多媒体数字信号的压缩与编码技术
《信息论与编码》T课 件
# 信息论与编码 PPT课件
第一章 信息的度量与表示
信息的概念与来源
介绍信息的定义，以及信息在各个领域中的来源和 应用。
香农信息熵的定义与性质
介绍香农信息熵的概念和其在信息论中的重要性。
信息量的度量方法
详细解释如何度量信息的数量和质量。
信息压缩的基本思路
探讨信息压缩的原理和常用方法。
第二章 信源编码
等长编码与不等长编码
讨论等长编码和不等长编码的特点 和应用领域。
霍夫曼编码的构造方法与 性质
详细介绍霍夫曼编码的构造和优越 性。
香农第一定理与香农第二 定理
解释香农第一定理和香农第二定理 在信源编码中的应用。