小学奥数分数求和专题总结
六年级上册数学竞赛试题分数裂项求和方法总结_通用版
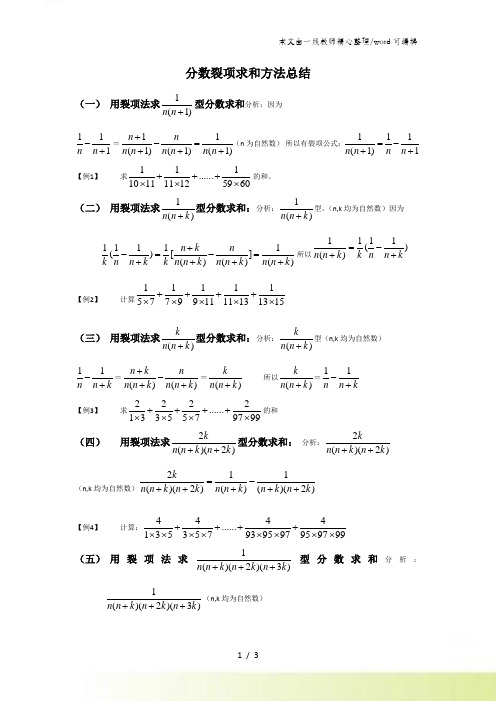
分数裂项求和方法总结(一) 用裂项法求1(1)n n +型分数求和分析:因为 111n n -+=11(1)(1)(1)n n n n n n n n +-=+++(n 为自然数) 所以有裂项公式:111(1)1n n n n =-++ 【例1】 求111 (101111125960)+++⨯⨯⨯的和。
(二) 用裂项法求1()n n k +型分数求和:分析:1()n n k +型。
(n,k 均为自然数)因为 11111()[]()()()n k n k n n k k n n k n n k n n k +-=-=++++所以1111()()n n k k n n k =-++【例2】 计算11111577991111131315++++⨯⨯⨯⨯⨯(三) 用裂项法求()k n n k +型分数求和:分析:()k n n k +型(n,k 均为自然数) 11n n k -+=()()n k n n n k n n k +-++=()k n n k + 所以()k n n k +=11n n k -+ 【例3】 求2222 (1335579799)++++⨯⨯⨯⨯的和 (四) 用裂项法求2()(2)k n n k n k ++型分数求和: 分析:2()(2)k n n k n k ++ (n,k 均为自然数)211()(2)()()(2)k n n k n k n n k n k n k =-+++++【例4】 计算:4444......135357939597959799++++⨯⨯⨯⨯⨯⨯⨯⨯ (五) 用裂项法求1()(2)(3)n n k n k n k +++型分数求和分析:1()(2)(3)n n k n k n k +++(n,k 均为自然数)【例5】 计算:111......1234234517181920+++⨯⨯⨯⨯⨯⨯⨯⨯⨯(六) 用裂项法求3()(2)(3)k n n k n k n k +++型分数求和: 分析:3()(2)(3)k n n k n k n k +++(n,k 均为自然数) 【例6】 计算:333 (1234234517181920)+++⨯⨯⨯⨯⨯⨯⨯⨯⨯ 【例7】计算:71+83+367+5629+6337+7241+7753+8429+883 【分析与解】解答此题时,我们应将分数分成两类来看,一类是把5629、6337、7241、7753这四个分数,可以拆成是两个分数的和。
四年级奥数专题 巧妙求和

四年级奥数专题巧妙求和【一】求1~20这20个连续自然数的所有数字之和。
练习1、求1~50这50个连续自然数的所有数字之和。
2、求3~19连续自然数的全部数字之和。
【二】一把钥匙只能开一把锁。
现在有4把钥匙和4把锁,但不知道哪把钥匙开哪把锁,最多要试多少次就能配好全部的钥匙和锁?练习1、现在有8对钥匙和锁混在一起,不知道哪把钥匙配哪把锁,最多要试多少次就可以把它们全部配成对?2、有9颗钢珠,其中8颗一样重,另有一颗比这8颗略轻,用一架天平最多称多少次,就可以找到那颗较轻的钢珠?【三】思雨读一本长篇小说,他第一天读20页,从第二天起,他每天读的页数都比前一天多2页,第11天读了40页,正好读完,这本书共有多少页?练习1、王师傅做一批零件,第一天做了40个,以后每天都比前一天多做3个,第15天做了82个,正好做完,这批零件共有多少个?2、张琳读一本故事书,她第一天读了15页,从第二天起,每天读的页数都比前一天多5页。
最后一天读了40页恰好读完,这本书共有多少页?【四】45把锁的钥匙都搞乱了,为了使每把锁都配上自己的钥匙,至多要试多少次?练习1、有60把锁的钥匙搞乱了,为了使每把锁都配上自己的钥匙,至多要试多少次?2、有一些锁的钥匙搞乱了,已知至多要试45次,就能使每把锁都配上自己的钥匙,问一共有几把锁的钥匙搞乱了?【五】某班有30个同学,每两个同学互通一次电话,那么他们一共通了多少次电话?练习1、竹苑小学进行象棋比赛,每个参赛选手都要和其他所有的选手各赛一场,如果有15人参加比赛,问一共要进行多少场比赛?2、一次生日party中,参加的有20位同学和3位老师,每两人之间握一次手。
那么一共握了几次手?【六】求1~99中连续自然数的所有数字之和。
练习1、求1~199的199个连续自然数的所有数字之和。
2、求1~999的999个连续自然数的所有数字之和。
3、求1~210连续自然数的全部数字之和。
4、求1~299连续自然数的全部数字之和。
完整版)六年级奥数专题分数的计算技巧

完整版)六年级奥数专题分数的计算技巧例2、计算: (1)73分析与解:(1)73可以化简为73÷(7+3)=73÷10=7.32)把题中的166÷41改写成(4+1/41),再运用乘法分配律计算比常规方法计算要简便得多。
166÷41=4+1/4173×(4+1/41)=292+73/41=299.78例3、计算:(1)1112) 166÷41可以把111写成(72+39),再把式子改写成(72+39)×(166÷41),再利用除法的运算性质使计算更简便。
1)(72+39)×(166÷41)=72×4+39×4=288+156=4442)166÷41=4+2/41所以,(2)的计算式可以改写为×(4+2/41)=+3080/41=.75例2、计算:(1) 73×(2) 166÷41解析:(1) 73可以改写成(72+1),然后运用乘法分配律,得到73×=72×+×=9×。
因此,73×=9.2) 将166分成41的倍数与另一个较小的数相加的形式,得到166=4×41+42.然后,运用除法的运算性质,得到166÷41=4+÷41=4.因此,166÷41=4.例3、计算:(1) ×39+×25+×40 (2) 1×(2-)+15÷17解析:(1) 根据乘法的交换律和结合律,将×39写成×13,将×写成×,然后运用乘法分配律,得到×39+×25+×=×13+×25+×=×(13+25+2)=×40=10×。
奥数里的分数应用原理总结

奥数里的分数应用原理总结1. 介绍奥数是指奥林匹克数学竞赛,是培养学生逻辑思维和数学能力的重要途径之一。
在奥数中,分数应用是一个重要的内容,我们来总结一下奥数里的分数应用原理。
2. 原理介绍分数是数学中的一种表示方法,表示一个整体被划分成若干部分的数。
在奥数中,分数应用主要包括四则运算、比较大小、化简、混合运算等。
2.1 四则运算分数的四则运算包括加法、减法、乘法和除法。
2.1.1 加法和减法两个分数相加或相减,需要满足相同的分母。
具体步骤如下: - 确定两个分数的分母是否相同,如果不同,先通分; - 将两个分数的分子进行对应的加法或减法运算; - 将运算结果的分子写在分数的上方,分母写在分数的下方。
2.1.2 乘法两个分数相乘,直接将两个分数的分子相乘,分母相乘。
具体步骤如下: - 将两个分数的分子相乘,将运算结果的分子写在分数的上方; - 将两个分数的分母相乘,将运算结果的分母写在分数的下方。
2.1.3 除法两个分数相除,可以将除法转化为乘法的形式。
具体步骤如下: - 将被除数的分子乘以除数的分母,将运算结果的分子写在分数的上方; - 将被除数的分母乘以除数的分子,将运算结果的分母写在分数的下方。
2.2 比较大小比较两个分数的大小,可以通过找到两个分数的公共分母进行比较。
具体步骤如下: - 确定两个分数的分母是否相同,如果不同,先通分; - 比较两个分数的分子的大小,如果分子相等,则比较分母的大小,分母越大,分数越小; - 如果分子不相等,比较两个分子的大小,分子越大,分数越大。
2.3 化简分数的化简是指将一个分数约分到最简形式。
具体步骤如下: - 找到分子和分母的最大公约数; - 将分子和分母分别除以最大公约数,得到最简分数。
2.4 混合运算混合运算是指分数与整数的组合运算,包括分数与整数的加减乘除等。
3. 实例分析下面通过一些实例来进一步理解奥数中分数应用的原理。
3.1 实例一:分数的四则运算假设有两个分数:1/3 和 2/5,我们来进行加法运算。
小学五年级奥数练习(分数的综合运算技巧详解 )

小学五年级奥数练习——分数地综合运算技巧详解(分数地复杂运算、分数地混合运算)一、知识点1.混合运算技巧在分数、小数地四则混合运算中,到底是把分数化作小数,还是把小数化作分数,这影响到运算过程地繁琐与简便程度,也影响到运算结果地精确度。
小数化成分数,或分数化成小数’,有如下几种技巧。
(1)在加减法中,有时遇到分数只能化成循环小数时’,不能把分数化成小数,此时要将包括循环小数在内地所有小数都化为分数;(2)在乘除法中,一般情况下,小数化成分数计算则比较简便;(3)一般情况下,在加减法中,分数化成小数比较方便;(4)在运算中,使用假分数还是带分数,需视情况而定;(5)在计算中经常用到除法’、比、分数、小数、百分数互相之间地变换,把这些常用地数互化成数表对学习非常重要。
2.复杂分数地运算注意点先找出分数线,确定分子部分和分母部分,然后这两部分分别进行计算,每部分地计算结果需要约分地要先约分,再改成“分子部分÷分母部分”地形式,最后求出结果。
3.比和比例地技巧化简比地方法:比地前项和后项同时乘以或除以相同地数(0除外’),最后地比值应写成最简整数比。
具体如下:(1)分数比:可以前项除以后项,在根据比值写出最’简单地整数比。
(2)小数比:可以先利用商不’变地性质将其转化为整数比,然后再化简;(3)整数比:可以根据商不变地性质或像分数约分(前后项同时除以它们’地最大公因数)那样进行化简;4.分数拆分从分母M 地约数中’任意找出两个m 和n ,有)()()()(11n m M n n m M m n m M n m M +++=++=B A 11+=;如10地约’数有:1,10,2,5。
如选1和2,有:)21(102)21(101)21(10)21(1101+++=++=151301+=;另外,a ,b ,c 为M 地约数:)()()()()(11c b a M c c b a M b c b a M a c b a M c b a M ++++++++=++++=5.循环小数循环小数与分数地互化,循环小数之间’简单地加、减法运算,涉及循环小数与分数地’运算主要利用运算定律进行简算。
小学数学奥数35个专题题型分类及解题技巧

小学奥数辅导35个专题汇总1.和差倍问题2.年龄问题的三个基本特征:①两个人的年龄差是不变的;②两个人的年龄是同时增加或者同时减少的;③两个人的年龄的倍数是发生变化的;3.归一问题的基本特点:问题中有一个不变的量,一般是那个“单一量”,题目一般用“照这样的速度”……等词语来表示。
关键问题:根据题目中的条件确定并求出单一量;4.植树问题5.鸡兔同笼问题基本概念:鸡兔同笼问题又称为置换问题、假设问题,就是把假设错的那部分置换出来;基本思路:①假设,即假设某种现象存在(甲和乙一样或者乙和甲一样):②假设后,发生了和题目条件不同的差,找出这个差是多少;③每个事物造成的差是固定的,从而找出出现这个差的原因;④再根据这两个差作适当的调整,消去出现的差。
基本公式:①把所有鸡假设成兔子:鸡数=(兔脚数×总头数-总脚数)÷(兔脚数-鸡脚数)②把所有兔子假设成鸡:兔数=(总脚数一鸡脚数×总头数)÷(兔脚数一鸡脚数)关键问题:找出总量的差与单位量的差。
6.盈亏问题基本概念:一定量的对象,按照某种标准分组,产生一种结果:按照另一种标准分组,又产生一种结果,由于分组的标准不同,造成结果的差异,由它们的关系求对象分组的组数或对象的总量.基本思路:先将两种分配方案进行比较,分析由于标准的差异造成结果的变化,根据这个关系求出参加分配的总份数,然后根据题意求出对象的总量.基本题型:①一次有余数,另一次不足;基本公式:总份数=(余数+不足数)÷两次每份数的差②当两次都有余数;基本公式:总份数=(较大余数一较小余数)÷两次每份数的差③当两次都不足;基本公式:总份数=(较大不足数一较小不足数)÷两次每份数的差基本特点:对象总量和总的组数是不变的。
关键问题:确定对象总量和总的组数。
7.牛吃草问题基本思路:假设每头牛吃草的速度为“1”份,根据两次不同的吃法,求出其中的总草量的差;再找出造成这种差异的原因,即可确定草的生长速度和总草量。
六年级数学奥数第二讲 分数裂项巧求和

(10)+++…+
(11)+++…+
计算:(5)+++…+ 例4. 计算:+++…+
(6)+++…+
分析与解:是不是觉得本题和例3有些相似,但又不完全一样?例3 中每一个分数的分子都是4(两个自然数的差),而这道题中每一个分 数的分子都是1,可以直接将每一个分数写成两个分数相减的形式吗? 该怎么计算呢? 这就启发我们思考,能否将每一个分数的分子也变成两个自然数的 差呢?利用分数的基本性质是完全可以的。所以给原题乘4,为了使原 题的值不变,然后再除以4.即:
+++…+ =(+++…+)×4÷4 =(+++…+)÷4 =(—+—+—+…+—)÷4 =(—)÷4 =÷4 = 【举一反三】 计算: (7)+++…+
(8)+++…+
例5. 计算:+++…+ +++…+
分析与解:先算出每一个分数中的分母,再仔细观察每一个分 数,找出规律然后计算。
=+++…+ =+++…+ (分子分母同时乘以2) =(+++…+)×2 (利用乘法分配律,把分子的2同时 =(—)×2 提到括号外面) =×2= 【举一反三】 计算:(9)+++…+
【典型例题】 例1.计算:+++…++
五年级奥数分数求和的技巧

五年级奥数分数求和的技巧
一、把十位数弄清楚
把学习数字的范围缩小到个位和十位数,再把十位数分类好,归类成小于等于6及大于6的两类。
二、个位数的求和运算
对于小于等于6的十位数,在个位上按常规方法做相应的运算,把加法按照数字从右往左从上到下依次排列,就可以更快地把个位数两两相加求和。
三、计算大于6的十位数
当十位数为7,8或者9时,我们可以把它们转换成一个十位数和一个个位数,分别进行记忆,然后把它们分别加上个位数,比如说7可以看做是6+1,8可以看做是6+2,9可以看做是6+3,然后再把6的分数和1、2、3的分数分别加起来就可以了。
四、综合利用技巧
我们可以先把小于等于6的十位数求和,然后把大于6的十位数把它们拆成十位数和个位数进行加减,最后综合处理,就可以较快地求出五年级奥数分数求和的结果了。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
分数求和的常用方法1、公式法,直接运用一些公式来计算,如等差数列求和公式等。
2、图解法,将算式或算式中的某些部分的意思,用图表示出来,从而找出简便方法。
3、裂项法,在计算分数加、减法时,先将其中的一些分数做适当的拆分,使得其中一部分分数可以互相抵消,从而使计算简便。
4、分组法,运用运算定律,将原式重新分组组合,把能凑整或约分化简的部分结合在一起简算。
5、代入法,将算式中的某些部分用字母代替并化简,然后再计算出结果。
典型例题一、公式法:和公式:(首项+末项)X项数+ 2来计算。
1 I2 |3 |4 | ( 2006 +20072008 + 2008 + 2008 + 2008 * + 2008 2008=(土+ 3007)x 2007 + 220081=1003-20082二、图解法:1 1 1 1… 1 1计算:一 +—+—+-- +-- +2 4 8 16 32 64分析:解法一,先画出线段图:从图中可以看出:1 + 1 + 1 + -1 + -1 + -1=1--1=632 4 8 16 32 64 64 64解法二:观察算式,可以发现后一个加数总是前一个加数的一半。
因此,只要添上一个加数1 、,…, 1 ................ ,一,一一,就能凑成一,依次向刖类推,可以求出算式之和。
64 32111111-+一 + 一 + ——F ------- F一2 4 8 16 32 641 1 1 1 1 , 1 1、 1=+ - + - + —+ 一+ ( 一 + 一 )——2 4 8 16 32 64 64 64.1 ,1 ,1 1 ,1 1、 1+ — + —+—+ (——+——) -----2 4 8 16 32 32 64分数求和计算:n^+M+工+2008 2008 2008 2008分析:这道题中相邻两个加数之间相差+ 2006 + 2007+ 2008 20081 ... ............... ......... ................,成等差数列,我们可以运用等差数列求2008— 1 ill2 4 S 10 321 1 -X 2-—— 264=63"64解法三:由于题中后一个加数总是前一个加数的一半, 2倍,然后两式相减,消去一部分。
1 1 1 1 1 1 设x= — + — + —+• + -- + ----2 4 8 16 32 64那么,2x= (1+ 1 + 1 1 1 1 、 —+ — + — + — ) X 22 48 16 32 64,1 ,11 1 1 =1 + — + — + —+ — + —2 48 16 32用②一①得2x-x=1+1 + 1+1 + 1 + 1- (1 + 1 + 1 + 1 + -1 + -1)2 4 8 16 32 2 4 8 16 32 6463 x=64所以,1 +1 +1 + -1 + 1 + -1=632 4 8 16 32 64 64三、裂项法分析:由于每个分数的分子均为 1,先分解分母去找规律: 2=1 X 2,6=2X 3, 12=3X 4, 20=4X 5, 30=5 X 6,……110=10X11,这些分母均为两个连续自然数的乘积。
=1 1 =1 — -11 10 111-+ - F ……+5 99 13 29 33再变数型:因为1=工=1_ 1 , 1=工=]_ 12 1 2 2 6 23 2 1 一一,,,一。
这样将连加您算变成加减混合您算, 111111 ----------------------------------------- --------------- ---------- ----------12 3 4 34中间分数互相抵消, 只留下头1+1 * 1 * 1 * 1 1 1+ •+ 一 + ——2 6 12 20 3090 110 1 , 1 1 , 1 1 1111=1 — — + ----- --- + ------- -+• + — - ------P---- --- 2 2 3 3 4 9 10 10 11 110 10 11 10 和尾两个分数,给计算带来方便。
根据这一特点,我们可以把原式扩大1、计算:,1 ,.,.,, H 1 ---------- 1 --------------- F ……+ 12 20 301 ----F90 1102、计算:+ --------- 33 37分析:因为_J L=I — 1, J L = 11 5 55 9 5373、计算:21 -4 4 4 一-4-一-j444 - 4-—-一一一一,一 一,4分析:因为一 3 1535 6399 1 143 1 195255=4 X 1 =4 X 1 =4X (1 一 )x , 3 3 1 3324… ----- 4 X 151 … =4 X15 工=4X(1- 1) x 13 5 3 5 24 1 1, 11、 1 ————=4X ------ =4X ( — )X3535 5 7 57 2-±=4X 1=4X-^=4X (1 - 1) X 1.255 255 15 17 15 172所以,先用裂项法求出分数串的和,使计算简便。
11 +—— 1 1 1 -+ ■ ------ +• ••…+ ------- + -1 5 5 99 1329 3333 3744444 、=(- ——++-------- + ••… •+ --------- + ---------) + 41 5 5 9 9 1329 33 33 371 1 1 1 11 1 1 1、,=(1 ■——+ —— —+ —— -- + , .•…+ ------- -——+ —- ——)+45 5 9 9 132933 3337=(1 ■ 1 )+ 43741 1~… ........ ... .... ..............—4一 =—-上。
所以,我们可以将题中的每一个加数都扩大33 37 33 37 的差进行简便计算。
9 21---———— ——一——一——一——一——3 15 35 63 99 143 195 255 1 1 1 1 1 1 1、 1 =21 - (1 - + ---- + ----- —+ ...... + — — — ) x —3 3 5 5 7 15 17 2 =21 - 2X (1 - 1)17 2 =19 —17… 1 5 119 29 9701 9899 4、计募: ---- 1 - + 一 + 一 + ------ ■••+ ---------F ----- 2 6 120 30 9702 9900 4 _ 4 _ 4 _ 4 _ 4 _ 土 _ 土 _ 4每个加数的分子均比分母少 分析:仔细观察后发现, 1.这样可变形为: 1=1 5 =1-】=1 一 6 6 _^=1 =1 — 9900"-1=1--X,12 12 3 42 311一 .然后再裂项相消。
99 1001920 2=1 - — =1 --------- --- , 20 4 51=12 9899=1- 9900 1411 —. ----------- =—— -------9 9 13 9 13 4 1 1 … -------- = ----- —— -29 33 29334倍后,再分裂成两个数1 5 11 19 29 9701 —+ — + ---- + --- + --- + .... + ------- +2 6 12 20 30 9702 =(1 - 1) + (1 - 1) + (1 -—)12 989921 =1X 99 -( — +21 ——+2 =99—(-1 61 1 1 —+——12 201 ----- +3 4=99一(1 一—)100+……++ (11 =99——1005、计算:11+——1 299001、,,-—)+ ......... +20)9900----------------- + ........ + ------------------------------1 2 3 4 1 2 3 (100)1,第二项的分母为两个数相加,依此类推,最后一个分1 2 3分析:可以看出,第一项的分母为母是100个数相加且都是等差数列。
这样,利用等差数列求和公式,或利用分数基本性质, 变分母为两个数相乘。
(1)解法一:1+ -----------1 21(1 2) 222 再裂项求和。
1=2X (2 31-上101(1 3) 32 3 41(1 4) 4+ ....... + -1 100(1 100) 100100 101】99=1 -101解法二:原式=2 (1 2) (1 2 3) 2 (1 23 4) 2 (1 2 99 100)=2X (-1100=2X ( 1- )101 1011 —)101 100=1堕1016、计算:1 2 3分析:可以把题中的每两个加数分解成两个分数之差: ...+ ----------------98 99 10098 99 100 1 原式=1x (一 2 11 1=—x ( 2 1 =Lx ( 2 4949 19800 (98 99 1 —) + 3 1 99 )100-------- ), 99 1001 1 -x ( 1 21此时, 可消中间,留两头进行巧算。
+……+98 991 , 1 …+ — X ( ----------2 98 9999 1005 ,6 . -, ---- + ----- ------- ------- + 2004 2004 2004 2004 2001 2002 4 , ---- + 2004 ——+ 2004 2004 20041999 2000 __ _____ 一 ---- 一 ----- + ------ + ----2004 2004 2004 2004.一 .......... … 2 ......... ... ,^一 …,一 , 分析:算式中共有2002个分数,从第二个分数 二^开始依次往后数,每四个分数为一组, 2004 四、分组法 :计算,10 9 + 2004 2004 2001 一到2001为止,共有500组,每组计算结果都是 0. 2004原式=^^+ ( 22004 ,10 + -------- …… 2004 =1 + 20022004 2004 2003 2004 2004 2004 2000 2004 1998 2004 1999 2004 七+直)+ 2004 ,2001、2004 2004 2004 2002 2004 2804 + 2004 五、代入法:计算(1、几1 1 1 1 1 1 1 小 设_ =A,— — =B,则 2 3 4 2 3 4 5 原式= :(1+A) X B- (1+B) X A 4 分析:可以把算式中相同的一部分式子,设字母代替,=B+ AE^ A — AB ,1 1 1 11 1 1() -()2 3 4 52 3 4=B — A =1 5 热点习题1、-)-(1+ 一 - 一 5 2 3 4 可化繁为简,化难为易。
