作业-计算题Word版
完整word版,建筑施工技术计算题汇总,文档

计算题建筑施工技术作业 11、采用轻型井点系统进行降水施工,自然地面标高,地下水位标高,基坑底面标高,实测地基土的渗透系数含水层厚度10m,井点管埋深。
井点管围成的面积1226m2,滤管长度1m,计算轻型井点系统的涌水量。
15m/d,解:①轻型井点系统布置根据本工程条件,轻型井点系统选用单层环形布置。
井点管长度6M,直径50MM,滤管长度,井点管露出地面,基坑中心要求的降水深度S为:S=井点管所需埋置深度H=②基坑涌水量计算由于含水层的厚度为10m,按无压非完整井计算,抽水影响深度按表计算:/——原地下水位线到井点底部的距离S×(S/+L)=×(+1.0)=<取2、某基坑底面尺寸50×20m,基坑底面标高,自然地面标高±,基坑边坡坡度1:,实测地下水位标高,地基土的渗透系数10m/d,含水层厚,按无压完整井计算基坑涌水量。
解:①轻型井点系统布置根据本工程条件,轻型井点系统选用单层环形布置。
总管直径选用127MM,布置于天然地面上〔如下图〕,基坑上口尺寸为:长:50+-0.00)××2=宽:20+-0.00)××2=井点管距离基坑壁为,那么总管长度为:2×[+2 1.0]×++2)]×井点管长度选用6M,直径50MM的钢管,滤管长度,井点管露出地面,基坑中心要求的降水深度S为:S=井点管所需埋置深度H=H1+h+IL=4.3+0.5+1/10 ×<不满足要求。
将总管埋设于地面下处。
即先挖去基坑上口长:50+(4.3-0.5)××2=宽:20+(4.3-0.5)××2=深的沟槽,然后在槽底铺设总管〔如下图〕,此时井点所需长度:H=×1/10满足要求。
抽水设备根据总管长度选用两套,其布置位置与总管的划分范围如下图。
②基坑涌水量计算按无压非完整井计算,H=6m3、某建筑物一层共有10根L梁〔图〕,计算钢筋下料长度并绘制L梁钢筋配料单。
完整word版)初一数学全册计算题天天练

完整word版)初一数学全册计算题天天练第1天初一数学上册计算题天天练1.计算下列有理数口算(直接写出得数):1.(-16) + (-8) = -242.-2 + 12 = 103.78 + (-85) = -74.(-14) - (+15) = -295.4 - (-16) = 206.(-4) × (-6) = 247.84 × (-1) = -848.(-48) ÷ 3 = -169.(-6) ÷ (-1/3) = 1810.-(-2) = 211.-2 = -212.(-2) = 213.(-1)2012 = 114.(-1)2013 = -115.-1/ = 016.-(-2) = 22.整式的加减——去括号、合并同类型:1) 2a + (a + b) - 2(a + b) = a - b2) 1 - (3xy - x) + [-2(2x + 3yz)] = -3xy - 2x - 3yz - 13.整式的加减——先化简、再求值:4a + 3a^2 - 3 - 3a^3) - (-a + 4a^3),其中a = -23a^3 + 4a^2 + 5a - 34.解一元一次方程:1) 2x + 5 = 5x - 72x - 5x = -7 - 53x = -12x = 42) 4 - 3(2 - x) = 5x4 - 6 + 3x = 5x3x - 5x = -22x = -2x = 1第2天1.有理数混合运算:1.(15/17)^3 × 1/(-2) × (-64) ÷ 3 × 2 = -80/172.-22 × (-1/3) + 8 ÷ (-2) = 22/33.(-39/7) × 9 = -351/72.整式的加减——去括号、合并同类型:3) 5(a + b) - 4(3a - 2b) + 3(2a - 3b) = 5a - 3b4) 3a - (5a - ab + b) - (7ab - 7b - 3a) = -4ab - 4a + 8b3.整式的加减——先化简、再求值:2x^2y - 2xy^2) - [(-3x^2y^2 + 3x^2y) + (3x^2y^2 - 3xy^2)],其中x = -1,y = 24.解一元一次方程:3) 3(x - 2) = 2 - 5(x - 2)3x - 6 = 2 - 5x + 108x = 14x = 7/44) 2(x + 3) - 5(1 - x) = 3(x - 1)2x + 6 - 5 + 5x = 3x - 37x = -8x = -8/7第3天1.有理数混合运算:4.1/3 ÷ (-1 + 1/3 ÷ 4/24) = -1/25.(-1)^-4 × (-1/2 + 1/4) × 6 = -36.(-1)^-1 - (-1)^-2 - 1 - (-1) = 02.整式的加减——去括号、合并同类型:5) (4x - x + 5) + (5x - x - 4) = 8x + 16) 4(2x - 3x + 1) - 2(4x - 2x + 3) = -2x - 23.整式的加减——先化简、再求值:4a^2 - 2ab - b^2) - (-a^2 + b^2 - 2ab) + (3a^2 - ab + b^2),其中a = -4,b = 44.解一元一次方程:5) 3(x + 1) - 2(x + 2) = 2x + 33x + 3 - 2x - 4 = 2x + 3x = 46) 3(x - 2) + 1 = x - (2x - 1)3x - 6 + 1 = x - 2x + 12x = 4x = 2第4天1.有理数混合运算:7.-4注:原文中没有第7小题的答案。
(完整word版)高中数学计算题专项练习一(3)

高中数学计算题专项练习一高中数学计算题专项练习一一.解答题(共30小题)1.(Ⅰ)求值:;(Ⅰ)解关于x的方程.2.(1)若=3,求的值;(2)计算的值.3.已知,b=(log43+log83)(log32+log92),求a+2b的值.4.化简或计算:(1)()﹣[3×()0]﹣1﹣[81﹣0.25+(3)]﹣10×0.027;(2).5.计算的值.6.求下列各式的值.(1)(2)已知x+x﹣1=3,求式子x2+x﹣2的值.7.(文)(1)若﹣2x2+5x﹣2>0,化简:(2)求关于x的不等式(k2﹣2k+)x<(k2﹣2k+)1ˉx的解集.8.化简或求值:(1)3a b(﹣4a b)÷(﹣3a b);(2).9.计算:(1);(2)(lg8+lg1000)lg5+3(lg2)2+lg6﹣1+lg0.006.10.计算(1)(2).11.计算(1)(2).12.解方程:log2(x﹣3)﹣=2.13.计算下列各式(Ⅰ)lg24﹣(lg3+lg4)+lg5(Ⅰ).14.求下列各式的值:(1)(2).15.(1)计算(2)若xlog34=1,求4x+4﹣x的值.16.求值:.17.计算下列各式的值(1)0.064﹣(﹣)0+160.75+0.25(2)lg25+lg5•lg4+lg22.18.求值:+.19.(1)已知a>b>1且,求log a b﹣log b a的值.(2)求的值.20.计算(1)(2)(lg5)2+lg2×lg50 21.不用计算器计算:.22.计算下列各题(1);(2).23.解下列方程:(1)lg(x﹣1)+lg(x﹣2)=lg(x+2);(2)2•(log3x)2﹣log3x﹣1=0.24.求值:(1)(2)2log525﹣3log264.25.化简、求值下列各式:(1)•(﹣3)÷;(2)(注:lg2+lg5=1).26.计算下列各式(1);(2).27.(1)计算;(2)设log23=a,用a表示log49﹣3log26.28.计算下列各题:(1);(2)lg25+lg2lg50.29.计算:(1)lg25+lg2•lg50;(2)30++32×34﹣(32)3.30.(1)计算:;(2)解关于x的方程:.高中数学计算题专项练习一参考答案与试题解析一.解答题(共30小题)1.(Ⅰ)求值:;(Ⅰ)解关于x的方程.考点:有理数指数幂的化简求值.专题:计算题.分析:(Ⅰ)利用对数与指数的运算法则,化简求值即可.(Ⅰ)先利用换元法把问题转化为二次方程的求解,解方程后,再代入换元过程即可.解答:(本小题满分13分)解:(Ⅰ)原式=﹣1++log2=﹣1﹣1+23=﹣1+8+=10.…(6分)(Ⅰ)设t=log2x,则原方程可化为t2﹣2t﹣3=0…(8分)即(t﹣3)(t+1)=0,解得t=3或t=﹣1…(10分)Ⅰlog2x=3或log2x=﹣1Ⅰx=8或x=…(13分)点评:本题考查有理指数幂的化简求值以及换元法解方程,是基础题.要求对基础知识熟练掌握.2.(1)若=3,求的值;(2)计算的值.考点:有理数指数幂的化简求值.专题:计算题.分析:(1)利用已知表达式,通过平方和与立方差公式,求出所求表达式的分子与分母的值,即可求解.(2)直接利用指数与对数的运算性质求解即可.解答:解:(1)因为=3,所以x+x﹣1=7,所以x2+x﹣2=47,=()(x+x﹣1﹣1)=3×(7﹣1)=18.所以==.(2)=3﹣3log22+(4﹣2)×=.故所求结果分别为:,点评:本题考查有理数指数幂的化简求值,立方差公式的应用,考查计算能力.3.已知,b=(log43+log83)(log32+log92),求a+2b的值.考点:有理数指数幂的化简求值;对数的运算性质.专题:计算题.分析:直接利用有理指数幂的运算求出a,对数运算法则求出b,然后求解a+2b的值解答:解:==.b=(log43+log83)(log32+log92)=(log23+log23)(log32+log32)==,Ⅰ,,Ⅰa+2b=3.点评:本题考查指数与对数的运算法则的应用,考查计算能力.4.化简或计算:(1)()﹣[3×()0]﹣1﹣[81﹣0.25+(3)]﹣10×0.027;(2).考点:有理数指数幂的化简求值.专题:计算题.分析:根据有理数指数幂的运算法则进行化简求值即可.解答:解:(1)原式=﹣(3×1)﹣1﹣﹣10×=﹣﹣1﹣3=﹣1.(2)原式=+﹣2=+﹣2=﹣2+﹣2.点评:本题考查有理数指数幂的运算法则,考查学生的运算能力,属基础题,熟记有关运算法则是解决问题的基础.5.计算的值.考点:有理数指数幂的化简求值.专题:计算题.分析:根据分数指数幂运算法则进行化简即可.解答:解:原式===.点评:本题主要考查用分数指数幂的运算法则进行化简,要求熟练掌握分数指数幂的运算法则.6.求下列各式的值.(1)(2)已知x+x﹣1=3,求式子x2+x﹣2的值.考点:有理数指数幂的化简求值.专题:计算题.分析:(1)直接利用有理指数幂的运算性质和对数的运算性质化简求值.(2)把已知的等式两边平方即可求得x2+x﹣2的值.解答:解:(1)==;(2)由x+x﹣1=3,两边平方得x2+2+x﹣2=9,所以x2+x﹣2=7.点评:本题考查了有理指数幂的化简求值,考查了对数的运算性质,是基础的计算题.7.(文)(1)若﹣2x2+5x﹣2>0,化简:(2)求关于x的不等式(k2﹣2k+)x<(k2﹣2k+)1ˉx的解集.考点:指数函数的单调性与特殊点;方根与根式及根式的化简运算.专题:计算题;转化思想.分析:(1)由﹣2x2+5x﹣2>0,解出x的取值范围,判断根号下与绝对值中数的符号,进行化简.(2)先判断底数的取值范围,由于底数大于1,根据指数函数的单调性将不等式进行转化一次不等式,求解即可.解答:解:(1)Ⅰ﹣2x2+5x﹣2>0Ⅰ,Ⅰ原式===(8分)(2)Ⅰ,Ⅰ原不等式等价于x<1﹣x,Ⅰ此不等式的解集为(12分)点评:本题考查指数函数的单调性与特殊点,求解本题的关键是判断底数的符号,以确定函数的单调性,熟练掌握指数函数的单调性是正确转化的根本.8.化简或求值:(1)3a b(﹣4a b)÷(﹣3a b);(2).考点:对数的运算性质;有理数指数幂的化简求值.专题:计算题.分析:(1)利用分数指数幂的运算法则即可得出;(2)利用对数的运算法则和lg2+lg5=1即可得出.解答:解:(1)原式==4a.(2)原式=+50×1=lg102+50=52.点评:本题考查了分数指数幂的运算法则、对数的运算法则和lg2+lg5=1等基础知识与基本技能方法,属于基础题.9.计算:(1);(2)(lg8+lg1000)lg5+3(lg2)2+lg6﹣1+lg0.006.考点:对数的运算性质;有理数指数幂的化简求值.专题:计算题.分析:(1)先将每一个数化简为最简分数指数幂的形式,再利用运算性质化简.(2)先将每一个对数式化简,再利用对数运算性质化简.解答:解:(1)===﹣45;(2)(lg8+lg1000)lg5+3(lg2)2+lg6﹣1+lg0.006=(3lg2+3)•lg5+3(lg2)2﹣lg6+(lg6﹣3)=3lg2•lg5+3lg5+3(lg2)2﹣3=3lg2(lg5+lg2)+3lg5﹣3=3lg2+3lg5﹣3=3﹣3=0.点评:本题考察运算性质,做这类题目最关键的是平时练习时要细心、耐心、不怕麻烦,考场上才能熟练应对!10.计算(1)(2).考点:对数的运算性质;有理数指数幂的化简求值.专题:函数的性质及应用.分析:(1)利用指数幂的运算性质即可得出;(2)利用对数函数的运算性质即可得出.解答:解:(1)原式=|2﹣e|﹣+﹣=e﹣2﹣+=e﹣2﹣e+=﹣2.(2)原式=+3=﹣4+3=2﹣4+3=1.点评:熟练掌握指数幂的运算性质、对数函数的运算性质是解题的关键.11.计算(1)(2).考点:对数的运算性质;有理数指数幂的运算性质.专题:计算题.分析:(1)直接利用对数的运算法则求解即可.(2)直接利用有理指数幂的运算法则求解即可.解答:解:(1)==(2)==9×8﹣27﹣1=44.点评:本题考查对数的运算法则、有理指数幂的运算法则的应用,考查计算能力.12.解方程:log2(x﹣3)﹣=2.考点:对数的运算性质.专题:计算题.分析:由已知中log2(x﹣3)﹣=2,由对数的运算性质,我们可得x2﹣3x﹣4=0,解方程后,检验即可得到答案.解答:解:若log2(x﹣3)﹣=2.则x2﹣3x﹣4=0,…(4分)解得x=4,或x=﹣1(5分)经检验:方程的解为x=4.…(6分)点评:本题考查的知识点是对数的运算性质,其中利用对数的运算性质,将已知中的方程转化为整式方程是解答醒的关键,解答时,易忽略对数的真数部分大于0,而错解为4,或﹣1.13.计算下列各式(Ⅰ)lg24﹣(lg3+lg4)+lg5(Ⅰ).考点:对数的运算性质;根式与分数指数幂的互化及其化简运算.专题:计算题.分析:(Ⅰ)利用对数的运算的性质可得结果;(Ⅰ)利用指数幂的运算性质可得结果;解答:解:(Ⅰ)lg24﹣(lg3+lg4)+lg5=lg24﹣lg12+lg5=lg=lg10=1;(Ⅰ)=×+﹣﹣1=32×23+3﹣2﹣1=72.点评:本题考查对数的运算性质、指数幂的运算性质,考查学生的运算能力,属基础题.14.求下列各式的值:(1)(2).考点:对数的运算性质;有理数指数幂的化简求值.专题:计算题.分析:根据对数和指数的运算法则进行求解即可.解答:解:(1)原式==log﹣9=log39﹣9=2﹣9=﹣7.(2)原式=== =.点评:本题主要考查对数和指数幂的计算,要求熟练掌握对数和指数幂的运算法则.15.(1)计算(2)若xlog34=1,求4x+4﹣x的值.考点:对数的运算性质;根式与分数指数幂的互化及其化简运算.分析:(1)利用指数幂的运算性质即可;(2)利用指数式和对数式的互化和运算性质即可.解答:解:(1)原式===3.(2)由xlog34=1,得x=log43,Ⅰ4x=3,,Ⅰ4x+4﹣x==.点评:熟练掌握对数和指数幂的运算性质是解题的关键.16.求值:.考点:对数的运算性质;有理数指数幂的化简求值.专题:计算题.分析:根据有理数指数幂的定义,及对数的运算性质,即可求出的值.解答:解:原式…(4分)…(3分)=…(1分)点评:本题考查的知识点是对数的运算性质,有理数指数幂的化简求值,其中掌握指数的运算性质和对数的运算性质,是解答本题的关键.17.计算下列各式的值(1)0.064﹣(﹣)0+160.75+0.25(2)lg25+lg5•lg4+lg22.考点:对数的运算性质;有理数指数幂的化简求值.专题:计算题.分析:(1)利用指数幂的运算性质可求;(2)利用对数运算性质可求;解答:解:(1)原式==0.4﹣1+8+=;(2)原式=lg25+2lg5•lg2+lg22=(lg5+lg2)2=(lg10)2=1点评:本题考查对数的运算性质、有理数指数幂的运算,属基础题,熟记有关运算性质是解题基础.18.求值:+.考点:对数的运算性质;有理数指数幂的化简求值.专题:计算题.分析:直接利用对数的运算法则,求出表达式的值即可.解答:解:原式==3+9+2000+1=2013.点评:本题考查对数的运算法则的应用,基本知识的考查.19.(1)已知a>b>1且,求log a b﹣log b a的值.(2)求的值.考点:对数的运算性质.专题:计算题.分析:(1)通过a>b>1利用,平方,然后配出log a b﹣log b a的表达式,求解即可.(2)直接利用对数的运算性质求解的值解答:解:(1)因为a>b>1,,所以,可得,a>b>1,所以log a b﹣log b a<0.所以log a b﹣log b a=﹣(2)==﹣4.点评:本题考查对数与指数的运算性质的应用,整体思想的应用,考查计算能力.20.计算(1)(2)(lg5)2+lg2×lg50考点:对数的运算性质;根式与分数指数幂的互化及其化简运算;有理数指数幂的化简求值.专题:计算题.分析:(1)把根式转化成指数式,然后利用分数指数幂的运算法则进行计算.(2)先把lg50转化成lg5+1,然后利用对数的运算法则进行计算.解答:解:(1)===(6分)(2)(lg5)2+lg2×lg50=(lg5)2+lg2×(lg5+lg10)=(lg5)2+lg2×lg5+lg2=lg5(lg5+lg2)+lg2=lg5+lg2=1(12分)点评:本题考查对数的运算法则和根式与分数指数幂的互化,解题时要注意合理地进行等价转化.21.不用计算器计算:.考点:对数的运算性质.专题:计算题.分析:,lg25+lg4=lg100=2,,(﹣9.8)0=1,由此可以求出的值.解答:解:原式=(4分)=(8分)=(12分)点评:本题考查对数的运算性质,解题时要认真审题,注意公式的灵活运用.22.计算下列各题(1);(2).考点:对数的运算性质.专题:计算题.分析:(1)直接利用对数的运算性质求解表达式的值.(2)利用指数的运算性质求解表达式的值即可.解答:解:(1)==9+﹣1=(2)===﹣45.点评:本题考查指数与对数的运算性质的应用,考查计算能力.23.解下列方程:(1)lg(x﹣1)+lg(x﹣2)=lg(x+2);(2)2•(log3x)2﹣log3x﹣1=0.考点:对数的运算性质.专题:计算题.分析:(1)先根据对数运算性质求出x,再根据对数的真数一定大于0检验即可.(2)设log3x=y,得出2y2﹣y﹣1=0,求出y的值,再由对数的定义求出x的值即可.解答:解:(1)原方程可化为lg(x﹣1)(x﹣2)=lg(x+2)所以(x﹣1)(x﹣2)=x+2即x2﹣4x=0,解得x=0或x=4经检验,x=0是增解,x=4是原方程的解.所以原方程的解为x=4(2)设log3x=y,代入原方程得2y2﹣y﹣1=0.解得y1=1,.log3x=1,得x1=3;由,得.经检验,x1=3,都是原方程的解.点评:本题主要考查对数的运算性质和对数函数的定义域问题.属基础题.24.求值:(1)(2)2log525﹣3log264.考点:对数的运算性质;有理数指数幂的化简求值.专题:计算题.分析:(1)首先变根式为分数指数幂,然后拆开运算即可.(2)直接利用对数式的运算性质化简求值.解答:解:(1)====.(2)2log525﹣3log264==4﹣3×6=﹣14.点评:本题考查了对数式的运算性质,考查了有理指数幂的化简求值,解答的关键是熟记有关性质,是基础题.25.化简、求值下列各式:(1)•(﹣3)÷;(2)(注:lg2+lg5=1).考点:对数的运算性质;有理数指数幂的化简求值.专题:计算题.分析:(1)利用指数幂的运算性质化简即可;(2)利用对数的运算性质化简即可.解答:解:(1)原式=﹣b﹣3÷(4)…..3分=﹣…..7分(2)解原式=…..2分=…..4分=…..6分=….7分.点评:本题考查对数的运算性质,考查有理数指数幂的化简求值,熟练掌握其运算性质是化简的基础,属于基础题.26.计算下列各式(1);(2).考点:对数的运算性质;有理数指数幂的化简求值.专题:计算题.分析:(1)利用指数幂的运算法则即可得出;(2)利用对数的运算法则和换底公式即可得出.解答:解:(1)原式=﹣1﹣+=.(2)原式=+lg(25×4)+2+1==.点评:本题考查了指数幂的运算法则、对数的运算法则和换底公式,属于基础题.27.(1)计算;(2)设log23=a,用a表示log49﹣3log26.考点:对数的运算性质;根式与分数指数幂的互化及其化简运算.专题:计算题.分析:(1)把第一、三项的底数写成平方、立方的形式即变成幂的乘方运算,第二项不等于0根据零指数的法则等于1,化简求值即可;(2)把第一项利用换底公式换成以2为底的对数,第二项利用对数函数的运算性质化简,log23整体换成a即可.解答:解:(1)原式=+1+=+1+=4;(2)原式=﹣3log22×3=log23﹣3(1+log23)=a﹣3(1+a)=﹣2a﹣3.点评:本题是一道计算题,要求学生会进行根式与分数指数幂的互化及其运算,会利用换底公式及对数的运算性质化简求值.做题时注意底数变乘方要用到一些技巧.28.计算下列各题:(1);(2)lg25+lg2lg50.考点:对数的运算性质;有理数指数幂的化简求值.专题:计算题.分析:(1)利用指数的运算法则,直接求解表达式的值即可.(2)利用对数的运算性质,直接化简求解即可.解答:解:(1)原式===.(5分)(2)原式lg25+lg2lg50=lg25+2lg2lg5+lg25=(lg2+lg5)2=1 (5分)点评:本题考查对数的运算性质,有理数指数幂的化简求值,考查计算能力.29.计算:(1)lg25+lg2•lg50;(2)30++32×34﹣(32)3.考点:对数的运算性质;有理数指数幂的化简求值.专题:计算题;函数的性质及应用.分析:(1)直接利用对数的运算性质即可求解(2)直接根据指数的运算性质即可求解解答:解:(1)原式=lg25+lg2(1+lg5)=lg25+lg2lg5+lg2=lg5(lg5+lg2)+lg2=lg5+lg2=1(2)原式=1+3+36﹣36=4.…(14分)点评:本题主要考查了对数的运算性质及指数的运算性质的简单应,属于基础试题30.(1)计算:;(2)解关于x的方程:.考点:对数的运算性质;有理数指数幂的运算性质;有理数指数幂的化简求值;函数的零点.专题:计算题.分析:(1)根据分数指数幂运算法则进行化简即可.(2)利用对数函数的性质和对数的运算法则进行计算即可.解答:解:(1)原式==﹣3;(2)原方程化为log5(x+1)+log5(x﹣3)=log55,从而(x+1)(x﹣3)=5,解得x=﹣2或x=4,经检验,x=﹣2不合题意,故方程的解为x=4.点评:本题主要考查分数指数幂和对数的运算,要求熟练掌握分数指数幂和对数的运算法则.。
二年级下册数学同步作业(可编辑修改word版)

一、直接写出得数第一部分计算题练习(一)40+60= 100-35= 48- 28= 52+20= 5 × 7=35÷ 8 =35 ÷ 9=9× 6 = 37÷ 8 =45÷ 7=49÷ 7=28÷ 7 =300+350= 320+260= 810+180= 200+80= 24÷ 6- 4 = 6 ×(5-3)= (15- 5)÷2=5×4-6= 3 千米×6=40 米÷5=二、(5×()里最大填几。
)<43 ()×3<17 ()×7<27 8×()<55 4×()<30 ()×7<47()×6<39 6×()<39三、用竖式计算。
213+325= 183+307= 624+150= 613+130=四、脱式计算。
32+21+35 24-8+14 3×8÷432÷4×963-(7+23)(23+25)÷8(30-2)÷47×(6+3)15-28÷427+24÷358+3×69×9-71五、写出下列各数。
1、我国已发现的鸟类大约有一千三百种。
写作:()2、世界海拔最高的山峰是珠穆朗玛峰,高约八千八百四十四米。
写作:()3、东方明珠电视塔高四百六十八米。
写作:()4、一个数个位和百位上的数都是 0,千位和十位上的数是 4,这个数写作()。
六、读出下面的各数。
9089 读作:()9809 读作:()9809 读作:()9890 读作:()七、比较下列各数的大小。
1202○1020210○2011001○10102dm○20cm200cm○2m1000m○1km 60dm○61m72cm○7dm8km○7000m八、按要求画线段。
(完整word版)六年级计算题100道

六年级数学计算题过关练习一班级: 姓名: 总分: 1、直接写出复数。
(20分)3 5×12= 1÷23=45÷8= 7×27=38×12=1 5×1625=14-15=13+14910÷320=14÷78=2、怎样简便就怎样算。
(40分)(1)3-712-512(2)57×38+58×57(3)815×516+527÷109(4)18×(49+56)3、解方程。
(20分)(1)78χ=1116(2)χ×(34+23)=7244、列式计算。
(20分)(1)一个数的35是30,这个数是多少?(2)比一个数多12%的数是112,这个数是多少?六年级数学计算题过关练习二班级: 姓名: 总分:1、直接写出得数。
(20分)12÷12= 1÷1%= 9.5+0.5=13+14= 0÷15×2= 1-1112= 78×514= 712÷74=45-12= 19×78×9=2、怎样简便就怎样算。
(40分)(1)23×7+23×5 (2)(16-112)×24-45)(3)(57×47+47)÷47 (4)15÷[(23+15)×113]3、解方程。
(16分)(1)χ-35χ=65 (2)6×112-12χ=124、列式计算。
(24分)(1)12加上23的和,等于一个数的23,这个数是多少?3 5比它的2倍少28,这个数是多少?(2)一个数的六年级数学计算题过关练习三班级: 姓名: 总分:1.直接写出得数。
(16分) 4.9:6.3=54+152= 87×74= 1―41―21= 83+43= 53÷103= 9÷43=32×61×109= 2.解方程。
(word完整版)初三中考化学专题练习--计算题(含参考答案最新)
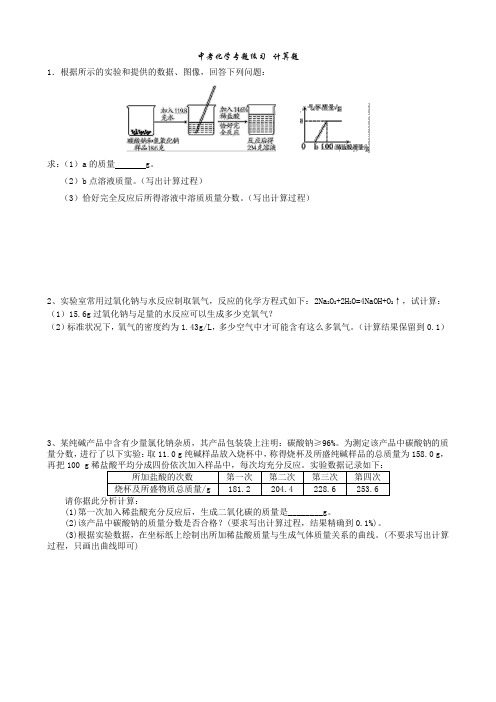
中考化学专题练习--计算题1.根据所示的实验和提供的数据、图像,回答下列问题:求:(1)a的质量 g。
(2)b点溶液质量。
(写出计算过程)(3)恰好完全反应后所得溶液中溶质质量分数。
(写出计算过程)2、实验室常用过氧化钠与水反应制取氧气,反应的化学方程式如下:2Na2O2+2H2O=4NaOH+O2↑,试计算:(1)15.6g过氧化钠与足量的水反应可以生成多少克氧气?(2)标准状况下,氧气的密度约为1.43g/L,多少空气中才可能含有这么多氧气。
(计算结果保留到0.1)3、某纯碱产品中含有少量氯化钠杂质,其产品包装袋上注明:碳酸钠≥96%。
为测定该产品中碳酸钠的质量分数,进行了以下实验:取11.0 g纯碱样品放入烧杯中,称得烧杯及所盛纯碱样品的总质量为158.0 g,再把100 g(1)第一次加入稀盐酸充分反应后,生成二氧化碳的质量是________g。
(2)该产品中碳酸钠的质量分数是否合格?(要求写出计算过程,结果精确到0.1%)。
(3)根据实验数据,在坐标纸上绘制出所加稀盐酸质量与生成气体质量关系的曲线。
(不要求写出计算过程,只画出曲线即可)4.工业盐酸中通常溶有少量的FeCl3而呈黄色,小红为测定某工业盐酸中HCl的含量进行如下实验:取某工业盐酸l00g,滴加一定溶质质量分数的NaOH溶液,测得加入NaOH溶液质量与反应生成的沉淀质量关系如图所示。
请回答下列问题:(1)FeCl3与NaOH恰好完全反应时,生成沉淀的质量是________g。
(2)计算氢氧化钠溶液的溶质质量分数。
(写出计算过程)(3)该工业盐酸中HCl的质量分数是_________。
5、钙是人体中的常量元素,缺钙时可通过食用保健药剂来增加摄入量。
某补钙药剂主要成分为碳酸钙,现将100g盐酸分成5等份,逐次加到用40g该药剂制成的粉末中(其他成分不与盐酸反应),得到部分数据与图象。
请根据有关信息回答问题:序号第1次第2次第3次第4次第5次加入盐酸的质量/g 20 20 20 20 20剩余固体的质量/g 35 30 25 20 a(1)a的数值为________,该品牌补钙药剂中CaCO3的质量分数是_________。
钻孔桩计算题Word版

1、某钻孔灌注桩采用导管水下灌注混凝土。
在灌注前检测数据为:孔径
D=1.8m,孔深H=45m,泥浆比重γw=1.1,导管直径d=0.3m,导管底部距离孔底H1=0.3m。
灌注过程中泥浆面高程维持不变,要求首灌导管埋深不小于H2=1m,请计算首灌混凝土方量?(混凝土比重γc= 2.4,保留1位小数)。
问题:
(1)请计算首灌混凝土方量?(混凝土比重γc= 2.4,保留1位小数)。
(7分)
(2)请简述混凝土灌注过程中防止钢筋骨架上浮的技术措施?(3分)
2、某钻孔灌注桩直径为1.80m,桩长为L=60m;主筋①②规格为HRB400 28mm,加强箍筋规格为HRB400 22mm,螺旋筋④⑤规格为HPB300 10mm;主筋净保护层厚度为100mm(即:主筋外表与混凝土表面的最小距离),螺旋筋③间距为200mm,加强筋间距为2000mm。
具体见下图:桥墩桩基钢筋构造图。
试计算:(1)Ⅰ-Ⅰ截面处主筋间距(按弧长)<mm,2分>;(2)单桩混凝土用量<m3,2分>;(3)单桩钢筋总用量< kg,按钢筋编号计算,6分>;(结果全部取整数)
桥墩桩基钢筋构造图(标注单位:cm)。
计算题Word版

计算题1.有一叶轮外径为460mm 的离心式风机,在转速为1450r/min 时,其流量为5.13m /s ,试求风机的全压与有效功率。
设空气径向流入叶轮,在叶轮出口处的相对速度方向为半径方向,设其p /T p ∞=0.85,ρ=1.2kg/3m 。
2.有一单级轴流式水泵,转速为375r/min ,入口直径为980mm ,水以1v =4.01m/s 的速度沿轴向流入叶轮,以2v =4.48m/s 的速度由叶轮流出,总扬程为H=3.7m ,求该水泵的流动效率h η。
3.有一离心式水泵,转速为480r/min ,总扬程为136m 时,流量V q =5.73m /s ,轴功率为P =9860KW ,其容积效率与机械效率均为92%,求流动效率。
设输入的水温度及密度为:t=20℃,ρ=1000kg/3m 。
4.用一台水泵从吸水池液面向50m 高的水池输送V q =0.33m /s 的常温清水(t=20℃,ρ=1000kg/3m ),设水管的内径为d =300mm ,管道长度L =300m ,管道阻力系数λ=0.028,求泵所需的有效功率。
5.设一台水泵流量V q =25L /s ,出口压力表读数为323730Pa ,入口真空表读数为39240Pa ,两表位差为0.8m ,(压力表高,真空表低),吸水管和排水管直径为1000mm 和750mm ,电动机功率表读数为12.5kW ,电动机效率g η=0.95,求轴功率、有效功率、泵的总功率(泵与电动机用联轴器直接连接)。
6.有一送风机,其全压是1962Pa 时,产生V q =403m /min 的风量,其全压效率为50%,试求其轴功率。
7.要选择一台多级锅炉给水泵,初选该泵转速n=1441r/min ,叶轮外径=2D 300mm ,流动效率h η=0.92,流体出口绝对速度的圆周分速为出口圆周速度的55%,泵的总效率为90%,输送流体密度ρ=9613/kg m ,要求满足扬程H =176m ,流量V q =81.63m /h ,试确定该泵所需要的级数和轴功率各为多少(设流体径向流入,并不考虑轴向涡流的影响)?8.一台G4-73型离心式风机,在工况1(流量V q =703003m /h ,全压p =1441.6Pa ,轴功率P =33.6k W )及工况2(流量V q =378003m /h ,全压p =2038.4Pa ,轴功率P=25.4k W )下运行,问该风机在哪种工况下运行较为经济?9.有一离心式送风机,转速n=1450r/min ,流量V q =1.53m /min ,全压p =1200Pa ,输送空气的密度为ρ=1.23/kg m 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、甲仓库A商品年需求量为30 000个,单位商品的购买价格为20元,每次订货成本为240元,单位商品的年保管费为10元,求:该商品的经济订购批量,每年的订货次数及平均订货间隔周期。
解:经济批量EOQ=(个)
每年的订货次数N=30 000/1 200=25(次)
平均订货间隔周期T=365/25=14.6(天)
2、上海某电子设备生产企业全年需要A材料4800吨,每次订货成本为400元,每吨材料年储备成本24元,请问经济订货批量是多少?每年进货的最佳订货次数是多少?
答:经济订货批量Q=√(2DS/H)=√(2×4800×400÷24)=400(吨)
最佳订货次数=4800÷400=12(次)
所以,经济订货批量是400吨,每年进货的最佳订货次数是12次。
3、假设某公司每年需外购零件4900个,该零件单位储存变动成本20元,已知订货批量是700个,请问一次订货成本是多少?
答:经济订货批量Q=√(2DS/H)
订货成本S=(Q2×H)÷2D=(7002×20)÷(2×4900)=1000(元)所以,一次订货成本是1000元。
4、某公司每年需要购入原材料9000 件,每件单价10 元,假设每次订购费用为20 元,单位年存储成本按原材料价值10%计算,那么该原材料经济订购批量为多少件?
5、已知:年需求量(D)=1000单位日平均需求量(d)=1000/365
订购成本 (S)=5美元/次持有成本(H)=1.25美元/单位.年
提前期(L)=5天单价(C)=12.50美元
问:最佳订购批量、订购点B及总采购成本分别是多少?
解:
最优订购批量为: Qopt= = = =89.4单位
再订购点为:
R= L=1000(5)/365=13.7单位 通过取近似数,可指定如下库存政策:当库存水平降至 14单位,则应再订购89单位的产品。
年总成本为:
TC=DC+(D/Q)S+(Q/2)H
=1000(12.50)+1000(5)/89+89(1.25)/2
=12611.81美元
2DS/H .252(1000)5/1
8000 d。
