SPSS上机实验案例分析
SPSS实验分析报告四
SPSS实验分析报告四第一篇：SPSS实验分析报告四SPSS实验分析报告四一、地区*日期*销售量（一）、提出假设原假设H0=“不同地区对销售量的平均值没有产生显著影响。
” H2=“不同日期对销售量的平均值没有产生显著影响。
” H3=“不同的地区和日期对销售量没有产生了显著的交互作用。
”（二）、两独立样本t检验结果及分析表（一）主旨間係數地区 2 3 日期 2 3數值標籤地区一地区二地区三周一至周三周四至周五周末N 9 9 9 9 9 9表（一）表示各个控制变量的分组情况，包括三个不同的地区以及三个不同日期的数据。
表（二）销售额多因素方差分析结果主体间效应的检验因變數: 销售量來源第 III 類平方和修正的模型 61851851.852adf 8平均值平方 7731481.481F 8.350顯著性.000 截距地区日期地区 * 日期錯誤總計 844481481.4812296296.296 2740740.741 56814814.8***.667 923000000.000 2 2 4 18 27 26844481481.481 1148148.148 1370370.370 14203703.704 925925.926912.040 1.240 1.480 15.340.000.313.254.000校正後總數 78518518.519 a.R平方 =.788（調整的 R平方 =.693）由表（二）可知，第一列是对观测变量总变差分解的说明；第二列是对观测变量总变差分解的结果；第三列是自由度；第四列是方差；第五列是F检验统计量的观测值；第六列是检验统计量的概率P值。
可以看到：观测变量的总变差SST为78518518.519，它被分解为四个部分，分别是：由地区（x2）不同引起的变差（2296296.296），由日期（x3）不同引起的变差(2740740.741)，由地区和日期交互作用（x2*x3）引起的变差（5.681E7），由随机因素引起的变差（Error 1.667E7）。
Spss上机报告1讲解
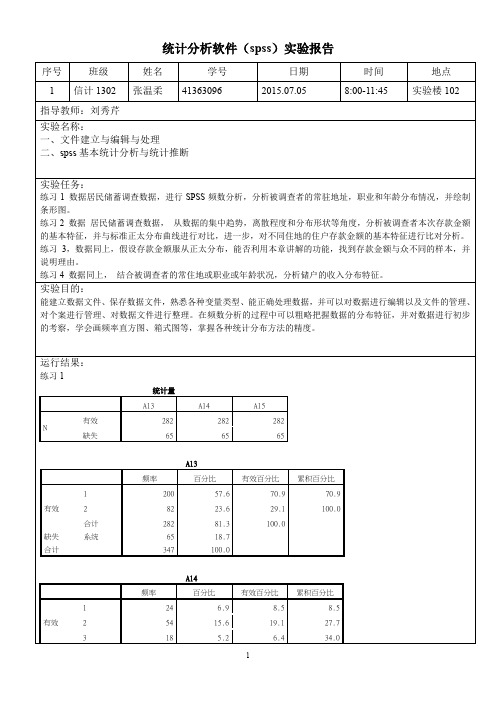
统计分析软件（spss）实验报告
练习2
统计量
A5
有效282
N
缺失65
均值4738.09
均值的标准误651.799
中值1032.43a
众数1000
标准差10945.569
方差119805486.302
偏度 5.234
偏度的标准误.145
峰度33.656
峰度的标准误.289
全距100000
极小值 1
极大值100001
和1336141
a. 利用分组数据进行计算。
居民收入较集中在2000元以下，高收入人群较少，收入在2000元以上的数据离散程度较大，分布形状与标准正态分布差距较大。
根据表格分析，不同地区的人群居民收入差距不是特别大啊，但2地区的居民收入离散程度较1地区收入人群大，在置信水平为95%的情况下可以说两地区的收入平均值是相等的。
统计量
A5
N 有效282
缺失65 平均值4738.09 标准平均值误差651.799 中位数1000.00 方式1000 标准偏差10945.569 方差119805486.302 偏度 5.234 标准偏度误差.145 峰度33.656 标准峰度误差.289 范围100000 最小值 1 最大值100001
运用spss对数据进行标准化分析，得到的标准值大于3时数据即为异常。
交叉表
A4
11。
统计学spss上机实验报告
实验一：用SPSS绘制统计图实验目的：掌握基本的统计学理论，使用SPSS实现基本统计功能（绘制统计图）。
对SPSS的理解：它是一款社会科学统计软件包，同时也广泛应用于经济，金融，商业等各个领域，基本功能包括数据管理，统计分析，图表分析，输出管理等。
实验算法：掌握SPSS的基本输入输出方法，并用SPSS绘制相应的统计图（例如：直方图，曲线图，散点图，饼形图等）。
操作过程：步骤1：启动SPSS。
单击Windows 的[开始]按钮（如图1-1所示），在[程序]菜单项[SPSS for Windows]中找到[SPSS 13.0 for Windows]并单击，得到如图1-2所示的选择数据源界面。
图1-1 启动SPSS图1-2 选择数据源界面步骤2 ：打开一个空白的SPSS数据文件，如图1-3。
启动SPSS 后，出现SPSS 主界面（数据编辑器）。
同大多数Windows 程序一样，SPSS 是以菜单驱动的。
多数功能通过从菜单中选择完成。
图1-3 空白的SPSS数据文件步骤3：数据的输入。
打开SPSS以后，直接进入变量视图窗口。
SPSS的变量视图窗口分为data view和variable view两个。
先在variable view中定义变量，然后在data view里面直接输入自定义数据。
命名为“我的文件”并保存在桌面。
如图1-4所示。
图1-4数据的输入步骤4：调用Graphs菜单的Bar功能，绘制直条图。
直条图用直条的长短来表示非连续性资料（该资料可以是绝对数，也可以是相对数）的数量大小。
步骤5：数据准备。
步骤6：选Graphs菜单的Bar过程，弹出Bar Chart定义选项。
在定义选项框的下方有一数据类型栏，系统提供3种数据类型：Summaries for groups of cases：以组为单位体现数据；Summaries of separate variables：以变量为单位体现数据；Values of individual cases：以观察样例为单位体现数据。
《统计信息应用软件》上机试验指导书(SPSS)
《统计信息应用软件上机实验指导书》（编写人李灿）湖南商学院信息系2005-4-10编写说明为了方便教师教学，提高学生运用统计信息应用软件的能力，以更好的适应信息社会对现代化定量分析人才的需求，为社会培养现代化的高级专门人才，以及更好地配合统计信息应用软件课程的案例教学改革，我在教学的过程中精心编写了此本《统计信息应用软件》上机试验指导书（SPSS12.0统计软件）。
在编写的过程中得到了信息系领导龚曙明教授、欧阳资生博士以及统计学教研室各位老师的支持，在此我表示感谢。
由于时间仓促，本人水平有限，错误之处敬请各位专家学者指正，本人邮箱：xlican@。
李灿2004．3目录试验一、数据统计处理 (3)试验二、单变量频率分配分析 (4)试验三、T-TEST过程 (6)试验四、聚类分析 (9)试验五、因子分析 (14)试验六、判别分析..........................................17. 试验七、多元方差分析 (21)试验一、数据统计处理试验目的：通过上机试验，使学生掌握数据统计处理基本原理，熟悉数据文件的处理，具体包括数据的输入、数据变量的定义、数据资料的统计处理等软件操作过程，能对软件输出结果进行分析。
实验题目：某班进行其中考试成绩分析，首先输入全班36人的学号、性别、数学、无力、化学、外语和语文成绩，如表1所示：存为aa.sys文件，现按以下要求操作。
（1（2）计算个人平均成绩，按平均分从大到小进行排序，挑选出学习成绩最好、最差的3个同学。
（3）求这5门课的平均成分和标准差。
（4）将各门成绩按5级分类（优、良、中、及格和不及格）贴标签，求其频数分布，查看哪一分数段人最多。
（5）将数学和物理成绩做一散点分布图。
（6）将数据文件、输出结果和图形分别存盘保存。
试验二、单变量频率分配分析试验目的：通过上机试验，使学生掌握频率分配分析基本原理，熟悉频率分配分析软件操作过程，能对软件输出结果进行分析。
SPSS上机例子
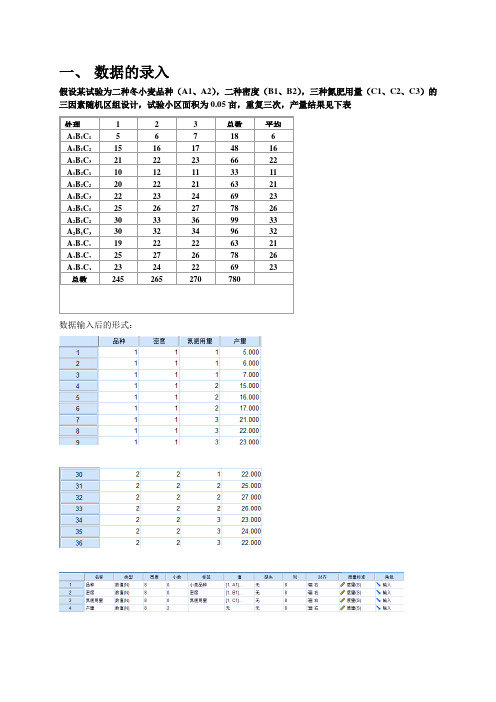
一、数据的录入假设某试验为二种冬小麦品种（A1、A2），二种密度（B1、B2），三种氮肥用量（C1、C2、C3）的三因素随机区组设计，试验小区面积为0.05亩，重复三次，产量结果见下表数据输入后的形式：处理 1 2 3 总数平均A1B1C1 5 6 7 18 6 A1B1C215 16 17 48 16 A1B1C321 22 23 66 22 A1B2C110 12 11 33 11 A1B2C220 22 21 63 21 A1B2C322 23 24 69 23 A2B1C125 26 27 78 26 A2B1C230 33 36 99 33 A2B1C330 32 34 96 32 A2B2C119 22 22 63 21 A2B2C225 27 26 78 26 A2B2C323 24 22 69 23 总数245 265 270 780二、一般统计或者三、假设检验1、独立样本的t检验工厂的两个化验室，每天对所配的水样，分别测定其含氯量（ppm），下面是7天的记录，问：两化验室测定结果之间有无显著差异？（α=0.01）。
日期 1 2 3 4 5 6 7化验室A 1.15 1.86 0.75 1.82 1.14 1.65 1.90 化验室B 1.00 1.90 0.90 1.80 1.20 1.70 1.95四、方差分析1、单因素方差分析例：黑龙江某地淋溶土上玉米氮肥品种肥效试验，每亩施N6斤，小区面积54m2 ，随机区组设计，重复四次，玉米产量见下表：重复产量（公斤/亩）CK 碳铵硫铵硝铵氰铵尿素氯铵氨水1 126.8 233.8 261.0 277.2 196.4 272.5 264.6 253.42 148.7 231.1 263.3 268.7 208.9 246.1 252.9 274.13 121.9 226.0 248.4 291.7 203.1 269.4 267.5 246.34 83.1 221.3 259.2 255.4 141.6 232.5 150.3 251.9第一种选择：第二种选择：2、两因素方差分析为了研究土壤和施肥量对作物产量的影响，随机选取30棵长势相同的植株分别种到6块试验地，其高中低酸性12 22 1213 19 1311 20 1412 18 119 21 11碱性20 32 1522 26 1717 34 1819 30 1420 31 15这里的单变量是指一个因变量而非一个自变量。
SPSS实验上机题
SPSS实验上机题实验1 数据文件建立与管理某航空公司38名职员性别和工资情况的调查数据，如下表所示，试在SPSS中进行如下操作：（1）定义变量，将gender定义为字符型变量，salary定义为数值型变量，在数据窗口录入数据，并保存数据文件，将其命名为“data1_1.sav”。
（2）打开文件data1_1.sav，练习增加一个个案，删除一个个案，增加一个变量、删除一个变量，以及个案和变量的复制、粘贴操作。
（3）将数据文件按性别分组；将数据文件按工资进行组距分组。
（4）查找工资大于40000美元的职工。
（5）按工资进行升序和降序排列，比较升序和降序排列结果有什么不同。
（6）练习数据的分类汇总操作，要求按照性别分类汇总样本的总数。
（7）练习数据选取操作，要求随机选取70%的数据。
（8）当工资大于40000美元时，职工的奖金是工资的20％；当工资小于40000美元时，职工的奖金是工资的10%，假设实际收入＝工资＋奖金，计算所有职工的实际收入，并将结果添加到income变量中。
实验2 数据特征的描述统计分析1.下表是一电脑公司某年连续120天的销售量数据(单位：台)。
试对其进行频数分析，计算均值、中位数、众数、四分位数,标准差、最大值、最小值、全距,偏度、峰度系数；画出直方图、茎叶图、箱线图；解释结果并说明其分布特征。
234159187155158172163183182177156165 143198141167203194196225177189203165 187160214168188173176178184209175210161152149211206196196234185189196172 150161178168171174160153186190172207 228162223170208165197179186175213176 153163218180192175197144178191201181 166196179171210233174179187173202182 154164215233168175198188237194205195 1742261801722111902001721871891881952.下表是某班同学月生活费资料，试对其进行描述分析，并对结果作出说明。
上机实验七 SPSS相关分析
上机实验七SPSS相关分析题目：1、分析数学和英语得分是否存在线性关系?数据来源：SPSS课程资料correlate2.sav假设：H0：数学和英语得分存在线性关系H1：数学和英语得分不存在线性关系基本结果：结论：Pearson相关系数为0.834，sig值为0.003，sig值小于0.05，所以数学和英语得分存在正相关；Spearman相关系数为0.770，sig值为0.009，sig值小于0.05，所以数学和英语得分存在正相关；无论是用Pearson、Spearman相关系数，都可以得出数学和英语得分存在正相关的结论，故接受H0假设，且SIG值均小于0.05，两者之间存在正相关线性关系。
题目：2、分析汽车销售额和燃油效率之间是否存在线性关系?数据来源：SPSS课程资料correlate1.sav假设：H0：汽车销售额和燃油效率之间存在线性关系H1：汽车销售额和燃油效率之间不存在线性关系基本结果：结论：Pearson相关系数为-0.492，sig值为0.000，sig值小于0.05，所以汽车销售额和燃油效率之间存在负相关；Spearman相关系数为-0.614，sig值为0.000，sig值小于0.05，所以汽车销售额和燃油效率之间存在负相关；无论是用Pearson、Spearman相关系数，都可以得出汽车销售额和燃油效率之间存在负相关的结论，且SIG值均小于0.05，故接受H0假设，两者之间存在负相关线性关系。
题目：3、试分析工资高低是否和教育水平相关?数据来源：SPSS课程资料Employee data.sav假设：H0：工资高低和教育水平相关H1：工资高低和教育水平不相关基本结果：结论：Pearson相关系数为0.661，sig值为0.000，sig值小于0.05，所以工资高低和教育水平之间存在正相关；Spearman相关系数为0.688，sig值为0.000，sig值小于0.05，所以工资高低和教育水平之间存在正相关；无论是用Pearson、Spearman相关系数，都可以得出工资高低和教育水平之间存在正相关的结论，且SIG值均小于0.05，故接受H0假设，两者之间存在正相关线性关系。
spss分析案例
spss分析案例SPSS分析案例。
在社会科学研究中，SPSS（Statistical Package for the Social Sciences）是一个非常常用的统计分析软件，它能够帮助研究者对数据进行有效的整理、分析和呈现。
本文将以一个实际的案例来介绍SPSS的使用，希望能够帮助读者更好地理解和运用这一工具。
案例背景：假设我们是一家餐饮公司的市场部门，想要了解不同地区的顾客对我们产品的满意度情况，以便进行有针对性的改进和营销活动。
我们收集了来自不同地区的顾客满意度调查数据，包括满意度评分和顾客所在地区。
数据准备：首先，我们需要将收集到的数据整理成SPSS可以识别的格式。
在SPSS中，我们可以将数据导入数据视图中，按照变量的不同类型进行设定，比如将地区设定为名义变量，满意度评分设定为数值型变量。
数据分析：接下来，我们可以进行数据分析了。
我们可以使用描述性统计方法来了解不同地区的顾客满意度评分的分布情况，比如平均值、标准差、最大值和最小值等。
这可以帮助我们直观地了解不同地区的满意度情况。
此外，我们还可以使用交叉表分析方法来探究地区和满意度评分之间的关系。
通过交叉表，我们可以清晰地看到不同地区的顾客在不同满意度评分下的分布情况，从而找出可能存在的关联关系。
结果呈现：最后，我们需要将分析结果进行呈现。
在SPSS中，我们可以利用图表功能来直观地展示数据分析的结果，比如制作柱状图或饼状图来展示不同地区的满意度评分分布情况。
此外，我们还可以利用报告功能来生成分析报告，将分析结果清晰地呈现给决策者。
结论：通过以上的分析，我们可以得出不同地区的顾客满意度情况，从而为下一步的改进和营销活动提供依据。
同时，我们也了解了如何使用SPSS来进行数据分析，希望本案例能够对读者有所帮助。
总结：SPSS作为一款强大的统计分析软件，可以帮助研究者对数据进行全面的分析和呈现。
通过本案例的介绍，希望读者能够更加熟练地运用SPSS，为自己的研究工作提供有力的支持。
spss上机报告2
统计分析软件（spss）实验报告结论：根据单因素方差分析得出这五种推销方法不存在显著性差异。
练习3_2（3）销售量日期周一到周三周四到周五周末地区一500060004000 600080007000400030005000地区二700080008000 500050006000500060004000地区三300020004000 600060005000800090006000结论：如果显著性水平α为0.05，由于有关日期和地区的F值大于显著性水平α，所以不同地区和不同日期对于该商品没有显著性影响。
同时，由于F日期·F地区小于显著性水平α，所以可以认为不同地区和日期对于该商品销售产生交互作用。
4.在全部的2044个样本中，很不满意579个，不满意1153个，满意224个，很满意88个。
所以，如果不同年龄段人群对该商品的满意状况分布一致的话，存在很不满意：不满意：满意：很满意＝579：1153：224：88.使用非参数检验中的卡放检验来分别检验青年、中年、老年人群是否服从以上比例。
首先进行加权个案，之后进行卡放检验。
青年结论：显著性水平0.000小于0.005，认为青年人满意程度水平不与总体趋势相同。
中年：结论：显著性水平0.000小于0.005，认为中年人满意程度水平不与总体趋势相同。
老年结论：显著性水平0.003小于0.005，认为老年人满意程度水平不与总体趋势相同。
5.相关性客户满意度得分综合竞争力得分客户满意度得分Pearson 相关性 1 .864**显著性（双尾）.000N 15 15综合竞争力得分Pearson 相关性.864** 1显著性（双尾）.000N 15 15**. 在置信度（双测）为 0.01 时，相关性是显著的。
结论：因为相关系数为0.864，大于0.8，所以客户满意度与加权竞争力之间存在较强的正相关关系。
6.相关性人均香烟消耗量1930年每百万男子中死于肺癌的人数人均香烟消耗量1930年Pearson 相关性 1 .737**显著性（双尾）.010N 11 11每百万男子中死于肺癌的人数Pearson 相关性.737** 1 显著性（双尾）.010N 11 11**. 在置信度（双测）为 0.01 时，相关性是显著的。
大学生spss数据分析案例
大学生spss数据分析案例大学生SPSS数据分析案例。
在大学教育中，数据分析是一个非常重要的环节，尤其是对于社会科学和商业管理专业的学生来说。
SPSS（Statistical Package for the Social Sciences）是一个专业的统计分析软件，广泛应用于学术研究和商业决策中。
本文将以一个大学生SPSS数据分析案例为例，介绍如何使用SPSS进行数据分析。
案例背景：某大学社会科学专业的学生对大学生活满意度进行了调查，并收集了相关数据，包括学生的性别、年级、专业、宿舍类型、课程质量、宿舍环境、社交活动等方面的信息。
现在需要对这些数据进行分析，以了解不同因素对大学生活满意度的影响。
数据准备：首先，需要将调查所得的数据录入SPSS软件中，确保数据的准确性和完整性。
在录入数据时，要注意将不同的变量分别录入不同的列中，以便后续的分析和处理。
数据分析：1. 描述统计分析。
首先，可以对各个变量进行描述统计分析，包括计算均值、标准差、频数分布等。
通过描述统计分析，可以直观地了解各个变量的分布情况，为后续的分析提供基础。
2. 相关性分析。
接下来，可以进行各个变量之间的相关性分析，通过相关系数的计算来了解不同变量之间的关联程度。
例如，可以分析学生的性别、年级、专业与大学生活满意度之间的相关性，以及宿舍类型、课程质量、社交活动等因素对大学生活满意度的影响程度。
3. 方差分析。
针对分类变量，可以进行方差分析，比较不同组别之间的均值差异是否显著。
例如，可以分析不同年级、不同专业的学生对大学生活满意度的差异情况，以及不同宿舍类型对大学生活满意度的影响是否显著。
4. 回归分析。
最后，可以利用回归分析来探讨不同因素对大学生活满意度的影响程度。
通过建立回归模型，可以了解各个自变量对因变量的影响情况，以及它们之间的关系强度和方向。
结论与建议：通过以上的数据分析，可以得出不同因素对大学生活满意度的影响程度，为学校和相关部门提供决策建议。
SPSS上机实验报告四
SPSS上机实验报告一、实验内容1.数据合并：（1）纵向拼接（添加个案）：合并数据a.sav和b.sav（2）横向合并（添加变量）：合并数据a.sav和c.sav2.对数据CCSS_Sample.sav作下列操作：（1）频率分析：对S0城市，S4学历分别做分析；（2）交叉列表：月份对城市做交叉分析；观察值；计算（行、列）百分百；（3）对多选题C0贷款情况进行分析：多响应频率分析；3.对数据Employee data.sav，分析员工的性别、受教育程度、少数名族、职位类别的分布情况，并尝试分析这些属性之间的关系以及这些属性和工资之间的关系.二、实验步骤1.合并数据（1）纵向拼接：打开spss软件，在菜单中打开a.sav文件，选择菜单：[数据]→[合并文件]→[添加个案],在弹出的窗口中将选择外部spss数据文件并在浏览中选择b.sav，点击继续，在弹出的窗口中将“非成对变量”中的所有变量添加到“新的活动数据集中的变量”，勾选“将个案表现为变量”，点击确定。
结果如图：（2）横向合并：打开a.sav,选择菜单：[数据]→[合并文件]→[添加变量]，在弹出的窗口中选择外部数据文c.sav,在弹出的窗口中勾选“按照排序文件中的关键变量匹配个案”，将“已排除变量”中的id添加到“关键变量”中，点击确定。
结果如图：2.（1）频率分析：在spss中打开CCSS_Sample.sav，选择菜单：[分析]→[描述统计]→[频率]，在弹出的窗口中双击左边框中的S0城市，S4学历加入到右边变量框中，如图：点击确定。
结果如图：分析：在北京，上海，广州工作的人数基本相同；大专毕业的人最多，其次是高中/中学毕业生和本科毕业生，硕士及以上学历的人非常少，仅占5%。
（2）交叉列表：打开CCSS_Sample.sav数据，选择菜单：[分析]→[描述统计]→[交叉表]，在弹出的窗口中从左边框中将月份添加到行中，将城市添加到列中，如图：单击[单元格]，勾选百分比中的行和列，如图：单击[继续]，再单击[确定]。
正交试验设计的spss分析报告
上机操作6：正交试验设计的spss分析习题：有一混合水平的正交试验，A因素为葡萄品种，A1、A2、A3、A4，B因素为施肥期，有B1、B2，C因素为施肥量，有C1、C2，重复三次，采用L8(4×24)正交表，试验结果如下表，试进行分析葡萄品种施肥时期及用量实验结果解： 1.定义变量，输入数据：在变量视图中写入变量名称“产量”、“区组”、“施肥量”、“施肥期”、“品种”“处理”，宽度均为8，小数均为0。
并在数据视图依次输入变量。
2．分析过程：（1）正态分布检验：工具栏“图形”——“P-P图”，在“变量”中放入“产量”，“检验分布”为“正态”，“确定”。
（2）方差齐性检验：a.工具栏“分析”——“比较均值”——“单因素ANOVA”。
b.在“因变量”中放入“产量”，在“固定因子”中放入“品种”。
c.点击“选项”，在“统计量”中点击“方差同质性检验”，“继续”。
d.“确定”。
工具栏“分析”——“比较均值”——“单因素ANOVA”。
e.在“因变量”中放入“产量”，在“固定因子”中放入“施肥期”。
f.点击“选项”，在“统计量”中点击“方差同质性检验”，“继续”。
g.“确定”。
在“因变量”中放入“产量”，在“固定因子”中放入“施肥量”。
h.点击“选项”，在“统计量”中点击“方差同质性检验”，“继续”。
i.“确定”。
在“因变量”中放入“产量”，在“固定因子”中放入“处理”。
点击“选项”，在“统计量”中点击“描述性”和“方差同质性检验”，“继续”。
j.“确定”。
（3）显著性差异检验：a.工具栏“分析”——“常规线性模型”——“单变量”。
b.在“因变量”中放入“产量”，在“固定因子”中分别放入“施肥期”、“施肥量”、“品种”“区组”。
c.点击“模型”，“定制”，将“施肥期”、“施肥量”、“品种”、“区组”放入“模型”下。
在“建立项”中选择“主效应”，“继续”。
d.点击“两两比较”，将“施肥期”、“施肥量”、“品种”放入“两两比较检验”中，点击“假定方差齐性”中的“Duncan”。
不同地区和不同日期对该商品销售量的影响实验报告 2
SPSS统计软件上机实验报告
班别姓名学号：信管12 龙珍珍201205402138
1、实验内容
分析不同地区和不同日期对该商品的销售是否产生显著影响
2、实验目的
通过本实验掌握多因素方差分析方法。
3、实验方案分析
在本题中，以不同的地区和不同的日期为控制变量，销售量为观测变量。
原假设为：不同的地区没有对销售量尝试显著影响；不同的日期的销售量没有显著差异；地区和日期对销售量没有产生交互影响。
4、操作过程
(1)选择菜单【分析】→【一般线性模型】→【单变量】，指定销售量到【因变量】框中，指定固定效应的控制变量到【固定因子】框中，如图：
选择【确定】
5、实验结果
6、讨论
由表“主体间效应的检验”可以看到：观测变量的总变差sst为7.830e7，它被分解为4个部分，分别是由地区（x1）不同引起的变差，由日期(x2)不同引起的变差，由地区不同和日期(x1*x2)不同交互作用引起的变差，由随机引起的误差。
F(x1)、F(x2)、F(x1*x2)的概率p值分别为0.439,0.303和0.00。
如果显著性水平为0.05，由于F(x1)、F(x2)的概率p值大于显著性水平，因此不应拒绝原假设，可以认为不同的地区，不同的日期的销售量总体均值没有显著性差异。
同时，由于F(x1*x2)的概率p值小于显著性水平，因此拒绝原假设，可以认为不同的地区和日期对销售量产生交互式影响。
7、结论
不同的地区和不同的日期对该商品没有显著性差异，但是不同的地区和日期对销售量产生交互式影响。
spss数据分析案例
spss数据分析案例SPSS数据分析案例。
在实际的数据分析工作中，SPSS（Statistical Product and Service Solutions）是一个非常常用的统计分析软件。
它提供了强大的数据处理和分析功能，可以帮助研究人员快速、准确地进行数据处理和分析。
本文将通过一个实际的案例，介绍如何使用SPSS进行数据分析，并展示分析结果。
案例背景：某公司想要了解员工满意度与工作绩效之间的关系，为了达到这个目的，他们进行了一项调查，收集了员工的满意度评分和绩效评分数据。
现在，他们希望通过这些数据，利用SPSS进行分析，找出员工满意度和工作绩效之间的关系。
数据收集：首先，我们收集了100名员工的满意度评分和绩效评分数据。
满意度评分采用了1-5的五级评分制，绩效评分采用了1-100的百分制评分。
数据导入：将收集到的数据导入SPSS软件中，创建一个新的数据集，并将员工的满意度评分和绩效评分数据分别录入到不同的变量中。
数据描述统计分析：首先，我们对数据进行描述性统计分析，包括计算满意度评分和绩效评分的均值、标准差、最大值、最小值等。
这些统计量可以帮助我们更好地了解数据的分布情况。
相关性分析：接下来，我们使用SPSS进行相关性分析，探索员工满意度评分和绩效评分之间的相关关系。
通过相关性分析，我们可以计算出两个变量之间的相关系数，进而判断它们之间是否存在显著的相关性。
回归分析：在确定了员工满意度评分和绩效评分之间存在相关性的基础上，我们可以进一步进行回归分析，建立员工满意度评分对绩效评分的预测模型。
通过回归分析，我们可以得到员工满意度评分对绩效评分的影响程度，以及其他可能影响绩效评分的因素。
结论：通过SPSS数据分析，我们发现员工满意度评分与绩效评分之间存在显著的正相关关系，即员工满意度评分越高，其绩效评分也越高。
这为公司提高员工绩效提供了重要的参考依据，可以通过提升员工满意度来提高整体绩效水平。
总结：在本案例中，我们利用SPSS软件进行了员工满意度和绩效之间的数据分析。
spss案例分析报告
spss案例分析报告一、引言在本次报告中，将使用SPSS软件进行案例分析，对某一具体问题进行统计分析和数据可视化，以便对问题进行深入的了解和解释。
二、问题描述本次案例分析的问题是研究一个新产品在市场上的受欢迎程度与其价格、广告投入和消费者年龄之间的关系。
希望通过统计分析找出这些变量之间的关联，以便制定更好的市场策略。
三、数据收集与准备1. 数据收集从市场调研公司获取了500个有效问卷，并收集了新产品的价格、广告投入以及消费者的年龄等相关数据。
2. 数据清洗对数据进行了清洗和整理，包括去除缺失值、异常值的处理，使得数据集可用于后续的分析。
四、数据分析1. 描述性统计分析通过SPSS软件进行了描述性统计分析，包括对新产品价格、广告投入和消费者年龄的平均值、标准差、最小值和最大值等指标的计算。
2. 相关性分析利用SPSS软件进行了相关性分析，研究新产品受欢迎程度与价格、广告投入以及消费者年龄之间的关系。
结果显示价格与受欢迎程度之间存在较强的负相关，广告投入与受欢迎程度之间存在较强的正相关，而消费者年龄与受欢迎程度之间则没有明显的相关性。
3. 回归分析为了进一步探讨价格和广告投入对受欢迎程度的影响程度，进行了回归分析。
通过SPSS软件计算出了价格和广告投入对受欢迎程度的回归方程，并利用F检验和t检验对该方程的显著性进行了验证。
五、结果与讨论1. 描述性统计分析结果显示，新产品的平均价格为XXX元，标准差为XXX元，对消费者而言具有一定的价格竞争力。
广告投入的平均值为XXX万元，标准差为XXX万元，表明公司在产品推广方面投入了相对较高的资源。
而消费者的年龄平均值为XXX岁，标准差为XXX岁，消费者整体上比较年轻。
2. 相关性分析结果显示，新产品的价格与受欢迎程度之间存在较强的负相关，即价格越高，受欢迎程度越低；广告投入与受欢迎程度之间存在较强的正相关，即广告投入越高，受欢迎程度越高。
这表明在制定市场策略时，应考虑价格和广告投入对受欢迎程度的影响。
SPSS上机实验案例分析
SPSS上机实验案例分析SPSS上机实验案例分析练习⼀：下表为10个⼈对两个不同的问题作出的回答（回答为“Yes”或“No”）后得到的练习⼆: 某百货公司连续40天的商品销售额（单位：万元）如下：根据上⾯的数据进⾏适当分组，编制频数分布表。
（2）按规定，销售收⼊在125万元以上为先进企业，115万元-125万元为良好企业，105万元-115万元为⼀般企业，105万元以下为落后企业，按先进企业、良好企业、⼀般企业、落后企业进⾏分组。
练习四：某班的统计学成绩如下表所⽰：条件1:总评成绩的构成：总评成绩=0.2*平时成绩+0.8*期末成绩（即总评成绩中，平时成绩占20%，期末成绩占80%）条件2：总评成绩请保留为整数（2）请按100-90分，89-80分，79-70分，69-60分，59分及以下，将该班全体同学按照期末成绩进⾏分组得出各组⼈数。
练习五：如下表中所⽰的是20个股票经纪商对于两种不同交易收取佣⾦数据的⼀个样本。
这两种交易分别为: 买卖500股每股50美元和买卖1000股每股5美元的股票。
（1）计算两种交易佣⾦的全距和四分位数间距。
（2）计算两种交易佣⾦的⽅差和标准差。
（3）计算两种交易佣⾦的变异系数。
（4）⽐较两种交易的成本变异程度。
练习六：某⽣产部门利⽤⼀种抽样程序来检验新⽣产出来的产品的质量，该部门使⽤下⾯的法则来决定检验结果：如果⼀个样本中的14个数据项的⽅差⼤于0.005，则⽣产线必须关闭整修。
假设搜集的数据如下：问此时的⽣产线是否必须关闭？为什么？练习七：将50个数据输⼊到SPSS⼯作表中。
并使⽤SPSS计算这些数据描述统计量（如最⼤值、平均值、⽅差、标准差等）练习⼋：⼴告协会记录了在半点时段和最佳时段电视节⽬中⼴告所占时间。
在主要通信⽹中晚8：30分时段的20个最佳时段的电视节⽬中，⼴告所占时间的数据如下（单位：分钟）求晚8：30分时段电视节⽬中⼴告所占时间均值的点估计的95％置信区间。
大学生spss数据分析案例
大学生spss数据分析案例SPSS数据分析是大学生在进行学术研究和毕业论文撰写过程中常常需要掌握的技能之一。
本文将以一个实际案例为例，介绍如何使用SPSS软件进行数据分析，以帮助大学生更好地理解和运用SPSS进行数据处理和分析。
首先，我们需要明确案例研究的背景和目的。
假设我们要研究大学生学习成绩与每周学习时间的关系，我们收集了一批大学生的学习成绩和每周学习时间的数据，现在需要用SPSS进行分析。
第一步，我们需要导入数据。
在SPSS软件中，点击“文件”-“导入数据”-“从数据库导入数据”，选择相应的文件并导入数据。
第二步，进行数据清洗。
在数据清洗过程中，我们需要检查数据是否存在缺失值、异常值等情况，可以使用SPSS中的数据查看功能和描述统计功能进行检查和处理。
第三步，进行描述性统计分析。
在SPSS中，我们可以使用“描述统计”功能来计算学习成绩和每周学习时间的均值、标准差、频数分布等统计指标，以便对数据有一个整体的了解。
第四步，进行相关性分析。
我们可以使用SPSS中的“相关分析”功能来计算学习成绩和每周学习时间之间的相关系数，以判断它们之间是否存在显著的相关性。
第五步，进行回归分析。
如果我们想进一步探究学习成绩与每周学习时间之间的因果关系，可以使用SPSS中的“线性回归”功能来进行回归分析，得出它们之间的回归方程和相关系数。
最后，我们需要对分析结果进行解释和总结。
在解释和总结过程中，我们需要使用清晰、准确的语言对分析结果进行解释，并结合案例研究的背景和目的进行合理的总结和结论。
通过以上案例分析，我们可以看到，SPSS软件作为一款专业的统计分析工具，能够帮助我们快速、准确地进行数据分析，为我们的学术研究和毕业论文撰写提供了有力的支持。
希望本文能够对大学生在SPSS数据分析方面有所帮助，引起大家对SPSS数据分析的重视和学习兴趣。
武汉理工大学实验报告：spss上机实验
SPSS上机考试姓名：班级：学号：实验一：聚类分析一、实验问题某校从高中二年级女生中随机抽取16名，测得身高和体重数据如下表：试分别利用最短距离法、最长距离法、重心法、类平均法、中间距离法将它们聚类(分类统计量采用绝对距离)，并画出聚类图。
二、实验步骤1、1.数据处理：在SPSS中的Data View中导入数据，并在Variable View中定义变量。
2、点击“Analyze-Classify-Hierarchical Cluster，打开Hierarchical Cluster的对话框，从左侧将2个聚类指标选入Variables栏中，将表示序号（字符串）选入Lable Cases By栏中按“Plots”按钮，在弹出的窗口中选中Dendrogram（谱系图）选项，按“Continue”返回主对话框。
再按“Method”按钮，在Cluster Method，下面就各种方法进行结果输出。
3.结果输出（1）最短距离法分类统计量采用绝对距离Block，采用最短距离法Nearest neighbor返回主对话框后点击“OK”即可得到聚类结果的树形图如下：（2）最长距离法分类统计量采用绝对距离Block，采用最短距离法Furthest neighbor返回主对话框后点击“OK”即可得到聚类结果的树形图如下：(3)重心法分类统计量采用绝对距离Block，采用最短距离法Centroid clustering返回主对话框后点击“OK”即可得到聚类结果的树形图如下：（4）类平均法-组间平均法分类统计量采用绝对距离Block，采用最短距离法Between-groups linkage返回主对话框后点击“OK”即可得到聚类结果的树形图如下：（5）中间距离法分类统计量采用绝对距离Block，采用最短距离法Median clustering返回主对话框后点击“OK”即可得到聚类结果的树形图如下：分析：就以中间聚类法为例，当采用绝对距离时，分为3类的时候分别为：①5 12 13 15 16 1 6 7②4 ③8 11 9 10 2 14基于上述各种聚类方法的分析可知，分为3类的时候各个方法相似度最高，所以将其分为3类最为合适。
SPSS数据分析与应用 第6章实训案例
SPSS数据分析与应用第6章实训案例本章介绍《SPSS数据分析与应用第6章实训案例》的背景和目的。
这个案例是为了帮助读者更好地理解和应用SPSS数据分析工具而设计的。
在本章中，我们将介绍一个具体的实训案例，包括案例的背景、数据的来源以及需要进行的数据分析任务。
通过这个案例，读者将研究如何使用SPSS软件进行数据分析，并掌握常用的数据分析方法和技巧。
在这一章节中，我们将详细介绍实际操作SPSS软件的步骤，包括数据导入、数据清洗、变量设置、数据分析等。
每个步骤都会给出详细的说明和示例，以帮助读者顺利完成实训案例。
在这一章节中，我们将展示实际进行数据分析后得到的结果，并进行对结果的解读和分析。
读者将通过实验结果的展示和分析，更好地理解数据分析方法和结果的含义。
在这个章节中，我们将对整个实训案例进行总结，并给出一些拓展的内容，包括其他可能的数据分析方法和应用场景。
读者将通过这个章节更好地巩固所学的知识，并拓展自己的数据分析能力。
这个章节将给出实训案例的参考答案，供读者参考和对比。
读者可以通过对比答案，进一步检查自己的数据分析能力和理解程度。
通过研究本章内容，读者将能够熟练使用SPSS软件进行数据分析，掌握常用的数据分析方法和技巧，并能够将数据分析应用于实际问题中。
本章介绍了《SPSS数据分析与应用第6章实训案例》中涉及的数据集和问题。
以下是详细描述：该案例涉及的数据集为某医院的病人信息和医疗费用数据集。
主要问题是研究不同因素对病人的医疗费用的影响。
在数据集中，每个病人都有一些基本信息，如年龄、性别、是否吸烟等。
此外，还有每个病人的医疗费用数据，包括住院费、手术费、药费等。
研究问题主要包括以下几个方面：病人的基本信息对医疗费用的影响：通过分析年龄、性别、是否吸烟等因素与医疗费用之间的关系，研究这些基本信息对医疗费用的影响程度。
不同费用项之间的关系：通过探究住院费、手术费、药费等不同费用项之间的相关性，了解各项费用之间的关系，为进一步分析提供依据。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
SPSS上机实验案例分析
练习一：下表为10个人对两个不同的问题作出的回答（回答为“Yes”或“No”）后得到的
练习二: 某百货公司连续40天的商品销售额（单位：万元）如下：
根据上面的数据进行适当分组，编制频数分布表。
（2）按规定，销售收入在125万元以上为先进企业，115万元-125万元为良好企业，105万元-115万元为一般企业，105万元以下为落后企业，按先进企业、良好企业、一般企业、落后企业进行分组。
练习四：某班的统计学成绩如下表所示：
条件1:总评成绩的构成：总评成绩=0.2*平时成绩+0.8*期末成绩（即总评成绩中，平时成绩占20%，期末成绩占80%）
条件2：总评成绩请保留为整数
（2）请按100-90分，89-80分，79-70分，69-60分，59分及以下，将该班全体同学按照期末成绩进行分组得出各组人数。
练习五：如下表中所示的是20个股票经纪商对于两种不同交易收取佣金数据的一个样本。
这两种交易分别为: 买卖500股每股50美元和买卖1000股每股5美元的股票。
（1）计算两种交易佣金的全距和四分位数间距。
（2）计算两种交易佣金的方差和标准差。
（3）计算两种交易佣金的变异系数。
（4）比较两种交易的成本变异程度。
练习六：某生产部门利用一种抽样程序来检验新生产出来的产品的质量，该部门使用下面的法则来决定检验结果：如果一个样本中的14个数据项的方差大于0.005，则生产线必须关闭整修。
假设搜集的数据如下：
问此时的生产线是否必须关闭？为什么？
练习七：
将50个数据输入到SPSS工作表中。
并使用SPSS计算这些数据描述统计量（如最大值、平均值、方差、标准差等）
练习八：广告协会记录了在半点时段和最佳时段电视节目中广告所占时间。
在主要通信网中晚8：30分时段的20个最佳时段的电视节目中，广告所占时间的数据如下（单位：分钟）
求晚8：30分时段电视节目中广告所占时间均值的点估计的95％置信区间。
练习九：某年度我国部分工业品产量如下表所示
请据表中数据对如下六个问题进行统计图形描述
（1）请选择一个适当图形描述各地区所含省市数目
（2）请选择一个适当图形描述各地区水泥的平均产量
（3）请选择一个适当图形描述每个地区水泥产量低于800万吨的省市数目
（4）请选择一个适当图形描述该年度全国生铁、钢、水泥、塑料的平均产量
（5）请选择一个适当图形描述该年度华北五省市工业品产量
（6）请选择一个适当图形描述各地区塑料总产量占全国总量的比例
练习十：以下数据记录了美国最大的旅馆业市场的客房使用率和平均房价的统计资料。
（1）用平均房价作自变量，画出这些数据的散点图；
（2）求客房使用率关于平均房价估计的回归方程；
（3）对于平均房价为80美元的一家旅馆，估计它的客房使用率
练习十一：某公司采集了美国市场上办公用房的空闲率和租金率的数据。
对于18个选取的销售地区，下面是这些地区的中心商业区的综合空闲率（%）和平均租金率（美元/平方英尺）的数据。
（1）用水平轴表示空闲率，对这些数据画出散点图。
（2）这两个变量之间显示出什么关系吗？
（3）求出在办公用房的综合空闲率已知时，能用来预测平均租金率的估计的回归方程。
（4）在0.05显著性水平下检验关系的显著性。
（5）估计的回归方程对数据的拟合好吗？请作出解释。
（6）在一个综合空闲率是25%的中心商业区，预测该市场的期望租金率。
（7）在劳德代尔堡的中心商业区，综合空闲率是11.3%，预测劳德代尔堡的期望租金率。
练习十二：某农场通过试验取得早稻收获量与春季降雨和春季温度的如下数据，计算回归参数和检验统计量：
试确定早稻收获量对春季降雨量和春季温度的二元线性回归方程，并解释回归系数的实际含义。
练习十三：Heller公司是一家生产割草机和割草机相关设备的企业，管理人员认为割草机的销售数量依赖于割草机的价格和竞争对手的价格。
令y―销售数量（千台）； x1―竞争厂商割草机的价格（美元）； x2－－Heller公司割草机的价格（美元）
Heller公司的管理人员希望建立割草机的销售数量与Heller公司割草机价格和竞争厂商割草机价格的回归方程，下表列出了10个城市的价格资料。
（1）建立估计的回归方程。
它能在竞争厂商割草机的价格和Heller公司割草机的价格已知时预测割草机的销售数量。
（2）如果在一个城市Heller公司割草机的销售价格为160美元，竞争厂商的割草机的价格为170美元，预测在该城市割草机的销售数量。