工程力学习题答案(1)
工程力学复习题1及答案
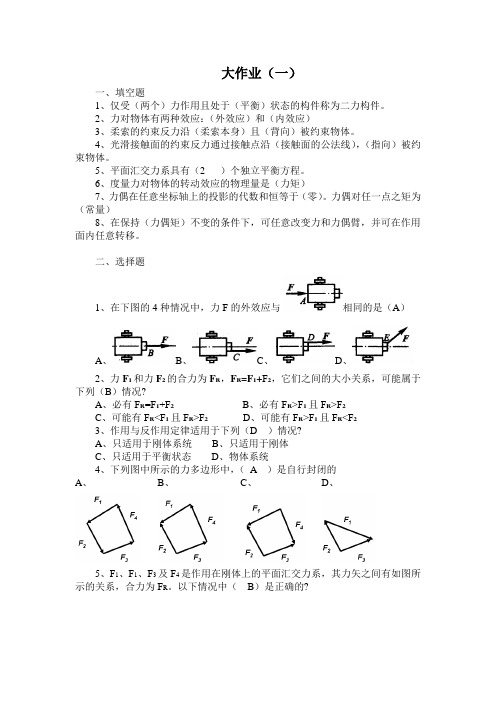
大作业（一）一、填空题1、仅受（两个）力作用且处于（平衡）状态的构件称为二力构件。
2、力对物体有两种效应：（外效应）和（内效应）3、柔索的约束反力沿（柔索本身）且（背向）被约束物体。
4、光滑接触面的约束反力通过接触点沿（接触面的公法线），（指向）被约束物体。
5、平面汇交力系具有（2 ）个独立平衡方程。
6、度量力对物体的转动效应的物理量是（力矩）7、力偶在任意坐标轴上的投影的代数和恒等于（零）。
力偶对任一点之矩为（常量）8、在保持（力偶矩）不变的条件下，可任意改变力和力偶臂，并可在作用面内任意转移。
二、选择题1、在下图的4种情况中，力F的外效应与相同的是（A）A、B、C、D、2、力F1和力F2的合力为F R，F R=F1+F2，它们之间的大小关系，可能属于下列（B）情况?A、必有F R=F1+F2B、必有F R>F1且F R>F2C、可能有F R<F1且F R>F2D、可能有F R>F1且F R<F23、作用与反作用定律适用于下列（D ）情况?A、只适用于刚体系统B、只适用于刚体C、只适用于平衡状态D、物体系统4、下列图中所示的力多边形中，（A ）是自行封闭的A、B、C、D、5、F1、F1、F3及F4是作用在刚体上的平面汇交力系，其力矢之间有如图所示的关系，合力为F R。
以下情况中（B）是正确的?A、F R=F4B、F R=2F4C、F R=-F4D、F R=-2F46、三铰刚架ABC如图所示，不计自重，仅受力F作用，铰链A反力FA的方位必满足（ C ）?A、通过B点B、通过D点C、通过E点D、通过C点7、在图中，如果两力偶均作用在杆AC上，铰链A或B的反力方位（ C ）?A、垂直于ACB、垂直于BCC、垂直于ABD、不确定三、画受力图1、重为P的均质圆轮在边缘A点用绳AB系住，绳AB通过轮心C，圆轮边缘D点靠在光滑的固定曲面上，试画圆轮的受力图解：（1）选圆轮为研究对象，画出其分离体图（2）在分离体圆轮上画出作用其上的主动力P（3）在分离体的每处约束，画出其约束力。
工程力学课后习题答案
第一章 静力学基本概念与物体的受力分析下列习题中，未画出重力的各物体的自重不计，所有接触面均为光滑接触。
1.1 试画出下列各物体（不包括销钉与支座）的受力图。
解：如图(g)(j)P (a)(e)(f)WWF F A BF DF BF AF ATF BA1.2画出下列各物体系统中各物体（不包括销钉与支座）以及物体系统整体受力图。
解：如图F BB(b)(c)C(d)DCF D(e)AF D(f)FD(g)(h)EOBO EFO(i)(j) BYFB XBFXE(k)1.3铰链支架由两根杆AB、CD和滑轮、绳索等组成，如题1.3图所示。
在定滑轮上吊有重为W的物体H。
试分别画出定滑轮、杆CD、杆AB和整个支架的受力图。
解：如图'D1.4题1.4图示齿轮传动系统，O1为主动轮，旋转方向如图所示。
试分别画出两齿轮的受力图。
解：1o xF2o xF2o yF o yFFF'1.5结构如题1.5图所示，试画出各个部分的受力图。
解：第二章 汇交力系2.1 在刚体的A 点作用有四个平面汇交力。
其中F 1＝2kN ，F 2=3kN ，F 3=lkN ， F 4=2.5kN ，方向如题2.1图所示。
用解析法求该力系的合成结果。
解 00001423cos30cos45cos60cos45 1.29Rx F X F F F F KN ==+--=∑ 00001423sin30cos45sin60cos45 2.54Ry F Y F F F F KN ==-+-=∑2.85R F KN ==0(,)tan63.07Ry R RxF F X arc F ∠==2.2 题2.2图所示固定环受三条绳的作用，已知F 1＝1kN ，F 2=2kN ，F 3=l.5kN 。
求该力系的合成结果。
解：2.2图示可简化为如右图所示023cos60 2.75Rx F X F F KN ==+=∑013sin600.3Ry F Y F F KN ==-=-∑2.77R F KN ==0(,)tan6.2Ry R RxF F X arc F ∠==-2.3 力系如题2.3图所示。
工程力学(第二版)习题册答案
一、填空题
1. 相 对 滑 动 相 对 滑 动 趋 势 接触面的切线 相反 2. 10N 20N 30N 30N 30N 3. 100N 竖直向上 平衡 4. 平稳无冲击 自锁
阻碍物体相对滑动
相对滑动趋势
二、选择题
1. A
三、简答题
1. ①问题中含有可能发生相对滑动的摩擦面，因此，存在摩擦力； ②受力图中要画出摩擦力，摩擦力总是沿着接触面的切线方向并与物体相对滑
7.
8.
9.
第二章 平面力系
第一节 共线力系的合成与平衡
一、填空题
1. 在同一条直线上
2. FR Fi FR 0
二、计算题
设向右为正方向。 则 FR=120+40-80-200=-120N 方向：水平向左
第二节 平面汇交力系的合成
一、填空题
1. 作用于同一平面内且各力作用线相交于一点的力系 共线力系 力的作用点 2. -F 或 F 0 0 -F 或 F 3. 合力在任一坐标轴上的投影 各分力在同一轴上投影的代数和 4. F4 F3 5. 自行封闭 6. 所有各力在 x 轴上投影的代数和为零 所有各力在 y 轴上投影的代数和为零 Fx 0 Fy 0
3. 后轮：摩擦力向前 前轮：摩擦力向后
4. 不下滑，处于自锁状态
四、计算题
FT 60 18 3N
五、应用题
1. （提示）从摩擦力与 F 对 B 点的力矩大小的比较进行考虑
第三章 空间力系 第一节 力在空间坐标轴上的投影与合成
一、填空题
1. 力的作用线不都在同一平面内呈空间分布的力系 2. 一次投影法 二次投影法
二、选择题
1. A 2.B
它所限制物体
三、简答题
1.柔性体约束只能承受拉力，不能承受压力。 2.被约束物体可以沿约束的水平方向自由滑动，也可以向离开约束的方向运动， 但不能向垂直指向约束的方向运动。 3.剪刀的两半部分可以绕销钉轴线相对转动，但不能在垂直销钉轴线的平面内沿 任意方向做相对移动。 4.木条不能沿圆柱销半径方向移动，但可以绕销轴做相对转动。 5.固定端约束既限制物体在约束处沿任何方向的移动，也限制物体在约束处的转 动。
工程力学习题答案
工程力学习题答案第一章 静力学基础知识思考题：1. ×;2. √;3. √;4. √;5. ×;6. ×;7. √;8. √习题一1 解：（a ）杆AB 在A 、B 、C 三处受力作用。
由于力p 和B R的作用线交于点O 。
如图（a ）所示，根据三力平衡汇交定理， 可以判断支座A 点的约束反力必沿 通过A 、O 两点的连线。
（b ）同上。
由于力p 和B R的作用线交于O 点，根据三力平衡汇交定理， 可判断A 点的约束反力方向如 下图（b ）所示。
2．不计杆重，画出下列各图中AB 解：（a ）取杆AB 处受绳索作用的拉力B T ，在A和E 两处还受光滑接触面约束。
约束力A N 和并指向杆。
其中力E N 与杆垂直，力A N 通过半圆槽的圆心O 。
AB 杆受力图见下图（a ）。
(b)由于不计杆重，曲杆BC 只在两端受铰销B 和C 对它作用的约束力B N 和C N ，故曲杆BC 是二力构件或二力体，此两力的作用线必须通过B 、C 两点的连线，且B N =C N 。
研究杆两点受到约束反力A N 和B N，以及力偶m 的作用而平衡。
根据力偶的性质，A N 和B N(d)由于不计杆重，杆AB 在A 、C 两处受绳索作用的拉力A T 和C T ，在B 点受到支座反力B N 。
A T 和C T 相交于O 点，根据三力平衡汇交定理，可以判断B N必沿通过B 、O 两点的连线。
见图(d ).第二章力系的简化与平衡思考题：1. √;2. ×;3. ×;4. ×;5. √;6. ×;7. ×;8. ×;9. √.1． 平面力系由三个力和两个力偶组成，它们的大小和作用位置如图示，长度单位为cm ，求此力系向O 点简化的结果，并确定其合力位置。
解：设该力系主矢为R ' ，其在两坐标轴上的投影分别为x R 、y R 。
由合力投影定理有：x i R x =∑ 1.53=-=-1.5kN2y i R y ==-∑ kNsin /i y R α'=∑0.8=-；cos /i x R α'=∑0.6=- 233α≈由合力矩定理可求出主矩：300()30.31015000.21008020000.5580i M M F ==⨯⨯-⨯---⨯=-∑m N合力大小为：' 2.5R R ==kN ，方向233α≈m 23.2=cm ，位于O 点的右侧。
(完整版)工程力学课后习题答案
工程力学练习册学校学院专业学号教师姓名第一章静力学基础 1第一章静力学基础1-1 画出下列各图中物体A，构件AB，BC或ABC的受力图，未标重力的物体的重量不计，所有接触处均为光滑接触。
（a）（b）（c）2 第一章静力学基础（d）（e）（f）（g）第一章静力学基础 3 1-2 试画出图示各题中AC杆（带销钉）和BC杆的受力图（a）（b）（c）（a）4 第一章静力学基础1-3 画出图中指定物体的受力图。
所有摩擦均不计，各物自重除图中已画出的外均不计。
（a）第一章静力学基础 5 （b）（c）（d）6 第一章静力学基础（e）第一章静力学基础7 （f）（g）8 第二章 平面力系第二章 平面力系2-1 电动机重P=5000N ，放在水平梁AC 的中央，如图所示。
梁的A 端以铰链固定，另一端以撑杆BC 支持，撑杆与水平梁的夹角为30 0。
如忽略撑杆与梁的重量，求绞支座A 、B 处的约束反力。
题2-1图∑∑=︒+︒==︒-︒=PF F FF F F B A yA B x 30sin 30sin ,0030cos 30cos ,0解得: N P F F B A 5000===2-2 物体重P=20kN ，用绳子挂在支架的滑轮B 上，绳子的另一端接在绞车D 上，如第二章 平面力系 9图所示。
转动绞车，物体便能升起。
设滑轮的大小及轴承的摩擦略去不计，杆重不计，A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时，求拉杆AB 和支杆BC 所受的力。
题2-2图∑∑=-︒-︒-==︒-︒--=030cos 30sin ,0030sin 30cos ,0P P F FP F F F BC yBC AB x解得: PF P F AB BC 732.2732.3=-=2-3 如图所示，输电线ACB 架在两电线杆之间，形成一下垂线，下垂距离CD =f =1m ，两电线杆间距离AB =40m 。
电线ACB 段重P=400N ，可近视认为沿AB 直线均匀分布，求电线的中点和两端的拉力。
(完整版)工程力学习题解答(详解版)
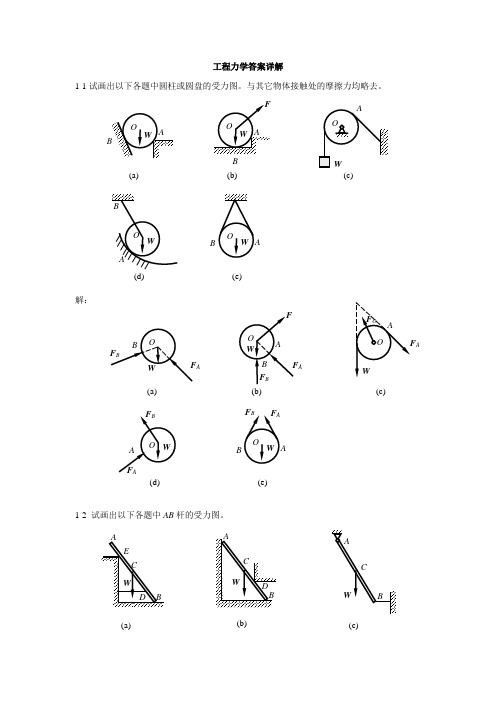
工程力学答案详解1-1试画出以下各题中圆柱或圆盘的受力图。
与其它物体接触处的摩擦力均略去。
解：1-2 试画出以下各题中AB 杆的受力图。
(a) B(b)(c)(d)A(e) A(a)(b) A(c)A(d)A(e)(c)(a)(b)解：1-3 试画出以下各题中AB 梁的受力图。
(d)(e)BB(a)B(b)(c)F B(a)(c)F (b)(d)(e)解：1-4 试画出以下各题中指定物体的受力图。
(a) 拱ABCD ；(b) 半拱AB 部分；(c) 踏板AB ；(d) 杠杆AB ；(e) 方板ABCD ；(f) 节点B 。
解：(a)F (b)W(c)(d) D(e)F Bx(a)(b)(c)(d)D(e)W(f)(a)D(b)B(c)BF D BF1-5 试画出以下各题中指定物体的受力图。
(a) 结点A，结点B；(b) 圆柱A和B及整体；(c) 半拱AB，半拱BC及整体；(d) 杠杆AB，切刀CEF及整体；(e) 秤杆AB，秤盘架BCD及整体。
解：(a)(b)(c)(d)ATF BAF(b)(e)(c)(d)(e)CAA C’CDDB2-2 杆AC 、BC 在C 处铰接，另一端均与墙面铰接，如图所示，F 1和F 2作用在销钉C 上，F 1=445 N ，F 2=535 N ，不计杆重，试求两杆所受的力。
解：(1) 取节点C 为研究对象，画受力图，注意AC 、BC 都为二力杆，(2) 列平衡方程：12140 sin 600530 cos6005207 164 o y AC o x BC AC AC BC F F F F F F F F F N F N=⨯+-==⨯--=∴==∑∑ AC 与BC 两杆均受拉。
2-3 水平力F 作用在刚架的B 点，如图所示。
如不计刚架重量，试求支座A 和D 处的约束力。
解：(1) 取整体ABCD 为研究对象，受力分析如图，画封闭的力三角形：(2)F 1F FDF F AF D211 1.122D A D D A F F FF F BC AB AC F F F F F =====∴===2-4 在简支梁AB 的中点C 作用一个倾斜45o 的力F ，力的大小等于20KN ，如图所示。
工程力学习题第1章答案
第1章 基本概念及基本原理思考题1-1 说明下列式子的意义和区别：(1)12F F = ，(2) 12=F F ， (3) 力1F 等效于力2F 。
答：式（1）表示2个力的大小相等。
式（2）表示2个力矢量相等，即2个力的大小相等，方向相同。
式（3）表示2个力的大小相等，方向和作用线均相等。
1-2 试区别12R +F =F F 和12R F F F =+两个等式代表的意义。
1-3 二力平衡条件与作用和反作用定律都是说二力等值、反向、共线，二者有什么区别？1-4 为什么说二力平衡条件、加减平衡力系原理和力的可传性等都只适用于刚体？1-5 什么叫二力构件? 分析二力构件受力时与构件的形状有无关系？ 1-6 如图所示，可否将作用于杆AC 上D 点的力F 沿其作用线移动，变成杆BC 上点的力F '，为什么？答：不可以，根据力的可传性定理的限制条件。
1-7 如图所示，杆AB 重为G ，B 端用绳子拉住，A 端靠在光滑的墙面，问杆能否平衡？为什么？答：不能，根据三力汇交定理内容。
习题1-11-2 如图所示，求F对点A的力矩。
1-3 如图所示，求P 对点O 的力矩。
解：（a ）Pl P m O =)(；（b ）0)(=P m O ；（c ）θsin )(Pl P m O = （d ）Pa P m O -=)(；（e ）)()(r l P P m O +=；（f ）αsin )(22P b a P m O +=1-4 如图示沿正立方体的前侧面AB 方向作用一力F ，则该力对哪些轴之矩 相等？1-5 图示力F 的作用线在平面OABC 内，对各坐标轴之矩哪些为零？1-6 如图所示长方体的三边 a EF =，b GB =，c AD =，沿三边作用力系1F ，2F ，3F 。
求此力系对点 H 之矩和对轴 HC 之矩。
注：下列习题凡未标出自重的物体，自重不计，接触处不计摩擦。
1-7 试画出图中所示各物体的受力图。
《工程力学》详细版习题参考答案
∑ Fx
=FAx
+
FBx
+
FCx
=− 1 2
F
+
F
−
1 2
F
=0
∑ Fy
= FAy
+
FBy
+
FCy
= − 3 2
F
+
3 F = 0 2
∑ M B= FBy ⋅ l=
3 Fl 2
因此，该力系的简化结果为一个力偶矩 M = 3Fl / 2 ，逆时针方向。
题 2-2 如图 2-19（a）所示，在钢架的 B 点作用有水平力 F，钢架重力忽 略不计。试求支座 A，D 的约束反力。
（a）
（b）
图 2-18
解：（1）如图 2-18（b）所示，建立直角坐标系 xBy。 （2）分别求出 A，B，C 各点处受力在 x，y 轴上的分力
思考题与练习题答案
FAx
= − 12 F ，FAy
= − 3 F 2
= FBx F= ，FBy 0
FCx
= − 12 F ，FCy
= 3 F 2
（3）求出各分力在 B 点处的合力和合力偶
（3）根据力偶系平衡条件列出方程，并求解未知量
∑ M =0 − aF + 2aFD =0
《工程力学》
可解得 F=Ay F=D F /2 。求得结果为正，说明 FAy 和 FD 的方向与假设方向相同。 题 2-3 如 图 2-20 （ a ） 所 示 ， 水 平 梁 上 作 用 有 两 个 力 偶 ， 分 别 为
3-4 什么是超静定问题？如何判断问题是静定还是超静定？请说明图 3-12 中哪些是静定问题，哪些是超静定问题？
（a）
工程力学课后习题答案
图2-13
1作为力图，BC杆受一对力偶作用。
2.对于AB杆系的平衡方程
所以:
1.以BC为研究对象，列出平衡方程。
1.以AB为研究对象，列出平衡方程。
2-18如图所示，三扭拱由两个半拱和三个铰A、B、c组成，已知每个半拱的重量为P=300kN，l=32m，h=10m。求支座A和b的约束反力。
图2-15
以整体为研究对象，从对称性认识:
以BC半拱为研究对象。
2-19在图示的框架中，物体重1200N，用一根细绳横过滑轮e水平系在墙上，尺寸如图，不考虑杆和滑轮的重量。求支座A和B处的约束反力和BC杆的内力FBC。
图2-19
以整体为研究对象。
解决方案:
以CDE杆和滑轮为研究对象。
解决方案:
2-20在图示的框架中，每根杆单位长度的重量为300N/m，载荷P=10kN，固定端在A处，铰链在B、C、d处，求固定端A和铰链处B、C的约束反力。
2-24平面桁架的支撑和荷载如图所示。求杆1，2，3的内力。(提示:先截掉AD、3、2杆，用切片法分析；然后取C节点)
2-25两个相同的匀质杆AB和BC在端点B用光滑铰链连接，A端和C端放在一个不光滑的水平面上，如图所示。当ABC处于等边三角形时，系统在垂直面内处于平衡状态。求杆端和水平面之间的摩擦系数。
工程学
练习册
1-1画出下图中物体A、分量AB、BC或ABC的受力图，不考虑无重力情况下物体的重量，所有接触点都是光滑的。
(一)
(二)
(三)
(
(五)
(六)
(g)
1-2试画出图中所示各题中AC杆(带销)和BC杆的受力图。
(a) (b) (c)
(一)
1-3画出图中指定物体的受力示意图。所有的摩擦力都不算，除了图中已经画出来的以外，所有东西的自重都不算。
工程力学课后习题答案（静力学和材料力学）
1 一 3 试画出图示各构件的受力图。
F
D
习题 1－3 图
C
F
D
C
A
B
FA
FB
习题 1－3a 解 1 图
F Ax
A
B
FAy
FB
习题 1－3a 解 2 图
C
BF
B
D
FB
FD
C
A
FA 习题 1－3b 解 2 图
W
FAx
FAy
习题 1－3c 解图
F
A
A
F
α
B C
FA
D
FAFD 习题 1－3d 解 2 图
FB2 x
B
FDy
C FB2 y
F Dx D
W
习题 1－4b 解 2 图
F'B1
B
F'B2x
F'B2 y F1
A B
F'B2x
习题 1－4c 解 1 图
F1 F'B2 y
FDx D FDy
F'B2x B
C
F'B2 y
W
F'B2 B
习题 1－4c 解 2 图
习题 1－4b 解 3 图
FA
A
B
F B1
习题 1－4d 解 1 图
可推出图（b）中 FAB = 10FDB = 100F = 80 kN。
FED αD
FDB FD′ B
FCB
α
B
F 习题 1－12 解 1 图
F AB 习题 1－12 解 2 图
1—13 杆 AB 及其两端滚子的整体重心在 G 点，滚子搁置在倾斜的光滑刚性平面上，如
工程力学第一章答案
范钦珊教育教学工作室FAN Qin-Shan’s Education & Teaching StudioeBook工程力学习题详细解答（教师用书）(第1章)2006-12-18(a) (b) 习题1-1图C(a-2)DR F(a-3)(b-1) 第1章 静力学基础1一1 图a 和b 所示分别为正交坐标系11y Ox 与斜交坐标系22y Ox 。
试将同一个力F 分别在两中坐标系中分解和投影，比较两种情形下所得的分力与投影。
解：（a ），图（c ）：11 s i n c o s j i F ααF F +=分力：11 cos i F αF x = ， 11 sin j F αF y =投影：αcos 1F F x = ， αsin 1F F y =讨论：ϕ= 90°时，投影与分力的模相等；分力是矢量，投影是代数量。
（b ），图（d ）： 分力：22)tan sin cos (i F ϕααF F x -= ，22sin sin j F ϕαF y =投影：αcos 2F F x = ， )cos(2αϕ-=F F y讨论：ϕ≠90°时，投影与分量的模不等。
1一2 试画出图a 和b 两种情形下各构件的受力图，并加以比较。
习题1－2图（c ） 22x（d ）比较：图（a-1）与图（b-1）不同，因两者之F R D 值大小也不同。
1一3 试画出图示各构件的受力图。
习题1－3图B或(a-2) B(a-1)(b-1)F(c-1)或(b-2)F D1一4 图a 所示为三角架结构。
荷载F 1作用在B 铰上。
AB 杆不计自重，BD 杆自重为W ，作用在杆的中点。
试画出图b 、c 、d 所示的隔离体的受力图，并加以讨论。
习题1－4图1(f-1)(e-3)'A(f-2)1O(f-3)F'F yB 21(c-1)AA B1B FDx y1F'F yB 2Dy FAxF(b-3)ED(a-3)B(b-2)(b-1)AxFF 'CF C1一5 试画出图示结构中各杆的受力图。
工程力学习题(一)
工程力学习题集刚体静力学基础思考题1.试说明下列式子的意义与区别。
（1）F1=F2和F1=F2（2）FR=F1+F2和FR=F1+F22.作用于刚体上大小相等、方向相同的两个力对刚体的作用是否等效？3.二力平衡公理和作用与反作用定律中，作用于物体上的二力都是等值、反向、共线,其区别在哪里？4.判断下列说法是否正确。
（1）物体相对于地球静止时，物体一定平衡；物体相对于地球运动时，则物体一定不平衡。
（2）桌子压地板，地板以反作用力支撑桌子，二力大小相等、方向相反且共线，所以桌子平衡。
（3）合力一定比分力大。
（4）二力杆是指两端用铰链连接的直杆。
5.平面中的力矩与力偶矩有什么异同？习题1.画出下列物体的受力图。
未画重力的物体的重量均不计，所有接触处都为光滑接触。
题1 图2.画下列各指定物体受力图。
未画重力的物体重量均不计，所有接触处的摩擦均不计。
题2图3.图示一排水孔闸门的计算简图。
闸门重为FG，作用于其它重心C。
F为闸门所受的总水压力，FT为启门力。
试画出：（1）FT不够大，未能启动闸门时，闸门的受力图。
题3图（2）力FT刚好将闸门启动时，闸门的受力图。
4.一重为FG1的起重机停放在两跨梁上，被起重物体重为FG2。
试分别画出起重机、梁AC和CD的受力图。
梁的自重不计。
题4图5.计算下列图中力F对O点之矩。
题5图6.挡土墙如图所示，已知单位长墙重FG=95KN。
墙背土压力F=66.7KN。
试计算各力对前趾点A的力矩，并判断墙是否会倾倒。
图中尺寸以米计。
题6图平面力系思考题1.一个平面力系是否总可用一个力来平衡？是否总可用适当的两个力来平衡？为什么？2.图示分别作用一平面上A、B、C、D四点的四个力F1、F2、F3、F4，这四个画出的力多边形刚好首尾相接。
问：（1）此力系是否平衡？（2）此力系简化的结果是什么？思1图思2图3.如图所示，如选取的坐标系的y轴不与各力平行，则平面平行力系的平衡方程是否可写出∑Fx＝0，∑Fy＝0和∑m0＝0三个独立的平衡方程？为什么？4.重物FG置于水平面上，受力如图，是拉还是推省力？若，摩擦系数为0.25，试求在物体将要滑动的临界状态下，F1与F2的大小相差多少？思3图思4图习题1.已知F1＝100N，F2＝150N，F3＝F4＝200N，各力的方向如图所示。
(完整版)工程力学课后习题答案
工程力学练习册学校 ______________学院 _______________专业 ______________学号 _______________教师 _______________姓名 ______________第一章静力学基础1-1画出下列各图中物体A,构件AB, BC或ABC的受力图，未标重力的物体的重量不计，所有接触处均为光滑接触。
1-3画出图中指定物体的受力图。
所有摩擦均不计，各物自重除图中已画出的外均不计。
(1 J AB杆(2)CTJff(3)整体(1 ) K段槊(2) CD段梁r 3)鹫佐t 1)滑轮日⑵ABff(3) DF 样C I 】CDW⑵曲杵⑶CA杵(e)t 1，直(并tlikkiv t n OA IT(g)第二章平面力系2-1电动机重P=5000N,放在水平梁AC的中央，如图所示。
梁的A端以皎链固定，另一端以撑杆BC支持，撑杆与水平梁的夹角为30 °。
如忽略撑杆与梁的重量，求绞支座A、B处的约束反力。
F x0, F B CO S30F A COS300F y0, F A sin30F B sin30P解得：F A F B P5000N2-2 物体重P=20kN，用绳子挂在支架的滑轮B上，绳子的另一端接在绞车D上，如图所示。
转动绞车，物体便能升起。
设滑轮的大小及轴承的摩擦略去不计，杆重不计，A 、B 、C 三处均为皎链连接。
当物体处于平衡状态时，求拉杆 AB 和支杆BC 所受的力。
2-3如图所示，输电线 ACB 架在两电线杆之间，形成一下垂线，下垂距离 CD=f=1m, 两电线杆间距离 AB=40m 。
电线ACB 段重P=400N,可近视认为沿 AB 直线均匀分布，求电 线的中点和两端的拉力。
F x0, F AB F BC F y0, F BC sin 30 解得：F BC 3.732P F AB 2.732Pcos30 Psin30 0 Pcos30 P 0F x 0,F A COS F C,F y 0, F A Sin F Gtan 1/10解得：F A 201NF C 2000 N2-4 图示为一拔桩装置。
工程力学试题
六、问答题（12分，共4题，每小题3分）
1.分离体与受力图有什么不同？
2.力矩与力偶矩有什么异同？
3.画受力图时需注意些什么问题？
4.作受力图时，是否可以根据主动力即把约束反力的方向单凭直观确定出来？如图a所示，由于主动力F铅垂向下，即可判断出A与B点处的约束力的方向皆铅垂向上，对不对？
A.图b
B.图c
C.图a
D.图b和图c
E.都平衡
F.以上都不正确
二、判断题（20分，共10题，每小题2分）
1.作用在一个刚体上的任意两个力成平衡的必要与充分条件是：两个力的作用线相同，大小相等，方向相反( )。
2.只要平面力偶的力偶矩保持不变，可将力偶的力和臂作相应的改变，而不影响其对刚体的效应。（）
14.扭转是轴的主要变形形式，轴上的扭矩可以用截面法来求得，扭矩的符号规定为：__________________________________________________________________________
15．力学将两分为两大类：静定梁和超静定梁。根据约束情况的不同静定梁可分为：__________、_________、_________三种常见形式。
D.没有二力杆
7.如题图所示，起吊机器时，通常采用两个吊环螺栓，称α为起吊角，若α角有三种情况供你选择，合理的选择是（）。
A.α＝90°
B.α>90°
C.α<90°
8.如图所示的四种支架都由杆AB和BC构成，A、B、C三点都是铰接，在A点悬挂重量为G的重物，若不计杆的自重，杆AB受力最小的是（）。
工程力学练习题和答案
工程力学试题（一）一、填空题（每题5分，共25分）1、图示结构受力矩为M=10 KN.m的力偶作用。
若a=1m ,各杆的自重不计。
则固定铰支座D的反力的大小为＿＿＿方向为＿＿＿。
2、空间一般力系有＿＿＿个独立的平衡方程；平面平行力系有＿＿＿个独立的平衡方程。
3、杆件的基本变形一般有＿＿＿＿、＿＿＿＿、＿＿＿＿、＿＿＿＿等四种。
而应变只有＿＿＿＿和＿＿＿＿两种。
4、用积分法求图示梁的挠曲线时，挠曲线方程要分为________段。
确定积分常数使用的边界条件是_______________；使用的连续条件是_______________。
5、两端铰支的细长压杆，长为l，直径为d，其柔度=＿＿＿＿。
二、计算题（本题15分）图示结构由丁字型梁ABC、直梁CE与支持DH组成，C、D电为铰接，均不计自重。
已知：q=200kN·m，L=2m。
试求固定端A处的反力。
三、计算题（本题15分）作图示梁的剪力图和弯矩图。
四、计算题（本题15分）图示铸铁制外伸梁，截面为T形，受力如图，截面对形心轴Z的轴惯矩Iz=7.63*10^(-6)m^4。
已知材料的许用拉应力[σ+]=30 MPa，许用压应力[σ-]=100MPa，试校核梁的正应力强度。
五、计算题（本题15分）试校核电机轴的强度。
已知：六、计算题（本题15分）图示滑套B可沿OC杆滑动，与B铰接的滑块可在水平滑道内运动，L=30cm。
设在图示φ=30°位置时，ω=0.2 rad/s。
试用合成运动的方法求滑块的速度。
工程力学试题二一、判断题（本大题共5小题，每小题2分，共10分）请在每小题后面的括号中正确的请填√，错误的填×1、凡在两个力作用下的构件称为二力构件。
（）2、杆件的轴力仅与杆件所受的外力有关，而与杆件的截面形状、材料无关。
（）3、纯弯曲梁横截面上任一点，既有正应力也有剪应力。
（）4、压杆通常在强度破坏之前便丧失稳定。
（）5、长为3m 的圆轴在扭矩作用下产生变形为50，则其不满足2 0/m的刚度要求。
工程力学(一)习题集及部分解答指导
工程力学学习参考资料第一章静力学基础一、判断题1-1．如物体相对于地面保持静止或匀速运动状态,则物体处于平衡。
（）1-2．作用在同一刚体上的两个力,使物体处于平衡的必要和充分条件是：这两个力大小相等、方向相反、沿同一条直线。
( ) 1-3．静力学公理中,二力平衡公理和加减平衡力系公理仅适用于刚体。
( ) 1-4．二力构件是指两端用铰链连接并且指受两个力作用的构件。
( ) 1-5．对刚体而言，力是滑移矢量，可沿其作用线移动。
（）1-6．对非自由体的约束反力的方向总是与约束所能阻止的物体的运动趋势的方向相反。
（）1-7．作用在同一刚体的五个力构成的力多边形自行封闭，则此刚体一定处于平衡状态。
（）1-8．只要两个力偶的力偶矩相等，则此两力偶就是等效力偶。
（）二、单项选择题1-1．刚体受三力作用而处于平衡状态,则此三力的作用线( )。
A、必汇交于一点B、必互相平行C、必都为零D、必位于同一平面内1-2．力的可传性（）。
A、适用于同一刚体B、适用于刚体和变形体C、适用于刚体系统D、既适用于单个刚体，又适用于刚体系统1-3．如果力F R是F1、F2二力的合力,且F1、F2不同向，用矢量方程表示为F R= F1+ F2，则三力大小之间的关系为()。
A、必有F R= F1+ F2B、不可能有F R= F1+ F2C、必有F R＞F1, F R＞F2D、必有F R＜F1, F R＜F21-4．作用在刚体上的一个力偶，若使其在作用面内转移，其结果是（）。
A、使刚体转动B、使刚体平移C、不改变对刚体的作用效果D、将改变力偶矩的大小三、计算题1-1．已知：F1=2000N，F2=150N，F3=200N，F4=100N，各力的方向如图1-1所示。
试求各力在x、y轴上的投影。
解题提示F x= + F cosαF y= + F sinα注意：力的投影为代数量；式中：F x、F y的“+”的选取由力F的指向来确定；α为力F与x轴所夹的锐角。
工程力学习题第一部分附答案
及 j′ 与 e1 (或 i )垂直。定义 j 为 j′ 的归一化矢量：
j = j′ = e2 − e1 cosθ ，(注意图中的几何关系)
j′
sinθ
-4-
第 2 章 刚体静力学基本概念
于是得到力 F 在两正交方向上的投影：
Fi = F ⋅ i = F ⋅ e1 = F1
Fj
=
F
⋅
j
=
F
⋅ e2
mx (F2 ) = −12N ⋅ cm ， my (F2 ) = 24N ⋅ cm ， mz (F2 ) = 32N ⋅ cm
2-7 轴 AB 在 Ayz 平面内，与铅锤的 Az 轴成α 角。悬臂 CD 垂直地固定在 AB 轴上，与 Ayz 平面成θ 角，如图所示。如 在 D 点作用铅直向下的力 FP 。并设 CD = a ， AC = h ， 试求力 FP 对 A 点之矩及对 AB 轴之矩。 解：由于力 FP 平行于 z 轴，所以，
力 F 对坐标原点 O 之矩
-1-
工程力学习题解答
i
jk
mO (F ) = − 3 − 4 − 6 = 3(15 j −10k) − 3 23 33
根据力系关系定理，力 F 对 OE 轴之矩
mOE (F ) = mO (F ) ⋅ e =
3(15 j −10k) ⋅ 3 (i + j + k) = 15 −10 = 5 3
由题意知， F ⋅ e1 = F1 ， F ⋅ e2 = F2 。
若令 e1 = i ，则问题的关键在于寻求与 i 垂直的单位矢量 j 。
定义矢量 j′ ： j′ = e2 − (e2 ⋅ e1)e1 = e2 − cosθe1 ，即图中的黑色矢量。显然有：
工程力学练习册习题答案
工程力学练习册学校学院专业学号教师姓名第一章静力学基础1-1 画出下列各图中物体A，构件AB，BC或ABC的受力图，未标重力的物体的重量不计，所有接触处均为光滑接触。
（a）（b ）（c ）1 / 85（d）（e）（f）（g）1-2 试画出图示各题中AC杆（带销钉）和BC杆的受力图85（a）（b）（c）（a）1-3 画出图中指定物体的受力图。
所有摩擦均不计，各物自重除图中已画出的外均不计。
（a）3 /（b）（c）（d）5 /85（e）（f）7 /85（g ）第二章 平面力系2-1 电动机重P=5000N ，放在水平梁AC 的中央，如图所示。
梁的A 端以铰链固定，另一端以撑杆BC 支持，撑杆及水平梁的夹角为30 0。
如忽略撑杆及梁的重量，求绞支座A 、B 处的约束反力。
题2-1图∑∑=︒+︒==︒-︒=PF F FF F F B A yA B x 30sin 30sin ,0030cos 30cos ,0解得:N P F F B A 5000===2-2 物体重P=20kN ，用绳子挂在支架的滑轮B 上，绳子的另一端接在绞车D 上，如图所示。
转动绞车，物体便能升起。
设滑轮的大小及轴承的摩擦略去不计，杆重不计，A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时，求拉杆AB 和支杆BC 所受的力。
9 /85题2-2图∑∑=-︒-︒-==︒-︒--=030cos 30sin ,0030sin 30cos ,0P P F FP F F F BC yBC AB x解得:PF P F BC AB 732.2732.3=-=2-3 如图所示，输电线ACB 架在两电线杆之间，形成一下垂线，下垂距离CD =f =1m ，两电线杆间距离AB =40m 。
电线ACB 段重P=400N ，可近视认为沿AB 直线均匀分布，求电线的中点和两端的拉力。
题2-3图以AC 段电线为研究对象，三力汇交NF N F F F FF F F C A GA yC A x 200020110/1tan sin ,0,cos ,0=======∑∑解得：ααα2-4图示为一拔桩装置。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第六章杆类构件的内力分析习题6.1试求图示结构1-1和2-2截面上的内力，指出AB 和CD 两杆的变形属于哪类基本变形，并说明依据。
（a ）（b ）题6.1图解：（a ）应用截面法：对题的图取截面2-2以下部分为研究对象，受力图如图一所示：B图一 图二 由平衡条件得：0,AM=∑6320N F ⨯-⨯=解得： N F =9KN CD 杆的变形属于拉伸变形。
应用截面法，取题所示截面1-1以右及2-2以下部分作为研究对象，其受力图如图二所示，由平衡条件有：0,OM=∑6210N F M ⨯-⨯-=（1）0,yF=∑60N S F F --=（2）将N F =9KN 代入（1）-（2）式，得：M =3 kN·m S F =3 KNAB 杆属于弯曲变形。
（b ）应用截面法 ，取1-1以上部分作为研究对象，受力图如图三所示，由平衡条件有：0,Fx =∑20NF-=图三F NMN F =2KN0,DM=∑210M -⨯=M =2KNAB 杆属于弯曲变形6.2求图示结构中拉杆AB 的轴力。
设由AB 连接的1和2两部分均为刚体。
题6.2图解：首先根据刚体系的平衡条件，求出AB 杆的内力。
刚体1的受力图如图一所示D图一图二平衡条件为：0,CM=∑104840D NF F⨯-⨯-⨯=（1）刚体2受力图如图二所示，平衡条件为：0,EM=∑240N DF F⨯-⨯=（2）解以上两式有AB杆内的轴力为：NF=5KN6.3试求图示各杆件1-1、2-2和3-3截面上的轴力，并做轴力图。
（a）（b）（c）（d）题6.3图解：（a）如图所示，解除约束，代之以约束反力，做受力图，如图1a所示。
利用静力平衡条件，确定约束反力的大小和方向，并标示在图1a中，作杆左端面的外法线n，将受力图中各力标以正负号，轴力图是平行于杆轴线的直线，轴力图线在有轴向力作用处要发生突变，突变量等于该处总用力的数值，对于正的外力，轴力图向上突变，对于负的外力，轴力图向下突变，轴力图如2a所示，截面1和截面2上的轴力分别为1NF=-2KN2NF=-8KN，（a ）nkN(a 1)(2)C（b ）CB4kNb 1）（b 2）（（b ）解题步骤和（a ）相同，杆的受力图和轴力图如（1b ）（2b ）所示，截面1和截面2上的轴力分别为1N F =4KN 2N F =6KN（c ）解题步骤和（a ）相同，杆的受力图和轴力图如（1c ）（2c ）所示，截面1，截面2和截面3上的轴力分别为1N F =3F 2N F=4F ，3N F =4FB CD（c ）4F（c 1）（c 2）（d）A D（d 1）（d 2）（d ）解题步骤和（a ）相同，杆的受力图和轴力图如（1d ）（2d ）所示，截面1和截面2上的轴力分别为1N F =2KN 2N F =2KN6.4求图示各轴1-1、2-2截面上的扭矩，并做各轴的扭矩图。
m (a)(b)题6.4图解（a ）如图所示，分别沿1-1，2-2截面将杆截开，受力图如1a 所示，用右手螺旋法则，并用平衡条件可分别求得：1T =16 kN·m 2T =-20 kN·m ，根据杆各段扭矩值做出扭矩图如2a 所示。
20kN m20kN mkN 20kN ·m(2)3kN (b)mm·m（b ）用和（a ）相同的办法求，如图1b 所示，用平衡条件可分别求得：1T =-3kN·m 2T =2 kN·m 根据杆各段扭矩值自左向右做出扭矩图如2b 所示6.5图示等截面圆轴上安装有4个皮带轮，其中D 轮为主动轮，由此输入功率100kW 。
轴的转速为300r/min n 。
轮A 、B 及C 均为从动轮，其输出功率分别为25kW 、35kW 、40kW 。
试讨论：1）图示截面1-1、2-2处的扭矩大小，作出该轴的扭矩图；2）试问各轮间的这种位置关系是否合理，若各轮位置可调，应当怎样布置？（提示：应当使得轴内最大扭矩最小）BCAD题6.5图解：（1）各轮的外力偶矩分别为：259550795.83300A M N m N m == 3595501114.17300B M N m N m ==4095501273.33300C M N m N m ==10095503183.33300D M N m N m ==3183.33N·m(a)(b)根据右手螺旋法则，并以左端面的外法线n 的正向为标准，凡是与n 的正向一致的标以正号， 反之标以负号，以图（a ）所示，自左向右画扭矩图，如图（b ）所示（2）不合理，由上面扭矩图可看出，在CD 段时，杆件的扭矩达到最大值，在这种扭矩作用下，构件很容易被破坏，若用强度较大的杆件，则AB 与BC 的扭力又远小于CD 段的扭力，故工程上一般将C轮与D 轮互换，得轴内最大扭矩最小，也就是说，一般主动轮处于各轮的中间位置，以降低其扭矩。
6.6试求图示各梁中指定控制面上的剪力、弯矩值。
（a ）（b ）M e（c ）（d ）22（e ）（f ）F题6.6图解：（a ）如图所示 解法一 截面法（a 1）F C22（a 2）欲求1-1截面的内力，可沿1-1截面将梁截开，取右部分为研究对象，受力图如1a 所示，截面上的内力按剪力和弯矩正负符号的规定设为正的，利用平衡条件有：0,yF=∑10S F F -=1S F F =10M =求2-2截面的内力时，可沿2-2截面 将梁展开，求右部分为研究对象，受力图如2a 所示，由于杆上无任何受力 情况，因此截面2-2的受力情况为：20S F =20M =解法二：外力简化法梁任意截面上的剪力和弯矩都是梁的内力，根据平衡条件，它们应分别与该截面以左（或以右）梁上所有外力向截面形心简化后的主矢和主矩大小相等，方向相反。
因此任意截面上的剪力等于该截面以左（或以右）梁上所有外力的代数和，使截面形心又顺时针转动趋势的外力取正值，反之取负值。
梁任意截面上的弯矩等于该截面以左（或以右）梁上所有外力对该截面形心之矩的代数和，使梁弯曲后曲率为正之矩取正值，反之取负值。
所以截面1-1的内力 1S F F =10M = 截面2-2的内力 20S F =20M =（b ）解法同（a ）一样，先解除支座约束，代之以约束反力，作受力图，利用静力学平衡条件得2e A M F a =2e B MF a=- 截面1-1的内力 12e S M F a =12e MM = 截面2-2的内力 22e S M F a =22e MM =-截面3-3的内力 32e S M F a =32e MM =-M e（c ） 解题思路如（a ）一样解除支座约束，代之以约束反力，利用静力学平衡条件得4A aq F =34C aq F =截面1-1的内力 14S aq F =214a q M = 截面2-2的内力 24S aq F =224a q M = （d ）解题思路如（a ）一样解除支座约束，代之以约束反力，利用静力学平衡条件得232A aq F =2B aqF = 截面1-1的内力 12S aqF =21M a q =- 截面2-2的内力 2S F aq =22M a q =- 截面3-3的内力 30S F =30M =（e ）解题思路如（a ）一样解除支座约束，代之以约束反力，利用静力学平衡条件得22A F aq =212A M a q =-截面1-1的内力 12S F aq =2112M a q =-截面2-2的内力 22S F aq =2232M a q =-（f ）解题思路如（a ）一样解除支座约束，代之以约束反力，利用静力学平衡条件得C FA F F =-2B F F =截面1-1的内力 1S F F =1M a F =- 截面2-2的内力 2S F F =-2M a F =6.7试写出图示各梁的剪力方程和弯矩方程，并作出剪力图和弯矩图。
（a ）（b ）（c）（d ）（e ）（f ）q2（g ）（h ）（i ）（j ）题6.7图解：（a ）列剪力方程和弯矩方程。
应用前一题提供的列剪力和弯矩方程的方法。
A F F =0A M =AB 段： ()S F x F = （0＜x ＜a ）()M x Fx = (0＜x ＜a )BC 段： ()0S F x= （a ≤x ≤2a ）()M x Fa = （a ≤x ＜2a ）作剪力图于弯矩图如图1a 所示（1（(b 1)A M（b ）列剪力和弯矩方程2A F aq =252A a qM =- AB 段： ()2S F x a q qx =-（0＜x ＜a ）()225222x qM x aqx a q =-- (0＜x ＜a )BC 段： ()S F x a q= （a ≤x ≤2a ） ()22M x aqx a q =- （a ≤x ＜2a ）作剪力图于弯矩图如图1b 所示（c ）列剪力和弯矩方程A F F =0C F =AB 段： ()S F x F = （0≤x ＜a ）()M x Fx = （0≤x ＜a ）BC 段： ()0S F x = （a ＜x ＜2a ）()0M x = （a ＜x ＜2a ）作剪力图于弯矩图如图1c 所示（c 1）（）ed 1(d) 列剪力和弯矩方程e A M F a =e C MF a=- AB 段： ()eS M F x a=（0＜x ＜a ） ()ee M M x x M a=- （0＜x ＜a ）BC 段： ()eS M F x a=（a ≤x ＜2a ） ()2ee M M x x M a=- （a ＜x ≤2a ） 作剪力图于弯矩图如图1d 所示(e) 列剪力和弯矩方程34A aq F =4C aqF = AB 段： ()34S F x a q q x =- （0＜x ≤a ）()23142M x aqx x q =- （0≤x ≤a ） BC 段： ()14S F x a q =- （a ≤x ＜2a ） ()21124M x a q aqx =- （a ≤x ≤2a ）作剪力图于弯矩图如图1e 所示1q（f 1）O2(f) 列剪力和弯矩方程2A aq F =12B F aq = AB 段： ()12S F x a q =（0＜x ≤a ） ()12M x aqx aq =- （0＜x ≤a ）BC 段： ()2S F x aq qx =- （a ≤x ＜2a ）()221222M x aqx a q x q =--（a ≤x ＜2a ） 作剪力图于弯矩图如图1f 所示 (g) 列剪力和弯矩方程23A F P F -=23D F PF -= AB 段： ()23S F PF x -= （0＜x ≤a ）()23F PM x x -= （0＜x ≤a ）BC 段： ()3S F PF x --= （a ≤x ＜2a ）()3F PM x Fa x +=- （a ≤x ＜2a ）CD 段： ()23S F PF x -+= （2a ≤x ＜3a ）()223P FM x Fa x aq -=+- （2a ≤x ＜3a ）作剪力图于弯矩图如图1g 所示1-F-P 3（）O1O(h) 列剪力和弯矩方程2A aq F =-2C aqF = AB 段： ()2S aqF x xq =- （0＜x ＜a ）()222x q aqM x x =- （0≤x ≤a ）BC 段： ()32S aqF x xq =- （a ＜x ＜2a ） ()22322aq x qM x x a q =-- （a ≤x ≤2a ）作剪力图于弯矩图如图1h 所示 (i) 列剪力和弯矩方程20B F KN =20C F KN =AB 段： ()5S F x x =- （0≤x ＜2m ）()252x M x =- （0≤x ≤2m ）BC 段： ()10S F x = （2m ＜x ＜3m ）()1030M x x =- （2m ≤x ≤3m ）CD 段： ()10S F x =- （3m ＜x ＜4m ）()1030M x x =-+ （3m ≤x ≤4m ）DE 段： ()105S F x x =- （4m ＜x ≤6m ）()2590302M x x x =-+-（4m ≤x ≤6m ） 作剪力图于弯矩图如图1i 所示E（）1（j ）列剪力和弯矩方程A F F =D F F =AB 段： ()S F x F = （0＜x ＜a ）()M x Fx = （0≤x ≤a ）BC 段： ()0S F x = （a ＜x ＜2a ）()M x Fa = （a ≤x ≤2a ）CD 段： ()S F x F =- （2a ＜x ＜3a ）()3M x Fa Fx =- （2a ≤x ≤3a ）作剪力图于弯矩图如图1j 所示6.8设梁的剪力图如图所示，试作弯矩图及载荷图。