数字图像处理(冈萨雷斯)-4 频域平滑及锐化滤波
数字图像处理- 图像平滑与锐化

数字图像处理
7
数字图像处理
8
巴特沃斯滤波器
通带波动下的切比雪夫滤波器
阻带波动下的切比雪夫滤波器
数字图像处理
椭圆函数滤波器
9
数字图像处理
10
数字图像处理
11
数字图像处理
12
数字图像处理
13
涉及4种图像初始、中间或最终结果,和三个主要 处理步骤。
图像结果包括原始图像、原始变换域、滤波后的变换域 和滤波后的图像; 处理步骤包括傅里叶正变换、低通滤波和傅lt; complex > CImageProcessing::Low_pass_filter( CTArray< complex > original_signal ) { long dimension = original_signal.GetDimension(); double threshold = 0; for( int index = 0; index < dimension; index ++ ) { double magnitude = sqrt( original_signal[ index ].m_re * original_signal[ index ].m_re + original_signal[ index ].m_im * original_signal[ index ].m_im ); if( magnitude > threshold ) threshold = magnitude; } threshold /= 100; for( int index = 0; index < dimension; index ++ ) { double magnitude = sqrt( original_signal[ index ].m_re * original_signal[ index ].m_re + original_signal[ index ].m_im * original_signal[ index ].m_im ); double eplon = 1.0 / sqrt( 1 + ( threshold / magnitude ) * ( threshold / magnitude ) ); original_signal[ index ].m_re *= eplon; original_signal[ index ].m_im *= eplon; } return original_signal; } 21 数字图像处理
数字图像处理(冈萨雷斯)

均匀噪声
高斯噪声
瑞利噪声
噪声
指数噪声
椒盐噪声
第14页,共62页。
①高斯噪声
高斯噪声的概率密度函数(PDF)
p(z) 1 e(z )2 /2 2 (5.2 1)
2
灰度值
✓ 当z服从上式分布时,其值有70%落在 , , 有 95%落在
范围内。 2 , 2
✓ 高斯噪声的产生源于电子电路噪声和由低照明度或高温带来的 传感器噪声。
其中zi值是像素的灰度值, p(zi )表示相应的归一化直方图.
第30页,共62页。
5.3 空间域滤波复原(唯一退化是噪声)
当唯一退化是噪声时,则退化系统H(u,v) 1
g( x, y) f ( x, y) ( x, y) (5.3 1)
G(u, v) F (u, v) N (u, v) (5.3 2)
的开关操作)
第22页,共62页。
例5.1 样本噪声图像和它们的直方图
✓ 用于说明噪声模型的测试图
✓ 由简单、恒定的区域组成 ✓ 仅仅有3个灰度级的变化
第23页,共62页。
例5.1 样本噪声图像和它们的直方图
高斯噪声
瑞利噪声
伽马噪声
图像
直方图
第24页,共62页。
例5.1 样本噪声图像和它们的直方图
➢在图像获取中从电 力或机电干扰中产生.
➢是空间相关噪声.
➢周期噪声可以通过 频率域滤波显著减少.
周期噪声
被不同频率的 正弦噪声干扰 了的图像
呈圆形分布 的亮点为噪 声频谱
第27页,共62页。
典型的周期噪声---正弦噪声
• Sinusoidal (单 一频率)
数字图像处理-冈萨雷斯-课件(英文)Chapter04 频域图像增强

F (u ) R(u ) I (u )
2
2
Example of 1-D Fourier Transforms
Notice that the longer the time domain signal, The shorter its Fourier transform
(Images from Rafael C. Gonzalez and Richard E. Wood, Digital Image Processing, 2nd Edition.
g(x,y) -M
0
For an image of size NxM pixels, its 2-D DFT repeats itself every N points in xdirection and every M points in y-direction.
M
2M
-N 0 N 2N
We display only in this range
2-D FFT Shift is a MATLAB function: Shift the zero frequency of F(u,v) to the center of an image.
2D FFTSHIFT
(Images from Rafael C. Gonzalez and Richard E. Wood, Digital Image Processing, 2nd Edition.
2-D DFT Properties
(Images from Rafael C. Gonzalez and Richard E. Wood, Digital Image Processing, 2nd Edition.
数字图像处理(冈萨雷斯)-4 频域平滑及锐化滤波PPT文档共40页

31、只有永远躺在泥坑里的人,才不会再掉进坑里。——黑格尔 32、希望的灯一旦熄灭,生活刹那间变成了一片黑暗。——普列姆昌德 33、希望是人生的乳母。——科策布 34、形成天才的决定因素应该是勤奋。——郭沫若 35、学到很多东西的诀窍,就是一下子不要学很多。——洛克
数字图像处理(冈萨雷斯)-4 频域平滑 及锐化滤波
36、“不可能”这个字(法语是一个字 ),只 在愚人 的字典 中找得 到。--拿 破仑。 37、不要生气要争气,不要看破要突 破,不 要嫉妒 要欣赏 ,不要 托延要 积极, 不要心 动要行 动。 38、勤奋,机会,乐观是成功的三要 素。(注 意:传 统观念 认为勤 奋和机 会是成 功的要 素,但 是经过 统计学 和成功 人士的 分析得 出,乐 观是成 功的第 三要素 。
数字图像处理实验指导书matlab冈萨雷斯

《数字图像处理》实验指导书实验一、空域图像处理一、 实验目的1熟悉CCS 集成开发环境的操作和基本功能;2熟悉MATLAB 基本图像操作;3结合实例学习如何在程序中增加图像处理算法;4理解和掌握图像的线性变换和直方图均衡化的原理和应用;5了解平滑处理的算法和用途,学习使用均值滤波、中值滤波和拉普拉斯锐化进行图像增强处理的程序设计方法;6 了解噪声模型及对图像添加噪声的基本方法。
二、 实验原理1 灰度线性变换就是将图像中所有点的灰度按照线性灰度变换函数进行变换。
)],([),(y x f T y x g =⎪⎩⎪⎨⎧<≤+-<≤+-≤≤=255),(]),([),( ]),([),(0 ),(),(y x f b g b y x f b y x f a g a y x f a y x f y x f y x g b a γβαn y m x ,2,1 ,,,2,1==2 直方图均衡化通过点运算将输入图像转换为在每一级上都有相等像素点数的输出图像。
按照图像概率密度函数PDF 的定义:1,...,2,1,0 )(-==L k n n r p k k r 通过转换公式获得:1,...,2,1,0 )()(00-====∑∑==L k n n r p r T s k j k j j j r k k3 均值(中值)滤波是指在图像上,对待处理的像素给定一个模板,该模板包括了其周围的临近像素。
将模板中的全体像素的均值(中值)来代替原来像素值的方法。
4 拉普拉斯算子如下:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--------111181111 拉普拉斯算子首先将自身与周围的8个像素相减,表示自身与周围像素的差异,再将这个差异加上自身作为新像素的灰度。
三、实验步骤1 启动MA TLAB程序,对图像文件分别进行灰度线性变换、直方图均衡化、均值滤波、中值滤波和拉普拉斯锐化操作;添加噪声,重复上述过程观察处理结果。
2 记录和整理实验报告四、实验仪器1计算机;2 MA TLAB程序;3记录用的笔、纸。
数字图像处理(岗萨雷斯 第三版)课后习题答案

第3章3.6原题:试解释为什么离散直方图均衡技术一般不能得到平坦的直方图?答:假设有一副图像,共有像素个数为n=MN(M行N列),像素灰度值取值范围为(0~255),那么该图像的灰度值的个数为L=256,为了提高图像的对比度,通常我们都希望像素的灰度值不要都局促到某一个狭窄的范围,也就是我们通常说的图像灰度值的动态分布小。
最好是在有效灰度值取值范围上,每个灰度值都有MN/L个像素,这个时候我们就可以得到一张对比度最理想的图像,也就是说像素的取值跨度大,像素灰度值的动态范围大。
因为直方图是PDF(概率密度函数)的近似,而且在处理中,不允许造成新的灰度级,所以在实际的直方图均衡应用中,很少见到完美平坦的直方图。
因此,直方图均衡技术不能保证直方图的均匀分布,但是却可以扩展直方图的分布范围,也就意味着在直方图上,偏向左的暗区和偏向右的亮区都有像素分布,只是不能保证每个灰度级上都有像素分布。
(百度答案:)由于离散图像的直方图也是离散的,其灰度累积分布函数是一个不减的阶梯函数。
如果映射后的图像仍然能取到所有灰度级,则不发生任何变化。
如果映射的灰度级小于256,变换后的直方图会有某些灰度级空缺。
即调整后灰度级的概率基本不能取得相同的值,故产生的直方图不完全平坦。
3.8原题:在某些应用中,将输入图像的直方图模型化为高斯概率密度函数效果会是比较好的,高斯概率密度函数为:其中m和σ分别是高斯概率密度函数的均值和标准差。
具体处理方法是将m和σ看成是给定图像的平均灰度级和对比度。
对于直方图均衡,您所用的变换函数是什么?答:直方图均衡变换函数的一般表达式如下:在回答这个问题时,有两点非常重要,需要学生表达清楚。
第一,这个表达式假定灰度值r只有正值,然而,高斯密度函数通常的取值范围是-∞~∞,认识到这点是非常重要的,认识到这点,学生才能以多种不同的方式来解决问题。
对于像标准差这样的假设,好的答案是,需要足够小,以便于当r为小于0时,在p r(r)曲线下的面积可以被忽略。
数字图像处理-空间域处理-空间滤波-锐化空间滤波器
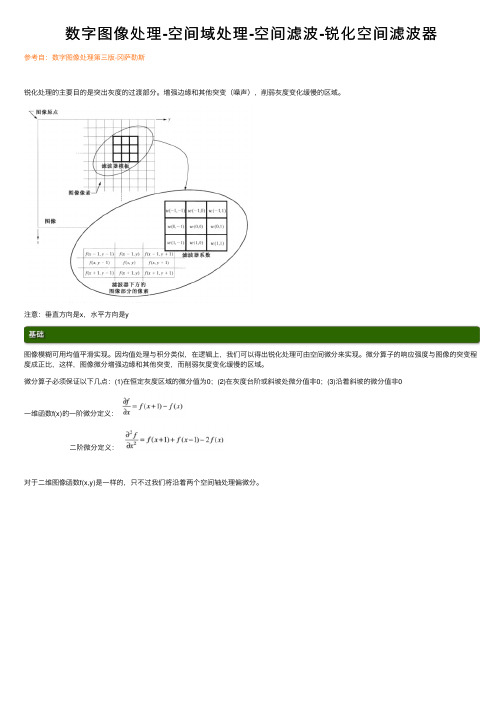
数字图像处理-空间域处理-空间滤波-锐化空间滤波器参考⾃:数字图像处理第三版-冈萨勒斯锐化处理的主要⽬的是突出灰度的过渡部分。
增强边缘和其他突变(噪声),削弱灰度变化缓慢的区域。
注意:垂直⽅向是x,⽔平⽅向是y基础图像模糊可⽤均值平滑实现。
因均值处理与积分类似,在逻辑上,我们可以得出锐化处理可由空间微分来实现。
微分算⼦的响应强度与图像的突变程度成正⽐,这样,图像微分增强边缘和其他突变,⽽削弱灰度变化缓慢的区域。
微分算⼦必须保证以下⼏点:(1)在恒定灰度区域的微分值为0;(2)在灰度台阶或斜坡处微分值⾮0;(3)沿着斜坡的微分值⾮0⼀维函数f(x)的⼀阶微分定义: ⼆阶微分定义:对于⼆维图像函数f(x,y)是⼀样的,只不过我们将沿着两个空间轴处理偏微分。
数字图像的边缘在灰度上常常类似于斜坡过渡,这样就导致图像的⼀阶微分产⽣较粗的边缘。
因为沿着斜坡的微分⾮0。
另⼀⽅⾯,⼆阶微分产⽣由0分开的⼀个像素宽的双边缘。
由此我们得出结论,⼆阶微分在增前细节⽅⾯⽐⼀阶微分好得多。
⼆阶微分-拉普拉斯算⼦我们要的是⼀个各向同性滤波器,这种滤波器的响应与滤波器作⽤的图像的突变⽅向⽆关。
也就是说,各向同性滤波器是旋转不变的,即将原图像旋转后进⾏滤波处理的结果和先对图像滤波然后再旋转的结果相同。
最简单的各向同性微分算⼦,即拉普拉斯算⼦⼀个⼆维图像函数f(x,y)的拉普拉斯算⼦定义为:任意阶微分都是线性操作,所以拉普拉斯变换也是⼀个线性算⼦。
于是:对应的滤波模板为下图a,这是⼀个旋转90°的各向同性模板,另外还有对⾓线⽅向45°的各向同性模板,还有其他两个常见的拉普拉斯模板。
a、b与c、d的区别是符号的差别,效果是等效的拉普拉斯是⼀种微分算⼦,因此它强调的是图像中灰度的突变。
将原图像和拉普拉斯图像叠加,可以复原背景特性并保持拉普拉斯锐化处理的效果。
如果模板的中⼼系数为负,那么必须将原图像减去拉普拉斯变换后的图像,从⽽得到锐化效果。
4平滑,锐化滤波-PPT资料51页

中的低频分量,但不 影响高频分量。
平滑滤波主要应用
平滑图像,减小噪声
去除噪声
•锐化滤波主要应用
增加反差,增强被模 糊的细节或边缘
分类1: (1) 平滑:模糊,消除噪声 (2) 锐化:增强被模糊的细节
分类2: (1) 线性:如邻域平均 (2) 非线性:如中值滤波
功能
特点
平滑(低通)
锐化(高通)
例子:使用3*3的模板对图像进行中值滤波
1 21 4 3 1 22 3 4 5 76 8 9 5 76 8 8 5 67 8 9
答案:
1 21 4 3 1 22 3 4 5 76 8 9 5 76 8 8 5 67 8 9
12143 1 22 23 34 4 5 75 66 86 9 5 76 67 88 8 56789
d2 f dx2
d(df ) / dx dx
d( f (x1) f (x))/dx
[ f (x1) f (x)][ f (x) f (x1)]
f (x1) f (x1)2f (x)
一、基于一阶微分的图像增强--梯度法(非线性)
•在图像处理中,一阶微分是通过梯度法来实现的。对 于函数f(x,y),其在(x,y)处的梯度是通过一个二维向量 来定义的:
4.5.2 线性平滑滤波器
2、加权平均
•用邻域内灰度值及本点灰度 加权值来代替该点灰度值
1 2 1
1 16
2
1
4 2
2
1
中心系数大 周围系数小
k4
k3
k2
1
k5
k0
k1
1
k6
k7
k8
1
R
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
的平滑效果
GLPF没有振铃
如果需要严格控制低频和高频之间截至频
率的过渡,选用BLPF,代价是可能产生振铃
4.8
频率域平滑滤波
4.8.4 低通滤波器的应用实例:模糊,平滑等
字符识别:通过模糊图像,桥接断裂字符的裂缝
印刷和出版业:从一幅尖锐的原始图像产生平滑、 柔和的外观,如人脸,减少皮肤细纹的锐化程度和 小斑点
第4章
频域图像增强
——图像的频域分析 频率域滤波
频率域平滑(低通)滤波器
频率域锐化(高通)滤波器
4.8 频率域平滑滤波
第4章 频率域滤波
• 图像的平滑除了在空间域中进行外,也可以在频率域中进
行。由于噪声主要集中在高频部分,为去除噪声改善图像 质量,滤波器采用低通滤波器 H 可达到平滑图像的目的
巴特沃思高通
高斯高通滤波器
高通滤波器的空间域表示:
理想高通滤波器 巴特沃思高通
4.9频率域锐化滤波器
高斯高通滤波器
Байду номын сангаас
4.9.1
理想高通滤波器(IHPF)
4.9频率域锐化滤波器
截断傅里叶变换中所有处于指定距离D0之内的低频成分
0 D( u, v ) D0 H IHPF ( u, v ) 1 D( u, v ) D0
4.9
频率域锐化滤波
4.9.5 钝化模板、高频提升滤波和高频加强滤波 为什么要进行高频提升和高频加强?
推导
H hp ( u, v ) 1 H lp ( u, v ) 1 D( u, v ) / D0 1 D( u, v ) / D0
2n
4.9.2 巴特沃思高通滤波器
二阶巴特沃思高通滤波示例:
D0=30 D0=60 D0=160
结论:BHPF的结果比IHPF的结果平滑得多
4.9
频率域锐化滤波
4.9.3
高斯(指数)高通滤波器
截频距原点为D0的高斯高通滤波器(GHPF)定义为
H GHPF (u, v) 1 e
2 D2 ( u ,v )/2 D0
(4.9 4)
高斯高通滤波示例:
D0=30 D0=60
4.9.3高斯高通滤波器
D0=160
结论:GHPF的结果比BHBF和IHPF的结果更平滑
圆环具有半径5,15,30,80和230个像素
图像功率为92.0%,94.6%,96.4%,98.0%和99.5%
4.8
频率域平滑滤波
理想低通滤波器举例4.16——具有振铃现象
原图
半径是5的理想低通滤波
滤除8%的总功率,模糊 说明多数尖锐细节在这 8%的功率之内
半径是15的理 想低通滤波 滤除5.4%的总功 率 半径是80的理 想低通滤波
半径是80的 BLPF滤波
半径是230的 BLPF滤波
所有的滤波器都有半径为5的 截至频率D0
4.8.2 巴特沃思低通滤波器 ILPF
巴特沃思低通滤波器
阶数n=2轻微 阶数n=5明显 无振铃和负值 振铃和负值 振铃和负值
阶数n=1
阶数n=20 与ILPF相似
注:二阶BLPF处于有效低通滤波和可接受的振铃特征之间
原图
半径是5的 GLPF滤波
采用该滤波器滤波在抑 制噪声的同时,图像边 缘的模糊程度较用 Butterworth滤波产生 的大些,无明显的振铃 效应
半径是15的 GLPF滤波
半径是30的 GLPF滤波
半径是80的 GLPF滤波
半径是230的 GLPF滤波
4.8
频率域平滑滤波
结论
GLPF不能达到有相同截止频率的二阶BLPF
处理卫星和航空图像:尽可能模糊细节,而保留大
的可识别特征。低通滤波通过消除不重要的特征来 简化感兴趣特征的分析
4.8
频率域平滑滤波
字符识别举例
如打印、传真、复印文本等, D0=80的高斯低通滤波器 字符失真、字符断裂等 修复字符
用于机器识别系统识别断裂字符的预处理
4.8
频率域平滑滤波
人脸图像处理
其中
100 u P(u, v ) / PT (4.8 4) v
4.3
频率域平滑滤波
理想低通滤波器举例
500×500的原图 图像的傅里叶频谱
结论:
①90%以上的功率 (能量)集中在半 径小于5的圆周内; ②随滤波器半径 的增加,越来越少 的功率被滤出掉, 使模糊减弱;
例4.19
1026 962
D0 962 5% 50
二值化的结果
4.9
频率域锐化滤波
三种高通滤波器小结
• 三种滤波函数的选用类似于低通。
• 理想高通有明显振铃现象,即图像的边缘有抖动现象;
• Butterworth高通滤波效果较好,但计算复杂,其优点是
H 有少量低频通过, (u, v ) 是渐变的,振铃现象不明显;
空间域拉普拉斯算子过滤后的图像可由计算 H (u, v )F (u, v ) 的反 傅里叶变换得到
2 f ( x, y) 1 4 2 (u P 2)2 (v Q 2)2 F (u, v) (4.9 7) 傅里叶变换对表示空间域拉普拉斯算子和频率域的双向关系
, D0 0 (4.9 2)
P Q 频率域的中心在 ( , ) 2 2
,从点(u,v)到中心(原点)
1 2
的距离如下
P 2 Q 2 D( u, v ) ( u ) (v ) 2 2
(4.8 2)
4.9.1理想高通滤波器
理想高通滤波示例:
D0=30 D0=60 D0=160
原图像
D0=100的GLPF滤波, D0=80的GLPF滤波,
细纹减少 细纹减少
4.8
频率域平滑滤波
卫星、航拍图像处理
原图像 D0=30的 GLPF滤波 D0=10的 GLPF滤波
目的:尽可能模糊细节,而保留大的可识别特征
4.9 频率域锐化
图像的边缘、细节主要位于高频部分,而图像的模糊是由于 高频成分比较弱产生的。频率域锐化就是为了消除模糊,突 出边缘。因此采用高通滤波器让高频成分通过,使低频成分 削弱,再经逆傅立叶变换得到边缘锐化的图像
当D(u,v)=D0时,H(u,v)=0.5(最大值是1,当D(u,v)=0) 它的特性是连续性衰减,而不象理想滤波器那样陡峭变化,
即明显的不连续性。因此采用该滤波器滤波在抑制噪声的
同时,图像边缘的模糊程度大大减小,没有振铃效应产生
4.8.2 巴特沃思低通滤波器 透视图 滤波器 阶数从1到4的滤波器横截面
频率域锐化滤波器主要有:
理想高通滤波器 巴特沃思高通滤波器 高斯高通滤波器 频率域的拉普拉斯算子
钝化模板、高频提升滤波和高频加强滤波
高通滤波器的频域表示:
透视图 图像表示 横截面
4.9频率域锐化滤波器
理想高通滤波器
巴特沃思滤波 器为理想滤波 器的尖锐化和 高斯滤波器 的完全光滑之 间的一种过渡
d 2 f ( x, y) d 2 f ( x, y) ( j 2u) n F ( u, v ) ( j 2v ) n F ( u, v ) 2 2 dy dx 4 2 ( u 2 v 2 )F ( u, v )
f ( x, y ) 4 (u v ) F (u, v)
4.8 频率域平滑滤波
理想低通滤波器 总图像功率值PT
P 1 Q 1 u 0 v 0
PT P ( u, v ) (4.8 3)
2
其中:
P (u, v ) F (u, v ) R2 (u, v ) I 2 (u, v )
原点在频率域的中心,半径为D0的圆包含%的功率
2
1
[1 4
2
D (u, v)]F (u, v) (4.9 9)
2
4.9
频率域锐化滤波
拉普拉斯锐化举例说明.例4.20
f ( x, y )
f ( x, y ) f ( x, y )
2
其中: 2 f ( x, y ) 1 H (u, v ) F (u, v ) (4.9 7)
理想低通滤波器:尖锐
巴特沃思低通滤波器:处于理想和高斯滤波器之间 高斯低通滤波器:平滑
4.8.1
高频成分
理想低通滤波器
4.8
频率域平滑滤波
截断傅里叶变换中的所有处于指定距离D0之外的
1 D( u, v ) D0 H ILPF ( u, v ) 0 D( u, v ) D0
• 指数高通效果比Butterworth差些,振铃现象不明显;
• 一般来说,不管在图像空间域还是频率域,采用高频滤
波不但会使有用的信息增强,同时也使噪声增强。因此
不能随意地使用
4.9
频率域锐化滤波
4.9.4 频率域的拉普拉斯算子
频率域的拉普拉斯算子定义:
d n f ( x) ( j 2 u)n F ( u) n dx
, D0 0 (4.8 1)
频率域的中心在 的距离如下
P Q ( , ) 2 2
,从点(u,v)到中心(原点)
P 2 Q 2 D( u, v ) ( u ) (v ) 2 2
1 2
(4.8 2)
4.8
频率域平滑滤波
理想低通滤波器
说明:在半径为D0的圆内,所有频率没有衰减地通过滤 波器,而在此半径的圆之外的所有频率完全被衰减掉
(u P 2)2 (v Q 2) 2 F (u, v) f ( x, y) 4
