九年级数学圆测试题及答案1
人教版九年级数学上册《24.1.1圆》同步测试题带答案
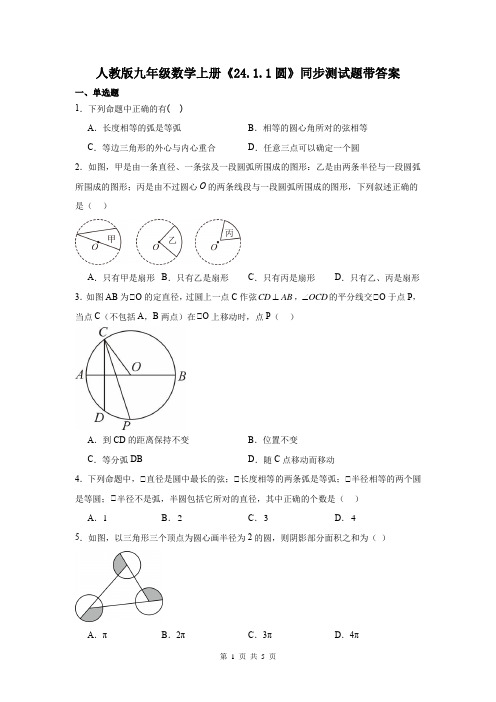
人教版九年级数学上册《24.1.1圆》同步测试题带答案一、单选题1.下列命题中正确的有( ) A .长度相等的弧是等弧 B .相等的圆心角所对的弦相等 C .等边三角形的外心与内心重合D .任意三点可以确定一个圆2.如图,甲是由一条直径、一条弦及一段圆弧所围成的图形:乙是由两条半径与一段圆弧所围成的图形;丙是由不过圆心O 的两条线段与一段圆弧所围成的图形,下列叙述正确的是( )A .只有甲是扇形B .只有乙是扇形C .只有丙是扇形D .只有乙、丙是扇形3.如图AB 为⊙O 的定直径,过圆上一点C 作弦CD AB ⊥,OCD ∠的平分线交⊙O 于点P ,当点C (不包括A ,B 两点)在⊙O 上移动时,点P ( )A .到CD 的距离保持不变B .位置不变C .等分弧DBD .随C 点移动而移动4.下列命题中,⊙直径是圆中最长的弦;⊙长度相等的两条弧是等弧;⊙半径相等的两个圆是等圆;⊙半径不是弧,半圆包括它所对的直径,其中正确的个数是( ) A .1B .2C .3D .45.如图,以三角形三个顶点为圆心画半径为2的圆,则阴影部分面积之和为( )A .πB .2πC .3πD .4π6.如图,在Rt ⊙ABC 中,⊙ACB =90°, AC =3,以点C 为圆心、CA 为半径的圆与AB 交于点D ,若点D 巧好为线段AB 的中点,则AB 的长度为( )A .32B .3C . 6D .9二、填空题7.到点O 的距离等于7cm 的点的集合是 .8.下图中,点O 是( ),线段OA 是圆的( ),线段BC 是圆的( ).9.已知,如图AB ,AD 是O 的弦 30B ∠=︒,点C 在弦AB 上,连结CO 并延长交O 于点D ,35D ∠=︒则BAD ∠的度数是 .10.如图,半径为r 的O 沿着边长为a 的正方形ABCD 的边作无滑动地滚动一周回到原来的位置,O 自身转动的圈数是 .(用含a r ,的代数式表示)11.下列说法:⊙直径是弦;⊙弦是直径;⊙大于半圆的弧是优弧;⊙长度相等的弧是等弧,其中正确的是 .12.顶点在圆外,并且两边都和圆相交的角叫做圆外角.圆外角的两边所夹的两条弧的度数与该角的度数之间的数量关系是:圆外角的度数等于 .三、解答题13.如图,O 的弦,AB CD 的延长线交于点P ,连接OP ,且OP 平分APC ∠.求证:PA PC =.14.如图,点O 是同心圆的圆心,大圆半径OA ,OB 分别交小圆于点C ,D ,求证:AB CD ∥.15.如图所示,AB 为O 的直径,CD 是O 的弦,AB CD ,的延长线交于点E ,已知220AB DE AEC =∠=︒,.求AOC ∠的度数.16.如图,O 的半径5cm OA =,AB 是弦,C 是AB 上一点,且OC OA ⊥,OC BC =求A ∠的度数.17.如图,破残的圆形轮片上,弦AB 的垂直平分线交弧AB 于C,交弦AB 于D .(1)求作此残片所在的圆的圆心(不写作法,保留作图痕迹); (2)若AB=8cm,CD=2cm,求(1)中所作圆的半径.18.如图,在O 中,AB 是直径,CD 是弦,延长AB ,CD 相交于点P ,且2AB DP = 18P ∠=︒ 求AOC ∠的度数.题号 1 2 3 4 5 6 答案CBBCD C7.以点O 为圆心,7cm 为半径的圆 8. 圆心 半径 直径 9.65︒ 10.21a r π+/21arπ+ 11.①③/③①12.两条弧度数差值的绝对值的一半 15.60AOC ∠=︒ 16.30︒17.(2) 圆的半径为5cm. 18.54。
人教版九年级数学上册第24章《圆》单元测试卷(含答案解析)

第24章《圆》单元测试卷一.选择题(共10小题)1.已知⊙O的半径为4,点O到直线m的距离为3,则直线m与⊙O公共点的个数为()A.0个B.1个C.2个D.3个2.如图,AB是⊙O的直径,AB⊥CD于E,AB=10,CD=8,则BE为()A.2B.3C.4D.3.53.正六边形内接于圆,它的边所对的圆周角是()A.60°B.120°C.60°或120°D.30°或150°4.⊙O的半径r=5cm,直线l到圆心O的距离d=4,则直线l与圆的位置关系()A.相离B.相切C.相交D.重合5.如图,AB是⊙O的直径,点C是⊙O上一点,点D在BA的延长线上,CD与⊙O交于另一点E,DE=OB=2,∠D=20°,则的长度为()A.πB.πC.πD.π6.如图,⊙O是△ABC 的外接圆,BC 是直径,D在圆上,连接AD、CD,若∠ADC=35°,则∠ACB=()A.70°B.55°C.40°D.45°7.如图,在△ABC中,AB=AC,∠ABC=45°,以AB为直径的⊙O交BC于点D,若BC=4,则图中阴影部分的面积为()A.π+1B.π+2C.2π+2D.4π+18.如图,△ABC是⊙O的内接三角形,∠C=30°,⊙O的半径为5,若点P是⊙O 上的一点,在△ABP中,PB=AB,则PA的长为()A.5B.C.5D.59.如图是某公园的一角,∠AOB=90°,弧AB的半径OA长是6m,C是OA的中点,点D在弧AB上,CD∥OB,则图中休闲区(阴影部分)的面积是()A.B.C.D.10.如图,AB是⊙O的直径,弦CD⊥AB,过点C作⊙O的切线与AB的延长线交于点P.若∠BCD=32°,则∠CPD的度数是()A.64°B.62°C.58°D.52°二.填空题(共8小题)11.如图,AB是⊙O的直径,点C、D在⊙O上,若∠ACD=25°,则∠BOD的度数为.12.如图,⊙O是△ABC的外接圆,BC为直径,BC=4,点E是△ABC的内心,连接AE并延长交⊙O于点D,则DE= .13.如图所示,点A在半径为20的圆O上,以OA为一条对角线作矩形OBAC,设直线BC交圆O于D、E两点,若OC=12,则线段CE、BD的长度差是.14.如图,半径为2的⊙O与含有30°角的直角三角板ABC的AC边切于点A,将直角三角板沿CA边所在的直线向左平移,当平移到AB与⊙O相切时,该直角三角板平移的距离为.15.如图,PA、PB切⊙O于A、B,点C在上,DE切⊙O于C,交PA、PB于D、E,已知PO=13cm,⊙O的半径为5cm,则△PDE的周长是.16.△ABC中,AB=CB,AC=10,S=60,E为AB上一动点,连结CE,过A作AF△ABC⊥CE于F,连结BF,则BF的最小值是.17.如图,等边三角形△ABC内接于半径为1的⊙O,则图中阴影部分的面积是.18.如图,已知线段AB=6,C为线段AB上的一个动点(不与A、B重合),将线段AC绕点A逆时针旋转120°得到AD,将线段BC绕点B顺时针旋转120°得到BE,⊙O外接于△CDE,则⊙O的半径最小值为.三.解答题(共7小题)19.十一期间,小明一家一起去旅游,如图是小明设计的某旅游景点的图纸(网格是由相同的小正方形组成的,且小正方形的边长代表实际长度100m,在该图纸上可看到两个标志性景点A,B.若建立适当的平面直角坐标系,则点A (﹣3,1),B(﹣3,﹣3),第三个景点C(1,3)的位置已破损.(1)请在图中画出平面直角坐标系,并标出景点C的位置;(2)平面直角坐标系的坐标原点为点O,△ACO是直角三角形吗?请判断并说明理由.20.如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC交⊙O于点F.(1)AB与AC的大小有什么关系?请说明理由;(2)若AB=8,∠BAC=45°,求:图中阴影部分的面积.21.已知AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C.(1)如图①,若∠P=35°,求∠ABP的度数;(2)如图②,若D为AP的中点,求证:直线CD是⊙O的切线.22.如图,已知锐角△ABC内接于⊙O,连接AO并延长交BC于点D.(1)求证:∠ACB+∠BAD=90°;(2)过点D作DE⊥AB于E,若∠ADC=2∠ACB,AC=4,求DE的长.23.如图,点I是△ABC的内心,AI的延长线和△ABC的外接圆相交于点D,与BC相交于点E.(1)求证:DI=DB;(2)若AE=6cm,ED=4cm,求线段DI的长.24.如图,已知扇形AOB的圆心角为直角,正方形OCDE内接于扇形AOB.点C、E、D分别在OA、OB、弧AB上,过点A作AF⊥DE交ED的延长线于F,如果正方形的边长为1,求阴影部分M、N的面积和.25.如图:△A BC是圆的内接三角形,∠BAC与∠ABC的角平分线AE、BE相交于点E,延长AE交圆于点D,连接BD、DC,且∠BCA=60°.(1)求证:△BED为等边三角形;(2)若∠ADC=30°,⊙O的半径为,求BD长.参考答案一.选择题(共10小题)1.【解答】解:∵d=3<半径=4∴直线与圆相交∴直线m与⊙O公共点的个数为2个故选:C.2.【解答】解:连接OC.∵AB是⊙O的直径,AB=10,∴OC=OB=AB=5;又∵AB⊥CD于E,CD=8,∴CE=CD=4(垂径定理);在Rt△COE中,OE=3(勾股定理),∴BE=OB﹣OE=5﹣3=2,即BE=2;故选:A.3.【解答】解:圆内接正六边形的边所对的圆心角=360°÷6=60°,根据圆周角等于同弧所对圆心角的一半,边所对的圆周角的度数是60×=30°或180°﹣30°=150°.故选:D.4.【解答】解:∴⊙O的半径为5cm,如果圆心O到直线l的距离为4cm,∴5>4,即d<r,∴直线l与⊙O的位置关系是相交,故选:C.5.【解答】解:连接OE、OC,如图,∵DE=OB=OE,∴∠D=∠EOD=20°,∴∠CEO=∠D+∠EOD=40°,∵OE=OC,∴∠C=∠CEO=40°,∴∠BOC=∠C+∠D=60°,∴的长度==π,故选:A.6.【解答】解:∵BC是⊙O的直径,∴∠BAC=90°,∵∠B=∠D=35°,∴∠ACB=55°,故选:B.7.【解答】解:连接OD、AD,∵在△ABC中,AB=AC,∠ABC=45°,∴∠C=45°,∴∠BAC=90°,∴△ABC是Rt△BAC,∵BC=4,∴AC=AB=4,∵AB为直径,∴∠ADB=90°,BO=DO=2,∵OD=OB,∠B=45°,∴∠B=∠BDO=45°,∴∠DOA=∠BOD=90°,∴阴影部分的面积S=S△BOD +S扇形DOA=+=π+2.故选:B.8.【解答】解:连接OA、OB、OP,∵∠C=30°,∴∠APB=∠C=30°,∵PB=AB,∴∠PAB=∠APB=30°∴∠ABP=120°,∵PB=AB,∴OB⊥AP,AD=PD,∴∠OBP=∠OBA=60°,∵OB=OA,∴△AOB是等边三角形,∴AB=OA=5,则Rt△PBD中,PD=cos30°•PB=×5=,∴AP=2PD=5,故选:D.9.【解答】解:连接OD,∵弧AB的半径OA长是6米,C是OA的中点,∴OC=OA=×6=3米,∵∠AOB=90°,CD∥OB,∴CD⊥OA,在Rt△OCD中,∵OD=6,OC=3,∴CD===3米,∵sin∠DOC===,∴∠DOC=60°,∴S阴影=S扇形AOD﹣S△DOC=﹣×3×3 =(6π﹣)平方米.故选:A.10.【解答】解:连接OC,∵CD⊥AB,∠BCD=32°,∴∠OBC=58°,∵OC=OB,∴∠OCB=∠OBC=58°,∴∠COP=64°,∵PC是⊙O的切线,∴∠OCP=90°,∴∠CPO=26°,∵AB⊥CD,∴AB垂直平分CD,∴PC=PD,∴∠CPD=2∠CPO=52°故选:D.二.填空题(共8小题)11.【解答】解:由圆周角定理得,∠AOD=2∠ACD=50°,∴∠BOD=180°﹣50°=130°,故答案为:130°.12.【解答】解:如图,连接BD,CD,EC.∵点E是△ABC的内心,∴∠DAB=∠DAC,∠ECA=∠ECD,∵∠DCB=∠DAB,∠DEC=∠EAC+∠ECA,∠ECD=∠ECB+∠DCB,∴∠DEC=∠DCE,∴DE=DC,∵BC是直径,∴∠BDC=90°,∵∠DAB=∠DAC,∴=,∴BD=DC,∵BC=4,∴DC=DB=2,∴DE=2,故答案为2.13.【解答】解:如图,设DE的中点为M,连接OM,则OM⊥DE.∵在Rt△AOB中,OA=20,AB=OC=12,∴OB===16,∴OM===,在Rt△OCM中,CM===,∵BM=BC﹣CM=20﹣=,∴CE﹣BD=(EM﹣CM)﹣(DM﹣BM)=BM﹣CM=﹣=.故答案为:.14.【解答】解:根据题意画出平移后的图形,如图所示:设平移后的△A′B′C′与圆O相切于点D,连接OD,OA,AD,过O作OE⊥AD,可得E为AD的中点,∵平移前圆O与AC相切于A点,∴OA⊥A′C,即∠OAA′=90°,∵平移前圆O与AC相切于A点,平移后圆O与A′B′相切于D点,即A′D与A′A为圆O的两条切线,∴A′D=A′A,又∠B′A′C′=60°,∴△A′AD为等边三角形,∴∠DAA′=60°,AD=AA′=A′D,∴∠OAE=∠OAA′﹣∠DAA′=30°,在Rt△AOE中,∠OAE=30°,AO=2,∴AE=AO•cos30°=,∴AD=2AE=2,∴AA′=2,则该直角三角板平移的距离为2.故答案为:2.15.【解答】解:连接OA、OB,如下图所示:∵PA、PB为圆的两条切线,∴由切线长定理可得:PA=PB,同理可知:DA=DC,EC=EB;∵OA⊥PA,OA=5,PO=13,∴由勾股定理得:PA=12,∴PA=PB=12;∵△PDE的周长=PD+DC+CE+PE,DA=DC,EC=EB;∴△PDE的周长=PD+DA+PE+EB=PA+PB=24,故此题应该填24cm.16.【解答】解:过B作BD⊥AC于D,∵AB=BC,∴AD=CD=AC=5,∵S=60,△ABC∴,即,BD=12,∵AF⊥CE,∴∠AFC=90°,∴F在以AC为直径的圆上,∵BF+DF>BD,且DF=DF',∴当F在BD上时,BF的值最小,此时BF'=12﹣5=7,则BF的最小值是7,故答案为:7.17.【解答】解:连接OB、OC,连接A O并延长交BC于H,则AH⊥BC,BH=CH.∵△ABC是等边三角形,OB=OA=1,∴BH=OB,∴BH=CH=,∴BC=,=•()2=,∴S△ABC∴S=π•12﹣=π﹣,阴故答案为π﹣.18.【解答】解:如图,连接OD、OA、OC、OB、OE.∵OA=OA,OD=OC,AD=AC,∴△OAD≌△OAC,∴∠OAC=∠OAD=∠CAD=60°,同法可证:∠OBC=∠OBE=∠ABE=60°,∴△AOB是等边三角形,∴当OC⊥AB时,OC的长最短,此时OC=OA•sin60°=3,故答案为3.三.解答题(共7小题)19.【解答】解:(1)如图;(2)△ACO是直角三角.理由如下:∵A(﹣3,1),C(1,3),∴OA==,OC==,AC==2,∵OA2+OC2=AC2,∴△AOC是直角三角形,∠AOC=90°.20.【解答】解:(1)AB=AC.理由是:连接AD.∵AB是⊙O的直径,∴∠ADB=90°,即AD⊥BC,又∵DC=BD,∴AB=AC;(2)连接OD、过D作DH⊥AB.∵AB=8,∠BAC=45°,∴∠BOD=45°,OB=OD=4,∴DH=2∴△OBD 的面积=扇形OBD的面积=,阴影部分面积=.21.【解答】(1)解:∵AB是⊙O的直径,AP是⊙O的切线,∴AB⊥AP,∴∠BAP=90°;又∵∠P=35°,∴∠AB=90°﹣35°=55°.(2)证明:如图,连接OC,OD、AC.∵AB是⊙O的直径,∴∠ACB=90°(直径所对的圆周角是直角),∴∠ACP=90°;又∵D为AP的中点,∴AD=CD(直角三角形斜边上的中线等于斜边的一半);在△OAD和△OCD中,,∴△OAD≌△OCD(SSS),∴∠OAD=∠OCD(全等三角形的对应角相等);又∵AP是⊙O的切线,A是切点,∴AB⊥AP,∴∠OAD=90°,∴∠OCD=90°,即直线CD是⊙O的切线.22.【解答】(1)证明:延长AD交⊙O于点F,连接BF.∵AF为⊙O的直径,∴∠ABF=90°,∴∠AFB+∠BAD=90°,∵∠AFB=∠ACB,∴∠ACB+∠BAD=90°.(2)证明:如图2中,过点O作OH⊥AC于H,连接BO.∵∠AOB=2∠ACB,∠ADC=2∠ACB,∴∠AOB=∠ADC,∴∠BOD=∠BDO,∴BD=BO,∴BD=OA,∵∠BED=∠AHO,∠ABD=∠AOH,∴△BDE≌△AOH,(AAS),∴DE=AH,∵OH⊥AC,∴AH=CH=AC,∴AC=2DE=4,∴DE=2.23.【解答】(1)证明:连接BI.∵点I是△ABC的内心,∴∠BAI=∠CAI,∠ABI=∠CBI.又∵∠DBI=∠CBI+∠DBC,∠DIB=∠ABI+∠BAI,∠DBC=∠DAC=∠BAI,∴∠DBI=∠DIB,∴DI=DB.(2)∵∠DBC=∠DAC=∠BAI,∠ADB=∠BDA,∴△BDE∽△ABD,∴,即BD2=D E•AD=DE•(AE+DE)=4×(6+4)=40,DI=BD=(cm).24.【解答】解:连接OD,∵正方形的边长为1,即OC=CD=1,∴OD=,∴AC=OA﹣OC=﹣1,∵DE=DC,BE=AC,弧BD=弧AD=长方形ACDF的面积=AC•CD=﹣1.∴S阴25.【解答】(1)证明:∵∠BAC与∠ABC的角平分线AE、BE相交于点E,∴∠EAB=∠CAB,∠EBA=∠CBA,∴∠AEB=180°﹣(∠EAB+∠EBA)=180°﹣(∠CAB+∠CBA)=180°﹣(180°﹣∠BCA)=120°,∴∠DEB=60°,由圆周角定理得,∠BDA=∠BCA=60°,∴△BED为等边三角形;(2)∵∠ADC=30°,∠BDA=60°,∴∠BDC=90°,∴BC是⊙O的直径,即BC=4,∵AE平分∠BAC,∴=,∴BD=DC=4.。
北师大版数学九年级下册第三章圆(第1~3节检测题)之二附答案

第三章圆(第1~3节检测题)3.1~3.3 车轮为什么做成圆形、圆的对称性、圆周角和圆心角的关系(B卷)(50分钟,共100分)班级:_______ 姓名:_______ 得分:_______ 发展性评语:_____________一、请准确填空(每小题3分,共24分)1.如图1,M是⊙O内一点,已知过点M的⊙O最长的弦为10 cm,最短的弦长为8 cm,则OM =_____ cm.2.如图2,⊙O的直径AC=2,∠BAD=75°,∠ACD=45°,则四边形ABCD的周长为_____(结果取准确值).3.如图3,⊙O的直径为10,弦AB=8,P是弦AB上一动点,那么OP长的取值范围是_____.OMOABC DOA BP图1 图2 图34.如图4,在⊙O中,两弦AD∥BC,AC、BD相交于点E,连接AB、CD,图中的全等三角形共有_____对.相似比不等于1的相似三角形共有_____对.5.如图5,在⊙O中,直径AB和弦CD的长分别为10 cm和8 cm,则A、B两点到直线CD的距离之和是_____.6.如图6,AB是⊙O的直径,C、D、E都是⊙O上的点,则∠1+∠2=_____.7.如图7,△ABC内接于⊙O,D是劣弧上的一点,E是BC延长线上一点,AE交⊙O于F,为使△ADB∽△ACE,应补充的一个条件是_____或_____.A BDEOABC DOAC DO1 2EAB COF图4 图5 图6 图78.如图8,在足球比赛场上,甲、乙两名队员互相配合向对方球门MN进攻,当甲带球冲到A点时,乙已跟随冲到B点,从数学角度看,此时甲是自己射门好,还是将球传给乙,让乙射门好?答:,简述理由:.图8二、相信你的选择(每小题3分,共24分)9.如图9,点P 是半径为5的⊙O 内一点,且OP =4,在过P 点的所有⊙O 的弦中,你认为弦长为整数的弦的条数为A.6条B.5条C.4条D.2条10.如图10,在平面直角坐标系中,⊙O ′与两坐标分别交于A 、B 、C 、D 四点,已知:A (6,0),B (0,-3),C (-2,0),则点D 的坐标为A.(0,2)B.(0,3)C.(0,4)D.(0,5)图9图10 图1111.如图11,已知AB 和CD 分别是半圆O 的直径和弦,AD 和BC 相交于点E ,若∠AEC =α,则S △CDE ∶S △ABE 等于A.sin 2αB.cos 2αC.tan 2αD.与α无关12.如图12,每张方格纸上都画有一个圆,只用不带刻度的直尺就能确定圆心位置的是A BD C图1213.如图13,已知:AB =2,BC =2,CD =1,∠ABC =45°,则四边形ABCD 的面积为A.333+ B.4223+ C.2223+D.433+。
2022年九年级中考数学考点训练——几何专题:《圆的综合》(一)及答案

备战2022最新年九年级中考数学考点训练——几何专题:《圆的综合》(一)1.对于平面内⊙C和⊙C外一点P,若过点P的直线l与⊙C有两个不同的公共点M,N,点Q为直线l上的另一点,且满足(如图1所示),则称点Q是点P关于⊙O的密切点.已知在平面直角坐标系xOy中,⊙O的半径为2,点P(4,0).(1)在点D(﹣2,1),E(1,0),F(3,)中,是点P关于⊙O的密切点的为.(2)设直线l方程为y=kx+b,如图2所示,①k=﹣时,求出点P关于O的密切点Q的坐标;②⊙T的圆心为T(t,0),半径为2,若⊙T上存在点P关于⊙O 的密切点,直接写出t的取值范围.2.A,B是⊙C上的两个点,点P在⊙C的内部.若∠APB为直角,则称∠APB为AB关于⊙C的内直角,特别地,当圆心C在∠APB 边(含顶点)上时,称∠APB为AB关于⊙C的最佳内直角.如图1,∠AMB是AB关于⊙C的内直角,∠ANB是AB关于⊙C的最佳内直角.在平面直角坐标系xOy中.(1)如图2,⊙O的半径为5,A(0,﹣5),B(4,3)是⊙O 上两点.①已知P1(1,0),P2(0,3),P3(﹣2,1),在∠AP1B,∠AP2B,∠AP3B,中,是AB关于⊙O的内直角的是;②若在直线y=2x+b上存在一点P,使得∠APB是AB关于⊙O的内直角,求b的取值范围.(2)点E是以T(t,0)为圆心,4为半径的圆上一个动点,⊙T 与x轴交于点D(点D在点T的右边).现有点M(1,0),N(0,n),对于线段MN上每一点H,都存在点T,使∠DHE是DE关于⊙T的最佳内直角,请直接写出n的最大值,以及n取得最大值时t的取值范围.3.定义:三角形一边上的点将该边分为两条线段,且这两条线段的积等于这个点到该边所对顶点连线的平方,则称这个点为三角形该边的“好点”.如图1,△ABC中,点D是BC边上一点,连结AD,若AD2=BD•CD,则称点D是△ABC中BC边上的“好点”.(1)如图2,△ABC的顶点是4×3网格图的格点,请仅用直尺画出AB边上的一个“好点”.(2)△ABC中,BC=9,tanB=,tanC=,点D是BC边上的“好点”,求线段BD的长.(3)如图3,△ABC是⊙O的内接三角形,OH⊥AB于点H,连结CH并延长交⊙O于点D.①求证:点H是△BCD中CD边上的“好点”.②若⊙O的半径为9,∠ABD=90°,OH=6,请直接写出的值.4.如图,⊙O是△ABD的外接圆,AB为直径,点C是弧AD的中点,连接OC,BC分别交AD于点F,E.(1)求证:∠ABD=2∠C.(2)若AB=10,BC=8,求BD的长.5.如图,在平面直角坐标系xOy中,A(0,8),B(6,0),C(0,3),点D从点A运动到点B停止,连接CD,以CD长为直径作⊙P.(1)若△ACD∽△AOB,求⊙P的半径;(2)当⊙P与AB相切时,求△POB的面积;(3)连接AP、BP,在整个运动过程中,△PAB的面积是否为定值,如果是,请直接写出面积的定值,如果不是,请说明理由.6.如图,已知Rt△ABC中,∠A=30°,AC=6.边长为4的等边△DEF沿射线AC运动(A、D、E、C四点共线).当等边△DEF的边DF、EF与Rt△ABC的边AB分别相交于点M、N(M、N不与A、B重合)时,设AD=x.(1)则△FMN的形状是,△ADM的形状是;(2)△ABC与△DEF重叠部分的面积为y,求y关于x的函数解析式,并写出的取值范围;(3)若以点M为圆心,MN为半径的圆与边AC、EF同时相切,求此时MN的长.7.如图,以点O为圆心,OE为半径作优弧EF,连接OE,OF,且OE=3,∠EOF=120°,在弧EF上任意取点A,B(点B在点A 的顺时针方向)且使AB=2,以AB为边向弧内作正三角形ABC.(1)发现:不论点A在弧上什么位置,点C与点O的距离不变,点C与点O的距离是;点C到直线EF的最大距离是.(2)思考:当点B在直线OE上时,求点C到OE的距离,在备用图1中画出示意图,并写出计算过程.(3)探究:当BC与OE垂直或平行时,直接写出点C到OE的距离.8.如图,在平面直角坐标系中,点A的坐标为(6,0),点B的坐标为(0,2),点M从点A出发沿x轴负方向以每秒3cm的速度移动,同时点N从原点出发沿y轴正方向以每秒1cm的速度移动.设移动的时间为t秒.(1)若点M在线段OA上,试问当t为何值时,△ABO与以点O、M、N为顶点的三角形相似?(2)若直线y=x与△OMN外接圆的另一个交点是点C.①试说明:当0<t<2时,OM、ON、OC在移动过程满足OM+ON =OC;②试探究:当t>2时,OM、ON、OC之间的数量关系是否发生变化,并说明理由.9.如图,将一副斜边相等的直角三角板按斜边重合摆放在同一平面内,其中∠CAB=30°,∠DAB=45°,点O为斜边AB的中点,连接CD交AB于点E.(1)求证:A,B,C,D四个点在以点O为圆心的同一个圆上;(2)求证:CD平分∠ACB;(3)过点D作DF∥BC交AB于点F,求证:BO2+OF2=EF•BF.10.如图,在△ABC中,∠BAC=90°,∠B=60°,AB=2.AD⊥BC 于D.E为边BC上的一个(不与B、C重合)点,且AE⊥EF于E,∠EAF=∠B,AF相交于点F.(1)填空:AC=;∠F=.(2)当BD=DE时,证明:△ABC≌△EAF.(3)△EAF面积的最小值是.(4)当△EAF的内心在△ABC的外部时,直接写出AE的范围.参考答案1.解:(1)当圆心在坐标原点时,直线l为y=0时,∵⊙O的半径为2,点P(4,0).∴M(2,0),N(﹣2,0),PM=2,PN=6,=,∵,∴=,设Q点坐标为(x,y),则QM=|2﹣x|,QN=|x﹣(﹣2)|=|x+2|,∴=,∴|2+x|=3|2﹣x|,∴2+x=6﹣3x,或2+x=3x﹣6,∴x=1,或x=4,∴E(1,0)是点P关于⊙O的密切点.故答案为:E.(2)①依题意直线l:y=kx+b过定点P(4,0),∵k=﹣∴将P(4,0)代入y=﹣x+b得:0=﹣×4+b,∴b=,∴y=﹣x+.如图,作MA⊥x轴于点A,NB垂直x轴于点B,设M(x,﹣x+),由OM=2得:x2+=4,∴5x2﹣4x﹣10=0,则M,N两点的横坐标xM,xN是方程5x2﹣4x﹣10=0的两根,解得xM=,xN=,∴AB=,PA=,PB=,∵,∴=,=,∴=,∴HA=,∴OH=OA﹣HA=﹣=1,∴Q(1,1).②点P关于⊙O的密切点的轨迹为切点弦ST(不含端点),如图所示:∴﹣1≤t<0或2<t≤3.2.解:(1)如图1,∵P1(1,0),A(0,﹣5),B(4,3),∴AB==4,P1A==,P1B==3,∴P1不在以AB为直径的圆弧上,故∠AP1B不是AB关于⊙O的内直角,∵P2(0,3),A(0,﹣5),B(4,3),∴P2A=8,AB=4,P2B=4,∴P2A2+P2B2=AB2,∴∠AP2B=90°,∴∠AP2B是AB关于⊙O的内直角,同理可得,P3B2+P3A2=AB2,∴∠AP3B是AB关于⊙O的内直角,故答案为:∠AP2B,∠AP3B;(2)∵∠APB是AB关于⊙O的内直角,∴∠APB=90°,且点P在⊙O的内部,∴满足条件的点P形成的图形为如图2中的半圆H(点A,B均不能取到),过点B作BD⊥y轴于点D,∵A(0,﹣5),B(4,3),∴BD=4,AD=8,并可求出直线AB的解析式为y=2x﹣5,∴当直线y=2x+b过直径AB时,b=﹣5,连接OB,作直线OH交半圆于点E,过点E作直线EF∥AB,交y 轴于点F,∵OA=OB,AH=BH,∴EH⊥AB,∴EH⊥EF,∴EF是半圆H的切线.∵∠OAH=∠OAH,∠OHB=∠BDA=90°,∴△OAH∽△BAD,∴,∴OH=AH=EH,∴OH=EO,∵∠EOF=∠AOH,∠FEO=∠AHO=90°,∴△EOF≌△HOA(ASA),∴OF=OA=5,∵EF∥AB,直线AB的解析式为y=2x﹣5,∴直线EF的解析式为y=2x+5,此时b=5,∴b的取值范围是﹣5<b≤5.(3)∵对于线段MN上每一个点H,都存在点T,使∠DHE是DE 关于⊙T的最佳内直角,∴点T一定在∠DHE的边上,∵TD=4,∠DHT=90°,线段MN上任意一点(不包含点M)都必须在以TD为直径的圆上,该圆的半径为2,∴当点N在该圆的最高点时,n有最大值,即n的最大值为2.分两种情况:①若点H不与点M重合,那么点T必须在边HE上,此时∠DHT =90°,∴点H在以DT为直径的圆上,如图3,当⊙G与MN相切时,GH⊥MN,∵OM=1,ON=2,∴MN==,∵∠GMH=∠OMN,∠GHM=∠NOM,ON=GH=2,∴△GHM≌△NOM(ASA),∴MN=GM=,∴OG=﹣1,∴OT=+1,当T与M重合时,t=1,∴此时t的取值范围是﹣﹣1≤t<1,②若点H与点M重合时,临界位置有两个,一个是当点T与M重合时,t=1,另一个是当TM=4时,t=5,∴此时t的取值范围是1≤t<5,综合以上可得,t的取值范围是﹣﹣1≤t<5.3.解:(1)如答图1,当CD⊥AB或点D是AB的中点是,CD2=AD•BD;(2)作AE⊥BC于点E,由,可设AE=4x,则BE=3x,CE=6x,∴BC=9x=9,∴x=1,∴BE=3,CE=6,AE=4,设DE=a,①如答图2,若点D在点E左侧,由点D是BC边上的“好点”知,AD2=BD•CD,∴a2+42=(3﹣a)(6+a),即2a2+3a﹣2=0,解得,a2=﹣2(舍去),∴.②如答图3,若点D在点E右侧,由点D是BC边上的“好点”知,AD2=BD•CD,∴a2+42=(3+a)(6﹣a),即2a2﹣3a﹣2=0,解得a1=2,(舍去)∴BD=3+a=3+2=5.∴或5.(3)①如答图4,连接AD,BD,∵∠CHA=∠BHD,∠ACH=∠DBH∴△AHC∽△DHB,∴,即AH•BH=CH•DH,∵OH⊥AB,∴AH=BH,∴BH2=CH•DH∴点H是△BCD中CD边上的“好点”.②.理由如下:如答图4,∵∠ABD=90°,∴AD是直径,∴AD=18.又∵OH⊥AB,∴OH∥BD.∵点O是线段AD的中点,∴OH是△ABD的中位线,∴BD=2OH=12.在直角△ABD中,由勾股定理知:AB===6.∴由垂径定理得到:BH=AB=3.在直角△BDH中,由勾股定理知:DH===3.又由①知,BH2=CH•DH,即45=3CH,则CH=.∴==,即.4.(1)证明:∵C是的中点,∴=,∴∠ABC=∠CBD,∵OB=OC,∴∠ABC=∠C,∴∠ABC=∠CBD=∠C,∴∠ABD=∠ABC+CBD=2∠C;(2)解:连接AC,∵AB为⊙O的直径,∴∠ACB=90°,∴AC==6,∵C是的中点,∴OC⊥AD,∴OA2﹣OF2=AF2=AC2﹣CF2,∴52﹣OF2=62﹣(5﹣OF)2,∴OF=1.4,又∵O是AB的中点,∴BD=2OF=2.8.5.解:(1)如图1,∵A(0,8),B(6,0),C(0,3),∴OA=8,OB=6,OC=3,∴AC=5,∵△ACD∽△AOB,∴,∴∴CD的=,∴⊙P的半径为;(2)在Rt△AOB中,OA=8,OB=6,∴==10,如图2,当⊙P与AB相切时,CD⊥AB,∴∠ADC=∠AOB=90°,∠CAD=∠BAO,∴△ACD∽△ABO,∴,即,∴AD=4,CD=3,∵CD为⊙P的直径,∴CP=,过点P作PE⊥AO于点E,∵∠PEC=∠ADC=90°,∠PCE=∠ACD,∴△CPE∽△CAD,∴,即,∴,∴,∴△POB的面积==;(3)①如图3,若⊙P与AB只有一个交点,则⊙P与AB相切,由(2)可知PD⊥AB,PD=,∴△PAB的面积=.②如图4,若⊙P与AB有两个交点,设另一个交点为F,连接CF,可得∠CFD=90°,由(2)可得CF=3,过点P作PG⊥AB于点G,则DG=,则PG为△DCF的中位线,PG=,∴△PAB的面积==.综上所述,在整个运动过程中,△PAB的面积是定值,定值为.6.解:(1)如图1,∵△DEF是等边三角形,∴∠FDE=∠F=60°.∵∠A=30°,∴∠AMD=∠FDE﹣∠A=30°,∴∠FMN=∠AMD=30°,∴∠MNF=90°,即△FMN是直角三角形,∵∠FDE=60°,∴∠AMD=∠FDE﹣∠A=30°,∴∠AMD=∠A,∴DM=DA,∴△ADM是等腰三角形;故答案为:直角三角形,等腰三角形;(2)如图2,△ADM是等腰三角形,∴DM=AD=x,FM=4﹣x,又∵∠FED=60°,∠A=30°,∴∠FNM=90°,∴MN=MF•sinF=(4﹣x),FN=,∴y==,=.当0<x≤2时,∴y=S四边形DENM=S△FDE﹣S△FMN=4,当2≤x<4时,CD=6﹣x,∵∠BCE=90°,∠PDC=60°,∴PC=(6﹣x),∴,=.(3)如图3,点M作MG⊥AC于点G,由(2)得DM=x,∵∠MDG=60°,∴MG=,MNF=90°∴MN⊥FC要使以点M为圆心,MN长为半径的圆与边AC、EF相切,则有MG=MN,∴,解得:x=2,∴圆的半径MN=.7.解:(1)如图1,连接OA、OB、OC,延长OC交AB于点G,在正三角形ABC中,AB=BC=AC=2,∵OA=OB,AC=BC,∴OC垂直平分AB,∴AG=AB=1,∴在Rt△AGC中,由勾股定理得:CG===,在Rt△AGO中,由勾股定理得:OG===2,∴OC=2﹣;如图2,延长CO交EF于点H,当CO⊥EF时,点C到直线EF的距离最大,最大距离为CH的长,∵OE=OF,CO⊥EF,∴CO平分∠EOF,∵∠EOF=120°,∴∠EOH=∠EOF=60°,在Rt△EOH中,cos∠EOH=,∴cos60°==,∴OH=,∴CH=CO+OH=,∴点C到直线EF的最大距离是.故答案为:2﹣;.(2)如图3,当点B在直线OE上时,由OA=OB,CA=CB可知,点O,C都在线段AB的垂直平分线上,过点C作AB的垂线,垂足为G,则G为AB中点,直线CG过点O.∴由∠COM=∠BOG,∠CMO=∠BGO∴△OCM∽△OBG,∴=,∴=,∴CM=,∴点C到OE的距离为.(3)如图4,当BC⊥OE时,设垂足为点M,∵∠EOF=120°,∴∠COM=180°﹣120°=60°,∴在Rt△COM中,sin∠COM=,∴sin60°==,∴CM=CO=(2﹣)=﹣;如图5,当BC∥OE时,过点C作CN⊥OE,垂足为N,∵BC∥OE,∴∠CON=∠GCB=30°,∴在Rt△CON中,sin∠CON=,∴sin30°==,∴CN=CO=(2﹣)=﹣;综上所述,当BC与OE垂直或平行时,点C到OE的距离为﹣或﹣.8.解:(1)由题意,得OA=6,OB=2.当0<t<2时,OM=6﹣3t,ON=t.若△ABO∽△MNO,则=,即=,解得t=1.若△ABO∽△NMO,则=,即=,解得t=1.8.综上,当t为1或1.8时,△ABO与以点O、M、N为顶点的三角形相似.(2)①当0<t<2时,在ON的延长线的截取ND=OM,连接CD、CN、CM,如图所示:∵直线y=x与x轴的夹角为450,∴OC平分∠AOB.∴∠AOC=∠BOC.∴CN=CM.又∵在⊙O中∠CNO+∠CMO=180°,∠DNC+∠CNO=180°,∴∠CND=∠CMO.∴△CND≌△CMO(SAS).∴CD=CO,∠DCN=∠OCM.又∵∠AOB=90°,∴MN为⊙O的直径,∴∠MCN=90°.∴∠OCM+∠OCN=90°.∴∠DCN+∠OCN=90°.∴∠OCD=90°.又∵CD=CO,∴OD=OC.∴ON+ND=OC.∴OM+ON=OC.②当t>2时,过点C作CD⊥OC交ON于点D,连接CM、CN,如图所示:∵∠COD=45°,∴△CDO为等腰直角三角形,∴OD=OC.∵MN为⊙O的直径,∴∠MCN=90°.又∵在⊙O中,∠CMN=∠CNM=45°,∴MC=NC.又∵∠OCD=∠MCN=90°,∴∠DCN=∠OCM.∴△CDN≌△COM(SAS).∴DN=OM.又∵OD=OC,∴ON﹣DN=OC.∴ON﹣OM=OC.9.证明:(1)如图,连接OD,OC,在Rt△ABC中,∠ACB=90°,点O是AB的中点,在Rt△ABD中,∠ADB=90°,点O是AB的中点,∴OD=OA=OB,∴OA=OB=OC=OD,∴A,B,C,D四个点在以点O为圆心的同一个圆上;(2)由(1)知,A,B,C,D四个点在以点O为圆心的同一个圆上,且AD=BD,∴,∴CD平分∠ACB;(3)由(2)知,∠BCD=45°,∵∠ABC=60°,∴∠BEC=75°,∴∠AED=75°,∵DF∥BC,∴∠BFD=∠ABC=60°,∵∠ABD=45°,∴∠BDF=180°﹣∠BFD﹣∠ABD=75°=∠AED,∵∠DFE=∠BFD,∴△DEF∽△BDF,∴,连接OD,则∠BOD=90°,OB=OD,在Rt△DOF中,根据勾股定理得,OD2+OF2=DF2,∴OB2+OF2=BF•EF,即BO2+OF2=EF•BF.10.解:(1)∵∠BAC=90°,∠B=60°,AB=2,tanB=,∴AC=AB•tanB=2tan60°=2;∵AE⊥EF,∴∠AEF=90°,∵∠EAF=∠B=60°,∴∠F=90°﹣∠EAF=90°﹣60°=30°.故答案为:2,30°;(2)证明:当BD=DE时,∵AD⊥BC于D,∴AB=AE,∵∠AEF=90°,∠BAC=90°,∴∠AEF=∠BAC,又∠EAF=∠B,∴△ABC≌△EAF(ASA);(3)∵∠AEF=90°,∠EAF=60°,tan∠EAF=,∴EF=AE•tan∠EAF=AE•tan60°=AE,∴S△EAF=AE•EF=AE×AE=AE2,当AE⊥BC时,AE最短,S△EAF最小,此时∠AEB=90°,sinB=,∴AE=AB•sinB=2sin60°=2×=,S△EAF=AE2=×3=,∴△EAF面积的最小值是,故答案为:;(4)当△EAF内心恰好落在AC上时,设△EAF的内心为N,连接EN,如图:∵N是△EAF的内心,∴AN平分∠EAF,EN平分∠AEF,∴∠EAC=∠AEF=×60°=30°,∵∠BAC=90°,∴∠BAE=∠BAC﹣∠EAC=90°﹣30°=60°,又∵∠B=60°,∴△ABE是等边三角形,∴AE=AB=2,∵E为BC上的一点,不与B、C重合,由(1)可知AC=2,∴当△EAF的内心在△ABC的外部时,.故答案为:.。
人教版 九年级数学上册 第24章 圆的概念及弧、弦、圆心角和圆周角 专题练习(含答案)

圆的概念及弧、弦、圆心角和圆周角专题练习(含答案)例1. 如图,线段AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠AOD等于()A.160°B.150°C.140°D.120°例2. 如图,以AB为直径的⊙O与弦CD相交于点E,且AC=2,AE CE=1.则弧BD 的长是()B C D例3.如图,已知A,B,C在⊙O上,ACB为优弧,下列选项中与∠AOB相等的是()A.2∠C B.4∠B C.4∠A D.∠B+∠C例4. 如图,已知⊙O的半径为13,弦AB长为24,则点O到AB的距离是()A.6 B.5 C.4 D.3巩固练习1.如下图,(1)若点O为⊙O的圆心,则线段__________是圆O的半径;线段________是圆O的弦,其中最长的弦是______;______是劣弧;______是半圆.(2)若∠A=40°,则∠ABO=______,∠C=______,∠ABC=______.2.如图,将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为________.3.⊙O中,∠AOB=100°,若C是AB上一点,则∠ACB等于( ).A.80°B.100°C.120°D.130°4.已知:如图,在同心圆中,大圆的弦AB交小圆于C,D两点.(1)求证:∠AOC=∠BOD;(2)试确定AC与BD两线段之间的大小关系,并证明你的结论.5. 已知:如图,AB为⊙O的直径,C,D为⊙O上的两点,且C为AD的中点,若∠BAD=20°,求∠ACO的度数6.如图,以ABCD的顶点A为圆心,AB为半径作⊙A,分别交BC、AD于E、F,交BA的延长线于G,试说明弧EF和弧FG相等.7. ⊙O中,M为AB的中点,则下列结论正确的是( ).A.AB>2AM B.AB=2AM C.AB<2AM D.AB与2AM的大小不能确定8. 如图,⊙O中,AB为直径,弦CD交AB于P,且OP=PC,试猜想AD与CB之间的关系,并证明你的猜想.9. 如图,⊙O中,直径AB=15cm,有一条长为9cm的动弦CD在ANB上滑动(点C与A,点D与B不重合),CF⊥CD交AB于F,DE⊥CD交AB于E.(1)求证:AE=BF;(2)在动弦CD滑动的过程中,四边形CDEF的面积是否为定值?若是定值,请给出证明并求这个定值;若不是,请说明理由.10.如图,若五边形ABCDE是⊙O的内接正五边形,则∠BOC=______,∠ABE=______,∠ADC=______,∠ABC=______.10题图11题图12题图11.如图,若六边形ABCDEF是⊙O的内接正六边形,则∠AED=______,∠FAE=______,∠DAB=______,∠EFA=______.12.如图,ΔABC是⊙O的内接正三角形,若P是AB上一点,则∠BPC=______;若M是BC上一点,则∠BMC=______.13.在⊙O中,若圆心角∠AOB=100°,C是AB上一点,则∠ACB等于( ).A.80°B.100°C.130°D.140°14.在圆中,弦AB,CD相交于E.若∠ADC=46°,∠BCD=33°,则∠DEB等于( ).A.13°B.79°C.38.5°D.101°15.如图,AC 是⊙O 的直径,弦AB ∥CD ,若∠BAC =32°,则∠AOD 等于( ).A .64°B .48°C .32°D .76°16.如图,弦AB ,CD 相交于E 点,若∠BAC =27°,∠BEC =64°,则∠AOD 等于( ).A .37°B .74°C .54°D .64°17.如图,四边形ABCD 内接于⊙O ,则x = 。
初三数学《圆》全章测试及答案

北京市第八中学分校202010月初三数学总复习圆 全章测试题班级: 姓名: 分数: 一、选择题 (每题4分,共32分)1.如图,AB 是⊙O 的直径,CD 是弦,AB ⊥CD 于点E, 若AB=10,CD=6,则OE 的长是( ).A.4B.3C.2D.12.半径分别为3和7的两个圆的圆心距为d ,若4<d≤11,则这两个圆的位置关系一定是( )A .相交B .相切C .内切或相交D .外切或相交 3.如图,在⊙O 中,P 是弦AB 的中点,CD 是过点P 的直径,则下列结论中不正确的是( )A .AB ⊥CD B .∠AOB=4∠ACDC .AD=BD D .PO=PD 4. 一个扇形的圆心角为60°,它所对的弧长为2πcm,则这个扇形的半径为( )A .6cmB .12cmC .2cm D .cm5.O 是△ABC 的外心,且∠ABC+∠ACB=100°,则∠BOC=( ). A .100° B .120° C .130° D .160°6.下列语句中,正确的个数是( )个.①相等的圆心角所对的弧相等;②同圆或等圆中,相等的圆周角所对的弦相等;③一边上的中线等于这条边一半的三角形是直角三角形;第1题第3题④等弧所对的圆周角相等;⑤一条弧所对的圆心角等于它所对的圆周角的一半A.2B.3C.4D.57.如图已知⊙O 是以数轴的原点O 为圆心,半径为1的圆,∠AOB =45°,点P 在数轴上运动,若过点P 与OA 平行的直线与⊙O 有公共点,设OP =x ,则x 的取值范围是( )A .0≤x ≤2B .-2≤x ≤2C .-1≤x ≤1D .x >28.设计一个商标图案如图中阴影部分,矩形ABCD 中,AB =2BC ,且AB =8cm ,以点A 为圆心,AD 为半径作圆与BA 的延长线相交于点F ,则商标图案的面积等于( )A .(4π+8)cm 2B .(4π+16)cm 2C .(3π+8) cm 2D .(3π +16)cm 2 二.填空题(每小题3分,共24分)9.如图,AB 是⊙O 的直径,弦CD⊙AB ,若⊙ABD =65°,则⊙ADC =__________.10.如图,AB 为半圆O 的直径,∠BAC =31°,D 为AC 上任意一点,则∠D的度数为__________.11.圆所在平面上的一点到该圆上的最小距离为4cm ,最大距离为10cm ,则该圆的半径为___________.12. 四边形ABCD 是⊙O 的内接四边形,且∠A ∶∠B ∶∠C=2∶3∶4,则 ∠D= 度。
人教版九年级上数学《24.1.1圆》练习题(含答案)

24.1.1 圆01 基础题知识点1 圆的有关概念1.下列条件中,能确定唯一一个圆的是(C)A .以点O 为圆心B .以2 cm 长为半径C .以点O 为圆心,5 cm 长为半径D .经过点A2.下列命题中正确的有(A)①弦是圆上任意两点之间的部分;②半径是弦;③直径是最长的弦;④弧是半圆,半圆是弧.A .1个B .2个C .3个D .4个3.过圆上一点可以作出圆的最长弦的条数为(A)A .1条B .2条C .3条D .无数条4.如图,在⊙O 中,弦有AC ,AB ,直径是AB ,优弧有ABC ︵,CAB ︵,劣弧有AC ︵,BC ︵.5.如图,在⊙O 中,点B 在⊙O 上,四边形AOCB 是矩形,对角线AC 的长为5,则⊙O 的半径长为5.知识点2 圆中的半径相等6.如图,MN 为⊙O 的弦,∠N =52°,则∠MON 的度数为(C)A .38°B .52°C .76°D .104°7.(朔州月考)如图,在△ABC中,∠ACB=90°,∠A=40°,以C为圆心,CB为半径的圆交AB于点D,连接CD,则∠ACD=(A)A.10°B.15°C.20°D.25°8.如图,AB为⊙O的直径,点C,D在⊙O上,已知∠BOC=70°,AD∥OC,则∠AOD =40°.9.如图,AB,AC为⊙O的弦,连接CO,BO并延长,分别交弦AB,AC于点E,F,∠B =∠C.求证:CE=BF.证明:∵OB,OC是⊙O的半径,∴OB=OC.又∵∠B=∠C,∠BOE=∠COF,∴△EOB≌△FOC(ASA).∴OE=OF.∴OE+OC=OF+OB,即CE=BF.10.如图,CE是⊙O的直径,AD的延长线与CE的延长线交于点B,若BD=OD,∠AOC =114°,求∠AOD的度数.解:设∠B=x.∵BD=OD,∴∠DOB=∠B=x.∴∠ADO=∠DOB+∠B=2x.∵OA=OD,∴∠A=∠ADO=2x.∵∠AOC=∠A+∠B,∴2x+x=114°,解得x=38°.∴∠AOD=180°-∠A-∠ADO=180°-4x=180°-4×38°=28°.02中档题11.如图,在△ABC中,AB为⊙O的直径,∠B=60°,∠BOD=100°,则∠C的度数为(C) A.50°B.60°C.70°D.80°12.下列四边形:①平行四边形;②菱形;③矩形;④正方形.其中四个顶点在同一个圆上的有(B)A.1个B.2个C.3个D.4个13.下面3个命题:①半径相等的两个圆是等圆;②长度相等的弧是等弧;③一条弦把圆分成两条弧,这两条弧不可能是等弧.其中真命题的个数为(B)A.0个B.1个C.2个D.3个14.如图,A,B是⊙O上两点,若四边形ACBO是菱形,⊙O的半径为r,则点A与点B 之间的距离为(B)A.2rB.3r C.r D.2r15.已知A ,B 是半径为6 cm 的圆上的两个不同的点,则弦长AB 的取值范围是0<AB ≤12cm. 16.如图,AB 是⊙O 的弦,半径OC ,OD 分别交AB 于点E ,F ,且AE =BF ,请你写出线段OE 与OF 的数量关系,并给予证明.解:OE =OF. 证明:连接OA ,OB. ∵OA ,OB 是⊙O 的半径, ∴OA =OB. ∴∠OAB =∠OBA. 又∵AE =BF ,∴△OAE ≌△OBF(SAS). ∴OE =OF.17.(教材P81练习T3变式)如图,在△ABC 中,BD ,CE 是两条高,点O 为BC 的中点,连接OD ,OE.求证:B ,C ,D ,E 四个点在以点O 为圆心的同一个圆上.证明:∵BD ,CE 是两条高, ∴∠BDC =∠BEC =90°. ∵点O 为BC 的中点, ∴OE =OB =OC =12BC.同理:OD =OB =OC =12BC.∴OB =OC =OD =OE.∴B ,C ,D ,E 四个点在以点O 为圆心的同一个圆上.03 综合题18.如图,过A ,C ,D 三点的圆的圆心为E ,过B ,F ,E 三点的圆的圆心为D ,∠A =63°,求∠B 的度数.解:连接EC ,ED. ∵AE =CE , ∴∠ACE =∠A =63°.∴∠AEC =180°-63°×2=54°. ∵DE =DB , ∴∠DEB =∠B.∴∠CDE =∠DEB +∠B =2∠B. ∵CE =DE ,∴∠ECD =∠CDE =2∠B. ∴∠AEC =∠ECD +∠B =3∠B. ∴3∠B =54°. ∴∠B =18°.。
人教版九年级数学中考真题分类(解答题)专练: 圆的综合(一)有答案

如果别人思考数学的真理像我一样深入持久,他也会找到我的发现。
——高斯人教版九年级数学中考真题分类(解答题)专练:圆的综合(一)1.(2020•齐齐哈尔)如图,AB为⊙O的直径,C、D为⊙O上的两个点,==,连接AD,过点D作DE⊥AC交AC的延长线于点E.(1)求证:DE是⊙O的切线.(2)若直径AB=6,求AD的长.2.(2020•泸州)如图,AB是⊙O的直径,点D在⊙O上,AD的延长线与过点B的切线交于点C,E为线段AD上的点,过点E的弦FG⊥AB于点H.(1)求证:∠C=∠AGD;(2)已知BC=6,CD=4,且CE=2AE,求EF的长.3.(2020•乐山)如图1,AB是半圆O的直径,AC是一条弦,D是上一点,DE⊥AB于点E,交AC于点F,连结BD交AC于点G,且AF=FG.(1)求证:点D平分;(2)如图2所示,延长BA至点H,使AH=AO,连结DH.若点E是线段AO的中点.求证:DH是⊙O的切线.4.(2020•安徽)如图,AB是半圆O的直径,C,D是半圆O上不同于A,B的两点,AD=BC,AC与BD相交于点F.BE是半圆O所在圆的切线,与AC的延长线相交于点E.(1)求证:△CBA≌△DAB;(2)若BE=BF,求证:AC平分∠DAB.5.(2020•德州)如图,点C在以AB为直径的⊙O上,点D是半圆AB的中点,连接AC,BC,AD,BD.过点D作DH∥AB交CB的延长线于点H.(1)求证:直线DH是⊙O的切线;(2)若AB=10,BC=6,求AD,BH的长.6.(2020•甘孜州)如图,AB是⊙O的直径,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D.(1)求证:∠CAD=∠CAB;(2)若=,AC=2,求CD的长.7.(2020•金华)如图,的半径OA=2,OC⊥AB于点C,∠AOC=60°.(1)求弦AB的长.(2)求的长.8.(2020•铜仁市)如图,AB是⊙O的直径,C为⊙O上一点,连接AC,CE⊥AB于点E,D 是直径AB延长线上一点,且∠BCE=∠BCD.(1)求证:CD是⊙O的切线;(2)若AD=8,=,求CD的长.9.(2020•衢州)如图,△ABC内接于⊙O,AB为⊙O的直径,AB=10,AC=6,连结OC,弦AD分别交OC,BC于点E,F,其中点E是AD的中点.(1)求证:∠CAD=∠CBA.(2)求OE的长.10.(2020•嘉兴)已知:如图,在△OAB中,OA=OB,⊙O与AB相切于点C.求证:AC=BC.小明同学的证明过程如下框:证明:连结OC,∵OA=OB,∴∠A=∠B,又∵OC=OC,∴△OAC≌△OBC,∴AC=BC.小明的证法是否正确?若正确,请在框内打“√”;若错误,请写出你的证明过程.参考答案1.(1)证明:连接OD,∵==,∴∠BOD=180°=60°,∵=,∴∠EAD=∠DAB=BOD=30°,∵OA=OD,∴∠ADO=∠DAB=30°,∵DE⊥AC,∴∠E=90°,∴∠EAD+∠EDA=90°,∴∠EDA=60°,∴∠EDO=∠EDA+∠ADO=90°,∴OD⊥DE,∴DE是⊙O的切线;(2)解:连接BD,∵AB为⊙O的直径,∴∠ADB=90°,∵∠DAB=30°,AB=6,∴BD=AB=3,∴AD==3.2.(1)证明:如图1,连接BD,∵AB是⊙O的直径,∴∠ADB=90°,∴∠DAB+∠DBA=90°,∵BC是⊙O的切线,∴∠ABC=90°,∴∠C+∠CAB=90°,∴∠C=∠ABD,∵∠AGD=∠ABD,∴∠AGD=∠C;(2)解:∵∠BDC=∠ABC=90°,∠C=∠C,∴△ABC∽△BDC,∴,∴=,∴AC=9,∴AB==3,∵CE=2AE,∴AE=3,CE=6,∵FH⊥AB,∴FH∥BC,∴△AHE∽△ABC,∴,∴==,∴AH=,EH=2,如图2,连接AF,BF,∵AB是⊙O的直径,∴∠AFB=90°,∴∠AFH+∠BFH=∠AFH+∠FAH=90°,∴∠FAH=∠BFH,∴△AFH∽△FBH,∴=,∴=,∴FH=,∴EF=﹣2.3.证明:(1)如图1,连接AD、BC,∵AB是半圆O的直径,∴∠ADB=90°,∵DE⊥AB,∴∠ADE=∠ABD,又∵AF=FG,即点F是Rt△AGD的斜边AG的中点,∴DF=AF,∴∠DAF=∠ADF=∠ABD,又∵∠DAC=∠DBC,∴∠ABD=∠DBC,∴=,∴即点D平分;(2)如图2所示,连接OD、AD,∵点E是线段OA的中点,∴,∴∠AOD=60°,∴△OAD是等边三角形,∴AD=AO=AH,∴△ODH是直角三角形,且∠HDO=90°,∴DH是⊙O的切线.4.(1)证明:∵AB是半圆O的直径,∴∠ACB=∠ADB=90°,在Rt△CBA与Rt△DAB中,,∴Rt△CBA≌Rt△DAB(HL);(2)解:∵BE=BF,由(1)知BC⊥EF,∴∠E=∠BFE,∵BE是半圆O所在圆的切线,∴∠ABE=90°,∴∠E+∠BAE=90°,由(1)知∠D=90°,∴∠DAF+∠AFD=90°,∵∠AFD=∠BFE,∴∠AFD=∠E,∵∠DAF=90°﹣∠AFD,∠BAF=90°﹣∠E,∴∠DAF=∠BAF,∴AC平分∠DAB.5.(1)证明:连接OD,∵AB为⊙O的直径,点D是半圆AB的中点,∴∠AOD=AOB=90°,∵DH∥AB,∴∠ODH=90°,∴OD⊥DH,∴直线DH是⊙O的切线;(2)解:连接CD,∵AB为⊙O的直径,∴∠ADB=∠ACB=90°,∵点D是半圆AB的中点,∴=,∴AD=DB,∴△ABD是等腰直角三角形,∵AB=10,∴AD=10sin∠ABD=10sin45°=10×=5,∵AB=10,BC=6,∴AC==8,∵四边形ABCD是圆内接四边形,∴∠CAD+∠CBD=180°,∵∠DBH+∠CBD=180°,∴∠CAD=∠DBH,由(1)知∠AOD=90°,∠OBD=45°,∴∠ACD=45°,∵DH∥AB,∴∠BDH=∠OBD=45°,∴∠ACD=∠BDH,∴△ACD∽△BDH,∴,∴=,解得:BH=.6.(1)证明:如图1,连接OC,,∵CD是切线,∴OC⊥CD.∵AD⊥CD,∴AD∥OC,∴∠1=∠4.∵OA=OC,∴∠2=∠4,∴∠1=∠2,即∠CAD=∠CAB.(2)解:如图2,连接BC,∵=,∴设AD=2x,AB=3x,∵AB是⊙O的直径,∴∠ACB=∠ADC=90°,∴∠ACB=90°,∵AD⊥DC,∴∠ADC=90°,∵∠DAC=∠CAB,∴△ACD∽△ABC,∴=,∴=,解得,x1=2,x2=﹣2(舍去),∴AD=4,∴CD==2.7.解:(1)∵的半径OA=2,OC⊥AB于点C,∠AOC=60°,∴AC=OA•sin60°=2×=,∴AB=2AC=2;(2)∵OC⊥AB,∠AOC=60°,∴∠AOB=120°,∵OA=2,∴的长是:=.8.(1)证明:连接OC,∵AB是⊙O的直径,∴∠ACB=90°,∵CE⊥AB,∴∠CEB=90°,∴∠ECB+∠ABC=∠ABC+∠CAB=90°,∴∠A=∠ECB,∵∠BCE=∠BCD,∴∠A=∠BCD,∵OC=OA,∴∠A=∠ACO,∴∠ACO=∠BCD,∴∠ACO+∠BCO=∠BCO+∠BCD=90°,∴∠DCO=90°,∴CD是⊙O的切线;(2)解:∵∠A=∠BCE,∴tan A==tan∠BCE==,设BC=k,AC=2k,∵∠D=∠D,∠A=∠BCD,∴△ACD∽△CBD,∴==,∵AD=8,∴CD=4.9.(1)证明:∵AE=DE,OC是半径,∴=,∴∠CAD=∠CBA.(2)解:∵AB是直径,∴∠ACB=90°,∵AE=DE,∴OC⊥AD,∴∠AEC=90°,∴∠AEC=∠ACB,∴△AEC∽△BCA,∴=,∴=,∴CE=3.6,∵OC=AB=5,∴OE=OC﹣EC=5﹣3.6=1.4.10.解:证法错误;证明:连结OC,∵⊙O与AB相切于点C,∴OC⊥AB,∵OA=OB,∴AC=BC.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
九年级数学圆测试题
一、选择题
1.若⊙O所在平面内一点P到⊙O上的点的最大距离为a,最小距离为b(a>b),则此圆的半径为()
A.
2b
a
+
B.
2
b
a-
C.
2
2b
a
b
a-
+
或D.b
a
b
a-
+或
2.如图24—A—1,⊙O的直径为
10,圆心O到弦AB的距离OM的长为3,
则弦AB的长是()
A.4 B.6
C
.7
D.8
3.已知点O为△ABC的外心,若∠A=80°,则∠BOC的度数为()A.40°B.80°C.160°D.120°
4.如图24—A—2,△ABC内接于⊙O,若∠A=40°,则∠OBC的度数为()A.20°B.40°C.50°D.70°
5.如图24—A—3,小明同学设计了一个测量圆直径的工具,标有刻度的尺子OA、OB在O点钉在一起,并使它们保持垂直,在测直径时,把O点靠在圆周上,读得刻度OE=8个单位,OF=6个单位,则圆的直径为()
A.12个单位B.10个单位
C.1个单位D.15个单位
1.(改编)如图,AD⊥BC于点D,AD=4cm,AB=8cm,AC=6cm,则⊙O的直径是()A.4cm B.12cm C.8cm D.16cm
2.如图,矩形与O相交,若AB=4,BC=5,DE=3,则EF的长为()A. 3.5 B. 6.5 C.7 D.8
3.若圆的一条弦把圆分成度数的比为1:3的两条弧,则劣弧所对的圆周角等于()
图24—A—5
图24—A—1 图24—A—2 图24—A—3 图24—A—4
A . 45°
B . 90°
C . 135°
D . 270°
4.(改编)已知,如图,在ABC 中,70A ∠=,O 截ABC 的三边所得的弦长相等,则BOC ∠=( )
A .
140
B . 135
C .
130
D . 125
5.(08威海市)如图,AB 是⊙O 的直径,点C ,D 在⊙O 上,OD ∥AC ,下列结论错误的是
A .∠BOD =∠BAC
B .∠BOD =∠COD
C .∠BA
D =∠CAD D .∠C =∠D 二、填空题(本题共8小题,每题4分,共32分)
6.在平面内到定点A 的距离等于3cm
的点组成的图形是 .
7.如图,在圆O 中,
AB 、AC 为互相垂直且相等的两条弦,OD ⊥AB ,OE ⊥AC ,垂足分别为D 、E ,若AC=2cm ,则圆O 的半径为____________cm 。
8.(改编)如图,在“世界杯”足球比赛中,甲带球向对方球门PQ 进攻,当他带球冲到A 点时,同样乙已经助攻冲到B 点,丙助攻到C 点。
有三种射门方式:第一种是甲直接射门;第二种是甲将球传给乙,由乙射门。
第三种是甲将球传给丙,由丙射门。
仅从射门角度考虑,应选择________种射门方式.
9.如图,直角坐标系中一条圆弧经过网格点A 、B 、C ,其中,B 点坐标为(4,4),则该圆弧所在圆的圆心坐标为 .
B O A C
D
10.(改编)如图,⊙O是等边三角形ABC的外接圆,点D是⊙O上异于B、C的一点,
则∠
BDC = .
11.(原创)如图,已知⊙D在直角坐标系且点D的坐标为(4,4), ⊙D过坐标系中的A、
B、C三点,则∠ABC=
12.(2008·达州市)如图,某花园小区一圆形管道破裂,修理工准备更换一段新管道,现在量得污水水面宽度为80cm,水面到管道顶部距离为20cm,则修理工应准备内直径是cm的管道.
13.半径为cm
5的圆O中有一点P,OP=4,则过P的最短弦长_________,最长弦是__________,
三.解答题
22.如图24—A—13,AD、BC是⊙O的两条弦,且AD=BC,
求证:AB=CD。
图24—A—13
23.如图24—A —14,已知⊙O 的半径为8cm ,点A 为半径OB 的延长
线上一点,射线AC 切⊙O 于点C ,BC 的长为cm 3
8,求线段AB 的长。
24.已知:△ABC 内接于⊙O ,过点A 作直线EF 。
(1)如图24—A —15,AB 为直径,要使EF 为⊙O 的切线,还需添加的条件是(只需写出三种情况):
① ;② ;③ 。
(2)如图24—A —16,AB 是非直径的弦,∠CAE=∠B ,求证:EF 是⊙O 的切线。
⌒ 图24—A —14
图24—A —15 图24—A —16。
