MATLAB跟轨迹分析
利用MATLAB进行根轨迹分析

利用MATLAB进行根轨迹分析根轨迹分析是一种用于研究系统稳定性和动态特性的方法,通过研究系统的传递函数来绘制系统极点随参数变化的轨迹。
MATLAB提供了强大的工具和函数来进行根轨迹分析。
根轨迹是由系统的极点随参数变化所形成的轨迹,它可以反映系统的稳定性、阻尼比、上升时间、超调量等动态性能指标。
根轨迹的绘制通常包括以下步骤:1.定义系统传递函数:首先,需要根据具体的控制系统问题定义系统的传递函数。
传递函数是描述输入与输出间关系的数学模型,通常用分子多项式和分母多项式的比值来表示。
2. 极点位置确定:根据系统传递函数的分母多项式,可以求解系统的极点位置。
MATLAB提供了roots函数来计算多项式的根。
3. 绘制根轨迹:通过参数变化,将系统的极点位置代入传递函数的分子多项式中,可以计算得出系统的零点。
然后,使用MATLAB的plot函数将所有极点和零点绘制在复平面上。
4.判断稳定性:通过观察根轨迹的形状,可以判断系统的稳定性。
如果所有极点都位于左半平面,系统是稳定的。
如果存在极点位于右半平面,系统是不稳定的。
5.分析动态特性:根轨迹的形状可以提供许多关于系统动态特性的信息。
例如,阻尼比可以通过根轨迹上极点到原点的距离和纵坐标之比来估计;超调量可以通过根轨迹的形状和最大振幅来估计。
MATLAB提供了许多用于根轨迹分析的函数和工具箱,包括rlocus函数、nyquist函数和bode函数等。
这些函数可以方便地绘制根轨迹、Nyquist图和Bode图,从而帮助工程师分析系统稳定性以及设计和调整控制器。
根轨迹分析在控制系统设计和调优中具有重要作用。
通过根轨迹的绘制和分析,工程师可以深入了解控制系统的动态特性,并根据需要调整系统参数来达到设计要求。
同时,根轨迹分析也是控制系统教学和研究中常用的方法和工具。
总之,MATLAB是进行根轨迹分析的强大工具,通过绘制根轨迹和分析根轨迹的形状和特性,可以帮助工程师深入了解控制系统的稳定性和动态特性,从而有效地设计和调整控制器。
用MATLAB绘制根轨迹

国防工业出版社
.
16
[M例a子tla]b系画统出的系开统环的传根递轨函迹数。为:Gk(s)s(s11)(s2) ,试利用 [解]打开Matlab,创建一个m文件,输入下列程序片段:
num=[0 0 0 1];%开环传递函数分子系数,降幂排列 den=[1 3 2 0]; %开环传递函数分母系数,降幂排列 r=rlocus(num,den);
(s)
|sd
可以求得分离点。
近似求法:分离点在[-4,0]之间。
s0
-0.5 -1 -1.5 -2.0 -2.5 -3 -3.5 -4
k gd 0
1.628 3
5.971 8.80 9.375 7.457 3.949
k gd 的最大值为9.375,这时s=-2.5,是近似分离点。
.
4
➢ 入射角:2 103 ➢ 与虚轴的交点(略)。这时的增益值:kgp14,64,195
解得:kg 44
k ( i s 1)
开环传递函数以G k (s)
i 1 n
的形式表示时,k称为开环放
大系数。
(T j s 1)
j 1
显然 k与 k g 的关系为:k kg
zi ,式中 p j 不计0极点。 pj
所以,开环放大系数:k 44 1.83
46
由于闭环极点之和等于开环极点之和,所以另一个闭环极点
n2 2nsn2
(s)
n2 s(s2)
共轭极点为:s1,2 nj 12n
在s平面上的分布如右图: 闭环极点的张角 为:
n
j 1 2n
co s(12 n)n 2 (n )2, co 1s
控制系统MATLAB仿真2-根轨迹仿真

Gk ( s)
k g ( s 0.5) s( s 1)( s 2)( s 5)
绘制系统的根轨迹,确定当系统稳定时,参数kg 的取值范围。 num=[1 0.5]; den=conv([1 3 2],[1 5 0]); G=tf(num,den); K=0:0.05:200; rlocus(G,K) [K,POLES]= rlocfind(G) figure(2) Kg=95; t=0:0.05:10; G0=feedback(tf(Kg*num,den),1); step(G0,t)
Root Locus 8
8 6 4 2 0 -2 -4 -6 -8 -8 x x x
6
4
2
Imaginary Axis
0
-2
-4
-6
-8 -8
-6
-4
-2
0 Real Axis
2
4
6
8
-6
-4
-2
0
2
4
6
8
(a) 直接绘制根轨迹
(b) 返回参数间接绘制根轨迹
图1 例1系统根轨迹
二、MATLAB根轨迹分析实例
用户可以通过Control Architecture窗口进行系 统模型的修改,如图9。
图9 rltool工具Control Architecture窗口
也可通过System Data窗口为不同环节导入已 有模型,如图10。
图10 rltool工具System Data窗口
可以通过Compensator Editor的快捷菜单进行 校正环节参数的修改,如增加或删除零极点、 增加超前或滞后校正环节等,如图11。
Step Response 2 1.8 1.6 1.4 1.2
Matlab实验三 绘制根轨迹

for
Principles of Automatic Control
实验三 绘制根轨迹 1: 绘制根轨迹 2: 参量分析
① 绘制根轨迹 rlocus(sys)
Gk
(s)
K *(s 1) (s 2)(s 3)
rlocus(num, den)
rlocus(sys,k)
②参量分析(根轨迹图上一顿乱点即可)
K1
(s a )nm
1
根轨迹渐进线的方程是新的根轨迹方程。
Байду номын сангаас
• 例: 绘制根轨迹及其渐近线
G(s)
K1
s(s 1)(s 2)
⑥讨论增加零点对根轨迹的影响 试试-2至-4之间的零点
G(s)
K1
s(s 1)(s 2)
r=rlocus(sys)
Gk
(s)
K *(s 1) (s 2)(s 3)
r=rlocus(num, den)
[r,k]=rlocus(sys)
[r,k]=rlocus(num, den)
③测量出根轨迹增益和对应闭环极点坐标,
在窗口显示
Gk
(s)
K *(s 1) (s 2)(s 3)
[k,poles] = rlocfind(sys)
[k,poles] = rlocfind(sys,p) P为已知的要研究的闭环极点。
④绘制零、极点以及在窗口显示零极点
pzmap(sys)
Gk
(s)
K *(s 1) (s 2)(s 3)
[p,z]=pzmap(sys) 求解零极点的好方法
⑤绘制根轨迹渐近线
一般人我不告诉他:
当根轨迹渐进线与实轴的交点已求出后, 可得到方程,这是根轨迹渐进线的方程。
利用MATLAB进行根轨迹分析

实验二 利用MATLAB 进行根轨迹分析一 实验目的1 掌握利用MA TLAB 绘制控制系统根轨迹图形等方法。
2 掌握利用绘制的根轨迹图形进行线性系统分析的方法二 实验内容1 初步掌握MA TLAB 根轨迹绘制以及分析中的基本命令;2 绘制系统的根轨迹图并进行性能分析三 实验步骤1 初步掌握MA TLAB 根轨迹绘制中的基本命令;可利用pzmap 函数绘制连续系统的零、极点图,也可以利用tf2zp 函数求出系统的零、极点。
如考虑函数432543232546()34276s s s s G s s s s s s ++++=+++++ 的零、极点及增益,并绘制其零、极点图。
执行如下程序:num=[3 2 5 4 6];den=[1 3 4 2 7 2];[Z,P,K]=tf2zp(num,den)pzmap(num,den)Title(‘Pole-Zore Map ’)或者num=[3 2 5 4 6];den=[1 3 4 2 7 2];sys1=tf(num,den)pzmap(sys1)Title(‘Pole-Zore Map ’)绘制结果如下:2 绘制系统的根轨迹考虑如下开环传递函数*2()()(3)(22)K G s H s s s s s =+++ 试绘制根轨迹执行如下命令:num=[0 0 0 0 1];den=[1 5 8 6 0];rlocus(num,den)grid绘制结果如下:四 作业1 设单位反馈系统的开环传递函数为(0.011)(0.021)K s s s ++,要求:(1)画出根轨迹;(2)从图中确定系统的临界稳定开环增益c K ;(3)从图中确定与系统临界阻尼比相应的开环增益K 。
2 设单位负反馈系统的开环传递函数(4)()(2)K s G s s s +=+,试绘制根轨迹图,并从图中找出系统具有最小阻尼比时的闭环极点和对应的增益K 。
MATLAB的根轨迹分析
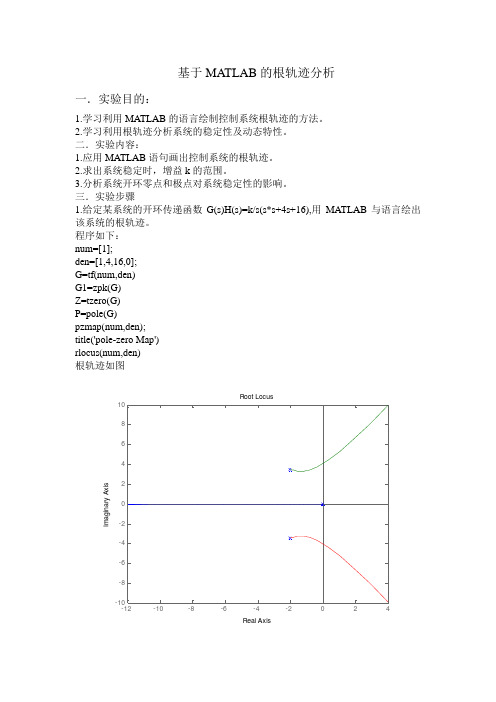
基于MATLAB 的根轨迹分析一.实验目的:1.学习利用MATLAB 的语言绘制控制系统根轨迹的方法。
2.学习利用根轨迹分析系统的稳定性及动态特性。
二.实验内容:1.应用MATLAB 语句画出控制系统的根轨迹。
2.求出系统稳定时,增益k 的范围。
3.分析系统开环零点和极点对系统稳定性的影响。
三.实验步骤1.给定某系统的开环传递函数G(s)H(s)=k/s(s*s+4s+16),用MATLAB 与语言绘出该系统的根轨迹。
程序如下:num=[1];den=[1,4,16,0];G=tf(num,den)G1=zpk(G)Z=tzero(G)P=pole(G)pzmap(num,den);title('pole-zero Map')rlocus(num,den)根轨迹如图-12-10-8-6-4-2024-10-8-6-4-20246810Root LocusReal Axis I m a g i n a r y A x i s结论:由上图可知增益k 的取值范围:0<k<642.将系统的开环传递函数改为:G(s)H(s)=k/s(s*s+4s+5),绘出该系统根轨迹图,观察增加了开环零点后根轨迹图的变化情况。
程序如下:num=[1,1];den=[1,4,5,0];G=tf(num,den)G1=zpk(G)Z=tzero(G)P=pole(G)pzmap(num,den);title('pole-zero Map')rlocus(num,den)根轨迹如图-2.5-2-1.5-1-0.50-5-4-3-2-1012345Root LocusReal Axis I m a g i n a r y A x i s结论:增加了开环零点后根轨迹的变化3.将系统的开环传递函数改为:G(s)H(s)=k/s(s-1)(s*s+4s+5),绘出该系统的根轨迹图,观察增加了开环零点后根轨迹的变化情况。
第14讲应用MATLAB的根轨迹分析

第四章 根轨迹分析法 解: 1)创建MATLAB环境。 (1)在MATLAB环境下输入如下文本程序 g=tf(1,conv([1,1,0],[1,3])); rlocus(g) (2)在根轨迹图上找到 s 3 3 .2 5 实部比为
ts 3 n
3 .2 5 0 .3 7 2 8 .7 3 ~ 5
3 2
T (s )
在MATLAB环境下输入如下文本程序: g=tf(1.81,[1,4,3,1.81]) step(g)
% 1 6 % , t p 5 .1 7 s, t s 7 .5 9s
自动控制原理
12
第四章 根轨迹分析法 2)单位斜坡函数输入时,
e ss e ss lim s
自动控制原理
13
第四章 根轨迹分析法
总 结
1. 根轨迹法是一种图解方法。它不用求解高次代数方程 即可将系统闭环特征方程的根解出来。
2. 根轨迹是以开环传递函数中的某个参数为参变量而画 出的闭环特征方程式的根轨迹图。 3. 根轨迹图不仅能直观地表示出参数的变化对系统性能 的影响,而且还可以用它求出指定参变量或指定阻尼比 相对应的闭环极点。根据确定的闭环极点和已知的闭环 零点,就能计算出系统的输出响应及其性能指标,从而 避免了求解高阶微分方程 的麻烦。
g 2
Imaginary Axis
0.88
1
(s 1) s (s 4 s 8 )(s 3)
2
1 K
g
0 0.88 1 2 3 0.38 -2 0.27 -1.5 Real Axis 0.19 0.12 0.06 -1 -0.5 4 5 0
MATLAB程序为 0.68 num=[1,1]; 0.5 -5 den=conv([1,4,8,0],[1,3]); -3 -2.5 g=tf(num,den) 图4-25 rlocus(g)
第九章根轨迹法MATLAB

对根轨迹使用[k,poles]=rlocfind(sys)进行操作,将十字光标指向根 轨迹与纵坐标的交点时,对应的开环增益与极点为: K=2.9957, ploes=-2.9919 -0.0040+1.4056i -0.0040-1.4056i。
当参数K从0→3变动时,根轨迹均在s平面虚轴左半部分,对应的 闭环系统稳定,一旦根轨迹穿越纵坐标到达其右侧,对应的 K > 3时, 闭环系统就进入不稳定状态。 当在根轨迹实轴阶段时(过阻尼状态),对应着系统闭环阶跃响 应无超调,闭环系统稳定。当在根轨迹圆上时,系统闭环特征方程 出现共轭复根(欠阻尼状态),系统闭环阶跃响应有超调量,但系 统还是稳定的。
[r, k]=rlocus (sys):此命令只返回系统特征方程根位置的复数矩阵和 相应的增益向量k,而不绘制零、极点图。
三、计算给定一组根的系统根轨迹增益
[k, poles]=rlocfind (sys):sys为LTI对象的开环传递函数,命令执 行后,可在根轨迹窗口中显示出十字光标,当用户选择根轨迹上 的一点时,其相应的增益由k记录,与增益对应的闭环极点(即特 征方程的根)由poles记录;
10
9.2 用根轨迹法判定系统的稳定性
采用[k, poles]=rlocfind (sys)(可在根轨迹窗口中显示出十字光 标,当用户选择根轨迹上的一点时,其相应的增益由k记录,与 增益对应的闭环极点(即特征方程的根)由poles记录)这条指令反 复进行操作,可以来判断系统的稳定性。
例9-5
已知一单位负反馈系统的开环传递函数为:
6
k= 0.4984
poles =
-2.0664 -0.0918 + 0.3349i -0.0918 - 0.3349i
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
z1
p1
×
p3
5.2 MATLAB跟轨迹相关指令
rlocus rlocfind pzmap
1. pzmap
功能:绘制系统的零极点图。 格式:[p,z]=pzmap(A,B,C,D) [p,z]=pzmap(num,den) pzmap(p,z)
说明:
对SISO系统,pzmap函数可绘制出传递函 数的零极点; 对MIMO系统,pzmap函数可绘制系统的特 征向量和传递零点。 当不带输出变量引用时,pzmap函数可在当 前图形窗口中绘制系统的零极点图,其中极 点用“×”表示,零点用“o”表示。P为极点 的列向量,z为零点的列向量。
即
|G(s)H(s)| K 1 | s zi |
i 1 m
| s pi |
i 1
n
1
G(s)H(s) (s-z i )- (s-p i ) 180 (2q 1), (q 0,1,2,
i 1 i 1ຫໍສະໝຸດ mn)(**)
★ 根据相角条件确定根轨迹上的点
可以指定阻尼比系数z与自然振荡角频率wn。
5. 3
跟轨迹分析与设计工具rltool
例如: 对于单位反馈控制系统的开环传递为
K ( s 1) G (s) s ( s 1)( s 4)
用rltool方法绘制分析系统性能。
num=[1 1]; den=conv([1 0],conv([1 -1],[1 4])); sys=tf(num,den); rltool(sys)
5.zgrid
功能:
在离散系统跟轨迹上加等阻尼线和等自然 振荡角频率
格式: zgrid(); zgrid(z,wn);
说明: (1)与pzmap(),rlocus()配合使用 (2)zgrid():
阻尼比间隔0.1,范围:0-1; 自然振荡角频率间隔为pi/10,范围0-pi
(3)zgrid(z,wn)
K ( s 1) GH ( s ) s ( s 1)( s 4) 。
(1) 画出系统的跟轨迹 (2) 确定使闭环系统稳定的增益值 K; (3) 分析系统的阶跃响应性能; 利用 rltool 对系统的性能进行分析
5. 4
用跟轨迹分析系统性能
所有极点位于虚轴左面——稳定
稳定性分析
暂态性能分析
4. sgrid
功能:
在连续系统跟轨迹上加等阻尼线和等自然 振荡角频率
格式: sgrid(); sgrid(z,wn);
说明: (1)与pzmap(),rlocus()配合使用 (2)sgrid(): 阻尼比间隔0.1,范围:0-1; 自然振荡角频率间隔为0.1,范围0-10 (3)sgrid(z,wn) 可以指定阻尼比系数z与自然振荡角频率wn。
3. rlocfind
功能: 计算给定一组根的根轨迹增益。 格式: [K,poles]=rlocfind(A,B,C,D) [K,poles]=rlocfind(A,B,C,D,P) [K,poles]=rlocfind(num,den) [K,poles]=rlocfind(num,den,P)
例5-1 有连续系统
0.05 s 0.045 G (s) 2 2 ( s 1.8 s 0.9)( s 5 s 6)
要求绘制出零极点图。
解:运行以下程序,得到如图所示的零极点图 num=[0.05,0.045]; den=conv([1,-1.8,0.9],[1,5,6]); pzmap(num,den); title('Pole-Zero Map')
第五章
5.1 5.2 5. 3 5. 4
MATLAB跟轨迹分析
根轨迹法基础 MATLAB根轨迹相关指令 根轨迹分析与设计工具rltool 用根轨迹分析系统性能
5.1
跟轨迹法基础
一、根轨迹方程 二、基本条件
根轨迹的相角条件 根轨迹的幅值条件
三、基本法则
一、跟轨迹方程 开环传递函数零极点形式:
打开bode图 K=6的临界增益
思考题
1. 已知某系统的闭环传递函数为
G( s)
2.5(s 6) , 2 ( s 2s 3)( s 5)
试试用 MATLAB 画出系统的零极点,并求出系统的零极点。
num=2.5*[1,6]; den=conv([1 2 3],[1 5]) pzmap(sys) [p,z]= pzmap(sys) title('零极点图')
2. rlocus
功能:绘制跟轨迹,求增益为k时的极点。 格式: rlocus(num,den) [R,K]=rlocus(num,den) [R,K]=rlocus(num,den,k) [R,K]=rlocus(A,B,C,D) [R,K]=rlocus(A,B,C,D,k)
说明:
rlocus函数可计算SISO开环模型的Evans 根轨迹,根轨迹以反馈增益的函数形式给 出了闭环极点的轨迹(假定为负反馈)。
6.已知单位负反馈系统,系统的开环传递函 数为
K G( s) s( s 1)( s 4)
画出系统的跟轨迹,并分析暂态特性。
特征方程:
1 G( S ) H ( S ) 0
根轨迹方程:
G( S ) H ( S ) 1
二、基本条件
幅值条件与相角条件
|G(s)H(s)| 1 -----------------------------------幅值条件 G(s)H(s) = 180 (2q 1), (q 0,1,2, ) ---相角条件
试使用 MATLAB 绘制系统的跟轨迹,并在跟轨迹上任选一点, 计算该点的增益 K 及其所有极点的位置
4. 已知单位负反馈系统, 系统的开环传递函数为
2 s 2 5s 1 GH ( s ) 2 s 2s 3 ,
试使用 MATLAB 绘制系统带网格线的根轨迹。
5. 综合实例 已知单位负反馈系统,系统的开环传递函数为
动态特性取决于主导极点 在主导极点的基础上增加闭环极点
系统的响应速度降低 超调量减小
在主导极点的基础上增加闭环零点
系统的响应速度加快 超调量增大
偶极子对动态特性影响可以忽略。
时间响应的稳态分量取决于输入函数 时间响应的暂态分量取决于闭环零极点
左右分布决定终值 虚实分布决定振型 远近分布决定快慢
例5-2:绘制如下系统的根轨迹图
0.05s 0.045 G (s) 2 ( s 1.8s 0.9)( s 2 5 s 6)
解: 下面的程序可以计算并绘制根轨迹图,如 图所示,然后用 rlocfind 函数在图中选 择极点位置(十字光标如图所示),得 到反馈增益的值。
G=tf([0.05,0.045],conv([1,-1.8,0.9],[1,5,6])) rlocus(G),K=rlocfind(G)
G ( s) H ( s) K1 ( s z1 ) ( s zm ) ( s p1 )( s p2 ) ( s pn )
n
K1 ( s zi )
i 1
m
(s p )
j 1 j
闭环传递函数:
( s ) G( s) 1 G( s) H ( s)
设某一系统的开环零极点如图,在S平面 中的任意一点 s 0 ,用相角条件可以判断 s 0 是不是根轨迹的点。 × s0 p2 O 1.从 s 0 到各零极点连直线 2.用量角器量(s0 p1 ) ,…等 各个角. 3.将量好的值代入(**) 式,若等式成立,则 s 0 就是 根轨迹上的点.
×
O
2. 已知单位负反馈系统,系统的开环传递函数为
GH ( s ) K ( s 1) , s(0.5s 1)(4s 1)
试使用 MATLAB 绘制系统的跟轨迹。
3. 已知单位负反馈系统,系统的开环传递函数为
G (s)
K ( s 5) ( s 1)( s 3)( s 12) ,
