立体几何之外接球问题含问题详解
立体几何中球的内切和外接问题(完美版)
则这个球的表面积是( )
A.16π
B.20π
C.24π
D.32π
4
举一反三-突破提升
2.正六棱柱的底面边长为 4,高为 6,则它的外接球的表面积为
A. 20 B. 25 C. 100 D. 200
4
举一反三-突破提升
已知正三棱锥 P-ABC 的主视图和俯视图如图所 示,
则此三棱锥的外接球的表面积为 ( )
ห้องสมุดไป่ตู้
切(如图).求:
(1)这个正三棱锥的表面积; (2)这个正三棱锥内切球的表面积与体积.
考点一 考点二 考点三
4
举一反三-突破提升
-30-
解:(1)底面正三角形中心到一边的距离为1 × 3×2 6 = 2,则正棱锥
32
侧面的斜高为 12 + ( 2)2 = 3.
∴S 侧=3×12×2 6 × 3=9 2.
,五个顶点都在同一个球面上,
P
设外接球半径为 R,在△OO1A 中有
D
解得 . ∴ .
O1
O C
A B
6
测棱相等的锥体顶点的投影在底面外接圆心
例 7、.若三棱锥 S-ABC 的底面是以 AB 为斜边的等腰直角三角形,AB=2,
SA=SB=SC=2,则该三棱锥的外接球的球心到平面 ABC 的距离为( )
B、体积为 3
D、外接球的表面积为 16
3
1正视图
1
3 1 侧视图
俯视图
点 A、B、C、D 均在同一球面上,其中
是正三角形,
AD 平面 ABC,AD=2AB=6,则该球的体积为 ( )
(A)
(B)
(C)
(D)
平面四边形 ABCD中, AB AD CD1, BD 2, BD CD ,
2022高考数学立体几何外接球专题(含解析)
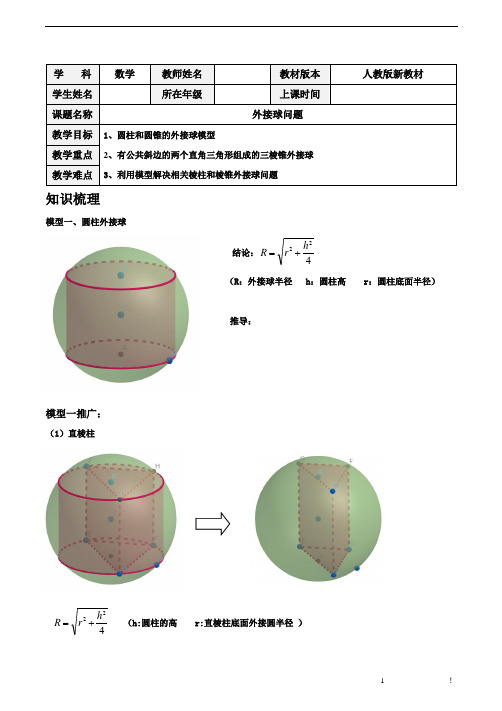
知识梳理模型一、圆柱外接球结论:422h r R +=(R:外接球半径 h:圆柱高 r:圆柱底面半径)推导:模型一推广:(1)直棱柱422h r R += (h:圆柱的高 r:直棱柱底面外接圆半径 )学 科 数学 教师姓名 教材版本 人教版新教材学生姓名所在年级上课时间课题名称外接球问题教学目标 1、圆柱和圆锥的外接球模型2、有公共斜边的两个直角三角形组成的三棱锥外接球3、利用模型解决相关棱柱和棱锥外接球问题教学重点 教学难点(2)侧面为三角形,底面为矩形,侧面和底面垂直的四棱锥(3)侧棱垂直于底面的棱锥【2017深二模】已知三棱锥S-ABC,△ABC是直角三角形,其斜边AB=8,SC⊥平面ABC,SC=6,则三棱锥的外接球的表面积为( )(A)64π(B)68π(C)72π(D)100π模型二、圆锥外接球结论:hh r R 222+=(R:外接球半径 h:圆锥高 r:圆锥底面半径)推导:模型二推广:(1)棱锥(上顶点在底面外心正上方)外接球hh r R 222+= (h:棱锥的高 r:棱锥底面外接圆半径 )【2018深一模】如图,网格纸上小正方形的边长为1,某几何体的三视图如图所示,则该几何体的外接球表面积为()A.B.C.16πD.25π【2017全国一卷文 16】已知三棱锥S−ABC的所有顶点都在球O的球面上,SC是球O的直径.若平面SCA⊥平面SCB,SA=AC,SB=BC,三棱锥S−ABC的体积为9,则球O的表面积为______________.【2019 全国一卷理 12】已知三棱锥P−ABC的四个顶点在球O的球面上,PA=PB=PC,△ABC是边长为2的正三角形,E,F分别是PA,AB的中点,∠CEF=90°,则球O的体积为A.B.C.D模型一、二总结题型:求几何体的外接球模型一: 422h r R += (圆柱模型) 模型二: h h r R 222+=(圆锥模型)适用于: 适用于:1、所有的圆柱、直棱柱 上顶点在底面外心正上方的棱锥2、侧棱垂直于底面的棱锥3、侧面为任意三角形,底面为矩形, 且侧面垂直于底面的四棱锥模型三、有公共斜边的两个直角三角形组成的三棱锥 ,球心在公共斜边的中点处如下图,∠ABC=∠ADC=90°,则O 为外接球球心1、在矩形ABCD 中,AB =4,BC =3,沿AC 将矩形ABCD 折成一个直二面角D AC B --,则四面体ABCD 的外接球的体积为A. π12125B.π9125C.π6125D.π31252.三棱锥S ABC -的所有顶点都在球O的球面上,且SA AC SB BC ====4SC =,则该球的体积为A 2563πB 323π C 16π D 64π专题练习类型一 构造法(补形法)【例1】已知是球上的点, , , ,则球的表面积等于________________.【例2】【辽宁省鞍山一中2019届高三三模】刘徽《九章算术•商功》中将底面为长方形,两个三角面与底面垂直的四棱锥体叫做阳马.如图,是一个阳马的三视图,则其外接球的体积为( )A .B .C .3πD .4π,,,S A B C O SA ABC ⊥平面AB BC ⊥1SA AB ==BC =O【举一反三】1、【山东省济宁市2019届高三一模】已知直三棱柱的底面为直角三角形,且两直角边长分别为1和,此三棱柱的高为,则该三棱柱的外接球的体积为A.B.C.D.2、【辽宁省师范大学附属中学2019届高三上学期期中】在三棱锥S−ABC中,,则三棱锥S−ABC外接球的表面积为()A.25ΠB.C.50ΠD.3、【河南省天一大联考2019届高三阶段性测试(五)】某多面体的三视图如图所示,其中正视图是一个直角边为2的等腰直角三角形,侧视图是两直角边分别为2和1的直角三角形,俯视图为一矩形,则该多面体的外接球的表面积为()A.7πB.8πC.9πD.10π类型二 正棱锥与球的外接【例3】正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为 ( ) A . B . C . D .【举一反三】1、球O 的球面上有四点S ,A ,B ,C ,其中O ,A ,B ,C 四点共面,△ABC 是边长为2的正三角形,平面SAB ⊥平面ABC ,则棱锥S-ABC 的体积的最大值为( )A .33 B . 3 C .2 3 D .42. 【四川省德阳市2018届高三二诊】正四面体ABCD 的体积为,则正四面体ABCD 的外接球的体积为______.814π16π9π274π3、【安徽省蚌埠市2019届高三下学期第二次检查】正三棱锥P −ABC 中,√2PA =AB =4√2,点E 在棱PA 上,且PE =3EA .正三棱锥P −ABC 的外接球为球O ,过E 点作球O 的截面α,α截球O 所得截面面积的最小值为__________.类型三 直棱柱的外接球【例4】直三棱柱的各顶点都在同一球面上,若,, 则此球的表面积等于 .【举一反三】1、【云南省2019年高三第二次统一检测】已知直三棱柱的顶点都在球O 的球面上,AB =AC =2,BC =2√2,若球O 的表面积为72Π,则这个直三棱柱的体积是( ) A .16 B .15C .D .2、已知三棱柱的6个顶点都在球的球面上,,,,则球的半径为()A B . C.D .3、 正四棱柱的各顶点都在半径为的球面上,则正四棱柱的侧面积有最111ABC A B C -12AB AC AA ===120BAC ∠=︒111ABC A B C -O 34AB AC ==,AB AC ⊥112AA =O 1321111ABCD A B C D -R值,为 .答案与解析类型一 构造法(补形法)【例1】已知是球上的点, , , ,则球的表面积等于________________. 【答案】 【解析】由已知S,A,B,C 是球O 表面上的点,所以 ,又,,所以四面体的外接球半径等于以长宽高分别以SA,AB,BC 三边长为长方体的外接球的半径,因为, ,所以,所以球的表面积.【指点迷津】当一三棱锥的三侧棱两两垂直时,可将三棱锥补成一个长方体,将问题转化为长方体(正方体)来解.长方体的外接球即为该三棱锥的外接球.【例2】【辽宁省鞍山一中2019届高三三模】刘徽《九章算术•商功》中将底面为长方形,两个三角面与底面垂直的四棱锥体叫做阳马.如图,是一个阳马的三视图,则其外接球的体积为( )A .B .C .3πD .4π,,,S A B C O SA ABC ⊥平面AB BC ⊥1SA AB ==BC =O 4πOA OB OC OS ===SA ABC ⊥平面AB BC ⊥S ABC -1SA AB ==BC =22,1R R ==O 244S R ππ==【答案】B【解析】由题意可知阳马为四棱锥,且四棱锥的底面为长方体的一个底面,四棱锥的高为长方体的一棱长,且阳马的外接球也是长方体的外接球,由三视图可知四棱锥的底面是边长为1的正方形,四棱锥的高为1,∴长方体的一个顶点处的三条棱长分别为1,1,1,∴长方体的对角线为,∴外接球的半径为,∴外接球的体积为.故选:B.【指点迷津】当一四面体或三棱锥的棱长相等时,可以构造正方体,在正方体中构造三棱锥或四面体,利用三棱锥或四面体与正方体的外接球相同来解即可.【举一反三】1、【山东省济宁市2019届高三一模】已知直三棱柱的底面为直角三角形,且两直角边长分别为1和,此三棱柱的高为,则该三棱柱的外接球的体积为A.B.C.D.【答案】C【解析】如图所示,将直三棱柱补充为长方体,则该长方体的体对角线为,设长方体的外接球的半径为R,则2R=4,R=2,所以该长方体的外接球的体积,故选C.2、【辽宁省师范大学附属中学2019届高三上学期期中】在三棱锥S−ABC中,,则三棱锥S−ABC外接球的表面积为()A.25蟺B.C.50蟺D.【答案】C【解析】解:如图,把三棱锥S−ABC补形为长方体,设长方体的长、宽、高分别为,则,∴三棱锥外接球的半径∴三棱锥S−ABC外接球的表面积为.故选:C.3、【河南省天一大联考2019届高三阶段性测试(五)】某多面体的三视图如图所示,其中正视图是一个直角边为2的等腰直角三角形,侧视图是两直角边分别为2和1的直角三角形,俯视图为一矩形,则该多面体的外接球的表面积为()A .7πB .8πC .9πD .10π 【答案】C 【解析】由三视图可得,该几何体为一个三棱锥,放在长、宽、高分别为2,1,2的长方体中,此三棱锥和长方体的外接球是同一个,长方体的外接球的球心在体对角线的中点处,易得其外接球的直径为,从而外接球的表面积为9π.故答案为:C.类型二 正棱锥与球的外接【例3】正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为 ( )A .B .C .D .【答案】A .814π16π9π274π【指点迷津】求正棱锥外接球的表面积或体积,应先求其半径,在棱锥的高上取一点作为外接球的球心,构造直角三角形,利用勾股定理求半径. 【举一反三】1、球O 的球面上有四点S ,A ,B ,C ,其中O ,A ,B ,C 四点共面,△ABC 是边长为2的正三角形,平面SAB ⊥平面ABC ,则棱锥S-ABC 的体积的最大值为( )A .33 B . 3 C .2 3 D .4 【答案】A【解析】 (1)由于平面SAB ⊥平面ABC ,所以点S 在平面ABC 上的射影H 落在AB 上,根据球的对称性可知,当S 在“最高点”,即H 为AB 的中点时,SH 最大,此时棱锥S -ABC 的体积最大.学科*网因为△ABC 是边长为2的正三角形,所以球的半径r =OC =23CH =23×32×2=233.在Rt △SHO 中,OH =12OC =33,所以SH =⎝ ⎛⎭⎪⎫2332-⎝ ⎛⎭⎪⎫332=1, 故所求体积的最大值为13×34×22×1=33.2. 【四川省德阳市2018届高三二诊】正四面体ABCD 的体积为,则正四面体ABCD 的外接球的体积为______. 【答案】【解析】 解:如图,设正四面体ABCD 的棱长为x ,过A 作AD ⊥BC , 设等边三角形ABC 的中心为O ,则AO =23AD =√33x ,,,即x=√2a.再设正四面体ABCD的外接球球心为G,连接GA,则,即.∴正四面体ABCD的外接球的体积为.故答案为:.3、【安徽省蚌埠市2019届高三下学期第二次检查】正三棱锥P−ABC中,√2PA=AB=4√2,点E在棱PA上,且PE=3EA.正三棱锥P−ABC的外接球为球O,过E点作球O的截面α,α截球O所得截面面积的最小值为__________.【答案】3π【解析】因为PA=PC=PB=4,AB=AC=BC=4√2,所以PA2+PC2=AC2,所以∠CPA=π2,同理∠CPB=∠BPA=π2,故可把正三棱锥补成正方体(如图所示),其外接球即为球O,直径为正方体的体对角线,故2R=4√3,设PA的中点为F,连接OF,则OF=2√2且OF⊥PA,所以OE=√8+1=3,当OE⊥平面α时,平面α截球O的截面面积最小,此时截面为圆面,其半径为√(2√3)2−32=√3,故截面的面积为3π.填3π.类型三 直棱柱的外接球 【例4】直三棱柱的各顶点都在同一球面上,若,, 则此球的表面积等于 . 【答案】【解析】在中,,可得,由正弦定理,可得外接圆半径r=2,设此圆圆心为,球心为,在中,易得球半径,故此球的表面积为.【指点迷津】直棱柱的外接球的球心在上、下底面的外接圆的圆心的连线上,确定球心,用球心、一底面的外接圆的圆心,一顶点构成一个直角三角形,用勾股定理得关于外接球半径的关系式,可球的半径. 【举一反三】1、【云南省2019年高三第二次统一检测】已知直三棱柱的顶点都在球O 的球面上,AB =AC =2,BC =2√2,若球O 的表面积为72蟺,则这个直三棱柱的体积是( ) A .16 B .15 C .D .【答案】A 【解析】 由题,,因为AB =AC =2,BC =2√2,易知三角形ABC 为等腰直角三角形, 故三棱柱的高故体积V =12脳2脳2脳8=16 故选A111ABC A B C -12AB AC AA ===120BAC ∠=︒ABC ∆2AB AC ==120BAC ∠=︒BC =ABC ∆O 'O RT OBO '∆R =2420R ππ=2、已知三棱柱的6个顶点都在球的球面上,若,,,则球的半径为 ( )A .B .C .D .【答案】C【解析】由球心作面ABC 的垂线,则垂足为BC 中点M.计算AM=,由垂径定理,OM=6,所以半径,选C.3、 正四棱柱的各顶点都在半径为的球面上,则正四棱柱的侧面积有最值,为 . 【答案】大111ABC A B C -O 34AB AC ==,AB AC ⊥112AA =O 213252132=1111ABCD A B C D -R。
立体几何高考专题--外接球的几种常见求法

立体几何高考专题--外接球的几种常见求法高三微专题:外接球在立体几何中,外接球问题是一个重点和难点。
其实质是确定球心O的位置和使用勾股定理求解外接球半径(其中底面外接圆半径r可根据正弦定理求得)。
一、由球的定义确定球心在空间中,如果一个定点与一个简单多面体的所有顶点的距离都相等,那么这个定点就是该简单多面体的外接球的球心。
简单多面体外接球问题是立体几何中的重点和难点。
二、球体公式球的表面积公式为S=4R²,球体积公式为V=4/3R³。
三、球体几个结论:1)长方体、正方体外接球直径等于体对角线长。
2)侧棱相等,顶点在底面投影为底面外接圆圆心。
3)直径所对的球周角为90°(大圆的圆周角)。
4)正三棱锥对棱互相垂直。
四、外接球几个常见模型1.长方体(正方体)模型例1:长方体的长、宽、高分别为3、2、1,其顶点都在球O的球面上,则球O的表面积为14。
练1:体积为8的正方体的顶点都在同一球面上,则该球的表面积为12。
2.正棱锥(圆锥)模型对于侧棱相等,底面为正多边形的正棱锥,其外接球的球心位置位于顶点与底面外心连线线段(或延长线)上。
半径公式为R²=(h-R)²+r²(其中R为外接球半径,r为底面外接圆半径,h为棱锥的高,r可根据正弦定理a=2rsinA求得)。
例2:已知各顶点都在同一个球面上的正四棱锥高为h,体积为V,则这个球的表面积为____。
正四棱锥的高为h,体积为V,易知底面面积为,底面边长为。
正四棱锥的外接球的球心在它的高上,记为,得,在中。
由勾股定理,所以球的表面积为。
练2:正三棱锥S-ABC中,底面ABC是边长为3的正三角形,侧棱长为2,则该三棱锥的外接球体积等于。
解析:ABC外接圆的半径为,三棱锥S-ABC的直径为2R=,外接球半径R=,外接球体积V=4/3R³=。
对于侧棱与底面垂直的直棱柱和圆柱,其外接球的球心位置在上下底面外心连线中点处。
立体几何之外接球问题含答案

立体几何之外接球问题一讲评课1课时总第课时月日1、已知如图所示的三棱锥的四个顶点均在球的球面上,和所在的平面互相垂直,,,,则球的表面积为( ? )A. B. C. D.2、设三棱柱的侧棱垂直于底面,所有棱的长都为,顶点都在一个球面上,则该球的表面积为(??)A.B. C.D.3、已知是球的球面上两点,,为该球面上的动点,若三棱锥体积的最大值为,则球的表面积为( ? ?)A. B. C. D.4、如图是某几何体的三视图,正视图是等边三角形,侧视图和俯视图为直角三角形,则该几何体外接球的表面积为(?)A.B. C.D.5、已知都在半径为的球面上,且,,球心到平面的距离为1,点是线段的中点,过点作球的截面,则截面面积的最小值为()A. B.C. D.6、某几何体的三视图如图所示,这个几何体的内切球的体积为(? )A.B.C. D.7、四棱锥的所有顶点都在同一个球面上,底面是正方形且和球心在同一平面内,当此四棱锥的体积取得最大值时,它的表面积等于,则球的体积等于(?)A. B. C. D.8、一个三条侧棱两两互相垂直并且侧棱长都为的三棱锥的四个顶点全部在同一个球面上,则该球的表面积为( ? )A.B. C.D.9、一个棱长都为的直三棱柱的六个顶点全部在同一个球面上,则该球的表面积为( ?)A.B.C. D.10、一个几何体的三视图如图所示,其中正视图是正三角形,则几何体的外接球的表面积为( ? )A. B. C. D.立体几何之外接球问题二讲评课1课时总第课时月日11、若圆锥的内切球与外接球的球心重合,且内切球的半径为,则圆锥的体积为__________.12、底面为正三角形且侧棱与底面垂直的三棱柱称为正三棱柱,则半径为的球的内接正三棱柱的体积的最大值为__________.13、底面为正三角形且侧棱与底面垂直的三棱柱称为正三棱柱,则棱长均为的正三棱柱外接球的表面积为__________.14、若一个正四面体的表面积为,其内切球的表面积为,则__________. 15、若一个正方体的表面积为,其外接球的表面积为,则__________. 16.已知边长为的正的三个顶点都在球的表面上,且与平面所成的角为,则球的表面积为__________. 16、在三棱锥中,平面,,,,则此三棱锥外接球的体积为__________18、底面是正多边形,顶点在底面的射影是底面中心的棱锥叫正棱锥.如图,半球内有一内接正四棱锥,该四棱锥的体积为,则该半球的体积为__________.17、三棱柱的底面是直角三角形,侧棱垂直于底面,面积最大的侧面是正方形,且正方形的中心是该三棱柱的外接球的球心,若外接球的表面积为,则三棱柱的最大体积为__________.20、一长方体的各顶点均在同一个球面上,且一个顶点上的三条棱长分别为,则这个球的表面积为__________.立体几何之三视图问题1讲评课 1课时 总第 课时 月 日3、一个几何体的三视图如下图所示,则这个几何体的体积是( ) A. B. C. D.4、如图,网格纸上小正方形的边长为,粗线画出的是某几何体的三视图,则它的体积为(??? ) A.B.C.D.5、某几何体的三视图如图所示,则它的表面积为( ? ?)A.B.C.D.6、某几何体三视图如图所示,则该几何体的体积为(?? ) A. B. C.D.7、多面体的底面矩形,其正(主)视图和侧(左)视图如图,其中正(主)视图为等腰梯形,侧(左)视图为等腰三角形,则该多面体的体积为( ???) A.B.C.D.8、某一简单几何体的三视图如图所示,该几何体的外接球的表面积是(?? ) A.B.C.D.9、如图,网格纸上小正方形的边长为,粗实线画出的是某多面体的三视图,则该多面体的各面中,面积的最大值是(?? ) A. B.C. D. 10、一个几何体的三视图如图,则这个几何体的表面积是(?? )A.B.C.D.11、若某空间几何体的三视图如图所示,根据图中数据,可得该几何体的表面积是(?? ) A.B.C.D.12、某几何体三视图如下图所示,则该几何体的体积是(?? )D.A. B. C.13、一个三棱锥的三视图如图所示,则该棱锥的外接球的体积为(?)A. B.C. D.14、已知一空间几何体的三视图如图所示,其中正视图与左视图都是等腰梯形,则该几何体的体积为(?)A.D.B. C.15、如图,网格纸上小正方形的边长为,粗实线画出的是某几何体的三视图,则该几何体的的体积为(?)C. D.A. B.立体几何之三视图问题2讲评课1课时总第课时月日16、某长方体的三视图如右图,长度为的体对角线在正视图中的长度为,在侧视图中的长度为,则该长方体的全面积为__________.17、一个空间几何体的三视图如下图所示,则该几何体外接球的表面积为__________.18、一个正三棱柱的三视图如图所示,求这个正三棱柱的表面积__________.19、已知一个四棱锥的底面是平行四边形,该四棱锥的三视图如图所示(单位:),则该四棱锥的体积为__________.20、一个几何体的三视图如图所示(单位:),则该几何体的体积为__________.21、已知一个几何体的三视图如图所示(单位:),则该几何体的体积为__________.22、某三棱锥的三视图如图所示,其中俯视图是正方形,则该三棱锥最长棱的长是__________.23、一个多面体的三视图如图所示,则该多面体的表面积为____.24、2016年11月18日13时59分,神舟十一号飞船返回舱在内蒙古中部预定区域成功着陆. 神舟十一号载人飞行,是我国迄今为止时间最长的一次载人航天飞行,在轨33天飞行中,航天员景海鹏、陈冬参与的实验和实验多达38项. “跑台束缚系统”是未来空间站长期飞行的关键锻炼设备,本次任务是国产跑台首次太空验证. 如图所示是“跑台束缚系统”中某机械部件的三视图(单位:),则此机械部件的表面积为__________.25、一个几何体的三视图如图所示,则该几何体的表面积为__________.立体几何之外接球问题答案解析第1题答案C第1题解析如图所示,∵,∴为直角,即过的小圆面的圆心为的中点,和所在的平面互相垂直,则圆心在过的圆面上,即的外接圆为球的大圆,由等边三角形的重心和外心重合易得球半径,球的表面积为,故选.第2题答案B第2题解析设球心为,设正三棱柱上底面为,中心为,因为三棱柱所有棱的长都为,则可知?,,又由球的相关性质可知,球的半径,所以球的表面积为,故选.第3题答案C第3题解析如图所示,当点位于垂直于面的直径端点时,三棱锥的体积最大,设球的半径为,此时,故,则球的表面积为,故选.第4题答案D第4题解析该几何体为三棱锥,设球心为,分别为和的外心,易求得,,∴球的半径,∴该几何体外接球的表面积为.第5题答案B第5题解析∵,∴,∴圆心在平面的射影为的中点,∴,∴.∴,当线段为截面圆的直径时,面积最小,∴截面面积的最小值为.第6题答案C第6题解析此几何体是底面边长为,高为的正四棱锥,可算出其体积为,表面积为. 令内切球的半径为,则,从而内切球的体积为,故选C.第7题答案B第7题解析由题意可知四棱锥的所有顶点都在同一个球面上,底面是正方形且和球心在同一平面内,当体积最大时,可以判定该棱锥为正四棱锥,底面在球大圆上,可得知底面正方形的对角线长度为球的直径,且四棱锥的高半径,进而可知此四棱锥的四个侧面均是边长为的正三角形,底面为边长为的正方形,所以该四棱锥的表面积为?,于是,,进而球的体积. 故选.第8题答案B第8题解析由题可知该三棱锥为一个棱长的正方体的一角,则该三棱锥与该正方体有相同的外接球,又正方体的对角线长为,则球半径为,则. 故选.第9题答案A第9题解析如图:设、为棱柱两底面的中心,球心为的中点.又直三棱柱的棱长为,可知,,所以,因此该直三棱柱外接球的表面积为,故选.?第10题答案D第10题解析此几何体是三棱锥,底面是斜边长为的等腰直角三角形,且顶点在底面内的射影是底面直角三角形斜边的中点.易知,三棱锥的外接球的球心在上.设球的半径为,则,∵,∴,解得:,∴外接球的表面积为.第11题答案第11题解析过圆锥的旋转轴作轴截面,得及其内切圆⊙和外切圆⊙,且两圆同圆心,即的内心与外心重合,易得为正三角形,由题意⊙的半径为,∴的边长为,∴圆锥的底面半径为,高为,∴.第12题答案第12题解析设球心为,正三棱柱的上下底面的中心分别为,,底面正三角形的边长为,则,由已知得底面,在中,,由勾股定理得,故三棱柱体积,又,所以,则.第13题答案第13题解析底面正三角形外接圆的半径为,圆心到底面的距离为,从而其外接圆的半径,则该球的表面积.第14题答案第14题解析设正四面体棱长为,则正四面体表面积为,其内切球半径为正四面体高的,即,因此内切球表面积为,则.第15题答案第15题解析设正方体棱长为,则正方体表面积为,其外接球半径为正方体体对角线长的,即为,因此外接球表面积为,则.第16题答案第16题解析设正的外接圆圆心为,易知,在中,,故球的表面积为.第17题答案第17题解析根据题意球心到平面的距离为,在的外接圆的半径为,所以球的半径为,所以此三棱锥的外接球的体积为,所以答案为:.第18题答案第18题解析设所给半球的半径为,则棱锥的高,底面正方形中有,所以其体积,则,于是所求半球的体积为.第19题答案第19题解析依题意,外接球的表面积为,所以.如图所示,三棱柱外接圆球心为,设,在直角三角形中,所以.三棱柱的体积为,当且仅当时取得最大值.第20题答案第20题解析由已知可得长方体的体对角线为球的直径:,所以.所以球的面积为.。
2025届立体几何微专题外接球问题
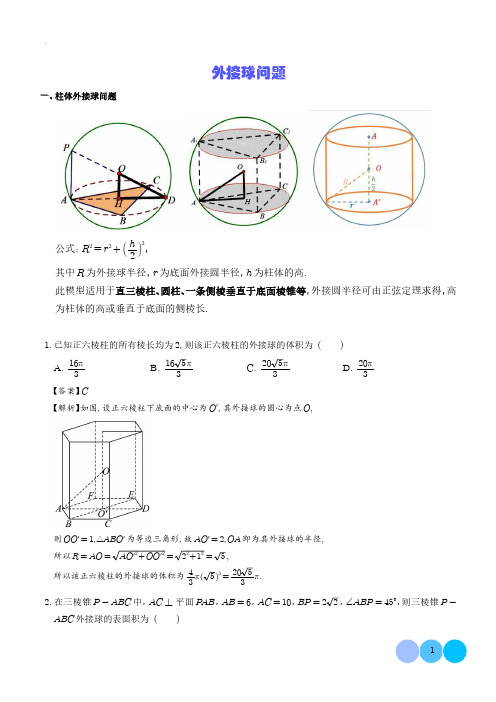
外接球问题一、柱体外接球问题公式:R 2=r 2+h 22,其中R 为外接球半径,r 为底面外接圆半径,h 为柱体的高.此模型适用于直三棱柱、圆柱、一条侧棱垂直于底面棱锥等,外接圆半径可由正弦定理求得,高为柱体的高或垂直于底面的侧棱长.1.已知正六棱柱的所有棱长均为2,则该正六棱柱的外接球的体积为()A.16π3B.165π3C.205π3D.20π3【答案】C【解析】如图,设正六棱柱下底面的中心为O ,其外接球的圆心为点O ,则OO =1,△ABO 为等边三角形,故AO =2,OA 即为其外接球的半径,所以R =AO =AO 2+OO 2=22+12=5,所以该正六棱柱的外接球的体积为43π5 3=2053π.2.在三棱锥P -ABC 中,AC ⊥平面P AB ,AB =6,AC =10,BP =22,∠ABP =45°,则三棱锥P -ABC 外接球的表面积为()A.144πB.128πC.140πD.148π【答案】C【解析】在△ABP中由余弦定理AP2=AB2+BP2-2AB⋅BP cos∠ABP=62+222-2×6×22×22=20,所以AP=25,设△ABP外接圆的半径为,则2r=APsin∠ABP=2522=210,所以r=10,又AC⊥平面P AB,AC=10,设三棱锥P-ABC外接球的半径为,则R2=r2+AC22=102+52=35,所以三棱锥P-ABC外接球的表面积S=4πR2=140π.3.直三棱柱ABC-A B C 的各个顶点都在球O的球面上,且AB=AC=1,BC= 2.若球O的表面积为3π,则这个三棱柱的体积是.【答案】1 2【解析】∵AB=AC=1,BC=2,∴AB⊥AC,∴直三棱柱ABC-A B C 外接球的球心O即为侧面BCC B 的中心,设球O半径为r,则4πr2=3π,∴r=32,即OC=r=3 2,∴直三棱柱ABC-A B C 的高h=2r2-12BC2=1,∴直三棱柱ABC-A B C 的体积V=S△ABC⋅h=12×1×1×1=124.圆柱的底面半径为1,侧面积为10π,则该圆柱外接球的表面积为.【答案】29π【解析】设圆柱的高为h,其外接球的半径为R,由圆柱的底面半径为1,侧面积为10π,得2πh=10π,解得h=5,由圆柱和球的对称性可知,球心位于圆柱上下底面中心连线的中点处,因此R=1+522=292,所以球的表面积为S=4πR2=29π.5.如图,该“四角反棱柱”是由两个相互平行且全等的正方形经过旋转、连接而成,其侧面均为等边三角形,已知该“四角反棱柱”的棱长为4,则其外接球的表面积为.【答案】32+82π【解析】如图,由题意可知旋转角度为π2,设上、下正方形的中心分别为O1,O2,连接O1O2,则O1O2的中点O即为外接球的球心,其中点B为所在棱的中点,OA即为该几何体的外接球的半径,O1A=22,O2B=2,AB=23,过点B作BC⊥O1A于点C,则AC=O1A-O2B=22-2,BC=AB2-AC2=8 2.易得四边形CBO1O2为矩形,即O1O2=BC=82,OO1=12O1O2=22,则OA=OO12+O1A2=8+22,即R=8+22,S=4πR2=32+82π,即该“四角反棱柱”的外接球的表面积为32+82π.二、长方体外接球问题公式:R=a2+b2+c22此模型适用于长方体、三条棱两两垂直的三棱锥、四棱锥等模型,其中a、b、c为长方体的长宽高,或者锥体的三条互相垂直的棱长.此类型外接球问题,可拓展出对棱相等模型:若三棱锥三组对棱分别对应相等,则三棱锥可看作为长方体的一部分,则其外接球公式为:R=λ2+μ2+ϕ28,其中λ、μ、ϕ为三组对棱的长.6.已知长方体的一条棱长为2,体积为16,则其外接球表面积的最小值为()A.5πB.12πC.20πD.80π【答案】C【解析】设长方体的长、宽、高分别为a,b,2,所以长方体的体积为V=2ab=16,解得:ab=8,设长方体的外接球的半径为R,所以2R=a2+b2+4,即4R2=a2+b2+4≥2ab+4=20,即R≥5,当且仅当a=b=22时取等,所以R min=5,所以其外接球表面积的最小值为S=4πR2=20π.7.已知三棱锥S-ABC的四个顶点都在球O的球面上,且SA=BC=2,SB=AC=7,SC=AB=5,则球O的体积是().A.83π B.3223π C.423π D.823π【答案】D【解析】将三棱锥放入长方体中,设长方体的长宽高分别为a,b,c,如图所示:则a2+b2=5a2+c2=7b2+c2=4,故a2+b2+c2=8,球O的半径R=12a2+b2+c2=2,故体积为43πR3=82π3.故选:D.将三棱锥放入长方体中,设长方体的长宽高分别为a,b,c,可得则a2+b2=5 a2+c2=7 b2+c2=4,得到球半径,计算体积得到答案.三、锥体外接球模型公式:R2=r2+h-R2此模型适用于圆锥、正棱锥等,其中R为外接球半径,r为底面圆的半径,h为锥体的高,特别的,正四面体的外接球半径公式为:R=64a.8.已知正三棱锥P-ABC的四个顶点都在半径为R的球面上,且AB=2,若三棱锥P-ABC的体积为32R,则该球的表面积为()A.32π27B.16π9C.64π27D.64π9【答案】D【解析】由题意得,△ABC为等边三角形,取△ABC的中心O1,设球心为O ,易得P ,O ,O 1共线,设三棱锥的高为h ,S △ABC =12×22×32=3,则V P -ABC =13⋅S △ABC ⋅h =32R ,则h =32R ,又OA =OP =R ,由正弦定理得,O 1A =12⋅2sin π3=233,在△OAO 1中,O 1O 2+O 1A 2=OA 2,即32R -R2+2332=R 2,解得R =43,则球的表面积为4πR 2=64π9.9.已知正四棱锥P -ABCD 的各顶点都在同一球面上,且该球的体积为36π,若正四棱锥P -ABCD 的高与底面正方形的边长相等,则该正四棱锥的底面边长为()A.16B.8C.4D.2【答案】C【解析】如图所示,设P 在底面的投影为G ,易知正四棱锥P -ABCD 的外接球球心在PG 上,不妨设球半径r ,OG =h ,AB =2a ,该球的体积为36π,即43πr 3=36π⇒r =3=OA =OP ,又正四棱锥P -ABCD 的高与底面正方形的边长相等,则AG =2a ,PG =2a ,AG 2+OG 2=r 2=PG -OG 2即2a -h2=92a 2+h 2=9⇒h =12a =4.四、垂面模型(两平面互相垂直)公式:R 2=r 21+r 22-l 24,其中R 为外接圆半径,r 1、r 2分别为两个垂直平面的外接圆半径,l 为公共边长.10.在体积为12的三棱锥A -BCD 中,AC ⊥AD ,BC ⊥BD ,平面ACD ⊥平面BCD ,∠ACD =π3,∠BCD =π4,若点A ,B ,C ,D 都在球O 的表面上,则球O 的表面积为()A.12πB.16πC.32πD.48π【答案】D 【解析】如图,取CD 的中点O ,连接AO ,BO ,因为AC ⊥AD ,BC ⊥BD ,所以OA =OB =OC =OD ,因此点O 就是球心,又∠BCD =π4,故△BCD 是等腰直角三角形,所以OB ⊥CD .因为平面ACD ⊥平面BCD ,平面ACD ∩平面BCD =CD ,所以OB ⊥平面ACD .设球O 半径为R ,则OB =R ,AC =R ,又∠ACD =π3,则AD =3R ,所以三棱锥A -BCD 的体积V =13S △ACD ⋅OB =13×12×AC ⋅AD ⋅OB =36R 3=12,所以R =23,所以球O 的表面积为4πR 2=48π.11.在三棱锥P -ABC 中,AB =BC =10,∠ABC =120°,D 为AC 的中点,PD ⊥平面ABC ,且PD =15,则三棱锥P -ABC 外接球的表面积为.【答案】500π【解析】在△ABC 中,AB =BC =10,∠ABC =120°,由余弦定理得AC 2=AB 2+BC 2-2AB ⋅BC ⋅cos ∠ABC =300,所以AC =103,设△ABC 的外接圆O 1的半径为r ,则由正弦定理得2r =AC sin ∠ABC =103sin120°,解得r =10结合图形分析:因为D 为AC 的中点,PD ⊥平面ABC ,且PD =15,在Rt △ABD 中,AD =12AC =53,BD =AB 2-AD 2=5,又O 1B =r =10,则圆心O 1到D 点的距离为O 1D =5,另设三棱锥P -ABC 的外接球球心O 到平面ABC 的距离为OO 1=d ,设外接球的半径为R ,则Rt △O 1OB 中,O 1B 2+OO 21=OB 2,即102+d 2=R 2,直角梯形O 1OPD 中,O 1D 2+PD -OO 1 2=OP 2,即52+15-d 2=R 2,解得d =5,R 2=125,所以S =4πR 2=500π..五、两面相交模型公式:R 2=m 2+n 2-2mn cos θsin 2θ+l 24,其中m 、n 为外心到公共边的距离,l 为公共边长,θ为二面角大小,若仅有一个面为钝角三角形,则取其补角.12.如图,在三棱锥P -ABC ,△P AC 是以AC 为斜边的等腰直角三角形,且CB =22,AB =AC =6,二面角P -AC -B 的大小为120°,则三棱锥P -ABC 的外接球表面积为.【答案】10π【解析】先分别作BC ,AC 中点E ,F ,连接AE ,PF ;再过点F 在平面ABC 内作AC 垂线,与AE 相交于点G ,AB 相交于点H ;分别过点F ,G 作平面P AC ,平面ABC 垂线,相交于点O ,连接AO ,如图所示,由题可知,二面角P -AC -B 的平面角为∠HFP =120°,点F ,G 分别为△P AC ,△ABC 的外心,故O 为该三棱锥外接球球心,AO 为外接球半径,可得,OF ⊥PF ,OG ⊥FH ,OG ⊥AG ,所以∠OFG =30°在△ABC 中,sin ∠CAE =CE AC=12BCAC=26=33所以tan ∠CAE =22,sin ∠BAC =sin2∠CAE =223,所以FG =AF tan ∠CAE =62×22=32,由正弦定理可知BCsin ∠BAC=2AG ⇒AG =32因为∠OFG =30°,OG ⊥FH 所以OG =FG tan30°=12因为OG ⊥AG所以有OA 2=AG 2+OG 2=52所以外接表面积为4πOA 2=10π13.如图,三棱锥P -ABC 的四个顶点都在球O 的球面上,P A ⊥PC ,△ABC 是边长为6的正三角形,二面角P -AC -B 的大小为120°,则球O 的体积为.【答案】52133π/5213π3【解析】取AC 的中点D ,连接BD ,设E 为△ABC 的外心,则点E 在BD 上且BE =2ED ,因为P A ⊥PC ,则D 为Rt △APC 的外心,根据球的几何性质,则OE ⊥平面ABC ,OD ⊥平面P AC ,因为二面角P -AC -B 的大小为120°,平面OAC ⊥平面P AC ,则二面角O -AC -B 的大小为30°,所以∠ODE =30°,因为△ABC 是边长为6的正三角形,则BD =6sin60°=33,所以ED =BD3=3,在Rt △OED 中,OD =EDcos30°=2,在Rt △ADO 中,因为AD =3,则OA =AD 2+OD 2=13,所以球O 的半径R =13,表面积为V 球=43πR 3=43π×1313=52133π.14.三棱锥A -BCD 中,BC =CD =2,BC ⊥CD ,△ABD 是正三角形,AC =14,则三棱锥A -BCD 的体积为;此三棱锥外接球的表面积为.【答案】63;56π3【解析】设BD的中点为P,连接CP,AP因为△ABD是正三角形,所以AB=AD,又因为BC=CD=2,所以有CP⊥BD,AP⊥BD,而CP∩AP=P,CP,AP⊂平面ACP,因此有BD⊥平面ACP,因为BC=CD=2,BC⊥CD,所以BD=BC2+CD2=4+4=22,CP=12BD=2因为△ABD是正三角形,BD的中点为P,所以AP=(22)2-12×222=6,而AC=14,根据余弦定理可知:cos∠APC=6+2-142×6×2=-32⇒∠APC=5π6因为BD的中点为P,所以三棱锥A-BCD的体积为:1 3S△ACP⋅BD=13×12×6×2×12×22=63因为BC=CD=2,BC⊥CD,BD的中点为P,所以P是△BCD的外心,设O1为△ABD的外心,过P作平面BCD的垂线,过O1作平面ABD的垂线,两个垂线的交点为球心O,在正△ABD中,O1P=13AP=63,O1A=23AP=263由上可知:∠APC=5π6,于是∠OPO1=5π6-π2=π3,于是有OO1=tan π3⋅O1P=3×63=2,在直角三角形OO1A中,OA=O1O2+O1A2=2+249=423因此此三棱锥外接球的表面积为4π⋅4232=56π3.六、台体的外接球模型公式:利用R2=r21+h-x2=r22+x2建立方程求解,其中h为台体高,r1、r2为底面圆(或外接圆)半径.15.已知某圆台的母线长为22,母线与轴所在直线的夹角是45°,且上、下底面的面积之比为1:4,则该圆台外接球的表面积为()A.40πB.64πC.80πD.128π【答案】C【解析】根据题意,将圆台补全为圆锥,记圆锥顶点为E,取圆锥的轴截面EAB,记该轴截面与圆台的交点为ABCD,记圆台上底面圆心为M,下底面圆心为N,根据圆台的对称性可知,其圆台的对称性可知,其外接球球心O在中轴线EN上,连接OC,OB如图所示:因为上、下底面的面积之比为1:4,则上底面半径与下底面半径之比为1:2,即BN=2MC,则有EB=2EC=2BC,EN=2MN,又由∠AEN=45°,则∠AEB=90°,而BC=22,则有MC=2,BN= 4,EN=4,则有NM=2,记圆台外接球半径为R,ON=h,在直角△OCM和直角△OBN中由勾股定理知:OM2+CM2=OC2,ON2+BN2=OB2,则有(h+2)2+4= h2+16,解可得h=2,故圆台外接球的半径R2=OB2=4+16=20,则该圆台外接球的表面积S=4πR2= 80π.16.已知正四棱台的顶点都在同一球面上,其上、下底面边长分别为2,22,高为3,则该球的表面积为()A.40πB.20πC.16πD.205π3【答案】B【解析】法一:正四棱台的对角面的外接圆为其外接球O 的大圆(如下图),对角面为等腰梯形AA C C ,其上下底边长分别为2,4,高为3,由正四棱台的对称性可知,球O 的球心O 在梯形上下底的中点连线O 1O 2所在直线上,设OO 1=d ,则OO 2=3-d ,球O 半径为OC =R =OC ,由Rt △OO 1C ,Rt △OO 2C 可得R 2=|3-d |2+22=d 2+12,解得d =2,R =5,所以所求的球O 的表面积为4πR 2=20π,法二:下底的外接圆不大于球的大圆,故球半径R ≥2(下底对角线长的一半),表面积4πR 2≥16π,排除D ;对角面等腰梯形AA C C 的对角线长32,故球半径R >322,表面积4πR 2>18π,排除C ;若4πR 2=40π,则R =10,易求球心到A C 的距离为d 1=3,球心到AC 的距离为d 2=6,无法满足d 1+d 2 =h =3,或d 1-d 2 =h =3,排除A .。
高中数学空间几何体的外接球专题(附经典例题与解析)
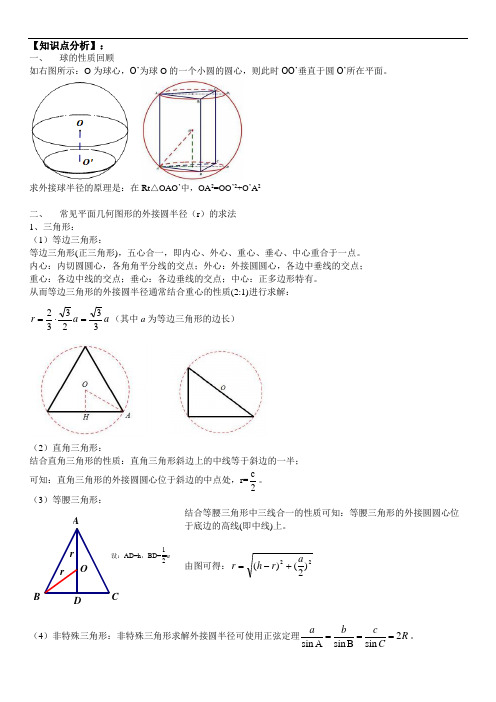
【知识点分析】: 一、 球的性质回顾如右图所示:O 为球心,O’为球O 的一个小圆的圆心,则此时OO’垂直于圆O’所在平面。
求外接球半径的原理是:在Rt △OAO ’中,OA 2=OO ’2+O ’A 2二、 常见平面几何图形的外接圆半径(r )的求法1、三角形:(1)等边三角形:等边三角形(正三角形),五心合一,即内心、外心、重心、垂心、中心重合于一点。
内心:内切圆圆心,各角角平分线的交点;外心:外接圆圆心,各边中垂线的交点;重心:各边中线的交点;垂心:各边垂线的交点;中心:正多边形特有。
从而等边三角形的外接圆半径通常结合重心的性质(2:1)进行求解:a a r 332332=⋅=(其中a 为等边三角形的边长)(2)直角三角形:结合直角三角形的性质:直角三角形斜边上的中线等于斜边的一半;可知:直角三角形的外接圆圆心位于斜边的中点处,r=2c 。
(3)等腰三角形: 结合等腰三角形中三线合一的性质可知:等腰三角形的外接圆圆心位于底边的高线(即中线)上。
由图可得:22)2()(a r h r +-=(4)非特殊三角形:非特殊三角形求解外接圆半径可使用正弦定理2sin sin sin a b c R C===A B 。
rrAD=h ,BD=12a B CO2、四边形常见具有外接圆的四边形有:正方形、矩形、等腰梯形,其中正方形与长方形半径求解方法转化为直角三角形,等腰梯形的外接圆圆心不在中学考察范围内。
外接圆圆心是在圆心到各个顶点距离相同的点;外接球球心则是球心到几何体各个顶点距离相同的点。
结论:几何体的外接球球心与底面外心的连线垂直于底面,(也即球心落在过底面外心的垂线上,)简单称之为:球心落在底面外心的正上方。
【相似题练习】2.半径为2的球的内接三棱锥P﹣ABC,PA=PB=PC=2,AB=AC=BC,则三棱锥的高为()A.3B.C.2D.3【知识点分析】:类型一:直(正)棱柱:上下两底面三角形的外心连线与侧棱平行与底面垂直,从而球心O 必位于上下两底面外心连线的中点处,即121'AA OO =,从而R 可求.【相似题练习】1.三棱柱ABC ﹣A 1B 1C 1中,底面ABC 是边长为2的正三角形,侧棱AA 1垂直于底面ABC ,且AA 1=4,则此三棱柱外接球的表面积为( )A .B .C .D .【知识点分析】:类型二:侧棱垂直底面的三棱锥,法一:补形法:该几何体可由正三棱柱沿平面PBC 切割得来,故可转化为原三棱柱的外接球;法二:先确定底面三角形ABC 的外心O’,从而球心位于O’的正上方,即OO’ ⊥平面ABC ,同时:OP=OA ,故,过O 作OM ⊥PA 于M ,此时M 必为PA 中点,从而四边形OMAO’为矩形,所以PA AM OO 21'==,在直角三角形OO’A 中有:222'OO r R +=.【相似题练习】2.已知在三棱锥P ﹣ABC 中,△ABC 是边长为2的正三角形,若PA ⊥底面ABC 且PA =2,则该三棱锥的外接球的表面积为( )A .32πB .28πC .24πD .20π3.在三棱锥P ﹣ABC 中,PA ⊥平面ABC ,PA =2,AB =4,AC =3,∠BAC =,则三棱锥P ﹣ABC 的外接球的半径R =( )A .B .C .D .【知识点分析】:类型三:正三棱锥:由底面正三角形边长可得r ,在直角三角形OO’A 中,222'OO r R +=,故只需确定OO’的长度即可,结合图形,OO’=PO’-OP=H-R ,代入222)(R H r R -+=即可求解.【相似题练习】3.正三棱锥P ﹣ABC 侧棱长为,侧棱与底面ABC 所成的角为60°,则该正三棱锥外接球半径为 .2.某几何体的三视图如图所示,其中网格纸上小正方形的边长为1,则该几何体的外接球的表面积为( )【知识点分析】:类型四:侧面垂直于底面的三棱锥:设△ABC和△PAB的外心分别为O’,O’’,则PM⊥AB,球心设为O,则OO’ ⊥平面ABC,OO’’⊥平面PAB,从而四边形OO’MO’’是矩形,可得:OO’=O’’M,在Rt△OO’C中用勾股定理求解.【讲透例题】1.在四面体A﹣BCD中,AB=5,BC=CD=3,DB=2,AC=4,∠ACD=60°,则该四面体的外接球的表面积为.解析:如图:取AB的中点O,在△ACD中,由余弦定理得:AD2=AC2+CD2﹣2×AC×CD cos60°=13,在△ABD中,∵AB2=BD2+AD2,∴∠ADB=90°,∴OA=OB=OD,在△ABC中,∵AB2=BC2+AC2,∴∠ACB=90°,∴OA=OB=OC,∴OA=OB=OC=OD,∴O为四面体ABCD的外接球的球心,其半径R=AB=,∴S球=4πR2=4π()2=25π.故答案为:25π.【相似题练习】4.在三棱锥P-ABC中,面PAB⊥面ABC,三角形ABC和三角形PAB均为等边三角形,且AB=3,求该几何体外接球半径.2.在边长为2的菱形ABCD中,,将菱形ABCD沿对角线AC折起,使得平面ABC⊥平面ACD,则所得三棱锥A﹣BCD的外接球表面积为()A.B.C.D.1.已知点A是以BC为直径的圆O上异于B,C的动点,P为平面ABC外一点,且平面PBC⊥平面ABC,BC=3,PB=2,PC=,则三棱锥P﹣ABC外接球的表面积为.5、如图,在四棱锥P﹣ABCD中,底面ABCD为长方形,PA⊥底面ABCD,AD=AP=2,AB=2,E为棱PD中点.(1)求证:PD⊥平面ABE;(2)求四棱锥P﹣ABCD外接球的体积.1.如图,在正四棱锥P﹣AMDE,底面AMDE的边长为2,侧棱PA=,B,C分别为AM,MD的中点.F为棱PE的中点,平面ABF与棱PD,PC,PM分别交于点G,H,K.(1)求证:AB∥FG;(2)求正四棱锥P﹣AMDE的外接球的表面积.1.如图,四凌锥P﹣ABCD而底面ABCD是矩形,侧面PAD是等腰直角三角形∠APD=90°,且平面PAD⊥平面ABCD.(Ⅰ)求证:平面PAD⊥平面PCD;(Ⅱ)在AD=2,AB=4,求三棱锥P﹣ABD的体积;(Ⅲ)在条件(Ⅱ)下,求四棱锥P﹣ABCD外接球的表面积.7、如图,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,已知其俯视图是正三角形,则该四棱锥的外接球的表面积是()A.B.C.19πD.22π课后作业:1.如图,一个正三棱柱的主视图是长为,宽为2的矩形,俯视图是边长为的正三角形,则它的外接球的表面积等于()A.16πB.12πC.8πD.4π2.某四面体的三视图如图所示,正视图、侧视图、俯视图都是边长为1的正方形,则此四面体的外接球的表面积为()A.πB.3πC.πD.π3.某四棱锥的三视图如图所示,则该棱锥的外接球的表面积为()A.3πB.C.6πD.12π4.四棱锥P﹣ABCD中,ABCD为矩形,AD=2,AB=2,PA=PD,∠APD=,且平面PAD⊥平面ABCD.(1)证明:PA⊥PC;(2)求四棱锥P﹣ABCD的外接球的体积.参考答案与解析12.(5分)已知A,B,C为球O的球面上的三个点,⊙O1为△ABC的外接圆.若⊙O1的面积为4π,AB=BC=AC=OO1,则球O的表面积为()A.64πB.48πC.36πD.32π【解答】解:由题意可知图形如图:⊙O1的面积为4π,可得O1A=2,则AO1=AB sin60°,,∴AB=BC=AC=OO1=2,外接球的半径为:R==4,球O的表面积:4×π×42=64π.故选:A.1.1.一个几何的三视图如图所示,它们都是腰长为1的等腰直角三角形,则该几何体的外接球的体积等于()A.B.C.πD.2π解析:由三视图可知:该几何体是一个如图所示的三棱锥,其中底面是一个两直角边都为1的直角三角形,PC⊥底面ABC,且PC=1.将此三棱锥恢复为棱长为1的正方体,可知该正方体的外接球的直径即为正方体的对角线,∴V外接球==.故选:B.1.半径为2的球的内接三棱锥P﹣ABC,PA=PB=PC=2,AB=AC=BC,则三棱锥的高为()A.3B.C.2D.3【解答】解:三棱锥P﹣ABC中,PA=PB=PC=2,AB=AC=BC,如图,过点p作PM⊥平面ABC的垂足为M,则球O的内接三棱锥P﹣ABC的球心O在PM所在直线上,∵球O的半径为2,∴OB=OP=2,∴由余弦定理得cos∠BPM==∴∠BPM=30°,∴在Rt△PMB中,∠PBM=60°,∴PM=PB sin∠PBM=3.故选:D.1.三棱柱ABC﹣A1B1C1中,底面ABC是边长为2的正三角形,侧棱AA1垂直于底面ABC,且AA1=4,则此三棱柱外接球的表面积为()A.B.C.D.【解答】解:∵正三棱柱ABC﹣A1B1C1的中,底面边长为2,高为4,由题意可得:三棱柱上下底面中心连线的中点,到三棱柱顶点的距离相等,说明中心就是外接球的球心,∴正三棱柱ABC﹣A1B1C1的外接球的球心为O,外接球的半径为r,表面积为:4πr2.球心到底面的距离为2,底面中心到底面三角形的顶点的距离为:=,所以球的半径为r==.外接球的表面积为:4πr2=π故选:D.2.已知在三棱锥P﹣ABC中,△ABC是边长为2的正三角形,若PA⊥底面ABC且PA=2,则该三棱锥的外接球的表面积为()A.32πB.28πC.24πD.20π【解答】解:由正弦定理可知,正△ABC的外接圆的直径为,∵PA⊥平面ABC,所以,该三棱锥的外接球的直径为,则.因此,该三棱锥的外接球的表面积为4πR2=20π.故选:D.3.在三棱锥P﹣ABC中,PA⊥平面ABC,PA=2,AB=4,AC=3,∠BAC=,则三棱锥P﹣ABC的外接球的半径R=()A.B.C.D.【解答】解:∵AC=3,AB=4,∠BAC=,∴由余弦定理可得BC=,∴△ABC外接圆的半径r=,设球心到平面ABC的距离为d,则d=PA=1.由勾股定理可得R =,故选:D .3.正三棱锥P ﹣ABC 侧棱长为,侧棱与底面ABC 所成的角为60°,则该正三棱锥外接球半径为 1 . 【解答】解:过点P 作PH ⊥平面ABC 于H ,则∵AH 是PA 在平面ABC 内的射影 ∴∠PAH 是直线PA 与底面ABC 所成的角,得∠PAH =60°, ∴Rt △PAH 中,AH =PA cos60°=,PH =PA sin60°=设三棱锥外接球的球心为O ,∵PA =PB =PC ,∴P 在平面ABC 内的射影H 是△ABC 的外心由此可得,外接球心O 必定在PH 上,连接OA 、OB 、OC ∵△POA 中,OP =OA , ∴∠OAP =∠OPA =30°,可得PA =OA =,∴三棱锥外接球的半径R =OA =1故答案为:1.2.某几何体的三视图如图所示,其中网格纸上小正方形的边长为1,则该几何体的外接球的表面积为( )A .16πB .12πC .9πD .8π【解答】解:根据几何体的三视图转换为直观图为:该几何体为底面为等腰直角三角形,高为2的三棱锥体. 如图所示:所以该三棱锥体的外接球的球心为O ,外接球的半径为OA =r ,则:,解得.故S =.故选:C .4.在三棱锥P-ABC 中,面PAB ⊥面ABC ,三角形ABC 和三角形PAB 均为等边三角形,且AB=3,求该几何体外接球半径.由题可得:333,2331'''=====AB r PM M O OO ,所以215'22=+=OO r R2.在边长为2的菱形ABCD中,,将菱形ABCD沿对角线AC折起,使得平面ABC⊥平面ACD,则所得三棱锥A﹣BCD的外接球表面积为()A.B.C.D.【解答】解:∵在边长为2的菱形ABCD中,;如图,由已知可得,△ABC与△ACD均为等边三角形,取AC中点G,连接BG,DG,则BG⊥AC,∴DG=⇒cos∠GDA=⇒∠GDA=⇒∠ADC=;∵二面角B﹣AC﹣D为直二面角,则BG⊥平面ACD,分别取△BCD与△ABD的外心E,F,过E,F分别作两面的垂线,相交于O,则O为三棱锥A﹣BCD的外接球的球心,由△BCA与△ACD均为等边三角形且边长为2,可得OE=OF=DG=.∴DE=DG﹣GE=.∴OD===.∴三棱锥A﹣BCD的外接球的表面积为4π×R2=4π×()2=.故选:C.1.已知点A是以BC为直径的圆O上异于B,C的动点,P为平面ABC外一点,且平面PBC⊥平面ABC,BC=3,PB=2,PC=,则三棱锥P﹣ABC外接球的表面积为10π.【解答】解:因为O为△ABC外接圆的圆心,且平面PBC⊥平面ABC,过O作面ABC的垂线l,则垂线l一定在面PBC内,根据球的性质,球心一定在垂线l,∵球心O1一定在面PBC内,即球心O1也是△PBC外接圆的圆心,在△PBC中,由余弦定理得cos B=,⇒sin B=,由正弦定理得:,解得R=,∴三棱锥P﹣ABC外接球的表面积为s=4πR2=10π,故答案为:10π.1.如图,在四棱锥P﹣ABCD中,底面ABCD为正方形,PA⊥底面ABCD,AD=AP=2,AB=2,E为棱PD 中点.(1)求证:PD⊥平面ABE;(2)求四棱锥P﹣ABCD外接球的体积.【解答】证明:(1)∵PA⊥底面ABCD,AB⊂底面ABCD,∴PA⊥AB,又∵底面ABCD为矩形,∴AB⊥AD,PA∩AD,又PA⊂平面PAD,AD⊂平面PAD,∴AB⊥平面PAD,又PD⊂平面PAD,∴AB⊥PD,AD=AP,E为PD中点,∴AE⊥PD,AE∩AB=A,AE⊂平面ABE,AB⊂平面ABE,∴PD⊥平面ABE.解:(II)四棱锥P﹣ABCD外接球球心是线段BD和线段PA的垂直平分线交点O,由已知BD===4,设C为BD中点,∴AM=2,OM=AP=1,∴OA===3,∴四棱锥P﹣ABCD外接球的体积是=36π.1.如图,在正四棱锥P﹣AMDE,底面AMDE的边长为2,侧棱PA=,B,C分别为AM,MD的中点.F为棱PE的中点,平面ABF与棱PD,PC,PM分别交于点G,H,K.(1)求证:AB∥FG;(2)求正四棱锥P﹣AMDE的外接球的表面积.【解答】(1)证明:在正方形AMDE中,因为B是AM的中点,所以AB∥DE.又因为AB⊄平面PDE,DE⊂平面PDE,所以AB∥平面PDE.因为AB⊂平面ABF,且平面ABF∩平面PDE=FG,所以AB∥FG.(2)解:连接AD,EM,相交于O′,易得AO′=,PO′=.由正四棱锥P﹣AMDE的对称性,得正四棱锥P﹣AMDE得外接球球心在线段PO′上,不妨设为O点.设OA=OP=R,则OO′=﹣R,∵AO2=AO′2+OO′2,∴R2=2+(﹣R)2,∴R=∴S=4πR2=,∴正四棱锥P﹣AMDE的外接球的表面积为.1.如图,四凌锥P﹣ABCD而底面ABCD是矩形,侧面PAD是等腰直角三角形∠APD=90°,且平面PAD⊥平面ABCD.(Ⅰ)求证:平面PAD⊥平面PCD;(Ⅱ)在AD=2,AB=4,求三棱锥P﹣ABD的体积;(Ⅲ)在条件(Ⅱ)下,求四棱锥P﹣ABCD外接球的表面积.【解答】解:(I)∵四边形ABCD是矩形,∴AD⊥CD,又∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,CD⊂平面ABCD,∴CD⊥平面PAD,∵CD⊂平面PCD,∴平面PAD⊥平面PCD.(II)过P作PE⊥AD,垂足为E,∵△PAD是等腰直角三角形,∠APD=90°,∴PE==1.∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PE⊂平面PAD,PE⊥AD,∴PE⊥平面ABCD,∴V棱锥P﹣ABD=S△ABD•PE=••2•4•1=.(III)取BD中点M,过M作MN⊥平面ABCD,则球心O在直线MN上,连接AM,则AM==.∵PE⊥平面ABCD,∴MN∥PE.∵四棱锥P﹣ABCD内接于球,,∴OA==.∴S⊙O=4πOA2=20π.∴E为外心,∴OM=1.如图,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,已知其俯视图是正三角形,则该四棱锥的外接球的表面积是()A.B.C.19πD.22π【解答】解:几何体的直观图如图:是长方体的一部分,上底面PCD的外接圆的半径:O1D==,几何体的外接球的半径为:OD==,该四棱锥的外接球的表面积是:4=π.故选:A.课后作业答案:1.如图,一个正三棱柱的主视图是长为,宽为2的矩形,俯视图是边长为的正三角形,则它的外接球的表面积等于()A.16πB.12πC.8πD.4π【解答】解:设正三棱柱的外接球的半径为R,则∵俯视图是边长为的正三角形∴底面三角形外接圆的半径为=1,∵正三棱柱的高为2∴正三棱柱的外接球的半径为=∴正三棱柱的外接球的表面积等于4π×=8π故选:C.2.某四面体的三视图如图所示,正视图、侧视图、俯视图都是边长为1的正方形,则此四面体的外接球的表面积为()A.πB.3πC.πD.π【解答】解:由三视图可知:该四面体是正方体的一个内接正四面体.∴此四面体的外接球的直径为正方体的对角线长=.∴此四面体的外接球的表面积为表面积==3π.故选:B.3.某四棱锥的三视图如图所示,则该棱锥的外接球的表面积为()A.3πB.C.6πD.12π【解答】解:由题意可知,几何体的直观图如图:是四棱锥D1﹣ABCD,是棱长为1的正方体的一部分,外接球奇数正方体的外接球,取得直径是体对角线,r=,外接球的表面积为:4=3π.故选:A.4.四棱锥P﹣ABCD中,ABCD为矩形,AD=2,AB=2,PA=PD,∠APD=,且平面PAD⊥平面ABCD.(1)证明:PA⊥PC;(2)求四棱锥P﹣ABCD的外接球的体积.【解答】证明:(1)设AD的中点为E,则∵PA=PD,∴PE⊥AD,∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,∴PE⊥平面ABCD,∵PA在平面ABCD内的射影为AE,AE⊥CD,∴PA⊥CD,∵PA⊥PD,CD∩PD=D,∴PA⊥平面PCD∴PA⊥PC;解:(2)连接AC交BD于F,球心O在底面的射影必为点F,取截面PEF,PE=,EF=1.假设OF=x,则由OA2=x2+4=1+得x=0,∴球的半径为2,∴四棱锥P﹣ABCD的外接球的体积为=.。
几何体外接球表面积及体积的求法有答案
几何体外接球表面积及体积的求法答案1.D【考点】由三视图求面积、体积.【专题】数形结合;转化法;空间位置关系与距离.【分析】根据三视图得出该几何体是圆柱,求出圆柱体的表面积和它外接球的表面积即可得出结论.【解答】解:根据三视图得,该几何体是底面半径为3,高为4的圆柱体,所以该圆柱体的表面积为S1=2π×32+2π×3×8=66π;根据球与圆柱的对称性,得它外接球的半径R满足(2R)2=62+82=100,所以外接球的表面积为S2=4πR2=100π;所以剩余几何体的表面积是S=S1+S2=66π+100π=166π.故选:D.【点评】本题考查了三视图的应用问题,也考查了利用三视图研究直观图的性质,球与圆柱的接切关系,球的表面积计算问题,是基础题目.2.D【考点】球的体积和表面积.【专题】计算题;空间位置关系与距离.【分析】由长方体的对角线公式,算出正四棱柱体对角线的长,从而得到球直径长,得球半径R=1,最后根据球的体积公式,可算出此球的体积.【解答】解:∵正四棱柱的底面边长为1,侧棱长为,∴正四棱柱体对角线的长为=2又∵正四棱柱的顶点在同一球面上,∴正四棱柱体对角线恰好是球的一条直径,得球半径R=1根据球的体积公式,得此球的体积为V=πR3=π.故选:D.【点评】本题给出球内接正四棱柱的底面边长和侧棱长,求该球的体积,考查了正四棱柱的性质、长方体对角线公式和球的体积公式等知识,属于基础题.3.C【考点】球内接多面体;球的体积和表面积.【专题】空间位置关系与距离.【分析】先画出图形,正四棱锥外接球的球心在它的底面的中心,然后根据勾股定理列方程,解出球的半径即可.【解答】解:如图,设正四棱锥底面的中心为E,过点A,B,C,D,S的球的球心为O,半径为R,则在直角三角形AEO中,AO=R,AE=BD=4,OE=SE﹣AO=8﹣R由AO2=AE2+OE2得R2=42+(8﹣R)2,解得R=5球半径R=5,故选C.【点评】本题主要考查球,球的内接体问题,考查计算能力和空间想象能力,属于中档题.4.D考点:球的体积和表面积.专题:计算题.分析:由AB=BC=CA=2,求得△ABC的外接圆半径为r,再由R2﹣(R)2=,求得球的半径,再用面积求解.解答:解:因为AB=BC=CA=2,所以△ABC的外接圆半径为r=.设球半径为R,则R2﹣(R)2=,所以R2=S=4πR2=.故选D点评:本题主要考查球的球面面积,涉及到截面圆圆心与球心的连垂直于截面,这是求得相关量的关键.5.C【考点】棱柱、棱锥、棱台的体积.【专题】计算题;空间位置关系与距离.【分析】根据题意作出图形,利用截面圆的性质即可求出OO1,进而求出底面ABC上的高SD,即可计算出三棱锥的体积.【解答】解:根据题意作出图形:设球心为O,过ABC三点的小圆的圆心为O1,则OO1⊥平面ABC,延长CO1交球于点D,则SD⊥平面ABC.∵CO1==,∴OO1==,∴高SD=2OO1=,∵△ABC是边长为1的正三角形,∴S△ABC=,∴V三棱锥S﹣ABC==.故选:C.【点评】本题考查棱锥的体积,考查球内接多面体,解题的关键是确定点S到面ABC的距离.6.C【考点】球的体积和表面积.【专题】空间位置关系与距离.【分析】将四面体补成长方体,通过求解长方体的对角线就是球的直径,然后求解外接球的表面积.【解答】解:由题意可采用割补法,考虑到四面体ABCD的四个面为全等的三角形,所以可在其每个面补上一个以,,为三边的三角形作为底面,且以分别x,y,z长、两两垂直的侧棱的三棱锥,从而可得到一个长、宽、高分别为x,y,z的长方体,并且x2+y2=29,x2+z2=34,y2+z2=37,则有(2R)2=x2+y2+z2=50(R为球的半径),得R2=,所以球的表面积为S=4πR2=50π.故选:C.【点评】本题考查几何体的外接球的表面积的求法,割补法的应用,判断外接球的直径是长方体的对角线的长是解题的关键之一.7.B【考点】球的体积和表面积.【专题】计算题;空间位置关系与距离.【分析】三棱锥A﹣BCD的三条侧棱两两互相垂直,所以把它扩展为长方体,它也外接于球,对角线的长为球的直径,然后解答即可.【解答】解:三棱锥A﹣BCD的三条侧棱两两互相垂直,所以把它扩展为长方体,它也外接于球,对角线的长为球的直径,d==,它的外接球半径是外接球的表面积是4π()2=14π故选:B.【点评】本题考查球的表面积,考查学生空间想象能力,是基础题.8.B【考点】球内接多面体.【专题】计算题;方程思想;综合法;空间位置关系与距离.【分析】三棱锥A﹣BCD的三条侧棱两两互相垂直,所以把它扩展为长方体,它也外接于球,对角线的长为球的直径,然后解答即可.【解答】解:三棱锥A﹣BCD的三条侧棱两两互相垂直,所以把它扩展为长方体,它也外接于球,对角线的长为球的直径,d==,它的外接球半径是,外接球的表面积是4π()2=14π故选:B.【点评】本题考查球的表面积,考查学生空间想象能力,是基础题.9.D【考点】棱柱、棱锥、棱台的体积.【专题】计算题;空间位置关系与距离.【分析】设该球的半径为R,则AB=2R,2AC=AB=,故AC=R,由于AB是球的直径,所以△ABC在大圆所在平面内且有AC⊥BC,由此能求出球的体积.【解答】解:设该球的半径为R,则AB=2R,2AC=AB=,∴AC=R,由于AB是球的直径,所以△ABC在大圆所在平面内且有AC⊥BC,在Rt△ABC中,由勾股定理,得:BC2=AB2﹣AC2=R2,所以Rt△ABC面积S=×BC×AC=,又PO⊥平面ABC,且PO=R,四面体P﹣ABC的体积为,∴V P﹣ABC==,即R3=9,R3=3,所以:球的体积V球=×πR3=×π×3=4π.故选D.【点评】本题考查四面体的外接球的体积的求法,解题时要认真审题,仔细解答,注意合理地化空间问题为平面问题.10.B【考点】球的体积和表面积;球内接多面体.【专题】计算题;空间位置关系与距离.【分析】以PA、PB、PC为过同一顶点的三条棱,作长方体如图,则长方体的外接球同时也是三棱锥P﹣ABC外接球.算出长方体的对角线即为球直径,结合球的表面积公式,可算出三棱锥P﹣ABC外接球的体积.【解答】解:以PA、PB、PC为过同一顶点的三条棱,作长方体如图则长方体的外接球同时也是三棱锥P﹣ABC外接球.∵长方体的对角线长为2,∴球直径为2,半径R=,因此,三棱锥P﹣ABC外接球的体积是πR3=π×()3=4π故选:B.【点评】本题给出三棱锥的三条侧棱两两垂直,求它的外接球的表面积,着重考查了长方体对角线公式和球的表面积计算等知识,属于基础题.11.D12.考点:球的体积和表面积;球内接多面体.专题:空间位置关系与距离.分析:求出BC,利用正弦定理可得△ABC外接圆的半径,从而可求该三棱锥的外接球的半径,即可求出三棱锥的外接球表面积.解答:解:∵AC=2,AB=1,∠BAC=120°,∴BC==,∴三角形ABC的外接圆半径为r,2r=,r=,∵SA⊥平面ABC,SA=2,由于三角形OSA为等腰三角形,则有该三棱锥的外接球的半径R═=,∴该三棱锥的外接球的表面积为S=4πR2=4π×()2=.故选:D.点评:本题考查三棱锥的外接球表面积,考查直线和平面的位置关系,确定三棱锥的外接球的半径是关键.12.A考点:球内接多面体;棱柱、棱锥、棱台的体积.专题:压轴题.分析:先确定点S到面ABC的距离,再求棱锥的体积即可.解答:解:∵△ABC是边长为1的正三角形,∴△ABC的外接圆的半径∵点O到面ABC的距离,SC为球O的直径∴点S到面ABC的距离为∴棱锥的体积为故选A.点评:本题考查棱锥的体积,考查球内角多面体,解题的关键是确定点S到面ABC的距离.13.【考点】棱柱、棱锥、棱台的体积.【专题】计算题;空间位置关系与距离.【分析】由于面SAB⊥面ABC,所以点S在平面ABC上的射影H落在AB上,根据球体的对称性可知,当S 在“最高点”,也就是说H为AB中点时,SH最大,棱锥S﹣ABC的体积最大.【解答】解:由题意画出几何体的图形如图由于面SAB⊥面ABC,所以点S在平面ABC上的射影H落在AB上,根据球体的对称性可知,当S在“最高点”,也就是说H为AB中点时,SH最大,棱锥S﹣ABC的体积最大.∵△ABC是边长为2的正三角形,所以球的半径r=OC=CH=.在RT△SHO中,OH=OC=OS∴∠HSO=30°,求得SH=OScos30°=1,∴体积V=Sh=××22×1=.故答案是.【点评】本题考查锥体体积计算,根据几何体的结构特征确定出S位置是关键.考查空间想象能力、计算能力.14.12π【考点】球的体积和表面积.【专题】计算题;空间位置关系与距离.【分析】利用平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为,求出球的半径,然后求解球O的表面积.【解答】解:因为平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为,所以球的半径为: =.所以球O的表面积为4π×3=12π.故答案为:12π.【点评】本题考查球的表面积的求法,考查空间想象能力、计算能力.15.【考点】球的体积和表面积.【专题】计算题.【分析】正方体的内切球的直径为正方体的棱长,外接球的直径为正方体的对角线长,设出正方体的棱长,即可求出两个半径,求出两个球的面积之比.【解答】解:正方体的内切球的直径为,正方体的棱长,外接球的直径为,正方体的对角线长,设正方体的棱长为:2a,所以内切球的半径为:a;外接球的直径为2a,半径为:a,正方体的内切球与外接球的面积之比:==.故答案为:.【点评】本题是基础题,考查正方体的外接球与内切球的面积之比,求出外接球的半径,是解决本题的关键.16.16π【考点】球的体积和表面积.【专题】计算题;方程思想;数形结合法;立体几何.【分析】正四棱锥P﹣ABCD的五个顶点在同一球面上,则其外接球的球心在它的高PO1上,记为O,如图.求出AO1,OO1,解出球的半径,求出球的表面积.【解答】解:正四棱锥P﹣ABCD的外接球的球心在它的高PO1上,记为O,PO=AO=R,PO1=3,OO1=3﹣R,在Rt△AO1O中,AO1=AC=,由勾股定理R2=3+(3﹣R)2得R=2,∴球的表面积S=16π故答案为:16π.【点评】本题考查球的表面积,球的内接体问题,解答关键是确定出球心的位置,利用直角三角形列方程式求解球的半径.需具有良好空间形象能力、计算能力.17.36π【考点】球的体积和表面积.【专题】计算题.【分析】由题意推出MN⊥平面SAC,即SB⊥平面SAC,∠ASB=∠BSC=∠ASC=90°,将此三棱锥补成正方体,则它们有相同的外接球,正方体的对角线就是球的直径,求出直径即可求出球的表面积.【解答】解:∵三棱锥S﹣ABC正棱锥,∴SB⊥AC(对棱互相垂直)∴MN⊥AC,又∵MN⊥AM而AM∩AC=A,∴MN⊥平面SAC即SB⊥平面SAC,∴∠ASB=∠BSC=∠ASC=90°,将此三棱锥补成正方体,则它们有相同的外接球,∴2R=2 ,∴R=3,∴S=4πR2=4π•(3)2=36π,故答案为:36π.【点评】本题是中档题,考查三棱锥的外接球的表面积,考查空间想象能力;三棱锥扩展为正方体,它的对角线长就是外接球的直径,是解决本题的关键.18.;。
高考数学立体几何专题:外接球
b2
1 a2 3
PO1
b2
1 a2 3
OO1
PO1
PO
b2 1 a2 R ; 3
在 RtOO1A 中:根据勾股定理得到:
OO12 AO12 AO2 (
b2 1 a2 R)2 ( 3 a)2 R2 b2 1 a2 2
第二部分:柱体的外接球半径 【计算步骤】 第一步:计算底面的外接圆的半径。 第二步:计算直柱体的外接球的半径。 直柱体的外接球的球心:上下底面的外接圆圆心连线的中点为球心。如下图所示:
第3页共8页
其中: O1 为下底面的外接圆的圆心, O2 为上底面的外接圆的圆心, O 为 O1O2 的中点(直柱体外接球的球心); r 为上下底面的外接圆的半径, R 为直柱体的外接球的半径。
2
训练:求下列图形的外接圆半径。
(Ⅰ)在 ABC 中: AB AC , AB 3 , AC 4 ; (Ⅱ)在 ABC 中: AB AC 3 , BC 2 5 ; (Ⅲ)在正 ABC 中: AB 3 ;
3 (Ⅳ)在 ABC 中, AB 2 , BC 3, AC 2 ; (Ⅴ)在矩形 ABCD 中: AB 6 , BC 3 ; (Ⅵ)在正方形 ABCD 中: AB 2 。
根据勾股定理得到: R2 r 2 ( h )2 r 2 h2 R r 2 h2 。
2
4
4
【训练一】:已知:在直三棱柱 ABC A1B1C1 中: AB AC , AB AC 2 , AA1 2 。 求解:直三棱锥 ABC A1B1C1 的外接球的半径。
【训练二】:已知:在正三棱柱 ABC A1B1C1 中: AB 3 , BB1 2 3 。 求解:直三棱锥 ABC A1B1C1 的外接球的半径。
高中数学立体几何外接球专题练习(含解析)
高中数学立体几何外接球专题练习(含解析)1.已知菱形ABCD满足|AB|=2,∠ABC=120°,将菱形ABCD沿对角线AC折成一个直二面角B-AC-D,则三棱锥B-ACD外接球的表面积为()。
A。
πB。
8πC。
7πD。
4π2.如图,四面体ABCD中,面ABD和面BCD都是等腰直角三角形,AB=BD=BC=1,∠CBD=60°,且二面角A-BD-C的大小为120°,∠BAD=45°,若四面体ABCD的顶点都在球O上,则球O的表面积为()。
A。
12πB。
20πC。
24πD。
36π3.如图,网格纸上小正方形的边长为2,粗实线及粗虚线画出的是某四棱锥的三视图,则该四棱锥的外接球的表面积为()。
A。
28πB。
32πC。
41πD。
31π4.已知一个几何体是由半径为2的球挖去一个三棱锥得到(三棱锥的顶点均在球面上).若该几何体的三视图如图所示(侧视图中的四边形为菱形),则该三棱锥的体积为()。
A。
4/3B。
2/3C。
8/3D。
16/35.已知一个几何体的三视图如图所示,则该几何体的表面积是()。
A。
2+2+2B。
4+4+2C。
2+4+4D。
4+4+46.某三棱锥的三视图如图所示,则它的外接球表面积为()。
A。
25πB。
20πC。
16πD。
40π7.如图是某几何体的三视图,则该几何体的表面积是()。
A。
18+2B。
15+2C。
12+2D。
18+48.在四面体ABCD中,AD⊥底面ABC,DE⊥AC,E为棱BC的中点,DG⊥BE,点G在AE上且满足AG=2GE,若四面体ABCD的外接球的表面积为S,则tan∠AGD=S/12.A。
1/2B。
1C。
2D。
49.在三棱锥S-ABC中,∠ASB=90°,SA=SB=SC=2,且三棱锥S-ABC的体积为8/3,则该三棱锥的外接球的表面积为()。
A。
4πB。
16πC。
36πD。
72π10.如图所示,正方形ABCD的边长为2,切去阴影部分围成一个正四棱锥,则当正四棱锥体积最大时,该正四棱锥外接球的表面积为()。
几何体的外接球与内切球的有关问题
几何体的外接球与内切球的有关问题一、外接球的问题简单多面体外接球问题是立体几何中的难点和重要的考点,此类问题实质是计算球的半径或确定球心O 的位置问题,其中球心的确定是关键. (一) 由球的定义确定球心球的定义:在空间中,如果一个定点与一个简单多面体的所有顶点的距离都相等,那么这个定点就是该简单多面体的外接球的球心.由上述性质,可以得到确定简单多面体外接球的球心的如下结论. 结论1:正方体或长方体的外接球的球心其体对角线的中点.结论2:正棱柱的外接球的球心是上下底面中心的连线的中点.结论3:直三棱柱的外接球的球心是上下底面三角形外心的连线的中点,由球心、底面中心及底面一顶点构成的直角三角形便可得球半径.(在1BOO Rt ∆中,21212OO BO BO +=,即222)2(hr R +=.) 结论4:正棱锥的外接球的球心在其高上,具体位置可通过构造直角三角形利用勾股定理求得. (以正三棱锥为例:设正三棱锥的底面△ABC 的边长为a ,高为h ,外接球球心为O ,半径为R . 在1AOO Rt ∆中,21212OO AO AO +=,即222)(33R h a R -+⎪⎪⎭⎫ ⎝⎛=.) 结论5:若棱锥的顶点可构成共斜边的直角三角形,则公共斜边的中点就是其外接球的球心,则公共斜3R a=222a b c R ++=BC边的一半就是其外接球的半径.(二)构造正方体或长方体确定球心长方体或正方体的外接球的球心是在其体对角线的中点处. 1.可构造正方体的类型:①正四面体:棱长对应正方体的面对角线.① ② ③②三条侧棱两两垂直的正三棱锥:底面棱长对应正方体的面对角线,侧棱对应正方体的棱长. ③四个面都是是直角三角形的三棱锥:最长的棱长对应正方体的体对角线. 2.可构造长方体和正方体的类型①同一个顶点上的三条棱两两垂直的四面体;②三个侧面两两垂直的三棱锥;③有三个面是直角三角形的三棱锥;①与②与③ ④④相对的棱相等的三棱锥:设对应长方体的长、宽、高分别为a 、b 、c ,则BC 2=a 2+b 2,AC 2=a 2+c 2,AB 2=b 2+c 2.所以对应长方体的体对角线为2222222AB AC BC c b a ++=++.⑤含有其它线面垂直关系的棱锥. (三) 由性质确定球心利用球心O 与截面圆圆心O’的连线垂直于截面圆,确定球心. 记球的半径为R ,截面圆的半径为r ,球心O 与截面圆圆心O’A BC DA BCPABCP的距离为d,则有R2=r2+d 2.(四) 圆柱外接球模型计算球的半径一个底面半径为r ,高为h 的圆柱,求它的外接球半径. 222)2(h r R +=(1) (2) (3)变形一:如果我们对圆柱上下底面对应位置处,取相同数量的点,比如都取三个点,如图(1)所示.我们可以得到(直)三棱柱,它的外接球其实就是这个圆柱的外接球,所以说直棱柱的外接球求半径符合这个模型. 在这里棱柱的高就是公式中的h ,而棱柱底面△ABC 外接圆的半径则是公式中的r .变形二:如果把三棱柱上面的C 1去掉,如图(2)所示,我们得到有一个侧面⊥矩形底面的四棱锥,其中r 为垂直底面的侧面△ABC 的外接圆半径,h 为垂直于那个侧面的底面边长AA 1.变形三:如果把上面的那个三棱柱上面的B 1,C 1两点去掉,如图(3)所示,我们得到一根侧棱⊥底面的三棱锥,其中r 为底面△ABC 外接圆半径,h 为垂直于底面的那条侧棱AA 1.二、内切球问题若一个多面体的各面都与一个球的球面相切, 则称这个多面体是这个球的外切多面体,这个球是这个多面体的内切球.结论1:内切球球心到多面体各面的距离均相等,外接球球心到多面体各顶点的距离均相等. 结论2:正多面体的内切球和外接球的球心重合.结论3:正棱锥的内切球和外接球球心都在高线上,但不重合. 结论4:基本方法:构造三角形利用相似比和勾股定理. 结论5:体积分割是求内切球半径的通用做法. (一)正方体的的内切球设正方体的棱长为a ,求(1)内切球半径;(2)与棱相切的球半径.Rr2h A BC1A 1B 1C A BC1A 1B A BC1A(1)内切球:截面图为正方形的内切圆,得2a R =. (2)棱切球:切点为正方体各棱的中点,截面图为为正方形的外接圆,得22a R =. (二)棱锥的内切球(分割法)将内切球的球心与棱锥的各个顶点连线,将棱锥分割成以原棱锥的面为底面,内切球的半径为高的小棱锥,根据分割前后的体积相等,列出关于半径的方程.设三棱锥的棱长为a ,内切球半径为r.V V V V VPAB O PBC O PAC O ABC O ABCP -----+++=r S r S r S r S PAB PBC PAC ABC 31313131+++= r S S S S PAB PBC PAC ABC )(31+++= 内切球r S ABC P -=31所以ABCP ABCP S V r --=3内切球一般地,记棱锥的体积为V ,表面积为S ,则内切球的半径为SV r 3=. (三)圆柱、圆锥的内切球(截面法)(1)圆柱的内切球:圆柱的轴截面为正方形,记圆柱的底面圆的半径r ,内切球的半径R ,则R =r . (2)圆锥的内切球:圆锥的轴截面为三角形的内切圆,记圆锥的底面圆的半径r ,内切球的半径R ,由于在△ABC 中,所以CS R 2=.备注:1.三角形内切圆的半径S S S S AO BAO C BO C ABC ∆∆∆∆++=r c b a cr br ar )(21212121++=++= 内切圆r C ABC ∆=21所以三角形内切圆的半径为CSr 2=,其中S 为△ABC 的面积,C 为△ABC 的周长. 2. 三角形外接圆的半径利用正弦定理R C c B b A a 2sin sin sin ===,CcB b A a R sin 2sin 2sin 2===. ①正三角形:a a R 3360sin 2=︒=,其中a 为正三角形的边长.②直角三角形:290sin 2cc R =︒=,其中c 为直角三角形的斜边.3. 正三角形的内切圆与外接圆的半径之比正三角形的内切圆与外接圆的两个圆心“二心合一”. 设正三角形的边长为a ,内切圆半径为r ,外接圆半径为R.由于a a R 3360sin 2=︒=,a a a a a a C S r 6360sin 2122=++︒⋅⋅⋅⨯==, 所以1:2:=r R ,即圆心O 为正三角形高h 的三等分点.4. 正四面体的内切球与外接球的半径之比正四面体的内切球与外接球的两个球心“二心合一”. 设正四面体A-BCD 的棱长为a ,内切球半径为r ,外接球 半径为R ,则OA=OB=R ,OE=r.∵底面△BCD 为正三角形,∴BE=a 33 在BEO Rt ∆中,222OE BE BO +=,即22233r a R +⎪⎪⎭⎫ ⎝⎛=,得a R 46= ∴1:3:=r R ,即球心O 为正四面体高h 的四等分点. 5.正三棱柱的内切球与外接球的半径之比正三棱柱的内切球与外接球的球心是重合的,过侧棱1AA 和它们的球心O 作截面如下图所示:设正三棱柱底面边长为a . 由于内切球投影到底面的圆是底面正三角形的内切圆,所以a R 632=,从而正三棱柱的高为a R h 3322==. 在O D A Rt 11∆中,得22222211211256333a a a R D A R =⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=+=,a R 1251=∴因此1:5:21=R R .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
标准文案立体几何之外接球问题一讲评课1课时 总第 课时月 日1、已知如图所示的三棱锥的四个顶点均在球的球面上,和所在的平面互相垂直,,,,则球的表面积为()A. B. C. D. 2、设三棱柱的侧棱垂直于底面,所有棱的长都为,顶点都在一个球面上,则该球的表面积为( )A.B.C.D.3、已知是球的球面上两点,,为该球面上的动点,若三棱锥体积的最大值为,则球的表面积为( )A.B.C.D.4、如图是某几何体的三视图,正视图是等边三角形,侧视图和俯视图为直角三角形,则该几何体外接球的表面积为( )A.B.C.D. 5、已知都在半径为的球面上,且,,球心到平面的距离为1,点是线段的中点,过点作球的截面,则截面面积的最小值为( )A.B.C.D.6、某几何体的三视图如图所示,这个几何体的内切球的体积为()A.B.C. D.7、四棱锥的所有顶点都在同一个球面上,底面是正方形且和球心在同一平面内,当此四棱锥的体积取得最大值时,它的表面积等于,则球的体积等于()A. B. C. D.8、一个三条侧棱两两互相垂直并且侧棱长都为的三棱锥的四个顶点全部在同一个球面上,则该球的表面积为( )A.B. C.D.9、一个棱长都为的直三棱柱的六个顶点全部在同一个球面上,则该球的表面积为( )A.B.C. D.10、一个几何体的三视图如图所示,其中正视图是正三角形,则几何体的外接球的表面积为( )A. B. C. D.立体几何之外接球问题二讲评课1课时总第课时月日11、若圆锥的内切球与外接球的球心重合,且内切球的半径为,则圆锥的体积为__________.12、底面为正三角形且侧棱与底面垂直的三棱柱称为正三棱柱,则半径为的球的内接正三棱柱的体积的最大值为__________.13、底面为正三角形且侧棱与底面垂直的三棱柱称为正三棱柱,则棱长均为的正三棱柱外接球的表面积为__________.14、若一个正四面体的表面积为,其内切球的表面积为,则__________.15、若一个正方体的表面积为,其外接球的表面积为,则__________.标准文案16.已知边长为的正的三个顶点都在球的表面上,且与平面所成的角为,则球的表面积为__________.16、在三棱锥中,平面,,,,则此三棱锥外接球的体积为__________18、底面是正多边形,顶点在底面的射影是底面中心的棱锥叫正棱锥.如图,半球内有一内接正四棱锥,该四棱锥的体积为,则该半球的体积为__________.17、三棱柱的底面是直角三角形,侧棱垂直于底面,面积最大的侧面是正方形,且正方形的中心是该三棱柱的外接球的球心,若外接球的表面积为,则三棱柱的最大体积为__________.20、一长方体的各顶点均在同一个球面上,且一个顶点上的三条棱长分别为,则这个球的表面积为__________.立体几何之三视图问题1讲评课1课时总第课时月日3、一个几何体的三视图如下图所示,则这个几何体的体积是()A. B. C. D. 4、如图,网格纸上小正方形的边长为,粗线画出的是某几何体的三视图,则它的体积为()A. B. C. D.5、某几何体的三视图如图所示,则它的表面积为()A. B.C.D.6、某几何体三视图如图所示,则该几何体的体积为()标准文案A. B. C. D.7、多面体的底面矩形,其正(主)视图和侧(左)视图如图,其中正(主)视图为等腰梯形,侧(左)视图为等腰三角形,则该多面体的体积为( )A.B.C.D.8、某一简单几何体的三视图如图所示,该几何体的外接球的表面积是( )A. B. C. D.9、如图,网格纸上小正方形的边长为,粗实线画出的是某多面体的三视图,则该多面体的各面中,面积的最大值是( )A. B. C. D.10、一个几何体的三视图如图,则这个几何体的表面积是()A. B. C. D.11、若某空间几何体的三视图如图所示,根据图中数据,可得该几何体的表面积是()A. B. C. D.12、某几何体三视图如下图所示,则该几何体的体积是()D.A. B. C.13、一个三棱锥的三视图如图所示,则该棱锥的外接球的体积为()标准文案A. B.C. D.14、已知一空间几何体的三视图如图所示,其中正视图与左视图都是等腰梯形,则该几何体的体积为()D.A.B. C.15、如图,网格纸上小正方形的边长为,粗实线画出的是某几何体的三视图,则该几何体的的体积为()C. D.A. B.标准文案立体几何之三视图问题2讲评课 1课时 总第 课时 月 日16、某长方体的三视图如右图,长度为的体对角线在正视图中的长度为,在侧视图中的长度为,则该长方体的全面积为__________.17、一个空间几何体的三视图如下图所示,则该几何体外接球的表面积为__________.18、一个正三棱柱的三视图如图所示,求这个正三棱柱的表面积__________.19、已知一个四棱锥的底面是平行四边形,该四棱锥的三视图如图所示(单位:),则该四棱锥的体积为__________.20、一个几何体的三视图如图所示(单位:) ,则该几何体的体积为__________.21、已知一个几何体的三视图如图所示(单位:),则该几何体的体积为__________.22、某三棱锥的三视图如图所示,其中俯视图是正方形,则该三棱锥最长棱的长是__________.23、一个多面体的三视图如图所示,则该多面体的表面积为____.24、2016年11月18日13时59分,神舟十一号飞船返回舱在内蒙古中部预定区域成功着陆. 神舟十一号载人飞行,是我国迄今为止时间最长的一次载人航天飞行,在轨33天飞行中,航天员景海鹏、陈冬参与的实验和实验多达38项. “跑台束缚系统”是未来空间站长期飞行的关键锻炼设备,本次任务是国产跑台首次太空验证. 如图所示是“跑台束缚系统”中某机械部件的三视图(单位:),则此机械部件的表面积为__________.25、一个几何体的三视图如图所示,则该几何体的表面积为__________.标准文案立体几何之外接球问题答案解析第1题答案 C第1题解析如图所示,∵,∴为直角,即过的小圆面的圆心为的中点,和所在的平面互相垂直,则圆心在过的圆面上,即的外接圆为球的大圆,由等边三角形的重心和外心重合易得球半径,球的表面积为,故选.第2题答案 B第2题解析 设球心为,设正三棱柱上底面为,中心为,因为三棱柱所有棱的长都为,则可知,,又由球的相关性质可知,球的半径,所以球的表面积为,故选.第3题答案 C第3题解析 如图所示,当点位于垂直于面的直径端点时,三棱锥的体积最大,设球的半径为,此时,故,则球的表面积为,故选.第4题答案D第4题解析该几何体为三棱锥,设球心为,分别为和的外心,易求得,,∴球的半径,∴该几何体外接球的表面积为.第5题答案B第5题解析∵,∴,∴圆心在平面的射影为的中点,∴,∴.∴,当线段为截面圆的直径时,面积最小,标准文案∴截面面积的最小值为.第6题答案 C第6题解析此几何体是底面边长为,高为的正四棱锥,可算出其体积为,表面积为.令内切球的半径为,则,从而内切球的体积为,故选C.第7题答案 B第7题解析 由题意可知四棱锥的所有顶点都在同一个球面上,底面是正方形且和球心在同一平面内,当体积最大时,可以判定该棱锥为正四棱锥,底面在球大圆上,可得知底面正方形的对角线长度为球的直径,且四棱锥的高半径,进而可知此四棱锥的四个侧面均是边长为的正三角形,底面为边长为的正方形,所以该四棱锥的表面积为,于是,,进而球的体积.故选.第8题答案 B第8题解析由题可知该三棱锥为一个棱长的正方体的一角,则该三棱锥与该正方体有相同的外接球,又正方体的对角线长为,则球半径为,则. 故选.第9题答案 A如图:设、为棱柱两底面的中心,球心为的中点.又直三棱柱的棱长为,可知,,所以,因此该直三棱柱外接球的表面积为,故选.第10题答案D第10题解析此几何体是三棱锥,底面是斜边长为的等腰直角三角形,且顶点在底面内的射影是底面直角三角形斜边的中点.易知,三棱锥的外接球的球心在上.设球的半径为,则,∵,∴,解得:,∴外接球的表面积为.第11题答案第11题解析过圆锥的旋转轴作轴截面,得及其内切圆⊙和外切圆⊙,且两圆同圆心,即的内心与外心重合,易得为正三角形,由题意⊙的半径为,∴的边长为,∴圆锥的底面半径为,高为,∴.第12题答案标准文案设球心为,正三棱柱的上下底面的中心分别为,,底面正三角形的边长为,则,由已知得底面,在中,,由勾股定理得,故三棱柱体积,又,所以,则.第13题答案第13题解析底面正三角形外接圆的半径为,圆心到底面的距离为,从而其外接圆的半径,则该球的表面积.第14题答案第14题解析设正四面体棱长为,则正四面体表面积为,其内切球半径为正四面体高的,即,因此内切球表面积为,则.第15题答案第15题解析设正方体棱长为,则正方体表面积为,其外接球半径为正方体体对角线长的,即为,因此外接球表面积为,则.第16题答案第16题解析设正的外接圆圆心为,易知,在中,,故球的表面积为.第17题答案第17题解析根据题意球心到平面的距离为,在的外接圆的半径为,所以球的半径为,所以此三棱锥的外接球的体积为,所以答案为:.第18题答案第18题解析设所给半球的半径为,则棱锥的高,底面正方形中有,所以其体积,则,于是所求半球的体积为.第19题答案第19题解析依题意,外接球的表面积为,所以.如图所示,标准文案三棱柱外接圆球心为,设,在直角三角形中,所以.三棱柱的体积为,当且仅当时取得最大值.第20题答案第20题解析由已知可得长方体的体对角线为球的直径:,所以.所以球的面积为.。
