实验七数据插值与曲线拟合实验并且附有答案
matlab插值与曲线拟合实验报告

湖南大学电气与信息工程学院 《数值计算》课程 上机实验报告姓名: 班级: 学号: 日期:指导老师:本次实验题号:第 3 次实验1) 实验目的:1) 用MATLAB 实现拉格朗日插值和分段线性插值。
2) 了解matlab 实现曲线拟合方法的实际应用。
二. 实验内容:1) 插值算法的应用:题目:用拉格朗日插值程序,分段线形插值函数分别研究f (X )的数据表,计算f(0.472) X 0.46 0.47 0.48 0.49 Y0.48465550.49375420.50274980.51166832) 曲线拟合方法的实际应用用电压V=10V 的电池给电容器充电,电容器上t 时刻的电压v(t)=V-(V-V0)e^(-t/T),其中V0是电容器的初始电压,T 是充电常数。
实验测量了一组数据如下,请根据数据表确定V0和T 的大小。
t 0.5 1 2 3 4 5 7 9 V(t) 6.366.487.268.228.668.999.439.63三. 算法介绍或方法基础1.1 拉格朗日插值法对于已给定的点 00(,),...,(,)k k x y x y 和待估计的点的横坐标x ,如上述理论,将其值代入1100,011()()()()():......()()()()kj j i k j i i j j i j j j j j j kx x x x x x x x x x l x x x x x x x x x x x -+=≠-+-----==-----∏计算出插值基函数的值,然后根据公式:():()ki i j L x y l x ==∑计算出纵坐标的估计值,由此完成对该点的插值过程,其中k 为该点插值的阶数。
1.2 线性分段插值利用已给定的点 00(,),...,(,)k k x y x y 对插值区间分为1k -段,将每段的端点(,)i i x y 与 11(,)i i x y ++作为数据点利用公式100010()()()()()f x f x p x f x x x x x -=+--在所构成的区间进行线性插值。
数据插值与曲线拟合

实验报告实验目的:掌握数据插值与曲线拟合的方法与应用。
掌握求数值倒数、数值积分、代数方程数值求解、常微分方程数值求解的方法 掌握定义符号对象、求符号函数极限及导数、求符号函数积分的方法实验内容:1 求22)ln(lim y x e x y ++2.计算I=dxdy y x dxdy x f D D )2(21)(--=⎰⎰⎰⎰,其中D 为直线2x y =所围部分 3.求下列变上限积分对变量x 的导数;.2dx x a x x ⎰+4 求高阶微分方程,022''=-++xyz z y y 确定了函数y z x z y x z z ∂∂∂∂=),.(format compact>> input('my name is:','s')my name is:liu yangans =liu yangclear>> fxy=sym('log(x+exp(y))/sqrt(x^2+y^2)')fxy =log(x + exp(y))/(x^2 + y^2)^(1/2)>> result=limit(limit(fxy,'x',1),'y',0)result =log(2)>> clearsyms x yf=(2-x-y)/2;y1=x;y2=x^2;X=solve('x-x^2=0')fdy=int(f,y,x^2,x)X =1fdy =(x*(x - 1)^2*(x + 4))/4>>I=int(fdy,x,X(1),X(2))I =11/120>> clear>> syms a x t y1 y2>> y1=sqrt(a+t)y1 =(a + t)^(1/2)>> y2=int(y1,t,x,x^2);Warning: Explicit integral could not be found. >> diff(y2,x)ans =2*x*(x^2 + a)^(1/2) - (a + x)^(1/2)clear>> y1=dsolve('D2y-10*Dy+9*y=exp(2*x)','Dy(0)=33/7,y(0)=6/7')y1 =exp(2*x)/9 - exp(t)*(exp(2*x)/8 - 3/8) + exp(9*t)*(exp(2*x)/72 + 27/56)clearsyms x y zf=x+2*y-2*sqrt(x*y*z);>> fx=diff(f,x);fy=diff(f,y);fz=diff(f,z);>> zx=-fx/fzzx =-(((y*z)/(x*y*z)^(1/2) - 1)*(x*y*z)^(1/2))/(x*y)>> zy=-fy/fzzy =-(((x*z)/(x*y*z)^(1/2) - 2)*(x*y*z)^(1/2))/(x*y)clear[x,y,z]=solve('x*y^2+z^2=0','y-z=1','x^2-5*x+6')x =2332y =1/3 + (2^(1/2)*i)/31/4 + (3^(1/2)*i)/41/4 - (3^(1/2)*i)/41/3 - (2^(1/2)*i)/3z =- 2/3 + (2^(1/2)*i)/3 - 3/4 + (3^(1/2)*i)/4 - 3/4 - (3^(1/2)*i)/4 - 2/3 - (2^(1/2)*i)/3。
插值与拟合试验

实验:插值与拟合实验目的1.掌握用MATLAB计算拉格朗日、分段线性、三次样条三种插值的方法,改变节点的数目,对三种插值的结果进行初步的分析。
2.掌握用MATLAB作线性最小二乘的方法。
3.通过实例学习如何用插值方法与拟合方法解决实际问题,注意二者的联系和区别。
实验内容选择一些函数,在n个节点上(n不要太大,如5~11)用拉格朗日、分段线性、三次样条三种插值方法,计算m个插值点的函数值(m要适中,如50~100)。
通过数值和图形输出,将三种插值结果与精确值进行比较。
适当增加n,再作比较,由此作初步分析。
y=exp(-x2),-2≤x≤2.取n=5,m=80用MATLAB计算插值数据比较如下:y是精确值,y1是分段线性值,y2是三次样条法插值,y3是拉格朗日插值由于对称性,只给出x>0的值程序:function y=lagr(x0,y0,x)%函数输入:n个节点以数组x0,y0输入,m个插值点以数组x输入?%函数输出:输出数组y为m个插值?n=length(x0);m=length(x);for i=1:mz=x(i);s=0.0;for k=1:np=1.0;for j=1:nif j~=kp=p*(z-x0(j))/(x0(k)-x0(j)); endends=p*y0(k)+s;endy(i)=s;end结果:x0=-2:0.5:2;y0=exp(-1*x0.^2);x=-2:0.05:2y=exp(-1*x.^2);y1=lagr(x0,y0,x);y2=interp1(x0,y0,x);y3=spline(x0,y0,x);[x;y;y1;y2;y3]'plot(x,y,'k--',x,y1,'r'),xlabel('x')ylabel('y/y1')title('拉格朗日插值(n=9,m=21)'),legend('原函数曲线','拉格朗日插值曲线'), pause,plot(x,y,'k--',x,y2,'r'),xlabel('x')ylabel('y/y2')title('分段线性插值(n=9,m=21)'),legend('原函数曲线','分段线性插值曲线'), pause,plot(x,y,'k--',x,y3,'r'),xlabel('x')ylabel('y/y1')title('三次样条插值(n=9,m=21)'),legend('原函数曲线','三次样条插值曲线'), x =Columns 1 through 9-2.0000 -1.9500 -1.9000 -1.8500 -1.8000 -1.7500 -1.7000 -1.6500 -1.6000Columns 10 through 18-1.5500 -1.5000 -1.4500 -1.4000 -1.3500 -1.3000 -1.2500 -1.2000 -1.1500Columns 19 through 27-1.1000 -1.0500 -1.0000 -0.9500 -0.9000 -0.8500 -0.8000 -0.7500 -0.7000Columns 28 through 36-0.6500 -0.6000 -0.5500 -0.5000 -0.4500 -0.4000 -0.3500 -0.3000 -0.2500Columns 37 through 45-0.2000 -0.1500 -0.1000 -0.0500 0 0.0500 0.1000 0.1500 0.2000Columns 46 through 540.2500 0.3000 0.3500 0.4000 0.4500 0.5000 0.5500 0.6000 0.6500Columns 55 through 630.7000 0.7500 0.8000 0.8500 0.9000 0.9500 1.0000 1.0500 1.1000Columns 64 through 721.1500 1.2000 1.2500 1.3000 1.3500 1.4000 1.4500 1.5000 1.5500Columns 73 through 811.6000 1.6500 1.7000 1.7500 1.8000 1.8500 1.9000 1.95002.0000ans =-2.0000 0.0183 0.0183 0.0183 0.0183 -1.9500 0.0223 0.0048 0.0270 0.0207 -1.9000 0.0271 0.0011 0.0357 0.0243 -1.8500 0.0326 0.0044 0.0444 0.0292 -1.8000 0.0392 0.0127 0.0531 0.0355 -1.7500 0.0468 0.0243 0.0619 0.0433 -1.7000 0.0556 0.0381 0.0706 0.0525 -1.6500 0.0657 0.0535 0.0793 0.0633 -1.6000 0.0773 0.0700 0.0880 0.0757 -1.5500 0.0905 0.0873 0.0967 0.0897 -1.5000 0.1054 0.1054 0.1054 0.1054 -1.4500 0.1222 0.1244 0.1316 0.1229 -1.4000 0.1409 0.1446 0.1579 0.1421 -1.3500 0.1616 0.1660 0.1841 0.1633 -1.3000 0.1845 0.1889 0.2104 0.1863 -1.2500 0.2096 0.2136 0.2366 0.2114 -1.2000 0.2369 0.2402 0.2629 0.2384 -1.1500 0.2665 0.2689 0.2891 0.2675-1.1000 0.2982 0.2998 0.3154 0.2988 -1.0500 0.3320 0.3328 0.3416 0.3322 -1.0000 0.3679 0.3679 0.3679 0.3679 -0.9500 0.4056 0.4050 0.4090 0.4058 -0.9000 0.4449 0.4439 0.4501 0.4455 -0.8500 0.4855 0.4844 0.4912 0.4867 -0.8000 0.5273 0.5261 0.5322 0.5288 -0.7500 0.5698 0.5687 0.5733 0.5716 -0.7000 0.6126 0.6117 0.6144 0.6145 -0.6500 0.6554 0.6547 0.6555 0.6571 -0.6000 0.6977 0.6972 0.6966 0.6989 -0.5500 0.7390 0.7388 0.7377 0.7397 -0.5000 0.7788 0.7788 0.7788 0.7788 -0.4500 0.8167 0.8168 0.8009 0.8159 -0.4000 0.8521 0.8524 0.8230 0.8507 -0.3500 0.8847 0.8850 0.8452 0.8827 -0.3000 0.9139 0.9142 0.8673 0.9117 -0.2500 0.9394 0.9397 0.8894 0.9372 -0.2000 0.9608 0.9610 0.9115 0.9588 -0.1500 0.9778 0.9779 0.9336 0.9763 -0.1000 0.9900 0.9901 0.9558 0.9892 -0.0500 0.9975 0.9975 0.9779 0.99720 1.0000 1.0000 1.0000 1.0000 0.0500 0.9975 0.9975 0.9779 0.9972 0.1000 0.9900 0.9901 0.9558 0.9892 0.1500 0.9778 0.9779 0.9336 0.9763 0.2000 0.9608 0.9610 0.9115 0.9588 0.2500 0.9394 0.9397 0.8894 0.9372 0.3000 0.9139 0.9142 0.8673 0.9117 0.3500 0.8847 0.8850 0.8452 0.8827 0.4000 0.8521 0.8524 0.8230 0.8507 0.4500 0.8167 0.8168 0.8009 0.8159 0.5000 0.7788 0.7788 0.7788 0.7788 0.5500 0.7390 0.7388 0.7377 0.7397 0.6000 0.6977 0.6972 0.6966 0.6989 0.6500 0.6554 0.6547 0.6555 0.6571 0.7000 0.6126 0.6117 0.6144 0.6145 0.7500 0.5698 0.5687 0.5733 0.5716 0.8000 0.5273 0.5261 0.5322 0.5288 0.8500 0.4855 0.4844 0.4912 0.4867 0.9000 0.4449 0.4439 0.4501 0.44550.9500 0.4056 0.4050 0.4090 0.40581.0000 0.3679 0.3679 0.3679 0.3679 1.0500 0.3320 0.3328 0.3416 0.33221.1000 0.2982 0.2998 0.3154 0.2988 1.1500 0.2665 0.2689 0.2891 0.2675 1.2000 0.2369 0.2402 0.2629 0.2384 1.2500 0.2096 0.2136 0.2366 0.2114 1.3000 0.1845 0.1889 0.2104 0.1863 1.3500 0.1616 0.1660 0.1841 0.1633 1.4000 0.1409 0.1446 0.1579 0.1421 1.4500 0.1222 0.1244 0.1316 0.1229 1.5000 0.1054 0.1054 0.1054 0.1054 1.5500 0.0905 0.0873 0.0967 0.0897 1.6000 0.0773 0.0700 0.0880 0.0757 1.6500 0.0657 0.0535 0.0793 0.0633 1.7000 0.0556 0.0381 0.0706 0.0525 1.7500 0.0468 0.0243 0.0619 0.0433 1.8000 0.0392 0.0127 0.0531 0.0355 1.8500 0.0326 0.0044 0.0444 0.0292 1.9000 0.0271 0.0011 0.0357 0.02431.9500 0.0223 0.0048 0.0270 0.02072.0000 0.0183 0.0183 0.0183 0.0183上图是根据插值数据作出的曲线。
数值分析实验报告--插值与拟合及其并行算法

《数值分析》实验报告实验五、插值与拟合及其并行算法一.实验目的:1.学会拉格朗日插值, 分段线性插值或三次样条插值以及曲 线拟合等数值分析问题,通过 MATLAB 编程解决这些数 值分析问题,并且加深对此次实验内容的理解。
2.加强编程能力和编程技巧,练习从数值分析角度看问题, 同时用 MATLAB 编写代码。
二.实验要求:学会在计算机上实现拉格朗日插值,分段线性插值或三次 样条插值以及曲线拟合等数值分析问题,分析几种插值方法的异 同。
三.实验内容:分别用下列题目完成①:拉格朗日插值及其误 差分析 ②:三次样条 ③: 曲线拟合及其误差分析,实验要求。
四.实验题目: (1)已知 sin 30 D = 0.5 , sin 45D = 0.707 1 ,sin 60 D = 0.866 0 ,用拉格朗日插值及其误差估计的MATLAB主程序求 sin 20D 的近似值,并估计其误差。
(2)观测得出函数 y=f(x)在若干点处的值为 f(0)=0, f(2)=16, f(4)=36, f(6)=54, f(10)=82 和 f'(0)=8, f'(10)=7, 试求 f(x)的三次样条函数,并计算 f(3)和 f(8)的近似值. ( 3 ) t=[2.1 7.9 10.1 13 14.5 15.3];r=[13.5 36.9 45.7 求出 r 与 t 之间的关系, 及三 57.3 62.78 74.9];根据给出数据, 种误差,并作出拟合曲线。
五.实验原理:(1)拉格朗日插值公式:P5 ( x) = ∑ y i l i ( x)i =05li ( x) =( x − x 0 ) " ( x − xi −1 )( x − xi +1 ) " ( x − x n ) ( xi − x0 ) " ( xi − xi −1 )( xi − xi +1 ) " ( xi − x n )(2)三次样条插值公式:Sn(x)={Si(x)=a i x +b i x +c i x+d i , x ∈ [x i −1 ,x i ] ,i=1,2,….,n}32(3)曲线拟合: 最小二乘法并不只限于多项式,也可以用于任何具体给出的函数 形式。
第七讲 插值与拟合实验

y i = f ( xi ) 。插值函数一般是已知函数的线性组合或称为加权平均。用代数多项式作为插
值函数的插值法称为多项式插值,相应的多项式称为插值多项式。 插值和拟合是函数逼近的简单但又十分重要的方法。 插值法可以导出数值微分、 数值积 分和微分方程数值解等多方面的计算方法, 是数值分析的基本课题。 同时插值和拟合在工程 实践和科学实验中有着非常广泛而又十分重要的应用。 本实验将主要研究几种基本的插值方法(如 Lagrange 插值、分段线性插值、三次样条 插值等)和数据的最小二乘拟合方法。要求学会 Mathematica 提供的插值函数和拟合函数的 使用方法,会用这些函数解决实际问题。
基函数。容易证明
⎧1 li ( x j ) = δ ij = ⎨ ⎩0
i= j , i, j = 0,1& Ln ( xi ) = y i , i = 0,1, " , n 。 还可以从其他角度出发,构造出插值多项式,如牛顿(Newton)插值公式。 Lagrange 插值法最大的优点是函数具有很好的解析性质(无穷次可微) ,但是它也存在 固有的缺点:可能出现严重的振荡现象,并且多项式函数的系数依赖于观测数据。 例 1 考虑函数
3、 三次样条插值 在工程设计和机械加工等实际问题中,要求插值函数有较高的光滑度。在数学上,光滑 程度的定量描述是:函数(曲线)的 k 阶导数存在且连续,则称该曲线具有 k 阶光滑性。自 然,光滑性阶数越高其曲线光滑程度就越好。而上面介绍的分段线性插值,只具有零阶光滑 性,也就是不光滑的。虽然,提高分段函数如多项式函数的次数,可以提高整体曲线的光滑 程度, 但是, 是否存在较低次多项式达到较高光滑性的方法?三次样条插值就是一个很好的 例子。 样条曲线本身就来源于飞机、船舶等外形曲线设计问题。在工程实际中,要求此类曲线 应该具有连续的曲率,即连续的二阶导数。人们普遍使用的样条曲线是分段三次多项式。 定义 设 在 区 间 [a,b] 上 给 定 一 组 节 点 a = x 0 < x1 < " < x n = b 上 的 函 数 值
插值与拟合实验报告

学生实验报告了解插值与拟合的基本原理和方法;掌握用MATLAB计算插值与作最小二乘多项式拟合和曲线拟合的方法;通过范例展现求解实际问题的初步建模过程;通过动手作实验学习如何用插值与拟合方法解决实际问题,提高探索和解决问题的能力。
这对于学生深入理解数学概念,掌握数学的思维方法,熟悉处理大量的工程计算问题的方法具有十分重要的意义。
二、实验仪器、设备或软件:电脑,MATLAB软件三、实验内容1.编写插值方法的函数M文件;2.用MATLAB中的函数作函数的拟合图形;3.针对实际问题,试建立数学模型,并求解。
四、实验步骤1.开启软件平台——MATLAB,开启MATLAB编辑窗口;2.根据各种数值解法步骤编写M文件;3.保存文件并运行;4.观察运行结果(数值或图形);5.写出实验报告,并浅谈学习心得体会。
五、实验要求与任务根据实验内容和步骤,完成以下具体实验,要求写出实验报告(实验目的→问题→数学模型→算法与编程→计算结果→分析、检验和结论→心得体会)。
1.天文学家在1914年8月的7次观测中,测得地球与金星之间距离(单位:米),并取得常用对数值,与日期的一组历史数据如下表:由此推断何时金星与地球的距离(米)的对数值为9.93518?解:输入命令days=[18 20 22 24 26 28 30];distancelogs=[9.96177 9.95436 9.94681 9.93910 9.93122 9.92319 9.91499]; t1=interp1(distancelogs,days,9.93518) %线性插值t2=interp1(distancelogs,days,9.93518,'nearest') %最近邻点插值t3=interp1(distancelogs,days,9.93518,'spline') %三次样条插值t4=interp1(distancelogs,days,9.93518,'cubic') %三次插值计算结果:t1 =24.9949t2 =24t3 =25.0000t4 =25.0000综上所得,可推断25日金星与地球的距离(米)的对数值为9.93518。
曲线拟合和插值运算原理和方法

实验10 曲线拟合和插值运算一. 实验目的学会MATLAB 软件中软件拟合与插值运算的方法。
二. 实验内容与要求在生产和科学实验中,自变量x 与因变量y=f(x)的关系式有时不能直接写出表达式,而只能得到函数在若干个点的函数值或导数值。
当要求知道观测点之外的函数值时,需要估计函数值在该点的值。
要根据观测点的值,构造一个比较简单的函数y=t (x),使函数在观测点的值等于已知的数值或导数值,寻找这样的函数t(x),办法是很多的。
根据测量数据的类型有如下两种处理观测数据的方法。
(1) 测量值是准确的,没有误差,一般用插值。
(2) 测量值与真实值有误差,一般用曲线拟合。
MATLAB 中提供了众多的数据处理命令,有插值命令,拟合命令。
1.曲线拟合已知离散点上的数据集[(1x ,1y ),………(n x ,n y )],求得一解析函数y=f (x),使f(x)在原离散点i x 上尽可能接近给定i y 的值,之一过程叫曲线拟合。
最常用的的曲线拟合是最小二乘法曲线拟合,拟合结果可使误差的平方和最小,即使求使21|()|n i ii f x y =-∑ 最小的f(x).格式:p=polyfit(x,Y ,n).说明:求出已知数据x,Y 的n 阶拟合多项式f(x)的系数p ,x 必须是单调的。
[例 1.9]>>x=[0.5,1.0,1.5,2.0,2.5,3.0]; %给出数据点的x 值>>y=[1.75,2.45,3.81,4.80,7.00,8.60]; %给出数据点的y 值>>p=polyfit (x,y,2); %求出二阶拟合多项式f(x)的系数>>x1=0.5:0.05:3.0; %给出x 在0.5~3.0之间的离散值>>y1=polyval(p,1x ); %求出f(x)在1x 的值>>plot(x,y,‟*r ‟, 11,x y ‟-b ‟) %比较拟合曲线效果计算结果为:p=0.5614 0.8287 1.1560即用f(x)=0.56142x +0.8287x+1.1560拟合已知数据,拟合曲线效果如图所示。
曲线拟合和插值
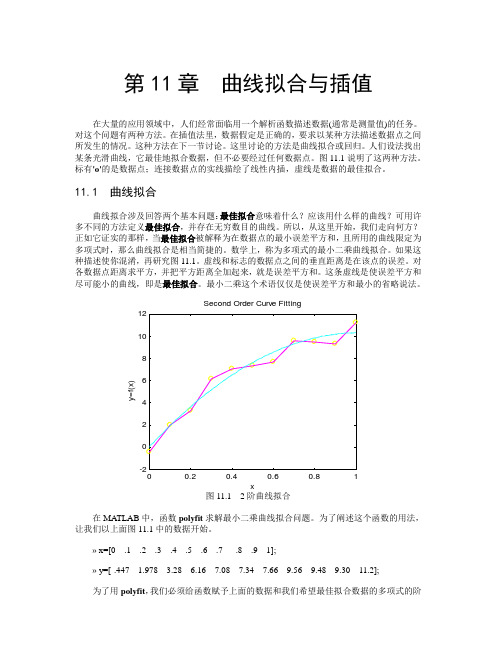
第11章曲线拟合与插值在大量的应用领域中,人们经常面临用一个解析函数描述数据(通常是测量值)的任务。
对这个问题有两种方法。
在插值法里,数据假定是正确的,要求以某种方法描述数据点之间所发生的情况。
这种方法在下一节讨论。
这里讨论的方法是曲线拟合或回归。
人们设法找出某条光滑曲线,它最佳地拟合数据,但不必要经过任何数据点。
图11.1说明了这两种方法。
标有'o'的是数据点;连接数据点的实线描绘了线性内插,虚线是数据的最佳拟合。
11.1 曲线拟合曲线拟合涉及回答两个基本问题:最佳拟合意味着什么?应该用什么样的曲线?可用许多不同的方法定义最佳拟合,并存在无穷数目的曲线。
所以,从这里开始,我们走向何方?正如它证实的那样,当最佳拟合被解释为在数据点的最小误差平方和,且所用的曲线限定为多项式时,那么曲线拟合是相当简捷的。
数学上,称为多项式的最小二乘曲线拟合。
如果这种描述使你混淆,再研究图11.1。
虚线和标志的数据点之间的垂直距离是在该点的误差。
对各数据点距离求平方,并把平方距离全加起来,就是误差平方和。
这条虚线是使误差平方和尽可能小的曲线,即是最佳拟合。
最小二乘这个术语仅仅是使误差平方和最小的省略说法。
图11.1 2阶曲线拟合在MA TLAB中,函数polyfit求解最小二乘曲线拟合问题。
为了阐述这个函数的用法,让我们以上面图11.1中的数据开始。
» x=[0 .1 .2 .3 .4 .5 .6 .7 .8 .9 1];» y=[-.447 1.978 3.28 6.16 7.08 7.34 7.66 9.56 9.48 9.30 11.2];为了用polyfit,我们必须给函数赋予上面的数据和我们希望最佳拟合数据的多项式的阶次或度。
如果我们选择n=1作为阶次,得到最简单的线性近似。
通常称为线性回归。
相反,如果我们选择n=2作为阶次,得到一个2阶多项式。
现在,我们选择一个2阶多项式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
试验七数据插值与曲线拟合实验
一、试验目的
1.掌握数据统计和分析的方法。
2.掌握数据插值与曲线拟合的方法及其应用。
二、试验内容
1.已知原始数据)5/
x
y
pi
x-
=
=,,插值点为
*
4:1:0x
*
e x p(
).
sin(
=,试用四种不同的插值方法进行插值,并在一副图中绘出四种4:3.0:0
pi
xi*
插值曲线。
x=0:1:4*pi;
y=sin(x).*exp(-x/5);
xi=0:0.3:4*pi;
y1=interp1(x,y,xi,'nearest');
y2=interp1(x,y,xi,'linear');
y3=interp1(x,y,xi,'spline');
y4=interp1(x,y,xi,'cubic');
plot(x,y,'r',xi,y1,'b',xi,y2,'g',xi,y3,'y',xi,y4,'k')
2.考虑下面的数据,一位举重教练收集了不同性别的举重动员每个年龄的最大举重磅数,他相信这三者之间存在着函数关系,请创建一个年龄数组,以便估算当前队伍中队员(要求13~20岁每一岁都有)的最大举重。
y=[270 290 330 350 380;250 270 310 330 360 ]';
X=[ones(size(t)) t t.^2];
Z=X\y; %得到系数
T=(13:20)';
Y=[ones(size(T)) T T.^2]*Z
运行结果:Y =
269.1990 249.1990
280.8565 260.8565
293.7351 273.7351
307.8351 287.8351
323.1562 303.1562
339.6987 319.6987 357.4623 337.4623 376.4473 356.4473
x=1990:1996;
y=[70 122 144 152 174 196 202]; k1=polyfit(x,y,1); %得到系数 y1=polyval(k1,x);
plot(x,y,'r',x,y1,'g');
title('ijÏçÕòÆóÒµ1990-1996ÄêµÄÉú²úÀûÈó') legend('qixian','1th order')
4. 先使用命令load 加载census.mat 得到一组数据(cdate,pop ),该数据是美国自1790到1990年(以10年为一单位)的总人口。
利用回归法拟合,预测出美国在2010年的人口总数,写出拟合模型),(2210cdate x pop y x a x a a y 为为其中++=,并绘出拟合图。
load census.mat cdate'; pop';
X=[ones(size(cdate)) cdate cdate.^2]; a=X\pop;
CDATE=[1970:1:2012]'; axis([1970 2012 0 750]);
POP=[ones(size(CDATE)) CDATE CDATE.^2]*a; plot(CDATE,POP,'r-',cdate,pop,'b*'); grid on;。
