全国大学生数学建模竞赛A题
全国大学生数学建模大赛国家一等奖论文A题

=
− − ( − 1)′
, = 1, 2, · · ·, 210
当逐渐增大,锚链受到的竖直向下方向的合力与支持力之差先逐渐接近于0,
再等于0,直至小于0。当合力小于0时,锚链以海床接触,此时海床提供向上的支持
力,其大小与′ 相等。因此可将小于0 的值都作零处理,故锚链接触海床时,
对于问题二,首先考虑第一个子问题,将风速36/直接代入问题一的模型中,
得出此条件下的吃水深度为0.723,各钢管倾斜角度(度)依次为8.960、9.014、9.068
、9.123,钢桶倾斜角(度)为9.179,锚链链接处的切线方向与海床的夹角(度)为18.414,
游动区域半径为18.80。发现此条件下,水声通讯系统设备的工作效果较差,且锚被
计与应用对海上科学发展有重要意义。
1.2 问题的提出
已知某近浅海传输节点(如图1所示),将浮标视作底面直径2为、高为2、质量
为1000的圆柱体,锚的质量为600,钢管共4节,每节长度为1,直径为50,
每节钢管的质量为10。水声通讯系统安装在一个长为1、外径为30的密封圆
柱形钢桶内,设备和钢桶总质量为100。
Step1: 遍历求解
令吃水深度ℎ的初始值为0.1,以0.0005为单位逐步增加至2。( 浮标高度为2,
完全浸没时吃水深度ℎ则为2 ),记录对应的数据,选取水下物体竖直方向高度和
与海域水深最接近的组别,进一步进行计算,结果如下表所示(具体程序见附录):
表 1: 不同风速的相关结果表
以风速24/的情况为例,绘制游动区域图:
题意的变量临界值。以水深16、系统各部分递推关系式和钢桶与竖直方向夹角小
于5°为约束条件,将多目标优化转化为单目标优化。通过调节决策变量中锚链的型
全国大学生数学建模竞赛a题(2255)

优秀论文选编A题之一(全国一等奖)奥运会临时超市网点设计广西师范大学,吴宗显、单俊辉、谭春亮;指导教师:数学建模组摘要:本文首先根据问卷调查数据计算观众出行、用餐和购物等方面的分布,分析各种分布的特点。
然后,根据观众出行、用餐分布,场馆分布情况和最短距离原则,测算出测算20个商区的人流量及其分布。
最后,根据商圈分析中零售引力法则(即里利法则)、哈夫概率模型、饱和理论,建立设计MS网点大小规模类型的数学模型。
在约定大规模MS网点的面积为1个单位的基础上,经过计算求解,得到小规模MS网点的面积为0.6个单位,并得出20个MS网点的设计方案,具体设计方案是:A区有2个大规模MS网点,分别设在A6小区和A1小区,其余8个小区均为小规模MS网点;B区有2个大规模MS网点,分别设在B6小区和B3小区,其余4个小区均为小规模MS网点;C区有1个大规模MS网点,设在C4小区,其余3个小区均为小规模MS网点。
奥运会临时超市网点设计一、问题的分析与基本假设(一)问题的分析题目要求完成如下工作:1、根据附录中给出的问卷调查数据,找出了观众在出行、用餐和购物等方面所反映的规律2、在一天内每位观众平均出行两次,一次为进出场馆,一次为餐饮,并且出行均采取最短路径前提下。
依据1的结果,测算图2中20个商区的人流量分布。
3、按照满足奥运会期间的购物需求、分布基本均衡和商业上赢利的要求,根据流量分布规律,在有两种大小不同规模的MS类型供选择情况下,给出图2中20个商区内MS网点的设计方案(即每个商区内不同类型MS的个数)。
(二)基本假设1、假定A区(国家体育场)容量为10万人,B区(国家体育馆)容量为6万人,C区(国家游泳中心)容量为4万人。
三个场馆的每个看台容量均为1万人,出口对准一个商区,各商区面积相同。
2、无论乘坐何种交通工具的观众所持的票号是随机的。
二、问卷调查数据的统计与分布规律我们把附录中三次调查的数据综合起来并进行的统计和分析得出的观众在出行、用餐和购物等方面的规律如下:1、整个人群的各种行为的分布规律(1)用不同的交通方式的人数及其分别所占总人数的比例除私车方式偏少一些(仅有9.0377%)外,其余方式分布都比较均匀,均为16%-20%,这说明场馆周围布局的交通车站是比较合理的。
2023国赛数学建模a题

2023国赛数学建模a题一、选择题(每题4分,共20分)下列函数中,是奇函数的是()A. y = x^2B. y = |x|C. y = 1/xD. y = x^3已知直线l 过点P(1, 2),且与直线y = 3x 平行,则直线l 的方程是()A. y = 3x - 1B. y = 3x + 1C. y = 3x - 5D. y = 3x + 5下列等式中正确的是()A. sin(π/2 + α) = cosαB. cos(π/2 + α) = sinαC. tan(π/2 + α) = -cotαD. sin(π - α) = -sinα设随机变量X 服从正态分布N(2, σ^2),若P(X < 4) = 0.9,则P(0 < X < 2) = ()A. 0.4B. 0.3C. 0.2D. 0.1在△ABC中,若 A = 60°,b = 1,S△ABC = √3,则 a = ()A. 1B. 2C. √3D. √2二、填空题(每题4分,共16分)函数y = √(x - 1) 的定义域是_______。
若直线x + y + k = 0 与圆x^2 + y^2 = 1 相切,则k = _______。
已知等差数列{an} 的前n 项和为Sn,若a1 = 1,S3 = 9,则a2 + a4 = _______。
若x, y 满足约束条件{ x + y ≤ 1, x - y ≥ -1, y ≥ 0 },则z = 2x + y 的最大值为_______。
三、解答题(共64分)10.(12分)求函数y = 2sin(2x - π/6) 的单调递增区间。
11.(12分)在△ABC中,已知a = 5,b = 8,cosC = 11/16,求sinA 的值。
12.(12分)已知函数f(x) = x^3 + ax^2 + bx + c 在x = 1 与x = -1 时取得极值。
(1)求a,b 的值;(2)若对于任意x ∈ [-2, 2],都有f(x) < c^2 成立,求 c 的取值范围。
2023数学建模国赛a题详解

2023数学建模国赛a题详解2023数学建模国赛A题要求我们通过研究某公司的数据集,分析并预测销售额的变化规律。
本文将详细解析解题思路和方法,并进行具体的数据分析和预测。
1. 问题描述与分析我们首先需要详细了解题目描述和所给的数据集。
根据题目要求,我们已经得知某公司的销售数据集包括了过去几年的销售额数据,每个季度为一个数据点。
我们的目标是利用这些数据进行分析和预测,找出销售额的变化规律,并给出未来一段时间内的销售额预测。
2. 数据处理与可视化在进行数据分析之前,我们首先需要对所给的数据进行处理和可视化。
我们可以借助Python编程语言中的数据分析库,如NumPy和Pandas,对数据进行导入和处理。
然后,我们可以使用Matplotlib或Seaborn等库来绘制可视化图表,以更好地理解数据的分布和趋势。
3. 数据分析与模型建立在对数据进行可视化之后,我们可以开始进行数据分析和模型建立。
根据经验,销售额的变化往往受多个因素的影响,比如季节性变化、市场需求、竞争压力等等。
我们可以通过构建适当的数学模型来描述这些因素与销售额之间的关系,并进行参数估计和模型验证。
以季节性变化为例,我们可以使用时间序列分析方法,如ARIMA模型或季节性指数平滑方法,来捕捉销售额随季节变化的规律。
此外,我们还可以考虑使用回归分析或神经网络等方法,以探索销售额与其他因素之间的复杂关系。
4. 模型评估与预测在模型建立之后,我们需要对模型进行评估和预测。
我们可以使用历史数据的一部分来验证模型的拟合效果,比较模型预测值与真实值的差异。
如果模型表现良好,则可以将其应用于未来一段时间内的销售额预测。
在进行预测时,我们应该注意模型的置信区间和误差范围。
销售额的预测结果往往是一个区间范围,而不是一个确定的数值。
这是由于预测中存在不确定性和随机性因素的影响。
我们可以使用Bootstrap方法或蒙特卡洛模拟等方法,来估计销售额的置信区间和误差范围。
2023数学建模国赛a题思路

2023数学建模国赛a题思路
2023数学建模国赛A题是关于水电站优化选址和建设的题目,可以按照以下步骤进行思路分析:
1. 问题一:水电站的最优选址
首先,需要考虑投入和收入、地质和水文条件、环境成本等各个因素,这些因素可以被看作优化模型中的约束条件。
目标函数可以是最优水电站的位置。
由于这是一个优化问题,需要定义目标函数并确定最大化或最小化的目标,同时定义约束条件,例如线性约束、非线性约束等。
2. 问题二:建设多个水电站
目标是使得能源最大,约束条件与问题一相同。
这需要对问题一的优化模型进行延申,对建设水电站的个数以及发电能力进行求解。
3. 问题三:红旗河项目
这是一个引水工程项目,目的是将雅鲁藏布江的水输送到西北地区,改善西北地区的缺水状况和自然环境。
这个问题需要结合地理知识和工程知识进行建模和求解。
以上是对2023数学建模国赛A题思路的分析,具体解题过程还需要根据实际问题进行建模和求解。
全国大学生数学建模竞赛题目A题
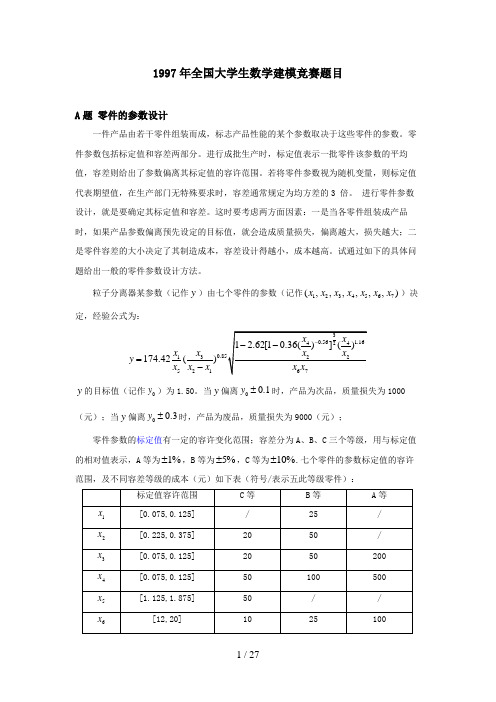
1997年全国大学生数学建模竞赛题目A 题 零件的参数设计一件产品由若干零件组装而成,标志产品性能的某个参数取决于这些零件的参数。
零件参数包括标定值和容差两部分。
进行成批生产时,标定值表示一批零件该参数的平均值,容差则给出了参数偏离其标定值的容许范围。
若将零件参数视为随机变量,则标定值代表期望值,在生产部门无特殊要求时,容差通常规定为均方差的3 倍。
进行零件参数设计,就是要确定其标定值和容差。
这时要考虑两方面因素:一是当各零件组装成产品时,如果产品参数偏离预先设定的目标值,就会造成质量损失,偏离越大,损失越大;二是零件容差的大小决定了其制造成本,容差设计得越小,成本越高。
试通过如下的具体问题给出一般的零件参数设计方法。
粒子分离器某参数(记作y )由七个零件的参数(记作1234567(,,,,,,)x x x x x x x )决定,经验公式为:31521174.42()x x y x x x =-y 的目标值(记作0y )为1.50。
当y 偏离00.1y ±时,产品为次品,质量损失为1000(元);当y 偏离00.3y ±时,产品为废品,质量损失为9000(元);零件参数的标定值有一定的容许变化范围;容差分为A 、B 、C 三个等级,用与标定值的相对值表示,A 等为1%±,B 等为5%±,C 等为10%±.七个零件的参数标定值的容许范围,及不同容差等级的成本(元)如下表(符号/表示五此等级零件):现进行成批生产,每批产量1000个。
在原设计中,七个零件参数标定值为10.1x=,20.3x=,30.1x=,40.1x=,51.5x=,616x=,70.75x=;容差均取最便宜的等级。
请你综合考虑y偏离0y造成的损失和零件成本,重新设计零件参数(包括标定值和容差),并与原设计比较,总费用降低了多少?B题截断切割某些工业部门(如贵重石材加工等)采用截断切割的加工方式。
2022年全国大学生数学建模竞赛A题

2022年全国大学生数学建模竞赛A题(请先阅读“全国大学生数学建模竞赛论文格式规范”)A题系泊系统的设计近浅海观测网的传输节点由浮标系统、系泊系统和水声通讯系统组成(如图1所示)。
某型传输节点的浮标系统可简化为底面直径2m、高2m的圆柱体,浮标的质量为1000kg。
系泊系统由钢管、钢桶、重物球、电焊锚链和特制的抗拖移锚组成。
锚的质量为600kg,锚链选用无档普通链环,近浅海观测网的常用型号及其参数在附表中列出。
钢管共4节,每节长度1m,直径为50mm,每节钢管的质量为10kg。
要求锚链末端与锚的链接处的切线方向与海床的夹角不超过16度错误!未找到引用源。
,否则锚会被拖行,致使节点移位丢失。
水声通讯系统安装在一个长1m、外径30cm的密封圆柱形钢桶内,设备和钢桶总质量为100kg。
钢桶上接第4节钢管,下接电焊锚链。
钢桶竖直时,水声通讯设备的工作效果最佳。
若钢桶倾斜,则影响设备的工作效果。
钢桶的倾斜角度(钢桶与竖直线的夹角)超过5度时,设备的工作效果较差。
为了控制钢桶的倾斜角度,钢桶与电焊锚链链接处可悬挂重物球。
图1传输节点示意图(仅为结构模块示意图,未考虑尺寸比例)系泊系统的设计问题就是确定锚链的型号、长度和重物球的质量,使得浮标的吃水深度和游动区域及钢桶的倾斜角度尽可能小。
问题1某型传输节点选用II型电焊锚链22.05m,选用的重物球的质量为1200kg。
现将该型传输节点布放在水深18m、海床平坦、海水密度为1.025某103kg/m3的海域。
若海水静止,分别计算海面风速为12m/和24m/时钢桶和各节钢管的倾斜角度、锚链形状、浮标的吃水深度和游动区域。
问题2在问题1的假设下,计算海面风速为36m/时钢桶和各节钢管的倾斜角度、锚链形状和浮标的游动区域。
请调节重物球的质量,使得钢桶的倾斜角度不超过5度,锚链在锚点与海床的夹角不超过16度。
问题3由于潮汐等因素的影响,布放海域的实测水深介于16m~20m之间。
全国大学生数学建模竞赛A题解析

三、解题思路(续)
(4)对于实际储油罐,建立罐体变位后罐内储油量
V与油位高度h及纵向倾斜角度 和 横向偏转角度 之间 的关系模型,即 V。F(,,h)
由于本问较复杂,需要分情况建立模型,可以先考 虑只发生纵向变位的情况。
三、解题思路(续)
球冠Ⅰ的体积表达式为:
其中
三、解题思路(续)
球冠III的体积表达式为:
atabnhaaltanz a2z2a2arcsinaz2a2dz, 0hLltan
V( ,h) atabn
haltan haLltanz
a2z2a2arcsinaz2a2dz,
(Ll)tanh2altan
LabaahLltanz a2z2a2arcsinaz2a2dz, 0hLltan
180
190
200
L 19265.60 21941.18 24674.88 27450.77 30253.25 33066.99 35876.76 38667.27 41423.11 44128.48
h 210
220
230
240
250
260
270
280
290
3400
L 46767.21 49322.44 51776.40 54109.93 56302.12 58329.27 60163.39 61768.90 63093.63 64026.17
ax
h
三、解题思路(续)
利用积分可以计算出油位高度为h时实验罐的截面 面积,于是得到油位高度与储油量的计算公式:
V (H ) 2 a b b a (h b )2 b h h 2 a b a rc s in h b b L
其中a,b,L分别是实验罐截面椭圆的长半轴、短半轴 和罐体长度,h为油位高度。
