15.5 算符与平均值
25 力学量的平均值、算符表示 平均值
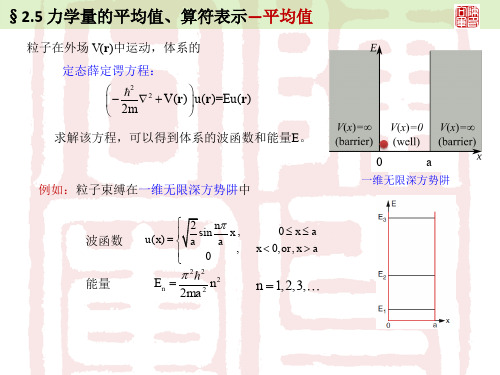
粒子在外场 V(r)中运动,体系的 定态薛定谔方程:
2 2 V ( r ) u (r )=Eu (r ) 2 m
求解该方程,可以得到体系的波函数和能量E。 0 例如:粒子束缚在一维无限深方势阱中
2 n sin x, u ( x) a a , 0 0 xa x 0, or , x a
定态薛定谔方程:
2 2 V (r ) u (r )=Eu (r ) 2m
ˆ (r)=Eu(r) Hu
§2.5 力学量的平均值、算符表示—算符表示
量子力学中,描述微观粒子的力学量均有对应的算符
(1) 位矢 r r (2) 势能 V(r) V(r) (3) 动量 p
如果粒子动量可以表示为 r点的函数 p(r, t),则可以用上述同样的方 法求平均值。但是,按照不确定关系,位置和动量不能同时具有确定的 取值!因此,“粒子在空间某点的动量 ”是没有意义的。
p(r, t)
§2.5 力学量的平均值、算符表示—平均值
将位置空间的波函数用平面单色波展开:
(r , t )
§2.6 单电子(H)原子—中心力场薛定谔方程
氢原子(类氢离子) 的薛定谔方程
3D 不含时的定态薛定谔方程
2 2 V r u Eu 2m
-e
+
+Ze
其中库仑势
Ze2 V r 4 0 r
电子束缚在原子核的中力场中,只与电子和核 间的径向距离有关。
a a 2 x a 2 x x u ( x) dx x sin 2 dx 0 0 a a 2
加权平均
§2.5 力学量的平均值、算符表示—平均值
高中化学计算方法总结:平均值法

方法总论平均值法高三化学组混合物的平均式量、元素的质量分数、生成的某指定物质的量总是介于组分的相应量的最大值M2与最小值M1之间,表达式为M1 < M < M2,已知其中两个量,可以确定另一个量的方法,称为平均值法。
一.平均相对分子质量1.在标准状况下,气体A的密度为1.25 g/L,气体B的密度为1.875 g/L,A和B 混合气体在相同状况下对H2的相对密度为16.8,则混合气体中A和B的体积比为A.1:2 B.2:1 C.2:3 D.3:2二.平均摩尔电子质量转移 1 mol电子时所对应的物质的质量就是摩尔电子质量。
如Al为27/3,Mg为24/2.2.由两种金属组成的合金50 g与Cl2完全反应,消耗Cl2 71 g,则合金可能的组成是A.Cu和Zn B.Ca和Zn C.Fe和Al D.Na和Al三.利用平均值的公式进行计算相对分子质量为M1、M2的物质按物质的量之比为a:b混合后,M=M1a/n t+M2b/n t。
3.有A、B、C三种一元碱,它们的相对分子质量之比为3:5:7,如果把7 mol A、5 mol B、3 mol C混合均匀,取混合碱5.36 g,恰好中和含0.15 mol HCl的盐酸,则A、B、C三种一元碱的相对分子质量分别是_____、_____、_____。
24,40,56。
四.平均双键数法基本思想:烷烃双键数为0,单烯烃双键数为1,炔烃双键数为2。
混合烃双键数根据具体情况确定,可利用双键数的平均值求解有关问题。
4.标准状况下的22.4 L某气体与乙烯的混合物,可与含溴8%的溴的CCl4溶液800 g恰好加成,则该气体可能是A.乙烷 B.丙烯 C.乙炔 D.1,3 丁二烯五.巧练5.已知Na2SO3和Na2SO4组成的混合物中,硫的质量分数为24.6%,则混合物中Na2SO3与Na2SO4的物质的量之比为A.1:3 B.3:1 C.4:1 D.1:46.现有铷和另一种碱金属形成的合金50 g,当它与足量水反应时,放出标准状况下的氢气22.4 L,这种碱金属可能是A.Li B.Na C.K D.Cs摩尔电子质量法根据在氧化还原反应中,得失电子相等的原则,立意是提供、得到或偏移 1 mol电子所需要和涉及的物质的质量,利用这种物质的质量来解决的方法称为摩尔电子质量法。
量子力学中平均值与期望值的概念与区别

量子力学中平均值与期望值的概念与区别量子力学是描述微观世界的一门物理学科,它引入了一些独特的概念和数学工具。
其中,平均值和期望值是量子力学中重要的概念,它们在理论和实验研究中起着关键的作用。
本文将探讨平均值和期望值的概念与区别。
一、平均值的概念与计算方法平均值是对一组数据的总体特征进行描述的统计量,它可以反映数据的集中程度。
在量子力学中,平均值用来描述物理量的期望取值。
以一个可观测量A为例,其平均值可以表示为:⟨A⟩= ∑(ai * Pi)其中,ai是A的一个可能取值,Pi是对应ai的概率。
平均值的计算方法是将所有可能取值与其对应的概率相乘,并将结果相加。
二、期望值的概念与计算方法期望值是对一个随机变量的平均值的度量,它表示了该随机变量在大量试验中的长期平均表现。
在量子力学中,期望值用来描述量子态的平均性质。
对于一个可观测量A和一个量子态ψ,其期望值可以表示为:E(A) = ⟨ψ|A|ψ⟩其中,|ψ⟩是量子态,A是可观测量。
期望值的计算方法是将量子态与可观测量的算符作用在一起,并对结果进行内积运算。
三、平均值与期望值的区别平均值和期望值在概念上有一定的区别。
平均值是对一组数据的总体特征进行描述,而期望值是对一个随机变量的长期平均表现进行度量。
在量子力学中,平均值描述了一个物理量的期望取值,而期望值描述了一个量子态的平均性质。
此外,平均值和期望值的计算方法也有所不同。
平均值的计算需要考虑各个可能取值的概率,而期望值的计算需要将量子态与可观测量的算符作用在一起,并对结果进行内积运算。
四、量子力学中的应用平均值和期望值在量子力学的理论和实验研究中有着广泛的应用。
通过计算平均值和期望值,可以了解物理量的平均取值和分布情况,从而揭示微观世界的规律和性质。
例如,在量子力学中,平均值和期望值可以用来描述粒子的位置、动量、能量等物理量。
通过计算这些物理量的平均值和期望值,可以了解粒子在不同量子态下的平均性质,从而揭示量子系统的行为和演化规律。
平均值与算符

i
同样可以证明另外两个式,
坐标和动量的其它对易关系如下,它们的证明是显然
的.
xpˆ y pˆ y x 0
xpˆ z
pˆ z
x
0
ypˆ x pˆ x y 0
ypˆ z
pˆ z
y
0
zpˆ x pˆ xz 0
Байду номын сангаас
zpˆ
y
pˆ yz
0
pˆ x pˆ y pˆ y pˆ x 0 pˆ y pˆ z pˆ z pˆ y 0 pˆ z pˆ x pˆ x pˆ z 0
x
2.算符
量子力学中的力学量通常以算符的形式出现。现用的
波函数是在坐标表象中的波函数,还可有别的表象,如 动量表象等。在不同的表象中,力学量的算符不同。
为在位置表象里求 p,x 只要把 px (x)换为
就可依照式(1)的方法求出。
pˆ x
i
x
pˆ x 称为动量x分量的算符。推广到三维空间则有: pˆ i
例如,动量的x分量px是可测的量,但px(x)写不 出来,因为px(x) 表示与每一特定的x有对应的值, 这是直接违反不确定关系的。
Px
*
(k
)Px
(k
)dk
Px hk
(k) 1 *(x)eikxdx
2
(x) (k)eikxdk
Px
*(x)(ih ) (x)dx
上面的第六式称为 Jacobi 恒等式。
证明5)式 [Oˆ ,UˆEˆ ] OˆUˆEˆ UˆEˆOˆ
OˆUˆEˆ UˆOˆEˆ UˆOˆEˆ UˆEˆOˆ
[Oˆ ,Uˆ ]Eˆ Uˆ[Oˆ , Eˆ ]
3. 基本对易关系
I(三章3讲)常用算符本征值问题

2 1 1 ˆ2 2 [ L (sin ) ] 2 2 sin sin 本征方程:
本征值: 本征函数: 正交归一性: 完备性: 简并度:
0
2
0
Ylm ( , )Yl* m ( , )sin d d ll mm
( p (r ''), p (r ')) (r '' r ')
平面波归一化计 算,你会了吗?
(二)位置算符
本征方程
ˆx x
ˆ x x
归一化常数: A 1
因为λ是常数,除了x=λ这一点外,x取其他任何值都有 0 即: ( x) A ( x ) 属于本征值λ的本征函数:
3. L2算符的本征值
2 1 1 ˆ2 2 [ L (sin ) ] 2 2 sin sin
因为它只与
, 有关,所以其本征函数应具有如下形式
Y ( , )
设它的本征值为: L
2
则其本征方程可写成:
ˆ2Y ( ,) L Y ( ,) 2Y ( ,) L
你会直角坐标与球坐标 的相互转换吗?
z
r
r
y
(II) 球坐标
直角坐标与球坐标之间的变换关系
2 2 2 2 r x y z cos z / r tan y / x
x
球 坐 标
x r sin cos y r sin sin z r cos
量子力学与统计物理
Quantum mechanics and statistical physics
平均值法01

专题29 平均值法在数学上,我们算过求平均数的题目,可表达为:m=(a+b)/2,且a>b>0时,a>m >b。
我们把它引入化学计算中,能使很多题目转繁为简,化难为易。
一、解题方法指导例题1 计算下列不同质量的20%的硫酸和10%的硫酸相混合后,所得溶液的溶质质量分数,并填表:10%的硫酸的质量20%的硫酸的质量混合后硫酸溶液的质量分数20g 70g40g 60g50g 50g60g 30g80g 20g思考:混合前后硫酸溶液中溶质、溶剂、溶液的量分别发生了什么变化?混合液的溶质质量分数与混合前两溶液的溶质质量分数大小有何关系?由此你可以得到哪些结论?(1)混合后的溶质质量分数总是介于10%-20%之间。
(2)只有等质量混合时混合液的溶质质量分数是混合前两溶液溶质质量分数之和的1/2。
(3)当20%的硫酸溶液质量大时,混合液的溶质质量分数就大于15%,反之亦然。
例题2 现有13.5g氯化铜样品,当它与足量的硝酸银充分反应后,得到AgCl 29g,则此样品中可能混有的物质是( )A、BaCl2B、KClC、ZnCl2D、CaCl2思考:此题反应化学方程式是什么?如果混有杂质会对AgCl的产量产生什么影响?解析:此类题目一般采用假设推理求平均值的方法。
先假设参加反应的物质为纯净物质,经计算得出一个平均值。
然后将假设所得结果,与实际数据相比较。
(1)设13.5g纯净物的CuCl2与AgNO3反应可得AgCl质量为XCuCl2 + 2AgNO3 == 2AgCl↓ + Cu(NO3)2135 28713.5g X135 :287 = 13.5g:X X = 28.7g(2)因为28.7g<29g,说明CuCl2样品中混有的杂质能与硝酸银反应,并且与同质量的CuCl2相比产生AgCl的质量多,即杂质中所含氯元素的质量分数高于CuCl2中氯元素的质量分数。
(3)分别计算出CuCl2、BaCl2、KCl、ZnCl2、CaCl2中氯元素的质量分数,然后比较得出答案。
1-05 算符
(壹x上) 量子力学基础第五节算符一、算符的定义和运算二、算符的本征方程、本征值、本征函数三、线性算符四、厄米算符小结作业思考题一、算符的定义和运算返回上页下页返回上页下页设符号代表某个运算规则,按此规则,由一个函数f 可唯一地确定另一个函数g ,记作符号称为算符.[算符的定义]Af g ˆ=AˆAˆ返回上页下页通常,算符记号上带有抑扬符“∧”.但是,对于单纯做乘法的算符,“∧”可省略.注可直接写做x ; ˆ()xx ⋅(5⋅)可直接写作5 .5ˆ例如,返回上页下页算符的等价性设和是两个算符,若对任意函数f 都有,则称和相等,记作.AˆB ˆf B f A ˆˆ=B A ˆˆ=[算符的运算]AˆB ˆ返回上页下页算符的加法(减法)AB f Af Bf ˆˆˆˆ()±=±Df x Df x f x ˆˆˆˆ(3)()()3()+=+例如,f x f x ()3()′=+规定:称为与的和(差).A ˆB ˆA Bˆˆ±运算规律:AB B A [交 换律 ]ˆˆˆˆ+=+AB C A B C 结合律] ˆˆˆˆˆˆ()()[++=++返回上页下页一般而言,(算符的乘法不满足交换律).ABBA ˆˆˆˆ≠对易子如果,即,则称和可对易;否则,就是不可对易的.A B ˆˆ[,]0=A BˆˆAB AB BA ˆˆˆˆˆˆ[,]=−规定:称为与的对易子.AB ˆˆ[,]A ˆB ˆAB BA ˆˆˆˆ=但不排除对某些特定的算符有.ABBA ˆˆˆˆ=返回上页下页对易子的恒等式(证明留作练习):]ˆ,ˆ[]ˆ,ˆ[A B B A−=n A A ˆˆ[,]0=二、算符的本征方程、本征值、本征函数返回上页下页返回上页下页则⎯⎯常数a 称为的本征值;非零函数f 称为的属于(对应于)本征值a 的本征函数;ˆAaf f A =ˆ设:是算符,f 是非零函数,a 是常数.如果AˆˆA称为的本征方程.ˆA af f A=ˆ返回上页下页(3)本征函数总是和本征值联系在一起,一个本征函数不能同时属于两个不同的本征值;(4)对应于同一个本征值,可能有不止一个线性无关的本征函数.说明(1) 本征函数f 要求是非零函数(不恒等于零);(2)一般而言,本征值(复数域),相应的,本征函数f 是复函数.a ∈ 假设,则有.本征函数f 是非零函数,于是a =b ,矛盾., 其中ˆˆ()Afaf Af bf a b ==≠()0a b f −=三、线性算符返回上页下页返回上页下页线性算符有如下的对易子恒等式:]ˆ,ˆ[]ˆ,ˆ[]ˆ,ˆ[B A k B k A B Ak ==]ˆ,ˆ[]ˆ,ˆ[]ˆˆ,ˆ[C A B A C B A+=+]ˆ,ˆ[]ˆ,ˆ[]ˆ,ˆˆ[C B C A C B A+=+C B A C A B C B Aˆ]ˆ,ˆ[]ˆ,ˆ[ˆ]ˆˆ,ˆ[+=B C A C B A C B Aˆ]ˆ,ˆ[]ˆ,ˆ[ˆ]ˆ,ˆˆ[+=[线性算符的对易子]例6. 由,计算对易子和D xˆˆ[,]1=x i D ˆ[,]− x D 2ˆ[,]]ˆ,[2D x x i Dˆ[,]− i x D ˆ[,]=− i D x ˆ[,]= D ˆ2−=D D ˆˆ−−=D D x D x Dˆ]ˆ,[]ˆ,[ˆ+=i = 解返回上页下页112211221122ˆˆˆ()D c f c f c f c f c Df c Df ′′+=+=+都是线性算符,2ˆˆˆ,,xD D 222112211221122ˆˆˆ()D c f c f c f c f c D f c D f ′′′′+=+=+11221122()x c f c f c xf c xf ⋅+=⋅+⋅因此,返回上页下页[线性算符的性质]若f 1,f 2是线性算符的属于同一个本征值a 的本征函数,则它们的任意非零线性组合c 1f 1+c 2f 2(即c 1,c 2是任意常数但要保证c 1f 1+c 2f 2是非零函数)仍然是属于a 的本征函数.证2211ˆ ,ˆ af f A af f A==∵ 1122ˆ()A c f c f ∴+2211ˆˆf A c f A c +=注此性质对更多本征函数也成立.Aˆ2211af c af c +=)(2211f c f c a +=当c 1f 1+c 2f 2为非零函数时,是对应于a 的本征函数.四、厄米算符返回上页下页返回上页下页如果算符满足:则称算符是厄米算符.d d **ˆˆ()f Ag g Af ττ=∫∫AˆAˆ[厄米算符的定义](f ,g 是任意的品优函数)说明(1)一般来说,算符的本征值是复数域上的数.但是,厄米算符的本征值一定是实数.(2)一般来说,算符的本征函数不一定正交.但是,对于线性厄米算符,①非简并本征值:有且有一个线性无关的本征函数,任选一个;②简并本征值:能够选出一个两两正交的最大线性无关组[线性厄米算符的性质2(2)].所选的的这一系列本征函数必定是两两正交的[线性厄米算符的性质2(1)].返回上页下页四、小结作业思考题返回上页下页小结返回上页下页1算符的概念;算符的加法、乘法、幂及其运算规则.m n m n m n mn A A A A A; ˆˆˆˆˆ()+==[加法交换律] ˆˆˆˆAB B A +=+加法结律 合 ]ˆˆˆˆˆˆ()()[AB C A B C ++=++ [乘法结合律]ˆˆˆˆˆˆ()()ABC AB C =返回上页下页2对易子ˆˆˆˆˆˆ[,]AB AB BA =−如果(即),则称和可对易.ˆA ˆB 重要的恒等式:ˆˆ[,]0AB =ˆˆˆˆAB BA =]ˆ,ˆ[]ˆ,ˆ[A B B A−=n A A ˆˆ[,]0=ˆˆ[,]AB返回上页下页3算符的本征方程、本征值、本征函数.af f A =ˆa 为常数,称为本征值;f 是非零函数,称为属于本征值a 的本征函数.的本征方程:ˆA4线性算符的概念和性质.()A c f c f c Af c Af 11221122ˆˆˆ+=+( f 1和f 2是任意函数;c 1和c 2是任意常数)返回上页下页线性算符的运算规律:线性算符的对易子恒等式:]ˆ,ˆ[]ˆ,ˆ[]ˆ,ˆ[B A k B k A B Ak ==ˆˆˆˆˆˆˆ[,][,][,]AB C A C B C +=+[左分配律] ˆˆˆˆˆˆˆ()AB C AB AC +=+[分 律] 右配ˆˆˆˆˆˆˆ()BC A BA CA +=+ˆˆˆˆˆˆˆ[,][,][,]AB C A B A C +=+C B A C A B C B Aˆ]ˆ,ˆ[]ˆ,ˆ[ˆ]ˆˆ,ˆ[+=B C A C B A C B Aˆ]ˆ,ˆ[]ˆ,ˆ[ˆ]ˆ,ˆˆ[+=返回上页下页(本征值的简并度:属于该本征值的全体本征函数中,最大线性无关组所含的函数个数)线性算符的性质:线性算符的属于同一个本征值的本征函数的任意非零线性组合,仍是属于同一个本征值的本征函数.返回上页下页5厄米算符的概念和性质. d d **ˆˆ()f Ag g Af ττ=∫∫(f ,g 是任意的品优函数)线性厄米算符的性质:1. 厄米算符的本征值必然是实数;2.(1)厄米算符属于不同本征值的本征函数必然是相互正交的;(2)线性算符的属于简并本征值的全体本征函数中,能够选出一个两两正交的最大线性无关组.作业p.145,第26,27,28题返回上页下页返回上页下页思考题下列哪些算符可对易⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅( )(A) ˆˆ,x y (B),x y ∂∂∂∂(C),x x ∂∂ (D),y x∂∂返回上页下页[提示]可对易⇔.将作用于二元函数f (x ,y )可得.[答案] (A)(B)(D)即 ˆˆˆˆˆˆ[,]00A B AB BA =−=ˆˆ,AB ˆˆˆˆABBA −ˆˆ[,]A B附录线性厄米算符性质的证明返回上页下页返回上页下页线性厄米算符的性质2(1)厄米算符的属于不同本征值的本征函数必然是相互正交的;(2)线性算符的属于同一个简并本征值的全体本征函数中,可选出两两正交的最大线性无关组.(1) 设是厄米算符,f , g 是分别属于两个不同特征值a , b 的本征函数,即ˆAd d **ˆˆ()f Ag g Af ττ=∫∫证; ()ˆˆAf af Agbg a b ==≠根据厄米算符的定义,有d d **()f bg g af ττ=∫∫d d ***b f g a gf ττ=∫∫返回上页下页上式中a *≠b (∵厄米算符的本征值是实数,a*=a ,而a ≠b ),从而有是相互正交的d 即*0,,g f g f τ=∫一般而言,{f 1,f 2,…,f n }不是两两正交的.但是,从最大线性无关组{f 1,f 2,…,f n }出发,利用施密特正交化方法,能够构造出一个等价的非零正交函数组{ϕ1,ϕ2,…,ϕn }.方法如下(参见数学复习):(2)设是线性算符,f 1,f 2,…,f n 是属于简并本征值a 一个最大线性无关组.ˆA。
高中化学平均值法计算方法总结
方法总论平均值法混合物的平均式量、元素的质量分数、生成的某指定物质的量总是介于组分的相应量的最大值M2与最小值M1之间,表达式为M1 < M < M2,已知其中两个量,可以确定另一个量的方法,称为平均值法。
一.平均相对分子质量1.在标准状况下,气体A的密度为 1.25 g/L,气体B的密度为 1.875 g/L,A和B 混合气体在相同状况下对H2的相对密度为16.8,则混合气体中A和B的体积比为A.1:2 B.2:1 C.2:3 D.3:2二.平均摩尔电子质量转移 1 mol电子时所对应的物质的质量就是摩尔电子质量。
如Al为27/3,Mg为24/2.2.由两种金属组成的合金50 g与Cl2完全反应,消耗Cl2 71 g,则合金可能的组成是A.Cu和Zn B.Ca和Zn C.Fe和Al D.Na和Al三.利用平均值的公式进行计算相对分子质量为M1、M2的物质按物质的量之比为a:b混合后,M=M1a/n t+M2b/n t。
3.有A、B、C三种一元碱,它们的相对分子质量之比为3:5:7,如果把7 mol A、5 mol B、3 mol C混合均匀,取混合碱 5.36 g,恰好中和含0.15 mol HCl的盐酸,则A、B、C三种一元碱的相对分子质量分别是_____、_____、_____。
24,40,56。
四.平均双键数法基本思想:烷烃双键数为0,单烯烃双键数为1,炔烃双键数为2。
混合烃双键数根据具体情况确定,可利用双键数的平均值求解有关问题。
4.标准状况下的22.4 L某气体与乙烯的混合物,可与含溴8%的溴的CCl4溶液800 g恰好加成,则该气体可能是A.乙烷 B.丙烯 C.乙炔 D.1,3丁二烯五.巧练5.已知Na2SO3和Na2SO4组成的混合物中,硫的质量分数为24.6%,则混合物中Na2SO3与Na2SO4的物质的量之比为A.1:3 B.3:1 C.4:1 D.1:46.现有铷和另一种碱金属形成的合金50 g,当它与足量水反应时,放出标准状况下的氢气22.4 L,这种碱金属可能是A.Li B.Na C.K D.Cs摩尔电子质量法根据在氧化还原反应中,得失电子相等的原则,立意是提供、得到或偏移 1 mol电子所需要和涉及的物质的质量,利用这种物质的质量来解决的方法称为摩尔电子质量法。
第15讲_Excel公式及函数
公式中的运算符有
算术运算符、关系运算符、文本运算符、 引用运算符------
: 区域界定
, 联合求并
空格 交叉求交
目录
上页 下页
结束
15.2 公式的输入与编辑
Excel单元格中的公式,以=号开头,
可在要得到计算结果的单元格中输入, 也可在编辑栏中输入。 然后还可填充复制到其他单元格。
上页 下页
结束
INT (……) IF (……)
使用方法:在输入公式时,要用到某函数,可直接键入,
也可在编辑栏左边名字框的下拉列表框中选取,并输入参数。
上页 下页
结束
“插入函数”对话框
目录
上页 下页
结束
15.4 单元格的引用方式
公式中,常需按单元格的地址引用其中的数据。 有三种引用方式:
相对引用: 实质指的是,相对于公式所在 的单元格,被引用的单元格所处的位置。
20. 在Excel中,求两个单元格区域A4:E9与B5:D10相交的单元格区域 内各数值的平均值,采用相对地址引用,应该表示为________。 A.AVERAGE(A4:E9,B5:D10) B.AVERAGE(A4:E9;B5:D10) C.AVERAGE(A4:E9:B5:D10) D.AVERAGE(A4:E9 B5:D10)
例: 在SjkKcCjB.xls工作簿的一个工作表中,计算总评。
第一讲算符及其本征值与本征函数
ˆ
ˆ
• A:泊松括号:
• •
ˆ, B ˆB ˆ ˆ] A ˆ B ˆA [A
ˆ, B ˆ 与B ˆ ] 0, 则 ˆ 对易, 若 [ A A B:
ˆ ,B ˆ ,B ˆ 0, 则 ˆ 不对易。 若A A
补充说明
• 算符相加满足交换律、结合律:
• • • •
ˆB ˆ, A ˆB ˆA ˆ B ˆ ˆB ˆA ˆ C ˆ C A
E
• 也就是等式左边的符号作用于波函数的结果等效 于右边的能量作用于波函数的结果。 • 对于定态的薛定谔方程,当势能不显含时间t,可 以认为E=H=T+U,恰好是经典力学中的哈密顿量。
在量子力学中出现的力学量,都有 与该力学量运算效果上等效的算符。 因此通过对比,我们可以归纳出下 列的几个等效关系:
d ˆx p i dx
d d d x px px x x x x ( x ) i i dx i dx i dx
y, p y i
z, p z i
• 类似有: x, p 0 y • 一般写成: •
简并度
• 不同的算符一般有不同的本征函数系和本征值谱, 因为算符不同,本征方程的数学形式不同,因而 方程解的函数形式不同。 ˆ 的某一本征 ˆ 的本征方程时,可能得出 A • 当解 A 值对应的不止一个是一个本征函数,而是f个线性 无关的本征函数,则称该本征值有f度简并,并且 属于该本征值的本征函数也有f个。 • 这时,当粒子处于该f个态中的任何一个,力学量 的值都是一样的。即:
ˆ ˆ GF 。
• 六、厄米算符:
ˆ d ( F ˆ ) d ,其中ψ 、φ 是 ˆ A ˆ ,即 * F 若 A
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
大学物理 第一版
*15.5 算符与平均值
d2 例2 下列函数ex ,sinx,2cosx,x3中,哪几个是算符 dx 2
的本征函数。若是,求出本征值。
d (e ) 1 e x dx 2 d 2 (sin x ) sin x 2 dx
2
x
ex是算符的本征函数,本征值为1
sinx是算符的本征函数,本征值为-1
d 2 (2 cos x ) 2 cos x 2cosx是算符的本征函数,本征值为-1 2 dx d (x ) 6x 2 dx
2 3
x3不是算符的本征函数
大学物理 第一版
*15.5 算符与平均值
三、力学量平均值
若任一力学量A: Â≠a ( a为常数),则说明该力学量 没有确定值(本征值),但可求其平均值。
大学物理 第一版
*15.5 算符与平均值
一、力学量算符
1 算符
就是对一个函数施行某种运算的符号。如sin、log等。
量子力学中常用力学量上方加“∧”来表示该力学量的算符。 量子力学中的算符都是线性厄米算符,即该算符既是线 性的,又是厄米的。
A.线性算符:
若一算符对常数乘以函数的运算等于该算符对函数的运 算的结果乘以常数;对函数和的运算等于该算符分别对 每个函数运算的结果的和,则该算符为线性算符,即:
则该算符为厄米算符。
大学物理 第一版
*15.5 算符与平均值
2 常用力学量及其算符
A 算符
i j k x y z 2 2 2 2 2 2 2 x y z
B 时空算符就是其本身:
ˆ ˆ t ˆ xx yy zz ˆt
3
大学物理 第一版
*15.5 算符与平均值
A
ˆ Ad
d
若已归一化,则:
ˆ A A d
ˆ x x d
d ˆ p x pd (i ) d dx
7
4
大学物理 第一版
*15.5 算符与平均值
二、本征பைடு நூலகம்方程 本征方程
ˆ F n n n
本征函数 本征值
n
n
有一个函数f1,算符作用于f1后,其结果等于 常数a乘以f1自身,即: Âf1= af1 ,f1称为Â的本征 函数,常数a称为Â的本征值,Âf1= af1 称为算符Â 的本征方程。
大学物理 第一版
*15.5 算符与平均值
Â(af1)=aÂf1 Â(f1+f2)= Âf1+ Âf2
d 是线性算符,而 如 dx
不是
B.厄米算符: 若算符满足
ˆ ˆ f1 Af1d f1 (Af1 ) d
或
ˆ ˆ f1 Af 2 d f 2 (Af1 ) d
C 动量算符定义为 : ˆ ih i Px 2 x x ˆ ih i Py 2 y y ˆ ih i Pz 2 z z D 能量算符
ˆ p i
h 2
ˆ L r (i)
2 ˆ E 2m
