甘肃省嘉峪关市一中2012届高三上学期期中试题数学理
甘肃省嘉峪关市一中2012-2013学年高一上学期期中考试数学试题

实用文档yxyx0y x(1) (2) (3)嘉峪关市一中2012-2013学年第一学期期中考试高一数学试题一.选择题(每小题5分,共60分)1. 设A={a ,b},集合B={a+1,5},若A∩B={2},则A∪B=( )A 、{1,2}B 、{1,5}C 、{2,5}D 、{1,2,5} 2.函数x y 24-=的定义域为( )A. ),2(+∞B. (]2,∞-C. (]2,0D. [)+∞,1 3. 下列哪个函数与函数y x =相同( )A 、2y x =B 、2x y x=C 、()2y x =D 、33y x =4. 函数y =0.5x 、 y =x -2 、y =log 0.3x 的图象如图所示,依次大致是( )A .(1)(2)(3)B .(2)(1)(3)C .(3)(1)(2)D .(3)(2)(1)5. 设2log 3P =,3log 2Q =,23log (log 2)R =,则( ) A.R Q P <<B.P R Q << C.Q R P << D.R P Q <<6. 已知函数f (x )=2log (0)3(0)xx x x >≤⎧⎨⎩,则f [f (14)]的值是( )A .9B .19C .-9D .-19实用文档7. 设集合{|12},{|}.A x x B x x a =<<=<若,A B ⊆则a 的范围是( ) A.2a ≥ B.1a ≤ C.1a ≥ D.2a ≤8. 用二分法计算23380x x +-=在(1,2)x ∈内的根的过程中:令f(x)= 2338x x +-得,(1)0f <,(1.5)0f >,(1.25)0f <,则方程的根落在区间( )A 、(1,1.5)B 、(1.5,2)C 、(1,1.25)D 、(1.25,1.5)9. 设集合}21,|{},,40|{2≤≤--==∈≤≤=x x y y B R x x x A ,则)(B A C R 为( )A .RB . }0,|{≠∈x R x xC . }0{D . φ10. 某工厂10年来某种产品总产量C 与时间t (年)的函数关系如下图所示,下列四种说法:①前五年中产量增长的速度越来越快; ②前五年中产量增长的速度越来越慢;③第五年后,这种产品停止生产; ④第五年后,这种产品的产量保持不变;其中说法正确的是( )A .①③B .②④C .②③D .①④11.设11{3,2,1,,1,2,3}23α∈----,则使幂y=x a 为奇函数且在(0,+∞)上单调递减的α值的个数为 ( )A. 1B. 2C. 3D. 4实用文档12.已知函数()|21|x f x =-,当a b c <<时()()()f a f c f b >>,那么以下结论正确的是( )A .22a b >B .22a c >C .222a c +<D .22a c -< 二.填空题(每小题5分,共20分)13. 当x ∈[1,9]时,函数f (x )=log 3x-2的值域为 . 14. 已知函数2()2(1)2f x x a x =+-+是偶函数,则f(-1)=_______________. 15. 满足}1,0,1{}0,1{-=-A 的集合A 共有 个.16.已知函数()()()1,01log ≠>-=a a a x f x a ,有以下命题:○1函数()x f 的图象在y 轴的一侧;○2函数()x f 为奇函数;○3函数()x f 为定义域上的增函数;○4函数()x f 在定义域内有最大值,则正确的命题序号是 .三.解答题(17小题10分,18—22小题每题12分,共70分) 17.求值:(1)14310333427(0.064)()[(2)]16|0.01|8-----+-++-;(2)77733log 2log 92log ()22-+.18.已知函数x x x f +--=11)(. (1)求函数)(x f 的定义域; (2)用定义判断)(x f 的奇偶性; 19.设函数⎩⎨⎧≥+-<++=0(,3)0(,)(2x x x c bx x x f ,且xy-4-444321-3-2-1-3-2-1321实用文档(4)(0),(2)1f f f -=-=-.(1)求函数)(x f 的解析式; (2)画出函数)(x f 的图象,并指出函 数)(x f 的单调区间.(3)若方程f(x)=k 有两个不等的实数根,求k 的值.20. 已知函数()log (1)(0,1)a f x x a a =+>≠ (1)求f(x)的单调区间;(2)当a=2时,求f(x)在区间[1,7]上的最大值和最小值;(3)若f(x)在区间[1,7]上的最大值比最小值大12,求a 的值.21.某公司生产某种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元,已知总收入满足函数:21400,(0400)()280000,400.x x x R x x ⎧-≤≤⎪=⎨⎪>⎩(1)将利润表示为月产量的函数f(x);(2)当月产量为何值时,公司所获利润最大?最大利润为多少元?(总收益=总成本-利润).22. 记函数f(x)的定义域为D ,若存在x 0∈D ,使f (x 0)=x 0成立,则称以x 0为函数f(x)的不动点.(1)当a =1,b =-2时,求f (x )=ax 2+(b+1)x+(b-1) ()0≠a 的“不动点”;实用文档(2)若函数f(x)=31x x a-+的图象上有且只有两个相异的“不动点”,试求实数a 的取值范围;(3)已知定义在实数集R 上的奇函数f (x )存在有限个“不动点”,求证:f(x)必有奇数个“不动点”.嘉峪关市一中2012-2013学年度第一学期期中考试高一数学参考答案一.选择题:DBDBA BADBC BC二.填空题:13. [-2,0] ; 14. 3; 15. 4;16. ①③.三.解答题:17.(1)14380; (2)0. 18.(1)(-1,1);(2)奇函数.19.(1)243,(0)()3,(0)x x x f x x x ⎧++<=⎨-+≥⎩;(2)图略.单调增区间为:[-1,0]; 单调减区间为:(-∞,-1]和[0,+∞).实用文档(3)k=-1或3.20.(1)当a>0时,f(x)的单调递增区间为:(-1,+∞);当a<0时,f(x)的单调递减区间为:(-1,+∞);(2)a=16或a=116. 21.(1)设月生产量为台,则总成本为20000+100,从而2130020000,(0400)()260000100,(400)x x x f x x x ⎧-+-≤≤⎪=⎨⎪->⎩.(2)当0400x ≤≤时,f(x)=21(300)250002x --+∴当x=300时,f(x)有最大值25000;当x>400时,f(x)=6000-100x 是减函数,又f (400)=f20000<25000,∴当x=300时,f(x)的最大值为25000元.即当月产量为300台时,公司所获最大利润为25000元.22.(1)f (x )=ax 2+(b+1)x+(b-1) ()0≠a 的“不动点”为-1和3; (2)a<-1或a>7;(3)证明:函数f(x)的“不动点”即方程f(x)=x 亦即f(x)-x=0的根.∵f(x)为奇函数,∴f(x)-x为奇函数.设方程f(x)-x=0在(0,+∞)上有k( k∈N)个实数根,则它在(-∞,0)上也有k 个实数根.又∵f(x)-x为奇函数,∴f(0)-0=0,即0是f(x)-x=0的根∴方程f(x)-x=0共有2k+1(k∈N)个实数根.∴函数f(x)有2k+1(k∈N)个“不动点”.即f(x)有奇数个“不动点”.实用文档。
甘肃省兰州一中2012届高三上学期期中考试(理综).pdf

C.分散系中分散质粒子的直径:Fe(OH)3悬浊液>Fe(OH)3胶体>FeCl3溶液
D.将碳酸钠溶液和碳酸氢钠溶液分别蒸干并灼烧,所得固体均为氢氧化钠
11.某溶液中含有NH、SO、SiO、Br-、CO、Na+,向该溶液中通入过量的Cl2,下列判断正确的是反应前后,溶液
中离子浓度基本保持不变的有NH、Na+ 有胶状生成
④酶催化作用的最适温度一定是37.5℃
⑤生长素对植物生长一定有促进作用 ⑥两个种群间的隔离一旦形成,这两个不同种群的个体之间一定不能进行交
配
A.全部正确 B.③⑥ C.①②③⑤ D.全都不对
6.如图两瓶体积相等的气体,在同温同压时瓶数相等
B.气体密度相等
C.气体质量相等
D.摩尔质量相等
.下列实验方法合理的是 A.用渗析的方法精制Fe(OH)3胶体
B.用水鉴别、四氯化碳、乙醇三种无色液体
C.可用澄清石灰水鉴别Na2CO3溶液和NaHCO3溶液
D.为准确测定盐酸与NaOH溶液反应的中和热,所用酸和碱的物质的量相等下列实验设计及其对应的离子方程式均
有气体产生溶液颜色发生变化 共发生了2个氧化还原反应
A. B.C. D.
12.若NA表示阿伏加德罗常数,下列说法正确的是
A.1 mol SiO2晶体中含有NASiO2个分子
B.7.8 g Na2O2中含有的离子总数目为0.4NA
C.标准状况下2.24L苯含有的碳原子数目为0.6NA
θ
c
b
a
a
A
B
0
1
2
3 cm
0
10
20
30
15
20
5
10
0
5
10
甘肃省河西部分高中(张掖中学、嘉峪关一中、山丹一中)高三数学上学期期中联考试题 理

2015-2016学年第一学期高三期中联考试卷 数学(理科)注:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题);满分150分,考试时间120分钟。
第I 卷 (选择题共60分)一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合{}220P x x x =-≥,Q {}12x x =<≤,则R P =I Q ð( ) A. [)0,1 B. (]0,2 C. ()1,2 D. []1,2 2.下列函数中,既不是奇函数,也不是偶函数的是( ) A .x x y 1+= B . x e x y += C .x x y 212+= D .21x y += 3.下列函数中,最小正周期为π且图象关于原点对称的函数是( ) A. cos 22y x π⎛⎫=+⎪⎝⎭B.sin 22y x π⎛⎫=+⎪⎝⎭C.sin 2cos 2y x x =+D.sin cos y x x =+ 4. 函数43y x =的图象是 ( )A .B .C .D .5. 设命题P :“**,()n N f n N ∀∈∈ 且()f n n ≤, 则⌝P 为( )A. ,()n N f n N **∀∈∉且()f n n >B. ,()n N f n N **∀∈∉或()f n n >C. 00,()n N f n N **∃∈∉且00()f n n >D. 00,()n N f n N **∃∈∉或00()f n n >6. 设x R ∈ ,则“21x -< ”是“220x x +-> ”的( )A. 充分不必要条件B. 必要不充分条件C . 充要条件 D. 既不充分也不必要条件7.在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c . 若22()6c a b =-+,3C π=,则△ABC 的面积是( )A.3B.2 C.2D.8.一段圆弧的长度等于其内接正三角形的边长,则其圆心角的弧度数为( )A.3πB.23π9.已知函数cos y x x ωω=+(0)ω>的图象与直线2y =的两个相邻交点的距离等于π,则()f x 的单调递增区间是( )A.5,1212k k ππππ⎡⎤-+⎢⎥⎣⎦,k Z ∈ B.511,1212k k ππππ⎡⎤++⎢⎥⎣⎦,k Z ∈ C.,36k k ππππ⎡⎤-+⎢⎥⎣⎦, k Z ∈ D.2,63k k ππππ⎡⎤++⎢⎥⎣⎦,k Z ∈ 10. 函数0.5()2log 1x f x x =-的零点个数为( ) A. 1 B. 2 C.3 D. 4 11.已知定义在R 上的函数()21x mf x -=- (m 为实数)为偶函数,记()()0.52(log 3),log 5,2a f b f c f m === ,则,,a b c 的大小关系为( )A.a b c << C. c b a <<B.c a b << D. a c b <<12.对二次函数2()f x ax bx c =++(a 为非零常数),四位同学分别给出下列结论,其中有且仅有一个结论是错误的,则错误的结论是( )A .1-是()f x 的零点B .1是()f x 的极值点C . 3是()f x 的极值 D. 点(2,8)在曲线()y f x =上第II 卷(非选择题共90分)二、填空题:本大题共4小题,每小题5分,共20分,把答案填在答题卡的相应位置。
嘉峪关市嘉峪关一中届高三模拟考试数学试题及答案(理)

嘉峪关市一中2013-2014学年高三第六次模拟考试数学(理科)试卷第Ⅰ卷一、选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.定义集合运算:A ⊙B={z ︳z= xy (x+y ),x ∈A ,y ∈B },设集合A={0,1},B={2,3},则集合A ⊙B 的所有元素之和为( ) A .0B .6C .12D .182.已知M (-2,7),N (10,-2),点P 是线段MN 上的点且,2→-→--=PM PN 则P 点的坐标是( ) A .(-14,-16)B .(22,-11)C .(6,1)D .(2, 4)3.若π<α<π223,则直线α+αsin cos y x=1必不经过( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限4.样本a 1,a 2,a 3,…,a 10的平均数为a ,样本b 1,b 2,…,b 10的平均数为b ,那么样本a 1,b 1,a 2,b 2,a 3,b 3,…,a 10,b 10的平均数是( ) A .a +b B .21(a +b ) C .2(a +b ) D .101(a +b ) 5.已知函数f (x )=x 2 - 4x + 3,集合M ={(x , y ) | f (x )+f (y )≤0},集合N ={(x , y ) | f (x ) - f (y )≥0},则集合M ∩N 的面积是( )A .4πB . 2πC .πD .2π6.等差数列{a n }前n 项和为S n ,满足S 20=S 40,则下列结论中正确的是( ) A .S 30是S n 中的最大值 B .S 30是S n 中的最小值 C .S 30=0 D .S 60=0 7.如图是一几何体的三视图,正视图是一等腰直角三角形,且斜边BD 长为2;侧视图一直角三角形;俯视图为一直角梯1==BC AB ,则此几何体的体积是( )。
甘肃省嘉峪关市一中高三数学上学期第三次模拟考试试题 理

嘉峪关市一中2015-2016学年高三第三次模拟考试数学(理科)一.选择题(每题5分,共60分)1. 已知扇形的半径是2,面积为8,则此扇形的圆心角的弧度数是( ) A.2 B.4 C.8 D.1 2.已知全集U=R ,集合A={x | x 2-x-6≤0},B={x|4x x->0},那么集合A I (C U B )=( ) A .{x|-2≤x<4} B .{x|x≤3或x ≥4} C .{x|-2≤x≤0} D .{x|0≤x≤3} 3.下列有关命题的叙述错误..的是( ) A .若⌝p 是q 的必要条件,则p 是⌝q 的允分条件 B .若p 且q 为假命题,则p ,q 均为假命题C .命题“x ∀∈R ,x 2-x>0”的否定是“∃x ∈R ,x 2-x <0”D .“x>2”是“112x <”的充分不必要条件 4.设等差数列{a n }前n 项和为S n ,若a 1=-11,a 4+a 6=-6,则当S n 取最小值时,n 等于( ) A .6B .7C .8D .95.设OA u u u r =(1,-2),OB u u u r =(a ,-1),OC u u u r =(-b ,0),a>0,b>0,O 为坐标原点.若A ,B ,C 三点共线,则12a b+的最小值是( ) A .2 B .4 C .6 D .86.设等比数列{}n a 的公比2q =,前n 项和为n S ,则42S a =( ) A. 2 B. 4 C.152D.1727. 已知复数i bi a i 42))(1(+=++),(R b a ∈,函数()2sin()6f x ax b π=++图象的一个对称中心是( ) A. (1,6π-) B. (,018π-) C.(,36π-) D.(5,118π) 8. 在ABC △中,内角,,A B C 所对的边长分别是,,a b c ,若A A B C 2sin )sin(sin =-+,则ABC △的形状为( )A 、等腰三角形B 、直角三角形C 、等腰直角三角形D 、等腰或直角三角形 10. 已知实数33,,,,x x y d c b a -=且曲线成等比数列的极大值点坐标为(b,c )则ad 等 于( )A .2B .1C .—1D .—211.已知()x x f x3log 31-⎪⎭⎫⎝⎛=,实数a 、b 、c 满足()()()f a f b f c ⋅⋅<0,且0<a <b <c ,若实数0x 是函数()x f 的一个零点,那么下列不等式中,不可能...成立的是( ) A .0x <aB .0x >bC .0x <cD .0x >c12.已知f (x )的定义域为(0,+∞),f ′(x )为f (x )的导函数,且满足f (x )<-xf ′(x ),则不等式f (x +1)>(x -1)f (x 2-1)的解集是( )A .(0,1)B .(1,+∞)C .(1,2)D .(2,+∞) 二、填空题(每小题5分,共20分)13.不等式x 2-2x <0表示的平面区域与抛物线y 2=4x 围成的封闭区域的面积为____. 14.已知O (0,0),M (1,12),N (0,1),Q (2,3),动点P (x ,y )满足不等式0≤OP →·OM →≤1,0≤OP →·ON →≤1,则z =OQ →·OP →的最大值为________.15.已知点A (3,0),B (0,3),C (cos α,sin α),若AC →·BC →=-1,则1+tan α2sin 2α+sin2α的值为_______.16. 若实数a ,b ,c 满足2a+2b=2a +b,2a+2b +2c =2a +b +c,则c 的最大值是________.三.解答题(17题10分,18-22题每题12分,共70分)17. 已知函数2()2cos )f x x x =--.(1)求()f x 的最小正周期;(2)求函数在区间ππ[,]63-上的最大值和最小值.18.ABC ∆中内角,,A B C 的对边分别为,,a b c ,向量2(2sin ,(cos 2,2cos 1)2B m B n B ==-u r r2(2sin ,3),(cos 2,2cos 1)2B m B n B =-=-u r r 且//m n u r r(1)求锐角B 的大小;(2)如果2b =,求ABC ∆的面积ABC S ∆的最大值.19.设数列{}n b 的前n 项和为n S ,且22n n b S =-;数列{}n a 为等差数列,且514,a =720a =.(1)求数列{}n b 的通项公式;(2)若(1,2,3),n n n n c a b n T =⋅=…为数列{}n c 的前n 项和,求证:72n T <. 20. 设函数f (x )=23+1x (x >0),数列{a n }满足a 1=1,a n =f ⎝ ⎛⎭⎪⎫1a n -1,n ∈N *,且n ≥2.(1)求数列{a n }的通项公式; (2)对n ∈N *,设S n =1a 1a 2+1a 2a 3+1a 3a 4+…+1a n a n +1,若S n ≥3t 恒成立,求实数t 的取值范围.21.已知函数()ln ()f x x mx m R =-∈.(1)若曲线()y f x =过点P (1,-1),求曲线()y f x =在点P 处的切线方程; (2)若()0f x ≤对(0,)x ∈+∞恒成立,求实数m 的取值范围;22.已知函数f (x )=ax +x ln x ,且图象在点⎝ ⎛⎭⎪⎫1e ,f ⎝ ⎛⎭⎪⎫1e 处的切线斜率为1(e 为自然对数的底数).(1)求实数a 的值; (2)设g (x )=f x -xx -1,求g (x )的单调区间;(3)当m >n >1(m ,n ∈Z)时,证明:mn n m >n m .2016高三三模理科数学答案一.选择题(每小题5分,共60分) CDBADC DCCADD二.填空题(每小题5分,共20分)13. 1632; 14. 4; 15. -9/5; 16. _2-log 23.三.解答题(17小题10分,18—22每小题12分,共70分)17. 解:(1)2()2cos )f x x x =--222(3sin cos cos )x x x x =-+-22(12sin 2)x x =-+-212sin 2x x =-+cos22x x =+ π= 2sin(2)6x +所以 ()f x 的周期为2π2ππ||2T ω===. (2)当ππ[,]63x ∈-时, π2π2[,]33x ∈-,ππ5π(2)[,]666x +∈- 所以当6x π=-时,函数取得最小值()16f π-=-………………11分当6x π=时,函数取得最大值()26f π=.18. 解:(1)n m ρρΘ// B BB 2cos 3)12cos 2(sin 22-=-∴ B B 2cos 32sin -=∴ 即 32tan -=B又B Θ为锐角 ()π,02∈∴B 322π=∴B 3π=∴B (2),23B b π==Q , 由余弦定理得222cos 2a c b B ac +-=即0422=--+ac c a .又ac c a 222≥+Θ 代入上式得4≤ac (当且仅当 2==c a 时等号成立).343sin 21≤==∆ac B ac S ABC (当且仅当 2==c a 时等号成立).19. 解.(1)由11111222,1,22,,3n n b S n b S S b b =-==-==令则又所以2122111222(),9222,2()213n n n n n n n n n b b b b n b S b b S S b b b ---=-+=≥=--=--=-=则当时,由可得即{}12112333n n n b b b ==⋅所以是以为首项,为公比的等比数列,于是.(2)数列{}n a 为等差数列,公差751()3,312n d a a a n =-==-可得从而12(31)3n n n n c a b n =⋅=-⋅2323123111112[258(31)],3333111112[ 25(34)(31)]333332111112[3333(31)]3333333n n n n n n n n T n T n n d T n ++∴=⋅+⋅+⋅++-⋅=⋅+⋅++-⋅+-⋅∴=⋅+⋅+⋅++⋅---⋅………从而13312727--⋅-=n n n n T . 27<∴n T20. 解:(1)由a n =f ⎝ ⎛⎭⎪⎫1a n -1可得,a n -a n -1=23,n ∈N *,n ≥2.所以{a n }是等差数列,又因为a1=1,所以a n =1+(n -1)×23=2n +13,n ∈N *.(2)S n =1a 1a 2+1a 2a 3+1a 3a 4+…+1a n a n +1,n ∈N *.因为a n =2n +13, 所以a n +1=2n +33,所以1a n a n +1=92n +12n +3=92⎝ ⎛⎭⎪⎫12n +1-12n +3.所以S n =92⎝ ⎛⎭⎪⎫13-12n +3=3n 2n +3,n ∈N *. 由S n ≥3t 得t 23n n ≤+,又{23n n +}递增,所以n=1时,(23n n +)min=15,所以t ≤15. 21.解:(1)()f x Q 过点(1,1)P -1ln1m ∴-=-,1m ∴=.()ln f x x x ∴=-1'()1f x x=-,'(1)0f =. ∴过点(1,1)P -的切线方程为1y =-.(2)()0f x ≤Q 恒成立,即ln 0x mx -≤恒成立,ln mx x ∴≥又()f x Q 定义域为(0,)+∞,ln xm x∴≥恒成立. 设ln ()x g x x =,21ln '()xg x x -=Q ∴当x=e 时,'()0g e = 当0x e <<时,'()0,()g x g x >为单调增函数 当x e >时,'()0,()g x g x <为单调减函数max 1()()g x g e e ∴==.∴当1m e≥时,()0f x ≤恒成立.22.解:(1)f (x )=ax +x ln x ,f ′(x )=a +1+ln x ,依题意f ′⎝ ⎛⎭⎪⎫1e =a =1,所以a =1.(2)因为g (x )=f x -x x -1=x ln xx -1,所以g ′(x )=x -1-ln xx -12.设φ(x )=x -1-ln x ,则φ′(x )=1-1x. 当x >1时,φ′(x )=1-1x>0,φ(x )是增函数,对任意x >1,φ(x )>φ(1)=0,即当x >1时,g ′(x )>0, 故g (x )在(1,+∞)上为增函数.当0<x <1时,φ′(x )=1-1x<0,φ(x )是减函数,对任意x ∈(0,1),φ(x )>φ(1)=0,即当0<x <1时,g ′(x )>0,故g (x )在(0,1)上为增函数.所以g (x )的递增区间为(0,1),(1,+∞).(3)证明:要证mn n m>n m,即证ln n m -ln mn >ln n -ln m ,即n -1n ln m >m -1m ln n ,m ln m m -1>n ln nn -1.(*) 因为m >n >1,由(2)知,g (m )>g (n ),故(*)式成立,所以mn n m>nm .。
甘肃省嘉峪关市一中高三数学上学期第二次模拟考试试题

嘉峪关市第一中学2012—2013学年高三第二次模拟考试数学试题(时间:120分钟 满分:150分)一、选择题(每小题5分,共60分) 1、已知向量()1,1-=,()x ,2=,若3=⋅,则=x ( )A 、 -1B 、-2C 、12D 、1 2、设集合{}41|<<=x x A ,{}032|2≤--=x xx B ,则()=B C A R I ()A 、()4,1 B 、()4,3 C 、()3,1 D 、()2,13、224(1)ii ++的共轭复数是( )A 、2i +B 、2i -+C 、2i -D 、2i --4、下列命题错误的是( )A 、对于命题p :∃x ∈R ,使得x 2+x+1<0,则-p 为:∀x ∈R ,均有x 2+x+1≥0 B 、命题“若x 2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x 2-3x+2≠0” C 、若p ∧q 为假命题,则p ,q 均为假命题 D 、“x>2”是“x 2-3x+2>0”的充分不必要条件5、执行如图所示的程序框图,若输入n 的值为6,则输出s 的值为( )A 、105B 、16C 、15D 、16、已知α,β表示两个不同的平面,m 为平面α内的一条直线,则“αβ⊥”是“m β⊥”的()A 、充要条件B 、充分不必要C 、既不充分也不必要D 、必要不充分7、△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,若ο60=A ,4=+c b ,3=∆ABCS 则a =( ) A 、3 B 、2 C 、1 D 、328、已知点()y x ,在抛物线x y 42=上,则32122++=x y z 的最小值()A 、2B 、3C 、4D 、09、有以下程序:根据如上程序,若函数()()m x f x g -=在R 上有且只有两个零点,则实数m 的取值范围是( )A 、1>mB 、10<<mC 、10=<m m 或D 、0<m10、函数xx xy --=226cos 的图像大致为( )A 、B 、C 、D 、 11、在区间[,]22ππ-上随机取一个数x ,cos 2x π的值介于0到21之间的概率为( ) A 、31 B 、π2 C 、21 D 、32w.w.w12、已知函数()c bx ax x x f +++=232131在1x 处取得极大值,在2x 处取得极小值,满足()1,11-∈x ,()4,12∈x ,则b a +2的取值范围是( )A 、()4,6--B 、()1,6-- C 、()6,10--D 、()1,10--二、填空题(每小题5分,共20分) 13、已知1312sin=x ,x 是第二象限的角,则=x tan14、直线052=+-y x 与圆822=+y x 相交于A 、B 两点,则=AB15、函数1)3(log 2-+=x y,()1,0≠>a a 的图像恒过定点A ,若A 在直线01=++ny mx 上,其中0>mn ,则nm 21+的最小值 16、如图所示,一个三棱锥的三视图是三个直角三角形(单位:cm ),则该三棱锥的外接球的表面积为 2cm 17、等差数列{}na 的前n 项和为nS,已知22=a ,05=S ,求(1)该数列{}na 的通项公式na(2)当n 为何值时,n S 取得最大值18、如图,四棱锥ABCD P -中,底面ABCD 是直角梯形,ο90=∠DAB ,BC AD //,PAB AD 面⊥,PAB ∆是等边三角形,2==AB DA ,AD BC 21=,E 是线段AB 的中点 (1)求证:CD PE ⊥ (2)求四棱锥ABCD P -的体积(3)求PC 与平面PDE 所成角的正弦值19、某公司的广告费支出x 与销售额y (单位:万元)之间有下列对应数据:x 2 4 5 6 8 y3040605070(1)画出散点图; (2)试求出线性回归方程.(3)试根据(2)求出的线性回归方程,预测销售额为115万元时约需多少广告费?参考公式:回归方程为a x b y ˆˆˆ+=,其中 ⎪⎪⎩⎪⎪⎨⎧⋅-=-⋅-=∑∑==x b y a x n x y x n y x b n i ini i i ˆˆˆ1221参考数值:2×30+4×40+5×60+6×50+8×70=1380, 22+42+52+62+82=14520、已知椭圆221:14x C y +=,椭圆2C 以1C 的长轴为短轴,且与1C 有相同的离心率 (1)求椭圆2C 的方程(2)设O 为坐标原点,点A ,B 分别在椭圆1C 和2C 上,2OB OA =u u u r u u u r,求直线AB 的方程21、(文科)已知函数()x ax x x f ln 2-+=()R a ∈(1)若0=a 时,求曲线()y f x =在点()()1,1f 处的切线方程(2)若函数()x f 在[]2,1上是减函数,求实数a 的取值范围(3)令()()2xx f x g-=,是否存在实数a ,当(]e x ,0∈(e 是自然常数)时,函数()x g的最小值是3,若存在,求出a 的值;若不存在,说明理由21、(理科)已知函数32,(1)()ln ,(1)x ax bx x f x c x x ⎧-++ <=⎨ ⎩≥的图像在点()()2,2--f 处的切线方程为02016=++y x(1)求实数a 、b 的值 (2)曲线()x f y=上存在两点M 、N ,使得△MON 是以坐标原点O 为直角顶点的直角三角形,且斜边MN 的中点在y 轴上,求实数c 的取值范围(3)当e c =时,讨论关于x 的方程()()R k kx xf ∈=的实根个数四、选做题(本题满分10分)请考生在第22、23、24三题中任选一题做答,如果多做,则按所做的第一题记分.做答时,用2B 铅笔在答题卡上把所选题目对应的题号涂黑.22、选修4—1:几何证明选讲在ABC ∆中,AB=AC ,过点A 的直线与其外接圆交于点P ,交BC 延长线于点D 。
甘肃省嘉峪关市一中12—13上学期高二数学(理)期中考试试卷

嘉峪关市一中2012-2013学年第一学期期中考试高二数学(理)试卷一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的1.0232>+-x x 是“2>x ”成立的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件2.顶点在原点,焦点是()5,0F 的抛物线方程是( ) A .y x 202=B .x y 202=C .x y 2012=D .y x 2012= 3.下列命题中的假命题...是( ) A .,lg 0x R x ∃∈= B .,tan 1x R x ∃∈= C .3,0x R x ∀∈>D .,20x x R ∀∈>4.设a >1>b >-1,则下列不等式中恒成立的是( ) A .ba 11< B .ba 11> C .a >b 2 D .a 2>2b5.若函数32()21f x x x =+-,则(1)f '-=( ) A .7- B .C .1-D .76.不等式2252xx x -->的解集是( )A .{}51x x x ≥≤-或 B .{}51x x x ><-或C .{}15x x -<<D .{}15x x -≤≤7.在平行六面体D C B A ABCD ''''-中,4=AB ,3=AD ,5='A A ,︒=∠90BAD ,︒='∠='∠60A DA A BA ,则对角线C A '的长度为( ) A .6B .65C .8D .858.函数c o s2y x =在点处的切线方程是( )A .024=-+πy xB .440x y π+-=C .024=--πy x D .024=++πy x9.已知点)0,3(M ,椭圆1422=+y x 与直线)3(+=x k y 交于点A 、B ,则A B M ∆的周长为( ) A .4B .8C .12D .1610.设函数()f x 是R 上以5为周期的可导偶函数,则曲线()y f x =在5x =处的切线的斜率( ) A .15-B .0C .D .511.设F 是双曲线C :221169x y -=的右焦点,l 是双曲线C 的一条渐近线,过F 作一条直线垂直与l ,垂足为P ,则sin OFP ∠的值为 A .53 B .54 C .45 D .35 12.已知函数()321132f x x a x b x c =+++在1x 处取得极大值,在2x 处取得极小值,满足x 1∈(-1,0),x 2∈(0,1)2(0,1)x ∈,则242a b a +++的取值范围是( )A .(0,2) B .(1,3)C .[0,3]D .[1,3]二、填空题:共6小题,每小题5分,共30分.请将答案填写在答题卷的横线上.13.已知方程12122=-+-my m x 表示焦点在y 轴上的椭圆,则m 的取值范围是________ 14.若xex f 1)(-=,则0(12)(1)l i mt f t f t→--=________ 15.函数l o g (3)1(0,a y x a a =+->≠的图象恒过定点A ,若点A 在直线10mx ny ++=上,其中0mn >,则nm 21+的最小值为________. 16.在正方体ABCD —A 1B 1C 1D 1中,E ,F 分别是面BCC 1B 1和面CDD 1C 1的中心,则异面直线A 1E 和B 1F 所成角的余弦值为________.17.设O 为坐标原点,12,F F 是椭圆22221(0)x y a b a b+=>>的左、右焦点,若在椭圆上存在点P 满足123F PF π∠=,且||OP =,则该椭圆的离心率为________ 18.以下命题正确..的有________. ①到两个定点21,F F 距离的和等于定长的点的轨迹是椭圆;②“若0=ab ,则0=a 或0=b ”的逆否命题是“若0≠a 且0≠b ,则ab ≠0”;③当f'(x 0)=0时,则f (x 0)为f (x )的极值 ④曲线y =2x 3-3x 2共有2个极值.三、解答题:本大题有6小题,共60分,解答应写出文字说明、证明过程或演算步骤.19.(本小题6分)已知p :方程22146x y k k +=--表示双曲线,q :过点(2,1)M 的直线与椭圆2215x y k+=恒有公共点,若p q ∧为真命题,求k 的取值范围.20.(本小题6分)求下列各函数的导数.(1)x xx y -+=12(2))2cos(x x y =21.(本小题12分)已知不等式2230x x --<的解集为A ,不等式260x x +-<的解集是B .(1)求A B ;(2)若不等式20x ax b ++<的解集是,A B 求20ax x b ++<的解集.22.(本小题12分)设.ln 2)(x x kkx x f --=(1)若0)2(='f ,求函数在点(2,)2(f )处的切线方程; (2)若)(x f 在其定义域内为单调增函数,求k 的取值范围23.(本小题12分)如图,在长方体1111ABCD A B C D -中,已知4AB =,3AD =,12AA =,E ,F 分别是棱AB ,BC 上的点,且1EB FB ==.(1)求异面直线1EC 与1FD 所成角的余弦值;(2)试在面1111A B C D 上确定一点G ,使DG ⊥平面EF D 1.过点(3, 0)B 的直线与椭圆C 交于不同的两点,M N , (Ⅰ)求椭圆C 的方程; (Ⅱ)求B M B N ⋅的取值范围数学答案一、选择题1—12 BACCC BDABB BD 二、填空题 13.)23,1(14.e2-(或12--e ) 15.816.61 17.1218.②④19.解:由p 得:(4)(6)0,46k k k -⋅-<∴<<, …………2分由q 得:22211,55,kk ⎧+≤⎪⎨⎪≠⎩5k ∴>.……………4分 又p q ∧为真命题,则56k <<,所以k 的取值范围是(5,6).……6分20.(1)xx x y 2112'2--= (2))]'2[cos()2cos(''x x x x y +=x x x x x x x 2sin 22cos )'2()2(sin 2cos -=⋅-=21.(1)}31|{}032|{2<<-=<--=x x x x x A }23|{}06|{2<<-=<-+=x x x x x B{}{}{} 133212A B x x x x x x ∴⋂=-<<⋂-<<=-<<(2)∵不等式20x ax b ++<的解集是{12},AB x x =-<<∴方程20x ax b ++=的根是121,2x x =-= ∴121212 1,212x x aa b x x b+=-+=-⎧∴=-=-⎨⋅=-⨯=⎩∴不等式20ax x b ++<为220x x -+-< 即2220(1)420x x -+>∆=--⨯<∴原不等式的解集为R22.(1)由x x kkx x f ln 2)(--=得22222)(x k x kx x x k k x f +-=-+=',令0)2(='f ,得54=k ,∵2ln 2254254)2(--⨯=f 2ln 256-=, 过点(2,)2(f )的直线方程为)1(02ln 256-=+-x y ,即2ln 256-=y ; (2)令)(,2)(2x f k x kx x h 要使+-=在其定义域(0,+∞)上单调递增,只需0)(≥x h 恒成立,由),0(1212020)(22+∞∈+=+≥≥+-≥x xx x x k k x kx x h 在即得上恒成立, ∵0>x ,∴21≥+xx ,∴xx 12+1≤,∴1≥k23.解:轴,轴的正向建立空间直角坐标系,则有,设1EC与1FD所成角为α,则1111cos||||(EC FDEC FDα⋅===∴异面直线1EC与1FD.(2)因点G在平面1111DCBA上,故可设)2,,(yxG.)2,,(yxDG=,1(2,4,2)FD=--,(1,1,0)EF=-.由10,DG FDDG EF⎧⋅=⎪⎨⋅=⎪⎩得⎩⎨⎧=+-=+--,0,0442yxyx解得⎪⎪⎩⎪⎪⎨⎧==.32,32yx故当点G在面1111DCBA上,且到11DA,11DC距离均为32时,DG⊥平面EFD1.24.解:(Ⅰ)由题意得22222411,,a ba b cca⎧+=⎪⎪⎪=+⎨⎪⎪=⎪⎩解得a=,b=故椭圆C 的方程为22163x y +=;(Ⅱ)由题意显然直线的斜率存在,设直线方程为(3)y k x =-,由22(3),1,63y k x x y =-⎧⎪⎨+=⎪⎩得2222(12)121860k x k x k +-+-=, 因为直线与椭圆C 交于不同的两点M 、N ,所以由42221444(12)(186)24(1)0k kk k ∆=-+-=->,解得11k -<<, 设M 、N 的坐标分别为11(,)x y ,22(,)x y ,则21221212k x x k +=+,212218612k x x k -=+,11(3)y k x =-,22(3)y k x =-, 所以1212(3)(3)B M B N xx y y ⋅=--+ 21212(1)[3()9]kx x xx =+-++223312k k +=+23322(12)k =++,因为11k -<<, 所以2332322(12)k <++≤.故BM B N ⋅的取值范围为(2, 3];。
《精编》甘肃省嘉峪关市高三数学上学期第一次考试试题 理 新人教A版.doc
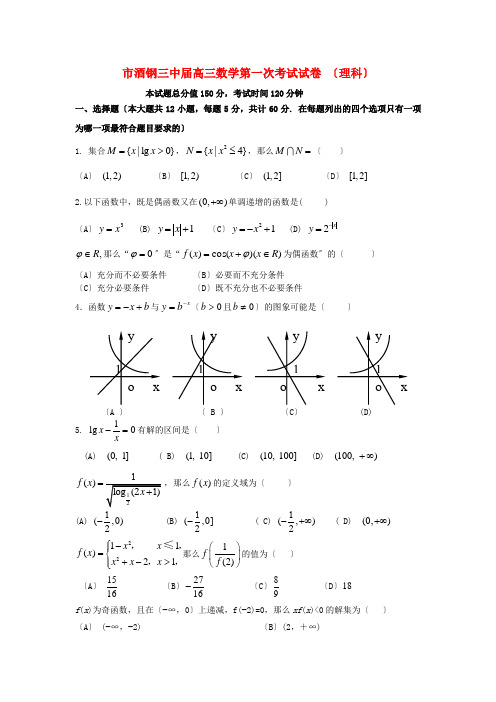
市酒钢三中届高三数学第一次考试试卷 〔理科〕本试题总分值150分,考试时间120分钟一、选择题〔本大题共12小题,每题5分,共计60分. 在每题列出的四个选项只有一项为哪一项最符合题目要求的〕1. 集合{|lg 0}M x x =>,2{|4}N x x =≤,那么MN =〔 〕〔A 〕 (1,2) 〔B 〕 [1,2) 〔C 〕 (1,2] 〔D 〕 [1,2] 2.以下函数中,既是偶函数又在(0,)+∞单调递增的函数是( ) 〔A 〕3x y = (B) 1y x =+ 〔C 〕21y x =-+ (D) 2xy -=,R ∈ϕ那么“0=ϕ〞是“))(cos()(R x x x f ∈+=ϕ为偶函数〞的〔 〕〔A 〕充分而不必要条件 〔B 〕必要而不充分条件 〔C 〕充分必要条件 〔D 〕既不充分也不必要条件4.函数b x y +-=与x b y -=〔0>b 且0≠b 〕的图象可能是〔 〕〔A 〕 〔 B 〕 〔C 〕 (D) 5.01lg =-x x 有解的区间是〔 〕(A) (0,1]( B) (1,10] (C) (10,100] (D) (100,)+∞()f x =,那么()f x 的定义域为〔 〕(A) (,)1-02 (B) (,]1-02 ( C) (,)1-+∞2( D) (,)0+∞ 2211()21x x f x x x x ⎧-⎪=⎨+->⎪⎩,,,,≤那么1(2)f f ⎛⎫⎪⎝⎭的值为〔 〕 〔A 〕1516〔B 〕2716-〔C 〕89〔D 〕18f (x )为奇函数,且在〔−∞,0〕上递减,f(−2)=0,那么xf (x )<0的解集为〔 〕〔A 〕 (−∞,−2) 〔B 〕(2,+∞)〔C 〕 (−∞,−2) ∪ (2,+∞) 〔D 〕〔 −2,2〕9.定义在R 上的函数()f x 满足()()()2f x y f x f y xy +=++〔x y ∈R ,〕,(1)2f =,那么(3)f -等于〔 〕 〔A 〕 2〔B 〕 3〔C 〕 6〔D 〕 9a 和b ,定义运算“⊗〞:,1,, 1.a ab a b b a b -≤⎧⊗=⎨->⎩ 设函数()()22()2,.f x x x x x R =-⊗-∈假设函数()y f x c =-的图像与x 轴恰有两个公共点,那么实数c 的取值范围是〔 〕〔A 〕(]3,21,2⎛⎫-∞-⋃- ⎪⎝⎭ 〔B 〕(]3,21,4⎛⎫-∞-⋃--⎪⎝⎭〔C 〕111,,44⎛⎫⎛⎫-⋃+∞ ⎪ ⎪⎝⎭⎝⎭〔D 〕311,,44⎛⎫⎡⎫--⋃+∞ ⎪⎪⎢⎝⎭⎣⎭11.定义在R 上的函数()x f 是奇函数又是以2为周期的周期函数,那么()()()741f f f ++等于 〔 〕〔A 〕 -1 (B) 0 (C) 1 (D) 4 12.设函数)(x f 是奇函数,并且在R 上为增函数,假设0≤θ≤2π时,f 〔m sin θ〕+f 〔1—m 〕>0恒成立,那么实数m 的取值范围是( D )(A) 〔0,1〕 (B) 〔-∞,0〕 (C) )21,(-∞ (D) 〔-∞,1〕二、填空题〔本大题共4小题,每题5分,共计20分〕13.函数y=-x 2-4mx+1 在[2,+∞〕上是减函数,那么m 的取值范围是14. 函数)2(log 221x x y -=的单调递减区间是_________.15. 方程 96370x x-•-=的解是 .())1,0(13log ≠>-+=a a x y a 的图象恒过定点A,假设点A 在直线01=++ny mx 上,其中0>mn ,那么nm 21+的最小值为 .三、解答题〔本大题有8小题,共70分. 解容许写出文字说明,证明过程或演算步骤〕 请考生在第22、23、24题中任选一题作答,如果多做,那么按所做的第一题记分. 17. 〔本小题总分值12分〕计算:〔1〕12lg )2(lg 5lg 2lg )2(lg 222+-+⋅+ (2) 3643==y x,求xyyx 2+的值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
嘉峪关市一中2001-2002学年第一学期期中考试
高三数学(理科)
一.选择题.(每小题5分, 12小题共60分)
1. 定义集合{}*A B x x A x B =∈∉且,若{}{}1,3,5,7,2,3,5A B ==,则*A B 的子集个数为( )
A.1
B.2
C.3
D.4
2.设{}n a 是等差数列,若273,13a a ==,则数列{}n a 前8项的和为( ) A.128 B.80 C.64 D.56
3.对于实数,,a b c ,则“a b >”是“22ac bc >”的 ( ) A .充分不必要条件 B .必要不充分条件 C .充要条件
D .既不充分也不必要条件
4. 下列函数图象中不正确的是
( )
5.设集合}21|{},20|{≤≤=≤≤=y y B x x A ,在下图中能表示从集合A 到集合B
的映射的是( )
6.已知函数()f x 的的图象与函数()()10g x x =+2lgx >的图象关于直线y x =对称,则函数()f x 的图象与y 轴的交点坐标是( )
A. 12
(0,10) B. 12
(0,10)- C. 2(0,10) D. 2(0,10)- 7. 函数22()log (65f x x x =-+)的单调递减区间为( ). A. (,2)-∞ B. (0,2) C. (,3)-∞ D. (3,)+∞ 8. 设等比数列{}n a 的公比1
2
q =
,(n=1,2,3……)各项和为10,则1a 为( ) A .-5 B .-2 C .2 D .5
9.已知集合A ={1,3,x},B ={1,x 2},A ∪B ={1,3,x},则这样的x 的不同的值有( )个 A.1
B.2
C.3
D.4
10.设数列{}n a 的前项和为n S ,且对任意正整数n ,4096n n a s +=.若2log n n b a =则数列{}n b 为( )
A .公差为-1的等差数列
B .公差为1的等差数列
C .公比数列为
12的等比数列 D .公比数列为-1
2
的等比数列 11.已知函数(1)f x +是偶函数,当121x x <<时,[21()()f x f x -](21x x -)>0恒成立,
设a f =(-1
2
),(2)b f =,(3)c f =, 则a ,b ,c 的大小关系为
( )
A .b a c <<
B .c b a <<
C .b c a <<
D .a b c <<
12.函数()f x 的定义域为R ,若(1)f x +与(1)f x -都是奇函数,则( D )
(A) ()f x 是偶函数 (B) ()f x 是奇函数 (C) ()(2)f x f x =+ (D) (3)f x +是奇函数
二.填空题. (每小题5分, 4小题共20分)
13.定义“等积数列”:在一个数列中,如果每一项与它的后一项的积都为同一个常数,
那么这个数列叫做等积数列,这个常数叫做该数列的公积,已知数列{}n a 是等积数且
12a =,公积为6,则18a = 14.设等比数列{}n a 的公比12q =
,前n 项和为n S ,则44
S
a = . 15.若曲线3()ln f x ax x =+存在垂直于y 轴的切线,则实数a 的取值范围是 16.给出下列四个命题:
①函数x y a =(0a >且1a ≠)与函数log x a y a =(0a >且1a ≠)的定义域相同; ②函数31()(3)3x x f x x =-
,当()()f a f b >时,22
a b >;③函数11221
x y =+-与2(12)2
x x
y x +=⋅都是奇函数;④函数2(1)y x =-与12x y -=在区间[0,)+∞上都是增函数,其中正确命题的序号是
三.解答题.(请同学们将以下题目的解答过程书写在答题卡相应的栏内)
17. (本小题满分10分) 已知数列{}n a 的前n 项和n S ;函数321
()103
f x x x =-,若'()
f x 的图象经过点(n ,n S )(1,2,3,n =….) (1)求{}n a 的通项公式. (2)求n S 的最小值。
18. (本小题满分12分) (本题满分12分) 已知集合A ={|(2)[(31)]0}x x x a --+<, B =2
2{|
0}(1)
x a
x x a -<-+. (1)当a =2时,求A B ; (2)求使B ⊆A 的实数a 的取值范围.
19. (本小题满分12分)已知函数()f x 的定义域R ,如果x>0,则()1f x >-.且满足
()()()1f x y f x f y +=++,1
()12
f =.
(1)证明()f x 的单调性; (2)解不等式
2()(4)6f x f x -+-≥
20(本小题满分12分)已知数列{}n a 的首项123a =,121
n
n n a a a +=+,(1,2,3,n =…) (1)证明:数列1
{
1}n
a -是等比数列; (2)求数列{}n
n
a 的前n 项和n S .
21(本小题满分12分)统计表明,某种型号的汽车在匀速行驶中每小时的耗油量y (升)关于行驶速度x (千米/小时)的函数解析式可以表示为:
313
8(0120)12800080
y x x x =
-+<≤已知甲、乙两地相距100千米.
(1)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升? (2)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升? 22(本题12分)已知函数2()(33)x f x x x e =-+⋅,其定义域为[]2,t -(2t >-),设
(2),()f m f t n -==.
(1)试确定t 的取值范围,使得函数()f x 在[]2,t -上为单调函数; (2)试判断,m n 的大小并说明理由;
(3)求证:对于任意的2t >-,总存在0(2,)x t ∈-,满足0'20()2
(1)3
x f x t e =-,并确定这
样的0x 的个数.。
