左孝凌离散数学课件2.3谓词公式与翻译
合集下载
左孝凌离散数学1

4
第一章 命题逻辑(Propositional Logic)1.3命题
公式与翻译
• 联结词旳优先级:┐、∧、∨、→、。
则:
P∧Q→R 是合式公式
等价于Wff : ((P∧Q)→R )命题公式外层旳括号能够省略
等价于Wff : (P∧Q)→R
不等价于Wff : P∧(Q→R)
第一章 命题逻辑(Propositional Logic)1.3命题
P Q ┐P∨Q
TT T TF F FT T
P→Q
T F T
FF T
T
第一章 命题逻辑(Propositional Logic) 1.4真值表 与等价公式
1.4.2 等价公式
同理(P∧Q)∨(┐P∧┐Q)与P↔ Q相应旳真值相同,如表1-4.6所示。
表1-4.6
P Q P↔Q TT T TF F FT F FF T
公式与翻译
• 1.3.2 复合命题旳符号化(翻译) • 自然语言旳语句用Wff 形式化:
① 要精确拟定原子命题,并将其形式化。 ② 要选用恰当旳联结词,尤其要善于辨认自然语言中旳联 结词(有时它们被省略),否定词旳位置要放精确。 ③ 必要时能够进行改述,即变化原来旳论述方式, 但要确保体现意思一致。 ④ 需要旳括号不能省略,而能够省略旳括号, 在需要提升公式可读性时亦可不省略。
例2:构造公式 (P Q) ∧R旳 真值表。
P Q R PQ (P Q) ∧R
00 0 00 1
01 0 01 1 10 0 10 1 11 0 11 1
20
第一章 命题逻辑(Propositional Logic) 1.4真值表 与等价公式
例2:构造公式 (P Q) ∧R旳 真值表。
Chapter2_谓词逻辑2(34谓词公式与变元约束)

离散数学
从上述两个例子可以看出,命题的符号表达式与论域有关。当 论域扩大时,需要添加用来表示客体特性的谓词,称此谓词为 特性谓词。特性谓词往往就是给定命题中量词后边的那个名词 。如上面两个例子中的“所有自然数”、“有些大学生”。 如何添加特性谓词,这是个十分重要的问题,这与前边的量词 有关。 特性谓词的添加方法如下: 如果前边是全称量词,特性谓词后边是蕴含联结词“→”;如 果前边是存在量词,特性谓词后边是合取联结词“∧”。
y的辖域为R(x,y)。
xyz(A(x,y)→B(x,y,z))∧C(t)
z的辖域
y的辖域
x的辖域
离散数学
一、概念 1、指导变元、作用域、约束变元、自由变元
量 词
约 束 变 元
自 由 变 元
(x) P( x, y)
指 导 变 元
辖 域
通常,一个量词的辖域是公式的子公式。因 此,确定一个量词的辖域即是找出位于该量词之后 的相邻接的子公式,具体地讲: 若量词后有括号,则括号内的子公式就是该 量词的辖域; 若量词后无括号,则与量词邻接的子公式为 该量词的辖域。 判定给定公式中个体变元是约束变元还是自 由变元,关键是要看它在公式中是约束出现,还是 自由出现。
离散数学
例题2
小王的父亲是个医生。
设函数f(x)=x的父亲,谓词D(x):x是个医生,a:小王,此命 题可以表示为D(f(a)).
例题3 如果x和y都是奇数,则x+y是偶数。
设 h(x,y)=x+y ,此命题可以表示为: xy((O(x)∧O(y))→E(h(x,y))
像上述的g(x)、f(x)、h(x,y)就是客体函数,一般地用小写的 英文字母f,g,h….表示客体函数。
离散数学左孝陵第四章

(1)f:X→Y中,若 x, y f ,则称x为自变量, 与x对应的y称作f作用下的象点(值); 也可用y=f(x)表示 x, y f ,y称作函数f在x点处的值。
§1 函数的概念
(2)X中每一个元素均有定义, ∴函数f的定义域 domf X (3)对应于某一个 x X ,其值f(x)是唯一的,即
设A=,则A的后继集合可写成: A+={}={},(A+)+={}{{}}={,{}} ((A+)+)+={,{}}{{,{}}}={,{},{,{}}} 令:=0 则+=0+=1,(+)+=1+=2 上述求0的后继集合而得到N={0,1,2,} Peano公理 (1)0N (这里规定0=) (2) nNn+N (这里n+是n的后继数) (3)若SN,且(ⅰ)0S (ⅱ)nSn+S,则可得S=N
f ( f 2 (i)) 2 f 2 (i) 1 2(2 f (i) 1) 1 f (i )
3
2(2(2i 1) 1) 1 8i 6 1 8i 7
§2逆函数和复合函数
《定理》:设f: X→Y,g:Y→Z, g f 是一合成函数,则: (1)如果f和g都是满射函数,则 g f 也是满射函数; (2)如果f和g都是入射函数,则 g f 也是入射函数; (3)如果f和g都是双射函数,则 g f 证明:(2)设任一 xi , x j X xi x j ∵f为入射函数,∴ f ( xi ) f ( x j ) 也是双射函数。
1.基数的概念 对于有限集:集合中不同元素的个数。 对于无限集:? 是否所有无限集的基数都一样? 为了比较两个集合的“大小”,确定有限集和无限集的概念, 我们首先引进自然数集合。
§1 函数的概念
(2)X中每一个元素均有定义, ∴函数f的定义域 domf X (3)对应于某一个 x X ,其值f(x)是唯一的,即
设A=,则A的后继集合可写成: A+={}={},(A+)+={}{{}}={,{}} ((A+)+)+={,{}}{{,{}}}={,{},{,{}}} 令:=0 则+=0+=1,(+)+=1+=2 上述求0的后继集合而得到N={0,1,2,} Peano公理 (1)0N (这里规定0=) (2) nNn+N (这里n+是n的后继数) (3)若SN,且(ⅰ)0S (ⅱ)nSn+S,则可得S=N
f ( f 2 (i)) 2 f 2 (i) 1 2(2 f (i) 1) 1 f (i )
3
2(2(2i 1) 1) 1 8i 6 1 8i 7
§2逆函数和复合函数
《定理》:设f: X→Y,g:Y→Z, g f 是一合成函数,则: (1)如果f和g都是满射函数,则 g f 也是满射函数; (2)如果f和g都是入射函数,则 g f 也是入射函数; (3)如果f和g都是双射函数,则 g f 证明:(2)设任一 xi , x j X xi x j ∵f为入射函数,∴ f ( xi ) f ( x j ) 也是双射函数。
1.基数的概念 对于有限集:集合中不同元素的个数。 对于无限集:? 是否所有无限集的基数都一样? 为了比较两个集合的“大小”,确定有限集和无限集的概念, 我们首先引进自然数集合。
(完整版)离散数学课堂PPT(左孝凌版)

例4将下列命题符号化。
(1)只要不下雨,我就骑自行车上班。
(2)只有不下雨,我才骑自行车上班。
(3)若 2+2=4,则太阳从东方升起。
(3)若 2+2≠4,则太阳从东方升起。
(4)若 2+2=4,则太阳从西方升起。
(5)若 2+2≠4,则太阳从西方升起。
解:在(1)、(2)中,设P:天下雨;Q:我骑自行车上
∧表示自然语言中的“既……又……”, “不仅……而且……”, “虽然……但是”
P Q P ∧Q
TT
T
TF
F
FT
F
FF
F
例3将下列命题符号化。 (1)李平既聪明又用功。 (2)李平虽然聪明,但不用功。 (3)李平不但聪明,而且用功。 (3)李平不是不聪明,而是不用功。
解:设P:李平聪明;Q:李平用功。 (1)P∧Q (2)P∧ᄀQ (3)P∧Q (4)ᄀ(ᄀP)∧ᄀQ
自然语言中的“或”具有二义性,有时表示
不相容的或。
例:“派小王或小李中的一人去开会” 。为排斥
性的或。
P:派小王去开会;Q:派小李去开会。 (P∧ᄀQ)∨(ᄀP∧Q) , (P∨Q)∧ᄀ(P∧Q)
定义1-2.4 设P、Q为两命题,复合命题“如果P, 则Q”称作 P与Q的蕴涵式,记作P→Q,→为蕴涵联 结词。
1.命题公式 命题公式:由命题常量、命题变元、联结词、括号 等组成的符号串。
命题公式中的命题变元称作命题公式的分量。
定义1-3.1 (1)单个命题常量或命题变 元,Q,R,…,Pi,Qi,Ri,… ,F,T是合式公式。 (2)如果A是合式公式,则(ᄀA)也是合式公式。 (3)如果A、B是合式公式,则(A∧B)、(A
左孝凌离散数学课件第02章谓词逻辑

15
第二章 谓词逻辑(Predicate Logic)
2.2命题函数与量词(Propositional functions & Quantifiers)
例如: H(x,y)∧H(y ,z)H(x,z)
若H(x,y)解释为: x大于y,当x,y,z都在实数中取值时,则这个 式子表示“若x大于y 且y 大于z,则x大于z” 。这是一个永 真式。
其中(1)、(2)、 (3)为一元谓词, (4) 、 (6)为二元谓词,
第二章 谓词逻辑(Predicate Logic)
2.1谓词的概念与表示(Predicate and Its Expression)
注: (1)单独一个谓词并不是命题,在谓词字母后 填上客体所得到的式子称之为谓词填式。 (2)在谓词填式中,若客体确定,则A(a1, a2...an)就变成了命题 (3)在多元谓词表达式中,客体字母出现的先 后次序与事先约定有关,一般不可以随意交换 位置(如,上例中H(s,t) 与H(t, s)代表两个不同 的命题) 。
离散数学(Discrete Mathematics)
9
第二章 谓词逻辑(Predicate Logic)
2.1谓词的概念与表示 2.2命题函数与量词 2.3谓词公式与翻译 2.4变元的约束 2.5谓词演算的等价式与蕴含式 2.6前束范式 2.7谓词演算的推理理论
第二章 谓词逻辑(Predicate Logic)
17
第二章 谓词逻辑(Predicate Logic)
2.2命题函数与量词(Propoቤተ መጻሕፍቲ ባይዱitional functions & Quantifiers)
2.2.2 量词(Quantifiers)
离散数学左孝陵版答案公开课一等奖优质课大赛微课获奖课件

第4页
§1 谓词概念与表示法
(1)谓词填式:谓词字母后填以客体所得式子。
例:H(a, b)
(2)若谓词字母联系着一个客体,则称作一元谓词;若谓 词字母联系着二个客体,则称作二元谓词;若谓词字母联 系着n个客体,则称作n元谓词。
(3)客体顺序必须是有要求。 例:河南省北接河北省。
nL
b
写成二元谓词为:L(n,b),但不能写成L(b,n) 。
例:P(x)表示x是质数。这是一个命题函数。 其值取决于个体域。 能够将命题函数命题,有两种办法:
第7页
§2 命题函数与量词
a)将x取定一个值。如:P(4),P(5) b)将谓词量化。如:xP(x),xP(x) 个体域给定形式有二种: ①详细给定。 如:{j, e, t} ②全总个体域任意域:所有个体从该域中取得。
第13页
§3谓词公式与翻译
写成符号形式:
x(M(x) D(x)), M(s) D(s)
2.因为对个体描述性质刻划深度不同,可翻译 成不同形式谓词公式。
第14页
§4变元约束
1.辖域:紧接在量词后面括号内谓词公式。 例: xP(x) , x(P(x) Q(x)) 。 若量词后括号内为原子谓词公式,则括号能够省去。
第18页
§4变元约束
6.个体域(叙述域,客体域):用特定集合表示 被约束变元取值范围。
(1)个体域不同,则表示同一命题谓词公式形 式不同。 例:“全部人必死。”令D(x),x是要死。
下面给出不同个体域来讨论:
(ⅰ)个体域为:{人类},
则可写成 xD(x);
(ⅱ)个体域为任意域(全总个体域),则人必 须首先从任意域中分离出来,
(b)每一个自然数都是偶数 x(N(x) E(x))
§1 谓词概念与表示法
(1)谓词填式:谓词字母后填以客体所得式子。
例:H(a, b)
(2)若谓词字母联系着一个客体,则称作一元谓词;若谓 词字母联系着二个客体,则称作二元谓词;若谓词字母联 系着n个客体,则称作n元谓词。
(3)客体顺序必须是有要求。 例:河南省北接河北省。
nL
b
写成二元谓词为:L(n,b),但不能写成L(b,n) 。
例:P(x)表示x是质数。这是一个命题函数。 其值取决于个体域。 能够将命题函数命题,有两种办法:
第7页
§2 命题函数与量词
a)将x取定一个值。如:P(4),P(5) b)将谓词量化。如:xP(x),xP(x) 个体域给定形式有二种: ①详细给定。 如:{j, e, t} ②全总个体域任意域:所有个体从该域中取得。
第13页
§3谓词公式与翻译
写成符号形式:
x(M(x) D(x)), M(s) D(s)
2.因为对个体描述性质刻划深度不同,可翻译 成不同形式谓词公式。
第14页
§4变元约束
1.辖域:紧接在量词后面括号内谓词公式。 例: xP(x) , x(P(x) Q(x)) 。 若量词后括号内为原子谓词公式,则括号能够省去。
第18页
§4变元约束
6.个体域(叙述域,客体域):用特定集合表示 被约束变元取值范围。
(1)个体域不同,则表示同一命题谓词公式形 式不同。 例:“全部人必死。”令D(x),x是要死。
下面给出不同个体域来讨论:
(ⅰ)个体域为:{人类},
则可写成 xD(x);
(ⅱ)个体域为任意域(全总个体域),则人必 须首先从任意域中分离出来,
(b)每一个自然数都是偶数 x(N(x) E(x))
离散数学19.谓词公式与翻译
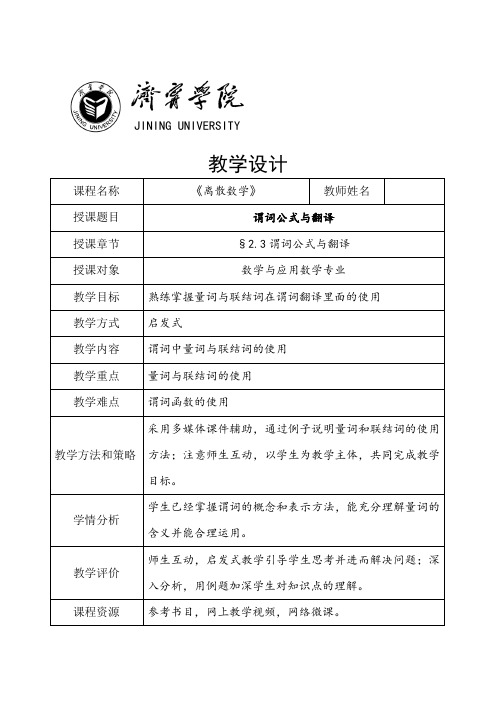
(4)并不是所有参加考试的人都能取得好成绩.
解:(1)令F(x): x是正数.M(x):x大于零.
则符号化为:(x)(F(x)M(x)).
(2)令E(x): x小于2. S(x):x是素数.则符号化为:
(x)(E(x)∧S(x)).
(3)令D(x): x是有理数.F(x):x能表示成分数.则符号化为:
学情分析
学生已经掌握谓词的概念和表示方法,能充分理解量词的含义并能合理运用。
教学评价
师生互动,启发式教学引导学生思考并进而解决问题;深入分析,用例题加深学生对知识点的理解。
课程资源
参考书目,网上教学视频,网络微课。
教学过程:
一、谓词合式公式
定义:称n元谓词A(x1,x2,...,xn)为原子谓词公式,其中x1,x2,...,xn是客体变元。
4)如果A是合式公式,x是A中的任何客体变元,则(x) A和(x) A也是合式公式;
5)只有经过有限次地应用规则(1)-(4)所得的公式是合式公式.
谓词合式公式也叫谓词公式,简称公式.
下面都是合式公式:
P,(P→Q),(Q(x)∧P),(x)(A(x)→B(x)),(x)C(x)
而下面都不是合式公式:
教学设计
课程名称
《离散数学》
教师姓名
授课题目
谓词公式与翻译
授课章节
§2.3谓词公式与翻译
授课对象
数学与应用数学专业
教学目标
熟练掌握量词与联结词在谓词翻译里面的使用
教学方式
启发式
教学内容
谓词中量词与联结词的使用
教学重点
量词与联结词的使用
教学难点
谓词函数的使用
教学方法和策略
采用多媒体课件辅助,通过例子说明量词和联结词的使用方法;注意师生互动,以学生为教学主体,共同完成教学目标。
解:(1)令F(x): x是正数.M(x):x大于零.
则符号化为:(x)(F(x)M(x)).
(2)令E(x): x小于2. S(x):x是素数.则符号化为:
(x)(E(x)∧S(x)).
(3)令D(x): x是有理数.F(x):x能表示成分数.则符号化为:
学情分析
学生已经掌握谓词的概念和表示方法,能充分理解量词的含义并能合理运用。
教学评价
师生互动,启发式教学引导学生思考并进而解决问题;深入分析,用例题加深学生对知识点的理解。
课程资源
参考书目,网上教学视频,网络微课。
教学过程:
一、谓词合式公式
定义:称n元谓词A(x1,x2,...,xn)为原子谓词公式,其中x1,x2,...,xn是客体变元。
4)如果A是合式公式,x是A中的任何客体变元,则(x) A和(x) A也是合式公式;
5)只有经过有限次地应用规则(1)-(4)所得的公式是合式公式.
谓词合式公式也叫谓词公式,简称公式.
下面都是合式公式:
P,(P→Q),(Q(x)∧P),(x)(A(x)→B(x)),(x)C(x)
而下面都不是合式公式:
教学设计
课程名称
《离散数学》
教师姓名
授课题目
谓词公式与翻译
授课章节
§2.3谓词公式与翻译
授课对象
数学与应用数学专业
教学目标
熟练掌握量词与联结词在谓词翻译里面的使用
教学方式
启发式
教学内容
谓词中量词与联结词的使用
教学重点
量词与联结词的使用
教学难点
谓词函数的使用
教学方法和策略
采用多媒体课件辅助,通过例子说明量词和联结词的使用方法;注意师生互动,以学生为教学主体,共同完成教学目标。
左孝凌离散数学PPT课件

25
第一章 命题逻辑(Propositional Logic) 1.2逻辑
联结词(Logical Connectives)
例3. 将下列命题符号化.
(1) 李平既聪明又用功.
(2) 李平虽然聪明, 但不用功.
(3)李平不但聪明,而且用功.
(4)李平不是不聪明,而是不用功.
解: 设 P:李平聪明. Q:李平用功.
第一章 命题逻辑(Propositional Logic)
1.1 命题及其表示方法
• 1.1.1 命题(Proposition) • 1.1.2 命题的表示方法 • 1.1.3 命题的分类
第一章 命题逻辑(Propositional Logic)
1.1 命题及其表示方法
1.1.1 命题
数理逻辑研究的中心问题是推理(inference),而 推理的前提和结论都是表达判断的陈述句,因而表达
第一部分 数理逻辑(Mathematical Logic)
❖1931年Godel不完全性定理的提出,以及递 归 函 数 可 计 算 性 的 引 入 , 促 使 了 1936 年 Turing 机 的 产 生 , 十 年 后 , 第 一 台 电 子 计 算机问世。
❖从 广 义 上 讲 , 数 理 逻 辑 包 括 四 论 、 两 演 算——即集合论、模型论、递归论、证明 论和命题演算、谓词演算,但现在提到数 理逻辑,一般是指命题演算和谓词演算。 本书也只研究这两个演算。
逻辑可分为:1. 形式逻辑(通过数学方法) 数理逻辑 2. 辩证逻辑 指引进一套符号体系的方法。
辩证逻辑是研究反映客观世界辩证发展过程的人类思 维的形态的。
第一部分 数理逻辑(Mathematical Logic)
❖ 形式逻辑是研究思维的形式结构和规律的科学,它撇 开具体的、个别的思维内容,从形式结构方面研究概 念、判断和推理及其正确联系的规律。
第一章 命题逻辑(Propositional Logic) 1.2逻辑
联结词(Logical Connectives)
例3. 将下列命题符号化.
(1) 李平既聪明又用功.
(2) 李平虽然聪明, 但不用功.
(3)李平不但聪明,而且用功.
(4)李平不是不聪明,而是不用功.
解: 设 P:李平聪明. Q:李平用功.
第一章 命题逻辑(Propositional Logic)
1.1 命题及其表示方法
• 1.1.1 命题(Proposition) • 1.1.2 命题的表示方法 • 1.1.3 命题的分类
第一章 命题逻辑(Propositional Logic)
1.1 命题及其表示方法
1.1.1 命题
数理逻辑研究的中心问题是推理(inference),而 推理的前提和结论都是表达判断的陈述句,因而表达
第一部分 数理逻辑(Mathematical Logic)
❖1931年Godel不完全性定理的提出,以及递 归 函 数 可 计 算 性 的 引 入 , 促 使 了 1936 年 Turing 机 的 产 生 , 十 年 后 , 第 一 台 电 子 计 算机问世。
❖从 广 义 上 讲 , 数 理 逻 辑 包 括 四 论 、 两 演 算——即集合论、模型论、递归论、证明 论和命题演算、谓词演算,但现在提到数 理逻辑,一般是指命题演算和谓词演算。 本书也只研究这两个演算。
逻辑可分为:1. 形式逻辑(通过数学方法) 数理逻辑 2. 辩证逻辑 指引进一套符号体系的方法。
辩证逻辑是研究反映客观世界辩证发展过程的人类思 维的形态的。
第一部分 数理逻辑(Mathematical Logic)
❖ 形式逻辑是研究思维的形式结构和规律的科学,它撇 开具体的、个别的思维内容,从形式结构方面研究概 念、判断和推理及其正确联系的规律。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
对个体刻划深度 的不同就可翻译成 不同的谓词公式.
练习
例1:在谓词逻辑中将下列命题符号化. (1)凡正数都大于零。 (2)存在小于2的素数。 (3)没有不能表示成分数的有理数。 (4)并不是所有参加考试的人都能取得好成绩。 解:
8
(1)凡正数都大于零 解:令M(x):x是正数。F(x): x大于零。则符号化为: (x)(M(x)F(x)) (2)存在小于2的素数。 解:令E(x): x 小于 2 。 S(x):x 是素数。则符号化为: (x)(E(x)∧S(x)) 真值为0。
再对x和y加以限制
R(x):x是大红书柜 Q(y):y是古书
C(x):x是红的 E(y):y是图书
a :这只 b:那些 此时可把命题符号化为:
A(a) B(a) C(a) D(b) E(b) F (a, b)
a:这只 b:那些 此时可把命题符号化为:
R(a) Q(b) F (a, b)
例题3 尽管有人聪明,但未必一切人都聪明。
解 设 M(x):x是人。 P(x):x是聪明的。 命题符号化为:
x(M ( x) P( x)) (x( M ( x) P( x)))
由于人们对命题的文字叙述含意理解的不同,强调的 重点不同,会影响到命题符号化的形式不同。见例题4。
例题4 这只大红书柜摆满了那些古书。
约定:最外层括号可以省略;量词后面如果有括号,则不能省略
3
2.3谓词公式与翻译
• 二、谓词公式的翻译(符号化)
把一个文字叙述的命题,用谓词公式表示出来,称为谓词 逻辑的翻译或符号化;一般,符号化的步骤如下: (1)正确理解给定命题。必要时把命题改述,使其中每个原子 命题、原子命题之间的关系明显表达出来。 (2)把每个原子命题分解成个体、谓词和量词;在全总论域讨 论时,要给出特性谓词。 (3)找出恰当量词。应注意全称量词后跟条件式,存在量词后 跟合取式。 (4)用恰当的联结词把给定命题表示出来。
10
练习2
• 1、 在谓词逻辑中将下列命题符号化. (1)所有运动员都钦佩某些教练. (2)有些运动员不钦佩教练. 设:L(x):x是运动员 J(y):y是教练 A(x,y):x钦佩y (1) (x)(L(x) (y)(J(y)∧A(x,y))) (2)(x)(L(x) ∧(y)(J(y)A(x,y)))
2.2命题函数与量词(Propositional functions & Quantifiers)
• 小结:本节介绍了谓词合式公式的概念,重 点掌握谓词公式的翻译. 作业: P63 (5)
14
12
练习2
(2)设:P(x,y):x在y连续. Q(x,y):x大于y. f在a点连续,当且仅当对每个ε>0, (2)符号化为:
P(f,a)(ε)(Q(ε,0) x-a ︱<δ,则︱f(x)-f(a)︱<ε。 ((δ )Q(δ,0)∧ (x)(Q(δ , ︱x-a︱)Q(ε, ︱f(x)-f(a)︱)) ))
练习1
(3)没有不能表示成分数的有理数。
解:令D(x): x是有理数。F(x):x能表示成分数。 则符号化为: (x)(D(x) F(x)) 或 (x)(D(x)∧ F(x)) 真值为1。
(4)并不是所有参加考试的人都能取得好成绩。
解:令M(x):x是人.Q(x):x参加考试。H(x):x能取得好成 绩。则符号化为: (x)( (M(x)∧Q(x))H(x) ) 或 (x)( (M(x)∧Q(x))∧ H(x) )
存在一个δ >0,使得对所有x,若︱
当且仅当: 每个ε>0: (ε)Q(ε,0) 存在δ >0:(δ) Q(δ,0) ∧ 对所有x,若︱x-a ︱<δ,则︱f(x)-f(a)︱<ε: (x)((Q(δ , ︱x-a︱)Q(ε, ︱f(x)-f(a)︱))
13
第二章 谓词逻辑(Predicate Logic)
11
练习2
• 2、在谓词逻辑中将下列命题符号化. (1) P63 (6)那位戴眼镜的用功的大学生在看这本大而厚 的巨著. (2)P63 (7) :f在a点连续,当且仅当对每个ε>0,存在一个
δ >0,使得对所有x,若︱x-a ︱<δ,则︱f(x)-f(a)︱<ε。
解: (1)设:S(x):x是大学生. A(x):x戴眼镜. B(x):x用功. E(y):y是大的. G(y):y是厚的. D(y):y是巨著. F(x,y):x看y.a:那位 b:这本 (1)符号化为: A(a)∧B(a)∧S(a)∧E(b)∧G(b)∧D(b)∧F(a,b)
例题1 并非每个实数都是有理数。
设 R(x):x是实数。 Q(x):X是有理数。
每个实数都是有理数表示为: (x)( R( x) Q( x))
(x)( R( x) Q( x)) 并非每个实数都是有理数表示为:
例题2 没有不犯错误的人
解 本语句即为“不存在不犯错误的人”。 设 M(x):x 是人。 F(x):x犯错误。 “存在不犯错误的人”表示为: “不存在不犯错误的人”表示为:(x(M ( x) F ( x)) 等价于“任何人都要犯错误”或“所有人都要犯错误”。 所以此命题也可符号化为: (x)(M ( x) F ( x))
解法1 这只大红书柜摆满了那些古书。 解法2 x y 设 A(x):x是书柜 设 F(x,y):x摆满了y
解法1中R(x)表示x是大红书柜, 解法2中A(x) ∧B(x) ∧C(x)也 可表示大红书柜,但用A(x) ∧B(x) ∧C(x)将更方便于对 书柜的大小颜色进行讨论
B(x):x是大的 D(y):y是古老的 F(x,y):x摆满了y
离散数学(Discrete Mathematics)
1
第二章 谓词逻辑
2.1谓词的概念与表示 2.2命题函数与量词 2.3谓词公式与翻译 2.4变元的约束 2.5谓词演算的等价式与蕴含式 2.6前束范式
2.7谓词演算的推理理论
2
2.3谓词公式与翻译
一、谓词公式
• 定义1:n元谓词A(x1,x2...xn) 称为谓词演算的原子公式。 • 定义2:谓词演算的合式公式,可由下述各条组成: ① 原子公式是合式公式。 ② 若A 是合式公式,则(A)也是合式公式。 ③ 若A,B是合式公式,则(A ∧ B),(A ∨ B),(A B), (A B)也是合式公式。 ④ 若A是合式公式,x是A中出现的任何变元 ,则(x)A , (x)A,也是合式公式。 ⑤ 只有有限次应用(1)~(4)得到的公式是合式公式.
练习
例1:在谓词逻辑中将下列命题符号化. (1)凡正数都大于零。 (2)存在小于2的素数。 (3)没有不能表示成分数的有理数。 (4)并不是所有参加考试的人都能取得好成绩。 解:
8
(1)凡正数都大于零 解:令M(x):x是正数。F(x): x大于零。则符号化为: (x)(M(x)F(x)) (2)存在小于2的素数。 解:令E(x): x 小于 2 。 S(x):x 是素数。则符号化为: (x)(E(x)∧S(x)) 真值为0。
再对x和y加以限制
R(x):x是大红书柜 Q(y):y是古书
C(x):x是红的 E(y):y是图书
a :这只 b:那些 此时可把命题符号化为:
A(a) B(a) C(a) D(b) E(b) F (a, b)
a:这只 b:那些 此时可把命题符号化为:
R(a) Q(b) F (a, b)
例题3 尽管有人聪明,但未必一切人都聪明。
解 设 M(x):x是人。 P(x):x是聪明的。 命题符号化为:
x(M ( x) P( x)) (x( M ( x) P( x)))
由于人们对命题的文字叙述含意理解的不同,强调的 重点不同,会影响到命题符号化的形式不同。见例题4。
例题4 这只大红书柜摆满了那些古书。
约定:最外层括号可以省略;量词后面如果有括号,则不能省略
3
2.3谓词公式与翻译
• 二、谓词公式的翻译(符号化)
把一个文字叙述的命题,用谓词公式表示出来,称为谓词 逻辑的翻译或符号化;一般,符号化的步骤如下: (1)正确理解给定命题。必要时把命题改述,使其中每个原子 命题、原子命题之间的关系明显表达出来。 (2)把每个原子命题分解成个体、谓词和量词;在全总论域讨 论时,要给出特性谓词。 (3)找出恰当量词。应注意全称量词后跟条件式,存在量词后 跟合取式。 (4)用恰当的联结词把给定命题表示出来。
10
练习2
• 1、 在谓词逻辑中将下列命题符号化. (1)所有运动员都钦佩某些教练. (2)有些运动员不钦佩教练. 设:L(x):x是运动员 J(y):y是教练 A(x,y):x钦佩y (1) (x)(L(x) (y)(J(y)∧A(x,y))) (2)(x)(L(x) ∧(y)(J(y)A(x,y)))
2.2命题函数与量词(Propositional functions & Quantifiers)
• 小结:本节介绍了谓词合式公式的概念,重 点掌握谓词公式的翻译. 作业: P63 (5)
14
12
练习2
(2)设:P(x,y):x在y连续. Q(x,y):x大于y. f在a点连续,当且仅当对每个ε>0, (2)符号化为:
P(f,a)(ε)(Q(ε,0) x-a ︱<δ,则︱f(x)-f(a)︱<ε。 ((δ )Q(δ,0)∧ (x)(Q(δ , ︱x-a︱)Q(ε, ︱f(x)-f(a)︱)) ))
练习1
(3)没有不能表示成分数的有理数。
解:令D(x): x是有理数。F(x):x能表示成分数。 则符号化为: (x)(D(x) F(x)) 或 (x)(D(x)∧ F(x)) 真值为1。
(4)并不是所有参加考试的人都能取得好成绩。
解:令M(x):x是人.Q(x):x参加考试。H(x):x能取得好成 绩。则符号化为: (x)( (M(x)∧Q(x))H(x) ) 或 (x)( (M(x)∧Q(x))∧ H(x) )
存在一个δ >0,使得对所有x,若︱
当且仅当: 每个ε>0: (ε)Q(ε,0) 存在δ >0:(δ) Q(δ,0) ∧ 对所有x,若︱x-a ︱<δ,则︱f(x)-f(a)︱<ε: (x)((Q(δ , ︱x-a︱)Q(ε, ︱f(x)-f(a)︱))
13
第二章 谓词逻辑(Predicate Logic)
11
练习2
• 2、在谓词逻辑中将下列命题符号化. (1) P63 (6)那位戴眼镜的用功的大学生在看这本大而厚 的巨著. (2)P63 (7) :f在a点连续,当且仅当对每个ε>0,存在一个
δ >0,使得对所有x,若︱x-a ︱<δ,则︱f(x)-f(a)︱<ε。
解: (1)设:S(x):x是大学生. A(x):x戴眼镜. B(x):x用功. E(y):y是大的. G(y):y是厚的. D(y):y是巨著. F(x,y):x看y.a:那位 b:这本 (1)符号化为: A(a)∧B(a)∧S(a)∧E(b)∧G(b)∧D(b)∧F(a,b)
例题1 并非每个实数都是有理数。
设 R(x):x是实数。 Q(x):X是有理数。
每个实数都是有理数表示为: (x)( R( x) Q( x))
(x)( R( x) Q( x)) 并非每个实数都是有理数表示为:
例题2 没有不犯错误的人
解 本语句即为“不存在不犯错误的人”。 设 M(x):x 是人。 F(x):x犯错误。 “存在不犯错误的人”表示为: “不存在不犯错误的人”表示为:(x(M ( x) F ( x)) 等价于“任何人都要犯错误”或“所有人都要犯错误”。 所以此命题也可符号化为: (x)(M ( x) F ( x))
解法1 这只大红书柜摆满了那些古书。 解法2 x y 设 A(x):x是书柜 设 F(x,y):x摆满了y
解法1中R(x)表示x是大红书柜, 解法2中A(x) ∧B(x) ∧C(x)也 可表示大红书柜,但用A(x) ∧B(x) ∧C(x)将更方便于对 书柜的大小颜色进行讨论
B(x):x是大的 D(y):y是古老的 F(x,y):x摆满了y
离散数学(Discrete Mathematics)
1
第二章 谓词逻辑
2.1谓词的概念与表示 2.2命题函数与量词 2.3谓词公式与翻译 2.4变元的约束 2.5谓词演算的等价式与蕴含式 2.6前束范式
2.7谓词演算的推理理论
2
2.3谓词公式与翻译
一、谓词公式
• 定义1:n元谓词A(x1,x2...xn) 称为谓词演算的原子公式。 • 定义2:谓词演算的合式公式,可由下述各条组成: ① 原子公式是合式公式。 ② 若A 是合式公式,则(A)也是合式公式。 ③ 若A,B是合式公式,则(A ∧ B),(A ∨ B),(A B), (A B)也是合式公式。 ④ 若A是合式公式,x是A中出现的任何变元 ,则(x)A , (x)A,也是合式公式。 ⑤ 只有有限次应用(1)~(4)得到的公式是合式公式.
