专题8.3 立体几何综合问题(原卷版)文科生
高三数学专项训练:立体几何解答题(文科)(一)

立体几何解答题吴丽康 2019-111.如图,三棱锥A —BPC 中,AP ⊥PC ,AC ⊥BC ,M 为AB 中点,D 为PB 中点,且△PMB 为正三角形.(Ⅰ)求证:DM //平面APC ;(Ⅱ)求 证:平面ABC ⊥平面APC ;(Ⅲ)若BC =4,AB =20,求三棱锥D —BCM 的体积.2.如图1,在四棱锥ABCD P -中,⊥PA 底面ABCD ,面ABCD 为正方形,E 为侧棱PD 上一点,F 为AB 上一点.该四棱锥的正(主)视图和侧(左)视图如图2所示.(Ⅰ)求四面体PBFC 的体积; (Ⅱ)证明:AE ∥平面PFC ;(Ⅲ)证明:平面PFC ⊥平面PCD .3.如图,四棱柱P ABCD -中, .//,,AB PAD AB CD PD AD F ⊥=平面是DC 上的点且1,2DF AB PH =为PAD ∆中AD 边上的高.(Ⅰ)求证://AB 平面PDC ; (Ⅱ)求证:PH BC ⊥;(Ⅲ)线段PB 上是否存在点E ,使EF ⊥平面PAB ?说明理由. 4.在四棱锥V ABCD -中,底面ABCD 是正方形,侧面VAD 是正三角形,平面VAD ⊥底面ABCD .(Ⅰ)如果P 为线段VC 的中点,求证://VA 平面PBD ; (Ⅱ)如果正方形ABCD 的边长为2, 求三棱锥A VBD -的体积.5.如图,在四棱锥中,底面为菱形,,为的中点。
(1)若,求证:平面;(2)点在线段上,,试确定的值,使;A B CVAB CD6.如图,已知三棱锥BPC A -中,PC AP ⊥,BC AC ⊥,M 为AB 中点,D 为PB 中点,且PMB ∆为正三角形。
(Ⅰ)求证:DM //平面APC ; (Ⅱ)求证:平面ABC ⊥平面APC ;(III )若4=BC ,20=AB ,求三棱锥BCM D -的体积.7.如图,E 是矩形ABCD 中AD 边上的点,F 为CD 边的中点,243AB AE AD ===,现将ABE ∆沿BE 边折至PBE ∆位置,且平面PBE ⊥平面BCDE .⑴ 求证:平面PBE ⊥平面PEF ; ⑵ 求四棱锥P BEFC -的体积.8.如图,平面四边形ABCD 的4个顶点都在球O 的表面上,AB 为球O 的直径,P 为球面上一点,且PO ⊥平面 ABCD ,2BC CD DA ===,点M 为PA 的中点. (1) 证明:平面//PBC 平面ODM ; (2) 求点A 到平面PBC 的距离.A BCDP MP B CFE(1)(2)O AD P BCM9.如图,四棱锥P —ABCD 中,底面ABCD 是边长为a 的正方形E , F 分别为PC ,BD 的中点,侧面PAD ⊥底面ABCD ,且PA=PD=2AD. (Ⅰ)求证:EF//平面PAD ; (Ⅱ)求三棱锥C —PBD 的体积.10.如图,在四棱锥P ABCD -中,平面PAD ⊥平面ABCD ,90ABC BCD ∠=∠=,PA PD DC CB a ====,2AB a =,E 是PB 中点,H 是AD 中点. (Ⅰ)求证://EC 平面APD ; (Ⅱ)求三棱锥E BCD -的体积.11.如图,在三棱锥S ABC -中,侧面SAB 与侧面SAC 均为等边三角形, 90BAC ∠=°,O 为BC 中点.(Ⅰ)证明:SO ⊥平面ABC ;(Ⅱ)求异面直线BS 与AC 所成角的大小.OSBACABCDFEP12.如图,已知AB ⊥平面ACD ,DE ∥AB ,△ACD 是正三角形,2AD DE AB ==,且F 是CD 的中点.(Ⅰ)求证AF ∥平面BCE ;(Ⅱ)设AB =1,求多面体ABCDE 的体积. 13.在四棱锥P -ABCD 中,∠ABC =∠ACD =90°,∠BAC =∠CAD =60°,PA ⊥平面ABCD ,E 为PD 的中点,PA =2AB =2.(Ⅰ)求四棱锥P -ABCD 的体积V ;(Ⅱ)若F 为PC 的中点,求证PC ⊥平面AEF ;PA BCDEF如图,四棱锥P —ABCD 中,底面ABCD 是边长为a 的正方形E , F 分别为PC ,BD 的中点,侧面PAD ⊥底面ABCD ,且PA=PD=22AD. (Ⅰ)求证:EF//平面PAD ; (Ⅱ)求三棱锥C —PBD 的体积.15.右图为一组合体,其底面ABCD 为正方形,PD ⊥平面ABCD ,//EC PD ,且22PD AD EC ===(Ⅰ)求证://BE 平面PDA ; (Ⅱ)求四棱锥B CEPD -的体积;(Ⅲ)求该组合体的表面积.CDFEP16.四棱锥S ABCD -中,底面ABCD 为平行四边形,侧面SBC ⊥底面ABCD ,E 为SD的中点,已知452ABC AB BC ∠===,,SB SC ==(Ⅰ)求证:SA BC ⊥;(Ⅱ)在BC 上求一点F ,使//EC 平面SAF ; (Ⅲ)求三棱锥D EAC -的体积.17.(本小题满分12分) 在三棱柱111ABC A B C -中,底面是边长为32的正三角形,点1A 在底面ABC 上的射影O 恰是BC 中点. (Ⅰ)求证:1AA BC ⊥;(Ⅱ)当侧棱1AA 和底面成45角时, 求11A BB C C V - (Ⅲ)若D 为侧棱1AA 上一点,当DADA 1为何值时,11BD A C ⊥.ABOCDA 1B 1C 1ABCD SE18.在四棱锥P-ABCD 中,平面PAD ⊥平面ABCD ,PA =PD ,底面ABCD 是菱形,∠A =60°,E 是AD 的中点,F 是PC 的中点. (Ⅰ)求证:BE ⊥平面PAD ; (Ⅱ)求证:EF∥平面PAB ;19.在几何体ABCDE 中,⊥=∠DC BAC ,2π平面ABC ,⊥EB 平面ABC ,1,2====CD BE AC AB .(1)设平面ABE 与平面ACD 的交线为直线l ,求证://l 平面BCDE ; (2)设F 是BC 的中点,求证:平面⊥AFD 平面AFE ; (3)求几何体ABCDE 的体积.20.在四棱锥P-ABCD 中,平面PAD ⊥平面ABCD ,PA =PD ,底面ABCD 是菱形,∠A =60°,E 是AD 的中点,F 是PC 的中点. (Ⅰ)求证:BE ⊥平面PAD ; (Ⅱ)求证:EF ∥平面PAB ;21.(本小题满分12分)如图,已知⊥AB 平面ACD ,⊥DE 平面ACD ,ACD ∆为等边三角形,AB DE AD 2==,F 为CD 中点.(1)求证://AF 平面BCE ; (2)求证:平面BCE ⊥平面CDE ; (3)求直线BF 与平面BCE 所成角的正弦值.BCDEFAPA ⊥底面ABCD ,PA(1)证明:平面PBE ⊥平面PAB (2)求二面角A —BE —P 的大小。
全国高考文科数学立体几何综合题型汇总(供参考)

新课标立体几何常考证明题汇总1、已知四边形ABCD 是空间四边形,,,,E F G H 分别是边,,,AB BC CD DA 的中点 (1) 求证:EFGH 是平行四边形(2) 若BD=AC=2,EG=2。
求异面直线AC 、BD 所成的角和EG 、BD 所成的角。
证明:在ABD ∆中,∵,E H 分别是,AB AD 的中点∴1//,2EH BD EH BD = 同理,1//,2FG BD FG BD =∴//,EH FG EH FG =∴四边形EFGH 是平行四边形。
(2) 90° 30 °考点:证平行(利用三角形中位线),异面直线所成的角2、如图,已知空间四边形ABCD 中,,BC AC AD BD ==,E 是AB 的中点。
求证:(1)⊥AB 平面CDE;(2)平面CDE ⊥平面ABC 。
证明:(1)BC AC CE AB AE BE =⎫⇒⊥⎬=⎭同理,AD BD DE AB AE BE =⎫⇒⊥⎬=⎭又∵CE DE E ⋂= ∴AB ⊥平面CDE (2)由(1)有AB ⊥平面CDE又∵AB ⊆平面ABC , ∴平面CDE ⊥平面ABC 考点:线面垂直,面面垂直的判定 AHGFEDCB AEDBC3、如图,在正方体1111ABCD A B C D -中,E 是1AA 的中点, 求证: 1//A C 平面BDE 。
证明:连接AC 交BD 于O ,连接EO , ∵E 为1AA 的中点,O 为AC 的中点 ∴EO 为三角形1A AC 的中位线 ∴1//EO AC 又EO 在平面BDE 内,1A C 在平面BDE 外∴1//A C 平面BDE 。
考点:线面平行的判定4、已知ABC ∆中90ACB ∠=,SA ⊥面ABC ,AD SC ⊥,求证:AD ⊥面SBC . 证明:90ACB ∠=∵° BC AC ∴⊥又SA ⊥面ABC SA BC ∴⊥BC ∴⊥面SAC BC AD ∴⊥又,SC AD SC BC C ⊥⋂=AD ∴⊥面SBC 考点:线面垂直的判定5、已知正方体1111ABCD A B C D -,O 是底ABCD 对角线的交点.求证:(1) C 1O ∥面11AB D ;(2)1AC ⊥面11AB D . 证明:(1)连结11A C ,设11111A CB D O ⋂=,连结1AO∵ 1111ABCD A B C D -是正方体 11A ACC ∴是平行四边形∴A 1C 1∥AC 且 11A C AC = 又1,O O 分别是11,A C AC 的中点,∴O 1C 1∥AO 且11O C AO =11AOC O ∴是平行四边形111,C O AO AO ∴⊂∥面11AB D ,1C O ⊄面11AB D ∴C 1O ∥面11AB D(2)1CC ⊥面1111A B C D 11!CC B D ∴⊥ 又1111A CB D ⊥∵, 1111B D AC C ∴⊥面 111AC B D ⊥即 同理可证11A C AD ⊥, 又1111D B AD D ⋂=∴1A C ⊥面11AB D考点:线面平行的判定(利用平行四边形),线面垂直的判定 AED 1CB 1DCBASDCBAD 1ODB AC 1B 1A 1CMP6、正方体''''ABCD A B C D -中,求证:(1)''AC B D DB ⊥平面;(2)''BD ACB ⊥平面.考点:线面垂直的判定7、正方体ABCD —A 1B 1C 1D 1中.(1)求证:平面A 1BD ∥平面B 1D 1C ; (2)若E 、F 分别是AA 1,CC 1的中点,求证:平面EB 1D 1∥平面FBD . 证明:(1)由B 1B ∥DD 1,得四边形BB 1D 1D 是平行四边形,∴B 1D 1∥BD , 又BD ⊄平面B 1D 1C ,B 1D 1⊂平面B 1D 1C , ∴BD ∥平面B 1D 1C .同理A 1D ∥平面B 1D 1C .而A 1D ∩BD =D ,∴平面A 1BD ∥平面B 1CD .(2)由BD ∥B 1D 1,得BD ∥平面EB 1D 1.取BB 1中点G ,∴AE ∥B 1G .从而得B 1E ∥AG ,同理GF ∥AD .∴AG ∥DF .∴B 1E ∥DF .∴DF ∥平面EB 1D 1.∴平面EB 1D 1∥平面FBD .考点:线面平行的判定(利用平行四边形)8、四面体ABCD 中,,,AC BD E F =分别为,AD BC 的中点,且22EF AC =, 90BDC ∠=,求证:BD ⊥平面ACD证明:取CD 的中点G ,连结,EG FG ,∵,E F 分别为,AD BC 的中点,∴EG12//AC =12//FG BD =,又,AC BD =∴12FG AC =,∴在EFG ∆中,222212EG FG AC EF +== ∴EG FG ⊥,∴BD AC ⊥,又90BDC ∠=,即BD CD ⊥,AC CD C ⋂= ∴BD ⊥平面ACD考点:线面垂直的判定,三角形中位线,构造直角三角形9、如图P 是ABC ∆所在平面外一点,,PA PB CB =⊥平面PAB ,M 是PC 的中点,N 是AB上的点,3AN NB =(1)求证:MN AB ⊥;(2)当90APB ∠=,24AB BC ==时,求MN 的长。
高考文科数学立体几何题型与方法(文科)

高考文科数学立体几何题型与方法〔文科〕一、考点回顾 1.平面〔1〕平面的基本性质:掌握三个公理与推论,会说明共点、共线、共面问题。
〔2〕证明点共线的问题,一般转化为证明这些点是某两个平面的公共点〔依据:由点在线上,线在面内,推出点在面内〕,这样,可根据公理2证明这些点都在这两个平面的公共直线上。
〔3〕证明共点问题,一般是先证明两条直线交于一点,再证明这点在第三条直线上,而这一点是两个平面的公共点,这第三条直线是这两个平面的交线。
〔4〕证共面问题一般用落入法或重合法。
〔5〕经过不在同一条直线上的三点确定一个面. 2. 空间直线.〔1〕空间直线位置分三种:相交、平行、异面. 相交直线—共面有反且有一个公共点;平行直线—共面没有公共点;异面直线—不同在任一平面内。
〔2〕异面直线判定定理:过平面外一点与平面内一点的直线和平面内不经过该点的直线是异面直线.〔不在任何一个平面内的两条直线〕〔3〕平行公理:平行于同一条直线的两条直线互相平行.〔4〕等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,则这两个角相等推论:如果两条相交直线和另两条相交直线分别平行,则这两组直线所成锐角〔或直角〕相等.〔5〕两异面直线的距离:公垂线的长度.空间两条直线垂直的情况:相交〔共面〕垂直和异面垂直.21,l l 是异面直线,则过21,l l 外一点P ,过点P 且与21,l l 都平行平面有一个或没有,但与21,l l 距离相等的点在同一平面内. 〔l 1或l 2在这个做出的平面内不能叫l 1与l 2平行的平面〕3. 直线与平面平行、直线与平面垂直.〔1〕空间直线与平面位置分三种:相交、平行、在平面内.〔2〕直线与平面平行判定定理:如果平面外一条直线和这个平面内一条直线平行,则这条直线和这个平面平行.〔"线线平行,线面平行"〕〔3〕直线和平面平行性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,则这条直线和交线平行.〔"线面平行,线线平行"〕〔4〕直线与平面垂直是指直线与平面任何一条直线垂直,过一点有且只有一条直线和一个平面垂直,过一点有且只有一个平面和一条直线垂直.PO A a4 若PA⊥α,a⊥AO,得a⊥PO〔三垂线定理〕,得不出α⊥PO. 因为a⊥PO,但PO不垂直OA.5 三垂线定理的逆定理亦成立.直线与平面垂直的判定定理一:如果一条直线和一个平面内的两条相交直线都垂直,则这两条直线垂直于这个平面.〔"线线垂直,线面垂直"〕直线与平面垂直的判定定理二:如果平行线中一条直线垂直于一个平面,则另一条也垂直于这个平面.推论:如果两条直线同垂直于一个平面,则这两条直线平行.〔5〕a.垂线段和斜线段长定理:从平面外一点向这个平面所引的垂线段和斜线段中,①射影相等的两条斜线段相等,射影较长的斜线段较长;②相等的斜线段的射影相等,较长的斜线段射影较长;③垂线段比任何一条斜线段短.[注]:垂线在平面的射影为一个点. [一条直线在平面内的射影是一条直线.〔×〕]b.射影定理推论:如果一个角所在平面外一点到角的两边的距离相等,则这点在平面内的射影在这个角的平分线上。
(完整)《立体几何》专题(文科)

(完整)《立体几何》专题(文科)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((完整)《立体几何》专题(文科))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(完整)《立体几何》专题(文科)的全部内容。
高三文科数学第二轮复习资料—-《立体几何》专题一、空间基本元素:直线与平面之间位置关系的小结.如下图:二、练习题:1.l 1∥l 2,a ,b 与l 1,l 2都垂直,则a ,b 的关系是A .平行B .相交C .异面D .平行、相交、异面都有可能2.三棱柱ABC-A 1B 1C 1的体积为V,P 、Q 分别为AA 1、CC 1上的点,且满足AP=C 1Q,则四棱锥B —APQC 的体积是A .B .C .D .3.设、、为平面, 、、为直线,则的一个充分条件是A .B .C .D . 4.如图1,在棱长为的正方体中, P 、Q 是对角 线,若的体积为 A . B . C . D .不确定5.圆台的轴截面面积是Q ,母线与下底面成60°角,则圆台的内切球的表面积是AB QC QD Q6.在正方体ABCD —A 1B 1C 1D 1中,E 、F 、G 、H 分别为棱BC 、CC 1、C 1D 1、AA 1的中点,O 为AC 与BD的交点(如图),求证: (1)EG∥平面BB 1D 1D; (2)平面BDF∥平面B 1D 1H; (3)A 1O⊥平面BDF ; (4)平面BDF⊥平面AA 1C .7.如图,斜三棱柱ABC —A’B'C’中,底面是边长为a 的正三角形,侧棱长为 b,侧棱AA'与底面相邻两边AB 、AC 都成450角,求V 21V 31V 41V 32αβγm nlm β⊥,,l m l αβαβ⊥=⊥,,m αγαγβγ=⊥⊥,,m αγβγα⊥⊥⊥,,n n m αβα⊥⊥⊥a AB C D A B C D -1111A C 1aPQ =2P B D Q -a3336a3318a332412Q 232π23π此三棱柱的侧面积和体积.8.在三棱锥P —ABC 中,PC=16cm ,AB=18cm ,PA=PB=AC=BC=17cm ,求三棱锥的体积V P-ABC .9.如图6为某一几何体的展开图,其中是边长为6的正方形,SD=PD=6,CR=SC ,AQ=AP ,点S 、D 、A 、Q 及P 、D 、C 、R 共线。
高三立体几何习题(文科含答案)

23正视图 图1侧视图 图22 俯视图 2图3立几习题21假设直线l 不平行于平面a ,且l a ∉,则 A .a 内的所有直线与异面 B .a 内不存在与l 平行的直线 C .a 内存在唯一的直线与l 平行 D .a 内的直线与l 都相交 2.1l ,2l ,3l 是空间三条不同的直线,则以下命题正确的选项是〔A 〕12l l ⊥,23l l ⊥13//l l ⇒〔B 〕12l l ⊥,23//l l ⇒13l l ⊥〔C 〕233////l l l ⇒1l ,2l ,3l 共面〔D 〕1l ,2l ,3l 共点⇒1l ,2l ,3l 共面3.如图1 ~ 3,某几何体的正视图〔主视图〕,侧视图〔左视图〕和俯视图分别是等边三角形,等腰三角形和菱形,则该几何体的体积为 A .3 B .4 C .3 D .24.某几何体的三视图如下图,则它的体积是〔 〕 A.283π- B.83π-D.23π5、如图,在四棱锥ABCD P -中,平面PAD ⊥平面ABCD ,AB=AD ,∠BAD=60°,E 、F 分别是AP 、AD的中点 求证:〔1〕直线E F ‖平面PCD ; (2)平面BEF ⊥平面PAD5〔本小题总分值13分〕如图,ABEDFC为多面体,平面ABED与平面ACFD垂直,点O在线段AD上,OD=,△OAB,△OAC,△ODE,△ODF都是正三角形。
OA=,21∥;〔Ⅰ〕证明直线BC EF-的体积.〔Ⅱ〕求棱锥F OBED6.〔本小题共14分〕如图,在四面体PABC中,PC⊥AB,PA⊥BC,点D,E,F,G分别是棱AP,AC,BC,PB的中点.〔Ⅰ〕求证:DE∥平面BCP;〔Ⅱ〕求证:四边形DEFG为矩形;〔Ⅲ〕是否存在点Q,到四面体PABC六条棱的中点的距离相等?说明理由.7.〔本小题总分值12分〕如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,点E在线段AD上,且CE∥AB。
立体几何(文科专用)(解析版)

专题09 立体几何1.【2019年高考全国Ⅱ卷文数】设α,β为两个平面,则α∥β的充要条件是 A .α内有无数条直线与β平行 B .α内有两条相交直线与β平行 C .α,β平行于同一条直线 D .α,β垂直于同一平面 【答案】B【解析】由面面平行的判定定理知:α内两条相交直线都与β平行是αβ∥的充分条件,由面面平行性质定理知,若αβ∥,则α内任意一条直线都与β平行,所以α内两条相交直线都与β平行是αβ∥的必要条件,故选B .【名师点睛】本题考查了空间两个平面的判定与性质及充要条件,渗透直观想象、逻辑推理素养,利用面面平行的判定定理与性质定理即可作出判断.面面平行的判定问题要紧扣面面平行判定定理,最容易犯的错误为定理记不住,凭主观臆断,如:“若,,a b a b αβ⊂⊂∥,则αβ∥”此类的错误.2.【2019年高考全国Ⅲ卷文数】如图,点N 为正方形ABCD 的中心,△ECD 为正三角形,平面ECD ⊥平面ABCD ,M 是线段ED 的中点,则()A .BM =EN ,且直线BM ,EN 是相交直线B .BM ≠EN ,且直线BM ,EN 是相交直线C .BM =EN ,且直线BM ,EN 是异面直线D .BM ≠EN ,且直线BM ,EN 是异面直线【答案】B【解析】如图所示,作EO CD ⊥于O ,连接ON ,BD ,易得直线BM ,EN 是三角形EBD 的中线,是相交直线.过M 作MF OD ⊥于F ,连接BF ,平面CDE ⊥平面ABCD ,,EO CD EO ⊥⊂平面CDE ,EO ∴⊥平面ABCD ,MF ⊥平面ABCD ,MFB ∴△与EON △均为直角三角形.设正方形边长为2,易知3,12EO ON EN ===,,35,,722MF BF BM ==∴=,BM EN ∴≠,故选B .【名师点睛】本题考查空间想象能力和计算能力,解答本题的关键是构造直角三角形.解答本题时,先利用垂直关系,再结合勾股定理进而解决问题.3.【2019年高考江苏卷】如图,长方体1111ABCD A B C D -的体积是120,E 为1CC 的中点,则三棱锥E −BCD的体积是 ▲ .【答案】10【解析】因为长方体1111ABCD A B C D -的体积为120,所以1120AB BC CC ⋅⋅=,因为E 为1CC 的中点,所以112CE CC =,由长方体的性质知1CC ⊥底面ABCD ,所以CE 是三棱锥E BCD -的底面BCD 上的高,所以三棱锥E BCD -的体积1132V AB BC CE =⨯⋅⋅=111111201032212AB BC CC =⨯⋅⋅=⨯=. 【名师点睛】本题蕴含“整体和局部”的对立统一规律.在几何体面积或体积的计算问题中,往往需要注意理清整体和局部的关系,灵活利用“割”与“补”的方法解题.由题意结合几何体的特征和所给几何体的性质可得三棱锥的体积.4.【2019年高考全国Ⅱ卷文数】如图,长方体ABCD –A 1B 1C 1D 1的底面ABCD 是正方形,点E 在棱AA 1上,BE ⊥EC 1.(1)证明:BE ⊥平面EB 1C 1;(2)若AE =A 1E ,AB =3,求四棱锥11E BB C C -的体积. 【答案】(1)见详解;(2)18.【解析】(1)由已知得B 1C 1⊥平面ABB 1A 1,BE ⊂平面ABB 1A 1,故11B C BE ⊥.又1BE EC ⊥,所以BE ⊥平面11EB C . (2)由(1)知∠BEB 1=90°.由题设知Rt △ABE ≌Rt △A 1B 1E , 所以1145AEB A EB ︒∠=∠=,故AE =AB =3,126AA AE ==.作1EF BB ⊥,垂足为F ,则EF ⊥平面11BB C C ,且3EF AB ==. 所以,四棱锥11E BB C C -的体积1363183V =⨯⨯⨯=. 【名师点睛】本题主要考查线面垂直的判定,以及四棱锥的体积的求解,熟记线面垂直的判定定理,以及四棱锥的体积公式即可,属于基础题型.一、考向分析:二、考向讲解考查内容解 题 技 巧 几何 体表 面积 与体 积1、空间几何体表面积的求法(1)以三视图为载体的几何体的表面积问题,关键是分析三视图确定几何体中各元素之间的位置关系及数量。
(完整)立体几何(文科)

立体几何(文科)1、如图1。
4所示四棱锥P。
ABCD中,底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=错误!,M为BC上一点,且BM=错误!.(1)证明:BC⊥平面POM;(2)若MP⊥AP,求四棱锥P。
ABMO的体积.516图42、四面体ABCD及其三视图如图14所示,平行于棱AD,BC的平面分别交四面体的棱AB,BD,DC,CA于点E,F,G,H。
图1。
4(1)求四面体ABCD的体积;错误!.(2)证明:四边形EFGH是矩形.3、如图1。
5,在三棱柱ABC .A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1,BC的中点.图1。
5(1)求证:平面ABE⊥平面B1BCC1;(2)求证:C1F∥平面ABE;(3)求三棱锥E。
ABC的体积.错误!.4、如图1.3,四棱锥P。
ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.(1)证明:PB∥平面AEC;(2)设AP=1,AD=错误!,三棱锥PABD的体积V=错误!,求A到平面PBC的距离.错误!图13。
5、如图16所示,三棱锥A . BCD 中,AB ⊥平面BCD ,CD ⊥BD 。
(1)求证:CD ⊥平面ABD ;(2)若AB =BD =CD =1,M 为AD 中点,求三棱锥A MBC 的体积.错误!图1。
66、如图1。
4所示,△ABC 和△BCD 所在平面互相垂直,且AB =BC =BD =2,∠ABC =∠DBC =120°,E ,F ,G 分别为AC ,DC ,AD 的中点.(1)求证:EF ⊥平面BCG ;(2)求三棱锥D 。
BCG 的体积.错误!。
7、如图, 四棱柱ABCD -A 1B 1C 1D 1的底面ABCD 是正方形, O 为底面中心, A 1O ⊥平面ABCD, 1AB AA ==1A(Ⅰ) 证明: A 1BD // 平面CD 1B 1; (Ⅱ) 求三棱柱ABD -A 1B 1D 1的体积.8、如图,在四棱锥P ABCD -中,PD ABCD ⊥面,//AB DC ,AB AD ⊥,5BC =,3DC =,4AD =,60PAD ∠=。
立体几何文科解答题
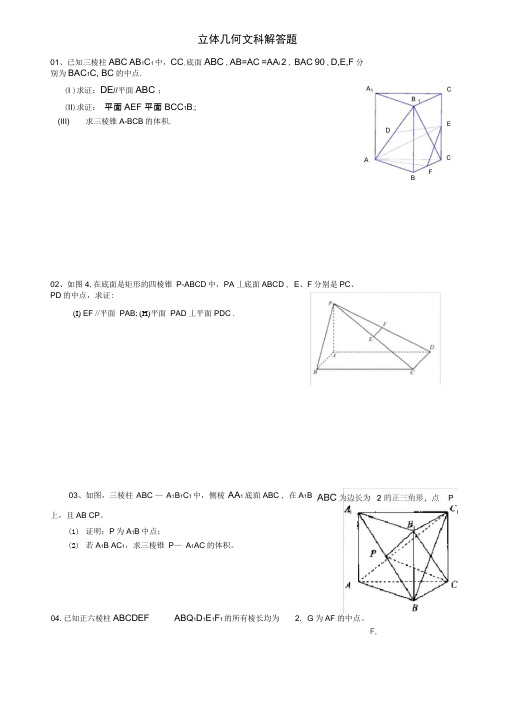
立体几何文科解答题01、已知三棱柱ABC AB1C1 中,CC, 底面ABC , AB=AC =AA i 2 , BAC 90°, D,E,F 分别为BAC1C, BC的中点.(I )求证:DE//平面ABC ;(II)求证:平面AEF 平面BCC1B,;(III) 求三棱锥A-BCB的体积.B 02、如图4,在底面是矩形的四棱锥P-ABCD中,PA丄底面ABCD , E、F分别是PC、PD的中点,求证:(I) EF //平面PAB; (H)平面PAD丄平面PDC .03、如图,三棱柱ABC —A1B1C1中,侧棱AA1 底面ABC , 在A1B上,且AB CP。
(1)证明:P为A1B中点;(2)若A1B AC1,求三棱锥P—A1AC的体积。
04.已知正六棱柱ABCDEF ABQ1D1E1F1的所有棱长均为2, G为AF的中点。
F,(1) 求证:F,G //平面BB.E.E ;(2) 求证:平面F-| AE丄平面DEE1D1;(3) 求四面体EGFF1的体积。
05、如图,(1) 已知求证:06、如图,已知ABCD为矩形,DQ 平面ABCD , AD DD1 1 , AB=2,点E是AB的中点.08、如图,矩形ABCD中,AD 平面ABE , AE BF 平面ACE . (I)求证:AE 平面BCE ;(H)求证;AE //平面BFD ;(川)求三棱锥C BGF的体积.EB BC 2,F为CE上的点,且E C B10、如图所示,在棱长为2的正方体ABCD ABGD i中,E、F分别为DD i、DB的中点.(1)求证:EF //平面ABC i D i ;(2)求证:EF BC ; (3)求三棱锥V B’EFC的体积. C i C11、在直四棱柱ABCD A i B i C i D i 中,AA i 2,底面是边长为1的正方形,E、F分别是棱B i B、DA 的中点.(I )直线BF //平面AD1E ;( n )求证:D1E 面AEC .JLE13、如图,在长方体 ABCD AB i C i D i 中,点E 在棱CC i 的延长线上,且 CC iC i EBC -AB 1 .2(I)求证:D 1E //平面 ACB 1 ; (n)求证:平面 D 1B 1E 平面DCB 1 ;(川)求四面体 D 1B1AC 的体积.丄AP ,垂足为 丘,将厶ADP沿AP 折起•使点D 位于D '位置,连D 'B 、D 'C 得四棱锥D '— ABCP .(I )求证D ' F 丄AP ;(II )若 PD=1并且平面 D ' AP 丄平面ABCP ,求四棱锥 D —ABCP 的体积12、如图6,正方形ABCD 所在平面与三角形 CDE 所在平面 相交于CD , AE 平面CDE ,且AE 3, AB 6 •(1) 求证:AB 平面ADE ; (2) 求凸多面体 ABCDE 的体积.14、已知P 在矩形 ABCD 边DC 上,AB=2 , BC=1 , F 在AB 上且 DFAEAF FBi6、如图,在底面是正方形的四棱锥G为AC上一点.(I)求证:BD丄FG;平面PBD,并说明理由.(II)确定点17 已知直P—ABCD 中,PA丄面ABCD , BD 交AC于点E, F是PC中点, 棱柱ABC A i B i C iACB 90 , AC BC 2, AA i 4。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【考点1】空间角,距离的求法 【备考知识梳理】 1.空间的角(1)异面直线所成的角:如图,已知两条异面直线,a b ,经过空间任一点O 作直线','a a b b .则把'a 与'b 所成的锐角(或直角)叫做异面直线与所成的角(或夹角).异面直线所成的角的范围是0,2π⎛⎤⎥⎝⎦. (2)平面的一条斜线和它在平面内的射影所成的锐角,叫做这条直线和这个平面所成的角.①直线垂直于平面,则它们所成的角是直角;②直线和平面平行,或在平面内,则它们所成的角是0︒的角.直线与平面所成角的范围是0,2π⎡⎤⎢⎥⎣⎦.(3)二面角的平面角:如图在二面角l αβ--的棱上任取一点O ,以点O 为垂足,在半平面α和β内分别作垂直于棱的射线OA 和OB ,则AOB ∠叫做二面角的平面角.二面角的范围是[]0,π.(4)等角定理:如果一个角的两边和另一个角的两边分别平行,并且方向相同,那么这两个角相等. 推论:如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等. 3.空间距离:(1)两条异面直线的距离:两条异面直线的公垂线在这两条异面直线间的线段的长度,叫做两条异面直线的距离;常有求法①先证线段AB 为异面直线b a ,的公垂线段,然后求出AB 的长即可.②找或作出过且与平行的平面,则直线到平面的距离就是异面直线b a ,间的距离.③找或作出分别过b a ,且与,分别平行的平面,则这两平面间的距离就是异面直线b a ,间的距离.(2)点到平面的距离:点P到直线的距离为点P到直线的垂线段的长,常先找或作直线所在平面的垂线,得垂足为A,过A作的垂线,垂足为B连PB,则由三垂线定理可得线段PB即为点P到直线的距离.在直角三角形PAB中求出PB的长即可.常用求法①作出点P到平面的垂线后求出垂线段的长;②转移法,如果平面α的斜线上两点A,B到斜足C的距离AB,AC的比为n m :,则点A,B到平面α的距离之比也为n m :.特别地,AB=AC时,点A,B到平面α的距离相等;③体积法(3)直线与平面的距离:一条直线和一个平面平行,这条直线上任意一点到平面的距离,叫做这条直线和平面的距离;(4)平行平面间的距离:两个平行平面的公垂线段的长度,叫做两个平行平面的距离. 【规律方法技巧】1.空间中各种角包括:异面直线所成的角、直线与平面所成的角以及二面角. (1)异面直线所成的角的范围是]2,0(π.求两条异面直线所成的角的大小一般方法是通过平行移动直线,把异面问题转化为共面问题来解决具体步骤如下:①利用定义构造角,可固定一条,平移另一条,或两条同时平移到某个特殊的位置,顶点选择在特殊的位置上;②证明作出的角即为所求的角;③利用三角形来求角; ④补形法:将空间图形补成熟悉的、完整的几何体,这样有利于找到两条异面直线所成的角θ. (2)直线与平面所成的角的范围是]2,0[π.求线面角方法:①利用面面垂直性质定理,巧定垂足:由面面垂直的性质定理,可以得到线面垂直,这就为线面角中的垂足的确定提供了捷径. ②利用三棱锥的等体积,省去垂足,在构成线面角的直角三角形中,其中垂线段尤为关键.确定垂足,是常规方法.可是如果垂足位置不好确定,此时可以利用求点面距常用方法---等体积法.从而不用确定垂足的位置,照样可以求出线面角.因为垂线段的长度实际就是点面距h,利用三棱锥的等体积,只需求出h ,然后利用斜线段长h =θsin 进行求解.③妙用公式,直接得到线面角 课本习题出现过这个公式:21cos cos cos θθθ=,如图所示:21,,θθθ=∠=∠=∠OBC ABO ABC .其中1θ为直线AB 与平面所成的线面角.这个公式在求解一些选择填空题时,可直接应用.但是一定要注意三个角的位置,不能张冠李戴.(3)确定点的射影位置有以下几种方法:①斜线上任意一点在平面上的射影必在斜线在平面的射影上;②如果一个角所在的平面外一点到角的两边距离相等,那么这一点在平面上的射影在这个角的平分线上;如果一条直线与一个角的两边的夹角相等,那么这一条直线在平面上的射影在这个角的平分线上;③两个平面相互垂直,一个平面上的点在另一个平面上的射影一定落在这两个平面的交线上;④利用某些特殊三棱锥的有关性质,确定顶点在底面上的射影的位置:a.如果侧棱相等或侧棱与底面所成的角相等,那么顶点落在底面上的射影是底面三角形的外心;b. 如果顶点到底面各边距离相等或侧面与底面所成的角相等,那么顶点落在底面上的射影是底面三角形的内心(或旁心);c. 如果侧棱两两垂直或各组对棱互相垂直,那么顶点落在底面上的射影是底面三角形的垂心;(4)二面角的范围[]0,π,解题时要注意图形的位置和题目的要求.求二面角的方法:①直接法.直接法求二面角大小的步骤是:一作(找)、二证、三计算.即先作(找)出表示二面角大小的平面角,并证明这个角就是所求二面角的平面角,然后再计算这个角的大小. 用直接法求二面角的大小,其关键是确定表示二面角大小的平面角.而确定其平面角,可从以下几个方面着手:①利用三垂线定理(或三垂线定理的逆定理)确定平面角,自二面角的一个面上一点向另一面引垂线,再由垂足向棱作垂线得到棱上的点(即垂足),斜足与面上一点连线和斜足与垂足连线所夹的角,即为二面角的平面角;;②利用与二面角的棱垂直的平面确定平面角, 自空间一点作与棱垂直的平面,截二面角得两条射线,这两条射线所成的角就是二面角的平面角;③利用定义确定平面角, 在棱上任取一点,过这点在两个平面内分别引棱的垂线,这两条射线所成的角,就是二面角的平面角;DBA Cα②射影面积法.利用射影面积公式cos θ=S S';此方法常用于无棱二面角大小的计算;对于无棱二面角问题还有一条途径是设法作出它的棱,作法有“平移法”“延伸平面法”等. 【考点针对训练】1. .【2016高考浙江文数】如图,在三棱台ABC-DEF 中,平面BCFE ⊥平面ABC ,∠ACB =90°,BE=EF=FC =1,BC =2,AC =3.(I )求证:BF ⊥平面ACFD ;(II )求直线BD 与平面ACFD 所成角的余弦值.2. 【2016届湖北省武汉市武昌区高三5月调研】如图,PA 垂直圆O 所在的平面,C 是圆O 上的点,Q 是PA 的中点,G 为AOC ∆的重心,AB 是圆O 的直径,且22AB AC ==.(1)求证://QG 平面PBC ; (2)求G 到平面PAC 的距离. 【考点2】立体几何综合问题 【备考知识梳理】空间线、面的平行与垂直的综合考查一直是高考必考热点.归纳起来常见的命题角度有: 以多面体为载体综合考查平行与垂直的证明. 探索性问题中的平行与垂直问题. 折叠问题中的平行与垂直问题. 【考点针对训练】1. 【2016届宁夏高三三轮冲刺】如图,在三棱锥P ABC -中,平面PAC ⊥平面ABC ,PA AC ⊥,AB BC ⊥.设,D E 分别为,PA AC 中点.(1)求证://DE 平面PBC ; (2)求证:BC ⊥平面PAB ;(3)试问在线段AB 上是否存在点F ,使得过三点D ,,E F 的平面内的任一条直线都与平面PBC 平行?若存在,指出点F 的位置并证明;若不存在,请说明理由.2. 【2016届四川南充高中高三4月模拟三】如图,在正方形ABCD 中,点,E F 分别是,AB BC 的中点,将,AED DCF ∆∆分别沿DE 、DF 折起, 使,A C 两点重合于P .(Ⅰ)求证:平面PBD ⊥平面BFDE ; (Ⅱ)求四棱锥P BFDE -的体积. 【应试技巧点拨】 1.如何求线面角(1)利用面面垂直性质定理,巧定垂足:由面面垂直的性质定理,可以得到线面垂直,这就为线面角中的垂足的确定提供了捷径. (2)利用三棱锥的等体积,省去垂足在构成线面角的直角三角形中,其中垂线段尤为关键.确定垂足,是常规方法.可是如果垂足位置不好确定,此时可以利用求点面距常用方法---等体积法.从而不用确定垂足的位置,照样可以求出线面角.因为垂线段的长度实际就是点面距h !利用三棱锥的等体积,只需求出h ,然后利用斜线段长h=θsin 进行求解.(3)妙用公式,直接得到线面角 课本习题出现过这个公式:21cos cos cos θθθ=,如图所示:21,,θθθ=∠=∠=∠OBC ABO ABC .其中1θ为直线AB 与平面所成的线面角.这个公式在求解一些选择填空题时,可直接应用.但是一定要注意三个角的位置,不能张冠李戴. 2.如何求二面角(1)直接法.直接法求二面角大小的步骤是:一作(找)、二证、三计算.即先作(找)出表示二面角大小的平面角,并证明这个角就是所求二面角的平面角,然后再计算这个角的大小. 用直接法求二面角的大小,其关键是确定表示二面角大小的平面角.而确定其平面角,可从以下几个方面着手:①利用三垂线定理(或三垂线定理的逆定理)确定平面角;②利用与二面角的棱垂直的平面确定平面角;③利用定义确定平面角;(2)射影面积法.利用射影面积公式cos θ=S S';此方法常用于无棱二面角大小的计算;对于无棱二面角问题还有一条途径是设法作出它的棱,作法有“平移法”“延伸平面法”等. 3.探索性问题探求某些点的具体位置,使得线面满足平行或垂直关系,是一类逆向思维的题目.一般可采用两个方法:一是先假设存在,再去推理,下结论;二是运用推理证明计算得出结论,或先利用条件特例得出结论,然后再根据条件给出证明或计算.4.在推证线面平行时,一定要强调直线不在平面内,否则,会出现错误.5.在解决直线与平面垂直的问题过程中,要注意直线与平面垂直定义,判定定理和性质定理的联合交替使用,即注意线线垂直和线面垂直的互相转化.6.面面垂直的性质定理是作辅助线的一个重要依据.我们要作一个平面的一条垂线,通常是先找这个平面的一个垂面,在这个垂面中,作交线的垂线即可. 【三年高考】1. 【2016高考新课标1文数】平面α过正文体ABCD —A 1B 1C 1D 1的顶点A ,11//CB D α平面,ABCD m α=平面,11ABB A n α=平面,则m ,n 所成角的正弦值为( )(A )2 (B )2 (C )3(D )132. 【2016高考浙江文数】如图,已知平面四边形ABCD ,AB =BC =3,CD =1,AD ADC =90°.沿直线AC 将△ACD 翻折成△CD 'A ,直线AC 与D 'B 所成角的余弦的最大值是______.3. 【2016高考北京文数】如图,在四棱锥ABCD P -中,⊥PC 平面ABCD ,,AB DC DC AC ⊥∥(I )求证:DC PAC ⊥平面; (II )求证:PAB PAC ⊥平面平面;(III )设点E 为AB 的中点,在棱PB 上是否存在点F ,使得//PA 平面C F E ?说明理由.4. 【2016高考天津文数】如图,四边形ABCD 是平行四边形,平面AED ⊥平面ABCD ,EF||AB ,AB=2,BC=EF=1,DE=3,∠BAD=60º,G 为BC 的中点.(Ⅰ)求证://FG 平面BED ;(Ⅱ)求证:平面BED ⊥平面AED ;(Ⅲ)求直线EF 与平面BED 所成角的正弦值.5. 【2016高考新课标1文数】如图,在已知正三棱锥P -ABC 的侧面是直角三角形,PA =6,顶点P 在平面ABC 内的正投影为点E ,连接PE 并延长交AB 于点G . (I )证明G 是AB 的中点;(II )在答题卡第(18)题图中作出点E 在平面PAC 内的正投影F (说明作法及理由),并求四面体PDEF 的体积.PABD CGE6. 【2015高考浙江,文7】如图,斜线段AB 与平面α所成的角为60,B 为斜足,平面α上的动点P 满足30∠PAB =,则点P 的轨迹是( )A .直线B .抛物线C .椭圆D .双曲线的一支7.【2015高考福建,文20】如图,AB 是圆O 的直径,点C 是圆O 上异于,A B 的点,PO 垂直于圆O 所在的平面,且1PO =OB =.(Ⅰ)若D 为线段AC 的中点,求证C A ⊥平面D P O ; (Ⅱ)求三棱锥P ABC -体积的最大值;(Ⅲ)若BC =E 在线段PB 上,求CE OE +的最小值.8.【2015高考四川,文18】一个正方体的平面展开图及该正方体的直观图的示意图如图所示. (Ⅰ)请按字母F ,G ,H 标记在正方体相应地顶点处(不需要说明理由) (Ⅱ)判断平面BEG 与平面ACH 的位置关系.并说明你的结论. (Ⅲ)证明:直线DF ⊥平面BEGAB FHED C G CD EAB9.【2015高考重庆,文20】如题(20)图,三棱锥P-ABC 中,平面PAC ⊥平面ABC ,∠ABC=2π,点D 、E 在线段AC 上,且AD=DE=EC=2,PD=PC=4,点F 在线段AB 上,且EF//BC. (Ⅰ)证明:AB ⊥平面PFE.(Ⅱ)若四棱锥P-DFBC 的体积为7,求线段BC 的长.题(20)图AC10. 【2014高考重庆文第20题】如题(20)图,四棱锥P ABCD -中,底面是以O 为中心的菱形,PO ⊥底面ABCD ,2,3AB BAD π=∠=,M 为BC 上一点,且12BM=. (Ⅰ)证明:BC⊥平面POM ;(Ⅱ)若MP AP ⊥,求四棱锥P ABMO -的体积.11. 【2014高考全国1文第19题】如图,三棱柱111C B A ABC -中,侧面C C BB 11为菱形,C B 1的中点为O ,且⊥AO 平面C C BB 11. (1)证明:;1AB C B ⊥(2)若1AB AC ⊥,,1,601==∠BC CBB求三棱柱111C B A ABC -的高.12.【2014高考江西文第19题】如图,三棱柱111C B A ABC -中,111,BB B A BC AA ⊥⊥. (1)求证:111CC C A ⊥;(2)若7,3,2===BC AC AB ,问1AA 为何值时,三棱柱111C B A ABC -体积最大,并求此最大值.【一年原创真预测】1.已知AB ⊥平面ACD ,DE ⊥平面ACD ,ACD ∆为等边三角形,22AD DE AB ===,F 为CD 的中点.(Ⅰ)求证:平面平面BCE DCE ⊥; (Ⅱ)求B CDE 点到平面的距离.2.如图,直三棱柱111ABC A B C -中,底面ABC △是等腰直角三角形,且AB CB ==,且AA 1=3,D 为11AC 的中点,F 在线段1AA 上,设11A F tAA =(102t <<),设11=B C BC M .MFDC 1B 1A 1CBA(Ⅰ)当取何值时,CF ⊥平面1B DF ;(Ⅱ)在(Ⅰ)的条件下,求四面体1F B DM -的体积.3.如图,三棱锥P ABC -中,BC ⊥平面PAB ,PA PB AB BC 6====,点M ,N 分别为PB,BC 的中点.(I )求证:AM ⊥平面PBC ; (Ⅱ)E 是线段AC 上的点,且AM 平面PNE .①确定点E 的位置;②求直线PE 与平面PAB 所成角的正切值.4.如图,在直角三角形ABC 中,∠BAC=60°,点F 在斜边AB 上,且AB=4AF ,D ,E 是平面ABC 同一侧的两点,AD ⊥平面ABC ,BE ⊥平面ABC ,AD=3,AC=BE=4.(Ⅰ)求证:CD ⊥EF ;(Ⅱ)若点M 是线段BC 的中点,求点M 到平面EFC 的距离.5. 如图所示,在边长为12的正方形11ADD A 中,点,B C 在线段AD 上,且3,4AB BC ==,作11//BB AA ,分别交111,A D AD 于点1B ,P .作11//CC AA ,分别交111,A D AD 于点1C ,Q .将该正方形沿11,BB CC 折叠,使得1DD 与1AA 重合,构成如图的三棱柱111ABC A B C -.(1)求证:AB ⊥平面11BCC B ; (2)求四棱锥A BCQP -的体积.【考点1针对训练】 1.2.【考点2针对训练】 1.又因为EF ⊄平面PBC ,BC ⊂平面PBC ,所以//EF PBC .又因为DE EF E =,所以平面//DEF 平面PBC ,所以平面DEF 内的任一条直线都与平面PBC 平行.2.【三年高考】 1. 【答案】A//',//'m m n n ,则,m n 所成的角等于','m n 所成的角.延长AD ,过1D 作11//D E B C ,连接11,CE B D ,则CE 为'm ,同理11B F 为'n ,而111//,//BD CE B F A B ,则','m n 所成的角即为1,A B BD 所成的角,即为60 ,故,m n所成角的正弦值为2,故选A. 2.3. 【解析】(I )因为C P ⊥平面CD AB ,所以C DC P ⊥.又因为DC C ⊥A ,所以DC ⊥平面C PA . (II )因为//DC AB ,DC C ⊥A ,所以C AB ⊥A .因为C P ⊥平面CD AB ,所以C P ⊥AB .所以AB ⊥平面C PA .所以平面PAB ⊥平面C PA .(III )棱PB 上存在点,使得//PA 平面C F E .证明如下:取PB 中点,连结F E ,C E ,CF .又因为E 为AB 的中点,所以F//E PA .又因为PA ⊄平面CF E ,所以//PA 平面C F E .4.5.6. 【答案】C【解析】由题可知,当点运动时,在空间中,满足条件的AP绕AB旋转形成一个圆锥,用一个与圆锥高成60角的平面截圆锥,所得图形为椭圆.故选C.7.解法二:(I)、(II)同解法一.8.【解析】(Ⅰ)点F ,G ,H 的位置如图所示9.【解析】如题(20)图.由,DE EC PD PC ==知,E 为等腰PDC D 中DC 边的中点,故PE AC ^,又平面PAC ⊥平面ABC ,平面PAC 平面ABC AC =,PE Ì平面PAC ,PE AC ^,所以PE ^平面ABC ,从而PE AB ^.因ABC=,,AB EF 2EF BC p衈故. 从而AB 与平面PFE 内两条相交直线PE ,EF 都垂直,所以AB ^平面PFE .(2)解:设BC=x ,则在直角ABC D中,从而11S AB BC=22ABC D =?由EFBC ,知23AF AE AB AC ==,得AEF ABC DD ,故224()S 39AEF ABC S D D ==,即4S 9AEF ABC S D D =.FCDEAB GHO由1AD=2AE ,11421S S =S S 22999AFB AFE ABC ABC D D D D =?=从而四边形DFBC 的面积为DFBC11S S -=29ABC ADF S D D =718=(1)知,PE PE ^平面ABC ,所以PE 为四棱锥P-DFBC 的高.在直角PEC D 中,=体积DFBC 117S 73318P DFBC V PE -=鬃=?,故得42362430x x -+=,解得2297x x ==或,由于0x >,可得3x x ==或.所以3BC =或BC =10.11.12.【解析】(1)证明:由1AA BC ⊥知1BB BC ⊥,又11BB A B ⊥,故1BB ⊥平面1,BCA 即11BB AC ⊥,又11//BB CC ,所以11.AC CC ⊥(2)设1,AA x =在11Rt A BB ∆中1BA同理1AC 在1A BC ∆中,2222111111cos 2A B AC BC BAC BAC A B AC +-∠==∠=⋅11111sin 2A BCS A B A C BA C ∆=⋅∠=从而三棱柱111ABC A B C -的体积为11133A BC V BB S ∆=⨯⨯=因=故当x =时,即1AA =时,体积V取到最大值【一年原创真预测】1.【解析】(Ⅰ)DE ⊥平面ACD ,F A ⊂平面CD A ∴DE AF ⊥,又等边三角形ACD 中AF CD ⊥, D CD D E =,D E ⊂平面CD E ,CD ⊂平面CD E ,∴平面AF ECD ⊥,取CE 的中点M ,连接BM,MF ,则MF 为△CDE 的中位线,故1////,2MF DE AB MF DE AB ==,所以四边形ABMF 为平行四边形,即MB//AF,MB⊂平面C B E ,F A ⊄平面C B E ,//BCE 平面AF ∴,平面平面BCE DCE ∴⊥.(Ⅱ)因为AB ⊥平面ACD ,DE ⊥平面ACD ,所以AB //DE ,故AB //平面DCE ,B CDE 点到平面的距离h 等于A CDE 点到平面的距离d ,由体积相等A DCE E ACD V V --=得,1133DCE ADC S d S DE ∆∆⋅=⨯,011112222sin 6023232d ⋅⨯⨯⋅=⨯⨯⨯⨯,解得h d ==.2.(Ⅱ)由已知得111111==22F B DM M B DF C B DF B CDF V V V V ----=,因为FD FC 1=22CDF S DF FC ⋅=△,由(Ⅰ)得1B D ⊥平面DFC ,故112=21=33B CDF V -⨯⨯,故1F B DM -的体积为13.3.②作EH AB ⊥于H ,则EH //BC ,∴EH ⊥平面PAB ,∴EPH ∠是直线PE 与平面PAB 所成的角.∵1AH AB 23==,π6=3PA PAH =∠, ∴PH ==1EH BC 23==,∴EH tan EPH PH 7∠==,即直线PE 与平面PAB 所成角的正切值为7.4.5.。
