2020高三数学立体几何专项训练文科
2020年高考文科数学《立体几何》题型归纳与训练

2020年高考文科数学《立体几何》题型归纳与训练【题型归纳】题型一立体几何证明例1如图五面体中,四边形ABCD是矩形,AD⊥面ABEF,AB//EF,AD=1,AB=1EF=22,2AF=BE=2,P、Q、M分别为AE、BD、EF的中点.(1)求证:PQ//面BCE;(2)求证:AM⊥面ADF.【答案】见解析【解析】(1)连结AC.因为四边形ABCD是矩形,且Q为BD的中点,所以Q为AC的中点.又因为P为AE的中点,所以PQ//EC,又因为PQ⊄面BCE,EC⊆面BCE,所以PQ//面BCE.(2)取EF的中点M,连结AM.因为AB//EM,且QB=EM=22,所以四边形ABEM为平行四边形,所以AM//BE,且AM=BE=2.在∆AMF中,A M=AF=2,MF=22.所以AM2+AF2=MF2,故AM⊥AF.由AD⊥面ABEF,得AD⊥AM,因为AD I AF=A,所以AM⊥面ADF.【易错点】定理证明所用知识点不清楚【思维点拨】证明几何体中的线面平行与垂直关系时,要注意灵活利用空间几何体的结构特征,抓住其中的平行与垂直关系.如该题中的(1)问需要利用五面体中的面ABCD是矩形,根据对角线的性质确定线段BD与AC的中点.(2)问中利用勾股定理验证线线垂直关系,这些都是证明空间平行与垂直关系的基础.例2在平行六面体ABCD-A B C D中,AA=AB,AB⊥B C.11111111A 1D1B1C1A DBC求证:(1)AB∥平面A B C;11(2)平面ABB A⊥平面A BC.111【答案】见解析【解析】(1)在平行六面体ABCD-A B C D中,AB∥A B.111111因为AB⊄平面A B C,A B⊂平面A B C,所以AB∥平面A B C.11111111A 1D1B1C1A DBC(2)在平行六面体ABCD-A B C D中,四边形ABB A为平行四边形.111111又因为AA=AB,所以四边形ABB A为菱形,因此AB⊥A B.11111又因为AB⊥B C,BC∥B C,所以AB⊥BC.111111又因为A B I BC=B,A B⊂平面A BC,BC⊂平面A BC,所以AB⊥平面A BC.111111因为AB⊂平面ABB A,所以平面ABB A⊥平面A BC.111111【易错点】定理证明所用知识点不清楚【思维点拨】证明几何体中的线面平行与垂直关系时,要注意灵活利用空间几何体的结构特征,抓住其中的平行与垂直关系.2(题型二 立体几何体积求解例 1 如图所示,在三棱锥V - ABC 中,平面VAB ⊥ 平面 ABC ,三角形VAB 为等边三角形, AC ⊥ BC ,且 AC = BC = 2 , O , M 分别为 AB ,V A 的中点.(1)求证:VB // 平面 MOC .V(2)求证:平面 MOC ⊥ 平面 VAB .M(3)求三棱锥V - ABC 的体积.AO BC【答案】 见解析【解析】(1)依题意, O , M 分别为 AB ,V A 的中点,则 O M 是 △VAB 的中位线,所以 OM //VB , OM ⊂ 平面 MOC ,VB ⊄ 平面 MOC ,故VB // 平面 MOC .(2)因为在 △ABC 中, AC = BC ,且 O 为 AB 的中点,所以 O C ⊥ AB ,又平面VAB ⊥ 平面 ABC ,平面VAB I 平面 ABC = AB , OC ⊂ 平面 ABC ,所以 OC ⊥ 平面VAB ,又 OC ⊂ 平面 MOC ,故平面 MOC ⊥ 平面VAB .(3)由(2)知, O C ⊥ 平面VAB ,所以V V - ABC= V C -VAB 1 1 3 3= ⋅ OC = ⨯ ⨯ 22 ⨯1 =3 △SVAB 3 4 3【易错点】定理证明所用知识点不清楚【思维点拨】证明几何体中的线面平行与垂直关系时,要注意灵活利用空间几何体的结构特征,抓住其中的平行与垂直关系.例 2 如图所示,在三棱锥 P – ABC 中, P A ⊥ AB , P A ⊥ BC , AB ⊥ BC , P A = AB = BC = 2 , D 为线段 AC 的中点, E 为线段 PC 上一点.(1)求证: P A ⊥ BD ;P(2)求证:平面 BDE ⊥ 平面 PAC ;ED C(3)当 P A // 平面 BDE 时,求三棱锥 E – BCD 的体积.AB【答案】 见解析 【解析】1)因为 P A ⊥ AB ,P A ⊥ BC ,AB I BC = B ,所以 P A ⊥ 平面 ABC .又因为 BD ⊂ 平面 ABC ,所以 PA ⊥ BD .(2)因为 AB ⊥ BC , AB = BC , D 为线段 AC 的中点,所以在等腰 △RtABC 中, BD ⊥ AC .又由(1)可知,P A ⊥ BD ,P A I AC = A ,所以 BD ⊥ 平面 PAC .由 E 为线段 PC 上一点,则 DE ⊂ 平面 PAC ,所以BD⊥ED.又因为BD⊂平面BDE,所以平面BDE⊥平面PAC.(3)当P A//平面BDE时,P A⊂平面PAC,且平面PAC I平面BDE=DE,可得P A//DE.由D是AC边的中点知,E为PC边的中点.故而ED=面BDC.12P A=1,ED∥P A,因为PA⊥平面ABC,所以ED⊥平由AB=BC=2,AB⊥BC,D为AC边中点知,BD=CD= 2.又BD⊥AC,有BD⊥DC,即∠BDC=90︒.因此,VE-BCD1111 =⋅ED=⨯⨯2⨯2⨯1=.3△SBCD323【易错点】注意体积几何证明题条件的严谨性【思维点拨】证明几何体中的线面平行与垂直关系时,要注意灵活利用空间几何体的结构特征,抓住其中的平行与垂直关系.掌握线面平行的性质定理的应用及其体积的求解方法.题型三几何体的外接球问题例1(1)已知各顶点都在同一球面上的正四棱柱的高为4,体积为16,则这个球的表面积是()A.16πB.20πC.24πD.32π(2)若三棱锥的三个侧面两垂直,且侧棱长均为3,则其外接球的表面积是.【答案】C;9π【解析】(1)V=a2h=16,a=2,4R2=a2+a2+h2=4+4+16=24,S=24π,选C;(2)4R2=3+3+3=9,S=4πR2=9π【易错点】外接球球心位置不好找【思维点拨】应用补形法找外接球球心的位置题型四立体几何的计算例1如图,已知三棱锥的底面是直角三角形,直角边边长分别为3和4,过直角顶点的侧棱长为4,且垂直于底面,该三棱锥的主视图是()【答案】B4, 【解析】显然由空间直角坐标系可知,该几何体在 xoy 面内的点保持不动,在 y 轴上的点在 xoy 面内的射影为坐标原点,所以该几何体的主视图就是其在面 xoy 面的表面图形,即主视图应为高为 4 ,底面边长为 3 的直角三角形.故选 B .【易错点】 该题易出现的问题是误以为 y 轴上的点在 xoy 面的射影落在 x 轴的正半轴上而误选 D , 【思维点拨】判断几何体的三视图应注意以下几个方面:(1)明确几何体的放置位置和角度,注意投影线和投影面;(2)准确把握几何体的结构特征,特别是几何体中的线面垂直关系等;(3)注意实线和虚线的区别.【巩固训练】题型一 立体几何的证明1.如图,在四棱锥 P - ABCD 中,底面 ABCD 为菱形, ∠BAD = 60° P A = PD = AD = 2 ,点 M 在线段PC 上,且 PM = 2MC , N 为 AD 的中点.(1)求证: AD ⊥ 平面 PNB ;(2)若平面 P AD ⊥ 平面 ABCD ,求三棱锥 P - NBM 的体积.【答案】(1)见解析;(2)23.【解析】(1)∵ P A = PD, N 为 AD 的中点,∴ PN ⊥ AD ,∵底面 ABCD 为菱形, ∠BAD = 60︒ ,∴ BN ⊥ AD ,∵ PN I BN = N ,∴ AD ⊥ 平面 PNB .(2)∵ PN = PD = AD = 2 ,∴ PN = NB = 3 ,∵平面 P AD ⊥ 平面 ABCD ,平面 P AD I 平面 ABCD = AD , PN ⊥ AD ,∴ PN ⊥ 平面 ABCD ,∴ PN ⊥ NB ,∴S3⨯3⨯3=. 22∵AD⊥平面PNB,AD//BC,∴BC⊥平面PNB.∵PM=2MC,∴VP-NRM =VM-PNB22132=V=⨯⨯⨯2=.3C-PNB33232.如图,在直三棱柱ABC-A B C中,D是AB的中点.111(1)证明:BC//平面A CD;11(2)若AC=CB,求证:A D⊥CD.1【答案】见解析.【解析】证明:(1)如图,连接AC,交A C于点O,连结OD.11据直三棱柱性质知四边形ACC A为平行四边形,所以O为AC的中点.111又因为D是AB的中点,所以BC//OD.1又因为BC⊄平面A CD,OD⊂平面A CD,111所以BC//平面A CD.11(2)因为AC=BC,D为AB的中点,所以CD⊥AB.据直三棱柱ABC-A B C性质知AA⊥平面ABC,又因为C D⊂平面1111所以AA⊥CD.1又因为AA I AB=A,AA,AB⊂平面ABB A,1111所以CD⊥平面ABB A,11又因为A D⊂平面ABB A,所以C D⊥A D,即A D⊥CD.11111ABC,题型二立体几何体积求解1.如图所示,四棱锥P-ABCD中,P A⊥底面ABCD,AD//BC,AB=AD=AC=3,P A=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.(1)证明MN//平面PAB;P6NA MB DC【答案】(1)(2) N -BCM 2 3 63 .AD = BC = 所以V △S ABC = ⨯ 4 ⨯ 2 5 = 2 3 6 3 . 1 2 ⨯ (2 + 4)(2)求四面体 N - BCM 的体积.1 1 14 5V = ⨯ P A ⋅= ⨯ 4 ⨯ 2 5 =△S ABC【解析】(1)取 PB 中点 Q ,连接 AQ 、 NQ ,因为 N 是 PC 中点, NQ //BC ,且 NQ = 1BC ,又2AM = 2 2 ⨯ 3 1 BC ,且 AM // BC ,所以 QN // AM ,且3 34 2QN = AM ,所以四边形 AQNM 是平行四边形.所以 MN // AQ .又 MN ⊄ 平面PAB , AQ ⊂ 平面 PAB ,所以 MN // 平面 PAB .PQ NAMD(2)由(1) QN // 平面 ABCD .BC所以VN -BCM= VQ -BCM1 = V2 P -BCM 1= V 2 P -BCA.N -BCM1 1 14 5 = ⨯ P A ⋅2.如图所示,四棱锥 P - ABCD 中,侧面 P AD 为等边三角形且垂直于底面 ABCD , PAB = BC = 1AD , ∠BAD = ∠ABC = 90o .2(1)证明:直线 BC // 平面 P AD ;(2)若 △PCD 面积为 2 7 ,求四棱锥 P - ABCD 的体积.【答案】(1)(2) V = ⨯⨯ 2 3 = 4 3 .32BACD【解析】(1)在平面 ABCD 内,因为 ∠BAD = ∠ABC = 90o ,所以 BC //AD .又 BC ⊄ 平面 P AD , AD ⊂ 平面 P AD ,故 BC // 平面 P AD .(2)取 AD 的中点 M ,联结 PM , CM .由 AB = BC = 1AD ,及 BC //AD , ∠ABC = 90o ,得四边形 ABCM 为正方形,则 CM ⊥ AD .2因为侧面 P AD 是等边三角形且垂直于底面 ABCD ,平面 P AD I 平面 ABCD = AD ,所以 PM ⊥ AD ,因为PM ⊂ 平面 P AD ,所以 PM ⊥ 平面 ABCD .因为 CM ⊂ 平面 ABCD ,所以 PM ⊥ CM .因为 △PCD 的面积为 2 7 ,所以 ⨯ 2x ⨯ 1 2 ⨯ (2 + 4)设 BC = x ,则 CM = x , CD = 2 x , PM = 3x , PC = PD = 2x .取 CD 的中点 N ,联结 PN ,则 PN ⊥ CD ,所以 PN =14 x .21 142 2x = 2 7 ,解得 x = -2 (舍去), x = 2 ,于是 AB = BC = 2 ,AD = 4 , PM = 2 3 .所以四棱锥 P - ABCD 的体积V = ⨯3 2⨯ 2 3 = 4 3 .题型三 几何体的外接球问题1. 在正三棱锥 S - ABC 中, M 、N 分别是棱 SC 、BC 的中点,且 AM ⊥ MN ,若侧棱 SA = 2 3 ,则正三棱锥 S - ABC 外接球的表面积是.【答案】 36π【解析】正三棱锥的对棱互垂直。
2020年高考文科数学原创专题卷:《立体几何》

原创文科数学专题卷专题立体几何考点32:空间几何体的结构特征、三视图、直观图,表面积和体积(1-8题,13-15题,17-22题)考点33:空间点、线、面的位置关系(9,10题)考点34:直线、平面平行的判定与性质(16,20题)考点35:直线、平面垂直的判定与性质(17-19,21,22题)考点36:异面直线所成的角,点到平面的距离(11,12题)考试时间:120分钟满分:150分说明:请将选择题正确答案填写在答题卡上,主观题写在答题纸上第I卷(选择题)一、选择题(本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是最符合题目要求的。
)1.【来源】2017届湖南省衡阳市高三上学期期末考试考点32易若正三棱锥的正视图与俯视图如下图所示,则它的侧视图的面积为()A. B. C. D.2.【2017课标3,理8】考点32 中难已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为()A.πB.3π4C.π2D.π43.【2017课标1,理7】考点32 中难某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形,这些梯形的面积之和为()A.10 B.12 C.14 D.164.【2017课标II,理4】考点32 中难如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分所得,则该几何体的体积为()A.90π B.63π C.42π D.36π5.【来源】2017届山西省五校联考考点32中难某几何体的三视图如图所示,则该几何体的表面积为()A. B. C. D. 6.【来源】2017届河北省衡水中学高三上学期六调考点32难如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体最长的棱长等于()A.B.C.D.7.【来源】2017届湖南长沙雅礼中学高三月考四 考点32 难如图,正方体1111D C B A ABCD -的棱长为3,以顶点A 为球心,2为半径作一个球,则图中球面与正方体的表面相交得到的两段弧长之和等于( )A .65π B .32π C. π D .67π8.【来源】2015仿照新课标卷一 冲刺卷数学1试卷 考点32 难. 已知几何体的三视图(单位:cm )如图所示,22222222俯视图侧视图正视图则该几何体的内切球的半径为( )A. 2B. 3C. 3D. 31+9.【来源】2016届浙江省宁波市高三上学期期末考试数学试卷 考点33易 已知m,n 是两条不同的直线,是三个不同平面,下列命题中正确的是( )A. 若,,则B. 若,,则C. 若,,则D. 若,,则 10.【来源】2016届浙江省宁波市高三上学期期末考试 考点33 难 如图,在正方形ABCD 中,点E,F 分别为边BC,AD 的中点,将沿BF 所在直线进行翻折,将沿DE 所在直线进行翻折,在翻折过程中( )A. 点A 与点C 在某一位置可能重合B. 点A 与点C 的最大距离为C. 直线AB 与直线CD 可能垂直D. 直线AF 与直线CE 可能垂直 11.【2017课标II 】 考点36 易已知直三棱柱111C C AB -A B 中,C 120∠AB =o ,2AB =,1C CC 1B ==,则异面直线1AB 与1C B 所成角的余弦值为( )A .32 B .155 C .105D .33 12.【来源】2012-2013学年福建省师大附中高二上学期期末考试 考点36 中难 如图,已知正方形ABCD 的边长为4,EF 、分别是AB AD 、的中点,GC ⊥平面ABCD ,且2GC =,则点B 到平面EFG 的距离为 ( )A .1010 B .11112 C .53 D .1 第Ⅱ卷(非选择题) 二.填空题(每题5分,共20分) 13.【2017山东,理13】考点32 易由一个长方体和两个14圆柱体构成的几何体的三视图如右图,则该几何体的体积为 .14.【来源】2016-2017学年江苏扬州中学高二上开学考试 考点32 中难在棱长为1的正方体1111ABCD A B C D -中,E 为1AB 的中点,在面ABCD 中取一点F ,使1EF FC +最小,则最小值为__________. 15.【2017课标1,理16】考点32 难如图,圆形纸片的圆心为O ,半径为5 cm ,该纸片上的等边三角形ABC 的中心为O .D 、E 、F 为圆O 上的点,△DBC ,△ECA ,△FAB 分别是以BC ,CA ,AB 为底边的等腰三角形.沿虚线剪开后,分别以BC ,CA ,AB 为折痕折起△DBC ,△ECA ,△FAB ,使得D 、E 、F 重合,得到三棱锥.当△ABC 的边长变化时,所得三棱锥体积(单位:cm 3)的最大值为_______.16.【来源】2017届安徽师大附中学高三上学期期中 考点34 难正方体1111ABCD A B C D -中,E 是棱1CC 的中点,F 是侧面11BCC B 内的动点,且1//A F 平面1D AE ,若正方体1111ABCD A B C D -的棱长是2,则F 的轨迹被正方形11BCC B 截得的线段长是________.三.解答题(共70分) 17.(本小题满分10分)【来源】2017届广东省高三上学期阶段性测评一 考点32 考点35 易 如图,三棱锥P ABC -中,PA PC =,底面ABC 为正三角形.(Ⅰ)证明:AC PB ⊥;(Ⅱ)若平面PAC ABC ⊥平面,2AB =,PA PC ⊥,求三棱锥P ABC -的体积. 18.(本小题满分12分)【来源】2016-2017学年河北枣强中学高二12月月考 考点32 考点35 中难 菱形ABCD 的边长为3,AC 与BD 交于O ,且60BAD ∠=,将菱形ABCD 沿对角线AC 折起得到三棱锥B ADC -(如图),点M 是棱BC 的中点,322DM =. (1)求证:平面ABC ⊥平面MDO ; (2)求三棱锥M ABD -的体积.19(12分)【来源】2017年高考全国卷1考点32 考点35 中难 如图,在四棱锥P-ABCD 中,AB//CD ,且90BAP CDP ∠=∠=o(1)证明:平面PAB ⊥平面PAD ;(2)若PA =PD =AB =DC ,90APD ∠=o,且四棱锥P-ABCD 的体积为83,求该四棱锥的侧面积. 20.【来源】2017年高考全国卷2 考点32 考点34 中难如图,四棱锥P-ABCD 中,侧面PAD 为等边三角形且垂直于底面ABCD ,AB=BC=12AD, ∠BAD=∠ABC=90°。
2020衡水名师文科数学专题卷:专题十一《立体几何》

2020衡水名师原创文科数学专题卷专题十一立体几何考点32:空间几何体的结构特征、三视图、直观图,表面积和体积(1-8题,13-15题,17-22题)考点33:空间点、线、面的位置关系(9,10题)考点34:直线、平面平行的判定与性质(16,20题)考点35:直线、平面垂直的判定与性质(17-19,21,22题)考点36:异面直线所成的角,点到平面的距离(11,12题)考试时间:120分钟满分:150分说明:请将选择题正确答案填写在答题卡上,主观题写在答题纸上1、已知图中的网格是由边长为12的小正方形组成的,一个几何体的三视图如图中的粗实线所示,则这个几何体的体积为()A.8 B.83C.163D.6432、某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:3cm)是( )A. 2B. 4C. 6D. 83、已知某几何体的三视图如图所示,则该几何体的体积为( )A.8B.12C.16D.244、某空间几何体的三视图如图所示,则该几何体的体积为()A.563B.568π3-C.643D.648π3-5、《九章算术》中将底面为长方形,且有一条侧棱与底面垂直的四棱锥称之为“阳马”. 现有一阳马,其正视图和侧视图是如图所示的直角三角形.若该阳马的顶点都在同一个球面上,则该球的体积为()A B .3C .D .24π 6、一个几何体的三视图如图所示,则此几何体的侧面积为( )A.48B.64C.80D.1207、已知水平放置的ABC △,按“斜二测画法”得到如图所示的直观图A B C '''△,其中''''1,''B O O C A O ===那么原ABC △的面积是( )A .BCD 8、《九章算术》是我国古代数学名著,在《九章算术》中将底面为矩形且有一侧棱垂直于底面的四棱锥称为“阳马”,若某阳马”的三视图如图所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,则该“阳马”的表面积为( )A. 1+B. 1+C. 2D. 2+9、平面内的一条直线将平面分成2部分,两条相交直线将平面分成4部分,三条两两相交且不共点的直线将平面分成7部分,…,则平面内六条两两相交且任意三条不共点的直线将平面分成的部分数为( )A .16B .20C .21D .2210、用符号表示“点A 在直线l 上,l 在平面α外”,正确的是( )A.,A l l α∈⊄B.,A l l α∈∉C.,A l l α⊂⊄D.,A l l α⊂∉11、一个正方体纸盒展开后如图所示,在原正方体纸盒中有下列结论:①AB EF ⊥;②AB 与CM 所成的角为60︒;③EF 与MN 是异面直线;④//MN CD .其中正确的是( )A.①②B.③④C.②③D.①③12、如图,在三棱锥—S ABC 中,SA 丄平面,32ABC SA AC AB BC ==,,丄,点P 是SC 的中点,则异面直线SA 与PB 所成角的正弦值为( )B. 313C. 13 13、一个圆柱和一个圆锥的轴截面分别是边长为a 的正方形和边长为a 的正三角形,则它们的表面积之比为__________.14、一个水平放置的三角形的斜二侧直观图是等腰直角三角形'''A B O ,若''1O B =,那么原△ABO 的面积是_______________.15、已知某三棱锥的三视图(单位:cm )如图所示,则该三棱锥的体积等于_____3cm .16、如图三棱柱'''ABC A B C -中,D 是BC 上一点,满足'//A B 面'AC D ,则D 是BC 的_____.17、如图,在以,,,,,A B C D E F 为顶点的多面体中,AF ⊥平面,//,//,ABCD DE AF AD BC AB CD =,60ABC ∠=︒,22BC AD ==.1.请在图中作出平面DEG ,使得//BF 平面DEG ,并说明理由;2.证明:AC ⊥平面ABF .18、如图,在四棱锥ABCD P -中,底面ABCD 是菱形,PA ⊥平面ABCD ,AB AC PA ==,F E ,分别是PD CD 、的中点.1.求证:CD ⊥平面PAE ;2.求异面直线AF 和PE 与所成角的余弦值。
2020版江苏省高考文科数学三轮复习 解析几何、立体几何精选试题(6页)

小题专题练(四)解析几何、立体几何(建议用时:50分钟)1.抛物线y2=4x的准线方程为________.2.已知双曲线x2a2-y23=1(a>0)的离心率为2,则a=________.3.一个六棱锥的体积为23,其底面是边长为2的正六边形,侧棱长都相等,则该六棱锥的侧面积为________.4.(2019·连云港调研)已知圆C:(x-3)2+(y-5)2=5,直线l过圆心且交圆C于A,B两点,交y轴于P点,若2P A→=PB→,则直线l的斜率k=________.5.如图,60°的二面角的棱上有A,B两点,直线AC,BD分别在这个二面角的两个半平面内,且都垂直于AB,已知AB=4,AC=6,BD=8,则CD 的长为________.6.已知圆C1:(x-2)2+(y-3)2=1,圆C2:(x-3)2+(y-4)2=9,M,N分别是圆C1,C2上的动点,P为x轴上的动点,则|PM|+|PN|的最小值为________.7.(2019·徐州调研)在三棱柱ABC-A1B1C1中,侧棱AA1与侧面BCC1B1的距离为2,侧面BCC1B1的面积为4,则此三棱柱ABC-A1B1C1的体积为________.8.已知圆C1:x2+(y-2)2=4,抛物线C2:y2=2px(p>0),C1与C2相交于A,B两点,|AB|=855,则抛物线C2的方程为____________.9.如图,在直角梯形ABCD中,BC⊥DC,AE⊥DC,M,N分别是AD,BE的中点,将△ADE沿AE折起,则下列说法正确的是________.(填上所有正确说法的序号)①不论D 折至何位置(不在平面ABC 内)都有MN ∥平面DEC ;②不论D 折至何位置都有MN ⊥AE ;③不论D 折至何位置(不在平面ABC 内)都有MN ∥AB ;④在折起过程中,一定存在某个位置,使EC ⊥AD .10.已知O 为坐标原点,过双曲线x 2-y 2b 2=1(b >0)上的点P (1,0)作两条渐近线的平行线,分别交两渐近线于A ,B 两点,若平行四边形OBP A 的面积为1,则双曲线的离心率为________.11.(2019·盐城模拟)已知圆C :(x -3)2+(y -4)2=1和两点A (-m ,0)、B (m ,0)(m >0),若圆上存在一点P ,使得∠APB =90°,则m 的最小值为________.12.已知半径为1的球O 中内接一个圆柱,当圆柱的侧面积最大时,球的体积与圆柱的体积的比值为________.13.(2019·宿迁质检)已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的左右焦点为F 1,F 2,若椭圆C 上恰好有6个不同的点P ,使得△F 1F 2P 为等腰三角形,则椭圆C 的离心率的取值范围是________.14.如图,椭圆C :x 2a 2+y 24=1(a >2),圆O :x 2+y 2=a 2+4,椭圆C 的左、右焦点分别为F 1,F 2,过椭圆上一点P 和原点O 作直线l 交圆O 于M ,N 两点,若|PF 1|·|PF 2|=6,则|PM |·|PN |的值为________.小题专题练(四)1.解析:易知抛物线y 2=4x 的准线方程为x =-p 2=-1.答案:x =-12.解析:因为c 2=a 2+3,所以e =c a =a 2+3a2=2,得a 2=1,所以a =1. 答案:1 3.解析:设该六棱锥的高是h .根据体积公式得,V =13×12×2×3×6×h=23,解得h =1,则侧面三角形的高为1+(3)2=2,所以侧面积S =12×2×2×6=12.答案:124.解析:依题意得,点A 是线段PB 的中点,|PC |=|P A |+|AC |=3 5.过圆心C (3,5)作y 轴的垂线,垂足为C 1,则|CC 1|=3,|PC 1|=(35)2-32=6.记直线l 的倾斜角为θ,则有|tan θ|=|PC 1||CC 1|=2,即k =±2. 答案:±25.解析:因为60°的二面角的棱上有A ,B 两点,AC ,BD 分别在这个二面角的两个半平面内,且都垂直于AB ,所以CD→=CA →+AB →+BD →,CA →·AB →=0,AB →·BD →=0, 因为AB =4,AC =6,BD =8,所以|AB→|=4,|AC →|=6,|BD →|=8, 所以CD→2=(CA →+AB →+BD →)2=CA →2+AB →2+BD →2+2CA →·BD → =36+16+64+2×6×8×cos 120°=68,所以CD 的长为217.答案:2176.解析:圆C 1关于x 轴对称的圆C ′1的圆心为C ′1(2,-3),半径不变,圆C 2的圆心为(3,4),半径r =3,|PM |+|PN |的最小值为圆C ′1和圆C 2的圆心距减去两圆的半径,所以|PM |+|PN |的最小值为(3-2)2+(4+3)2-1-3=52-4.答案:52-47.解析:补形法将三棱柱补成四棱柱,如图所示.记A 1到平面BCC 1B 1的距离为d ,则d =2.则V 三棱柱=12V 四棱柱=12S 四边形BCC 1B 1·d =12×4×2=4.答案:48.解析:由题意,知圆C 1与抛物线C 2的其中一个交点为原点,不妨记为B ,设A (m ,n ).因为|AB |=855,所以⎩⎨⎧m 2+n 2=855,m 2+(n -2)2=4,解得⎩⎪⎨⎪⎧m =85,n =165,即A ⎝ ⎛⎭⎪⎫85,165.将点A 的坐标代入抛物线方程得⎝ ⎛⎭⎪⎫1652=2p ×85,所以p =165,所以抛物线C 2的方程为y 2=325x . 答案:y 2=325x9.解析:如图,设Q ,P 分别为CE ,DE 的中点,可得四边形MNQP 是矩形,所以①②正确;不论D 折至何位置(不在平面ABC 内)都有MN 与AB 是异面直线,不可能MN ∥AB ,所以③错;当平面ADE ⊥平面ABCD 时,可得EC ⊥平面ADE ,故EC ⊥AD ,④正确.故填①②④.答案:①②④10.解析:依题意,双曲线的渐近线方程为y =±bx ,则过点P 且与渐近线平行的直线方程为y =±b (x -1),联立⎩⎪⎨⎪⎧y =bx y =-b (x -1)得|y |=b 2,所以平行四边形OBP A 的面积S ▱OBP A =2S △OBP =2×⎝ ⎛⎭⎪⎫12×1×|y |=b 2=1,所以b =2,所以双曲线的离心率e =c a =1+221= 5.答案: 511.解析:显然AB =2m ,因为∠APB =90°,所以OP =12AB =m ,所以要求m 的最小值即求圆C 上点P 到原点O 的最小距离,因为OC =5,所以OP min =OC -r =4,即m 的最小值为4.答案:412.解析:如图所示,设圆柱的底面半径为r ,则圆柱的侧面积为S =2πr ×21-r 2=4πr 1-r 2≤4π×r 2+(1-r 2)2=2π(当且仅当r 2=1-r 2,即r =22时取等号).所以当r =22时,V 球V 圆柱=4π3×13π⎝ ⎛⎭⎪⎫222×2=423. 答案:42313.解析:6个不同的点有两个为短轴的两个端点,另外4个分别在第一、二、三、四象限,且上下对称、左右对称.不妨设P 在第一象限,PF 1>PF 2,当PF 1=F 1F 2=2c 时,PF 2=2a -PF 1=2a -2c ,即2c >2a -2c ,解得e =c a >12,又因为e <1,所以 12<e <1;当PF 2=F 1F 2=2c 时,PF 1=2a -PF 2=2a -2c ,即2a-2c >2c 且2c >a -c ,解得13<e <12,综上可得13<e <12或12<e <1.答案:⎝ ⎛⎭⎪⎫13,12∪⎝ ⎛⎭⎪⎫12,1 14.解析:由已知|PM |·|PN |=(R -|OP |)(R +|OP |)=R 2-|OP |2=a 2+4-|OP |2,|OP |2=|OP →|2=14(PF 1→+PF 2→)2=14(|PF 1→|2+|PF 2→|2+2|PF 1→|·|PF 2→|cos ∠F 1PF 2)=12(|PF 1→|2+|PF 2→|2)-14(|PF 1→|2+|PF 2→|2-2|PF 1→||PF 2→|cos ∠F 1PF 2)=12[(2a )2-2|PF 1||PF 2|]-14×(2c )2=a 2-2,所以|PM |·|PN |=(a 2+4)-(a 2-2)=6.答案:6。
专题04 立体几何——2020年高考真题和模拟题文科数学分项汇编(解析版)

为真命题, 为真命题.
故答案为:①③④.
【点睛】本题考查复合命题的真假,同时也考查了空间中线面关系有关命题真假的判断,考查推理能力,属于中等题.
11.【2020年高考全国Ⅲ卷文数】已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为_________.
【答案】
【解析】易知半径最大球为圆锥的内切球,球与圆锥内切时的轴截面如图所示,
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
【答案】B
【解析】依题意 是空间不过同一点的三条直线,
当 在同一平面时,可能 ,故不能得出 两两相交.
当 两两相交时,设 ,根据公理 可知 确定一个平面 ,而 ,根据公理 可知,直线 即 ,所以 在同一平面.
综上所述,“ 在同一平面”是“ 两两相交”的必要不充分条件.
因为BC∥平面EB1C1F,所以四棱锥B−EB1C1F的顶点B到底面EB1C1F的距离等于点M到底面EB1C1F的距离.
作MT⊥PN,垂足为T,则由(1)知,MT⊥平面EB1C1F,故MT=PMsin∠MPN=3.
底面EB1C1F的面积为
所以四棱锥B−EB1C1F的体积为 .
【点睛】本题主要考查了证明线线平行和面面垂直,及其求四棱锥的体积,解题关键是掌握面面垂直转为求证线面垂直的证法和棱锥的体积公式,考查了分析能力和空间想象能力,属于中档题.
(1)证明:平面PAB⊥平面PAC;
(2)设DO= ,圆锥的侧面积为 ,求三棱锥P−ABC的体积.
【解析】(1)由题设可知,PA=PB=PC.
由于△ABC是正三角形,故可得△PAC≌△PAB.
△PAC≌△PBC.
立体几何(解答题)-高考真题文科数学分项汇编(原卷版)
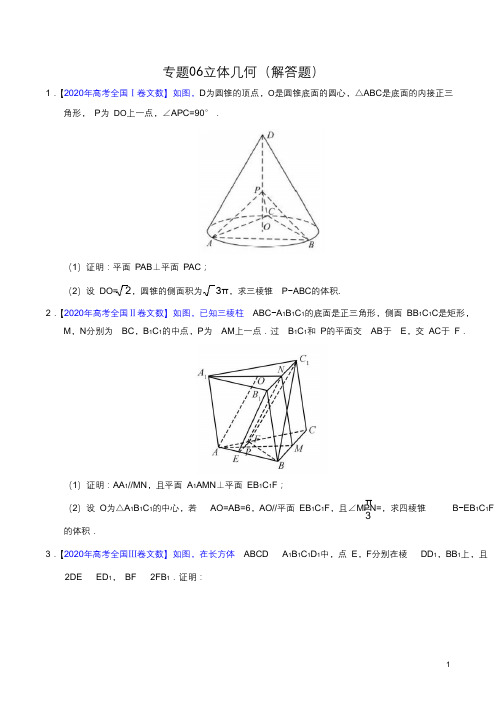
专题06立体几何(解答题)1.【2020年高考全国Ⅰ卷文数】如图,D为圆锥的顶点,O是圆锥底面的圆心,△ABC是底面的内接正三角形,P为DO上一点,∠APC=90°.(1)证明:平面PAB⊥平面PAC;(2)设DO= 2,圆锥的侧面积为3π,求三棱锥P−ABC的体积.2.【2020年高考全国Ⅱ卷文数】如图,已知三棱柱ABC−A1B1C1的底面是正三角形,侧面BB1C1C是矩形,M,N分别为BC,B1C1的中点,P为AM上一点.过B1C1和P的平面交AB于E,交AC于F.(1)证明:AA1//MN,且平面A1AMN⊥平面EB1C1F;π(2)设O为△A1B1C1的中心,若AO=AB=6,AO//平面EB1C1F,且∠MPN=,求四棱锥B−EB1C1F3的体积.3.【2020年高考全国Ⅲ卷文数】如图,在长方体ABCD A 1B1C1D1中,点E,F分别在棱DD1,BB1上,且2DE ED1,BF 2FB1.证明:(1)当AB BC时,EF AC;(2)点C1在平面AEF内.4.【2020年高考江苏】在三棱柱ABC-A1B1C1中,AB⊥AC,B1C⊥平面ABC,E,F分别是AC,B1C的中点.(1)求证:EF∥平面AB1C1;(2)求证:平面AB1C⊥平面ABB1.5.【2020年高考浙江】如图,在三棱台ABC—DEF中,平面ACFD⊥平面ABC,∠ACB=∠ACD=45°,DC =2BC.(Ⅰ)证明:EF⊥DB;(Ⅱ)求直线DF与平面DBC所成角的正弦值.6.【2019年高考全国Ⅰ卷文数】如图,直四棱柱ABCD–A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.(1)证明:MN∥平面C1DE;(2)求点C到平面C1DE的距离.7.【2019年高考全国Ⅱ卷文数】如图,长方体ABCD–A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.(1)证明:BE⊥平面EB1C1;(2)若AE=A E,AB=3,求四棱锥E BB1C1C的体积.18.【2019年高考全国Ⅲ卷文数】图1是由矩形ADEB,Rt△ ABC和菱形BFGC组成的一个平面图形,其中AB=1,BE=BF=2,∠FBC=60°.将其沿AB,BC折起使得BE与BF重合,连结DG,如图2.(1)证明:图2中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;(2)求图2中的四边形ACGD的面积.9.【2019年高考北京卷文数】如图,在四棱锥P ABCD中,PA 平面ABCD,底部ABCD为菱形,E 为CD的中点.(1)求证:BD⊥平面PAC;(2)若∠ABC=60°,求证:平面PAB⊥平面PAE;(3)棱PB上是否存在点F,使得CF∥平面PAE?说明理由.10.【2019年高考天津卷文数】如图,在四棱锥P ABCD中,底面ABCD为平行四边形,△PCD为等边三角形,平面PAC 平面PCD,PA CD,CD 2, AD 3.(1)设G,H分别为PB,AC的中点,求证:GH∥平面PAD;(2)求证:PA 平面PCD;(3)求直线AD与平面PAC所成角的正弦值.11.【2019年高考江苏卷】如图,在直三棱柱ABC-A1B1C1中,D,E分别为BC,AC的中点,AB=BC.求证:(1)A1B1∥平面DEC1;(2)BE⊥C1E.12.【2019年高考浙江卷】如图,已知三棱柱ABC A1B1C1,平面A1ACC1 平面ABC,ABC 90,BAC 30,A1A A1C AC,E,F分别是AC,A1B1的中点.(1)证明:EF BC;(2)求直线EF与平面A1BC所成角的余弦值.13.【2018年高考全国Ⅰ卷文数】如图,在平行四边形ABCM中,AB AC 3,∠ACM 90,以 AC 为折痕将△ACM折起,使点M到达点D的位置,且AB⊥ DA.(1)证明:平面ACD⊥平面ABC;BP DQ 2 DA ,求三棱锥Q ABP的体积.Q(2)为线段AD上一点,P为线段BC上一点,且 314.【2018年高考全国Ⅱ卷文数】如图,在三棱锥P ABC中,AB BC 2 2,PA PB PC AC 4,O为AC的中点.(1)证明:PO 平面ABC;(2)若点M在棱BC上,且MC 2MB,求点C到平面POM的距离.15.【2018年高考全国Ⅲ卷文数】如图,矩形ABCD所在平面与半圆弧CD所在平面垂直,M是CD上异于C,D的点.(1)证明:平面AMD⊥平面BMC;(2)在线段AM上是否存在点P,使得MC∥平面PBD?说明理由.16.【2018年高考北京卷文数】如图,在四棱锥P−ABCD中,底面ABCD为矩形,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,E,F分别为AD,PB的中点.(1)求证:PE⊥BC;(2)求证:平面PAB⊥平面PCD;(3)求证:EF∥平面PCD.17.【2018年高考天津卷文数】如图,在四面体ABCD中,△ABC是等边三角形,平面ABC⊥平面ABD,点M为棱AB的中点,AB=2,AD=2 3,∠BAD=90°.(1)求证:AD⊥BC;(2)求异面直线BC与MD所成角的余弦值;(3)求直线CD与平面ABD所成角的正弦值.18.【2018年高考江苏卷】在平行六面体ABCD A1B1C1D1中,AA1 AB, AB1 B1C1.求证:(1)AB∥平面A1B1C;(2)平面ABB1A1 平面A1BC.19.【2018年高考浙江卷】如图,已知多面体ABCA1B1C1,A1A,B1B,C1C均垂直于平面ABC,∠ABC=120°,A1A=4,C1C=1,AB=BC=B1B=2.(1)证明:AB1⊥平面A1B1C1;(2)求直线AC1与平面ABB1所成的角的正弦值.。
2020年高考数学(文)重难点专练03 立体几何(解析版)

重难点03 立体几何【命题趋势】立体几何一直在高中数学中占有很大的分值,未来的高考中立体几何也会持续成为高考的一个热点,文科高考中立体几何主要考查三视图的相关性质利用,简单几何体的体积,表面积以及外接圆问题.另外选择部分主要考查在点线面位置关系,简单几何体三视图.选择题主要还是以几何体的基本性质为主,解答题部分主要考查平行,垂直关系以及简单几何体的变面积以及体积.本专题针对高考高频知识点以及题型进行总结,希望通过本专题的学习,能够掌握高考数学中的立体几何的题型,将高考有关的立体几何所有分数拿到.【满分技巧】基础知识点考查:一般来说遵循三短一长选最长.要学会抽象问题具体会,将题目中的直线转化成显示中的具体事务,例如立体坐标系可以看做是一个教室的墙角有关外接圆问题:一般图形可以采用补形法,将几何体补成正方体或者是长方体,再利用不在同一个平面的四点确定一个立体平面原理,从而去求.内切圆问题:转化成正方体的内切圆去求.求点到平面的距离问题:采用等体积法.求几何体的表面积体积问题:应注意巧妙选取底面积与高.【考查题型】选择,填空,解答题【限时检测】(建议用时:45分钟)一、单选题1.(2013·山东高考模拟(文))设m ,n 是两条不同的直线, α,β,γ是三个不同的平面.有下列四个命题:①若//αβ,m α⊂,n β⊂,则//m n ; ①若m α⊥,//m β,则αβ⊥; ① 若n α⊥,n β⊥,m α⊥,则m β⊥;① 若αγ⊥,βγ⊥,m α⊥,则m β⊥. 其中错误..命题的序号是 A .①①B .①①C .①①①D .①①【答案】B【解析】【分析】根据平面平行的几何特征及直线关系的定义,可判断①错误;根据线面平行的性质定理,线面垂直的第二判定定理及面面垂直的判定定理,可得①正确;根据线面垂直的几何特征及面面平行的判定方法,可得①正确;根据面面垂直的几何特征,及线面垂直的几何特征,可判断①错误.【详解】若α①β,m①α,n①β,则m 与n 不相交,但可能平行也可能异面,故①错误;若m①α,m①β,由线面平行的性质定理可得:存在直线b①β,使b①a ,根据线面垂直的第二判定定理可得b①α,再由面面平行的判定定理得:α①β,故①正确;若n①α,n①β,则α①β,又由m①α,则m①β,故①正确;若α①γ,β①γ,α与β可能平行也可能相交(此时两平面交线与γ垂直),当α①β时,若m①α,则m①β,但α与β相交时,若m①α,则m 与β一定不垂直,故①错误; 故答案为:B【点睛】(1) 本题考查直线与平面平行与垂直的判定,考查空间想象能力,逻辑思维能力.(2)证明一个命题是真命题,需要证明,说明一个命题是假命题,可以通过举反例,要灵活选择. 2.(2019·河北高三月考(文))《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马;将四个面都为直角三角形的三棱锥称之为鳖臑.若三棱锥P ABC -为鳖臑,PA ⊥平面ABC ,2PA AB ==,AC =P ABC -的四个顶点都在球O 的球面上,则球O 的表面积为( )A .12πB .16πC .20πD .24π 【答案】C【解析】由题意得PC 为球O 的直径,而PC ==即球O 的半径R =所以球O的表面积24π20πS R ==.本题选择C 选项.【点睛】:与球有关的组合体问题,一种是内切,一种是外接.解题时要认 真分析图形,明确切点和接点的位置,确定有关元素间的数量关系,并作出合适的截面图,如球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径;球外接于正方体,正方体的顶点均在球面上,正方体的体对角线长等于球的直径.3.(2019·北京人大附中高考模拟(文))如图,在下列三个正方体1111ABCD A B C D -中,,,E F G 均为所在棱的中点,过,,E F G 作正方体的截面.在各正方体中,直线1BD 与平面EFG 的位置关系描述正确的是A .1BD ∥平面EFG 的有且只有①;1BD ⊥平面EFG 的有且只有①①B .1BD ∥平面EFG 的有且只有①;1BD ⊥平面EFG 的有且只有①C ..1BD ∥平面EFG 的有且只有①;1BD ⊥平面EFG 的有且只有①D .1BD ∥平面EFG 的有且只有①;1BD ⊥平面EFG 的有且只有①【答案】A【解析】【分析】①连结BD ,根据面面平行的判定定理可证平面1BDD P 平面EFG ,进而可得1BD P 平面EFG ;①①都可以根据线面垂直的判定定理,用向量的方法分别证明1BD EG ⊥,1BD EF ⊥,即可证明1BD ⊥平面EFG ;从而可得出结果.【详解】①连结BD ,因为,,E F G 均为所在棱的中点,所以BD GF P ,BD EF P ,从而可得BD P 平面EFG ,1DD P 平面EFG ;根据1BD DD D ⋂=,可得平面1BDD P 平面EFG ;所以1BD P 平面EFG ;①设正方体棱长为1,因为,,E F G 均为所在棱的中点,所以 ()()11111111B 22BD GE DD DB DA DD DA D DA ⎛⎫=-*=- ⎪⎝⎭***u u u u r u u u r u u u u r u u u r u u u u r u u u u r u u u u r u u u r u u u u r , ()11cos45cos6002=︒︒=即1BD EG ⊥; 又 ()()1111111C B 22BD EF DD DB DC DD D D DC ⎛⎫=-*=- ⎪⎝***⎭u u u u r u u u r u u u u r u u u r u u u u r u u u u r u u u r u u u r u u u u r ()11cos45cos6002=︒︒=,即1BD EF ⊥; 又EG EF E ⋂=,所以1BD ⊥平面EFG ;①设正方体棱长为1,因为,,E F G 均为所在棱的中点,所以()()()2111111111A 2222BD EG DD DB DG DE DD DB DC DD D DD DB DC DB DA ⎛⎫=-*-=-*+**-=-+ ⎪⎝*⎭u u u u r u u u r u u u u r u u u r u u u r u u u r u u u u r u u u r u u u r u u u u r u u u r u u u u r u u u r u u u r u u u r u u u r ,111102222=⨯+⨯=即1BD EG ⊥; 又()()()2111111111A A 2222BD EF DD DB AF AE DD DB DD DC D DD DB DC DB D ⎛⎫=*-*-=-*++=-- ⎪⎭*⎝*u u u u r u u u r u u u u r u u u r u u u r u u u r u u u u r u u u r u u u u r u u u r u u u r u u u u r u u u r u u u r u u u r u u u r1111102222=-⨯-⨯=1BD EF ⊥; 又EG EF E ⋂=,所以1BD ⊥平面EFG ;故选A【点睛】本题主要考查线面平行与线面垂直的判定,灵活掌握判定定理即可,属于常考题型. 4.(2019·山东高考模拟(理))如图,在下列四个正方体中,P ,R ,Q ,M ,N ,G ,H 为所在棱的中点,则在这四个正方体中,阴影平面与PRQ 所在平面平行的是( )A .B .C .D .【答案】A【解析】【分析】根据线面平行判定定理以及作截面逐个分析判断选择.【详解】A 中,因为11////PQ AC A C ,所以可得//PQ 平面11A BC ,又1//RQ AB ,可得//RQ 平面11A BC ,从而平面//PQR 平面11A BCB 中,作截面可得平面PQR I 平面1A BN HN =(H 为C 1D 1中点),如图:C 中,作截面可得平面PQR I 平面HGN HN =(H 为C 1D 1中点),如图:D 中,作截面可得1,QN C M 为两相交直线,因此平面PQR 与平面11A MC 不平行, 如图:【点睛】本题考查线面平行判定定理以及截面,考查空间想象能力与基本判断论证能力,属中档题.二、填空题5.(2019·吉林高考模拟(文))一个倒置圆锥形容器,底面直径与母线长相等,容器内存有部分水,向容器内放入一个半径为1的铁球,铁球恰好完全没入水中(水面与铁球相切)则容器内水的体积为__________.【答案】5π3.【分析】先由题意作出轴截面,根据圆锥的底面直径与母线长相等,得到∠APC =30∘,再记铁球的半径为r ,得r =1,求出圆锥的高,以及圆锥底面圆半径,最后由V 圆锥=V 水+V 铁球,即可求出结果.【详解】如图所示,作出轴截面,由题意,圆锥的底面直径与母线长相等,可得AP =AB ,则AP =2AC ,所以∠APC =30∘,记铁球的半径为r ,即OC =OD =r =1,在ΔODP 中,sin∠OPD =OD OP =12,则OP =2r =2,所以PC =3r =3,因此AC =√3r =√3,PA =2√3r =2√3,所以铁球所在圆锥的体积为V 圆锥=V 水+V 铁球,即V 水=V 圆锥−V 铁球=13S 圆C •PC −43πr 3=13π(√3)2•3−43π=53π.故答案为53π【点睛】本题主要考查圆锥内切球的相关计算,熟记体积公式即可,属于常考题型.6.(2019·广东高考模拟(文))已知矩形ABCD ,1AB =,BC =,将ADC V 沿对角线AC 进行翻折,得到三棱锥D ABC -,则在翻折的过程中有下列结论:①三棱锥D ABC -的体积最大值为14; ①三棱锥D ABC -的外接球体积不变;①异面直线AB 与CD 所成角的最大值为90o .其中正确的是____.(填写所有正确结论的编号)【答案】①①①【分析】考虑在翻折的过程中,当面ACD ⊥面ACB 时,D 到底面的距离最大,进而得到棱锥体积最大,可判断①正确;取AC 的中点O ,可得O 为棱锥的外接球的球心,计算可判断①正确;假设AB CD ⊥,由线面垂直的判断和性质,可判断①正确.【详解】解:矩形ABCD ,1AB =,BC =,可得2AC =,在翻折的过程中,当面ACD ⊥面ACB 时,D 到底面的距离最大,且为直角三角形ACD 斜边AC可得三棱锥D ABC -的体积最大值为1111324⋅⋅=,故①正确; 取AC 的中点O ,连接OB ,OD ,可得OA OB OC OD ===,即O 为三棱锥D ABC -的外接球的球心,且半径为1,体积为43π,故①正确;若AB CD ⊥,又AB BC ⊥,可得AB ⊥平面BCD ,即有AB BD ⊥,由1AB =及AD =可得BD =,将ADC V 沿对角线AC 翻折得过程中,存在某个位置使得BD =成立,故①正确.故答案为:①①①.【点睛】 本题主要考查了空间思维能力,还考查了球的体积公式,还考查了线面垂直的判断、性质及计算能力,属于难题.三、解答题7.(2019·湖南高考模拟(文))在平行四边形ABCD 中,3AB =,2BC =,过A 点作CD的垂线,交CD 的延长线于点E ,AE =连结EB ,交AD 于点F ,如图1,将ADE ∆ 沿AD 折起,使得点E 到达点P 的位置,如图2.(1)证明:平面BFP ⊥平面BCP ;(2)若G 为PB 的中点,H 为CD 的中点,且平面ADP ⊥平面ABCD ,求三棱锥G BCH -的体积.【答案】(1)见解析; (2)316. 【解析】【分析】(1)证明BE AD ⊥.PF AD ⊥,BF AD ⊥.推出PF BC ⊥,BF BC ⊥,得到BC ⊥ 平面BFP ,然后证明平面BFP ⊥平面BCP .(2)解法一:证明PF ⊥平面ABCD .取BF 的中点为O ,连结GO ,得到GO ⊥平面ABCD .然后求解棱锥的高.解法二:证明PF ⊥平面ABCD .三棱锥G BCH -的高等于12PF .说明BCH V 的面积是四边形ABCD 的面积的14,通过ABCD 13P ABCD V S PF -=⨯⋅平行四边形,求解三棱锥G BCH -的体积. 【详解】(1)证明:如题图1,在Rt BAE V 中,3AB =,AE =60AEB ∠=︒. 在Rt AED V 中,2AD =,所以30DAE ∠=︒.所以BE AD ⊥.如题图2,,PF AD BF AD ⊥⊥.又因为AD BC P ,所以PF BC ⊥,BF BC ⊥,PF BF F ⋂=,所以BC ⊥平面BFP ,又因为BC ⊂平面BCP ,所以平面BFP ⊥平面BCP .(2)解法一:因为平面ADP ⊥平面ABCD ,平面ADP ⋂平面ABCD AD =,PF ⊂平面ADP ,PF AD ⊥,所以PF ⊥平面ABCD .取BF 的中点为O ,连结GO ,则GO PF P ,所以GO ⊥平面ABCD .即GO 为三棱锥G BCH -的高.且11sin3022GO PF PA ==⨯︒=. 因为,三棱锥G BCH -的体积为11113332462416BCH BCD G BCH V S GO S -=⋅=⨯⨯=⨯=V V 三棱锥.解法二:因为平面ADP ⊥平面ABCD ,平面ADP ⋂平面ABCD AD =,PF ⊂平面ADP ,所以PF ⊥平面ABCD .因为G 为PB 的中点.所以三棱锥G BCH -的高等于12PF . 因为H 为CD 的中点,所以BCH V 的面积是四边形ABCD 的面积的14, 从而三棱锥G BCH -的体积是四棱锥P ABCD -的体积的18.ABCD 平行四边形面ABCD 113332P ABCD V S PF -=⨯⋅=⨯=平行四边形, 所以三棱锥G BCH -的体积为316. 【点睛】 本题考查直线与平面垂直,平面与平面垂直的判断定理的应用,几何体的体积的求法,考查空间想象能力以及计算能力.8.(2019·辽宁高考模拟(文))如图,在正三棱柱111ABC A B C -中,12AB AA ==,E ,F 分别为AB ,11B C 的中点.(①)求证:1B E ∕∕平面ACF ;(①)求三棱锥1B ACF -的体积.【答案】(①)见解析(①)3 【解析】【分析】(①)取AC 的中点M ,连结EM ,FM ,由三角形性质得//EM BC 且12EM BC =,结合已知得到1//EM B F 且1EM B F =,则四边形1EMFB 为平行四边形,可得1//B E FM ,再由线面平行的判定可得1//B E 平面ACF ;(①)设O 为BC 的中点,由已知得到AO ⊥平面11BCC B ,然后利用等积法求三棱锥1B ACF -的体积.【详解】(①)证明:取AC 的中点M ,连结EM ,FM ,在ABC ∆中,①E 、M 分别为AB ,AC 的中点,①EM BC ∕∕且12EM BC =, 又F 为11B C 的中点,11B C BC ∕∕,①1B F BC ∕∕且112B F BC =, 即1EM B F ∕∕且1EM B F =,故四边形1EMFB 为平行四边形,①1B E FM ∕∕,又MF ⊂平面ACF ,1B E ⊄平面ACF ,①1B E ∕∕平面ACF ;(①)解:设O 为BC 的中点,①棱柱底面是正三角形,2AB =,①有AO =又因为ABC ∆为正三角形,且O 为BC 的中点,所以AO BC ⊥,又由正三棱柱,所以平面11BCC B ⊥平面ABC ,由面面垂直的性质定理可得AO ⊥平面11BCC B ,即三棱锥1A B CF -所以1111112332B ACF A B CF B CF V V S AO --∆==⨯⨯=⨯⨯=. 【点睛】本题主要考查了直线与平面平行的判定与证明,以及利用等体积法七届多面体的体积问题,其中解答中熟记线面位置关系的判定与性质,以及合理利用等体积法求解体积是解答的关键,着重考查了空间想象能力,以及推理与运算能力,属于基础题. 9.(2019·吉林高考模拟(文))在四棱柱1111ABCD A B C D -中,底面ABCD 为平行四边形,1AA ⊥平面ABCD .24AB AD ==,3DAB π∠=(1)证明:平面1D BC ⊥平面1D BD ;(2)若直线1D B 与底面ABCD 所成角为6π,M ,N ,Q 分别为BD ,CD ,1D D 的中点,求三棱锥C MNQ -的体积.【答案】(1)见证明;(2) C MNQ V -=【解析】【分析】(1)推导出D 1D ①平面ABCD ,D 1D ①BC ,AD ①BD ,由AD ①BC ,得BC ①BD ,从而BC ①平面D 1BD ,由此能证明平面D 1BC ①平面D 1BD .(2)由1D D ⊥平面ABCD 得16D BD π∠=,可以计算出1D D ,再利用锥体体积公式求得Q CMN V -,根据等体积法即为C MNQ V -.【详解】(1)①1D D ⊥平面ABCD ,BC ⊂平面ABCD ,①1D D BC ⊥.又4AB =,2AD =,3DAB π∠=,①BD ==①222AD BD AB +=,①AD BD ⊥.又①//AD BC ,①BC BD ⊥.又①1D D BD D ⋂=,BD ⊂平面1D BD ,1D D ⊂平面1D BD ,①BC ⊥平面1D BD ,而BC ⊂平面1D BC ,①平面1D BC ⊥平面1D BD ;(2)①1D D ⊥平面ABCD ,①1D BD ∠即为直线1D B 与底面ABCD 所成的角,即16D BD π∠=,而BD =①12DD =. 又14C MNQ Q CMN Q BDC V V V ---==,①11121432C MNQ V -=⨯⨯⨯⨯=. 【点睛】 本题考查面面垂直的证明,考查线面角的定义及求法,考查了三棱锥体积的常用求法,涉及空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是中档题.10.(2020·河北石家庄二中高三月考(文))如图所示,在等腰梯形ABCD 中, //AD BC ,2AD CD AB ===, 60ABC ∠=o ,将三角形ABD 沿BD 折起,使点A 在平面BCD 上的投影G 落在BD 上.(1)求证:平面ACD ⊥平面ABD ;(2)若点E 为AC 的中点,求三棱锥G ADE -的体积.【答案】(1)见解析;(2) 【解析】试题分析:(1)要证平面ACD ⊥平面ABD ,只需证CD ⊥平面ABD ,分析条件易得AG CD ⊥和BD DC ⊥;(2)由G ADE G ACD A CDG 11V V V 22---==,只需求A CDG V -即可. 试题解析:(1)证明:在等腰梯形ABCD 中,可设2AD CD AB ===,可求出BD = 4BC =,在BCD V 中, 222BC BD DC =+,①BD DC ⊥,①点A 在平面BCD 上的投影G 落在BD 上,①AG ⊥平面BCD ,平面ABD ⊥平面BCD ,①AG CD ⊥,又BD DC ⊥, AG BD G ⋂=,①CD ⊥平面ABD ,而CD ⊂平面ACD ,①平面ACD ⊥平面ABD .(2)解:因为2AD AB ==,所以ABD ADB ∠=∠,又AD BC P ,所以ADB CBD ∠=∠,因为60ABC ∠=︒,所以30ABD ∠=︒,解得1AG =,因为E 为AC 中点,三棱锥G ADE -的体积与三棱锥G CDE -的体积相等, 所以1122G ADE G ACD A CDG V V V ---==,因为1112323A CDG V -=⨯⨯⨯=126G ADE A CDG V V --==. 11.(2020·广东实验中学高三月考(文))如图,在直三棱柱111ABC A B C -中,,E F 分别为11,AC BC 的中点,1C F AB ⊥,12AB BC AA===.(1)求证:1//C F 平面ABE ;(2)求三棱锥1E ABC -的体积.【答案】(1)见解析;(2)23. 【解析】试题分析:(1)设D 为边AB 的中点,连接ED ,FD ,①D ,F 分别为AB ,BC 的中点,根据三角形中位线定理以及题设条件可证明四边形1EC FD 为平行四边形,可得1C F ED P ,从而根据线面平行的判定定理可得结论;(2)先证明AB ⊥平面11BCC B ,知AB BC ⊥,从而可得三角形ABC 的面积为2,三角形ABF 的面积为1,利用等积变换可得11E ABC C EAB F EAB V V V ---== 121233E ABF V -==⨯⨯=. 试题解析:(1)设D 为边AB 的中点,连接ED ,FD①D ,F 分别为AB ,BC 的中点,①DF AC P ,12DF AC =, 又①1EC AC P ,112EC AC =,①1DF EC P ,1DF EC =,① 四边形1EC FD 为平行四边形.①1C F ED P ,又ED ⊂平面EAB ,1C F ⊄平面EAB ,①1C F P 平面ABE ,(2)在直三棱柱中1CC AB ⊥,又1C F AB ⊥,1CC ⊂平面11BCC B ,1C F ⊂平面11BCC B ,111CC C F C ⋂=,①AB ⊥平面11BCC B ,知AB BC ⊥,可得三角形ABC 的面积为2,三角形ABF 的面积为1,由(1)1C F P 平面ABE 知:1C 到平面EAB 的距离等于F 到平面EAB 的距离 ①11E ABC C EAB F EAB V V V ---==三棱锥三棱锥三棱锥 121233E ABF V -==⨯⨯=三棱锥. 【方法点晴】本题主要考查线面平行的判定定理、线面垂直的判定定理、利用等积变换求三棱锥体积,属于难题.证明线面平行的常用方法:①利用线面平行的判定定理,使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线,可利用几何体的特征,合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.①利用面面平行的性质,即两平面平行,在其中一平面内的直线平行于另一平面. 本题(1)是就是利用方法①证明的.12.(2020·宁夏高三月考(文))如图,在四棱锥P ABCD -中,平面PAB ⊥ 平面ABCD ,四边形ABCD 为正方形,①PAB 为等边三角形,E 是PB 中点,平面AED 与棱PC 交于点F .(①)求证://AD EF ;(①)求证:PB ⊥平面AEFD ;(III )记四棱锥P AEFD -的体积为1V ,四棱锥P ABCD -的体积为2V ,直接写出12V V 的值.【答案】(1)见解析(2)见解析(3)1238V V = 【解析】【分析】 (①)由ABCD 为正方形,可得//AD BC .再由线面平行的判定可得//AD 平面PBC ..再由面面平行的性质可得//AD EF ;(①)由ABCD 为正方形,可得AD AB ⊥.结合面面垂直的性质可得AD ⊥平面PAB .从而得到AD PB ⊥..再由已知证得PB AE ⊥.由线面垂直的判定可得PB ⊥平面AEFD ;(①)由(①)知,1C AEFD V V -=,利用等积法把2V 用1V 表示,则12V V 的值可求. 【详解】(I )证明:因为正方形ABCD ,所以//AD BC .因为AD ⊄平面PBC ,BC ⊂平面PBC ,所以//AD 平面PBC .因为AD ⊂平面AEFD ,平面AEFD ⋂平面PBC EF =,所以//AD EF .(II )证明:因为正方形ABCD ,所以AD AB ⊥.因为平面PAB ⊥平面ABCD ,平面PAB ⋂平面ABCD AB =,AD ⊂平面ABCD ,所以AD ⊥平面PAB .因为PB ⊂平面PAB ,所以AD PB ⊥.因为PAB ∆为等边三角形,E 是PB 中点,所以PB AE ⊥.因为AE ⊂平面AEFD ,AD ⊂平面AEFD ,AE AD A ⋂=,所以PB ⊥平面AEFD .(III )解:由(①)知,122133C AEFDE ABCF ADC C AEFD V V V V V V ,=,----=== 513BC AEFD V V -∴=, 则1158133P ABCD V V V V -+==, 1238V V ∴= . 【点睛】本题考查直线与平面平行的判定和性质,考查线面垂直的判定,考查空间想象能力与思维能力,训练了利用等积法求多面体的体积,是中档题.。
衡水中学2020届高三二轮数学专题09 立体几何(文科专用)(测)(解析版)

衡水中学2020届高三二轮数学立体几何单元—测【满分:100分 时间:90分钟】一、选择题(12*5=60分)1.若,l m 是两条不同的直线,m 垂直于平面α ,则“l m ⊥ ”是“l ∥α”的A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件【答案】B【解析】由“m α⊥且l m ⊥”推出“l α⊂或l α∥”,但由“m α⊥且l α∥”可推出“l m ⊥”,所以“l m ⊥”是“l α∥”的必要而不充分条件,故选B .2. 下列命题中错误的是A .如果平面αβ⊥平面,那么平面α内一定存在直线平行于平面βB .如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面βC .如果平面αγ⊥平面,平面βγ⊥平面,=l αβ ,那么l γ⊥平面D .如果平面αβ⊥平面,那么平面α内所有直线都垂直于平面β 【答案】D【解析】对于D ,若平面平面,则平面内的某些直线可能不垂直于平面,即与平面的关系还α⊥βαββ可以是斜交、平行或在平面内,其余选项易知均是正确的.β3. 如图所示,ABCD A 1B 1C 1D 1是长方体,O 是B 1D 1的中点,直线A 1C 交平面AB 1D 1于点M ,则下列结论正确的是( )A .A ,M ,O 三点共线B .A ,M ,O ,A 1不共面C .A ,M ,C ,O 不共面D .B ,B 1,O ,M 共面【答案】A【解析】连接A 1C 1,AC ,则A 1C 1∥AC ,∴A 1,C 1,A ,C 四点共面,∴A 1C ⊂平面ACC 1A 1,∵M ∈A 1C , ∴M ∈平面ACC 1A 1,又M ∈平面AB 1D 1,∴M 在平面ACC 1A 1与平面AB 1D 1的交线上,同理O 在平面ACC 1A 1与平面AB 1D 1的交线上.∴A ,M ,O 三点共线.答案:A4. 在梯形ABCD 中,2ABC π∠=,//AD BC ,222BC AD AB ===.将梯形ABCD 绕AD 所在的直线旋转一周而形成的曲面所围成的几何体的体积为 (A)23π (B) 43π (C) 53π (D) 2π 【答案】C 【解析】2215121133V πππ=⋅⋅-⋅⋅=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020高三数学立体几何专项训练文科1.在四棱锥P-ABCD中,底面ABCD为矩形,PA垂直于平面ABCD,E是PD的点。
Ⅰ) 证明PB平行于平面AEC。
Ⅱ) 设AP=1,AD=3,求三棱锥P-ABD的体积V和A点到平面PBD的距离。
2.在四棱锥P-ABCD中,AB平行于CD且AB等于2CD,E为PB的中点。
1) 证明CE平行于平面PAD。
2) 是否存在一点F在线段AB上,使得平面PAD平行于平面CEF?若存在,证明结论;若不存在,说明理由。
3.在四棱锥P-ABCD中,平面PAC垂直于平面ABCD,且PA垂直于AC且等于AD等于2,四边形ABCD满足BC平行于AD,AB垂直于AD且等于1,点E和F分别为侧棱PB和PC上的点,且PEPF等于λ(λ不等于0)。
1) 证明EF平行于平面PAD。
2) 当λ等于2时,求点D到平面AFB的距离。
4.四棱柱ABCD-A1B1C1D1的底面ABCD是正方形。
1) 证明平面A1BD平行于平面CD1B1.2) 若平面ABCD与平面B1D1C相交于直线l,证明B1D1平行于l。
5.在平行四边形ABCD外一点P,PC的中点为M,在DM上取一点G,过G与AP作平面交平面BDM于H。
证明AP平行于GH。
6.在四棱锥P-ABCD中,PA垂直于底面ABCD,AB垂直于AD,AC垂直于CD,且∠ABC等于60度,PA等于AB等于BC,E是PC的中点。
证明:1) CD垂直于AE;2) PD垂直于平面ABE。
7.在四棱锥P-ABCD中,平面PAB垂直于平面ABCD,四边形ABCD为正方形,△PAB为等边三角形,E是PB的中点,平面AED与棱PC交于点F。
1) 证明AD平行于EF;2) 证明PB垂直于平面AEFD;3) 设四棱锥P-AEFD的体积为V1,四棱锥P-ABCD的体积为V2,求V1和V2的值。
8.在四棱锥P-ABCD中,底面ABCD是边长为a,∠DAB 等于60度的菱形,侧面PAD为正三角形,其所在平面垂直于底面ABCD,G为AD的中点。
1) 证明BG垂直于平面PAD;2) 证明AD垂直于PB。
3、在四棱锥P-ABCD中,若E为BC边的中点,则是否存在一点F在棱PC上,使得平面DEF垂直于平面ABCD?请证明您的结论。
9、在四棱锥P-ABCD中,已知PC垂直于平面ABCD,AB平行于DC,DC垂直于AC,AD与BC交于点M。
证明:DC垂直于平面PAC;平面PAB垂直于平面PAC;是否存在点F在棱PB上,使得PA平行于平面CEF?10、在四棱锥P-ABCD中,底面ABCD为矩形,E在棱PC上且不等于点P或C,平面ABE与棱PD交于点F。
证明:AB平行于EF;若AF垂直于EF,则平面PAD垂直于平面ABCD。
11、在四棱锥P-ABCD中,PA垂直于平面ABCD,PA=AB=BC=3,AD=CD=1,∠ADC=120°,M为AC与BD的交点,N在线段PB上且PN=PB。
证明:MN平行于平面PDC;求直线MN与平面PAC所成角的正弦值。
12、在四棱锥ABCD中,PA垂直于CD,AD平行于BC,AD=BC,∠ADC=∠PAB=90°。
证明:存在点M在平面PAD 内,使得直线CM平行于平面PAB;平面PAB垂直于平面PBD。
13、在直三棱柱ABCA1B1C1中,D和E分别为AB和BC的中点,F在侧棱B1B上,且B1D垂直于A1F,A1C1垂直于A1B1.证明:DE平行于平面A1C1F;平面B1DE垂直于平面A1C1F。
14、在三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,B1C的中点为O,且AO垂直于平面BB1C1C。
证明:B1C垂直于AB;若AC垂直于B1A1且∠CBB1=60°,则求该三棱柱的高。
15、在四棱锥P-ABCD中,AD垂直于平面PDC,AD平行于BC,PD垂直于PB,AD=1,BC=3,CD=4,PD=2.求异面直线AP与BC所成角的余弦值;证明:PD垂直于平面PBC;求直线AB与平面PBC所成角的正弦值。
16、在三棱台ABCDEF中,平面BCFE垂直于平面ABC,且∠ACB=90°,BE=EF=FC=1,BC=2,AC=3.1) 证明BF垂直于平面ACFD。
2) 求直线BD与平面ACFD所成角的余弦值。
17、在图中,矩形ABCD所在平面与半圆弧CD所在平面垂直,M是CD上异于C、D的点。
1) 证明平面AMD垂直于平面XXX。
2) 判断在线段AM上是否存在点P,使得MC平行于平面PBD,并说明理由。
118、在直角梯形ABCD中,AD∥BC,∠BAD=22°,AB=BC=AD=a,E是AD的中点,O是AC与BE的交点。
将△ABE沿BE折起到△A1BE的位置,得到四棱锥A1BCDE。
1) 证明CD垂直于平面A1OC。
2) 当平面A1BE垂直于平面BCDE时,四棱锥A1BCDE的体积为362,求a的值。
119、在直角梯形ABCD中,∠ADC=90°,AB∥CD,AD=CD=AB=2,E为AC的中点,将△ACD沿AC折起,使折起后的平面ACD与平面ABC垂直,在几何体D-ABC 中:1) 证明BC垂直于平面ACD。
2) 点F在棱CD上,且满足AD∥平面BEF,求几何体F-BCE的体积。
20、在长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E、F分别在A1B1、D1C1上,过点E、F的平面α与此长方体的面相交,交线围成一个正方形EFGH。
1) 证明A1E=D1F。
2) 判断A1D与平面α的关系。
证明:如图所示,取XXX的中点H,连接EH和DH。
因为E为PB的中点,所以EH∥AB且EH=AB。
又因为AB∥CD且CD=AB,所以EH∥CD且EH=CD。
因此四边形DCEH是一个平行四边形,所以CE∥DH。
又因为DH⊂平面PAD且CE⊄平面PAD,所以CE∥平面PAD。
证明:如图所示,取AB的中点F,连接CF和EF。
因为E为PB的中点,所以EF∥BC。
又因为BC∥AD,所以EF∥AD。
又因为EF⊄平面PAD,AD⊂平面PAD,所以EF∥平面PAD。
又因为CD=AB,所以AF=CD。
又因为AF∥CD,所以四边形AFCD是一个平行四边形,所以CF∥AD。
又因为CF⊄平面PAD,所以CF∥平面PAD。
由(1)可知CE∥平面PAD,又CE∩CF=C,故平面CEF∥平面PAD。
因此存在AB的中点F满足要求。
证明:如图所示,因为PB=PC=λ(λ≠0),所以EF∥BC。
又因为BC∥AD,所以EF∥AD。
又因为EF⊄平面PAD,AD⊂平面PAD,所以EF∥平面PAD。
又因为λ=PEPF,所以F是PC的中点。
在Rt△PAC中,PA=2,AC=2,所以PC=PA2+AC2=6.又因为平面PAC⊥平面ABCD,且平面P AC∩平面ABCD=AC,所以PA⊥平面ABCD。
因此PA⊥BC。
又因为AB⊥AD,BC∥AD,所以BC⊥AB。
又因为PA∩AB=A,PA,AB⊂平面PAB,所以BC⊥平面PAB,所以BC⊥PB。
因此在Rt△PBC中,BF=PC=6/√22.又因为AB=1,所以S△ABD=1.设点D到平面AFB的距离为d,在等腰三角形BAF中,BF=AF=5/√2.又因为点F到平面ABD的距离为1,所以S△ABF=11/54.由V F-ABD=V D-AFB,得1×1=d×11/54,解得d=33/4554,即点D到平面AFB的距离为33/4554.证明由题设可知BB1∥DD1且BB1=DD1,所以四边形BB1D1D是一个平行四边形,所以BD∥B1D1.又因为BD⊄平面CD1B1,B1D1⊂平面CD1B1,所以BD∥平面CD1B1.因为A1D1∥B1C1∥BC且A1D1=B1C1=BC,所以四边形A1BCD1是一个平行四边形,所以A1B∥D1C。
又因为A1B⊄平面CD1B1,所以A1B∥平面CD1B1.C ⊂平面 CD,因此 A1B∥平面CD。
又因为BD∩A1B=B,BD,A1B ⊂平面A1BD,所以平面A1BD∥平面CD。
由此可得平面A1BD∥平面CD,又因为平面ABCD∩平面B1D1C1=直线l,平面ABCD∩平面A1BD=直线BD,因此直线l∥直线BD。
在四棱柱ABCD-A1B1C1D1中,四边形BDD1B1为平行四边形,因此B1D1∥BD,所以B1D1∥l。
连接AC交BD于点O,连接MO,因为PM=MC,AO=OC,所以PA∥MO。
因为PA⊄平面MBD,MO⊂平面MBD,所以PA∥平面MBD。
因为平面PAHG∩平面MBD=GH,所以AP∥GH。
1) 在四棱锥P-ABCD中,因为PA⊥底面ABCD,CD⊂平面ABCD,所以PA⊥CD。
因为AC⊥CD,且PA∩AC=A,所以CD⊥平面PAC。
而AE⊂平面PAC,所以CD⊥AE。
2) 由PA=AB=BC,∠ABC=60°,可得AC=PA。
因为E 就是PC的中点,所以AE⊥PC。
由(1)知AE⊥CD,且PC∩CD=C,所以AE⊥平面PCD。
而PD⊂平面PCD,所以AE⊥PD。
因为XXX⊥底面ABCD,所以PA⊥AB。
又因为AB⊥AD且PA∩AD=A,所以AB⊥平面PAD。
而PD⊂平面PAD,所以AB⊥PD。
又因为AB∩AE=A,所以PD⊥平面ABE。
1) 因为ABCD为正方形,所以AD∥BC。
因为AD⊄平面PBC,BC⊂平面PBC,所以AD∥平面PBC。
因为AD⊂平面AEFD,平面AEFD∩平面PBC=EF,所以AD∥EF。
2) 因为四边形ABCD就是正方形,所以AD⊥AB。
因为平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB,AD⊂平面ABCD,所以AD⊥平面PAB。
因为PB⊂平面PAB,所以AD⊥PB。
因为△PAB为等边三角形,E就是PB中点,所以PB⊥AE。
因为AE⊂平面AEFD,AD⊂平面AEFD,AE∩AD=A,所以PB⊥平面AEFD。
3) 由(1)知,V1=VC-AEFD,VE-ABC=VF-ADC=VC-AEFD=V1.因此,VBC-AEFD=V1,即Vp-ABCD=V1.1.在菱形ABCD中,证明BG垂直于平面PAD。
因为∠DAB=60°,G是AD的中点,所以BG垂直于AD。
又因为平面PAD垂直于平面ABCD,且平面PAD与平面ABCD的交线为AD,所以BG垂直于平面PAD。
2.在图中连接PG,证明AD垂直于PB。
因为△PAD是正三角形,G是AD的中点,所以PG垂直于AD。
由(1)知,BG 垂直于AD,又因为PG与BG相交于点G,所以AD垂直于平面PGB。
因为PB在平面PGB内,所以AD垂直于PB。
3.当F为PC的中点时,证明平面DEF垂直于平面ABCD。
