圆锥曲线第二定义在一些题目中的应用(供参考)
圆锥曲线中第二定义的三类用法(共10张PPT)
第二定义
第二定义：椭圆或双曲线中的一点P，满足条件
PF2 PD
e
（式右x 准线a2对应右焦点），其中PF2 称作焦半径，准线公
c
第二定义
例：在平面直角坐标系
xoy
中双曲线
x2 3
y2
1
的右准线与它的两条渐近线分别交于点P,Q，
其中 焦点是 ，F1, F2 ，则四边形 的面积是_______.
x2 a2
y2 b2
1 的左焦点 ，交椭圆于A,B 两点，且有 | AF | 3 | B F | ，求椭圆的离心率.
解析：AF, B F 为左焦点上的焦半径，所以过A,B 两点
分别作垂直于准线的直线且和准线交于D,E 两点，
从B 点作 BH AD .
因为| AF | 3 | B F | ，设 BF m ，则 AF 3m
是右 ，根
据第二定义
PF2 PD
e
，解得
PF2
5 4
PD
5
所以
|
PM
|
4 5
|
PF2
|
PM
PD
因此当P,M,D三点共线时 PM PD 取得最小值，最小
值为从 M到右准线的距离 MH, MH 6 16 14 55
第二定义
本次课重点需要注意三点 ：
（1）是第二定义的用法； （2）是注意例2这个题目的常规做法，此外下次课会给出这种例题的常用结论； （3）需要注意焦半径的取值范围，这个范围是求离心率取值范围题目中常用的
在 RT PF1F2 中，满足 PF12 所以在 RT PF1F2 中，SPF1F
1
圆锥曲线_经典例题
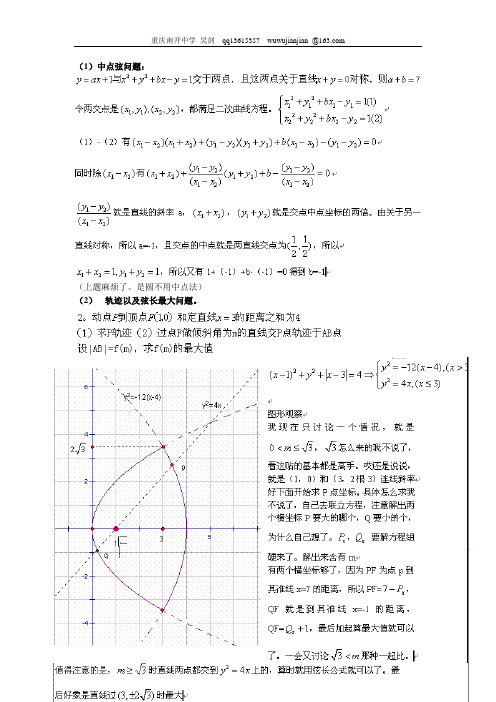
（1）中点弦问题：（上题麻烦了。
是圆不用中点法）（2）轨迹以及弦长最大问题。
（3）利用通径最断解题（4）利用第二定义求离心率?我在楼上说的方法不很好，有焦点弦和准线了，当然要想第二定义过P做PD垂直准线于D,那么可得,PF/PD=e,PD/PM=1/2所以PF/e=1/2PM,又PF/PM=sin60/sin45=根3/根2,所以最终可得离心率为根6 ?????????和楼上算的怎么不一样?（5）抛物线的一证明，过抛物线焦点F 的直线交抛物线于A,B 两点,通过点A 和抛物线的顶点的直线与抛物线的准线交于点D,求证:直线DB 平行于抛物线的对称轴.我没搞懂为什么必须用平几？为什么学解析几何，就是想把我们从烦琐的平几中解放出来，前人开创这个来干吗的呀？建系我就不说了，看图加解答。
令22y px=，1122(,),(,)A x y B x y ，:()2p A B y k x =-连立两方程消x 可得212y y p =-，其实这是一个结论又令0(,)2p D y -，则01101122y y y p y p x x =⇒=--，又2112y x p=，则有2021p y y y -==。
完（6）抛物线（7）很好的一题，圆锥曲线都实用这题的问题不在思路上，而是在计算上。
看我的。
这题做了你们可以自己再去做下05江西文21题。
练练。
第一问我不想说了就是重新高考的思路，算出椭圆方程为22340x y +-=（为哈要弄成这样？因为一般式对于一会直线联立不容易出错，我的习惯）开动了。
分析下意思，就是直线CP 与直线CQ 要关于C 点对称才行。
所以这题思路，令出两直线方程，都过C 点，斜率相反数，解出两点坐标，算出斜率为定。
解：若斜率不存在，CP ，CQ 重合，故两直线都有斜率，令:(1)11C P y k x kx k =-+=-+。
:(1)11C Q y k x kx k =--+=-++由222221(13)6(1)3610340y kx k k x k k x k k x y =-+⎧⇒+--+--=⎨+-=⎩，从这里就要解出P x 来。
二次曲线的定义及应用
例1、已知：P为双曲线 （a>0, b>0）上 一点，F1，F2为焦点，A1，A2为其顶点。求证： 以PF1为直径的圆与以A1A2为直径的圆相切。
x2 y2 2 1 2 a b
练习：已知：过抛物线y2=2px(p>0)焦点F的直 线与抛物线交于P，Q两点，求证：以线段PQ 为直径的圆与准线相切。
例2、设F1、F2是椭圆的两个焦点，M是椭圆上 的任意一点，从任一焦点向△F1MF2的顶点M的 外角平分线作垂线，垂足为P，则P的轨迹为 （ ） A、圆 B、椭圆 C、双曲线 D、抛物线
例3、如图：椭圆 为左焦点，A、B是两个顶点，P为椭圆上 一点，PF1⊥x轴，且PO//AB，求椭圆的离 心率e
用美的教育 造就美的新人
二次曲线的定义与应用
解析几何复习一
珠海市第一中学
袁长林
圆：平面内到定点的距离等于定长的点的轨迹 圆锥曲线的定义 1. 椭圆：平面内到两个定点的距离之和等于定长（定长大于 两个定点间的距离）的动点的轨迹叫做椭圆。即：{P| |PF1|+|PF2|=2a, (2a>|F1F2|)}。 2. 双曲线：平面内到两个定点的距离的差的绝对值为定值 （定值小于两个定点的距离）的动点轨迹叫做双曲线。即 {P|||PF1|-|PF2||=2a, (2a<|F1F2|)}。 3. 圆锥曲线的统一定义：平面内到定点的距离与到定直线的 距离的比e是常数的点的轨迹叫做圆锥曲线。当0<e<1时为椭 圆：当e=1时为抛物线；当e>1时为双曲线。
。
x2 y 2 2 1 2 a b （a>b>0），F1
例4、椭圆 的焦点为F1和F2，点P在椭 圆上，若线段PF1的中点在y轴上，求：|PF 1 12 3
圆锥曲线常用知识归类
圆锥曲线常用知识归类1.圆锥曲线的两个定义：（1）第一定义中要重视“括号”内的限制条件：椭圆中，与两个定点F 1，F 2的距离的和等于常数2a ，且此常数2a 一定要大于21F F ，当常数等于21F F 时，轨迹是线段F 1F 2，当常数小于21F F 时，无轨迹；双曲线中，与两定点F 1，F 2的距离的差的绝对值等于常数2a ，且此常数2a 一定要小于|F 1F 2|，定义中的“绝对值”与2a ＜|F 1F 2|不可忽视。
若2a ＝|F 1F 2|，则轨迹是以F 1，F 2为端点的两条射线，若2a ﹥|F 1F 2|，则轨迹不存在。
若去掉定义中的绝对值则轨迹仅表示双曲线的一支。
（2）第二定义中要注意定点和定直线是相应的焦点和准线，且“点点距为分子、点线距为分母”，其商即是离心率e 。
圆锥曲线的第二定义，给出了圆锥曲线上的点到焦点距离与此点到相应准线距离间的关系，要善于运用第二定义对它们进行相互转化。
2.圆锥曲线的标准方程（标准方程是指中心（顶点）在原点，坐标轴为对称轴时的标准位置的方程）：（1）椭圆：焦点在x 轴上时12222=+by a x （0a b >>）⇔{cos sin x a y b ϕϕ==（参数方程，其中ϕ为参数），焦点在y 轴上时2222bx a y +＝1（0a b >>）。
方程22Ax By C +=表示椭圆的充要条件是什么？（ABC ≠0，且A ，B ，C 同号，A ≠B ）。
（2）双曲线：焦点在x 轴上：2222b y a x - =1，焦点在y 轴上：2222bx a y -＝1（0,0a b >>）。
方程22Ax By C +=表示双曲线的充要条件是什么？（ABC ≠0，且A ，B 异号）。
（3）抛物线：开口向右时22(0)y px p =>，开口向左时22(0)y px p =->，开口向上时22(0)x py p =>，开口向下时22(0)x py p =->。
第2讲 圆锥曲线第二定义与焦半径公式(解析版)
第2讲圆锥曲线第二定义与焦半径公式参考答案与试题解析一．选择题（共5小题）1．已知点P 是双曲线22184x y -=上的动点，1F ，2F 为该双曲线的左右焦点，O 为坐标原点，则12||||||PF PF OP +的最大值为()A．B ．2CD【解答】解：由题意，分子最大且分母最小时，即P 在顶点处取得最大值，不妨取顶点，0)，则12||||||PF PF OP +=，故选：D ．2．已知双曲线222:1(0)4x y C a α-=>的右支上的点0(P x ，0)y 满足121||3||(PF PF F =，2F 分别是双曲线的左右焦点），则00(cy c x +为双曲线C 的半焦距）的取值范围是()A．)+∞B ．[2，25)2C．252D ．[2，【解答】解：由双曲线的第二定义可知10||PF ex a =+，20||PF ex a =-， 右支上的点0(P x ，0)y 满足12||3||PF PF =，0003()2ex a ex a ex a ∴+=-⇒=，由c e a=，解得202a x c=，P 在右支上，可得202a x a c= ，可得12ca< ，即12e < ，则22220022201164(1)422x c c y e x a a e+=+-=+-，令2e t =，14t < ，可得2202011611613244()4222c y e t t x e t t+=+-=+-=+-而132()()2f t t t=+在(1，4]递减，132()[62t t +∈，332，2002522c y x ∴+<，故选：B ．3．已知点P 是双曲线22221(0,0)x y a b a b-=>>上的动点，1F ，2F 分别是其左、右焦点，O 为坐标原点，若12||||||PF PF OP +的最大值是，则此双曲线的离心率是()AB．2C ．32D ．2【解答】解：不妨设P 为右支上的一点，(,)P x y 其中x a ，1||PF ex a =+，2||PF ex a =-，||OP ==∴12||||)||PF PF x a OP +==∴当x a =时，取得最大值，∴=，∴e =故选：B ．4．已知F 为抛物线2:4C y x =的焦点，过F 作两条互相垂直的直线1l ，2l ，直线1l 与C 交于A ，B 两点，直线2l 与C 交于D ，E 两点，则当||||AB DE +取得最小值时，四边形ADBE 的面积为()A ．32B ．16C ．24D ．8【解答】解：因为AB DE ⊥，要使||||AB DE +最小，而||||AB DE + 由抛物线的对称性可得A 与D ，B 与E 关于x 轴对称，所以可得直线DE 的斜率为1，又过抛物线的焦点(1,0)，所以直线DE 的方程为：1y x =-，214y x y x=-⎧⎨=⎩，整理可得2440y y --=，124y y +=，124y y =-，所以可得||8DE ===，所以11883222ABCD S DE AB =⋅=⨯⨯=四边形．故选：A ．5．过椭圆22143x y +=的右焦点F 作两条相互垂直的直线分别交椭圆于A ，B ，C ，D 四点，则11||||AB CD +的值为()A ．18B ．16C ．1D ．712【解答】解：由椭圆22143x y +=，得椭圆的右焦点为(1,0)F ，当直线AB 的斜率不存在时，:1AB x =，则:0CD y =．此时||3AB =，||4CD =，则11117||||3412AB CD +=+=；当直线AB 的斜率存在时，设:(1)(0)AB y k x k =-≠，则1:(1)CD y x k=--．又设点1(A x ，1)y ，2(B x ，2)y ．联立方程组22(1)3412y k x x y =-⎧⎨+=⎩，消去y 并化简得2222(43)84120k x k x k +-+-=，∴221212228412,3434k k x x x x k k -+==++，2212(1)||34k AB k +∴=+，由题知，直线CD 的斜率为1k-，同理可得2212(1)||43k CD k +=+．∴22117(1)7||||12(1)12k AB CD k ++==+为定值．故选：D ．二．填空题（共3小题）6．已知P 是椭圆22:184x y C +=上的动点，1F ，2F 分别是其左右焦点，O 是坐标原点，则12||||||PF PF PO - 的取值范围是[．【解答】解：设P 的坐标为(,)m n 椭圆22:184x y C +=中，28a =，24b =，2c ∴==，得椭圆的准线方程为2a x c=±，即4x =±作出椭圆的右准线，设P 在右准线上的射影为Q ，连结PQ ，根据圆锥曲线的统一定义，得2||||PF e PQ =，2||||)22PF e PQ m ∴==-=，同理可得1||2PF=，||PO =，∴12))||||22||m PF PF PO +--= 点(,)P m n 在椭圆22184x y +=上，得22184m n +=，∴2224(1482m m n =-=-，由此可得12||||||PF PF PO -= ，得22122||||4()8||PF PF m m PO -=+ ，2[0m ∈ ，2]a 即2[0m ∈，8]，得224[08m m ∈+，2]，∴12||||[||PF PF PO -∈，．故答案为：[7．已知F 为抛物线2:4C y x =的焦点，过F 作两条互相垂直的直线1l ，2l ，直线1l 与C 交于A 、B 两点，直线2l 与C 交于D 、E 两点，则11||||AB DE +的值为14．【解答】解：根据题意可得，抛物线24y x =的焦点坐标为(1,0)F ，准线方程为1x =-，设直线1:(1)(0)l y k x k =-≠， 直线1l ，2l 互相垂直，∴直线2l 的斜率为1k -，即得21:(1)l y x k=--，设1(A x ，1)y ，2(B x ，2)y ，3(C x ，3)y ，4(E x ，4)y ，则分别将直线1l ，2l 的方程与抛物线方程联立组成方程组可得，22222(1)(24)04y k x k x k x k y x=-⎧⇒-++=⎨=⎩；21(1)4y x k y x⎧=--⎪⎨⎪=⎩⇒2222121(4)0x x k k k -++=由韦达定理可得，212224k x x k ++=，2342241k x x k ++=，由抛物线性质可知，抛物线上的点到焦点的距离等于到准线的距离，∴2212222444||112k k AB x x k k ++=+++=+=，2234224||112441k DE x x k k +=+++=+=+，∴2221111||||44444k AB DE k k +=+=++．故答案为：14．8．已知F 为抛物线2:4C y x =的焦点，过F 作两条互相垂直的直线1l ，2l ，直线1l 与C 交于A 、B 两点，直线2l 与C 交于D 、E 两点，则||4||AB DE +的最小值为36．【解答】解：抛物线2:4C y x =的焦点(1,0)F ，准线方程为1x =-，设直线1l 的方程为(1)y k x =-，0k ≠，联立方程组24(1)y xy k x ⎧=⎨=-⎩，则2222(42)0k x k x k -++=，设1(A x ，1)y ，2(B x ，2)y ，可得12242x x k+=+，由抛物线的定义可得1224||24AB x x k=++=+，由12l l ⊥，可将上式中的k 换为1k-，可得2||44DE k =+，则221||4||204(4)2036AB DE k k +=+++= ．当且仅当2k =±时，上式取得等号，则||4||AB DE +的最小值为36．故答案为：36．三．解答题（共6小题）9．已知斜率为k 的直线l 与椭圆22:143x y C +=交于A ，B 两点，线段AB 的中点为(1M ，)(0)m m >．（1）证明：12k <-；（2）设F 为C 的右焦点，P 为C 上一点，且0FP FA FB ++=．证明：||FA ，||FP ，||FB 成等差数列，并求该数列的公差．【解答】解：（1）设1(A x ，1)y ，2(B x ，2)y ， 线段AB 的中点为(1,)M m ，122x x ∴+=，122y y m+=将A ，B 代入椭圆22:143x y C +=中，可得2211222234123412x y x y ⎧+=⎪⎨+=⎪⎩，两式相减可得，121212123()()4()()0x x x x y y y y +-++-=，即12126()8()0x x m y y -+-=，12126384y y k x x m m-∴==-=--点(1,)M m 在椭圆内，即211,(0)43m m +<>，解得302m <<∴3142k m =-<-．①（2）由题意得(1,0)F ，设3(P x ，3)y ，则1231110x x x -+-+-=，1230y y y ++=，由（1）及题设得3123()1x x x =-+=，312()20y y y m =-+=-<．又点P 在C 上，所以34m =，从而3(1,)2P -，3||2FP = ．于是1||22x FA =- ．同理2||22xFB =- ．所以121||||4()32FA FB x x +=-+= ，故||||2||FA FB FP += ，即||FA ，||FP ，||FB成等差数列．设改数列的公差为d ，则1212||||||||||2d FB FA x x =-=-= ②将34m =代入①得1k =-．所以l 的方程为74y x =-+，代入C 的方程，并整理得2171404x x -+=．故122x x +=，12128x x =，代入②解得||28d =．所以该数列的公差为28或28-．10．已知斜率为k 的直线l 与椭圆22:198x y C +=交于A 、B 两点，线段AB 的中点为(1M ，)(0)t t >．（Ⅰ）证明：13k <-；（Ⅱ）设F 为C 的右焦点，Q 为C 上的一点，且0FQ FA FB ++= ，证明：||FA ，||FQ，||FB成等差数列．【解答】（本小题满分12分）证明：（Ⅰ）设1(A x ，1)y ，2(B x ，2)y ，则有221122221(1)981(2)98x y x y ⎧+=⋯⋯⎪⎪⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⎨⎪+=⋯⋯⎪⎩（2分）（1）-（2）得12121212()()()()098x x x x y y y y +-+-+=．122x x += ，122y y t +=．∴12122()2()098x x t y y --+=．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯（3分）∴121289y y k x x t-==--．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯（4分）由题设可知点(1,)M t 在椭圆内，∴21198t +<，解得803t <<，∴818319983k t =-<-=- ．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯（5分）（Ⅱ） 0FQ FA FB ++=，M 为AB 的中点，∴2FQ FM =-，⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯（6分）(1,)M t ，(1,2)Q t ∴-．点(1,2)Q t -在椭圆上，∴214198t +=．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯（7分）又403t t >∴=．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯（8分）由（Ⅰ）知89k t =-，所以23k =-．∴直线l 的方程为42(1)33y x -=--，即223y x =-+．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯（9分）由直线l 的方程与椭圆方程联立，得22223198y x x y ⎧=-+⎪⎪⎨⎪+=⎪⎩消y 化简得2230x x --=，解得11x =-，23x =．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯（10分）从而得8(1,)3A -，(3,0)B ，又8(1,0),(1,)3F Q -，∴10||3FA ==，8||3FQ = ，||2FB = ．⋯⋯⋯⋯⋯⋯⋯（11分）∴||FA ，||FQ ，||FB成等差数列．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯（12分）11．已知1F 、2F 是椭圆22221(0)x y a b a b+=>>的左、右焦点，且离心率12e =，点P 为椭圆上的一个动点，△12PF F 的内切圆面积的最大值为43π．（1）求椭圆的方程；（2）若A ，B ，C ，D 是椭圆上不重合的四个点，满足向量1F A 与1F C 共线，1F B 与1F D共线，且0AC BD =，求||||AC BD + 的取值范围．【解答】解：（1）由几何性质可知，当，△12PF F 的内切圆面积的最大值时，即，12PF F S 取最大值，且121()22PF F max S c b bc == ，由243r ππ=，解得3r =，又由△12PF F 的周长为22a c +定值，∴223bc a c =+，又12c e a ==，可得2a c =，即b =，2c ∴=，b =4a =，故椭圆方程为2211612x y +=，（2）①当直线AC 和BD 中有一条垂直x 轴时，||||6814AC BD +=+=，②当直线AC 的斜率存在但不为0时，设AC 的方程为：(2)y k x =+，由22(2)11612y k x x y =+⎧⎪⎨+=⎪⎩得2222(34)1616480k x k x k +++-=，代入弦长公式得，2224(1)||34k AC k +=+ ，同理由221(2)11612y x kx y ⎧=-+⎪⎪⎨⎪+=⎪⎩，消去y ，代入弦长公式得2224(1)||34k BD k +=+ ，2222222168(1)168||||11(34)(43)121(1)k AC BD k k k k +∴+==+++-++，令21(0,1)1t k =∈+，则212(12t t -++∈，49]4，由①②可知||||AC BD + 的取值范围是96[7，14]．12．已知椭圆22221(0)x y a b a b +=>>经过点)2-，且椭圆的离心率12e =，过椭圆的右焦点F 作两条互相垂直的直线，分别交椭圆于点A 、B 及C 、D ．（Ⅰ）求椭圆的方程；（Ⅱ）求证：11||||AB CD +为定值；（Ⅲ）求9||||16AB CD +的最小值．【解答】解：()I 由12c e a ==，得2214c a =，222244()a c a b ∴==-，2234a b ∴=．（1），⋯（1分）由椭圆过点知，223314a b+=．（2）⋯（2分）联立（1）、（2）式解得24a =，23b =．⋯（3分）故椭圆的方程是22143x y +=．⋯（4分）11()||||II AB CD +为定值712⋯（5分）证明：椭圆的右焦点为(1,0)F '，分两种情况．1︒当直线AB 的斜率不存在时，:1AB x =，则:0CD y =．此时||3AB =，||4CD =，117||||12AB CD +=；⋯（6分）2︒当直线AB 的斜率存在时，设:(1)(0)AB y k x k =-≠，则1:(1)CD y x k=--．又设点1(A x ，1)y ，2(B x ，2)y ．联立方程组22(1)3412y k x x y =-⎧⎨+=⎩，消去y 并化简得2222(43)84120k x k x k +-+-=，∴2122843k x x k +=+，212241243k x x k -=⋯+ （7分）∴12|||AB x x ==-==2212(1)43k k +=+，⋯（8分）由题知，直线CD 的斜率为1k-，同理可得2212(1)||43k CD k +=⋯+（9分）所以2211777||||12(1)12k AB CD k ++==+为定值．⋯（10分）（Ⅲ）解：由()II 知117||||12AB CD +=，∴912911||||(||||)()16716||||AB CD AB CD AB CD +=++⋯（11分）9||1225||16()716||||CD AB AB CD =++122521(7164+= ，⋯（12分）当且仅当9||||16||||CD AB AB CD =，即3||||4AB CD =，即||3AB =，||4CD =时取等号⋯（13分）∴9||||16AB CD +的最小值为214．⋯（14分）13．已知椭圆22122:1(0)x y C a b a b +=>>的长轴长为4，离心率为12，一动圆2C 过椭圆1C 右焦点F ，且与直线1x =-相切．（1）求椭圆1C 的方程及动圆圆心轨迹2C 的方程；（2）过F 作两条互相垂直的直线，分别交椭圆1C 于P ，Q 两点，交曲线2C 于M ，N 两点，求四边形PMQN 面积的最小值．【解答】解：（1）由已知可得2222423112a a b a c c c e a =⎧=⎧⎪⇒⇒=-=⎨⎨===⎩⎪⎩，则所求椭圆方程221:143x y C +=．由已知可得动圆圆心轨迹为抛物线，且抛物线C 的焦点为(1,0)，准线方程为1x =-，则动圆圆心轨迹方程为22:4C y x =．（2）当直线MN 的斜率不存在时，||4MN =，此时PQ 的长即为椭圆长轴长，||4PQ =，从而11||||44822PMQN S MN PQ =⋅=⨯⨯=．设直线MN 的斜率为k ，则0k ≠，直线MN 的方程为：(1)y k x =-，直线PQ 的方程为1(1)y x k=--，设1(M x ，1)y ，2(N x ，2)y ，3(P x ，3)y ，4(Q x ，4)y ，由2(1)4y k x y x=-⎧⎨=⎩，消去y 可得2222(24)0k x k x k -++=，由抛物线定义可知：2221222244||||||1124k MN MF NF x x k k +=+=+++=+=+，由221(1)143y x k x y ⎧=--⎪⎪⎨⎪+=⎪⎩，消去y 得222(34)84120k x x k +-+-=，从而234212(1)|||34k PQ x x k +=-=+，∴222224211412(1)(1)||||(4)24223434PMQN k k S MN PQ k k k k ++=⋅=+=++，令21k t +=，0k > ，则1t >，则22222221242424211||||34(1)(0,3)2123(1)4(1)3213PMQN t t S MN PQ t t t t t t t t t =⋅===--+∈-+-----，所以2248213PMQN S t t =>--，所以四边形PMQN 面积的最小值为8．14．平面直角坐标系xOy 中，已知F 为椭圆22221x y a b+=的右焦点，且24a b +=，过F 作两条互相垂直的直线交椭圆分别于A 、B 与C 、D ．以F 为极点，x 轴正半轴为极轴建立极坐标系．（Ⅰ）求椭圆的极坐标方程与1||AB 的代数表达式；（Ⅱ）求11||||AB CD +的取值范围．【解答】解：由已知24b a =-，（Ⅰ）设(,0)F c，2222a a c b p c c c c -=-===c e a a==，以右焦点F 为极点，x 轴正半轴为极轴，建立极坐标系，则椭圆的极坐标方程为1cos ep e ρθ=+，即22cos ab ac c ρθ=+，其中c =设(A A ρ，)θ，则(B B ρ，)θπ+，222||1cos 1cos()1cos 1cos 1A B ep ep ep ep ep AB e e e e e cos ρρθπθθθθ∴=+=+=+=++++--，2211||2e cos AB ep θ-=，即22221||2a c cos AB ab θ-=；（Ⅱ）由（Ⅰ）得，22222222(112||||22a c cos a c cos AB CD ab ab πθθ-+-+=+2222222222222222422222(4)a c cos a c sin a c a b a a ab ab ab ab a a θθ---+-+=+===-．24a b += ，222240c a b a a ∴=-=+->，且4a <，4a <<．记f （a ）242(4)a a a a -+=-，则f '（a ）22(4)(34)2(4)a a a a +-=-，当142a -<<时，f '（a ）0>，f （a ）为增函数，则f （a）1(8+∈，)+∞，即11||||AB CD +∈，)+∞．。
圆锥曲线的第二定义
圆锥曲线的第二定义（平面内到定点与到定直线距离的比为常数e的点的轨迹）是圆锥曲线概念的重要组成部分。
揭示了圆锥曲线之间的内在联系，它不仅是研究圆锥曲线图象和性质的基础，而且在很多数学问题的求解过程中，具有不可低估的特殊功能。
一、导向功能圆锥曲线第二定义对许多问题的求解，具有明显的导向作用，优先考虑第二定义，有助于启迪思路，理顺解题线索。
例1：椭圆x2/25+y2/9=1上有一点P，如果它到左准线的距离为5/2，那么P到右焦点的距离是。
[分析]解题之前一定要认真审题，对有关曲线上一点到焦点、准线距离的问题，首先联想到圆锥曲线的第二定义。
[解]设P到左准线距离为|PM|由椭圆第二定义|PF1|/|PM|=e∴|PF1|=e|PM|=4/5×5/2=2又∵|PF1|+|PF2|=2a=10∴|PF2|=8例2：F2是椭圆x2/a2+y2/b2=1(a＞b>0)的右焦点，P(x0,y0)是椭圆上任一点，则|PF2|的值为：A. ex0-aB. a-ex0C. ex0-aD.e-ax0[分析]针对题中要求|PF2|的值，且各选项中含有e，从椭圆第二定义入手，问题不攻自破。
[解]设点P(x0,y0)到椭圆右准线x=a2/c的距离为|PN|，则|PN|=a2/c-x0 根据椭圆第二定义|PF2|=e|PN|=e(a2/c-x0)=a-ex0，故选B。
二、简化功能巧用圆锥曲线的第二定义，可以简化复杂的变形与讨论，使问题简捷获解。
例3：过抛物线y2=4x的焦点的一条直线交抛物线于A、B两点，若线段的中点的横坐标为3，则|AB|= 。
[分析]若按求焦点，设直线方程、联立方程组求|AB|过程繁琐，因此从定义出发。
[解]过A、B两点向准线引垂线AM、BN设AB中点为C(3,y0)，过C向准线引垂线CH，则CH是直角梯形ABNM的中位线。
∴|AM|+|BN|=2|CH|抛物线y2=4x的焦点为F(1,0)，准线为x=-1所以有|AB|=|AF|+|BF|=|AM|+|BN|=2|CH|=2（3+1）=8例4：已知椭圆方程为x2/b2+y2/a2=1(a>b>0)，求与这个椭圆有公共焦点的双曲线，使得以它们的交点为顶点的四边形面积最大，并求相应的四边形的顶点坐标。
圆锥曲线的第二定义双曲线的第二定义
圆锥曲线的第二定义-双曲线的第二定义巧用圆锥曲线第二定义解题整警巧用圆锥曲线第二定义解题黔西南民族职业技术学院姚忠安【摘要】圆锥曲线第二定义，揭示了圆锥曲线的内在联系。
应用圆锥曲线第二定义求解圆锥曲线的轨迹方程、离心率、与圆锥曲线有关的最值等非常简单，它能使问题化繁为简，提高准确率，达到事半功倍的效果。
【关键词】圆锥曲线第二定义轨迹离心率最值条件中的三个，用圆锥曲线定义来解决比较简单。
求圆锥曲线的离心率二例４过椭圆的左焦点Ｆ作直线与椭圆交于Ａ、Ｂ．两点，ｌ：Ｂ：ｌＩＦＩＡＦ＝５３，且直线与长轴的夹角为６。
，求椭圆的离心率。
０解：如图，作椭圆的左准线ｌ过Ａ、Ｂ两点分别作左准线的垂线，垂足分别为ｃ、Ｄ，由圆锥曲线的定ＩＩ君Ｉｌ圆锥曲线第二定义：平面内动点Ｍ定ＸＹ到点Ｆ的距离与它到定直线１距离的比是常数ｅ的点的轨迹，当０ｅ１是椭圆；当ｅ１是抛＜＜时＝时物线；当ｅ１是双曲线。
ｅ离心率，Ｆ焦点。
＞时是是求圆锥曲线的轨迹方程一例１经过点Ｍ轴率ｅ专的点Ｐｘｙ的轨迹方程。
：解：依题意，所求的点Ｐ的轨迹方程是以ｙ轴为右准线的椭圆方程，设椭圆的右焦点Ｆ因ｘ，。
为Ｐ在椭圆上且过椭圆的右顶点，由第二定义知点即Ｘ４工，。
ｙｏ＿－ＸＩ＝ＸＯＹ＝，所以椭圆右焦点，８ＣＸ６ｌＯ０。
ｆ一２，・为Ｆ，又’Ｍ在椭圆上，由一、Ｆ＼～定，止喜即／４＋。
｛，ｊ）一ｘ化简得Ｐ的轨迹方程为：即，椭圆的离心率为ｅ＝１＋９））右焦点，Ｘ为右准线，离．５０为＝２心率ｅ的圆锥曲线的轨迹方程。
＝２解：依题意，所求曲线的轨迹方程为双曲线，设Ｍ曲线上任一点，由圆锥曲线第二定ｘＹ为例５已知一抛物线以椭圆三＋。
１的左焦点．；Ｆ为顶点，以椭圆的右焦点Ｆ为焦点，Ｐ抛物线与椭圆的一个交点，如果椭圆的离为一ｌ，心率满足＝，求ｅ的值。
解：如图，设椭圆的左准线与抛物线的准线分别为ｌ。
，过点Ｐ作１垂线，垂足分别为Ａ、、ｌ．的、ｌ义，有＝，与２即喜，简２化得所线的为：；一善：求曲方程堕ｌ例３已知圆锥曲线过点Ａ．一４一８，它的一个焦点为Ｆ＝Ｂ，由圆锥曲线第二定义可知，一ｅ即ｌ，ｌ＝ｅＩｐＩ①又。
高三第二轮专题复习课案例分析——圆锥曲线定义的应用
２ 通过问题探究 ，掌握解决与圆锥曲线定义相 ． ２ 关问题的基本方法 求动 点 轨迹 ，如 果 出现 两 定点 或一 条 定直 线 ，
可 以通 过 图形 的几何 性 质 ，如线 段 中垂 线 、 角平 分 线 、 切线 长 等性 质 ，应 用平 面 几何 思 想 ，把 问题 转 化 为应 用 圆锥 曲线 的定义 来 求 轨迹 ，也是 解 决此 类 问题 的通 法 ．
切 线 方程为 Ｙ＝２ 一２ ｔ ． ｐ
Ｍ （ Ｙ） 因为 ９＝Ａ Ａ，由定 比分 点 坐标公 式 得 ｘ， 则 Ｑ
高三第二轮专题复 习课案例分析
— —
圆锥 曲线 定义 的应 用
肖
骁
福建 省 厦 门外 国语 学校 （６０ ２ ３ １１ ） 构 ， 重应 试训 练 ，导致 我省 基础教 育 大大 落后 ． 注 ”
一
３。 Ｙ ）＋ ＝４ 外切 的动 圆 圆心 Ｐ轨迹 方程 ．
段 为直 径 的圆 ，与 以双 曲线 实 轴 为 直径 的 圆相
２１ ０２年第 ３ 期
福建 中学数 学
１ ７
切 ．（ 证法 与例 ２相 似 ） （）连结 抛物 线 上任一 点与 其 中一个 焦点 的线 ２ 段 为 直径 的 圆 ，与 Ｙ轴相 切 ．
ａ— Ｄ
Ｐ作
方程 ．
的平分线上的垂线于 Ｇ，求点 Ｇ的轨迹
探 究 ３ 已知 Ａ Ｂ Ａ Ｃ的内切 圆边 Ｂ Ｃ于 Ｄ ，且
Ｂ Ｄ＝８， Ｃ ＝２，求点 的轨迹 方程 ． Ｄ
探 究 ４ 中心在 原点 ，焦 点在 Ｘ 的双 曲线 的两 轴
焦点 ，ｃ， 是双曲线右支上任意一点 ， 则
关的通性 问题 ．这样不仅可以提高综合解题能力 ， 同 时可 以激 发 学 生 的兴 趣 和热 情 ，从而 提 升学 生的 数学素养 ． 例 ３求证连结椭圆上任一点与其中一个焦点的
圆锥曲线中的第二定义应用
F 1F 2P 圆锥曲线第二定义的应用解析几何，把坐标系引入几何图形中，将几何的基本元素—点，与代数的基本研究对象—数对应起来，从而将几何问题转化为代数问题，将曲线或曲面转化为方程、函数进行解决。
在高中数学中利用解析几何的方法来研究几何图像的主要有：直线、圆、椭圆、双曲线、抛物线等。
在学习这些内容的时候，椭圆、双曲线、双曲线除了有它们的定义外，还有一个第二定义。
第二定义在解决问题方面的应用是有着很重要的地位。
下面我们就结合题目来看一下第二定义在解决问题的应用。
例题：已知，221243x y P F F 是椭圆上一点，分别是椭圆+=1上的左右焦点，12k PF PF =∙那么k 的最大值与最小值的差为 解法一：根据椭圆的定义知识可知122PF PF a +=，设1PF m =则24PF m =-，因此212k (4)4PF PF m m m m =∙=∙-=- (0,4)m ∈，此为关于m 的一元二次方程，且开口方向向下，故而有最大值 对称轴为2m =，将2m =代入可得k 的最大值为4。
(0,4)m ∈关于2m =对称则04m m ==或取到最小值，可是问题在于04m m ≠≠且因为1PF 不可能为零。
因此，m 的取值范围就有了问题，m 最小可以取到的不是无限的向零逼近。
可是m 最小可以取到多少呢？如果m 的精确地取值范围无法确定，这个问题就解决不了。
BA F 2F 1P 解法二：过点P 向两条准线做垂线，交两垂线为A 、B 两点。
由双曲线的第二定义可知，1PF PA e =且2PF PB e =则212k PF PF e PA PB =∙= 设PB x =则8PA x =-，12c e a == 那么1(8)4k x x =- []2,6x ∈此为关于m 的一元二次方程，且开口方向向下，对称轴为4x =，因此4k x =时取到最大值4，x=2或6时取到最小值3这样一来最大值与最小值的差为1.对于第一种解法里面的m 的最小值与最大值我们也可以确定下来了[]1,3m ∈。
高中数学《第二章圆锥曲线与方程复习参考题》151PPT课件 一等奖名师
学1:移项，实数的平方为非负数
x2
=(1 -
y2 b2
) a2
0
预想学生活动2:平方和等于1，
联想 sin2α+ cos2α= 1
设 x2 a2
cos2
,
y2 b2
= sin2
预想学生活动3:两个实数的平方和等于１，
这两个实数都不大于１
x2 a2
y2 1, b2
情感、态度与价值观：
通过学生自主探究、合作交流使学生亲自 体验研究知识的艰辛，从中体味成功的喜悦， 由此激发其更加积极主动的学习精神和探索勇 气；通过多媒体展示，使学生体会椭圆方程结 构的和谐美和椭圆的对称美.
3、教材重点、难点分析
重点：掌握椭圆的范围、对称性、顶点的概念、
离心率等性质并会简单应用；
设计意图：倡导学生主动参与，乐于研究，勤于动手，在师生互 动共同探索的过程中加深对椭圆范围和对称性的理解，培养学生 获取新知识的能力。
方程 16x2 + 25y2 = 400 表示什么样的曲线，你能 利用以前学过的知识准确的画出它的图形吗？
x = 0时y = 4,y = 0时x = 5 当x = 0时, y =±4 当y = 0 时,x =±5
三、教学过程分析
（一）问题引入
设置问题1
方程 16x2 + 25y2 = 400 表示什么
样的曲线，你能利用以前学过的知识准确 的画出它的图形吗？
预想学生活动：
x = 0时y = 4,y = 0时x = 5 当x = 0时, y =±4 当y = 0 时,x =±5
这样作图准确吗？你的依据是什么？
椭圆性质4——离心率
小组合作试验、讨论
试验探究：学生每小组都用长为10cm的线绳，在直
新教材北师大版高中数学选择性必修第一册第二章圆锥曲线 知识点考点重点难点解题规律归纳总结
第二章 圆锥曲线1 椭圆 ........................................................................................................................... - 1 -1.1 椭圆及其标准方程 ......................................................................................... - 1 - 1.2 椭圆的简单几何性质 ..................................................................................... - 6 - 2 双曲线 ..................................................................................................................... - 11 -2.1 双曲线及其标准方程 ................................................................................... - 11 - 2.2 双曲线的简单几何性质 ............................................................................... - 15 - 3 抛物线 ..................................................................................................................... - 19 -3.1 抛物线及其标准方程 ................................................................................... - 19 - 3.2 抛物线的简单几何性质 ............................................................................... - 23 - 4 直线与圆锥曲线的位置关系 .................................................................................. - 28 -4.1 直线与圆锥曲线的交点 ............................................................................... - 28 - 4.2 直线与圆锥曲线的综合问题 ....................................................................... - 28 -1 椭圆1.1 椭圆及其标准方程1．椭圆的定义平面内到两个定点F 1，F 2的距离之和等于常数(大于|F 1F 2|)的点的集合(或轨迹)叫作椭圆．这两个定点叫作椭圆的焦点，两焦点间的距离叫作椭圆的焦距．1．椭圆定义中，将“大于|F 1F 2|”改为“等于|F 1F 2|”或“小于|F 1F 2|”，其他条件不变，点的轨迹是什么？[提示] 当距离之和等于|F 1F 2|时，动点的轨迹就是线段F 1F 2；当距离之和小于|F 1F 2|时，动点的轨迹不存在．2．椭圆的标准方程焦点在x 轴上 焦点在y 轴上 标准方程 x 2a 2＋y 2b 2＝1 (a >b >0) y 2a 2＋x 2b 2＝1 (a >b >0) 焦点 (－c ，0)，(c ，0)(0，－c )，(0，c )a 、b 、c 的关系c 2＝a 2－b 22．椭圆x 29＋y 216＝1的焦点是在x 轴上，还是在y 轴上？[提示] 椭圆x 29＋y 216＝1的焦点在y 轴上．疑难问题类型1 椭圆定义及应用【例1】 (1)椭圆x 225＋y 29＝1上一点A 到焦点F 的距离为2，B 为AF 的中点，O 为坐标原点，则|OB |的值为( )A ．8B ．4C ．2D ．32(2)已知B (－5，0)、C (5，0)，且△ABC 的周长等于24，则顶点A 的轨迹方程为________．(3)已知F 1，F 2是椭圆x 2a 2＋y 2b 2＝1(a ＞b ＞0)的焦点，过F 1的直线AB 与椭圆交于A 、B 两点，则△ABF 2的周长为________．(1)B (2)x 249＋y 224＝1(y ≠0) (3)4a [(1)设F ′为椭圆的另一焦点，则|AF |＋|AF ′|＝2a ＝10，∴|AF ′|＝8，∵O ，B 分别为FF ′，AF 的中点．∴|OB |＝12|AF ′|＝4．(2)由已知得，|AB |＋|AC |＝14，由椭圆的定义可知，顶点A 的轨迹是椭圆， 又2c ＝10，2a ＝14，即c ＝5，a ＝7， 所以b 2＝a 2－c 2＝24．当点A 在直线BC 上，即y ＝0时，A 、B 、C 三点不能构成三角形，所以点A 的轨迹方程是x 249＋y 224＝1(y ≠0)．(3)∵|AF1|＋|AF2|＝2a，|BF1|＋|BF2|＝2a，∴△ABF2的周长＝|AB|＋|AF2|＋|BF2|＝|AF1|＋|BF1|＋|AF2|＋|BF2|＝2a＋2a＝4a．]由椭圆定义可知，椭圆上任一点到椭圆的两个焦点距离之和为定值，所以椭圆定义有以下应用：(1)实现两个焦半径之间的相互转化；,(2)将两个焦半径之和看成一个整体，求解定值问题.类型2求椭圆的标准方程[探究问题]1．同一椭圆在不同坐标系下的方程相同吗？[提示]不同．2．在椭圆标准方程的推导过程中，为什么令b2＝a2－c2，b＞0?[提示]令b2＝a2－c2可以使方程变得简单整齐，在今后讨论椭圆的几何性质时，b还有明确的几何意义．3．椭圆x2a2＋y2b2＝1和y2a2＋x2b2＝1(a＞b＞0)有何异同点？[提示]因为椭圆标准方程中的两个参数a，b确定了椭圆的形状、大小，所以椭圆x2a2＋y2b2＝1和y2a2＋x2b2＝1(a＞b＞0)的形状、大小相同，但这两个椭圆的位置不同，焦点坐标也不同．【例2】写出适合下列条件的椭圆的标准方程：(1)焦点坐标为(－4，0)，(4，0)，并且过点(－5，3)；(2)经过点P1(6，1)，P2(－3，－2)．[思路点拨](1)设出相应焦点位置的椭圆方程，利用关系式b2＝a2－c2及点(－5，3)在椭圆上求待定系数；(2)由于焦点位置不明确，可将其设成Ax 2＋By 2＝1(A >0，B >0)的形式，再进一步确定A ，B ．[解] (1)依题意知椭圆的焦点在x 轴上，可设它的标准方程为x 2a 2＋y 2b 2＝1(a ＞b ＞0)．由已知得c ＝4，所以a 2－b 2＝16．①因为点(－5，3)在椭圆上，所以(－5)2a 2＋(3)2b 2＝1，即5a 2＋3b 2＝1．② 由①②得a 2＝20，b 2＝4．因此，所求椭圆的标准方程为x 220＋y 24＝1．(2)设椭圆的方程为Ax 2＋By 2＝1(A >0，B >0)，由已知得 ⎩⎨⎧6A ＋B ＝13A ＋2B ＝1， 解得A ＝19，B ＝13．∴所求的椭圆的标准方程为x 29＋y 23＝1．1．求椭圆标准方程的方法(1)定义法：根据椭圆的定义，判断出轨迹是椭圆，然后写出其方程． (2)待定系数法：设出椭圆的标准方程，再依据条件确定a 2、b 2的值，其一般步骤是：①定位：确定椭圆的焦点在x 轴还是y 轴上，从而设出相应的标准方程的形式． ②定量：根据已知条件，建立关于a 、b 、c 的方程组，求出a 2、b 2，从而写出椭圆的标准方程．2．椭圆的标准方程在形式上可统一为Ax 2＋By 2＝1，其中A 、B 是不等的正常数．类型3 椭圆标准方程的简单应用【例3】 (1)已知方程x 25－2m ＋y 2|m |－1＝1表示焦点在y 轴上的椭圆，则实数m的取值范围为________．(2)已知椭圆方程为kx 2＋3y 2－6k ＝0，焦距为4，则k 的值为________． (1)⎝ ⎛⎭⎪⎫2，52 (2)1或5 [(1)∵椭圆焦点在y 轴上，∴其标准方程应为y 2a 2＋x 2b 2＝1(a ＞b ＞0)，∴|m |－1＞5－2m ＞0，解得2＜m ＜52，∴m 的取值范围为2＜m ＜52．(2)将方程kx 2＋3y 2－6k ＝0化为x 26＋y 22k ＝1．∵焦距为4，∴2c ＝4，即c ＝2．当焦点在x 轴上时，6－2k ＝4，解得k ＝1； 当焦点在y 轴上时，2k －6＝4，解得k ＝5． 综上，k ＝1或5．]1．判断焦点所在坐标轴的依据是看x 2项，y 2项的分母哪个大，焦点在分母大的对应的坐标轴上．2．对于方程x 2m ＋y 2n ＝1(m ＞0，n ＞0)，当m >n >0时，方程表示焦点在x 轴上的椭圆；当n ＞m ＞0时，方程表示焦点在y 轴上的椭圆．特别地，当n ＝m ＞0时，方程表示圆心在原点的圆．归纳总结1．平面内到两定点F 1，F 2的距离之和为常数，即|MF 1|＋|MF 2|＝2a ， 当2a >|F 1F 2|时，轨迹是椭圆；当2a ＝|F 1F 2|时，轨迹是一条线段F 1F 2； 当2a <|F 1F 2|时，轨迹不存在．2．涉及椭圆的焦点三角形问题，可结合椭圆的定义列出|PF 1|＋|PF 2|＝2a 求解，回归定义是求解椭圆的焦点三角形问题的常用方法．3．用待定系数法求椭圆的标准方程时，若已知焦点的位置，可直接设出标准方程；若焦点位置不确定，可分两种情况求解，也可设Ax 2＋By 2＝1(A >0，B >0，A ≠B )求解，避免分类讨论．1.2椭圆的简单几何性质椭圆的几何性质焦点的位置焦点在x轴上焦点在y轴上图形标准方程x2a2＋y2b2＝1(a＞b＞0)y2a2＋x2b2＝1(a＞b＞0)对称性对称轴x轴和y轴，对称中心(0，0)范围－a≤x≤a且－b≤y≤b －b≤x≤b且－a≤y≤a顶点A1(－a，0)、A2(a，0)，B1(0，－b)、B2(0，b)A1(0，－a)、A2(0，a)，B1(－b，0)、B2(b，0)轴长短轴长＝2b，长轴长＝2a焦点F1(－c，0)、F2(c，0)F1(0，－c)、F2(0，c)焦距|F1F2|＝2c离心率e＝ca(0＜e＜1)(1)椭圆方程x2a2＋y2b2＝1(a＞b＞0)中，a，b，c的几何意义是什么？(2)椭圆上的点到焦点的最大距离与最小距离分别是什么？[提示](1)在方程x2a2＋y2b2＝1(a＞b＞0)中，a，b，c的几何意义如图所示．即a，b，c正好构成了一个以对称中心，一个焦点、一个短轴顶点构成的直角三角形．(2)最大距离：a＋c；最小距离：a－c．疑难问题类型1 椭圆的几何性质 [探究问题]1．椭圆x 2a 2＋y 2b 2＝1(a ＞b ＞0)上，到中心O 和焦点F 1(－c ，0)的距离最近和最远的点分别在什么位置？[提示] 椭圆上，到中心O 的距离最近的点是短轴端点B 1和B 2；到中心O 的距离最远的点是长轴端点A 1和A 2．点(a ，0)，(－a ，0)与焦点F 1(－c ，0)的距离，分别是椭圆上的点与焦点F 1的最远距离和最近距离．2．利用椭圆方程如何判断点P (x 0，y 0)与椭圆x 2a 2＋y 2b 2＝1(a ＞b ＞0)的位置关系？ [提示] 点P (x 0，y 0)与椭圆x 2a 2＋y 2b 2＝1(a ＞b ＞0)的位置关系： 点P 在椭圆上⇔x 20a 2＋y 20b 2＝1； 点P 在椭圆内部⇔x 20a 2＋y 20b 2＜1； 点P 在椭圆外部⇔x 20a 2＋y 20b 2＞1．3．椭圆的离心率是如何刻画椭圆的扁平程度的？ [提示] e 的大小决定了椭圆的扁圆程度． 因为a 2＝b 2＋c 2，所以ba ＝1－e 2，因此，当e 越趋近于1时，ba 越接近于0，椭圆越扁； 当e 越趋近于0时，ba越接近于1，椭圆越接近于圆．【例1】 (1)椭圆x 225＋y 29＝1与x 29－k ＋y 225－k ＝1(0＜k ＜9)的( )A ．长轴长相等B ．短轴长相等C ．离心率相等D ．焦距相等(2)已知椭圆的标准方程为x 2100＋y 264＝1，O 为坐标原点，则椭圆上的点P 到椭圆中心|OP |的范围为( )A ．[6，10]B ．[6，8]C ．[8，10]D ．[16，20](3)(一题两空)椭圆4x 2＋9y 2＝36的长轴长为________，短轴长为________． (1)D (2)C (3)6 4 [(1)椭圆x 225＋y 29＝1中c 21＝25－9＝16，椭圆x 29－k ＋y 225－k＝1中c 22＝25－k －(9－k )＝16，∴两椭圆焦距相等．(2)设P (x 0，y 0)，则|OP |＝x 20＋y 20．由椭圆的范围，知|x 0|≤a ＝10，|y 0|≤b ＝8， 又∵P 在椭圆上，∴x 20100＋y 2064＝1， ∴y 20＝64－1625x 20，∴|OP |＝925x 20＋64.∵0≤x 20≤100，∴64≤925x 20＋64≤100，∴8≤|OP |≤10．(3)把已知方程化为椭圆的标准方程为：x 29＋y 24＝1，∴a ＝3，b ＝2，∴长轴长为2a ＝6，短轴长为2b ＝4．]用标准方程研究几何性质的步骤 (1)将椭圆方程化为标准形式.(2)确定焦点位置.(焦点位置不确定的要分类讨论) (3)求出a ，b ，c . (4)写出椭圆的几何性质.类型2 由椭圆的简单性质求方程【例2】 求适合下列条件的椭圆的标准方程： (1)焦点在y 轴上，a ＝2，离心率e ＝12；(2)一焦点坐标为(－3，0)，一顶点坐标为(0，5)； (3)过点(3，0)，离心率e ＝63．[思路点拨](1)由a＝2，e＝ca＝12，易得c，代入b2＝a2－c2可求得b2，此时可写出焦点在y轴上的椭圆方程；(2)由已知可以确定焦点在x轴上及c，b的值，从而可写出椭圆的标准方程；(3)不能确定焦点所在的坐标轴，需分类讨论．[解](1)由a＝2，e＝12，可得a2＝4，且c2＝12，即c＝1，所以b2＝a2－c2＝4－1＝3．已知椭圆的焦点在y轴上，所以所求的标准方程为y24＋x23＝1．(2)由椭圆的一个焦点坐标为(－3，0)，可知椭圆的焦点在x轴上，且c＝3．又由一顶点坐标为(0，5)，可得b＝5，所以a2＝b2＋c2＝25＋9＝34．因此所求的标准方程为x234＋y225＝1．(3)当椭圆的焦点在x轴上时，因为a＝3，e＝63，所以c＝6，从而b2＝a2－c2＝3，所以椭圆的标准方程为x29＋y23＝1；当椭圆的焦点在y轴上时，因为b＝3，e＝63，所以a2－b2a＝63，所以a2＝27，所以椭圆的标准方程为y227＋x29＝1．综上，所求椭圆的标准方程为x29＋y23＝1或y227＋x29＝1．已知椭圆的简单性质求标准方程：(1)先看题目的条件能否确定焦点所在的坐标轴，当不能确定焦点所在的坐标轴时，需分焦点在x轴上或在y轴上进行讨论.(2)然后依据关系式e＝ca，b2＝a2－c2确定a，b的值，从而求出椭圆的标准方程.类型3求椭圆的离心率【例3】已知F1，F2是椭圆的两个焦点，过F1且与椭圆长轴垂直的直线交椭圆于A，B两点，若△ABF2是正三角形，求该椭圆的离心率．[思路点拨]根据已知条件得出a、c的关系即可．[解]不妨设椭圆的焦点在x轴上，因为AB⊥F1F2，且△ABF2为正三角形，所以在Rt△AF1F2中，∠AF2F1＝30°，令|AF1|＝x，则|AF2|＝2x，所以|F1F2|＝|AF2|2－|AF1|2＝3x＝2c，由椭圆的定义，可知|AF1|＋|AF2|＝2a＝3x，∴e＝2c2a＝3x3x＝33．求椭圆的离心率通常有两种方法：(1)若给定椭圆的方程，则根据焦点位置先求a2、b2，再求出a、c的值，利用公式e＝ca直接求解；(2)若椭圆的方程未知，则根据条件建立a、b、c之间的关系式，化为关于a、c的齐次方程，再将方程两边同除以a的最高次幂，得到e的方程，解方程求得e.归纳总结1．已知椭圆的方程讨论椭圆的性质时，若不是标准形式，应先化成标准形式．2．根据椭圆的几何性质，可以求椭圆的标准方程，其基本思路是“先定位，再定量”，常用的方法是待定系数法．3．椭圆的范围给出了椭圆上的点的横坐标、纵坐标的取值范围，常用来求解与椭圆有关的最值与范围问题．4．椭圆的对称性是椭圆的重要几何性质，在解题时，恰当使用对称性能简化求解过程．2双曲线2.1双曲线及其标准方程1．双曲线的定义平面内到两个定点F1，F2的距离之差的绝对值等于常数(大于零且小于|F1F2|)的点的集合(或轨迹)叫作双曲线．这两个定点叫作双曲线的焦点，两个焦点间的距离叫作双曲线的焦距．1．双曲线定义中，将“小于|F1F2|”改为“等于|F1F2|”或“大于|F1F2|”的常数，其他条件不变，点的轨迹是什么？[提示]当距离之差等于|F1F2|时，动点的轨迹就是两条射线，端点分别是F1、F2，当距离之差大于|F1F2|时，动点的轨迹不存在．2．双曲线定义中，将“差的绝对值”改为“差”，其他条件不变，点的轨迹是什么？[提示]动点的轨迹是双曲线的一支．2．双曲线的标准方程焦点在x轴上焦点在y轴上标准方程x2a2－y2b2＝1(a>0，b>0)y2a2－x2b2＝1(a>0，b>0)焦点F1(－c，0)，F2(c，0)F1(0，－c)，F2(0，c)焦距|F1F2|＝2ca、b、c的关系c2＝a2＋b23．确定双曲线的标准方程需要知道哪些量？[提示]a，b的值及焦点所在的位置．疑难问题类型1双曲线的定义及应用双曲线中，焦点三角形的面积问题【例1】 已知双曲线x 29－y 216＝1的左，右焦点分别是F 1，F 2，若双曲线上一点P 使得∠F 1PF 2＝60°，求△F 1PF 2的面积．[解] 由x 29－y 216＝1，得a ＝3，b ＝4，c ＝5．由定义和余弦定理得|PF 1|－|PF 2|＝±6，|F 1F 2|2＝|PF 1|2＋|PF 2|2－2|PF 1|·|PF 2|cos 60°，所以102＝(|PF 1|－|PF 2|)2＋|PF 1|·|PF 2|， 所以|PF 1|·|PF 2|＝64，所以S △F 1PF 2＝12|PF 1|·|PF 2|·sin ∠F 1PF 2＝12×64×32＝163．利用双曲线定义求点的轨迹方程【例2】 已知定点A (0，7)，B (0，－7)，C (12，2)，以C 为一个焦点作过A ，B 的椭圆，求另一焦点F 的轨迹方程．[思路点拨] 考查点F 的几何性质，利用双曲线的定义求解． [解] 设F (x ，y )为轨迹上的任意一点， 因为A ，B 两点在以C ，F 为焦点的椭圆上，所以|F A |＋|CA |＝2a ，|FB |＋|CB |＝2a (其中a 表示椭圆的长半轴长)． 所以|F A |＋|CA |＝|FB |＋|CB |．所以|F A |－|FB |＝|CB |－|CA |＝122＋92－122＋(－5)2＝2，即|F A |－|FB |＝2． 由双曲线的定义知，F 点在以A ，B 为焦点，2为实轴长的双曲线的下半支上．所以点F 的轨迹方程是y 2－x248＝1(y ≤－1)．1．利用双曲线的定义解决与焦点有关的问题，一是要注意||PF 1|－|PF 2||＝2a 的变形使用，特别是与|PF 1|2＋|PF 2|2，|PF 1|·|PF 2|间的关系．2．利用双曲线的定义求曲线的轨迹方程， 其基本步骤为 ①寻求动点M 与定点F 1，F 2 之间的关系；②根据题目的条件计算是否满足||MF 1|－|MF 2||＝2a (常数，a >0)；③判断：若2a <2c ＝|F 1F 2|，满足定义，则动点M 的轨迹就是双曲线，且2c ＝|F 1F 2|，b 2＝c 2－a 2，进而求出相应a ，b ，c ；④根据F 1，F 2所在的坐标轴写出双曲线的标准方程．类型2 求双曲线的标准方程【例3】 (1)已知双曲线过点(3，－42)和⎝ ⎛⎭⎪⎫94，5，求双曲线的标准方程；(2)求与双曲线x 216－y 24＝1有公共焦点，且过点(32，2)的双曲线方程． [思路点拨] 用待定系数法求解．[解] (1)设所求双曲线方程为Ax 2－By 2＝1()AB >0， 则⎩⎪⎨⎪⎧9A －32B ＝1，8116A －25B ＝1， 解得⎩⎪⎨⎪⎧A ＝－19，B ＝－116，∴双曲线的标准方程为y 216－x 29＝1．(2)法一：设所求双曲线方程为x 2a 2－y 2b 2＝1(a >0，b >0)， 由题意易求得c ＝25．又双曲线过点(32，2)， ∴(32)2a 2－4b 2＝1．又∵a 2＋b 2＝(25)2， ∴a 2＝12，b 2＝8．故所求双曲线方程为x 212－y 28＝1．法二：设双曲线方程为x 216－k －y 24＋k ＝1(－4<k <16)，将点(32，2)代入得k ＝4， ∴所求双曲线方程为x 212－y 28＝1．待定系数法求双曲线方程的步骤类型3曲线类型的判定【例4】已知曲线C：x2t2＋y2t2－1＝1(t≠0，t≠±1)．(1)求t为何值时，曲线C分别为椭圆、双曲线；(2)求证：不论t为何值，曲线C有相同的焦点．[思路点拨]方程Ax2＋By2＝1表示的轨迹是由参数A，B的值及符号确定，因此要确定轨迹，需对A，B进行讨论．[解](1)当|t|>1时，t2>0，t2－1>0，且t2≠t2－1，曲线C为椭圆；当|t|<1时，t2>0，t2－1<0，曲线C为双曲线．(2)证明：当|t|>1时，曲线C是椭圆，且t2>t2－1，因此c2＝a2－b2＝t2－(t2－1)＝1，∴焦点为F1(－1，0)，F2(1，0)．当|t|<1时，双曲线C的方程为x2t2－y21－t2＝1，∵c2＝a2＋b2＝t2＋1－t2＝1，∴焦点为F1(－1，0)，F2(1，0)．综上所述，无论t为何值，曲线C有相同的焦点．方程Ax2＋By2＝1(A，B≠0)表示双曲线的充要条件为AB<0，若A<0，B>0，则方程表示焦点在y轴上的双曲线；若B<0，A>0，则方程表示焦点在x轴上的双曲线.即双曲线的焦点位置是由x2，y2的系数的正负决定的.归纳总结1．对双曲线定义的理解(1)定义中距离的差要加绝对值，否则只为双曲线的一支．设F1，F2表示双曲线的左，右焦点，若|MF1|－|MF2|＝2a，则点M在右支上；若|MF2|－|MF1|＝2a，则点M在左支上．(2)双曲线定义的应用：①若||MF1|－|MF2||＝2a(0<2a<|F1F2|)，则动点M的轨迹为双曲线．②若动点M在双曲线上，则||MF1|－|MF2||＝2a．2．求双曲线标准方程的步骤(1)定位：在标准方程的前提下，确定焦点位于哪条坐标轴上，以确定方程的形式．(2)定量：确定a2，b2的数值．提醒：若焦点的位置不明确，应注意分类讨论，也可以设双曲线方程为mx2＋ny2＝1的形式，其中mn<0．2.2双曲线的简单几何性质双曲线的性质标准方程x2a2－y2b2＝1(a＞0，b＞0)y2a2－x2b2＝1(a＞0，b＞0)图形性质焦点F1(－c，0)，F2(c，0)F1(0，－c)，F2(0，c)焦距|F1F2|＝2c范围x≥a或x≤－a，y∈R y≥a或y≤－a，x∈R 顶点(－a，0)，(a，0)(0，－a)，(0，a)对称性对称轴：x轴、y轴；对称中心：坐标原点轴长实轴长＝2a，虚轴长＝2b渐近线xa±yb＝0或y＝±ba xxb±ya＝0或y＝±ab x离心率e＝ca(e＞1)(1)渐近线相同的双曲线是同一条双曲线吗？(2)双曲线的离心率和渐近线的斜率有怎样的关系？[提示](1)渐近线相同的双曲线有无数条，但它们实轴与虚轴的长的比值相同．(2)e2＝c2a2＝1＋b2a2，ba是渐近线的斜率或其倒数．疑难问题类型1双曲线的简单性质【例1】求双曲线9y2－4x2＝－36的顶点坐标、焦点坐标、实轴长、虚轴长、离心率和渐近线方程．[思路点拨]先将双曲线的形式化为标准方程，再研究其性质．[解]双曲线的方程化为标准形式是x29－y24＝1，∴a2＝9，b2＝4，∴a＝3，b＝2，c＝13．又曲线的焦点在x轴上，∴顶点坐标为(－3，0)，(3，0)，焦点坐标为(－13，0)，(13，0)，实轴长2a＝6，虚轴长2b＝4，离心率e＝ca＝133，渐近线方程为y＝±23x．1．由双曲线方程探究其简单几何性质时，需先看所给方程是否为标准方程，若不是，需先把方程化为标准方程，这是依据方程求参数a，b，c值的关键．2．写顶点坐标、焦点坐标、渐近线方程时，需先由方程确定焦点所在的坐标轴，否则易出错，需注意双曲线方程与渐近线方程的对应关系．类型2利用双曲线的性质求双曲线方程【例2】求适合下列条件的双曲线的标准方程．(1)实轴长为16，离心率为5 4；(2)双曲线C的右焦点为(2，0)，右顶点为(3，0)．[思路点拨]由双曲线的几何性质，列出关于a，b，c的方程，求出a，b，c 的值．[解](1)设双曲线的标准方程为x2a2－y2b2＝1或y2a2－x2b2＝1(a>0，b>0)．由题意知2a＝16，ca＝54，c2＝a2＋b2，解得c＝10，a＝8，b＝6，所以双曲线的标准方程为x264－y236＝1或y264－x236＝1．(2)设双曲线方程为x2a2－y2b2＝1(a>0，b>0)．由已知得a＝3，c＝2，∴b2＝c2－a2＝1．∴双曲线的标准方程为x23－y2＝1．1．求双曲线方程，关键是求a，b的值，在解题过程中应熟悉a，b，c，e等元素的几何意义及它们之间的联系，并注意方程思想的应用．2．若已知双曲线的渐近线方程ax±by＝0，可设双曲线方程为a2x2－b2y2＝λ．类型3双曲线的离心率【例3】已知以双曲线C的两个焦点及虚轴的两个端点为顶点的四边形中，有一个内角为60°，求双曲线C的离心率．[思路点拨]确定四边形中为60°的内角，通过解三角形得a，b，c的关系，进而求出离心率．[解]设双曲线方程为x2a2－y2b2＝1(a>0，b>0)，如图所示，由于在双曲线中c>b，故在Rt△OF1B2中，只能是∠OF1B2＝30°，所以bc＝tan 30°，c＝3b，所以a＝2b，离心率e＝ca＝32＝62．求双曲线离心率的两种方法(1)直接法：若已知a，c可直接利用e＝ca求解.(2)方程法：若无法求出a，b，c的具体值，但根据条件可确定a，b，c之间的关系，可通过b2＝c2－a2，将关系式转化为关于a，c的齐次方程，借助于e＝ca，转化为关于e的n次方程求解.归纳总结1．由已知双曲线的方程求双曲线的几何性质时，注意首先应将方程化为标准形式，并要特别注意焦点所在的位置，防止将焦点坐标和渐近线方程写错．2．注意双曲线性质间的联系，尤其是双曲线的渐近线斜率与离心率之间的联系，并注意数形结合，从直观入手．3．椭圆、双曲线的标准方程都可写成Ax2＋By2＝1的形式，当A>0，B>0且A≠B 时表示椭圆，当AB<0时表示双曲线．3 抛物线3.1 抛物线及其标准方程1．抛物线的定义平面内与一个定点F 和一条定直线l (l 不经过点F )的距离相等的点的集合(或轨迹)叫作抛物线，定点F 叫作抛物线的焦点，定直线l 叫作抛物线的准线．1．抛物线的定义中，若点F 在直线l 上，那么动点的轨迹是什么？ [提示] 点的轨迹是过点F 且垂直于直线l 的直线． 2．抛物线的标准方程 图形标准 方程 y 2＝2px (p ＞0) y 2＝－2px(p ＞0) x 2＝2py (p ＞0) x 2＝－2py (p ＞0) 焦点 坐标 ⎝ ⎛⎭⎪⎫p 2，0 ⎝ ⎛⎭⎪⎫－p 2，0 ⎝ ⎛⎭⎪⎫0，p 2 ⎝ ⎛⎭⎪⎫0，－p 2 准线 方程x ＝－p 2x ＝p 2y ＝－p 2y ＝p 22．抛物线的标准方程y 2＝2px (p >0)中p 的几何意义是什么？ [提示] 焦点到准线的距离．3．已知抛物线的标准方程，怎样确定抛物线的焦点位置和开口方向？ [提示] 一次项变量为x (或y )，则焦点在x 轴(或y 轴)上；若系数为正，则焦点在正半轴上；系数为负，则焦点在负半轴上．焦点确定，开口方向也随之确定．疑难问题类型1 抛物线的定义【例1】 已知F 是抛物线y 2＝x 的焦点，A ，B 是该抛物线上的两点，|AF |＋|BF |＝3，则线段AB 的中点到y 轴的距离为( )A ．34B ．1C ．54D ．74[思路点拨] 如图，过A 、B 分别作准线l 的垂线AD ，BC ，垂足分别为D ，C ，M 是线段AB 的中点，MN 垂直准线l 于N ，由于MN 是梯形ABCD 的中位线，所以|MN |＝|AD |＋|BC |2．C [由抛物线的定义知|AD |＋|BC |＝|AF |＋|BF |＝3，所以|MN |＝32，又由于准线l 的方程为x ＝－14，所以线段AB 中点到y 轴的距离为32－14＝54，故选C ．]1．解答本题的关键是利用抛物线的定义把到焦点的距离转化为到准线的距离．2．与抛物线有关的问题中，涉及到焦点的距离或到准线的距离时，一般是利用定义对两个距离进行相互转化．类型2 求抛物线的标准方程求抛物线的焦点坐标或准线方程【例2】 求下列抛物线的焦点坐标和准线方程． (1)y 2＝40x ；(2)4x 2＝y ；(3)6y 2＋11x ＝0．[解] (1)焦点坐标为(10，0)，准线方程为x ＝－10． (2)由4x 2＝y 得x 2＝14y ． ∵2p ＝14，∴p ＝18．∴焦点坐标为(0，116)，准线方程为y ＝－116．(3)由6y 2＋11x ＝0，得y 2＝－116x ， 故焦点坐标为(－1124，0)，准线方程为x ＝1124．求抛物线的标准方程【例3】 求满足下列条件的抛物线的标准方程．(1)过点(－3，2)； (2)已知抛物线焦点在y 轴上，焦点到准线的距离为3．[思路点拨] 确定p 的值和抛物线的开口方向，写出标准方程．[解] (1)设所求的抛物线方程为y 2＝－2p 1x (p 1＞0)或x 2＝2p 2y (p 2＞0)，∵过点(－3，2)，∴4＝－2p 1×(－3)或9＝2p 2×2．∴p 1＝23或p 2＝94．故所求的抛物线方程为y 2＝－43x 或x 2＝92y ．(2)由题意知，抛物线标准方程为x 2＝2py (p ＞0)或x 2＝－2py (p ＞0)且p ＝3， ∴抛物线标准方程为x 2＝6y 或x 2＝－6y ．1．根据抛物线方程求准线方程或焦点坐标时，应先把抛物线的方程化为标准方程，这样才能准确写出抛物线的准线方程．2．求抛物线方程的主要方法是待定系数法，若已知抛物线的焦点位置，则可设出抛物线的标准方程，求出p 值即可，若抛物线的焦点位置不确定，则要分情况讨论，另外，焦点在x 轴上的抛物线方程可统一设成y 2＝ax (a ≠0)，焦点在y 轴上的抛物线方程可统一设成x 2＝ay (a ≠0)．类型3 抛物线的实际应用【例4】 一辆卡车高3 m ，宽1.6 m ，欲通过断面为抛物线型的隧道，已知拱口宽恰好是拱高的4倍，若拱口宽为a m ，求使卡车通过的a 的最小整数值．[思路点拨] 解答本题首先建系，转化成抛物线的问题，再利用抛物线的方程解决问题．[解] 以隧道顶点为原点，拱高所在直线为y 轴建立直角坐标系，则点B 的坐标为⎝ ⎛⎭⎪⎫a 2，－a 4，如图所示．设隧道所在抛物线方程为x 2＝my ，则⎝ ⎛⎭⎪⎫a 22＝m ·⎝ ⎛⎭⎪⎫－a 4，∴m ＝－a ．即抛物线方程为x 2＝－ay ． 将(0.8，y )代入抛物线方程，得0.82＝－ay ，即y ＝－0.82a ． 欲使卡车通过隧道，应有y －⎝ ⎛⎭⎪⎫－a 4＞3，即a 4－0.82a ＞3． ∵a ＞0，∴a ＞12.21．∴a 应取13．1．解答本题的关键是把实际问题转化为数学问题，利用数学模型，通过数学语言(文字、符号、图形、字母等)表达、分析、解决问题．2．在建立抛物线的标准方程时，以抛物线的顶点为坐标原点，对称轴为一条坐标轴建立坐标系．这样可使得标准方程不仅具有对称性，而且曲线过原点，方程不含常数项，形式更为简单，便于应用．归纳总结1．焦点在x 轴上的抛物线，其标准方程可以统设为y 2＝mx (m ≠0)，此时焦点为F ⎝ ⎛⎭⎪⎫m 4，0，准线方程为x ＝－m 4；焦点在y 轴上的抛物线，其标准方程可以统设为x 2＝my (m ≠0)，此时焦点为F ⎝ ⎛⎭⎪⎫0，m 4，准线方程为y ＝－m 4． 2．设M (x 0，y 0)是抛物线y 2＝2px (p >0)上一点，焦点为F ，则根据抛物线的定义，抛物线的焦半径|MF |＝x 0＋p 2．3．对于抛物线上的点，利用定义可以把其到焦点的距离与到准线的距离相互转化．4．对于抛物线的四种形式的标准方程，应准确把握、熟练应用，能利用图形分析性质，学习时应能根据一种类型归纳出另外三种的相关性质，注意数形结合思想的应用．3.2 抛物线的简单几何性质1．抛物线的几何性质 标准方程 y 2＝2px (p ＞0) y 2＝－2px (p ＞0)x 2＝2py (p ＞0) x 2＝－2py (p ＞0) 图形性质 范围x ≥0，y ∈R x ≤0，y ∈R y ≥0，x ∈R y ≤0，x ∈R 对称轴 x 轴 y 轴顶点(0，0) 离心率e ＝1 2．过焦点的弦若直线过抛物线y 2＝2px (p >0)的焦点F ，与抛物线交于A (x 1，y 1)、B (x 2，y 2)两点，则(1)抛物线的焦半径|AF |＝x 1＋p 2，|BF |＝x 2＋p 2；(2)过焦点的弦|AB |＝x 1＋x 2＋p ；(3)当直线AB 垂直于抛物线的对称轴时，弦AB 叫作抛物线的通径，它的长为2p ，通径是过焦点最短的弦．直线与抛物线只有一个公共点，那么直线与抛物线一定相切吗？[提示] 可能相切，也可能相交，当直线与抛物线的对称轴平行或重合时，直线与抛物线相交且只有一个公共点．疑难问题类型1抛物线几何性质的应用【例1】正三角形的一个顶点位于坐标原点，另外两个顶点在抛物线y2＝2px(p>0)上．求这个正三角形的边长．[思路点拨]正三角形及抛物线都是轴对称图形，如果能证明x轴是它们的公共对称轴，则容易求出等边三角形的边长．[解]设正三角形OAB的顶点A，B在抛物线上，且坐标分别为(x1，y1)，(x2，y2)，则y21＝2px1，y22＝2px2．由|OA|＝|OB|，得x21＋y21＝x22＋y22，即(x1＋x2)(x1－x2)＝2px2－2px1．∴(x1－x2)(x1＋x2＋2p)＝0．∵x1>0，x2>0，2p>0，∴x1－x2＝0，即x1＝x2．由此可知|y1|＝|y2|，即点A、B关于x轴对称，∴AB⊥x轴，且∠AOx＝30°，∴y1x1＝tan 30°＝33．∵x1＝y212p，∴y1＝23p，|AB|＝2y1＝43p．∴这个正三角形的边长为43p．抛物线各元素间的关系,抛物线的焦点在其对称轴上，顶点就是抛物线与对称轴的交点，准线与对称轴垂直，准线与对称轴的交点和焦点关于顶点对称，顶点到焦点的距离与顶点到准线的距离均为p 2.类型2与中点弦、焦点弦有关的问题【例2】 (1)过点Q (4，1)作抛物线y 2＝8x 的弦AB ，恰被点Q 所平分，则AB 所在直线的方程为________．(2)已知过抛物线y 2＝2px (p >0)的焦点，斜率为22的直线交抛物线于A ，B 两点，且|AB |＝9．则该抛物线的方程为________．[思路点拨] (1)法一：设A (x 1，y 1)，B (x 2，y 2)，用点差法求k AB ；法二：设直线AB 的方程，建立方程求解．(2)设出直线方程，直线方程与抛物线方程联立，根据焦点弦长公式求解．(1)4x －y －15＝0 (2)y 2＝8x [(1)法一：设以Q 为中点的弦AB 的端点坐标为A (x 1，y 1)，B (x 2，y 2)，则有y 21＝8x 1，y 22＝8x 2，∴(y 1＋y 2)(y 1－y 2)＝8(x 1－x 2)．又y 1＋y 2＝2，∴y 1－y 2＝4(x 1－x 2)，即4＝y 1－y 2x 1－x 2， ∴k ＝4．∴所求弦AB 所在直线的方程为y －1＝4(x －4)，即4x －y －15＝0．法二：设弦AB 所在直线的方程为y ＝k (x －4)＋1．联立⎩⎨⎧ y 2＝8x ，y ＝k (x －4)＋1，消去x ，得ky 2－8y －32k ＋8＝0， 设A (x 1，y 1)，B (x 2，y 2)(x 1<x 2)，由根与系数的关系得y 1＋y 2＝8k ．又y 1＋y 2＝2，∴k ＝4．∴所求弦AB 所在直线的方程为4x －y －15＝0．(2)设直线AB 的方程为y ＝22⎝ ⎛⎭⎪⎫x －p 2， 联立⎩⎪⎨⎪⎧ y 2＝2px ，y ＝22⎝ ⎛⎭⎪⎫x －p 2，化简得4x 2－5px ＋p 2＝0，∴x 1＋x 2＝5p 4，∵|AB |＝9＝x 1＋x 2＋p ，∴5p 4＋p ＝9，∴p ＝4，∴抛物线的方程为y 2＝8x ．]直线与抛物线相交的弦长问题直线和抛物线相交于A(x1，y1)，B(x2，y2)两点，直线的斜率为k．(1)一般的弦长公式：|AB|＝1＋k2|x1－x2|．(2)焦点弦长公式：当直线经过抛物线y2＝2px(p>0)的焦点时，弦长|AB|＝x1＋x2＋p．(3)“中点弦”问题解题策略两种方法类型3抛物线中的最值问题【例3】已知抛物线y2＝2x的焦点是F，点P是抛物线上的动点，又有点A(3，2)，求|P A|＋|PF|的最小值，并求出取最小值时点P的坐标．[思路点拨]利用抛物线的定义可将|PF|转化为P到准线的距离来考虑．[解]由定义知，抛物线上点P到焦点F的距离等于点P到准线l的距离d，则|P A|＋|PF|＝|P A|＋d．将x＝3代入抛物线方程y2＝2x，得y＝±6．∵6＞2，∴点A在抛物线内部．由图可知，当P A⊥l时，|P A|＋d最小，最小值为7 2，即|P A|＋|PF|的最小值为7 2，此时点P纵坐标为2，代入y2＝2x，得x＝2．∴此时点P坐标为(2，2)．1．本题若设P(x，y)，利用两点间的距离公式建模求解，难以得到答案，而由抛物线的定义将|PF|转化为点P到准线的距离，则当P，A，Q三点共线时，|P A|＋|PF|取得最小值，从而使问题迎刃而解．2．解决这类题，就是用抛物线的定义与平面几何的知识把折线段变为直线段，即知最小值．归纳总结1．抛物线只有一个焦点，一个顶点，一条对称轴，一条准线，无对称中心．2．抛物线上一点与焦点F的连线的线段叫做焦半径，设抛物线y2＝2px(p>0)上任一点A(x0，y0)，则|AF|＝x0＋p 2．3．抛物线的顶点也在抛物线上，作为抛物线上的一个特殊点，它到焦点的距离也等于到准线的距离，解题时注意应用．4．直线与抛物线有一个交点，是直线与抛物线相切的必要不充分条件．。
专题七 解析几何 第二讲 圆锥曲线的概念与性质,与弦有关的计算问题——2022届高考理科数学三轮
③|F1A|＋|F1B|＝
2 p
；④以弦
AB
为直径的圆与准线相切．
[典型例题]
1.已知椭圆 T : x2 y2 1(a b 0) 的长半轴为 2，且过点 M 0,1 .
a2 b2 若过点 M 引两条互相垂直的直线 l1 ， l2 ，P 为椭圆上任意一点，
记点 P 到 l1 ， l2 的距离分别为 d1 ， d2 ，则 d12 d22 的最大值为( B )
C. x2 y
D. x2 1 y 2
[解析]
本题考查抛物线的定义、标准方程. 抛物线 C : x2 2 py( p 0) 的准线方程为 y p .因为 | AF | 4 ，
2 所以由抛物线的定义得 p 3 4 ，解得 p 2 ，
2 所以抛物线 C 的方程为 x2 4 y .故选 A.
因为 | BC | 2 | BF | ，所以 | BC | 2 | BN | ，所以 BC 2 ，所以 BN 2 ，
CF 3
p3
所以 BN BF 4 ， BC 8 ，
3
3
[解析]
所以 CF 4 ,因为 p CF ， AM CA
所以 2 CF 4 4 , AM CF AF 4 AF 4 AM 4
则 d12 d22 x2 (1 y)2 ，因为 P 在椭圆上，所以 x2 4 4 y2 ，
所以
d12
d
2 2
5
3y2
2y
5
3
y
1 2 3
1 3
，
y [1,1]，
[解析]
所以当
y
1 3
时，
பைடு நூலகம்d12
d22
有最大值
16 3
，所以
圆锥曲线第二定义与焦半径公式知识点练习含答案(高考数学提升复习)
第2讲 圆锥曲线第二定义与焦半径公式一．选择题（共5小题）1．已知点P 是双曲线22184x y -=上的动点，1F ，2F 为该双曲线的左右焦点，O 为坐标原点，则12||||||PF PF OP +的最大值为( )A ．B ．2C D2．已知双曲线222:1(0)4x y C a α-=>的右支上的点0(P x ，0)y 满足121||3||(PF PF F =，2F 分别是双曲线的左右焦点），则00(cy c x +为双曲线C 的半焦距）的取值范围是( )A ．)+∞B ．[2，25)2C ．25)2D ．[2，3．已知点P 是双曲线22221(0,0)x y a b a b -=>>上的动点，1F ，2F 分别是其左、右焦点，O 为坐标原点，若12||||||PF PF OP +( )A B C ．32D ．24．已知F 为抛物线2:4C y x =的焦点，过F 作两条互相垂直的直线1l ，2l ，直线1l 与C 交于A ，B 两点，直线2l 与C 交于D ，E 两点，则当||||AB DE +取得最小值时，四边形ADBE的面积为( ) A ．32B ．16C ．24D ．85．过椭圆22143x y +=的右焦点F 作两条相互垂直的直线分别交椭圆于A ，B ，C ，D 四点，则11||||AB CD +的值为( ) A ．18B ．16C ．1D ．712二．填空题（共3小题）6．已知P 是椭圆22:184x y C +=上的动点，1F ，2F 分别是其左右焦点，O 是坐标原点，则12||||||PF PF PO -的取值范围是 ．7．已知F 为抛物线2:4C y x =的焦点，过F 作两条互相垂直的直线1l ，2l ，直线1l 与C 交于A 、B 两点，直线2l 与C 交于D 、E 两点，则11||||AB DE +的值为 ． 8．已知F 为抛物线2:4C y x =的焦点，过F 作两条互相垂直的直线1l ，2l ，直线1l 与C 交于A 、B 两点，直线2l 与C 交于D 、E 两点，则||4||AB DE +的最小值为 ．三．解答题（共6小题）9．已知斜率为k 的直线l 与椭圆22:143x y C +=交于A ，B 两点，线段AB 的中点为(1M ，)(0)m m >． （1）证明：12k <-；（2）设F 为C 的右焦点，P 为C 上一点，且0FP FA FB ++=．证明：||FA ，||FP ，||FB 成等差数列，并求该数列的公差．10．已知斜率为k 的直线l 与椭圆22:198x y C +=交于A 、B 两点，线段AB 的中点为(1M ，)(0)t t >．（Ⅰ）证明：13k <-；（Ⅱ）设F 为C 的右焦点，Q 为C 上的一点，且0FQ FA FB ++=，证明：||FA ，||FQ ，||FB 成等差数列．11．已知1F 、2F 是椭圆22221(0)x y a b a b +=>>的左、右焦点，且离心率12e =，点P 为椭圆上的一个动点，△12PF F 的内切圆面积的最大值为43π．（1）求椭圆的方程；（2）若A ，B ，C ，D 是椭圆上不重合的四个点，满足向量1F A 与1F C 共线，1F B 与1F D 共线，且0AC BD =，求||||AC BD +的取值范围．12．已知椭圆22221(0)x y a b a b +=>>经过点，且椭圆的离心率12e =，过椭圆的右焦点F 作两条互相垂直的直线，分别交椭圆于点A 、B 及C 、D ． （Ⅰ）求椭圆的方程； （Ⅱ）求证：11||||AB CD +为定值； （Ⅲ）求9||||16AB CD +的最小值．13．已知椭圆22122:1(0)x y C a b a b +=>>的长轴长为4，离心率为12，一动圆2C 过椭圆1C 右焦点F ，且与直线1x =-相切．（1）求椭圆1C 的方程及动圆圆心轨迹2C 的方程；（2）过F 作两条互相垂直的直线，分别交椭圆1C 于P ，Q 两点，交曲线2C 于M ，N 两点，求四边形PMQN 面积的最小值．14．平面直角坐标系xOy 中，已知F 为椭圆22221x y a b+=的右焦点，且24a b +=，过F 作两条互相垂直的直线交椭圆分别于A 、B 与C 、D ．以F 为极点，x 轴正半轴为极轴建立极坐标系．（Ⅰ）求椭圆的极坐标方程与1||AB 的代数表达式； （Ⅱ）求11||||AB CD +的取值范围．第2讲 圆锥曲线第二定义与焦半径公式参考答案与试题解析一．选择题（共5小题）1．已知点P 是双曲线22184x y -=上的动点，1F ，2F 为该双曲线的左右焦点，O 为坐标原点，则12||||||PF PF OP +的最大值为( )A ．B ．2C D【解答】解：由题意，分子最大且分母最小时，即P 在顶点处取得最大值，不妨取顶点，0)，则12||||||PF PF OP +=，故选：D ．2．已知双曲线222:1(0)4x y C a α-=>的右支上的点0(P x ，0)y 满足121||3||(PF PF F =，2F 分别是双曲线的左右焦点），则00(cy c x +为双曲线C 的半焦距）的取值范围是( )A ．)+∞B ．[2，25)2C ．25)2D ．[2，【解答】解：由双曲线的第二定义可知10||PF ex a =+，20||PF ex a =-， 右支上的点0(P x ，0)y 满足12||3||PF PF =， 0003()2ex a ex a ex a ∴+=-⇒=，由c e a=， 解得202a x c=，P 在右支上，可得202a x a c=， 可得12ca<，即12e <，则22220022201164(1)422x c c y e x a a e+=+-=+-， 令2e t =，14t <， 可得2202011611613244()4222c y e t t x e t t+=+-=+-=+- 而132()()2f t t t =+在(1，4]递减，132()[62t t +∈，33)2， 2002522c y x ∴+<， 故选：B ．3．已知点P 是双曲线22221(0,0)x y a b a b -=>>上的动点，1F ，2F 分别是其左、右焦点，O 为坐标原点，若12||||||PF PF OP+( )AB C ．32D ．2【解答】解：不妨设P 为右支上的一点，(,)P x y 其中x a ， 1||PF ex a =+，2||PF ex a =-，||OP =∴12||||)||PF PF x a OP +=∴当x a =时，取得最大值，∴=∴e =故选：B ．4．已知F 为抛物线2:4C y x =的焦点，过F 作两条互相垂直的直线1l ，2l ，直线1l 与C 交于A ，B 两点，直线2l 与C 交于D ，E 两点，则当||||AB DE +取得最小值时，四边形ADBE的面积为( ) A ．32B ．16C ．24D ．8【解答】解：因为AB DE ⊥，要使||||AB DE +最小，而||||2|||AB DE AB + 由抛物线的对称性可得A 与D ，B 与E 关于x 轴对称， 所以可得直线DE 的斜率为1，又过抛物线的焦点(1,0)， 所以直线DE 的方程为：1y x =-，214y x y x=-⎧⎨=⎩，整理可得2440y y --=，124y y +=，124y y =-，所以可得||8DE =， 所以11883222ABCD S DE AB =⋅=⨯⨯=四边形． 故选：A ．5．过椭圆22143x y +=的右焦点F 作两条相互垂直的直线分别交椭圆于A ，B ，C ，D 四点，则11||||AB CD +的值为( ) A ．18B ．16C ．1D ．712【解答】解：由椭圆22143x y +=，得椭圆的右焦点为(1,0)F ， 当直线AB 的斜率不存在时，:1AB x =， 则:0CD y =．此时||3AB =，||4CD =，则11117||||3412AB CD +=+=； 当直线AB 的斜率存在时，设:(1)(0)AB y k x k =-≠，则1:(1)CD y x k =--．又设点1(A x ，1)y ，2(B x ，2)y ． 联立方程组22(1)3412y k x x y =-⎧⎨+=⎩， 消去y 并化简得2222(43)84120k x k x k +-+-=，∴221212228412,3434k k x x x x k k -+==++， 22222221212222841212(1)||()41()4343434k k k AB x x x x kk k k -+∴=+-=+-=+++， 由题知，直线CD 的斜率为1k-，同理可得2212(1)||43k CD k +=+．∴22117(1)7||||12(1)12k AB CD k ++==+为定值． 故选：D ．二．填空题（共3小题）6．已知P 是椭圆22:184x y C +=上的动点，1F ，2F 分别是其左右焦点，O 是坐标原点，则12||||||PF PF PO -的取值范围是 [ ．【解答】解：设P 的坐标为(,)m n椭圆22:184x y C +=中，28a =，24b =，2c ∴=，得椭圆的准线方程为2a x c=±，即4x =±作出椭圆的右准线，设P 在右准线上的射影为Q ，连结PQ ， 根据圆锥曲线的统一定义，得2||||PF e PQ =，2||||)PF e PQ m ∴=-=，同理可得1||PF =， ||PO m =∴12))||||||PF PF PO --=点(,)P m n 在椭圆22184x y+=上，得22184m n +=，∴2224(1)482m m n =-=-， 由此可得12||||||PF PF PO -=，得22122||||4()8||PF PF m m PO -=+，2[0m ∈，2]a 即2[0m ∈，8]，得224[08m m ∈+，2]，∴12||||[||PF PF PO -∈．故答案为：[7．已知F 为抛物线2:4C y x =的焦点，过F 作两条互相垂直的直线1l ，2l ，直线1l 与C 交于A 、B 两点，直线2l 与C 交于D 、E 两点，则11||||AB DE +的值为 14．【解答】解：根据题意可得，抛物线24y x =的焦点坐标为(1,0)F ，准线方程为1x =-， 设直线1:(1)(0)l y k x k =-≠， 直线1l ，2l 互相垂直，∴直线2l 的斜率为1k -，即得21:(1)l y x k=--， 设1(A x ，1)y ，2(B x ，2)y ，3(C x ，3)y ，4(E x ，4)y ，则分别将直线1l ，2l 的方程与抛物线方程联立组成方程组可得，22222(1)(24)04y k x k x k x k y x=-⎧⇒-++=⎨=⎩； 21(1)4y x k y x⎧=--⎪⎨⎪=⎩⇒2222121(4)0x x k k k -++= 由韦达定理可得，212224k x x k++=，2342241k x x k ++=， 由抛物线性质可知，抛物线上的点到焦点的距离等于到准线的距离，∴2212222444||112k k AB x x k k ++=+++=+=， 2234224||112441k DE x x k k +=+++=+=+， ∴2221111||||44444k AB DE k k +=+=++． 故答案为：14． 8．已知F 为抛物线2:4C y x =的焦点，过F 作两条互相垂直的直线1l ，2l ，直线1l 与C 交于A 、B 两点，直线2l 与C 交于D 、E 两点，则||4||AB DE +的最小值为 36 ．【解答】解：抛物线2:4C y x =的焦点(1,0)F ，准线方程为1x =-， 设直线1l 的方程为(1)y k x =-，0k ≠，联立方程组24(1)y xy k x ⎧=⎨=-⎩，则2222(42)0k x k x k -++=，设1(A x ，1)y ，2(B x ，2)y ， 可得12242x x k +=+， 由抛物线的定义可得1224||24AB x x k =++=+，由12l l ⊥，可将上式中的k 换为1k -，可得2||44DE k =+， 则222211||4||204(4)208436AB DE k k k+=+++=．当且仅当2k =±时，上式取得等号， 则||4||AB DE +的最小值为36． 故答案为：36．三．解答题（共6小题）9．已知斜率为k 的直线l 与椭圆22:143x y C +=交于A ，B 两点，线段AB 的中点为(1M ，)(0)m m >．（1）证明：12k <-；（2）设F 为C 的右焦点，P 为C 上一点，且0FP FA FB ++=．证明：||FA ，||FP ，||FB 成等差数列，并求该数列的公差．【解答】解：（1）设1(A x ，1)y ，2(B x ，2)y ， 线段AB 的中点为(1,)M m ，122x x ∴+=，122y y m +=将A ，B 代入椭圆22:143x y C +=中，可得2211222234123412x y x y ⎧+=⎪⎨+=⎪⎩， 两式相减可得，121212123()()4()()0x x x x y y y y +-++-=，即12126()8()0x x m y y -+-=，12126384y y k x x m m-∴==-=-- 点(1,)M m 在椭圆内，即211,(0)43m m +<>， 解得302m <<∴3142k m =-<-．① （2）由题意得(1,0)F ，设3(P x ，3)y ，则1231110x x x -+-+-=，1230y y y ++=，由（1）及题设得3123()1x x x =-+=，312()20y y y m =-+=-<．又点P 在C 上，所以34m =，从而3(1,)2P -，3||2FP =．于是1||(22xFA x =-．同理2||22x FB =-． 所以121||||4()32FA FB x x +=-+=，故||||2||FA FB FP+=，即||FA ，||FP ，||FB 成等差数列．设改数列的公差为d ，则1212||||||||||2d FB FA x x =-=-=②将34m =代入①得1k =-． 所以l 的方程为74y x =-+，代入C 的方程，并整理得2171404x x -+=． 故122x x +=，12128x x =，代入②解得||d =．所以该数列的公差为28或28-． 10．已知斜率为k 的直线l 与椭圆22:198x y C +=交于A 、B 两点，线段AB 的中点为(1M ，)(0)t t >．（Ⅰ）证明：13k <-；（Ⅱ）设F 为C 的右焦点，Q 为C 上的一点，且0FQ FA FB ++=，证明：||FA ，||FQ ，||FB 成等差数列．【解答】（本小题满分12分）证明：（Ⅰ）设1(A x ，1)y ，2(B x ，2)y ， 则有221122221(1)981(2)98x y x y ⎧+=⋯⋯⎪⎪⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⎨⎪+=⋯⋯⎪⎩（2分）（1）-（2）得12121212()()()()098x x x x y y y y +-+-+=．122x x +=，122y y t +=．∴12122()2()098x x t y y --+=．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯（3分） ∴121289y y k x x t -==--．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯（4分）由题设可知点(1,)M t 在椭圆内，∴21198t +<，解得803t <<， ∴818319983k t =-<-=-．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯（5分） （Ⅱ）0FQ FA FB ++=，M 为AB 的中点，∴2FQ FM =-，⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯（6分）(1,)M t ，(1,2)Q t ∴-．点(1,2)Q t -在椭圆上，∴214198t +=．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯（7分）又403t t >∴=．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯（8分）由（Ⅰ）知89k t =-，所以23k =-．∴直线l 的方程为42(1)33y x -=--，即223y x =-+．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯（9分）由直线l 的方程与椭圆方程联立，得22223198y x x y ⎧=-+⎪⎪⎨⎪+=⎪⎩消y 化简得2230x x --=，解得11x =-，23x =．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯（10分） 从而得8(1,)3A -，(3,0)B ， 又8(1,0),(1,)3F Q -，∴10||(3FA =-=，8||3FQ =，||2FB =．⋯⋯⋯⋯⋯⋯⋯（11分）∴||FA ，||FQ ，||FB 成等差数列．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯（12分）11．已知1F 、2F 是椭圆22221(0)x y a b a b +=>>的左、右焦点，且离心率12e =，点P 为椭圆上的一个动点，△12PF F 的内切圆面积的最大值为43π．（1）求椭圆的方程；（2）若A ，B ，C ，D 是椭圆上不重合的四个点，满足向量1F A 与1F C 共线，1F B 与1F D 共线，且0AC BD =，求||||AC BD +的取值范围．【解答】解：（1）由几何性质可知，当，△12PF F 的内切圆面积的最大值时， 即，12PF F S取最大值，且121()22PF F maxSc b bc ==，由243r ππ=，解得r =，又由△12PF F 的周长为22a c +定值，∴22bc a c =+， 又12c e a ==，可得2a c =，即b =2c ∴=，b =4a =，故椭圆方程为2211612x y +=，（2）①当直线AC 和BD 中有一条垂直x 轴时，||||6814AC BD +=+=， ②当直线AC 的斜率存在但不为0时，设AC 的方程为：(2)y k x =+，由22(2)11612y k x x y =+⎧⎪⎨+=⎪⎩得2222(34)1616480k x k x k +++-=，代入弦长公式得，2224(1)||34k AC k +=+，同理由221(2)11612y x kx y ⎧=-+⎪⎪⎨⎪+=⎪⎩，消去y ，代入弦长公式得2224(1)||34k BD k +=+， 2222222168(1)168||||11(34)(43)121(1)k AC BD k k k k +∴+==+++-++，令21(0,1)1t k =∈+， 则212(12t t -++∈，49]4， 由①②可知||||AC BD +的取值范围是96[7，14]． 12．已知椭圆22221(0)x y a b a b +=>>经过点，且椭圆的离心率12e =，过椭圆的右焦点F 作两条互相垂直的直线，分别交椭圆于点A 、B 及C 、D ． （Ⅰ）求椭圆的方程； （Ⅱ）求证：11||||AB CD +为定值； （Ⅲ）求9||||16AB CD +的最小值． 【解答】解：()I 由12c e a ==，得2214c a =，222244()a c a b ∴==-，2234a b ∴=．（1），⋯（1分）由椭圆过点知，223314a b+=．（2）⋯（2分） 联立（1）、（2）式解得24a =，23b =．⋯（3分）故椭圆的方程是22143x y +=．⋯（4分）11()||||II AB CD +为定值712⋯（5分） 证明：椭圆的右焦点为(1,0)F '，分两种情况．1︒当直线AB 的斜率不存在时，:1AB x =，则:0CD y =．此时||3AB =，||4CD =，117||||12AB CD +=；⋯（6分） 2︒当直线AB 的斜率存在时，设:(1)(0)AB y k x k =-≠，则1:(1)CD y x k =--．又设点1(A x ，1)y ，2(B x ，2)y ． 联立方程组22(1)3412y k x x y =-⎧⎨+=⎩， 消去y 并化简得2222(43)84120k x k x k +-+-=，∴2122843k x x k +=+，212241243k x x k -=⋯+（7分）∴12|||AB x x =-12()x x +426416((4k -=2212(1)43k k +=+，⋯（8分） 由题知，直线CD 的斜率为1k-，同理可得2212(1)||43k CD k +=⋯+（9分） 所以2211777||||12(1)12k AB CD k ++==+为定值．⋯（10分）（Ⅲ）解：由()II 知117||||12AB CD +=， ∴912911||||(||||)()16716||||AB CD AB CD AB CD +=++⋯（11分） 9||1225||16()716||||CD AB AB CD =++122521(7164+=，⋯（12分） 当且仅当9||||16||||CD AB AB CD =，即3||||4AB CD =，即||3AB =，||4CD =时取等号⋯（13分） ∴9||||16AB CD +的最小值为214．⋯（14分）13．已知椭圆22122:1(0)x y C a b a b +=>>的长轴长为4，离心率为12，一动圆2C 过椭圆1C 右焦点F ，且与直线1x =-相切．（1）求椭圆1C 的方程及动圆圆心轨迹2C 的方程；（2）过F 作两条互相垂直的直线，分别交椭圆1C 于P ，Q 两点，交曲线2C 于M ，N 两点，求四边形PMQN 面积的最小值．【解答】解：（1）由已知可得2222423112a a b a c c c e a =⎧=⎧⎪⇒⇒=-=⎨⎨===⎩⎪⎩， 则所求椭圆方程221:143xy C +=．由已知可得动圆圆心轨迹为抛物线，且抛物线C 的焦点为(1,0)，准线方程为1x =-，则动圆圆心轨迹方程为22:4C y x =．（2）当直线MN 的斜率不存在时，||4MN =， 此时PQ 的长即为椭圆长轴长，||4PQ =， 从而11||||44822PMQN S MN PQ =⋅=⨯⨯=． 设直线MN 的斜率为k ，则0k ≠，直线MN 的方程为：(1)y k x =-，直线PQ 的方程为1(1)y x k=--，设1(M x ，1)y ，2(N x ，2)y ，3(P x ，3)y ，4(Q x ，4)y ， 由2(1)4y k x y x=-⎧⎨=⎩，消去y 可得2222(24)0k x k x k -++=， 由抛物线定义可知：2221222244||||||1124k MN MF NF x x k k +=+=+++=+=+， 由221(1)143y x k x y ⎧=--⎪⎪⎨⎪+=⎪⎩，消去y 得222(34)84120k x x k +-+-=，从而234212(1)|||34k PQ x x k +=-=+，∴222224211412(1)(1)||||(4)24223434PMQNk k S MN PQ k k k k ++=⋅=+=++， 令21k t +=，0k >，则1t >，则22222221242424211||||34(1)(0,3)2123(1)4(1)3213PMQNt t S MN PQ t t t t t t tt t =⋅===--=-+∈-+-----，所以2248213PMQN S t t=>--， 所以四边形PMQN 面积的最小值为8．14．平面直角坐标系xOy 中，已知F 为椭圆22221x y a b+=的右焦点，且24a b +=，过F作两条互相垂直的直线交椭圆分别于A 、B 与C 、D ．以F 为极点，x 轴正半轴为极轴建立极坐标系．（Ⅰ）求椭圆的极坐标方程与1||AB 的代数表达式；（Ⅱ）求11||||AB CD +的取值范围． 【解答】解：由已知24b a =-，（Ⅰ）设(,0)F c，2222a a c b p c c c c -=-==，c e a =，以右焦点F 为极点，x 轴正半轴为极轴，建立极坐标系，则椭圆的极坐标方程为1cos epe ρθ=+，即22cos ab ac c ρθ=+，其中c == 设(A A ρ，)θ，则(B B ρ，)θπ+，222||1cos 1cos()1cos 1cos 1A B ep ep ep ep epAB e e e e e cos ρρθπθθθθ∴=+=+=+=++++--， 2211||2e cos AB ep θ-=，即22221||2a c cos AB abθ-=； （Ⅱ）由（Ⅰ）得，22222222()112||||22a c cos a c cos AB CD ab ab πθθ-+-+=+2222222222222222422222(4)a c cos a c sin a c ab a a ab ab ab ab a a θθ---+-+=+===-． 24a b +=，222240c a b a a ∴=-=+->，且4a <，4a <<． 记f （a ）242(4)a a a a -+=-，则f '（a ）22(4)(34)2(4)a a a a +-=-4a <<时，f '（a ）0>，f （a ）为增函数，则f （a）∈)+∞，即11||||AB CD +∈)+∞．。
2020年高考数学圆锥曲线中第二定义的三类用法(共10张PPT)
1
2
PF22
PF1
F1F22 ，即
PF2
1 2
(e2 x02
e2 4)
x02 1
6
注意：此题有更简单的做法， 上述方法只是为了巩固焦半
径的知识
第二定义
（2）离心率问题
例2：倾斜角为
6
的直线过椭圆
x2 y2 a2 b2
1 的左焦点 ，交椭圆于A,B 两点，且有 | AF | 3 | B F | ，求椭圆的离心率.
，解得
PF2
5 4
PD
5
所以
|
PM
|
4 5
|
PF2
|
PM
PD
因此当P,M,D三点共线时 PM PD 取得最小值，最小
值为从 M到右准线的距离 MH, MH 6 16 14 55
第二定义
本次课重点需要注意三点 ：
（1）是第二定义的用法； （2）是注意例2这个题目的常规做法，此外下次课会给出这种例题的常用结论； （3）需要注意焦半径的取值范围，这个范围是求离心率取值范围题目中常用的
解析：AF, B F 为左焦点上的焦半径，所以过A,B 两点
分别作垂直于准线的直线且和准线交于D,E 两点，
从B 点作 BH AD .
因为| AF | 3| B F | ，设 BF m ，则 AF 3m
又因为 AF
AD
所以 AH
BF BE
2m
e
，则
BE
BF e
m e
,
AD
AF ,
e
3m e
为双曲线的左右焦点，
求
|
PM
|
4 5
|
PF2
圆锥曲线第二定义在解题中的应用
圆锥曲线第二定义在解题中的应用摘要：新课程改革要求在数学教学中构建数学知识体系，全面提高学生数学思维能力的运用。
圆锥曲线是高中数学学习的内容，同时也是高考内容考查的重点。
利用圆锥曲线第二定义解题，不仅可以提高解题效率，而且有利于培养学生分析问题和解决问题的能力。
关键词：圆锥曲线；第二定义；应用现在高中教材中的圆锥曲线包括椭圆、双曲线和抛物线三种。
它们不仅是平面解析几何教学中的重点和难点，而且也是高考压轴题经常涉及和考查的对象。
三种圆锥曲线的定义既是教材重要的基本内容，也是解决许多问题的一种方法。
圆锥曲线的第二定义把焦点、准线和离心率巧妙地联系起来，在解相关的题目时，如能巧妙运用第二定义，能起到化繁为简的作用，使问题简洁明快的得以解决，在解题中起到事半功倍的效果。
一、圆锥曲线的第二定义圆锥曲线第二定义也称其为统一定义，其定义为平面内与一个定点和一条定直线的距离之比为常数e（e＞0）的点的轨迹，其中定点是曲线的焦点，定直线是对应于焦点的准线，e为离心率。
当e ＞1时，轨迹为双曲线；当e=1时，轨迹为抛物线；当0＜e＜1时，轨迹为椭圆。
从定义中我们可以看出第二定义揭示了圆锥曲线之间的内在联系，它刻画了点与点的距离、点到线的距离之间的数量关系。
它不仅是研究圆锥曲线图像与性质的基础，而且还在解决众多的数学问题中，具有不可低估的特殊功能。
二、圆锥曲线的第二定义在解题中的应用有关圆锥曲线的问题运算量大，求解过程复杂，如能正确、灵活地运用圆锥曲线的相关定义去分析解题，往往会使问题化繁为简，提高解题思路的精确率。
圆锥曲线的第二定义可应用于求解离心率、最值、轨迹问题以及相关的证明题。
下面我们介绍其相关的一些应用。
1.证明焦半径公式已知圆锥曲线方程以及曲线上一点的横坐标，求解这一点与圆锥曲线焦点之间的距离。
我们常规的做法是利用圆锥曲线的方程求出焦点坐标，根据这点的横坐标求解出这点坐标，然后利用距离公式得出结果。
如果方程比较复杂，那势必增加运算量。
人教A版高中数学选修2-1第二章 圆锥曲线与方程-圆锥曲线基本题型总结习题
圆锥曲线基本题型总结：提纲：一、定义的应用：1、定义法求标准方程：2、涉及到曲线上的点到焦点距离的问题：3、焦点三角形问题：二、圆锥曲线的标准方程：1、对方程的理解2、求圆锥曲线方程（已经性质求方程）3、各种圆锥曲线系的应用：三、圆锥曲线的性质：1、已知方程求性质：2、求离心率的取值或取值范围3、涉及性质的问题：四、直线与圆锥曲线的关系：1、位置关系的判定：2、弦长公式的应用：3、弦的中点问题：4、韦达定理的应用：一、定义的应用：1.定义法求标准方程：（1）由题目条件判断是什么形状，再由该形状的特征求方程：（注意细节的处理）1.设F1，F2为定点，|F1F2|＝6，动点M满足|MF1|＋|MF2|＝6，则动点M的轨迹是()A．椭圆B．直线C．圆D．线段【注：2a>|F1 F2|是椭圆，2a=|F1 F2|是线段】A.x 225＋y 29＝1 (y ≠0) B.y 225＋x 29＝1 (y ≠0) C.x 216＋y 216＝1 (y ≠0) D.y 216＋x 29＝1 (y ≠0) 【注：检验去点】3.已知A (0，－5)、B (0,5)，|P A |－|PB |＝2a ，当a ＝3或5时，P 点的轨迹为( ) A.双曲线或一条直线 B.双曲线或两条直线 C.双曲线一支或一条直线D.双曲线一支或一条射线 【注：2a<|F 1 F 2|是双曲线，2a=|F 1 F 2|是射线，注意一支与两支的判断】4.已知两定点F 1(－3,0)，F 2(3,0)，在满足下列条件的平面内动点P 的轨迹中，是双曲线的是( ) A.||PF 1|－|PF 2||＝5 B.||PF 1|－|PF 2||＝6 C.||PF 1|－|PF 2||＝7D.||PF 1|－|PF 2||＝0 【注：2a<|F 1 F 2|是双曲线】5.平面内有两个定点F 1(－5,0)和F 2(5,0)，动点P 满足|PF 1|－|PF 2|＝6，则动点P 的轨迹方程是( ) A.x 216－y 29＝1(x ≤－4)B.x 29－y 216＝1(x ≤－3) C.x 216－y 29＝1(x ≥4)D.x 29－y 216＝1(x ≥3) 【注：双曲线的一支】 6.如图，P 为圆B ：(x ＋2)2＋y 2＝36上一动点，点A 坐标为(2,0)，线段AP 的垂直平分线交直线BP 于点Q ，求点Q 的轨迹方程.7.已知点A(0，3)和圆O 1：x 2＋(y ＋3)2＝16，点M 在圆O 1上运动，点P 在半径O 1M 上，且|PM|＝|PA|，求动点P 的轨迹方程．（2）涉及圆的相切问题中的圆锥曲线：8.已知圆A ：(x ＋3)2＋y 2＝100，圆A 内一定点B (3，0)，圆P 过B 且与圆A 内切，求圆心P 的轨迹方程. 已知动圆M 过定点B (－4,0)，且和定圆(x －4)2＋y 2＝16相切，则动圆圆心M 的轨迹方程为( ) A.x 24－y 212＝1 (x >0)B.x 24－y 212＝1 (x <0) C.x 24－y 212＝1D.y 24－x 212＝1 【注：由题目判断是双曲线的一支还是两支】 9.若动圆P 过点N (－2,0)，且与另一圆M ：(x －2)2＋y 2＝8相外切，求动圆P 的圆心的轨迹方程. 【注：双曲线的一支，注意与上题区分】10.如图，已知定圆F 1：x 2＋y 2＋10x ＋24＝0，定圆F 2：x 2＋y 2－10x ＋9＝0，动圆M 与定圆F 1、F 2都外切，求动圆圆心M 的轨迹方程.11.若动圆与圆(x －2)2＋y 2＝1相外切，又与直线x ＋1＝0相切，则动圆圆心的轨迹是( ) A.椭圆 B.双曲线 C.双曲线的一支 D.抛物线12.已知动圆M 经过点A (3,0)，且与直线l ：x ＝－3相切，求动圆圆心M 的轨迹方程. 【注：同上题做比较，说法不一样，本质相同】13.已知点A (3,2)，点M 到F ⎝⎛⎭⎫12，0的距离比它到y 轴的距离大12.（M 的横坐标非负） (1)求点M 的轨迹方程； 【注：体现抛物线定义的灵活应用】(2)是否存在M ，使|MA |＋|MF |取得最小值？若存在，求此时点M 的坐标；若不存在，请说明理由. 【注：抛物线定义的应用，涉及抛物线上的点到焦点的距离转化成到准线的距离】（3）其他问题中的圆锥曲线：14.已知A ，B 两地相距2 000 m ，在A 地听到炮弹爆炸声比在B 地晚4 s ，且声速为340 m/s ，求炮弹爆炸点的轨迹方程. 【注：双曲线的一支】2.15.如图所示，在正方体ABCD —A 1B 1C 1D 1中，P 是侧面BB 1C 1C 内一动点，若P 到直线BC 与到直线C 1D 1的距离相等，则动点P 的轨迹所在的曲线是( )A ．直线B ．圆C ． 双曲线D ．抛物线【注：体现抛物线定义的灵活应用】2.涉及到曲线上的点到焦点距离的问题：16.设椭圆x 2m 2＋y 2m 2－1＝1 (m >1)上一点P 到其左焦点的距离为3，到右焦点的距离为1，则椭圆的离心率为( )A.22 B.12 C.2－12 D.3417.椭圆x 216＋y 27＝1的左右焦点为F 1，F 2，一直线过F 1交椭圆于A 、B 两点，则△ABF 2的周长为( )A ．32B ．16C ．8D ．418.已知双曲线的方程为x 2a 2－y 2b2＝1，点A ，B 在双曲线的右支上，线段AB 经过双曲线的右焦点F 2，|AB |＝m ，F 1为另一焦点，则△ABF 1的周长为( )A ．2a ＋2mB ．4a ＋2mC ．a ＋mD ．2a ＋4m19.若双曲线x 2－4y 2＝4的左、右焦点分别是F 1、F 2，过F 2的直线交右支于A 、B 两点，若|AB |＝5，则△AF 1B 的周长为________.20.设F 1、F 2是椭圆x 216＋y 212＝1的两个焦点，P 是椭圆上一点，且P 到两个焦点的距离之差为2，则△PF 1F 2是( )A ．钝角三角形B ．锐角三角形C ．斜三角形D ．直角三角形21．椭圆x 29＋y 22＝1的焦点为F 1、F 2，点P 在椭圆上．若|PF 1|＝4，则|PF 2|＝________，∠F 1PF 2的大小为________．【注：椭圆上的点到焦点的距离，最小是a -c ，最大是a+c 】22.已知P 是双曲线x 264－y 236＝1上一点，F 1，F 2是双曲线的两个焦点，若|PF 1|＝17，则|PF 2|的值为________.【注：注意结果的取舍，双曲线上的点到焦点的距离最小为c -a 】23.已知双曲线的方程是x 216－y 28＝1，点P 在双曲线上，且到其中一个焦点F 1的距离为10，点N 是PF 1的中点，求|ON |的大小(O 为坐标原点). 【注：O 是两焦点的中点，注意中位线的体现】24.设F 1、F 2分别是双曲线x 25－y 24＝1的左、右焦点．若点P 在双曲线上，且1PF u u u u r ·2PF u u u u r ＝0，则|1PF u u u u r ＋2PF u u u u r |等于( ) A ．3 B ．6 C ．1 D ．225.已知点P 是抛物线y 2＝2x 上的一个动点，则点P 到点(0,2)的距离与点P 到该抛物线准线的距离之和的最小值是( ) A.172B.3C. 5D.92【注：抛物线定义的应用，将抛物线上的点到焦点的距离转化成到准线的距离】26.已知抛物线y 2＝4x 上的点P 到抛物线的准线的距离为d 1，到直线3x －4y ＋9＝0的距离为d 2，则d 1＋d 2的最小值是( ) A.125 B.65 C ．2 D.55【注：抛物线定义的应用，将抛物线上的点到准线的距离转化成到焦点的距离】27.设点A 为抛物线y2＝4x 上一点，点B(1,0)，且|AB|＝1，则A 的横坐标的值为( )A ．－2B ．0C ．－2或0D ．－2或2 【注：抛物线的焦半径，即定义的应用】3.焦点三角形问题：椭圆的焦点三角形周长2c 2a 2C PF PF C 21F PF 21+∆＝＋＋＝ 椭圆的焦点三角形面积：推导过程：2tan sin cos 121sin 21cos 1 -)cos (12 (1)-(2)(2)2a (1)COS 2-2 1 b 2b PFPF S 2bPFPF 4c 4a PFPF PF PF 4c PF PF PF PF 2221F PF 22122212212212221θθθθθθθ=+==+==+⎪⎩⎪⎨⎧=+=+∆得双曲线的焦点三角形面积：2tanbS 2F PF 21θ=∆28.设P 为椭圆x 2100＋y 264＝1上一点，F 1、F 2是其焦点，若∠F 1PF 2＝π3，求△F 1PF 2的面积．【注：小题中可以直接套用公式。
圆锥曲线第二定义备课讲稿
(1 )第一定义中要重视“括号”内的限制条件： 椭圆中，与两个定点 F , F 的距离的和等于常数応，且此常数2。
一定要大于冈月J ,当常数等于国鸟I 时，轨迹是线段 F F ， 当常数小于 戸1巧1时，无轨迹；双曲线中，与两定点 F ，F2的距离的差的绝对值等于常数 丄'，且此常数-:i一定要小于|FF=|，定义中的“绝对值”与二二V|F ：F ； |不可忽视。
若二 =|F -F^ |，则轨迹是以 F ,已为端点的两条射线，若 匕 > 尸F |，则轨迹不存在。
若去 掉定义中的绝对值则轨迹仅表示双曲线的一支。
比女口：(2)第二定义中要注意定点和定直线是相应的焦点和准线，且“ 点点距为分子、点线距为分母”，其商即是离心率。
圆锥曲线的第二定义，给出了圆锥曲线上的点到焦点距离 与此点到相应准线距离间的关系，要善于运用第二定义对它们进行相互转化 。
①已知定点在P 的轨迹中是椭圆的是C .|^|4|FF 2|=ti（答: C ）；②方程■- ' ；一一+一 「表示的曲线是(答：双曲线的左支)、求焦点弦长二、求离心率的弦的长度等于F i 到准线l i 的距离，求椭圆的离心率。
解：如图，AB 是过F i 垂直于x 轴的弦，|片6为F i 到准线l i 的距离，AD 丄11于D ，则 |AD|=|F i C|,由题意知 |AF i | 2 |AB |o由椭圆的第二定义知:2）如已知点」.及抛物线 1丁上一动点X i例i 过抛物线y 2 4x 的焦点F 作直线交抛物线于A （ x i ，y i ）、B （ X 2，y 2），若X 2 6，求|AB|的长。
解：设AB 的中点为E ,点A 、E 、B 在抛物线准线I : 由第二定义知：1上的射影分别为G 、 H 、|AB| |AF||BF|| AG | |BM | 2| EH | 2 x i x 22（1例2设椭圆 2x ~~2 a 2^7=i (a>b>0)的右焦点为F i ，右准线为bl i ，若过F i 且垂直于x 轴P(x,y )，则y+|PQ|的最小值是1 1|AF 1| RABI -|AB| 1 e |AD| IF 1CI |AB| 2三、求点的坐标 1,求点P 的坐标。
圆锥曲线第二定义的应用 ppt课件
点M在左支上
y
x
F1
F2
抛物线的焦半径公式：
点 P ( x 0 , y 0 )在对应抛物线上
,
y 2 2 px ( p 0 ) :| PF
|
x0
p; 2
y 2 2 px ( p 0 ) :| PF
| x 0
p; 2
x 2 2 py ( p 0 ) :| PF
|
y0
直线m与椭圆的交点到直线l的距离最近。
且d 4025 15 41
y
4252 41
dm maixn
4025 42 52
65 41
41
x o
思考：最大的距离是多少？
例 变 形3： 已 知 椭 圆 2 x5 2y921， 直 线 l： 4x-5y400.椭 圆 上
是 否 存 在 一 点 ， 它 到 直 线 l的 距 离 最 小 大？ y 最 小 大距 离 是 多 少 ？
例 3： 已 知 椭 圆 x2y21， 直 线 l： 4x-5y400.椭 圆 上 25 9
是 否 存 在 一 点 ， 它 到 直 线 l的 距 离 最 小 ？ y 最 小 距 离 是 多 少 ？
解 ： 设 直 线 m 平 行 于 l，
则 l可 写 成 ： 4 x 5 y k 0
x o
4x5y k 0
M
A
F1
O
F2
X
（1） 求 MA MF2的范围
解：椭圆的方程为
x2 y2 1
a3,b 5,c2
95
e 2 3
F1(2,0)
F2 (2, 0)
l1
:
x
p 2
l2 : x
p 2
圆锥曲线第二定义在一些题目中的应用(供参考)
圆锥曲线第二定义在一些题目中的应用北京一零一中学数学组何效员圆锥曲线的第二定义：平面上到定点与到定直线的距离的比为常数e 的点的轨迹是圆锥曲线概念的重要组成部分，它揭示了圆锥曲线之间的内在联系，是圆锥曲线在极坐标系下 具 有统一形式的基本保证。
利用圆锥曲线的第二定义，在某些情形下，可以更方便的求解一些 题目。
但当我们利用第二定义时，有时候会忽略一个条件，即平面上的这个定点不能在定直线上，否则得到的曲线不是圆锥曲线。
如：考虑坐标平面上，至U 定点 (1,1)与到定直线x 1的距离之比为常数 e 的点的轨迹讨论如下：①当e 1时，点的轨迹方程为y 1,(x 1),T J* j1直线去掉一点；\1/ n② 当e 1时，点的轨迹方程为y 1Je 2 1(x 1),/1\ 工(x 1)，两条直线去掉一点；③当e 1时，点的轨迹不存在。
下面我们就一些具体的题目来体会第二定义的妙用。
求其最小值无疑是困难，观察2|MF | ,设M 点到右准线的距离d ,IMF| c 1 e,21 MF | d ，这样da 2a 2|MP | 2 | MF |就转化为在椭圆上寻找一点到P( 1,1)的距离与到直线 x4c22x的距离和最小，当且仅当MP 直线x 4时，点M 在点P 和直线x 4之间时取2 2例2已知椭圆方程为 爲冷 1( a b 0)，求与这个椭圆有公共焦点的双曲线，使得a b它们的交点为顶点的四边形的面积最大，并求出相应的四边形的顶点坐标。
分析：本体若通过椭圆与双曲线方程联立求解交点坐标，继而讨论四边形面积的表达式，求出使面积最大时 的双曲线方程，计算会十分麻烦，考虑到椭圆和双 曲线有共同的焦点，不妨利用第二定义求解。
设所求双曲线方程为2 2-y7 与 1 (m, n 0)，其中 m n2 2 2 2 2c a b m n ，设两曲线在第一象限内的交点2c a IPF 2I e|RQ| elRRI -| — a c得，此时M 的坐标为双曲线的上准线，过卩舁乍RQ12 于 R ,X12 z am(— c%) a(y 1 2m 、 "，口)，解得 cy 1am，代入椭圆方程2 y 2 a2話1，得bn c利用双曲线与椭圆的对称性知S 4x 1 y 1,abmn 4 c 22 abc 22ab , 等号当且仅当 m-c 时取得, 2故所求双曲线方程为a 2b 2例3 已知椭圆2x~2 a2y_2，相应的四个顶点坐标为0的两个焦点分别为 F 1 c,0 ya).F 2 c,0，过点P(X i , %), hh 分别为椭圆,2I c 1 m y 1||y 1 |, m c文档来源为：从网络收集整理.word 版本可编辑.欢迎下载支持3分析: 解法 a 2E ,0的直线与椭圆相交于c(1)求椭圆的离心率; (2)求直线AB 的斜率。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
圆锥曲线第二定义在一些题目中的应用
北京一零一中学数学组 何效员 圆锥曲线的第二定义：平面上到定点与到定直线的距离的比为常数e 的点的轨迹是圆锥曲线概念的重要组成部分，它揭示了圆锥曲线之间的内在联系，是圆锥曲线在极坐标系下 具有统一形式的基本保证。
利用圆锥曲线的第二定义，在某些情形下，可以更方便的求解一些题目。
但当我们利用第二定义时，有时候会忽略一个条件，即平面上的这个定点不能在定直线上，否则得到的曲线不是圆锥曲线。
如：考虑坐标平面上，到定点(1,1)与到定直线1x =的距离之比为常数e 的点的轨迹讨论如下：
① 当1e =时，点的轨迹方程为1,(1)y x =≠，
直线去掉一点；
② 当1e >时，点的轨迹方程为211(1),y e x -=±--
(1)x ≠，两条直线去掉一点；
③ 当1e <时，点的轨迹不存在。
下面我们就一些具体的题目来体会第二定义的妙用。
例1 已知椭圆22
143
x y +=内一点(1,1)P -，F 为右焦点，椭圆上有一点M 使 ||2||MP MF +的值最小，求点M 的坐标。
分析：若按常规思路，设点(,)M x y ，右焦点(1,0)F ，
则2222
||2||(1)(1)2(1)MP MF x y x y +=-+++-+，
求其最小值无疑是困难，观察2||MF ，设M 点到右准线的距离d ，
||1
2
MF c e d a ===，2||MF d ∴=，这样 ||2||MP MF +就转化为在椭圆上寻找一点到(1,1)P -的距离与到直线2
4a x c
== M
P
F M
x = 4
O
y
x
的距离和最小，当且仅当MP ⊥直线4x =时，点M 在点P 和直线4x =之间时取得，此时M 的坐标为26
(
,1)3
-. 例2 已知椭圆方程为22
221(0)y x a b a b
+=>>，求与这个椭圆有公共焦点的双曲线，使得
它们的交点为顶点的四边形的面积最大，并求出相应的四边形的顶点坐标。
分析：本体若通过椭圆与双曲线方程联立求解交点坐标，
继而讨论四边形面积的表达式，求出使面积最大时 的双曲线方程，计算会十分麻烦，考虑到椭圆和双 曲线有共同的焦点，不妨利用第二定义求解。
设所求双曲线方程为
22
2
21(,0)y x m n m n
-=>，其中 22222c a b m n =-=+，设两曲线在第一象限内的交点111(,)P x y ，12,l l 分别为椭圆，双曲线的上准线，过1P 作11PQ l ⊥于Q ，1
2PR l ⊥于R ， 22
1211111||||||||||c a c m PF e PQ e PR y y a c m c
===
-=-， 2211()()a m m y a y c c ∴-=-，解得 1am
y c
=，代入椭圆方程22221y x a b +=，得
1bn
x c
=
，利用双曲线与椭圆的对称性知 22
1122
4422abmn m n S x y ab ab c c +==≤⋅=，等号当且仅当22m n c ==时取得，故所求双曲线方程为22
2
2
2
a b y x --=，相应的四个顶点坐标为22(,)b a ±±. 例3 已知椭圆()22
2210x y a b a b
+=>>的两个焦点分别为()1,0F c -和()2,0F c ，过点
2,0a E c ⎛⎫
⎪⎝⎭
的直线与椭圆相交于,A B 两点，且1212//,2F A F B F A F B = （1）求椭圆的离心率； （2）求直线AB 的斜率。
分析：本题是2009年天津卷文科第22题的前两问，参考答案是用常规方法，即设直线AB
的方程与椭圆方程联立，利用B 为AE 之中点求解，方法虽易理解，但计算繁杂，极易出错，而利用椭圆的第二定义，求解过程简洁，极富数学美感。
为对比，先将两种解法列出。
解法一 （1） 由1212//,2F A F B F A F B =，得2211||||1||||2EF F B EF F A ==，从而2
212
a c
c a c c
-=+， 整理得2
2
3a c =，故离心率33
c e a =
=. （2）解：由（1）知，22222b a c c =-=，所以椭圆的方程可以写为2
2
2
236x y c +=， 设直线AB 的方程为2
()a y k x c
=-即(3)y k x c =-，
由已知设1122(,),(,)A x y B x y ，则它们的坐标满足方程组2
2
2
(3)236y k x c x y c
=-⎧⎨
+=⎩，
消去y 整理，得2
2
2
22
2
(23)182760k x k cx k c c +-+-=
依题意， 22
3348(13)0,33
c k k ∆=->-
<<， 而2222
12122
2
18276,2323k k c c x x x x k k -+==++，由题设知，点B 为线段AE 的中点，所以1232x c x +=
联立三式，解得2222
1222
9292,2323k c c k c c x x k k -+==++，将结果代入韦达定理中解得
2
3
k =±
.
文档来源为:从网络收集整理.word 版本可编辑.欢迎下载支持.
解法二 （2） 设椭圆方程为 2
2
2
236x y c +=，
过E 作l x ⊥轴，知l 为椭圆的右准线， 过,A B 分别作'AA l ⊥于'A ，'BB l ⊥ 于'B ，知'//'AA BB ，
22||||
|'||'|
AF BF e AA BB ==，即22|||'||||'|AF AA BF BB =，在'EAA ∆中，根据相似三角形对应 线段成比例，
|'|||2|'|||
AA AE BB BE ==，221||2||||AF BF AF ∴==， 则点A 在短轴顶点，所以(0,2),A c ± 直线AB 的斜率为2233
AB c k c =±
=±。
利用圆锥曲线的第二定义，我们在极坐标系中可以很方便地得到圆锥曲线的统一方程：
1cos ep
e ρθ
=
-，（其中e 为离心率，p 为焦准距）。
利用这个方程，我们很容易得到下面这
个结论：
过双曲线22
221x y a b
-=的右焦点且与右支交于两点的弦，当且仅当弦与x 轴垂直时，取
得最小长度2
2b a
.
以双曲线右焦点F 为极点，对称轴为极轴， 如图所示建立极坐标系，易知双曲线右支的方程 为
2
,(,)1cos ep c b e p e a c
ρθ===-，
设,A B 两点的坐标分别是12(,),(,)ρθρπθ+，
212222221cos 1cos()1cos ep ep ep b ep e e e a ρρθθπθ+=+=≥=--+-，当且仅当2
πθ=时，
等号成立.
利用这个结论，我们可以很轻松地证明1997年全国高中数学联赛一试第8题。
y
O
x
A '
B 'F 1
F 2
E
B
A
文档来源为:从网络收集整理.word版本可编辑.欢迎下载支持.
例4证明：过双曲线
2
21
2
y
x-=的右焦点作直线l交双曲线于A、B两点，若实数λ使得
||
ABλ
=的直线恰好有3条，则4
λ=.
圆锥曲线第二定义在解题中的妙用不可胜数，本文只是稍加举例，更多的应用还有待我们去探索体会.。