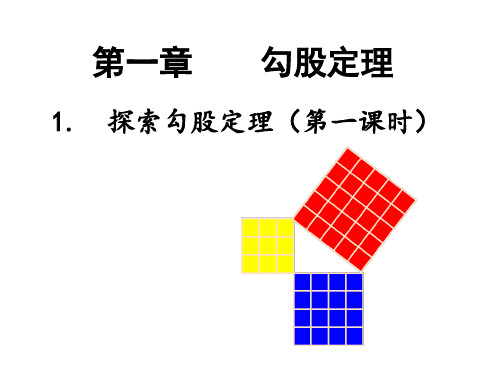
北师大版八年级数学上册：1.1 探索勾股定理课件(共17张PPT)

合集下载

北师大版八年级数学上册1.1《探索勾股定理》课件

c=
。
2.在△ABC中，∠C=90°,若c=13，ቤተ መጻሕፍቲ ባይዱ=12，则
a=
。
3.若直角三角形中，有两边长是3和4，则第三
边长的平方为（）
A 25 B 14 C 7 D 7或25
二、提高训练
4．一个长为10 m为梯子斜靠在墙上，梯子的顶端距
地面的垂直高度为8m，梯子的顶端下滑2 m后，底端
滑动
m．
5．已知Rt△ABC中，∠C＝90°，若 a+b=14cm， c=10cm，则Rt△ABC的面积为（）
视察这三个正方形
你发现图中三个正方形的面积之间存在什么关系吗？
换个角度来看呢？
你发现了什么？
结论1 以等腰直角三角形两直角边为边长的小正方形的面积的和，等于以斜边为边长的正方形的面积.
分小组动手操作实践
用四张全等的等腰直角三角形纸片，拼成一个正方形。（不能重叠，不能有间隙）
∵c2= 4×12 a2 ∴c2=2a2
（1）如果三角形的三边长分别为a,b,c，则 a2+b2=c2
( ×)
（2）如果直角三角形的三边长分别为a,b,c，则a2+b2=c2
( ×)
( 3) 如果直角三角形的三边长分别为a,b,c，且c为斜边，
则 a+b=c
( ×)
(4) 如果直角三角形的三边长分别为a,b,c，且c为斜边，
则 b2=c2-a2
2002年国际数学家大会会标 ——弦图.
四、课堂小结定理内容
重要的思想方法及数学思想
勾股定理
从特殊到一般、数形结合思想
定理运用
五、布置作业
1．习题1.1. 2．阅读《读一读》——勾股世界.

北师大版八年级数学上册1.1 第1课时勾股定理的认识课件(共23张PPT)

探究新知
1.在纸上画若干个直角三角形，分别测量它们的
三条边，看看三边长的平方之间有怎么样的关系？
c
a
b
直角三角形的两直角边的平方和等于斜边的平方，这就是
著名的“勾股定理”。
如果直角三角形的两条直角边为a、b，斜边为c，那么有
a2+b2=c2.
数学小知识
我国古代称直角三角形的较短的直角边为勾，较长的直角
求的长.
解：因为 ⊥ ，
所以 ∠ = ∠ = 90∘ .
在 Rt △ 中， 2 = 2 − 2 = 102 − 82 = 36 ，
所以 = 6 .
设 = = ，则 = − 6 .
在 Rt △ 中， 2 = 2 + 2 ，
所以 △ =
1

2
1
2
⋅ = × 25 × 12 = 150 .
6. 如图，直线上有三个正方形，， .若，的面积分别
为 5 和 11 ，则的面积为( C )
A. 4
B. 6
C. 16
D. 55
7. 如图，在 △ 中， = ， = 10 ， ⊥ ，垂足为， = 8 .
（2）已知 = 12 ， = 16 ，求 .
【解】在 Rt △ 中， ∠ = 90∘ ， = 12 ， = 16 ，
所以 2 = 2 + 2 = 122 + 162 = 400 .
所以 = 20 .
例2 如图，在 △ 中， ⊥ 于点，且 + = 32 ，
因为 ∠ = 90∘ ，所以 2 + 2 = 2 .

北师大八年级上册1.1探索勾股定理课件(18张PPT)

∴正方形C的边长为： 36 6cm
c b
a
课堂总结
赵爽弦图邹元治证明法
勾股定理
a2 b2 c2
上下求索
如图以直角三角形三边长为直径作半圆、正三角形、扇
形（圆心角相等），三边上的图形面积分别为SA、SB、SC，则三个半圆的面积间存在何种关系？
a2 b2 c2
在直角三角形中，两个直角边平方的和等于斜边的平方
利用拼图来验证勾股定理：
1、准备四个全等的直角三角形（设直角三角形的两条直角边分别为a,b，斜边为c.）
2、你能用这四个直角三角形拼成一个的正方形吗？
c a
b
赵爽弦图
cb aa
c2
大正方形的面积可以表示为______________；也可以表示为_______4__a2_b___(_b___a_)2__
c2 4 ab (b a)2 2
2ab b2 2ab a2 a2 b2
a2 b2 c2
邹元治证明法
a bc
c a
b
大正方形的面积可以表示为___(_a____b_)_2_____；
也可以表示为____c_2 __4__a_2b______
(a b)2 c2 4 ab 2
我们通常所说的20英寸或50厘米的电视机，是指其银屏对角线的长度
例2：如图，四边形A、B、C都是正方形，三角形D是直角三角形，其中正方形A的面积为100cm²，正方形B的边长为8cm，正方形C 的边长_________.
解：由勾股定理得：
b2+c2=a2 即 SB+SC=SA ∴SC=SA-SB 解得：SC=100-82=36
勾股定理的证明年级：八年源自（上）◇勾股树 ◇毕达哥拉斯树

北师大版八年级数学上册第一章 1.1 《探索勾股定理》课件 (共22张PPT)

2、你能用这四个直角三角形拼成一个正方形吗？
方法 1
3、你能否就你拼出的图证明a2+b2=c2？方法 2
c a
方法 3
b
赵爽弦图
大正方形的面积可以表示为 c2 也可以表示为 (b a)2 4 1 ab 2
c a
b
c 2 (b a)2 4 1 ab 2
a2 2ab b2 2ab a2 b2 即a 2 b2 c 2
A
c
a
c
b
B
b
a
E
C
1 2
ab
1 2
ab
1 2
c
2
1 2
(2ab
c2)
1876年，美国总统伽菲尔德利用上图验证了勾股定理，人们为
比较两式可知：a2+b2=c2 了纪念他对勾股定理的证明，
就把这一证法称为 “总统证法”
相传两千五百多年前，一次毕达哥拉斯去朋友家做客，发现朋友家用砖铺成的地面反映直角三角形三边的某种数量关系!
发现了什么？
解：设树高为xm
(x-9)m
9m
┓ ┓
12m
如图所示，一棵大树在一次强烈台风中于离地面9米处折断倒下，树梢顶落在离树根12米处.大树在折断之前高多少？
9m
┓
解：设树高为xm
(x-9)m 由题可知：81+144=（x-9）2
∴225=（x-9）2
12m
∴x-9=15或x-9=-15（舍）
∴x=24
答：树高为24m.
练一练
1.在△ABC中,∠C=90°,若AB=10, BC=6，那么AC2为
几何问题要利用图形来解决问题
B

北师大版八年级数学上册《1.1.1勾股定理》教学课件(共19张PPT)

例1 高为2.5 m的木梯，架在高为2.4 m的墙上(如图)，
这时梯脚与墙的距离是多少?
A
解：在Rt△ABC中，根据勾股定理，得：
BC2=AB2-AC2=2.52-2.42=0.49，
所以BC=0.7.
即梯脚与墙的距离是0.7 m.
C
B
例2 求斜边长为17 cm、一条直角边长为15 cm的直角三角形的另一边长.
正方形C的面积应该怎么计算呢？
C A
B
图①
➢ 分“割”成若干个直角边为整数的三角形 SC=12×2×3×4+1×1=13；
➢ 把C“补”成边长为5的正方形 SC=5×5-12×2×3×4=13.
观察：
C A
B
图①
正方形A中含有__4__个小正方形，即A的面积是___4__. 正方形B中含有__9__个小正方形，即B的面积是___9__. 正方形C中含有_1_3__个小正方形，即C的面积是__1_3__.
第一章勾股定理
1.1 探索勾股定理
第1课时勾股定理
学习目标
1.经历探索勾股定理的过程，了解勾股定理的探究方法；
2.掌握勾股定理，并能运用勾股定理解决一些简单问题.
新知引入
一个直角三角形的两条直角边长分别是3和4，你知道它的第三边长吗？
实际上，利用勾股定理我们可以很容易地解决这个问题. 勾股定理是一个古老的定理，人类很早就发现了这个定理.
观察：
A＇
C＇
B＇
图②
正方形A＇中含有__1_6_个小正方形，即 A＇的面积是__1_6__.
正方形B＇中含有__9__个小正方形，即 B＇的面积是__9___.
正方形C＇中含有__2_5_个小正方形，即 C＇的面积是__2_5__.

北师大版八年级数学上册课件：1.1探索勾股定理(一)(共27张PPT)

一、勾股定理概念理解
（1）勾股定理揭示的是直角三角形__三_边__
的关系；（2）勾股定理只适合于_直__角__ 三角形；
（3）如果a用2b2c2 a、b和c分别表示直角三角形
的两直角边和斜边，
则有：
，它还可以表述为
直__角_三__角__形_两__直_角__边__的_平__方_和__等__于_斜__边__的_平__方_。。
7，则第三边的平方是______.
_______.
64
72 49
AB2BC2AC2___. B
面积是D 24，这个三角形的斜边是则第三边的平方为_____.
C
（2）一直角三角形的两边为5,13，
直角三角形两直角边的平方和等于斜边的平方。
（3）如果用a、b和c分别表示直角三角形的两直角边和斜边，
方案设计：如图是一个直径为20米的半圆拱桥，那么一个长、宽、高分别为15,12,8.
三角形的面积是________.
已知直角三角形的两边长6,
3、面积恒等法（学习以下几个题目）
②第5页图1-5
资料作业：点拨到第2页
作业本长6,
补充2：把一块三角形（△ABC）土地挖去一个直角三角形（∠ADC）后，测得CD=6米，AD=8米，BC=24米，AB=26米，求剩余土地
我国早在三千多年就知道了这个定理,
（2）一直角三角形的两边为5,13，
④第7页第2题
2002年世界数学家大
④第7页第2题
（3）如果用a、b和c分别表示直角三角形的两直角边和斜边，
则有：
，它还可以表述为 ________________________________。
方案设计：如图是一个直径为20米的半圆拱桥，那么一个长、宽、高分别为15,12,8.

北师大版八年级数学上册第一章第一节《探索勾股定理》ppt课件

400m
A
分析
1、根据题意画出图形,根据题中所给出的信息, 你能得到什么结论呢? 2、由题可知,∠ABC=90°,AB=400米 ,AC=500米,BC即为敌方汽车10秒所行使的距离,故在直角三角形中求出BC的长即为解答此题的关键; 3、求出BC的长后,根据“速度=路程÷时间” 即可解答此题了.
换一个直角三角形还依旧满足这种关系吗？
满足
C
面积
A
A 16 B9 C 25
B
C
A
B
面积
A1 B9 C 10
想一想
将直角三角形设为a，b，c，你能得到什么？
Байду номын сангаас
C
Aa c
Bb
Sa+Sb=Sc
a2+b2=c2
想一想：两直角边a、b与斜边c 之间的关系？
结论
勾股定理 (毕达哥拉斯定理)
直角三角形两直角边的平方和等于斜边的平方.
解答
B
C
解:根据题意画出图形; 根据题意可知,∠ABC=90° 400m
AB=400米,AC=500米, BC即为汽车10秒行驶的距离 A
∵ 在△ABC中,∠ABC=90°,AB=400米,AC=500米 BC AC2 AB2 5002 4002 300m
∴ 敌方汽车速度为300÷10=30米/秒
答:敌方汽车速度为30米/秒.
练习2
如图，一根电线杆在离地面5米处断裂，电线杆顶部落在离电线杆底部12米处，电线杆折断之前有多高？
解：∵ＢＣ⊥ＡC，
∴在Ｒt△ＡＢＣ中，
ＡＣ＝１２，ＢＣ＝５,
B
根据勾股定理，
AB2 AC2 BC2
5米

北师大版初中八年级数学上册 1.1.1 认识勾股定理课件(共20张PPT)

( 55 ) 25
30
( 34)
95 61
( 42 ) 18
60
200 ( 350)
150
总结归纳
C A
B
SA+SB=SC
ac b
ac b
a2+b2=c2
a2+b2=c2
总结归纳
勾股定理
直角三角形两直角边的平方和等于斜边的平方．如果a，b和c分别表示直角三角形的两直角边和斜边，那么a2+b2=c2．
第一章勾股定理
1.1 探索勾股定理
第1课时认识勾股定理
导入新课
情境引入
如图，这是一幅美丽的图案，仔细观察，你能发现这幅图中的奥秘吗？带着疑问我们来一起探索吧.
数学家毕达哥拉斯的故事
相传2005年前，毕达哥拉斯有一次在朋友家做客时，发现朋友家的用砖铺成的地面…
毕达哥拉斯就从地面上这十分常见的图形中，发现了令世人震惊的定理：
方法一：割
方法二：补
方法三：拼
分割为四个直角三角形和一个小正方形.
补成大正方形，用大正方形的面积减去四个直角三角形的面积.
将几个小块拼成若干个小正方形，图中两块红色（或绿色）可拼成一个小正方形.
填一填：观察右边两幅图：完成下表（每个小
A的面积 B的面积 C的面积
左图 4
9
13
右图 16
9
25
怎样计算正方形C的面积呢？
分析表中数据，你发现了什么？
A的面积 B的面积 C的面积
左图 4
9
13
右图 16
9
25
C A
B
SA+SB=SC
结论：以直角三角形两直角边为边长的小正方形的面积的和，等于以斜边为边长的正方形的面积.

北师大版八年级上册1.1探索勾股定理课件(共30张PPT)

36
B.
特殊 △ ：直角三角形----Rt△ABC
2c
（3）在Rt△ABC中，∠C=90°，若BC：AB=8：17，且AC=30，求AB2 和AC2 +BC2的值；
C 2 B （3）在Rt△ABC中，∠C=90°，若BC：AB=8：17，且AC=30，求AB2 和AC2 +BC2的值；
已知Rt△ABC，∠C=90°
如何解决
2.分析方法
问题: 如何验证以c为边长的正方形的面积是否为2 ？
方法2.用网格1帮助
A
1c
C1 B
A
1c
C1 B
如何解决
2.分析方法
你能用上述方法验证问题（2）的结论吗？（2）在Rt△ABC中，∠C=90°，AB=25，AC=20，求BC的长；
（3）在Rt△ABC中，∠C=90°，若BC：AB=8：17，且AC=30，求AB2 和AC2 +BC2的值；
例3.已知直角三角形的两直角边分长别为6cm和8cm，求以第三边为边长的正方形的面积。
例4 .强大的台风使得一根长24米的旗杆在某处折断倒下，旗杆顶部落在离旗杆底部12米处，求旗杆折断处离地面有多高？
例4 强大的台风使得一根长24米的旗杆在某处折断倒下，旗杆顶部落在离旗杆底部12米处，求旗杆折断处离地面有多高？
是（ D ）.
A. 4:6:7
B. 6:8:12
C. 1:2:3
D.5:12:13
3.在Ｒｔ△ABC中，∠Ｃ＝９０°，a、b、c 为其
三边.(1)若 a 6，b 8 ，则 c 10 ；
(2)若a 5，c 13 ，则 b 12 ；
4. 如图，Ｒｔ△ABC中，B 90 ，AB=3 cm，AC=5

北师版八年级数学上册1.1 探索勾股定理课件(共17张PPT)

2b c
3
a2+b2=c2
猜想:两直角边a、b与斜边c 之间的关系？
20C中, ∠C=90°.
a=5cm
A
b=12cm
bc
c= 13cm
CaB
a 2+b 2= 169cm2
c 2= 169cm2
a2+b2=c2
2020/6/18
9
勾股定理:(gou-gu theorem)
2
图2-1
3 1
2
图2-2
（3）你能发现两图中三个正方形1，2， 3的面积之间有什么关系吗？
（图202中0/6/18每个小方格代表一个单位面积）
5
探索正方形3的面积
3 2
1
图3-1
3 2
1
图3-2
2020/6/18
6
3 2
1
图2-3
（图中每个小方格代表一个单位面积）
2020/6/18
7
推广:一般的直角三角形,上述结论成立吗？ 1 a
46
c
58
2020/6/18
14
4.求斜边长为17cm、一条直角边长为15cm的直角三角形的面积.
2020/6/18
15
归纳小结
1．知识：勾股定理：直角三角形两直角边的平方和等于斜边的平方．如果用a,b,c分别表示直角三角形的两直角边和斜边，那么a2+b2=c2
2．方法：（1）观察—探索—猜想—验证—归纳—应用；（2）“割、补、拼、接”法.
1 求下图中字母表示的正方形的面积.
A625 225
400
②
81 B 144
225
2020/6/18

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

B. S1 = S2 + S3 D. 无法确定
S1 S2
S3
反思
勾股定理
学到了什么？
割补法直角三角形
需要注意什么？
直角边的关系
作业
暑假新动向 96、97页
A
（2）若c=13，b=12，则 a= 5 .
B
C
变形
公式变形： c2 a2 b2 a2 c2 b2 b2 c2 a2
在直角三角形中，已知两边长度即可求第三边长度。
应用
（3）如图，AB=BC=CD=DE=1，且BC⊥AB，
CD⊥AC，DE ⊥AD，则线段AE的长为（ B ） E D
A. 1.5
S小 = a 2 S大 = b 2 = 2a 2
a
a
b
b2 = a2 + a2
b
探究
a
a
绿色正方形的面积又如何用a表示呢？
c
算一算
S=
若记绿色正方形的边长为c，面积为S；小方格的边长为a，面积为S小.
a a
c 2 = 13a 2
c2 = 4a2 + 9a2 =(2a)2+(3a)2
c
观察
引入
毕达哥拉斯（ Pythagoras ，约公元前580年—约500年）古希腊数学家、哲学家。他与他的信徒们组成了一个新的学派 —— 毕达哥拉斯学派。勾股定理又称毕达哥拉斯定理。
毕达哥拉斯
引入
探究
a a
黄色正方形的面积如何用a表示呢？
b
算一算
若记黄色正方形的边长为b，面积为S大；小方格的边长为a，面积为S小.
B. 2
C. 2.5
D. 3 C
B
A
Байду номын сангаас 应用
（4）如图，直角△ABC中，∠ACB=90°,AC=3,BC=4,以点A
为圆心，AC长为半径画弧，交AB于点D，则BD= 2 .
A D
C
B
应用
（5）如图，分别以直角三角形的三边为直径作半圆，则三个
半圆的面积S1 ，S2 ，S3之间的关系是（ B ）
A. S1 > S2 + S3 C. S1 < S2 + S3
b2 = a2 + a2
(斜边) 2 = (直角边) 2 + (另一直角边) 2
c2 = (2a)2+(3a)2
结论
勾股定理：直角三角形两直角边的平方和等于斜边的平方. 如果用a，b和c分别表示三角形的两直角边和斜边，那么a2 +b2 =c2
应用
在直角△ABC中，∠C=90°
（1）若a=6，b=8，则 c= 10 .

北师大版八年级数学上册：1.1 探索勾股定理 课件(共17张PPT)