有中介的调节变量和有调节的中介变量解读
调节变量和中介变量(温忠麟)

调节变量和中介变量
温忠麟 华南师范大学应用心理研究中心 香港考试及评核局研究发展部
引言
因果关系:自变量
因变量
第三者:调节变量(moderator) 中介变量(mediator)
如何分析? 如何区分?
1 调节变量与调节效应分析
1.1 调节变量的定义 如果两个变量之间的关系(如Y与X的关
带潜变量乘积项的结构方程分析
1. 参数非线性约束方法(Kenny & Judd, 1984; Joreskog & Yang , 1996; Algina & Moulder, 2001)
2. 广义乘积指标(GAPI)方法( Wall & Amemiya, 2001) 3. 无约束方法(Marsh, Wen & Hau, 2004, 2006, 2007)
拟极大似然估计(QML)方法(Klein & Muthen, 2002) 贝叶斯(Bayesian)方法
2 中介变量和中介效应
2.1 中介变量的定义 考虑自变量X对因变量Y的影响,如果X通过 影响变量M来影响Y,则称M为中介变量。 (Judd & Kenny,1981; Baron & Kenny, 1986)
中介效应检验程序
(温忠麟、张雷、侯杰泰、刘红云,2004 ,心理学报)
外源变量
潜外变源 量
内生变量
潜内变生 量
外 源 指 标
内 生 指 标
3 调节变量与中介变量的比较
(温忠麟、侯杰泰、张雷,2005,心理学报 )
4.1 有中介的调节模型
(温忠麟、张雷、侯杰泰,2006,心理学报 )
UX
有中介的调节效应显著意味着:
中介变量、调节变量与协变量概念、统计检验及其比较

中介变量、调节变量与协变量概念、统计检验及其比较一、本文概述在社会科学和自然科学的研究中,变量之间的关系是复杂且多样的。
中介变量、调节变量和协变量是理解和分析这些复杂关系的重要概念。
本文旨在深入探讨这三种变量的概念、统计检验方法及其在实证研究中的应用,并对它们进行比较,以帮助读者更好地理解并应用这些变量在各自的研究中。
我们将详细定义中介变量、调节变量和协变量的概念,解释它们在研究中的作用和重要性。
然后,我们将介绍如何通过统计方法检验这些变量,包括常用的回归分析、路径分析、协方差分析等技术。
我们将重点关注这些统计检验方法的原理、步骤和适用条件,以便读者能够在实际研究中正确应用。
我们还将对中介变量、调节变量和协变量进行比较,分析它们之间的异同点,以及在研究中的优势和局限性。
这将有助于读者更好地理解这三种变量在实证研究中的适用场景,以及如何在具体研究中选择合适的变量和方法。
我们将通过一些实证研究案例来演示中介变量、调节变量和协变量的应用,以便读者能够更直观地理解这些概念和方法在实际研究中的应用。
通过本文的阅读,读者将能够更深入地理解中介变量、调节变量和协变量的概念、统计检验方法及其在实证研究中的应用,为未来的研究提供有益的参考和指导。
二、中介变量概念及统计检验中介变量,又称为中介效应,是一个在自变量和因变量之间起桥梁作用的变量。
它的存在意味着自变量对因变量的影响并非直接,而是通过中介变量这一“中介”来实现的。
在理解这个概念时,我们可以将自变量视为“原因”,因变量视为“结果”,而中介变量则是这一因果关系链条中的“过程”或“机制”。
统计检验方面,常用的中介效应检验方法包括Baron和Kenny(1986)提出的逐步回归法,以及Sobel检验和Bootstrap方法等。
逐步回归法要求先检验自变量对中介变量的影响(第一步),再检验中介变量对因变量的影响(第二步),最后检验在控制中介变量后,自变量对因变量的直接影响是否显著减弱或消失(第三步)。
调节变量和中介变量

自变量、因变量和乘积项放到多元回归方程中检验交互作用。 乘积项的系数如果显著,就说明调节作用存在。
5.调节作用的分析和解释
调节变量和自变量都是定类变量:
1)在不同的组中分别计算因变量的均值,然后用得到的值 来做图,直观的表示出调节作用的模式。
2)在案调节变量所分的不同组中,检验自变量对结果变量 回归的斜率。
3.2 中介作用的检验和分析
1.建立因果关系
两个变量X与Y之间存在因果关系,如果X与Y之间 是完全没有关系的,接下来的步骤就不用做了。
这种关系是不是虚假的相关。
Wegener和Fabrigar提出:即使用非实验的研究,人们也 可以通过把其他变量的作用控制掉的方法或收集几个时间 点的数据的方法,来实现比较严格的因果关系研究。
交互作用分类
增强型交互作用:随着X2变大,X1对Y的正面影 响越来越强
干扰型交互作用:随着X2变大,X1对Y的正面影 响逐渐减弱
2.3 检验调节作用的方法
检验调节作用最普遍的方法是多元调节回归分析: MMR
MMR具体步骤
1.用虚拟变量代表类别变量
所需的虚拟变量的数目等于类别变量水平个数减一。 如2个类别变量的时候,D1=1;D1=0
“视情况而定”“因人而异” “在什么样的情况下”“对于哪些人”
Z
X
Y
2.1 调节作用的原理
调节变量影响自变量和因变量之间的关系,即可以是对关 系方向的影响,又可以是对关系强度的影响。
2.2 调节作用与交互作用
交互作用:两个变量(X1和X2)共同作用时对Y的 影响不等于两者分别影响Y的简单数学和。两个 自变量可以是对称也可以是不对称的。
调节变量和中介变量
本章大纲
调节效应的四种解释

调节效应的四种解释调节效应是指在某种条件下,一种因素对另一种因素的影响程度会随着第三种因素的变化而发生变化。
在研究中,调节效应是非常重要的,因为它可以帮助我们更好地理解变量之间的关系。
在本文中,我们将探讨四种解释调节效应的方法。
1. 交互作用交互作用是指两个或多个因素之间的相互作用。
在这种情况下,一个因素的影响程度取决于另一个因素的水平。
例如,假设我们正在研究两种药物对高血压的治疗效果。
我们发现,一种药物在年轻人中更有效,而另一种药物在老年人中更有效。
这就是交互作用的例子。
2. 中介效应中介效应是指一个因素通过影响另一个因素来影响结果变量。
例如,假设我们正在研究压力对心理健康的影响。
我们发现,压力会导致睡眠质量下降,而睡眠质量下降会导致心理健康问题。
因此,睡眠质量是压力和心理健康之间的中介变量。
3. 调节变量调节变量是指一个因素可以影响另一个因素对结果变量的影响。
例如,假设我们正在研究饮食对健康的影响。
我们发现,饮食对健康的影响程度取决于个体的体重。
因此,体重是饮食和健康之间的调节变量。
4. 模型比较模型比较是指比较不同模型之间的差异,以确定哪个模型最好地解释数据。
例如,假设我们正在研究社交媒体使用对心理健康的影响。
我们可以比较不同模型,例如,一个模型考虑社交媒体使用和睡眠质量对心理健康的影响,而另一个模型只考虑社交媒体使用对心理健康的影响。
通过比较这些模型,我们可以确定哪个模型最好地解释数据。
调节效应是研究中非常重要的概念。
通过了解交互作用、中介效应、调节变量和模型比较等方法,我们可以更好地理解变量之间的关系,并更好地解释数据。
调节变量和中介变量精选全文

变革型领导
员工工作绩效和组织公民行为
中介变量解释关系后的作用机制
中介变量可以解释变量之间为什么会存在关系以及这个关系如 何发生的。
二、调节变量的原理和检验方法
调节变量定义:
如果变量X与变量Y有关系,但是X与Y的关系受第三个变 量Z的影响,那么变量Z就是调节变量。
变量Y与变量X的关系是变量Z的函数,Z便称为X与Y关系 的调节变量。
因变量有几种测量方法,尽量选择测量信度高的 方法和测量敏感度较高的方法。
2.5 检验调节变量的其他方法
多层线性模型:HLM 结构方程模型:SEM
三、中介变量的原理和检验方法
3.1 中介作用的原理
凡是X影响Y,并且X是通过一个中间的变量M对Y产生影 响的,M就是中介变量。
完全中介:c=0 部分中介:c>0
“视情况而定”“因人而异” “在什么样的情况下”“对于哪些人”
Z
X
Y
2.1 调节作用的原理
调节变量影响自变量和因变量之间的关系,即可以是对关 系方向的影响,又可以是对关系强度的影响。
2.2 调节作用与交互作用
交互作用:两个变量(X1和X2)共同作用时对Y的 影响不等于两者分别影响Y的简单数学和。两个 自变量可以是对称也可以是不对称的。
交互作用分类
增强型交互作用:随着X2变大,X1对Y的正面影 响越来越强
干扰型交互作用:随着X2变大,X1对Y的正面影 响逐渐减弱
2.3 检验调节作用的方法
检验调节作用最普遍的方法是多元调节回归分析: MMR
MMR具体步骤
1.用虚拟变量代表类别变量
所需的虚拟变量的数目等于类别变量水平个数减一。 如2个类别变量的时候,D1=1;D1=0
调节变量和中介变量

Click to edit company s l o g a n .
第十四章 调节变量和中介变量
本章大纲
1 2 3
调节变量和中介变量在研究中的作用
调节变量的原理和检验方法
中介变量的原理和检验方法
一、调节变量和中介变量在研究中的意义
我们的很多知识都是建立在变量间的相关关系 或因果关系的基础上的,随着研究的深入,一 些简单的关系已经不能够提供足够的信息,也 难以概括复杂的情况。所以研究者们才提出了 调节变量和中介变量的研究挖掘更多信息的方 法。
Z
X
Y
2.1 调节作用的原理
调节变量影响自变量和因变量之间的关系,即可以是对关 系方向的影响,又可以是对关系强度的影响。
2.2 调节作用与交互作用
交互作用:两个变量(X1和X2)共同作用时对Y的 影响不等于两者分别影响Y的简单数学和。两个 自变量可以是对称也可以是不对称的。
调节作用:一个变量(X1)影响了另外一个变量 (X2)对Y的影响。自变量和调节变量是不能互 换的。
2.3 检验调节作用的方法
检验调节作用最普遍的方法是多元调节回归分析: MMR
MMR具体步骤
1.用虚拟变量代表类别变量
所需的虚拟变量的数目等于类别变量水平个数减一。 如2个类别变量的时候,D1=1;D1=0
2.对连续变量进行中心化或标准化
目的:减小回归方程中的变量间多重共线性 中心化:用这个变量中测量的每个数据点减去均值,使得新得到的数 据样本均值为0
2.2 调节作用与交互作用
Y 0 1 X1 2 X 2 3 X1 X 2
β1,β2反映了主效应的大小,β3反映了交互效用 和调节作用的大小。 对Y关于X2求偏导数
(完整word版)调节效应和中介效应

调节变量(Moderator)vs 中介变量(Mediator)1、调节变量的定义变量Y与变量X 的关系受到第三个变量M 的影响,就称M为调节变量。
调节变量可以是定性的,也可以是定量的.在做调节效应分析时,通常要将自变量和调节变量做中心化变换。
简要模型:Y = aX + bM + cXM + e 。
Y与X 的关系由回归系数a + cM 来刻画,它是M 的线性函数, c衡量了调节效应(moderating effect)的大小。
如果c显著,说明M 的调节效应显著。
2、调节效应的分析方法显变量的调节效应分析方法:分为四种情况讨论。
当自变量是类别变量,调节变量也是类别变量时,用两因素交互效应的方差分析,交互效应即调节效应;调节变量是连续变量时,自变量使用伪变量,将自变量和调节变量中心化,做Y=aX+bM+cXM+e 的层次回归分析:1、做Y对X和M的回归,得测定系数R12。
2、做Y对X、M和XM的回归得R22,若R22显著高于R12,则调节效应显著。
或者,作XM的回归系数检验,若显著,则调节效应显著;当自变量是连续变量时,调节变量是类别变量,分组回归:按 M的取值分组,做 Y对 X的回归。
若回归系数的差异显著,则调节效应显著,调节变量是连续变量时,同上做Y=aX +bM +cXM +e的层次回归分析.潜变量的调节效应分析方法:分两种情形:一是调节变量是类别变量,自变量是潜变量;二是调节变量和自变量都是潜变量。
当调节变量是类别变量时,做分组结构方程分析。
做法是,先将两组的结构方程回归系数限制为相等,得到一个χ2值和相应的自由度。
然后去掉这个限制,重新估计模型,又得到一个χ2值和相应的自由度。
前面的χ2减去后面的χ2得到一个新的χ2,其自由度就是两个模型的自由度之差.如果χ2检验结果是统计显著的,则调节效应显著;当调节变量和自变量都是潜变量时,有许多不同的分析方法,最方便的是Marsh,Wen和Hau提出的无约束的模型。
调节变量和中介变量模型举例
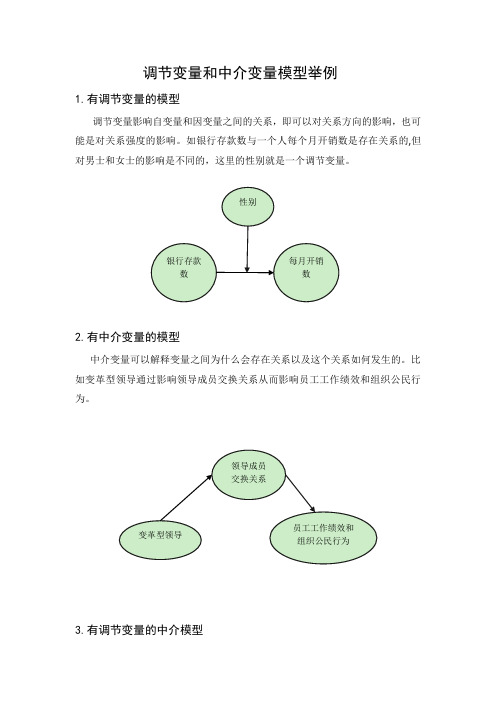
调节变量和中介变量模型举例
1.有调节变量的模型
调节变量影响自变量和因变量之间的关系,即可以对关系方向的影响,也可能是对关系强度的影响。
如银行存款数与一个人每个月开销数是存在关系的,但对男士和女士的影响是不同的,这里的性别就是一个调节变量。
2.有中介变量的模型
中介变量可以解释变量之间为什么会存在关系以及这个关系如何发生的。
比如变革型领导通过影响领导成员交换关系从而影响员工工作绩效和组织公民行为。
3.有调节变量的中介模型
在很多的模型中,可能既有中介变量又有调节变量,如良好的校园氛围会影响一个人的学业成就,但是校园氛围是通过学校依恋这一中介变量对学业成就进行影响,在这个过程中,学生自控能力的差别会影响这种关系,所以学生自控能力是这个模型里的调节变量.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
有中介的调节变量和有调节的中介变量有中介的调节变量(Mediated Moderator )
有中介的调节效应的检验程序:
1)、做Y 对X 、U 和UX 的回归,UX 的系数显著;(这一步说明U 对Y 与X 关系的调节效应显著。
)
2)、做W 对X 、U 和UX 的回归,UX 的系数显著;
3)、做Y 对X 、U 、UX 和W 的回归,W 的系数显著。
如果在第3)步中,UX 的系数不显著,则U 的调节效应完全通过中介变量W 而起作用。
有调节的中介变量(Mod erated Mediator)
有中介的调节效应的检验程序:
1)、做Y 对X 和U 的回归,X 的系数显著;
2)、做W 对X 和U 的回归,X 的系数显著;
3)、做Y 对X 、U 和W 的回归,W 的系数显著;(到此为止说明W 的中介效应显著。
)
4)、做Y 对X 、U 、W 和UW 的回归,UW 的系数显著。
从上面分析步骤可知,检验有调节的中介效应时,先要检验中介效应,然后检验调节效应。
混合模型(Mixed Model )
1)、U 的直接调节效应显著,即UX →Y 的系数显著;
2)、W 的中介效应显著,即X →W ,W →Y 的系数显著;
3)、由UX →W 的系数显著和W →Y 的系数显著,可知U 是有中介的调节变量,即除了直接调节效应外,U 通过W 还对Y 有间接调节效应。
4)、由UX →Y 的系数显著,U 是X →W 的调节变量,再由UW →Y 的系数显著,U 是W →Y
的调节变量,从而X →W 和W →Y 的中介过程受到U 的影响,所以从这个角度看W 是有调节的中介变量。
Notes :
在通常的调节模型中,Y 对X 的回归系数是调节变量U 的线性函数,而在混合模型中,调节不是通常的线性调节,而是二次调节,即Y 对X 的回归系数是调节变量U 的二次函数。
当U 在一定区域内,X 对Y 的效应不显著。
(可通过方程推导该区域)。
