第十二单元与复习
2020年中考历史全程复习课件知识12中华民族的抗日战争

(4)请你列举当时激发了中华民族抗战意志的另外两首 抗日救亡歌曲。 提示:《义勇军进行曲》《黄河大合唱》。
【感悟历史】 (5)回顾十四年抗战艰辛历程,你最大的感悟是什么? 提示:①我们要继承和发扬中华民族抗战精神。 ②树立民族自尊心和自信心,进一步增强民族使命感和 爱国主义情感。 ③我们要以民族大义为重,谋求两党合作,促进祖国统一。 (任答一点、言之有理即可)
③确立_毛__泽__东__思__想__为中国共产党的指导思想并写入党 章。 (3)意义:为争取_抗__日__战__争__的最后胜利准备了条件,并 为中国共产党和中国人民指明了战后的奋斗方向。
3.抗日战争的胜利: (1)胜利标志:_1_9_4_5_年8月15日,日本天皇宣布无条件投 降;1945年9月2日,日本正式签署投降书。
结 只有在中国共产党领导下,全民族团结一致,共 论 同努力,才能取得国家独立,民族富强
2.抗日战争期间四次事变
事变 九一八事变
西安事变 七七事变 八一三事变
时间 1931年9月18日 1936年12月12日 1937年7月7日 1937年8月13日
3.抗日战争期间日军制造的暴行
事件
九一八 事变
七七事 变
【漫画说史】
这是漫画家张仃1946年完成的作品《东北军脚下的镣 铐》。漫画反映的信息是九一八事变后,蒋介石实行不 抵抗政策,导致了东北三省全部沦陷。
【图示记忆】 从九一八事变到西安事变
【漫画说史】
漫画《七七与切切》,从“七七事变”和日本民族的切 腹传统,反映了日军发动全面侵华战争,犹如剖腹自杀, 自取灭亡。
2.第二次国共合作: (1)国共态度:国共两党分别发表声明抗议日本侵略。 (2)红军改编:工农红军改编为_国__民__革__命__军__第__八__路__军__、__ _国__民__革__命__军__新__编__第__四__军__。 (3)合作标志:1937年9月,国民党公开发表国共合作宣 言,以国共合作为主体的_抗__日__民__族__统__一__战__线__正式建立。 _全__民__族__抗__战__的局面开始形成。
历史一轮通史复习:第十二单元 新中国成立初期曲折发展的历程
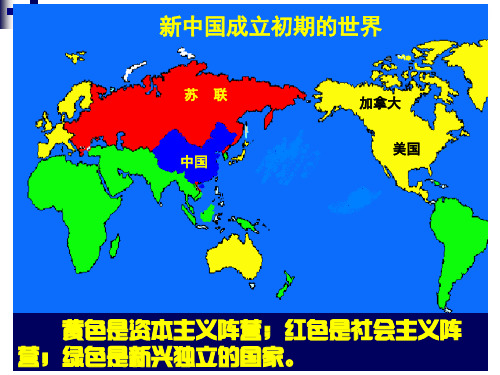
(07年广东)材料一:长期以来,很多学者将中 国近代史的基本线索概括为“两个过程”,即帝 新中国的建立标志着反帝反封建的民主革 国主义和封建主义相结合,把中国变为半殖民地 命任务的完成;中国历史新纪元。 和殖民地的过程,同时也是中国人民反抗帝国主 义和封建主义的过程,主张以这一基本线索作为 指导中国近代史研究的准则。 材料二:近二三十年来,有些学者注重从现 新中国的建立为现代化开辟了的道路: 代化角度研究中国近代史,认为中国的现代化就 政治: 人民民主;建立了中国特色民主制度 是从传统农业社会向现代工业社会的转变,涉及 经济:经济制度;向社会主义过渡创造条件 到政治、经济、文化等方面。 1840年以来中国错 文化:指导思想;为社会主义文化发展奠基 综复杂的历史,可以用“从传统到现代”这一思 路作解释。 ⑬ 结合材料一和材料二的观点,分析中华人 民共和国建立的影响。
美籍华裔历史学家黄仁宇: 近代化,以经济工业化和政治民主化为主要标 志。在中国,近代化也就是工业化与政治、经济、 文化等方面实现社会的转型。 中国近代化是一个长期的艰巨的过程,不完成 反帝反封建的任务和取得民族独立,要想实现近 代化是根本不可能的。
第十二单元 新中国成立初期曲折发展的历程 (1949-1976)
新 中 国 的 政 治 建 构
பைடு நூலகம்
根本制度:人民代 表大会制度
政党制度:中国共 产党领导的多党合 作和政治协商制度
阅读教材 梳理归纳
民族制度:民族区 域自治制度
两个 基本 制度
三大制度是如何建立的?(落实预习、核对答案) 中共领导的多党合作和政治协商制度建立
三个时间 一届政协 一部临宪 一个职能
1949
(3)新中国的建立,开辟了中国历史的 新纪元,标志着反帝反封建的民主革命任 务的完成。为现代化开辟了广阔的道路。 ①政治:成为一个独立自主的国家,进入 了人民民主的新时代,建立了中国特色的 民主政治制度;②经济:建立了新的经济 制度,为新民主主义过渡到社会主义,实 现国家繁荣和人民共同富裕创造了必要的 前提;③思想文化:确立马克思主义毛泽 东思想为指导思想,为社会主义文化的全 面繁荣提供了必要条件。
人教版(新课程标准)八年级上册生物第十二章 生命的起源和生物的进化 单元复习题

人教版(新课程标准)八年级上册生物第十二章生命的起源和生物的进化单元复习题姓名:________ 班级:________ 成绩:________一、单选题1 . 在没有被破坏的地层中,下面关于化石在地层中分布情况的叙述,错误的是()A.在古老的地层中可以找到低等生物的化石B.在新近的地层中可以找到高等生物的化石C.在新近的地层中可以找到低等生物的化石D.在极古老的地层中可以找到高等生物的化石2 . 下列有关生命起源和生物进化的叙述,错误的是()A.生命起源于原始海洋B.化石是研究进化的重要证据C.人类的祖先是类人猿D.生物多样性是自然选择的结果3 . 生命起源和生物进化问题吸引了许多科学家探究的目光。
下列关于生命起源和生物进化的有关说法中,错误的是()A.生命起源于原始海洋B.生物多样性是生物亿万年进化的结果C.化石为生物进化提供了重要证据D.生物的遗传,导致了生物的进化4 . 生命的起源很久以来一直吸引着人们去探求,也不断有各种各样的争论。
而生命起源的化学进化学说被许多学者认同。
下列关于生命起源的化学进化学说,说法不正确的是()A.米勒的模拟实验为化学进化学说的第一个阶段提供了有力支持。
B.我国科学家利用氨基酸合成结晶牛胰岛素支持了化学进化学说第二个阶段的推测。
C.化学进化学说的最后一个阶段,从有机物到原始生命的演变,缺乏足够的实验证据。
D.米勒的模拟实验证实了,原始地球上能够形成有机物,进而演变成了原始生命。
5 . 地质学家把地球的发展史分为若干地质年代,下列排列顺序正确的是()A.前寒武纪时期→古生代→中生代→新生代B.前寒武纪时期→太古代→中生代→古生代→新生代C.古生代→中生代→前寒武纪时期→新生代D.古生代→前寒武纪时期→中生代→新生代→元古代6 . “进化树”(如图)简明地表示了生物的进化历程和亲缘关系,以下说法错误的是()A.A代表原始生命,它生活在原始海洋中B.A由于营养方式不同,进化成代表不同生物类群的两大主干,其分类单位是界C.鸟类和哺乳类都是由B古代爬行类进化来的,C与蕨类植物的区别是用种子繁殖D.从进化树中可以看出,生物进化的总体趋势是由小体型到大体型,由水生到陆生,由低等到高等7 . 原始大气的可能成分是()A.水蒸气、氨气、甲烷B.甲烷、氧气、水蒸气C.水蒸气、氧气、沼气D.氧气、氨气、沼气8 . 关于生命起源,下列叙述中正确的是()A.生命起源于非生命物质B.生命起源于原始陆地C.现代地球上可能再形成原始生命D.原始大气中具有氧气9 . 如图为在我国发现的“郑氏始孔子鸟”化石复原图,它虽然看起来接近鸟类,却具有更多恐龙的体形特征,如具有牙齿、翅膀上长有爪子等。
人教版八年级数学 上册 第十二章 全等三角形 单元综合与测试 B卷(含答案)
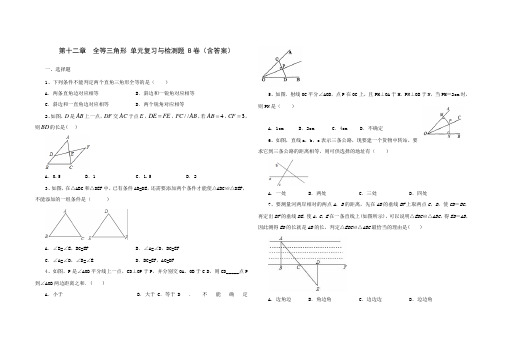
第十二章 全等三角形 单元复习与检测题 B 卷(含答案)一、选择题1、下列条件不能判定两个直角三角形全等的是( ) A .两条直角边对应相等 B .斜边和一锐角对应相等 C .斜边和一直角边对应相等D .两个锐角对应相等2、如图,D 是AB 上一点,DF 交AC 于点E ,DE FE =,//FC AB ,若4AB =,3CF =,则BD 的长是( )A .0.5B .1C .1.5D .23、如图,在△ABC 和△DEF 中,已有条件AB=DE ,还需要添加两个条件才能使△ABC ≌△DEF ,不能添加的一组条件是( )A .∠B=∠E ,BC=EFB .∠A=∠D ,BC=EFC .∠A=∠D ,∠B=∠ED .BC=EF ,AC=DF4、如图,P 是∠AOB 平分线上一点,CD ⊥OP 于P ,并分别交OA 、OB 于C D ,则CD_____点P 到∠AOB 两边距离之和.( )A .小于B .大于C .等于 D.不能确定5、如图.射线OC 平分∠AOB ,点P 在OC 上,且PM ⊥OA 于M .PN ⊥OB 于N ,当PM =2cm 时,则PN 是( )A .1cmB .2cmC .4cmD .不确定6、如图,直线a ,b ,c 表示三条公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )A .一处B .两处C .三处D .四处7、要测量河两岸相对的两点A ,B 的距离,先在AB 的垂线BF 上取两点C ,D ,使CD =BC ,再定出BF 的垂线DE ,使A ,C ,E 在一条直线上(如图所示),可以说明△EDC ≌△ABC ,得ED =AB ,因此测得ED 的长就是AB 的长,判定△EDC ≌△ABC 最恰当的理由是( )A .边角边B .角边角C .边边边D .边边角8、已知一等腰三角形的腰长为5,底边长为4,底角为β.满足下列条件的三角形不一定与已知三角形全等的是( )A .两条边长分别为4,5,它们的夹角为βB .两个角是β,它们的夹边为4C .三条边长分别是4,5,5D .两条边长是5,一个角是β9、如图,在ABC 中,AC BC =,过点B 作射线BF ,在射线BF 上取一点E ,连接AE ,使得CBF CAE ∠=∠,过点C 作射线BF 的垂线,垂足为点D ,若2DE =,4AE =,则BD 的长度为( )A .7B .6C .4D .210、如图,方格纸中△DEF 的三个顶点分别在小正方形的顶点上,像这样的三个顶点都在格点上的三角形叫格点三角形,则图中与△DEF 全等的格点三角形最多有A .8个B .7个C .6个D .4个二、填空题11、如图,如果△ABC ≌△DEF ,△DEF 周长是32cm ,DE=9cm ,EF=13cm ,∠E=∠B ,则AC=______cm .12、如图,小明用直尺和圆规作一个角等于已知角,则说明A O B AOB '''∠=∠的依据是______.13、已知△ABC ≌△DEF ,△ABC 的周长为12,则△DEF 的周长为______14、如图,D 为Rt △ABC 中斜边BC 上的一点,且BD=AB ,过D 作BC 的垂线,交AC 于E ,若AE=12cm ,则DE 的长为__cm .15、已知AD 是△ABC 的角平分线,DE ⊥AB 于E ,且DE =3cm ,则点D 到AC 的距离为_____.16、在四边形ABCD 中,∠BAD+∠BCD=180°, AC 平分∠BAD ,过点C 作CE ⊥AD ,垂足为E , CD=4,AE=10,则四边形ABCD 的周长是____________________.17、在数学活动课上,小明提出这样一个问题:∠B=∠C=90°,E 是BC 的中点,DE 平分∠ADC ,如图.大家一起热烈地讨论交流,小英第一个得出如下结论:(1)AE 平分∠DAB ;(2)△EBA ≌△DCE ;(3)AB+CD=AD ;(4)AE ⊥DE ;(5)AB ∥CD .其中正确的结论是_____.(将你认为正确结论的序号都填上)18、如图所示,直线a经过正方形ABCD的顶点A,分别过正方形的顶点B、D作BF⊥a于点F,DE⊥a于点E,若DE=8,BF=5,则EF的长为__.三、解答题19、已知△ABC≌△DFE,∠A=100°,∠B=50°,DF=12cm,求∠E的度数及AB的长.20、如图,点A,B,D,E在同一直线上,AB=ED,AC∥EF,∠C=∠F.求证:AC=EF.21、如图,∠C=∠CAM=90°,AC=8,BC=4,P,Q两点分别在线段AC和射线AM上运动,且PQ=A B.若△ABC和△PQA全等,求AP的长度.22、如图,已知△EFG≌△NMH,∠F与∠M是对应角.(1)写出图中相等的线段与角.(2)若EF=2.1cm,FH=1.1cm,HM=3.3cm,求MN和HG的长度.23、如图,在ABC∆中,D是BC边上的一点,AB DB=,BE平分ABC∠,交AC边于点E,连接DE.(1)求证:ABE DBE ∆≅∆;(2)若100A ∠=︒,50C ∠=︒,求AEB ∠的度数.24、如图,△ABC 为等腰三角形,AB=AC ,∠D=∠E ,∠BAD=∠CAE . (1)写出一对全等的三角形:△ ≌△ ; (2)证明(1)中的结论; (3)求证:点G 为BC 的中点.25、已知AB=AC ,D ,E 是BC 边上的点,将△ABD 绕点A 旋转,得到△ACD',连接D'E(1)如图1,当∠BAC=120°,∠DAE=60°时,求证DE=D'E ,(2)如图2,当DE=D'E 时,∠DAE 与∠BAC 有怎样的数量关系?请写出,并说明理由.参考答案:一、1、D 2、B 3、B 4、B 5、B 6、D 7、B 8、D 9、B 10、A 二、 11、10 12、SSS 13、12 14、12 15、 3cm 16、 2817、(1)(3)(4)(5). 18、13三、解答题19、∠E=30°,AB=12cm . 【分析】根据全等三角形性质得出∠D=∠A=100°,∠F=∠B=50°,利用三角形内角和定理即可求出∠E 的度数,再根据DF=AB ,即可求出AB 的长.【详解】∵△ABC ≌△DFE ,∴∠D=∠A=100°,∠F=∠B=50°,DF=AB ∴∠E=180°-100°-50°=30°,∵DF=12cm , ∴AB=12cm .【点睛】本题主要考查全等三角形的性质,掌握全等三角形的对应边、对应角相等是解题的关键. 20、证明见解析. 【解析】试题分析:根据全等三角形的片对于性质,再由原子条件即可证明△ABC ≌△EDF (AAS ),推出AC=EF 即可.试题解析:证明:∵AC ∥EF , ∴∠A=∠E . 在△ABC 和△DEF 中, {∠A =∠E∠C =∠F AB =ED , ∴△ABC ≌△EDF . ∴AC=EF .考点:全等三角形的判定与性质. 21、4或8 【解析】试题分析:分△ABC ≌△PQA 和△ABC ≌△QPA 两种情况求AP 的长. 试题解析:当△ABC ≌△PQA 时,AP =CA =8; 当△ABC ≌△QPA 时,AP =CB =4.22、(1)见解析;(2)MN=2.1cm ;HG= 2.2cm . 【分析】(1)根据△EFG ≌△NMH ,∠F 与∠M 是对应角可得到两个三角形中对应相等的三边和三角;(2)根据(1)中的对等关系即可得MN 和HG 的长度.【详解】(1)∵△EFG ≌△NMH ,∠F 与∠M 是对应角,∴EF=NM ,EG=NH ,FG=MH ,∠F=∠M ,∠E=∠N ,∠EGF=∠NHM , ∴FH=GM ,∠EGM=∠NHF ; (2)∵EF=NM ,EF=2.1cm , ∴MN=2.1cm ;∵FG=MH ,FH+HG=FG ,FH=1.1cm ,HM=3.3cm , ∴HG=FG-FH=HM-FH=3.3-1.1=2.2cm .23、(1)见解析;(2)65︒ 【分析】(1)由角平分线定义得出ABE DBE ∠∠=,由SAS 证明ABE DBE ∆≅∆即可; (2)由三角形内角和定理得出30ABC ∠=︒,由角平分线定义得出1152ABE DBE ABC ∠∠∠︒===,在ABE ∆中,由三角形内角和定理即可得出答案.【详解】(1)证明:BE 平分ABC ∠,∴ABE DBE ∠∠=,在ABE ∆和DBE ∆中,AB DB ABE DBE BE BE =⎧⎪∠=∠⎨⎪=⎩,∴()ABE DBE SAS ∆≅∆;(2)100A ∠=︒,50C ∠=︒,∴30ABC ∠=︒,BE平分ABC∠,∴1152ABE DBE ABC∠∠∠︒===,在ABE∆中,1801801001565AEB A ABE∠=︒∠∠=︒︒︒=︒----.【点睛】本题考查了全等三角形的判定与性质、角平分线的定义、三角形内角和定理;熟练掌握三角形内角和定理和角平分线定义,证明三角形全等是解题的关键.24、(1)△ABE≌△ACD.(2)详见解析.(3)详见解析.【分析】(1)结论:△ABE≌△ACD.(2)根据AAS即可证明;(3)只要证明FB=FC,可得AF垂直平分线段BC即可解决问题;【详解】(1)解:结论:△ABE≌△ACD.(2)证明:∵∠BAD=∠CAE,∴∠BAE=∠CAD,在△ABE和△ACD中,{E DBAE CADAB AC∠=∠∠=∠=,∴△ABE≌△ACD.故答案为ABE,ACD.(3)证明:∵AB=AC,∴∠ABC=∠ACB,∵△ABE≌△ACD,∴∠ABE=∠ACD,∴∠FBC=∠FCB,∴BF=CF,∵AB=AC,∴AF垂直平分线段BC,∴BG=GC,∴点G为BC的中点.【点睛】本题考查了全等三角形的判定和性质、等腰三角形的判定和性质等知识,解题的关键是准确寻找全等三角形解决问题.25、(1)详见解析;(2)∠DAE=12∠BAC,理由详见解析.【分析】(1)根据旋转的性质和全等三角形的判定定理SAS证得△DAE≌△D′AE,则由“全等三角形的对应边相等”的性质证得结论;(2)∠DAE=12∠BAC.根据旋转的性质和全等三角形的判定定理SSS证得△DAE≌△D′AE,则由“全等三角形的对应角相等”的性质推知∠DAE=12∠BAC.【详解】(1)证明:如图,∵△ABD旋转得到△ACD',∴∠DAD'=∠BAC=120°,AD=AD'.∵∠DAE=60°,∴∠EAD'=∠DAD'-∠DAE=120°-60°=60°. ∴∠DAE=∠D'AE,又∵AE=AE,AD=AD',∴△DAE≌△D'AE(SAS).∴DE=D'E.(2)解:∠DAE=12∠BAC.理由:如图,∵△ABD旋转得到△ACD', ∴∠DAD'=∠BAC,AD=AD'. ∵DE=D'E,AE=AE,∴△DAE≌△D'AE(SSS).∴∠DAE=D'AE=12∠DAD'.∴∠DAE=12∠BAC.【点睛】本题考查的知识点是全等三角形的判定与性质及旋转的性质以及等腰三角形的性质,解题的关键是熟练的掌握全等三角形的判定与性质及旋转的性质以及等腰三角形的性质.。
第十二单元 整理与复习

三位数除以一位数的复习课题:整理与复习教学内容:教科书第109—110页的内容。
知识目标:1.组织学生对本学期学习内容和学习情况进行回顾,促进学生对学习的反思。
2.引导学生联系生活复习用连除解决实际问题;巩固三位数除以一位数,两位数乘以一位数的笔算。
技能目标:1.培养学生在反思中提高复习的针对性和有效性的能力;2.运用数学知识解决生活问题的能力。
情感目标:通过回顾,了解学生对有关教学内容的兴趣和态度,感受自己在数学学习上的收获和进步,培养学生自我评价和相互评价的能力,实事求是学习态度和对数学的积极感情。
教学重点:组织学生对本学期学习内容和自己的学习情况进行回顾。
教学难点:在反思与交流中自我评价和相互评价,感受收获、进步与不足。
教学课时:1课时。
教学过程:一、回顾反思,交流评价:1,谈话引入师:你能回顾一下这个学期学习的内容,根据自己的学习情况,说说你的收获吗?(学生自由发言。
)生1:这学期我们学习了商是三位数的除法、平移和旋转、认识小数……生2:我们还学习了轴对称图形、认识了千米和吨,我还可以把这些知识应用到生活中……2.填写表格,汇报交流:师:在这里有一张表格,(大屏幕演示)你可以先仔细思考一下,我学得最好的内容我最感兴趣的内容我觉得学习有困难的内容对老师的建议1. 集体交流,反馈信息; 师:现在,你愿意把你的想法和大家交流吗?针对不同的问题一一汇报:问题1:你认为你学得最好的内容是什么?为什么?问题2:你最感兴趣的问题是什么?为什么?问题3;你觉得有困难的内容是什么?在小组的讨论中你解决了吗?问题4:你对老师有哪些建议呢?2.师小结:a 、 同学们在这个学期的学习里,都学到了很多知识,有很多的收获。
希望同学们能好好整理一下,把学得不够理想再好好复习复习。
二、动物赛跑。
谈话:小朋友们,你们喜爱看动物赛跑吗?今天老师给你们带来了许多动物,想看吗?1.下面是动物一分钟跑得路程,你帮它算一算,看谁跑得最快?谁跑得最慢?2. 出示各种动物图。
初中物理总复习课件第十二单元浮力2022年(全国通用)

3
二、阿基米德原理
考向一 阿基米德原理的应用:浮力的大小
典例三:(2021·广东中考真题)小明看到清淤作业人员正在将水塘底部的淤泥搬运到船上。他 想:水面高度会变化吗?于是进行了探究:首先,将石块a和不吸水的木块b置于装有水的烧杯中 ,如图所示;然后,将石块a从水中拿出并轻轻放在木块b上,它们处于漂浮状态,则水面高度
3
二、阿基米德原理
知识清单
要点诠释二:探究影响浮力大小的因素 【实验目的】探究影响浮力大小的因素。 【实验器材】弹簧测力计、烧杯2个、水、圆柱体(A)、盐水。 【实验原理】(1)浸在液体中的物体都会受到向上的浮力;(2)浮力大小遵循阿基米德原理 。 【实验步骤】一、实验装置如图。
3
二、阿基米德原理
3
三、物体的沉浮
考向一 物体沉浮的条件
典例一:(2021·湖南衡阳市)甲、乙、丙、丁是四个体积、形状相同的小球而材质不同的小球
,把它们放入水中静止后的情况如图所示,则它们在水中所受浮力相等的是(C )。
A.甲和乙
B.乙和丙
C.丙和丁
D.甲和丁
3
三、物体的沉浮
考向一 物体题)两个完全相同的烧杯A、B中分别盛有两种不同液体,将两个
3
三、物体的沉浮
知识清单
要点诠释:浮力的应用 3.密度计 密度计是利用物体浮在液面的条件来工作的,用密度计测量液体的密度时,它受到的浮力总等于 它的重力,由于密度计制作好后它的重力就确定了,所以它在不同液体中漂浮时所受到的浮力都 相同,根据可知:待测液体的密度越大,密度计浸入液体中的体积则越小,露出部分的体积就越 大;反之待测液体密度越小,密度计浸入液体中的体积则越大,露出部分的体积就越小,所以密 度计上的刻度值是“上小下大”。
初中数学人教版八年级上册第十二章 全等三角形单元复习-章节测试习题(2)

章节测试题1.【题文】如图,在△ABC中,AB=AC,AD是角平分线,点E在AD上,请写出图中两对全等三角形,并选择其中的一对加以证明.【答案】△ABE≌△ACE,△EBD≌△ECD,△ABD≌△ACD.以△ABE≌△ACE为例,证明见解答【分析】由AB=AC,AD是角平分线,即可利用(SAS)证出△ABD≌△ACD,同理可得出△ABE≌△ACE,△EBD≌△ECD.【解答】△ABE≌△ACE,△EBD≌△ECD,△ABD≌△ACD.以△ABE≌△ACE为例,证明如下:∵AD平分∠BAC,∴∠BAE=∠CAE.在△ABE和△ACE中,,∴△ABE≌△ACE(SAS).2.【题文】杨阳同学沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息汇集如下:如图,AB∥OH∥CD,相邻两平行线间的距离相等,AC,BD相交于O,OD⊥CD,垂足为D,已知AB=20米,请根据上述信息求标语CD的长度.【答案】20米.【分析】已知AB∥CD,根据平行线的性质可得∠ABO=∠CDO,再由垂直的定义可得∠CDO=90°,可得OB⊥AB,根据相邻两平行线间的距离相等可得OD=OB,即可根据ASA定理判定△ABO≌△CDO,由全等三角形的性质即可得CD=AB=20m.【解答】∵AB∥CD,∴∠ABO=∠CDO,∵OD⊥CD,∴∠CDO=90°,∴∠ABO=90°,即OB⊥AB,∵相邻两平行线间的距离相等,∴OD=OB,在△ABO与△CDO中,,∴△ABO≌△CDO(ASA),∴CD=AB=20(m)3.【题文】我们把两组邻边相等的四边形叫做“筝形”.如图,四边形ABCD是一个筝形,其中AB=CB,AD=CD. 对角线AC,BD相交于点O,OE⊥AB,OF⊥CB,垂足分别是E,F.求证OE=OF.【答案】证明见解答.【分析】欲证明OE=OF,只需推知BD平分∠ABC,所以通过全等三角形△ABD≌△CBD(SSS)的对应角相等得到∠ABD=∠CBD,问题就迎刃而解了.【解答】证明:∵在△ABD和△CBD中,AB=CB,AD=CD,BD=BD,∴△ABD≌△CBD(SSS),∴∠ABD=∠CBD,∴BD平分∠ABC.又∵OE⊥AB,OF⊥CB,∴OE=OF.4.【题文】已知△ABN和△ACM的位置如图所示,AB=AC,AD=AE,∠1=∠2.(1)求证:BD=CE;(2)求证:∠M=∠N.【答案】(1)证明见解答(2)证明见解答【分析】(1)由SAS证明△ADB≌△AEC,得出对应边相等即可(2)证出∠BAN=∠CAM,由全等三角形的性质得出∠B=∠C,由AAS证明△ACM≌△ABN,得出对应角相等即可.【解答】(1)在△ADB和△AEC中,∴△ADB≌△AEC∴BD=CE(2)∵∴即又△ADB≌△AEC∴180°-即.5.【题文】如图①,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.(1)请你判断并写出FE与FD之间的数量关系(不需证明);(2)如图②,如果∠ACB不是直角,其他条件不变,那么在(1)中所得的结论是否仍然成立?若成立,请证明;若不成立,请说明理由.【答案】(1)FE=FD(2)答案见解答【分析】(1)先在AC上截取AG=AE,连结FG,利用SAS判定△AEF≌△AGF,得出∠AFE=∠AFG,FE=FG,再利用ASA判定△CFG≌△CFD,得到FG=FD,进而得出FE=FD;(2)先过点F分别作FG⊥AB于点G,FH⊥BC于点H,则∠FGE=∠FHD=90°,根据已知条件得到∠GEF=∠HDF,进而判定△EGF≌△DHF(AAS),即可得出FE=FD.也可以过点F作FG⊥AB于G,作FH⊥BC于H,作FK⊥AC于K,再判定△EFG≌△DFH(ASA),进而得出FE=FD.【解答】(1)FE与FD之间的数量关系为:FE=FD.理由:如图,在AC上截取AG=AE,连结FG,∵AD是∠BAC的平分线,∴∠1=∠2,在△AEF与△AGF中,∴△AEF≌△AGF(SAS),∴∠AFE=∠AFG,FE=FG,∵∠B=60°,AD,CE分别是∠BAC,∠BCA的平分线,∴2∠2+2∠3+∠B=180°,∴∠2+∠3=60°,又∵∠AFE为△AFC的外角,∴∠AFE=∠CFD=∠AFG=∠2+∠3=60°,∴∠CFG=180°-60°-60°=60°,∴∠GFC=∠DFC,在△CFG与△CFD中,,∴△CFG≌△CFD(ASA),∴FG=FD,∴FE=FD;(2)结论FE=FD仍然成立.如图,过点F分别作FG⊥AB于点G,FH⊥BC于点H,则∠FGE=∠FHD=90°,∵∠B=60°,且AD,CE分别是∠BAC,∠BCA的平分线,∴∠2+∠3=60°,F是△ABC的内心,∴∠GEF=∠BAC+∠3=∠1+∠2+∠3=60°+∠1,∵F是△ABC的内心,即F在∠ABC的角平分线上,∴FG=FH,又∵∠HDF=∠B+∠1=60°+∠1,∴∠GEF=∠HDF,在△EGF与△DHF中,,∴△EGF≌△DHF(AAS),∴FE=FD.6.【答题】下列说法正确的是()A. 两个面积相等的图形一定是全等形B. 两个长方形是全等图形C. 两个全等图形形状一定相同D. 两个正方形一定是全等图形【答案】C【分析】根据全等图形的概念即可得出答案.【解答】A、面积相等,但图形不一定完全重合,故错误,B、两个长方形,图形不一定完全重合,故错误;C、全等图形∵完全重合,∴形状一定相同,故正确,D、两个正方形,面积不相等,也不是全等图形,故答案选C.7.【答题】已知图中的两个三角形全等,则∠α的度数是()A. 72°B. 60°C. 58°D. 50°【答案】D【分析】根据全等三角形对应角相等可知∠α是a、c边的夹角,然后写出即可.【解答】∵两个三角形全等,∴∠α的度数是50°.选D.8.【答题】如图,在下列条件中,不能证明△ABD≌△ACD的是().A. BD=DC,AB=ACB. ∠ADB=∠ADC,BD=DCC. ∠B=∠C,∠BAD=∠CADD. ∠B=∠C,BD=DC【答案】D【分析】两个三角形有公共边AD,可利用SSS,SAS,ASA,AAS的方法判断全等三角形.【解答】∵AD=AD,A、当BD=DC,AB=AC时,利用SSS证明△ABD≌△ACD,正确;B、当∠ADB=∠ADC,BD=DC时,利用SAS证明△ABD≌△ACD,正确;C、当∠B=∠C,∠BAD=∠CAD时,利用AAS证明△ABD≌△ACD,正确;D、当∠B=∠C,BD=DC时,符合SSA的位置关系,不能证明△ABD≌△ACD,错误.选D.9.【答题】如图,∠B=∠E=90°,AB=DE,AC=DF,则△ABC≌△DEF的理由是()A. SASB. ASAC. AASD. HL【答案】D【分析】本题考查了直角三角形全等的判定.【解答】∵在Rt△ABC与Rt△DEF中,,∴Rt△ABC≌Rt△DEF(HL),选D.10.【答题】如图,AC=CE,∠ACE=90°,AB⊥BD,ED⊥BD,AB=5cm,DE=3m,则BD等于()A. 6cmB. 8cmC. 10cmD. 4cm【答案】B【分析】由题中条件求出∠BAC=∠DCE,可得直角三角形ABC与CDE全等,进而得出对应边相等,即可得出结论.【解答】∵AB⊥BD,ED⊥BD,∴∠B=∠D=∠ACE=90°,∴∠BAC+∠ACB=90°,∠ACB+∠ECD=90°,∴∠BAC=∠ECD,∵在Rt△ABC与Rt△CDE中,∴Rt△ABC≌Rt△CDE(AAS),∴BC=DE=3cm,CD=AB=5cm,∴BD=BC+CD=3+5=8cm,故答案选B.11.【答题】如图,在Rt△ABC和Rt△BAD中,AB为斜边,AC=BD,BC,AD相交于点E,下列说法错误的是()A. AD=BCB. ∠DAB=∠CBAC. △ACE≌△BDED. AC=CE【答案】D【分析】本题考查了全等三角形的判定与性质.【解答】在和中,,∴≌,∴,正确,,正确,在和中,,∴在≌,∴正确.无从得证.选.12.【答题】如图,有一池塘,要测池塘两端A,B的距离,可先在平地上取一个直接到达A和B的点C,连接AC并延长到D,使CD=CA,连接BC并延长到E,使CE=CB,连接DE,那么量出DE的长,就是A、B的距离.我们可以证明出△ABC≌△DEC,进而得出AB=DE,那么判定△ABC和△DEC全等的依据是()A. SSSB. SASC. ASAD. AAS【答案】B【分析】本题考查了全等三角形的应用.【解答】解:如图,连接AB,∵在△ACB和△DCE中,,∴△ACB≌△DCE(SAS),∴AB=DE选B13.【答题】如图,在△ABC中,点O到三边的距离相等,∠BAC=60°,则∠BOC =()A. 120°B. 125°C. 130°D. 140°【答案】A【分析】由条件可知O为三角形三个内角的角平分线的交点,则可知∠OBC+∠OCB=(∠ABC+∠ACB)=(180°﹣∠A).在△BOC中利用三角形的内角和定理可求得∠BOC.【解答】∵O到三边的距离相等,∴BO平分∠ABC,CO平分∠ACB,∴∠OBC+∠OCB=(∠ABC+∠ACB)=(180°﹣∠A).∵∠A=60°,∴∠OBC+∠OCB=60°,∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣60°=120°.选A.14.【答题】如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为40和28,则△EDF的面积为()A. 12B. 6C. 7D. 8【答案】B【分析】过点D作DH⊥AC于H,根据角平分线上的点到角的两边距离相等可得DF=DH,再利用“HL”证明Rt△DEF和Rt△DGH全等,根据全等三角形的面积相等可得S△DEF=S△DGH,然后列式求解即可.【解答】解:如图,过点D作DH⊥AC于H,∵AD是△ABC的角平分线,DF⊥AB,∴DF=DH,在Rt△DEF和Rt△DGH中,,∴Rt△DEF≌Rt△DGH(HL),∴S△DEF=S△DGH,∵△ADG和△AED的面积分别为40和28,∴△EDF的面积=×(40-28)=6.选B.15.【答题】如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF,给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有()A. ①②③④B. ①②④C. ①②③D. ②③④【答案】A【分析】根据等腰三角形、全等三角形的判定与性质即可得到答案.【解答】∵BF∥AC,∴∠C=∠CBF,∵BC平分∠ABF,∴∠ABC=∠CBF,∴∠C=∠ABC,∴AB=AC,∵AD是△ABC的角平分线,∴BD=CD,AD⊥BC,故②③正确,在△CDE与△DBF中,∴△CDE≌△DBF,∴DE=DF,CE=BF,故①正确;∵AE=2BF,∴AC=3BF,故④正确;故答案为①②③④.16.【答题】已知△ADF≌△CBE,∠A=20°,∠B=120°,则∠BCE=______.【答案】20°【分析】根据全等三角形的基本性质即可得到答案.【解答】∵△ADF≌△CBE,∴∠BCE=∠DAF=∠A=20°,故答案为20°.17.【答题】如图,△ABC≌△CDA,则AB与CD的位置关系是______.【答案】AB∥CD【分析】根据全等三角形的性质得出边和角的关系,进一步可得到AB与CD的关系即可得到答案.【解答】∵△ABC≌△CDA,则∠ACD=∠BAC,∴AB∥CD,故答案为AB∥CD.18.【答题】如图,在中,点A的坐标为,点B的坐标为,点C 的坐标为,点D在第二象限,且与全等,点D的坐标是______.【答案】(-4,2)或(-4,3)【分析】本题考查了全等三角形的性质、点的坐标.【解答】把点C向下平移1个单位得到点D(4,2),这时△ABD与△ABC全等,分别作点C,D关于y轴的对称点(-4,3)和(-4,2),所得到的△ABD与△ABC 全等.故答案为(-4,2)或(-4,3).19.【答题】如图,△ABC中,AD⊥BC于D,要使△ABD≌△ACD,若加条件∠B=∠C,则可用______判定.【答案】AAS【分析】根据全等三角形的判定从而得到答案.【解答】已知AD⊥BC于D,AD=AD,若加条件∠B=∠C,显然根据的判定为AAS,故答案为AAS.20.【答题】如图,四边形ABCD的对角线AC,BD相交于点O,△ABO≌△ADO.下列结论:①AC⊥BD;②CB=CD;③DA=DC;④△ABC≌△ADC,其中正确结论的序号是______.【答案】①②④【分析】根据全等三角形的性质得出∠AOB=∠AOD=90°,OB=OD,AB=AD,再根据全等三角形的判定定理得出△ABC≌△ADC,进而得出其它结论.【解答】∵△ABO≌△ADO,∴∠AOB=∠AOD=90°,OB=OD,∴AC⊥BD,故①正确;∵四边形ABCD的对角线AC、BD相交于点O,∴∠COB=∠COD=90°,在△ABC和△ADC中,∴△ABC≌△ADC(SAS),故④正确∴BC=DC,故②正确;故答案为①②④.。
第十二章 全等三角形【过知识】数学八年级上册单元复习一遍过(人教版)

又∵∠1=∠2,∴PE=PF, ∠PEA=∠PFC=90 °.
∵ ∠PCB+ ∠BAP=180 °,∠BAP+∠EAP=180 °,
∴ ∠EAP=∠PCB.
在△APE和△CPF中, ∠PEA=∠PFC=90 °, ∠EAP=∠FCP, PE=PF,
∴ △APE ≌ △CPF(AAS), ∴ AP=CP.
∵AD⊥BC, ∴∠ADB=∠ADC=90°. 在Rt△ADB和Rt△ADC中,
AD=AD,
AB=AC,
B
∴ Rt△ADB ≌ Rt△ADC(HL).
∴BD=CD.
A
D
C
方法总结
利用全等三角形可以测量一些不易测量的距离和长 度,还可对某些因素作出判断,一般采用以下步骤: (1)先明确实际问题;
(2)根据实际抽象出几何图形;
解:∵ BE⊥CE,AD⊥CE,
B
∴∠E = ∠ADC = ∠CAD + ∠ACD = 90°.
E
∵∠BCE + ∠ACD = ∠ACB = 90°,
∴∠BCE = ∠CAD.
又∵ BC = AC,
D
∴△BCE ≌ △CAD (AAS).
∴ CE = AD = 2.5 cm,BE = CD.
C
A
∴ BE = CD = CE – DE = 2.5 – 1.7 = 0.8 (cm).
接DF.
(1)图中有全等三角形吗?
(2)图中有面积相等但不全等的三角形吗?
解:(1)有,△ABD ≌△CDB.A
D
(2)有,如 △ABD 和
△AFD,△AFD 和 △BCD,
△ABF 和 △DBF,△ABE 和
E
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十二单元整理与复习
整理与复习(1)
上课时间:6月7日,累计课时:61。
教学内容:~112部分练习
教学目标:
1、复习本学期的计算(三位数除以一位数,两位数乘两位数)
2、复习轴对称、统计、平移和旋转的有关知识
整理与复习(2)
上课时间:6月8日,累计课时:62。
教学内容:~113部分练习
教学目标:
1、整理复习千米与吨的知识,了解这是两个比较大的单位。
2、整理与复习分数的一些知识,进一步认识分数的意义。
3、整理与复习年月日的知识,掌握其中较多的知识点及计算。
整理与复习(3)
上课时间:6月9日,累计课时:63。
教学内容:~114部分练习
教学目标:
1、复习观察物体,知道观察物体的时候一般可以分别从物体的正面、侧面、上面进行观察,并得到不同的观察结果。
2、复习面积单元,进一步了解面积的有关知识。
3、复习解决实际问题,掌握解决问题的基本方法,注意规范解答。
