深空光通信下行链路调制编码预算
光通信中的编码调制技术

光通信中的编码调制技术随着信息交流的快速发展,光通信作为现代通信技术的重要支柱,扮演着连接世界的关键角色。
而在光通信中,编码调制技术则是其核心部分之一。
本文将探讨光通信中的编码调制技术,介绍其原理、应用和未来发展。
一、光通信中的编码调制技术简介光通信中的编码调制技术是指将信息信号转换为适合传输的光信号形式的过程。
通过选择适当的调制方式和编码方案,可以提高光信号的传输效率和抗干扰能力。
在光通信领域,常用的编码调制技术包括脉冲振幅调制(PAM)、脉冲位置调制(PPM)、差分相移键控(DPSK)、相干正交振幅调制(CO-OFDM)等。
二、编码调制技术的原理和工作方式编码调制技术的原理主要基于调制器和解调器之间的相互作用。
调制器将信息信号转换为光信号,而解调器则将光信号重新转换为原始信息信号。
不同的调制方式和编码方案采用不同的调制器和解调器实现。
以脉冲振幅调制为例,该调制方式通过改变光信号的振幅来表达信息。
调制过程首先将基带信号转换为连续时间脉冲序列,然后将脉冲信号与光载波相乘,生成调制后的光信号。
在解调过程中,接收端通过采样和滤波等操作将光信号转换为原始信息信号。
三、编码调制技术的应用领域编码调制技术在光通信中的应用非常广泛。
首先,它可以提高光通信系统的传输速率和容量。
通过采用高阶调制方式,光通信系统可以实现更高的比特率,提高数据传输的效率。
其次,编码调制技术可以提高光通信系统的可靠性和抗干扰能力。
在传输过程中,光信号会受到各种干扰因素的影响,如光纤损耗、色散和噪声等。
采用合适的编码方式可以提高信号的抗干扰性,降低误码率。
此外,编码调制技术还可以扩展光通信系统的传输距离。
通过采用前向纠错编码和调制技术,可以提高信号的传输性能,有效延长光信号在光纤中传输的距离。
四、编码调制技术的未来发展趋势随着信息时代的不断进步,光通信领域也在不断创新和发展。
编码调制技术作为光通信的核心技术之一,也在不断演化。
未来,编码调制技术将继续朝着更高比特率、更高容量和更低误码率的方向发展。
【简说卫星链路预算】卫星中继数据链链路预算

【简说卫星链路预算】卫星中继数据链链路预算链路预算的目的和作用卫星链路预算的目的和作用,简单的讲就是帮助新用户经济合理地选配收发站的硬件配置,协助老用户确认改变线路的可行性,给出合理性建议,即做到少花钱多办事、不多花冤枉钱。
什么时候需要链路预算下面以新用户组建卫星网为例说明什么时候需要用到链路预算。
1、首先用户根据实际情况及需求选定网络结构由于目前甚小口径终端VSAT的迅猛发展、普及,使得VSAT 一词几乎成了卫星通信的代名词。
一般小于4.5m天线的地面站被认为是VSAT站,但在VSAT网中有时中心站HUB的配置又很高(天线:6m-20m),可能是大、中型站,因此也难怪人们提到卫星通信就自然地认为是VSAT系统。
VSAT网络有如下几种结构,通常网络越复杂,投入的成本越高,租用的卫星带宽越多。
2、既已选定网络结构,下面该选择通信卫星和工作频段了卫星的选择主要是看朝向卫星方向有无遮挡及卫星覆盖是否满足要求。
由于目前几大卫星制造商所制造的卫星从性能指标上基本相差不大,针对中国区域的卫星覆盖也大同小异,且不同卫星的对比测试较难实现相同的测试条件,故即使测试,结果也并不能说明问题――孰优孰劣,因此说对卫星的选择很大一部分是由市场因素决定的。
工作频段的选择主要看业务形式。
C波段的主要优势就是不易受降水影响,缺点就是天线口径较大,Ku波段则正好相反。
故对通信保障要求严格,系统可用度要求高的业务应尽量选择C波段,如防洪、抢险、救灾等应急及机要通信,越是下雨越是需要保障通信。
对于系统可用度要求不高,但对于便携性、灵活性要求高,如SNG、动中通等业务则宜选用Ku波段。
3、用户初步接触设备商提出要求,设备商提供组网配置建议4、用户根据设备商建议向卫星公司提供相关信息,希望其提供有关链路预算有关信息包括:A、站址信息――发射、接收站的经纬度、海拔;B、载波信息――信息速率、调制方式、编码方式、接收门限、滚降系数等;C、用户期望信息――希望的天线的尺寸、功放大小、占用带宽等。
深空光通信链路特性分析及功率预算

单位在深空光通信方面取得 了一些阶段性成果 , 但关于深空光通信链路方程 、 大气信道特性、 信噪比和误码 率等方面的详细报道很少。文献[ ] 2 对空 间光通信链路进行了重点研究 , 分析 了影 响光通信链路 的各方面
因素, 但是没有建立能够积极反应光通信链路特性 的链路方程。文献 [ ] 3 对空间光通信系统的探测器信噪 比和误码率进行 了重点研究 , 但是没有详细分析链路方程 、 信噪比和误码率 的具体关系。本文结合国内外研 究成果 , 具体分析了大气信道特性和光学系统特性 , 出了对传统链路方程的修正方法 , 提 建立 了一个具有实 用和操作价值的链路方程 , 通过地面间光通信室外演示实验验证了该链路方程的合理性 。此外 , 对探测器信 噪比和通信误码率进行了具体分析 , 对光束发散角和探测器灵敏度进行 了实验测试 , 验证 了信噪 比和误码率 计算 方 法 的准确 性 。在 上述 理论 分 析和 实 验基 础 上 , 立 了 信 噪 比、 建 误码 率 和链 路 方 程 3者 之 间 的具 体 联
功率预算往往 需要很复杂的折 中考虑。重点分析 了链路距离、 光学天线直径、 光束发散角、 大气 信道损耗 、 光学系统损耗 、 探测器灵敏度等 因素对链路方程 、 探测器信噪比和通信误码率 的影 响。提 出了结合链路方程、 信噪比和误码率对发射功率进行预算的新方法。开展 了7k m地面 间光通 信 室外 演示验 证 实验 , 大 气 信 道 损耗 、 学 系 统 损耗 等 进 行 了测试 ; 展 了光 束 发 散 对 光 开
F( MZ M) B
式 中 : ) A D的过 噪声 因子 。可 以描 述为 F( 为 P F( )= e +( 一K ( —2 M) Kf f M 1 e) 1 / (5 1)
链路预算公式与说明
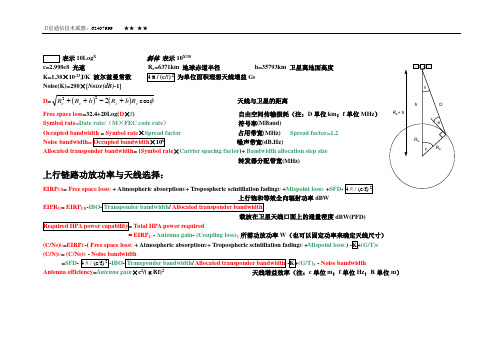
表示10Log X 斜体 表示10X/10c=2.998e8 光速地球赤道半径 h=35793km 卫星离地面高度K=1.38×10-23J/K 波尔兹曼常数 为单位面积理想天线增益G 0Noise(K)=290×[Noise(dB)-1]D =()()f cos 222e e e e R h R h R R +-++ 天线与卫星的距离 Free space loss =32.4+20Log(D ×f ) 自由空间传输损耗(注:D 单位km ;f 单位MHz )Symbol rate =Date rate /(M ×FEC code rate ) 符号率(MBaud)占用带宽(MHz) Spread factor=1.2噪声带宽(dB.Hz)Allocated transponder bandwidth = (Symbol rate ×Carrier spacing factor )+ Bandwidth allocation step size转发器分配带宽(MHz) 上行链路功放功率与天线选择:EIRP US = Free space loss U + Atmospheric absorption U + Tropospheric scintillation fading U +Mispoint loss U +SFD 上行饱和等效全向辐射功率dBWEIPR U = EIRP US -IBO载波在卫星天线口面上的通量密度dBW(PFD)Total HPA power required= EIRP U - Antenna gain - (Coupling loss)U 所需功放功率W (也可以固定功率来确定天线尺寸)(C/N 0)U =EIRPU -( Free space loss U + Atmospheric absorption U + Tropospheric scintillation fading U +Mispoint lossU (G/T)S(C/N)U = (C/N=SFD IBO (G/T)S - Noise bandwidthAntenna efficiency =Antenna gain ×c 2/(πRf)2 天线增益效率(注:c 单位m ;f 单位Hz ;R 单位m )Antenna noise =⎰⎰πππ200sin ),(),(41f q q f q f q d d T R =⎰⎰Ωπ42),(),(1d A T B f q f q λ 以波长为单位,天线有效面积为权重的亮温度对全天空的积分≈15×Antenna efficiency+(1-Antenna efficiency )×[15×sin θ/(cos θ+sin θ)+(140+θ)×cos θ/(cos θ+sin θ)]G/T= Antenna gainEIRP D = EIRP S -OBO(C/No)D =EIRP D –(Free space loss D + Atmospheric absorption D + Tropospheric scintillation fading D + Mispoint loss D G/T(C/N)D =(C/No)D -Noise bandwidth=EIRP D –(Free space loss D + Atmospheric absorption D + Tropospheric scintillation fading D + Mispoint loss D G/T -Noise bandwidthC/(N+I)C/(N+I) = C/(No+Io) - Noise bandwidthEb/(No+Io)频谱仪读到的MARKE DELTA= C/(N+I) +1=(C+N+I)/(N+I)Es/N 0一、转发器参数SFD、G/T、EIRP、载波输入回退CIBO(Carrier InputBackoff)和载波输出回退COBO(Carrier Output Backoff)G/T 被称为figure of merit,即接收系统的品质因素。
光通信中的编码技术研究和优化

光通信中的编码技术研究和优化光通信作为一种高速、大容量的数据传输技术,已经成为现代通信领域的重要研究方向。
在光通信系统中,编码技术的研究和优化对于提高传输速率和降低误码率至关重要。
本文将探讨光通信中的编码技术,并分析其研究与优化的方法与挑战。
一、光通信中的编码技术概述光通信中的编码技术是指将数字信号转化为适合在光纤中传输的光信号的过程。
它通过在信号中引入冗余来增强信号的可靠性,并采用调制技术将数字信号转换为光信号。
在光通信系统中,常用的编码技术包括块编码、前向纠错编码、调制编码等。
1. 块编码块编码是光通信系统中常用的一种编码技术。
它将输入数据分成固定长度的块,并在每个块中引入一定数量的冗余。
这样做的目的是使接收端能够在发生传输错误时,通过冗余信息进行错误检测和纠正。
块编码的常见方法包括汉明编码、RS编码等。
2. 前向纠错编码前向纠错编码是一种能够在接收端进行差错检测和纠正的编码技术。
它利用编码器在发送端对数据进行编码,并在接收端使用纠错解码器进行解码。
常见的前向纠错编码方法包括卷积码、LDPC码等。
3. 调制编码调制编码是将数字信号转换为模拟光信号的过程。
它利用不同的调制方式,在光信号上引入不同的特征,以实现高速、大容量的数据传输。
调制编码常用的方法有正交振幅调制、相移键控等。
二、光通信中编码技术的研究与优化方法在光通信系统中,编码技术的研究和优化旨在提高传输速率和降低误码率。
以下是一些常见的研究与优化方法:1. 码字设计和分组策略码字的设计和分组策略是提高编码效率和抗干扰能力的重要手段。
通过合理设计码字的结构和分组策略,可以提高编码的可靠性和传输效率。
2. 纠错编码算法的改进纠错编码算法的改进可以有效降低误码率。
通过研究和优化纠错编码算法,可以提高编码的纠错能力,使光通信系统具备更好的抗干扰和抗噪声能力。
3. 调制方式的优化调制方式的优化对于提高光通信系统的传输速率至关重要。
通过研究和改进调制方式,可以实现更高的比特传输率和更长的传输距离。
卫星链路预算(链路计算)-专业精简版(带公式计算)

参数 140.0 36.00 39.0 -88.00 -3.5 3.0 6.0 6225.000 4000.000
2.40 北京 116.40 39.90 37965.56 145.74 37.82 60 41.67 0.50 1.00 7.43 2.00 北京 116.40 39.90 37953.47 145.74 37.82 65 36.59 20.00 16.59 0.50 0.30 199.91 196.07 QPSK 256.00 204/204 3/4 170.67 204.80 238.93 4.60
一、卫星参数 1. 轨道位置 (deg.E) 2. 转发器带宽 (MHz) 3. EIRP (dBw) 4. 相应衰减下SFD (dBw/m2) 5. G/T (dB/k) 6. 转发器输出回退OBO (dB) 7. 转发器输入回退IBO (dB) 8. 上行频率 (MHz) 9. 下行频率 (MHz) 二、地面站参数 1. 发信站参数 1)天线口径 (m) 2)城市 3)经度 (deg.E) 4)纬度 (deg.N) 5)至卫星距离 (km) 6)天线方位 (deg) 7)天线仰角 (deg) 8)天线效率 (%) 9)天线增益 (dB) 10)馈源损耗 (dB) 11)功放至馈源插入损耗 (dB) 12)功放预算输出功率 (dBW) 2. 收信站参数 1)天线口径 (m) 2)城市 3)经度 (deg.E) 4)纬度 (deg.N) 5)至卫星距离 (km) 6)天线方位 (deg) 7)天线仰角 (deg) 8)天线效率 (%) 9)天线增益 (dB) 10)接收系统噪声温度 (dBk) 11)天线增益与等效噪声温度之比 (dB/k) 三、空间损耗 1. 上行雨衰 (dB) 2. 下行雨衰 (dB) 3. 上行自由空间损耗 (dB) 4. 下行自由空间损耗 (dB) 四、 载波参数 1. 调制方式 2. 载波信息速率 (kbps) 3. RS编码 4. 前向纠错码率 5. 载波符号速率(ksps) 6. 载波噪声带宽 (khz) 7. 载波分配带宽(khz) 8. 门限 Eb/N0 (dB)
深空通信中的编码与调制技术研究

空通信中的编码与调制技术研究研究方案:深空通信中的编码与调制技术研究引言:随着人类对太空探索的深入,深空通信越来越成为一个重要的课题。
深空通信中的编码与调制技术是实现高速、可靠传输的关键。
本研究旨在综合当前的研究成果,提出创新方法并为实际问题解决提供有价值的参考。
一、研究目标1. 深入了解深空通信中的编码与调制技术的现状和问题;2. 提出新的观点和方法,解决实际问题;3. 实验或调查采集相关数据;4. 对采集到的数据进行整理和分析;5. 在已有研究成果的基础上进行创新和发展。
二、方案实施1. 文献综述通过综合研究相关领域的文献,了解深空通信中的编码与调制技术的现状和问题,掌握最新研究成果,为后续工作奠定基础。
2. 新方法提出基于文献综述的结果,结合自身研究经验和创新思维,提出解决深空通信中编码与调制问题的新观点和方法,并阐明其原理和优势。
3. 实验设计或调查方案根据研究目标,设计一系列合理的实验方案或调查方案,以验证提出的新方法的有效性和实用性。
4. 实验或调查数据采集按照实验设计或调查方案,进行实验或调查数据的采集,并确保所采集的数据具备代表性和可靠性。
5. 数据整理与分析将采集到的数据进行整理,进行统计分析。
通过对数据的分析,验证提出的新方法的有效性,并从中获得有价值的结论。
6. 结果的比对与分析将已有研究成果与本研究提出的新方法进行比对和分析,分析其优势和不足,并提出改进措施。
7. 结果验证与讨论将实验结果或调查结果与已有研究成果进行对比,验证所提出的新方法的有效性和实用性,并对结果进行深入讨论,探索其在实际应用中的价值和潜力。
8. 结论与展望总结研究的成果,提出对深空通信中编码与调制技术研究的展望,指出未来可以进一步改进和提高的方面,并为解决实际问题提供有价值的参考和建议。
结语:通过制定上述研究方案,我们可以进一步深入深空通信中的编码与调制技术的研究,提出新的观点和方法,并验证其有效性和实用性。
基于CCSDS的深空通信链路预算的设计

0 为天线半 功率 波束带 宽;单位 弧度; D( m) 为抛 物面 天 线主 反射 器 i 2 1 径直 径;T 1 为
1 3 — 6 . 4 1 g ( 1 + 0 ) ( 2 . 1 0 )
大 气 中分子 有 磁偶 极子 ,水蒸 气分 子有
电偶分 子,均 能从电磁波 中吸收能量 ,使 电磁
‘
崖利天。 。
降 雨衰耗 为无 线 电波 在穿 过 雨区时 所 受 到 的衰 减量计算平均 年度中 p % 时间可 能达到
( 2 4 )
.
等效 全 向辐 射功率 表 示 了地 面站发射 系
上 行 链 路 指 无 线 电 信 号 经 由 深 空 测 控 地 面 站 天 线 发 射 到 探 测 器 的 链 路 ’反 之 称 为 下 行 统 的能 力 脚
,
2 . 1 . 1 探 测 器及 地 面 站 天 线 损 耗
( 、 2 . 7 )
式中,d为链路的距离 ,单位 k m;f 为频
,
【 关键词 】通信链路 地 面站 探测器 通信信
道 C C S D S
地面 站参 数包 括发 射 天线直 径、 天线 功 率
率、天线仰角 、天线效率等 。天线增 益指天线 将发射功率往指定方 向发射能力 ,公式为
焦损耗如下 :
=
声功 率,p 为经 由探测 器噪 声放 大倍数 ,T 为
在 下行链 路衰减 倍数 ,N。为地面 站噪 声。链 路预算 即预 算出通 信信 道中各种损耗并且量化 为 电平值 ,通过 已知参数的加减,得到接收端
的载 噪 比值 。
…。 去 : 潭
天 线 效 率 ;G 为 天 线 增 益 。
e
式中,k为波尔兹曼常数 ,T e 为接收机 的
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
I. Introduction
NASA is developing optical links to support deep-space communication to a satellite orbiting Mars at data rates on the order of 10 to 100 Mbits/second. The maximum supportable data rate changes by an order of magnitude as the range, atmospheric conditions, Sun-Earth-probe angle and Sun-probe-Earth angle vary. A characterization of these conditions for the Mars link is detailed in a companion article [1]. For optimum data throughput, the modulation and coding should be correspondingly changed during a mission. In this article, we describe the selection of coding and modulation for various operating points and illustrate achievable user data rates. As in [1], the transmitted signal is divided into slots of duration Ts seconds, during which a pulse may be transmitted. For the purpose of coding and modulation design, the link may be parameterized by the maximum average detected signal photons/pulse, Ppk , the average detected signal photons/slot, Pav , and the average detected noise photons/slot, nb . Ppk and Pav are proportional to the peak and average received optical signal power, respectively, and may be thought of as peak and average power constraints. The laser transmitter may have additional constraints on the minimum and maximum separation between transmitted pulses. Efficient signaling under these constraints is discussed in [2] and will not be considered here. Hence we may reduce each operating point to the triple (Pav , Ppk , nb ) and determine coding and modulation that maximize the achievable user bits/slot. Units are normalized by the slot width and
1
results stated in bits/slot, which may be divided by the slot width in seconds to give bits/second. The analysis may be repeated in a similar manner to maximize bits/(signal)photon, a measure of energy efficiency. We choose to maximize bits/slot, a measure of time, or bandwidth, efficiency, as this is the parameter of primary importance for links of interest—we typically have a fixed average power budget and desire to maximize the channel throughput. Although the design procedure is analogous, a link design that maximizes bits/photon will not necessarily maximize bits/second. We model the channel as Poisson to simplify presentation and facilitate comparisons with known results. More accurate models exist for particular detectors, e.g., the Webb+Gaussian model for avalanche photodiode (APD) detectors [3] and the Polya model for photomultiplier tubes (PMTs) [4], and may be used to provide more accurate link estimates. Much of the analysis here extends in a straightforward manner to other models. The optical detector output is quantized and synchronized, providing either slot counts or symbol estimates to the channel decoder. Using this information, the decoder, which may also perform the function of demodulation, generates estimates of the transmitted user data. The fidelity of the system may be measured in terms of the bit-error rate (BER) at the output of the decoder, with a target typically on the order of 10−5 to 10−6 . Where relevant, link budgets in this article require a BER ≤ 10−6 . It is well-known that the deep-space optical link operates efficiently at high peak-to-average power ratios, e.g., [5,6], which may be achieved by modulating the data using M -ary pulse-position modulation (PPM). In PPM, each log2 M user bits map to the location of a single pulsed slot in an M -slot frame. For most of this article, we assume the data are modulated with PPM and focus on choosing the optimum order. In Section II.E, we illustrate the losses incurred by restricting the modulation to PPM. The error-control code (ECC) rate is determined by the order and target bits/second. The baseline candidate coding and modulation for the deep-space optical channel is Reed–Solomon (RS) coded pulseposition modulation (PPM), denoted RSPPM [7]. This baseline is compared with an iteratively decoded serial concatenation of a convolutional code and coded PPM, denoted SCPPM. We illustrate gains of ≈2.5 dB in average power using SCPPM relative to RSPPM for nb = 1.0. The article is odiscuss the behavior of optical channel capacity for a Poisson channel using PPM. We show the impact of peak and average power constraints and dead time on capacity. In Section III, we illustrate a method to choose a modulation order and ECC code rate. In Section IV, we demonstrate the performance of specific coded modulation schemes. In Section V, we show how a symbol-error rate (SER) constraint affects capacity and how to trade off SER and throughput. In Section VI, we work through a sample link design and link budget.
