例题-桁架-截面法
用结点法计算图示桁架的内力

例5-2-2用结点法计算图示桁架的内力用结点法计算图示桁架的内力。
解:(1)求支座反力由桁架整体平衡∑M 1 = 0 ∑M 8= 0 得:F 8y ×8–30×2–30×4=0 F 8y =22.5kN (↑)F 1y ×8–30×4–30×6–20×8 = 0F 1y = 57.5 kN (↑)由∑F y = 0 校核校核,,满足满足。
A-PDF OFFICE TO PDF DEMO: Purchase from to remove the watermark(2) 求各杆轴力由结点法的特殊情况判断出零杆为由结点法的特殊情况判断出零杆为::杆23, 杆67, 杆57。
其它杆力计算如下其它杆力计算如下::结点8: ∑F y =0 F 86y = –22.5 kNF N86=(F 86y /l 86y )×l 86= –50.3 kNF 86x =(F 86y /l 86y )×l 86x = –45 kN∑F x =0F N87=45kN F N46=F N86= –50.3kNFN57=F N87=45kN结点结点11: ∑F y =0 F 13y =20–57.5= –37.5kNF N13=(F 13y /l13y )×l 13= –83.9 kNF 13x =(F 13y /l 13y )×l 13x = –75 kN∑F x =0FN1 =75 kNF N25=F N12=75kN结点3: ∑M = 04F 35x ×2+30×2–37.5×4+75×2=0 F 35x = –30kN F N35=(F 35x /l 35x )×l 35= –33.5 kNF 35y =(F 35x /l 35x )×l 35y = –15 kN∑M 5 = 0 F 34x ×2–30×2+37.5×4 =0F 34x = –45kNF N34=(F 34x /l 34x )×l 34= –50.3 kNF 34y =(F 34x /l 34x )×l 34y = –22.5 kN结点结点55: ∑F y =0F N54=15kN 由结点由结点44∑F = 0校核校核,,满足满足。
用截面法求桁架的内力

FN1 = –0.5F = –5KN FN2 = –0.707F= –7.07KN FN3 = F=10KN
F
G
F
FN1
FN2
A
aC
FN3
1.5F
a
3m 3m
例2:己知F=10KN,求各杆内力?
解:
FF
1.求支反力,由对称性知:
2m
F
G
FRA=FRB=F
D
E
2.求各杆的内力 A.先取特殊结点C
FNAC = FNBC= FNFG= F=10KN
FNAG FNAC
例3:己知F=10KN,判别结构中的零杆,
求1.2.3杆 F 内力?
解:
1.求支反力, 由对称性知: FHA
F
F
F
Ⅰ
1
C
2
A
3
Ⅰ
B
F FHB
4×2=8m
FVA=FVB=2.5F
FVA 4×8=32m FVB
FHA=FHB=-0.5F 2.判别结构中的零杆
ΣУ=0
FRA
FRA-3F- FN3sinα+FN2sinα=0
FN2 = -0.354F= -3.54KN
FN3= 0.354F=3.54KN
F
FN1 FN2 FN3 FN4
例5:己知F=30KN,判别结构中的零杆,
求1.2.3杆内力?
解: 1.用Ⅰ-Ⅰ截面 求1.2.3杆的内力
Ⅰ
1
2F
3
1.5a 1.5a
2.求1.2.3杆的内力
F
F
Σ MD=0
E
C
FN1
-FN1×4- (FVA-F)×4 +F×12-FHA×4= 0
结构力学 静定结构的受力分析
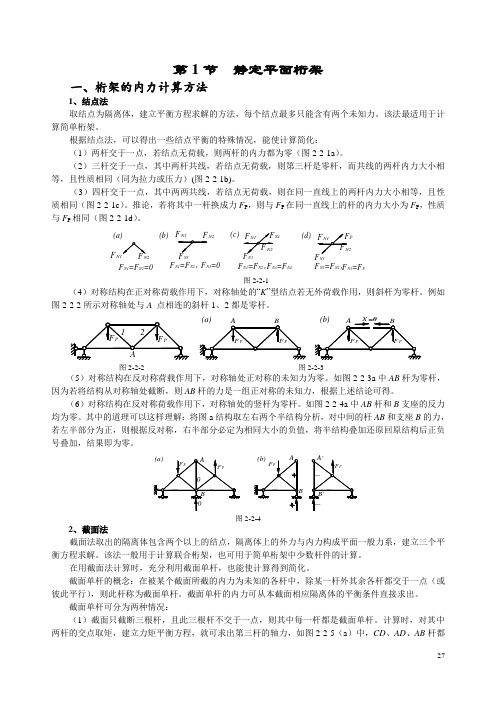
第1节 静定平面桁架一、桁架的内力计算方法1、结点法取结点为隔离体,建立平衡方程求解的方法,每个结点最多只能含有两个未知力。
该法最适用于计算简单桁架。
根据结点法,可以得出一些结点平衡的特殊情况,能使计算简化:(1)两杆交于一点,若结点无荷载,则两杆的内力都为零(图2-2-1a )。
(2)三杆交于一点,其中两杆共线,若结点无荷载,则第三杆是零杆,而共线的两杆内力大小相等,且性质相同(同为拉力或压力)(图2-2-1b)。
(3)四杆交于一点,其中两两共线,若结点无荷载,则在同一直线上的两杆内力大小相等,且性质相同(图2-2-1c )。
推论,若将其中一杆换成力F P ,则与F P 在同一直线上的杆的内力大小为F P ,性质与F P 相同(图2-2-1d )。
F N3F N3=0F N1=F N2=0F N3=F N4(a)(b)(c)F N4(d)F N3=F PF PN1F F N2F N1F N2F N1F N2F N1F N2F N3F N3F N1=F N2,F N1=F N2,F N1=F N2,图2-2-1(4)对称结构在正对称荷载作用下,对称轴处的“K ”型结点若无外荷载作用,则斜杆为零杆。
例如图2-2-2所示对称轴处与A 点相连的斜杆1、2都是零杆。
1A2F PF PAF PF PBF PF PBA(b)(a)X =0图2-2-2 图2-2-3(5)对称结构在反对称荷载作用下,对称轴处正对称的未知力为零。
如图2-2-3a 中AB 杆为零杆,因为若将结构从对称轴处截断,则AB 杆的力是一组正对称的未知力,根据上述结论可得。
(6)对称结构在反对称荷载作用下,对称轴处的竖杆为零杆。
如图2-2-4a 中AB 杆和B 支座的反力均为零。
其中的道理可以这样理解:将图a 结构取左右两个半结构分析,对中间的杆AB 和支座B 的力,若左半部分为正,则根据反对称,右半部分必定为相同大小的负值,将半结构叠加还原回原结构后正负号叠加,结果即为零。
桁架内力计算

21
一、节点法 (1)一般先研究整体,求支座约束力; (2)逐个取各节点为研究对象; (3)求杆件内力; (4)所选节点的未知力数目不大于2,由此 开始计算。
练习1
判断结构中的零杆
F F
F
FP
2015-3-5
15
结点法
基本概念 结点法 截面法 联合法 小结
۞
练习2
计算桁架各杆件内力
2F a
4×a
第一步:求支座反力 第二步:判断零杆和单杆,简化问题 第三步:逐次去结点,列平衡方程 第四步:自我检查
16
2015-3-5
结点法
基本概念 结点法 截面法 联合法 小结
目 ≤ 独立方程数(即2个);
小结
基本思路:尽可能简化问题,一般先求支座反力,
然后逐次列结点平衡方程。
2015-3-5 10
结点法
۞
例题1
如图所示为一施工托架计算简图,求图示 荷载作用下各杆轴力(单位:kN)。
基本概念 结点法 截面法 联合法 小结
8 A
1.5m
8
C 6 E8 G F
8
B
截面法
基本概念
۞ 例题2
求图示桁架25、34、35三杆内力(单位:kN)。 10 20
I 4
7 2m 8
结点法
10
3
a
截面法 联合法 小结
1
2
5 I8 m
6
解: 1)求支座反力。2)截面法,取分离体受力 分析,求内力。
截面法求桁架杆件内力

截面法1截面法可以快速求出某一内力,通常取结构 的一部分为隔离体,其上力系为平面一般力系。
每个隔离体上有3个独立平衡方程。
一般表示 为: ∑ FX = 0 投影法 ∑ FY = 0 力矩法 ∑M = 0 计算要点: 尽量使一个方程解一个未知数,避免求解 联立方程。
一. 力矩法例:求图示桁架1、2、3杆的轴力。
2VAVB解:由整体平衡条件求得支座反力 VA=VB HA=0作Ⅰ--Ⅰ截面,截开1、2、3杆的轴力 取截面以左为隔离体。
Ⅰ3Ⅰ(1)求1杆轴力N1K14选取未知力N2和N3 延长线的交点K1作 为取矩点。
N1 对K1点取矩,由 ∑MK1 = 0 从而求出所求未知 力N1。
VA(2)求2杆轴力N2N2 K2 VAY252X2由∑MK2 = 0 ,比例关系从而求出所求未知力Y2。
2杆轴力N2(3)求3杆轴力N3Y3 N3 X3K3 VA6由 ∑MK3 = 0比例关系从而求出所求未知力X3。
3杆轴力N3力矩法要点:7欲求某指定杆内力,则作一截面,截开待求 杆; 隔离体上除所求未知力外,其余未知力的延 长线均交于某一点K。
对K点取矩,从而求出所求未知力 。
(1)选择其余未知力延长线的交点K作为取矩 点,从而用∑MK=0,求出指定杆内力。
(2)将斜杆的内力放在某一个合适的点上分 解,使其一个分力通过取矩点K。
例1. 求图示桁架杆件a、b、c的轴力890kN30kN作Ⅰ—Ⅰ截面Ⅰ9Ⅰ求NaNa 求Na时,对另 外两个未知力的 交点C取矩,10C由 ΣMc=0,得 Na×4+30×8=030kN解得: Na =- 60kN求NbD Xb E Yb Nb30kN11求Nb时,对点D取矩。
将Nb 其在E点处分解 为水平和竖向分量。
由ΣMD=0,得 Yb×12+40×4 - 30×12=0 解得 Yb=16.67 kN由比例关系得到:N b = 2Yb = 2 × 16.67 = 23.57kN求NcYc XcD Nc12求Nc时,对点E取矩。
内力分析的基本方法-截面法

8kN 4kN E
4kN D C 4kN
C 4m n 1
A
D 4kN
N4
N1 N2 N3 N4
由结点E可知: N2 = -N3
取m-m截面以上为对象 由∑x= 0 得
解:取n-n截面以上为对象 ∑MD= 0 N1 ×6+8×3+4×4 = 0 得: N1 = -6.67 kN
N2=-6.67 kN
所以:
2、突变:在集中力作用处,剪力图有突变,弯矩图 有一尖角;在集中力偶作用处,弯矩图有突变,剪力 图无变化。 3、端值情况
详见教材p98表3-1
18
规律作图方法:
1、水平线图:段内任取截面求内力(一般取段端截面) 2、斜直线图:段内任取两截面求内力(一般取段两端 截面)
3、抛物线图:段内取两端截面及中间截面求弯矩
RA
RB 1、计算支座反力
得: QD= qL/2 Σmc= 0 MD–RA×L+qL×L/2 = 0 得: MD= qL2 取E--E截面右段为对象
ME
E
解得:RA=3qL/2 (竖直向上) RB=qL/2 (竖直向上)
2、取D--D截面左段为对象, 画出受力图 q D
MD
qL2
QE E
RA
D
ΣΎ= 0 Σmc= 0
2.5
=-2kNm(上拉) 静定平面刚架内力计算
一、刚架定义 刚架是由梁、柱等直杆组成的具有刚结点的结构, 其中全部或部分结点为刚结点。如图所示 D P C PC D
A
二、刚架的特点
B
A
B
1、结构内部空间较大,便于利用。 2、刚架的内力、变形峰值比用铰结点连接时小。
3、刚结点能传递力和力矩;而铰结点则只能传递力。
结构力学 06静定桁架和组合结构--习题.

N
3
3 5
75
50
0
即
N2
N3
125 3
N2 20.8kN(压) N3 20.8kN(拉)
-4 -4 2m -4 -4
结构力学电子教程
6 静定桁架和组合结构
6.4 作图示组合结构的内力图。
(a)
A
q=1kN/m I
F
C
G
I-I截面右部分: q=1kN/m
B
C
B
4kN
G
4kN D +4
2m 2m
解: 反力如图。
E
I
2m
+4 4
4kN
2m
2
2
4k
Q (kN)
4
M (kNm)
+4
N (kN)
结构力学电子教程
6 静定桁架和组合结构
建筑力学(第二版)
张曦 主编
结构力学电子教程
6 静定桁架和组合结构
习题14-10 试用结点法求图示桁架各杆的轴力。
(a)
A
C
60kN
30kN
M C
0:
N1 4 303
0
N1 22.5kN(拉)
M D
0 : N2 4 306 0
N2
45kN(压)
(3)II-II截面右部分
X
3 0 : 22.5 45 N3 5 0
N3
37.5kN(拉)
结构力学电子教程
30 20kN
D
NDC
NDE
30 5kN
静定结构的内力—静定平面桁架(建筑力学)

截断的五根杆件中,除杆ED外,其余 四杆均汇交于结点C,由力矩方程 ΣMC=0即可求得FNED。
静定平面桁架的内力计算
(2)欲求图复杂桁架中杆CB的轴力 可用Ⅰ-Ⅰ截面将桁架截开,在
被截断的四根杆件中,除杆CB外,
其余三杆互相平行,选取y轴与此三
静定平面桁架的工程实例和计算简图
1 静定平面桁架的工程实例
桁架是由直杆组成,全部由铰结点连接而成的结构。
屋架
桥梁
静定平面桁架的工程实例和计算简图
纵梁
横梁 主桁架
工业厂房
静定平面桁架的工程实例和计算简图
2 静定平面桁架的计算简图
(1)桁架各部分名称
斜杆 Diagonal chard
弦杆
上弦杆 Top chard
静定平面桁架的内力计算
MD 0 Fx 0
FNc 4 FAy 3 20 3 0 FNc 52.5kN FNbx FNa FNc 0
FNbx FNa FNc 15kN
由比例关系可得
FNb
lb lbxy
FNbx
3.61m 3m
15kN
18.05kN
静定平面桁架的内力计算
主内力:按理想桁架算出的内力,各杆只有轴力。 次内力:实际桁架与理想桁架之间的差异引起的杆件弯曲,由此引起的内力。
实际桁架不完全符合上述假定, 但次内力的影响是次要的。
静定平面桁架的工程实例和计算简图
3 静定平面桁架的分类
(1)按几何组成规律分类 简单桁架 由基础或一个铰接三角形开始,依
次增加二元体而组成的桁架 联合桁架 由几个简单桁架按照几何不变体系
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
版权所有
5
钟艳玲 张强
1m 1m
例
jm-3
图示桁架,
r F铅直向下,求杆Fra bibliotek1,2,
3
的内力。
解 (1) 取 I-I 截面左半部分
I L H EB
工 程 力 学
r
ME (Fi ) 0
F 6 F1 2 0
K M
rJ F
G 3 D2
F
C I1A
第
130
F1 3F
2m 2m 2m 2m
章
r
动量原理平面力系 的
例 jm-1 图示桁架尺寸为 AB=BC=BD=a;AD DC DE 2a。
集中力 F1 F2 F3 F。试计算 1, 3, 6 杆的内力。 r
工 解 (1) 用截面 I-I 将桁架截开
程 力
(2) 以右半部分为研究对象
学
MD (Fi ) 0
A 1 I F1 2
3
B
4 5
C r F2
L
K M
rJ
H FHE E
rr
G
F FGE 2
r
F
C
F1
平
F
衡
版权所有
6
钟艳玲 张强
1m 1m
例
jm-3
图示桁架,
r F
铅直向下,求杆
1,
2,
3
的内力。
解 (2) 取 II-II 截面左半部分
II LH
EB
工 程 力 学
r
MH (Fi ) 0
K M
F 4 FFC 2 0
rJ F
G 3 D2 F II C 1 A
r
的 平
MB (Fi ) 0
衡
FN2 a sin 30 F2 a cos30
r FH
FN2
3 2
3F
F3 2a cos30 FH 3a cos30 0
版权所有
4
钟艳玲 张强
例 jm-2 图示桁架受三铅垂力作用,且 F1 F2 F3 F , 杆长 AB=BD=DE=EH=a,求 2r, 3, 4 杆的内力。
章
动量原理平面力系 的
F3
5F 2
1.12F
Fiy 0
平
衡
F2 F3 sin 0
版权所有 钟艳玲 张强
F2 0.5F
L H EB
1m 1m
K M
G 3 D2
rJ
F
C 1A
F
2m 2m 2m 2m
F1 3F FFC 2F
y
r
r F3
F2
r FFC
C
r F1 x
cos 2 2
第 130
FN1 a F2 a 0 FN1 F
章
MC (Fi ) 0
D
r
6
F3
动量原理平面力系 的
F1 a F3 a FN3 2a 0 FN3 2F
EI
r
A
FN1
r F1
B
C r
平 衡
MA(Fi ) 0
r
F1 a F3 a F2 2a FN6 2a 0 rFN3
第
130
FFC 2F
2m 2m 2m 2m
章
r
动量原理平面力系 的 平
L FLH H
K
r FKH
r FFG
rJ F
F
r FFC
衡
版权所有
7
钟艳玲 张强
例
jm-3
图示桁架,
r F
铅直向下,求杆
1,
2,
3
的内力。
解 (3) 取节点 C
工
程 力
Fix 0
学
F1 FFC
第 130
F3 cos 0
版权所有 钟艳玲 张强
FN4 F
3
例 jm-2 图示桁架受三铅垂力作用,且 F1 F2 F3 F ,
杆长 AB=BD=DE=EH=a,求 2r, 3, 4 杆的内力。
F2
工
r
程 力
D
F3
3r
6
学
第 130 章
1
B r
FN3
4
5
7
E
9
A
FN4
2
r FN2
C
30o
8
30o
H
动量原理平面力系
(2) 取 I-I 截面右半部分
F2
工
r
程 力
D
F3
3r
6
学
第 130 章
1
B r
FN3
4
5
7
E
9
A
FN4
2
r FN2
C
30o
8
30o
H
动量原理平面力系
(2) 取 I-I 截面右半部分
r
r FH
的 平
MC (Fi ) 0
衡
FN3 2a sin 30cos30
FN3 2F
F3 a cos30 FH 2a cos30 0
D
F2
版权所有 钟艳玲 张强
FN6 2 2F
FN6
r
F3
1
例 jm-2 图示桁架受三铅垂力作用,且 F1 F2 F3 F ,
杆长 AB=BD=DE=EH=a,求 2r, 3, 4 杆的内力。
工 程 力
r F1
I
3
F2
r
D
F3
6
学
第 130 章
B
1
4 57
E
9
r FAx
A
30o
2
30o
30o
30o
C
8
H
动量原理平面力系
r
I
FAy
解 (1) 以整体为研究对象
r
r FH
的 平
MA(Fi ) 0
衡
F1 a cos30 F2 2a cos30
版权所有 钟艳玲 张强
FH
3F 2
F3 3a cos30 FH 4a cos30 0
2
例 jm-2 图示桁架受三铅垂力作用,且 F1 F2 F3 F , 杆长 AB=BD=DE=EH=a,求 2r, 3, 4 杆的内力。
F2
工
r
程 力
D
F3
3r
6
学
第 130 章
1
B r
FN3
4
5
7
E
9
A
FN4
2
r FN2
C
30o
8
30o
H
动量原理平面力系
(2) 取 I-I 截面右半部分
r
r FH
的 平
MA(Fi ) 0
衡
FN4 2a sin 30cos30 F2 2a cos30
F3 3a cos30 FH 4a cos30 0
12 22 5
sin 1 1
12 22 5
8
