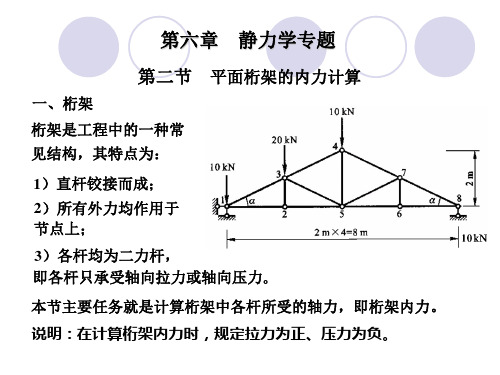
平面桁架的内力计算

【解】取桁架整体为研究对象。根据结构及载荷的对称性
理论力学
例题1
第 三 章
平面任意力系
C
6
D
8
F
F=20kN 1
A
3
2
B
5
4
7
E
9
10
11 12
G H
13
理论力学
例题1
第 三 章
平面任意力系
C
6
D
8
F
F=20kN 1
A
3
2
B
5
4
7
E
9
10
11 12
G H
13
理论力学
第 四 节 平 面 简 单 桁 架 的 内 力 计 算
理论力学
第 三 章
平面任意力系
1、平面桁架
节点数 （汇交力系）
3 4
5 7
6
7
……
3＋n 3+2n
杆件 3 5 （内力未知数）
9 11 ……
3＋2n+3=6+2n 未知数：
(3＋n)×2＝6＋2n 方程数：
理论力学
第 三 章
平面任意力系
2、节点法
每个节点都受到一个平面汇交力系的作用， 所以每个节点可以列两个方程，所以共有 2n+6个方程，每个杆件有一个内力为未知 数，另外外界会有三个位置数，所以有 2n+6个未知数。
理论力学
0 FR
第 三 章
平面任意力系
平衡条件和平衡方程
MO 0
与简化中心的位置无关
复 习
F
x
0
F
0
y
0
M F 0
o
平衡方程的一矩式
二矩式
F
x
M F 0 M F 0
A
B
B C
其中A、B两点连线不能垂直X坐标轴 三矩式
M F 0 M F 0 M F 0
5
F7 5
E
11 12
G H
A
FAy
4 m’F4F
10
F
13
FH
理论力学
例题2
第 三 章
平面任意力系
C
F6
3 5
B
6
D
8 9
F
1
FAx
F7 5
11 12
G H
A
2
F
4
FAy
F4
E
10
13
理论力学 内力S1。
a /2
第 三 章
平面任意力系
图示为一平面组合桁架.已知力P,求AB杆的
E F
P
C
D
a /2 B a/3 a/3 a/3
13
3m
3m
3m
求解：4、5、6杆的内力
理论力学
例题2
第 三 章
平面任意力系
C
m 6
D
8 9
F
1
FAx
3
2
F B
5
4 m’ F
7
E
11 12
G H
A
FAy
10
F
13
FH
【解】取桁架整体为研究对象。根据结构及载荷的对称性
理论力学
例题2
第 三 章
平面任意力系
C
F m 6
6
D
8 9
F
1
FAx
3
2
F B
A
其中A、B、C三点不能共线
理论力学
我们学过：
第 三 章
平面任意力系
一、静定与静不定问题的概念 平面汇交力系 X 0 两个独立方程，只能求两个 Y 0 独立未知数。
平面力偶系mi 0 一个独立方程，只能求一个独立未知数。
X 0 三个独立方程，只能求三个独立未知数。 平面 Y 0 任意力系
SAE C O SCD SBF
截开连接杆AE,CD 和BF并取下半个桁 架为研究对象画受 力图.
mO(Fi) = 0
节点法：取节点为研究对象，考虑其平衡， 以求解杆内力的方法
理论力学
例题1
平 面 简 单 桁 架 的 内 力 计 算
第 三 章
平面任意力系
C D A F
3m
F
4m
F=20kN
B F G
H
E
F
3m
3m
3m
理论力学
例题1
第 三 章
平面任意力系
C D A B F F
F
F=20kN
FAx
G
H
FAy
E
F
FH
F=20kN 1
A
3
2
B
5
4
7
E
9
10
11 12
G H
13
求出左半部分各杆件的内力后，可根据对称性得到右半 部分各杆件的内力，即
F8=F6=-30kN F9=F5=12.5kN F10=F4=22.5kN F11=F3=20kN F12=F1=22.5kN F13=F2=-37.5kN F7=0kN
第 三 章
平面任意力系
一、平面桁架
理论力学
第 三 章
平面任意力系
二、平面桁架
桁架是一种由杆件彼此在两端用铰链连接而成的结构，它 受力后几何形状不变。 桁架中杆件的铰链接头称为节点。
平面简单桁架采用以下几种假设
1．桁架的杆件都是直的，并且都在同一平面内。
2．杆件用光滑的铰链连接。
3．桁架所受的力都是作用在节点上，而且在桁架的平面内。 4．桁架杆件的重量略去不计，或平均分配在杆件两端的节点 上。
A
理论力学
第 三 章
E
平面任意力系
F
解：取整体为研
P
究对象画受力图. a /2 Xi = 0
XA + P = 0
C
D
XA = - P
mA(Fi) = 0
a /2 B a/3 a/3 a/3
aRB - aP = 0
RB = P Yi = 0 YA + P = 0
XA A YA
RB
YA = - P
理论力学
第 三 章
平面任意力系
4、截面法
C
6
3 5
B
D
8
9
F
1
A
7
E
11 12
G
H
2
4
10
13
用适当截面切取桁架的一部分作为考查对象，考 虑其平衡，求得割断杆件内力的一种方法。
理论力学
第 三 章
平面任意力系
例题十三 C
6
D
8 9
F
F=20kN 1
A
3
2
F B
5
4
F
7
E
11 12
G
4m
H
10
F
3m
mO ( Fi ) 0
独立方程数目≥未知数数目时，是静定问题（可求解）
独立方程数目<未知数数目时，是静不定问题（超静定问题）
理论力学
[ 例]
第 三 章
平面任意力系
静定（未知数三个）
静不定（未知数四个）
静不定问题在强度力学（材力,结Hale Waihona Puke Baidu,弹力）中用位 移协调条件来求解。
理论力学 平 面 简 单 桁 架 的 内 力 计 算
理论力学
第 三 章
平面任意力系
3、零力杆
零力杆: 在一定荷载作用下,桁架中内力为零的杆件。
S1= 0
1 1 2
S1= 0
P S2
2
S2= 0
S1= 0
S3
1 3 2
S2
理论力学
第 三 章
平面任意力系
三、零力杆
A
判定图示桁架中的零杆.
I H G F
E
B
C
D
P
P
解:AB和BC是零杆. CI是零杆. EG是零杆. EH是零杆.
第 三 章
平面任意力系
例题1
C
6
D
8
F
F=20kN 1
A
3
2
B
5
4
7
E
9
10
11 12
G H
13
列出节点C的平衡方程， 解得F5=12.5kN，F6=30kN 列出节点D的平衡方 程，解得 F7=0
理论力学
第 四 节 平 面 简 单 桁 架 的 内 力 计 算
第 三 章
平面任意力系
例题1
C
6
D
8
F
理论力学
第 三 章
平面任意力系
平 面 简 单 桁 架 的 内 力 计 算
对整体进行构 成分析 桁架由两个简
E
F
P
单桁架 ABC 和
DEF用AE,CD,BF 三根杆连接而成. 这类问题应先
a /2 C D
a /2 A
截断连接杆,求出
其内力.
P
a/3 P a/3 a/3
B
P
理论力学
第 三 章
平面任意力系