离散数学及其应用(徐凤生版)数学习题答案
离散数学及其应用集合论部分课后习题答案
作业答案：集合论部分P90:习题六5、确定下列命题是否为真。
（2）ÆÎÆ（4）{}ÆÎÆ（6）{,}{,,,{,}}a b a b c a b Î解答：（2）假（4）真（6）真8、求下列集合的幂集。
（5）{{1,2},{2,1,1},{2,1,1,2}}（6）{{,2},{2}}Æ解答：（5）集合的元素彼此互不相同，所以{2,1,1,2}{1,2}=，所以该题的结论应该为{,{{1,2}},{{2,1,2}},{{2,1,1,1}},{{1,2},{2,1,2},{2,1,1,1}}}Æ（6）{,{{,2}},2,{{,2},{2}}}ÆÆÆ9、设{1,2,3,4,5,6}E =，{1,4}A =，{1,2,5}B =,{2,4}C =,求下列集合。
（1）A B（2）()A B 解答：（1）{1,4}{3,4,6}{4}A B ==（2）(){1}{2,3,4,5,6}A B ==31、设A,B,C 为任意集合，证明()()()()A B B A A B A B --=-证明：()(){|}{|()()}{|()()()()}{|()()}{|()()}{|()()}{|()()}{|()(A B B A x x A B x B A x x A x B x B x A x x A x B x B x B x A x A x B x A x x A x B x B x A x x A B x A x B x x A B x A x B x x A B x A B x x AB x A--=Î-ÚÎ-=ÎÙÏÚÎÙÏ=ÎÚÎÙÏÚÎÙÎÚÏÙÏÚÏ=ÎÚÎÙÏÚÏ=ÎÙÏÚÏ=ÎÙÎÚÎ=ÎÙÎ=ÎÙÎ)}B A B AB=-34、设A,B 为集合，证明：如果()()A B B A AB --=，则AB =Æ。
离散数学及应用课后习题答案
离散数学及应用课后习题答案【篇一：离散数学及其应用图论部分课后习题答案】p165:习题九1、给定下面4个图（前两个为无向图，后两个为有向图）的集合表示，画出它们的图形表示。
（1）g1??v1,e1?，v1?{v1,v2,v3,v4,v5}，e1?{(v1,v2),(v2,v3),(v3,v4),(v3,v3),(v4,v5)} （2）g2??v2,e2?，v2?v1，e1?{(v1,v2),(v2,v3),(v3,v4),(v4,v5),(v5,v1)} （3）d1??v3,e3?,v3?v1,e3?{?v1,v2?,?v2,v3?,?v3,v2?,?v4,v5?,?v5,v 1?} （4）d2??v4,e4?,v4?v1,e3?{?v1,v2?,?v2,v5?,?v5,v2?,?v3,v4?,?v4,v 3?} 解答：（1）（2）10、是否存在具有下列顶点度数的5阶图？若有，则画出一个这样的图。
（1）5，5，3，2，2；（2）3，3，3，3，2；（3）1，2，3，4，5；（4）4，4，4，4，4 解答：（1）（3）不存在，因为有奇数个奇度顶点。
14、设g是n(n?2)阶无向简单图，g是它的补图，已知?(g)?k1,?(g)?k2，求?(g)，(g)。
解答：?(g)?n?1?k2；?(g)?n?1?k1。
15、图9.19中各对图是否同构？若同构，则给出它们顶点之间的双射函数。
解答：（c）不是同构，从点度既可以看出，一个点度序列为4，3，3，3，3而另外一个为4，4，3，3，1（d）同构，同构函数为12f(x)345解答：（1）三条边一共提供6度；所以点度序列可能是x?ax?bx?c x?dx?e16、画出所有3条边的5阶简单无向图和3条边的3阶简单无向图。
①3，3，0，0，0，0；②3，2，1，0，0，0；③3，1，1，1，0，0；④2，2，2，0，0，0；⑤2，2，1，1，0，0；⑥2，1，1，1，1，0；⑦1，1，1，1，1，1；由于是简单图，①②两种情形不可能图形如下：（2）三条边一共提供6度，所以点度序列可能为①3，3，0；②3，2，1；③2，2，2 由于是简单图，①②两种情形不可能21、在图9.20中，下述顶点序列是否构成通路？哪些是简单通路？哪些是初级通路？哪些是回路？哪些是简单回路？哪些是初级回路？（1）a,b,c,d,b,e；（2）a,b,e,d,b,a；（3）a,d,c,e,b；（4）d,b,a,c,e;（5）a,b,c,d,e,b,d,c；（6）a,d,b,e,c,b,d；（7）c,d,a,b,c；（8）a,b,c,e,b 解答：（1）构成通路，且为初级通路，因为点不重复（2）构成了回路，但是不为简单回路和初级回路，因为有重复的边(a,b) （3）构成了初级通路，因为点不重复；（4）不构成通路，因为边(a,c)不存在；（5）构成通路，但是不为简单通路和初级通路，因为有重复的边(d,c) （6）构成了回路，但是不为简单回路和初级回路，因为有重复的边(d,b) （7）构成了初级通路；（8）简单通路，但是不为初级通路，有重复边。
离散数学习题答案解析
离散数学习题答案解析(总16页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--离散数学习题答案习题一及答案：（P14-15）14、将下列命题符号化：（5）李辛与李末是兄弟解：设p：李辛与李末是兄弟，则命题符号化的结果是p（6）王强与刘威都学过法语∧解：设p：王强学过法语；q：刘威学过法语；则命题符号化的结果是p q（9）只有天下大雨，他才乘班车上班→解：设p：天下大雨；q：他乘班车上班；则命题符号化的结果是q p （11）下雪路滑，他迟到了解：设p：下雪；q：路滑；r：他迟到了；则命题符号化的结果是()∧→p q r 15、设p：2+3=5.q：大熊猫产在中国.r：太阳从西方升起.求下列复合命题的真值：（4）()(())∧∧⌝↔⌝∨⌝→p q r p q r解：p=1，q=1，r=0，∧∧⌝⇔∧∧⌝⇔，p q r()(110)1p q r⌝∨⌝→⇔⌝∨⌝→⇔→⇔(())((11)0)(00)1∴∧∧⌝↔⌝∨⌝→⇔↔⇔()(())111p q r p q r19、用真值表判断下列公式的类型：（2）()→⌝→⌝p p q解：列出公式的真值表，如下所示：由真值表可以看出公式有3个成真赋值，故公式是非重言式的可满足式。
20、求下列公式的成真赋值： （4）()p q q ⌝∨→解：因为该公式是一个蕴含式，所以首先分析它的成假赋值，成假赋值的条件是：()10p q q ⌝∨⇔⎧⎨⇔⎩⇒0p q ⇔⎧⎨⇔⎩ 所以公式的成真赋值有：01，10，11。
习题二及答案：（P38）5、求下列公式的主析取范式，并求成真赋值： （2）()()p q q r ⌝→∧∧解：原式()p q q r ⇔∨∧∧q r ⇔∧()p p q r ⇔⌝∨∧∧()()p q r p q r ⇔⌝∧∧∨∧∧37m m ⇔∨，此即公式的主析取范式， 所以成真赋值为011，111。
*6、求下列公式的主合取范式，并求成假赋值： （2）()()p q p r ∧∨⌝∨解：原式()()p p r p q r ⇔∨⌝∨∧⌝∨∨()p q r ⇔⌝∨∨4M ⇔，此即公式的主合取范式， 所以成假赋值为100。
离散数学及其应用图论部分课后习题答案
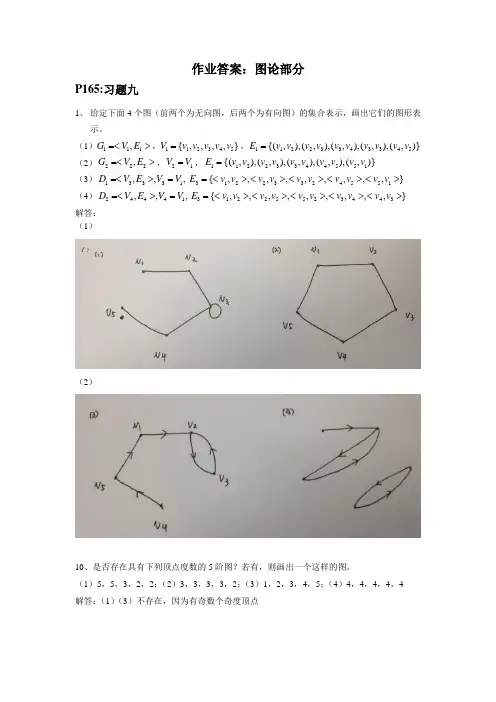
作业答案：图论部分P165:习题九1、 给定下面4个图（前两个为无向图，后两个为有向图）的集合表示，画出它们的图形表示。
（1）111,G V E =<>，112345{,,,,}V v v v v v =，11223343345{(,),(,),(,),(,),(,)}E v v v v v v v v v v = （2）222,G V E =<>，21V V =，11223344551{(,),(,),(,),(,),(,)}E v v v v v v v v v v = （3）13331,,,D V E V V =<>=31223324551{,,,,,,,,,}E v v v v v v v v v v =<><><><><> （4）24441,,,D V E V V =<>=31225523443{,,,,,,,,,}E v v v v v v v v v v =<><><><><> 解答： （1）（2）10、是否存在具有下列顶点度数的5阶图？若有，则画出一个这样的图。
（1）5，5，3，2，2；（2）3，3，3，3，2；（3）1，2，3，4，5；（4）4，4，4，4，4 解答：（1）（3）不存在，因为有奇数个奇度顶点。
14、设G 是(2)n n ≥阶无向简单图，G 是它的补图，已知12(),()G k G k δ∆==，求()G ∆，()G δ。
解答：2()1G n k ∆=--；1()1G n k δ=--。
15、图9.19中各对图是否同构？若同构，则给出它们顶点之间的双射函数。
解答：（c ）不是同构，从点度既可以看出，一个点度序列为4，3，3，3，3而另外一个为4，4，3，3，1（d ）同构，同构函数为12()345x a x bf x x c x d x e=⎧⎪=⎪⎪==⎨⎪=⎪=⎪⎩ 16、画出所有3条边的5阶简单无向图和3条边的3阶简单无向图。
第1章 离散数学习题解答
1. 下列句子中，哪些是命题？哪些不是命题？如果是命题，指出它的真值。
⑴中国有四大发明。
⑵计算机有空吗?⑶不存在最大素数。
⑷ 21+3＜5。
⑸老王是山东人或河北人。
⑹ 2与3都是偶数。
⑺小李在宿舍里。
⑻这朵玫瑰花多美丽呀!⑼请勿随地吐痰!⑽圆的面积等于半径的平方乘以p。
⑾只有6是偶数，3才干是2的倍数。
⑿雪是黑色的当且仅当太阳从东方升起。
⒀如果天下大雨，他就乘班车上班。
解：⑴⑶⑷⑸⑹⑺⑽⑾⑿⒀是命题，其中⑴⑶⑽⑾是真命题，⑷⑹⑿是假命题，⑸⑺⒀的真值目前无法确定；⑵⑻⑼不是命题。
2. 将下列复合命题分成若干原子命题。
⑴李辛与李末是兄弟。
⑵因为天气冷，所以我穿了羽绒服。
⑶天正在下雨或湿度很高。
⑷刘英与李进上山。
⑸王强与刘威都学过法语。
⑹如果你不看电影，那么我也不看电影。
⑺我既不看电视也不过出，我在睡觉。
⑻除非天下大雨，否则他不乘班车上班。
解：⑴本命题为原子命题；⑵p：天气冷；q：我穿羽绒服；⑶p：天在下雨；q：湿度很高；⑷p：刘英上山；q：李进上山；⑸p：王强学过法语；q：刘威学过法语；⑹p：你看电影；q：我看电影；⑺p：我看电视；q：我外出；r：我睡觉；⑻p：天下大雨；q：他乘班车上班。
3. 将下列命题符号化。
⑴他一面吃饭，一面听音乐。
⑵ 3是素数或2是素数。
⑶若地球上没有树木，则人类不克不及生存。
⑷ 8是偶数的充分需要条件是8能被3整除。
⑸停机的原因在于语法错误或程序错误。
⑹四边形ABCD是平行四边形当且仅当它的对边平行。
⑺如果a和b是偶数，则a+b是偶数。
解：⑴p：他吃饭；q：他听音乐；原命题符号化为：p∧q⑵p：3是素数；q：2是素数；原命题符号化为：p∨q⑶p：地球上有树木；q：人类能生存；原命题符号化为：p→q⑷p：8是偶数；q：8能被3整除；原命题符号化为：p↔q⑸p：停机；q：语法错误；r：程序错误；原命题符号化为：q∨r→p⑹p：四边形ABCD是平行四边形；q：四边形ABCD的对边平行；原命题符号化为：p↔q。
离散数学及其应用第2版课后练习题含答案
离散数学及其应用第2版课后练习题含答案1. 引言《离散数学及其应用》是一本经典的离散数学教材，是计算机科学和数学专业的必修课程。
本文将为读者提供《离散数学及其应用》第2版课后练习题的答案，并希望能够帮助读者加深对离散数学的理解。
2. 答案解析第一章习题 1.11.给定一组七个数字 {1, 3, 3, 4, 6, 9, 12}，请给出这组数字的中位数。
答案：中位数为 4。
2.给出两个整数 a 和 b 的三进制表示： a = 111011，b = 101101。
求 a + b。
答案：a + b = 1011000。
3.证明奇奇数的积为奇数。
答案：令两个奇数分别为 2n + 1 和 2m +1，则有：(2n + 1) × (2m + 1) = 4nm + 2n + 2m + 1 = 2(2nm + n + m) + 1，即奇奇数的积还是一个奇数。
习题 1.21.证明：如果一个整数 n 能同时被 2 和 3 整除，则它也能被 6 整除。
答案：首先，n 能同时被 2 和 3 整除，则分别有 n = 2k 和 n = 3m。
联立方程组 2k = 3m，得 k = (3/2)m。
因此，n = 2k = (3m/2) × 2 = 3m× (2/2) = 6m，可以被 6 整除。
2.求 10010 的八进制表示。
答案：将 10010 转换为四位一组的二进制数，得 0010 0100。
将 0010 和 0100 分别转换为八进制数，得 2 和 4。
因此，10010 的八进制表示为 24。
3.已知 547a5 是 11 的倍数，求 a 的值。
答案：根据 11 的倍数的规律，将 547a5 中的奇数位数字相加，再将偶数位数字相加，然后将两个和的差求出来： (5 + 7 + a) - (4 + 5) = 13 + a - 9 = a + 4。
因为547a5 是 11 的倍数，所以 a + 4 也必须是 11 的倍数。
离散数学及其应用(课后习题)
离散数学及其应用（课后习题）习题1.12. 指出下列命题是原子命题还是复合命题。
（3）大雁北回，春天来了。
（4）不是东风压倒西风，就是西风压倒东风。
（5）张三和李四在吵架。
解：（3）和（4）是复合命题，（5）是原子命题。
习题1.21. 指出下列命题的真值：（1）若224+>，则太阳从西方升起。
解：该命题真值为T （因为命题的前件为假）。
（3）胎生动物当且仅当是哺乳动物。
解：该命题真值为F （如鸭嘴兽虽是哺乳动物，但不是胎生动物）。
2. 令P ：天气好。
Q ：我去公园。
请将下列命题符号化。
（2）只要天气好，我就去公园。
（3）只有天气好，我才去公园。
（6）天气好，我去公园。
解：（2）P Q →。
（3）Q P →。
（6）P Q ↔。
习题1.32. 将下列命题符号化（句中括号内提示的是相应的原子命题的符号表示）： （1）我去新华书店（P ），仅当我有时间（Q ）。
（3）只要努力学习（P ），成绩就会好的（Q ）。
（6）我今天进城（P ），除非下雨（Q ）。
（10）人不犯我（P ），我不犯人（Q ）；人若犯我，我必犯人。
解：（1）P Q →。
（3）P Q →。
（6）Q P ⌝→。
（10）()()P Q P Q ⌝→⌝∧→。
习题1.41. 写出下列公式的真值表： （2）()P Q R ∨→。
解：该公式的真值表如下表：2. 证明下列等价公式：（2）()()()P Q P Q P Q ∨∧⌝∧⇔⌝↔。
证明：()(()()) ()()) ()() ()()P Q P Q P Q P Q P Q P Q P Q P Q P Q ⌝↔⇔⌝∧∨⌝∧⌝⇔⌝∧∧⌝⌝∧⌝⇔⌝∧∧∨⇔∨∧⌝∧（4）()()()P Q P R P Q R →∧→⇔→∧。
证明：()()()() () ()P Q P R P Q P R P Q R P Q R →∧→⇔⌝∨∧⌝∨⇔⌝∨∧⇔→∧3. 甲、乙、丙、丁4人参加考试后，有人问他们谁的成绩最好，甲说，不是我。
离散数学课后习题答案 (2)
离散数学课后习题答案1. 第一章习题答案1.1 习题一答案1.1.1 习题一.1 答案根据题意，设集合A和B如下：Set A and BSet A and B在此情况下，我们可以得出以下结论：•A的幂集为{ {}, {a}, {b}, {a, b} }；•B的幂集为{ {}, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3} }；•A和B的笛卡尔积为{ (a, 1), (a, 2), (a, 3), (b, 1), (b, 2), (b, 3) }。
因此，习题一.1的答案为：•A的幂集为{ {}, {a}, {b}, {a, b} }；•B的幂集为{ {}, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3} }；•A和B的笛卡尔积为{ (a, 1), (a, 2), (a, 3), (b, 1), (b,2), (b, 3) }。
1.1.2 习题一.2 答案根据题意，集合A和B如下所示：Set A and BSet A and B根据集合的定义，习题一.2要求我们判断以下命题的真假性：a)$A \\cap B = \\{ 2, 3 \\}$b)$\\emptyset \\in B$c)$A \\times B = \\{ (a, 2), (b, 1), (b, 3) \\}$d)$B \\subseteq A$接下来，我们来逐个判断这些命题的真假性。
a)首先计算集合A和B的交集：$A \\cap B = \\{ x\\,|\\, x \\in A \\, \\text{且} \\, x \\in B \\} = \\{ 2, 3 \\}$。
因此，命题a)为真。
b)大家都知道，空集合是任意集合的子集，因此空集合一定属于任意集合的幂集。
根据题意，$\\emptyset \\in B$，因此命题b)为真。
c)计算集合A和B的笛卡尔积：$A \\times B = \\{ (x, y) \\,|\\, x \\in A \\, \\text{且} \\, y \\in B \\} = \\{ (a, 1), (a, 2), (a, 3), (b, 1), (b, 2), (b, 3) \\}$。
离散数学课后习题答案
1-1，1-2（1） 解：a) 是命题，真值为T。
b) 不是命题。
c) 是命题，真值要根据具体情况确定。
d) 不是命题。
e) 是命题，真值为T。
f) 是命题，真值为T。
g) 是命题，真值为F。
h) 不是命题。
i) 不是命题。
（2） 解：原子命题：我爱北京天安门。
复合命题：如果不是练健美操，我就出外旅游拉。
（3） 解：a) (┓P ∧R)→Qb) Q→Rc) ┓Pd) P→┓Q（4） 解：a)设Q:我将去参加舞会。
R:我有时间。
P:天下雨。
Q (R∧┓P):我将去参加舞会当且仅当我有时间和天不下雨。
b)设R:我在看电视。
Q:我在吃苹果。
R∧Q:我在看电视边吃苹果。
c) 设Q:一个数是奇数。
R:一个数不能被2除。
（Q→R）∧(R→Q):一个数是奇数，则它不能被2整除并且一个数不能被2整除，则它是奇数。
(5) 解：a) 设P：王强身体很好。
Q：王强成绩很好。
P∧Qb) 设P：小李看书。
Q：小李听音乐。
P∧Qc) 设P：气候很好。
Q：气候很热。
P∨Qd) 设P： a和b是偶数。
Q：a+b是偶数。
P→Qe) 设P：四边形ABCD是平行四边形。
Q ：四边形ABCD的对边平行。
PQf) 设P：语法错误。
Q：程序错误。
R：停机。
（P∨ Q）→ R(6) 解：a) P:天气炎热。
Q:正在下雨。
P∧Qb) P:天气炎热。
R:湿度较低。
P∧Rc) R:天正在下雨。
S:湿度很高。
R∨Sd) A:刘英上山。
B:李进上山。
A∧Be) M:老王是革新者。
N:小李是革新者。
M∨Nf) L:你看电影。
M:我看电影。
┓L→┓Mg) P:我不看电视。
Q:我不外出。
R:我在睡觉。
P∧Q∧Rh) P:控制台打字机作输入设备。
Q:控制台打字机作输出设备。
P∧Q1-3（1）解：a) 不是合式公式，没有规定运算符次序（若规定运算符次序后亦可作为合式公式）b) 是合式公式c) 不是合式公式（括弧不配对）d) 不是合式公式（R和S之间缺少联结词）e) 是合式公式。
离散数学及其应用(徐凤生版)数学习题答案
习题一1.判断下列语句是否是命题，为什么？若是命题，判断是简单命题还是复合命题？(1)离散数学是计算机专业的一门必修课。
(2)李梅能歌善舞。
(3)这朵花真美丽！(4)３＋２＞６。
(5)只要我有时间，我就来看你。
(6)x＝５。
(7)尽管他有病，但他仍坚持工作。
(8)太阳系外有宇宙人。
(9)小王和小张是同桌。
(10)不存在最大的素数。
解在上述10个句子中，(3)是感叹句，因此它不是命题。
(6)虽然是陈述句，但它没有确定的值，因此它也不是命题。
其余语句都是可判断真假的陈述句，所以都是命题。
其中：(1)、(4) 、(8) 、(9) 、是简单命题，、(2) 、(5) 、(7)、(10) 是复合命题。
2.判断下列各式是否是命题公式，为什么？(1)(P→(P∨Q))。
(2)(⌝P→Q)→(Q→P)))。
(3)((⌝P→Q)→(Q→P))。
(4)(Q→R∧S)。
(5)(P∨QR)→S。
(6)((R→(Q→R)→(P→Q))。
解 (1)是命题公式。
(2)不是命题公式，因为括号不配对。
(3)是命题公式。
(4)是命题公式。
(5)不是命题公式，因为QR没有意义。
(6)不是命题公式，因为R→(Q→R)→(P→Q) 没有意义。
3.将下列命题符号化：(1)我们不能既划船又跑步。
(2)我去新华书店，仅当我有时间。
(3)如果天下雨，我就不去新华书店。
(4)除非天不下雨，我将去新华书店。
(5)张明或王平都可以做这件事。
(6)“2或4是素数，这是不对的”是不对的。
(7)只有休息好，才能工作好。
(8)只要努力学习，成绩就会好的。
(9)大雁北回，春天来了。
(10)小张是山东人或河北人。
解 (1)符号化为⌝(P ∧Q )，其中，P ：我们划船，Q ：我们跑步。
(2)符号化为Q →R ，其中，R ：我有时间，Q ：我去新华书店。
(3)符号化为P →⌝Q ，其中，P ：天下雨，Q ：我去新华书店。
(4)符号化为⌝P →Q ，其中，P ：天下雨，Q ：我去新华书店。
离散数学课后习题答案
离散数学课后习题答案离散数学课后习题答案离散数学是计算机科学中的一门重要课程，它涵盖了诸多数学概念与技巧，为计算机科学的理论基础打下了坚实的基础。
在学习离散数学的过程中，课后习题是巩固知识、提高能力的重要途径。
然而，有时候我们会遇到一些难以解答的问题，需要参考一些答案来进行思考与学习。
本文将为大家提供一些离散数学课后习题的答案，希望能对大家的学习有所帮助。
一、集合论1. 设A={1,2,3}，B={2,3,4}，求A∪B和A∩B的结果。
答案：A∪B={1,2,3,4}，A∩B={2,3}。
2. 证明：任意集合A和B，有(A-B)∪(B-A)=(A∪B)-(A∩B)。
答案：首先，对于任意元素x，如果x属于(A-B)∪(B-A)，那么x属于A-B或者x属于B-A。
如果x属于A-B，那么x属于A∪B，但x不属于A∩B；如果x属于B-A，同样有x属于A∪B，但x不属于A∩B。
所以(A-B)∪(B-A)属于(A∪B)-(A∩B)。
另一方面，对于任意元素x，如果x属于(A∪B)-(A∩B)，那么x属于A∪B，但x不属于A∩B。
所以x属于A或者x属于B。
如果x属于A，但x不属于B，那么x属于A-B；如果x属于B，但x不属于A，那么x属于B-A。
所以x属于(A-B)∪(B-A)。
所以(A∪B)-(A∩B)属于(A-B)∪(B-A)。
综上所述，(A-B)∪(B-A)=(A∪B)-(A∩B)。
证毕。
二、逻辑与证明1. 证明：如果p为真命题，那么¬p为假命题。
答案：根据命题的定义，命题要么为真，要么为假，不存在其他情况。
所以如果p为真命题，那么¬p为假命题。
2. 证明：对于任意整数n，如果n^2为偶数，则n为偶数。
答案：假设n为奇数，即n=2k+1（k为整数）。
那么n^2=(2k+1)^2=4k^2+4k+1=2(2k^2+2k)+1。
根据偶数的定义，2(2k^2+2k)为偶数，所以n^2为奇数。
离散数学及其应用数理逻辑部分课后习题答案
作业答案：数理逻辑部分P14：习题一1、下列句子中，哪些是命题？在是命题的句子中，哪些是简单命题？哪些是真命题？哪些命题的真值现在还不知道？（3 答：简单命题，真命题。
（9）吸烟请到吸烟室去！ 答：不是命题。
（12）8是偶数的充分必要条件是8能被3整除。
答：复合命题，假命题。
14、讲下列命题符号化。
（6）王强与刘威都学过法语。
答：:p 王强学过法语；:q 刘威学过法语。
符号化为：p q ∧（10）除非天下大雨，他就乘班车上班。
答：:p 天下大雨；:q 他乘班车上班。
符号化为：p q →（13）“2或4是素数，这是不对的”是不对的。
答：:p 2是素数；:q 4是素数。
符号化为：(())p q ⌝⌝∨15、设:p 2+3=5. :q 大熊猫产在中国。
:r 太阳从西方升起。
求下列复合命题的真值。
（2）(())r p q p →∧↔⌝（4）()(())p q r p q r ∧∧⌝↔⌝∨⌝→ 解答： p 真值为1；q 真值为1；r 真值为0.（2）p q ∧真值为1；()r p q →∧真值为1；p ⌝真值为0；所以(())r p q p →∧↔⌝真值为0.（4）p q r ∧∧⌝真值为1，p q ⌝∨⌝真值为0，()p q r ⌝∨⌝→真值为1；所以()(())p q r p q r ∧∧⌝↔⌝∨⌝→真值为1.19、用真值表判断下列公式的类型。
（4）()()p q q p →→⌝→⌝所以为重言式。
（7）所以为可满足式。
P36:习题二3、用等值演算法判断下列公式的类型，对不是重言式的可满足式，再用真值表法求出其成真赋值。
（1）()p q q ⌝∧→ 解答：()(())(())()10p q q p q q p q q p q q ⌝∧→⇔⌝⌝∧∨⇔⌝⌝∨⌝∨⇔⌝⌝∨⌝∨⇔⌝⇔所以为永假式。
（2）(())()p p q p r →∨∨→ 解答：(())()(())()()()1()1p p q p r p p q p r p p q p r p r →∨∨→⇔⌝∨∨∨⌝∨⇔⌝∨∨∨⌝∨⇔∨⌝∨⇔ 所以因为永真式。
离散数学课后习题答案
第1章习题解答1．1 除（3），（4），（5），（11）外全是命题，其中，（1），（2），（8），（9），（10），（14），（15）是简单命题，（6），（7），（12），（13）是复合命题。
分析首先应注意到，命题是陈述句，因而不是陈述句的句子都不是命题。
本题中，（3）为疑问句，（5）为感叹句，（11）为祈使句，它们都不是陈述句，所以它们都不是命题。
其次，（4）这个句子是陈述句，但它表示的判断结果是不确定。
又因为（1），（2），（8），（9），（10），（14），（15）都是简单的陈述句，因而作为命题，它们都是简单命题。
（6）和（7）各为由联结词“当且仅当”联结起来的复合命题，（12）是由联结词“或”联结的复合命题，而（13）是由联结词“且”联结起来的复合命题。
这里的“且”为“合取”联结词。
在日常生活中，合取联结词有许多表述法，例如，“虽然……，但是… … ”、“不仅……，而且… … ”、“一面……，一面… … ”、“……和… … ”、“……与……”等。
但要注意，有时“和”或“与”联结的是主语，构成简单命题。
例如，（14）、（15）中的“与”与“和”是联结的主语，这两个命题均为简单命题，而不是复合命题，希望读者在遇到“和”或“与”出现的命题时，要根据命题所陈述的含义加以区分。
1．2 （1）p : 2是无理数，p 为真命题。
（2）p : 5能被2 整除，p 为假命题。
（6）p →q 。
其中，p : 2是素数，q：三角形有三条边。
由于p 与q 都是真命题，因而p →q 为假命题。
（7）p →q ，其中，p：雪是黑色的，q：太阳从东方升起。
由于p 为假命题，q 为真命题，因而p →q 为假命题。
（8）p : 2000年10 月1 日天气晴好，今日（1999 年2 月13 日）我们还不知道p 的真假，但p 的真值是确定的（客观存在的），只是现在不知道而已。
（9）p：太阳系外的星球上的生物。
它的真值情况而定，是确定的。
离散数学习题答案解析
离散数学习题答案习题一及答案：（P14-15） 14、将下列命题符号化：（5）李辛与李末是兄弟解：设p ：李辛与李末是兄弟，则命题符号化的结果是p （6）王强与刘威都学过法语解：设p ：王强学过法语；q ：刘威学过法语；则命题符号化的结果是p q ∧（9）只有天下大雨，他才乘班车上班解：设p ：天下大雨；q ：他乘班车上班；则命题符号化的结果是q p → （11）下雪路滑，他迟到了解：设p ：下雪；q ：路滑；r ：他迟到了；则命题符号化的结果是()p q r ∧→15、设p ：2+3=5.q ：大熊猫产在中国. r ：太阳从西方升起. 求下列复合命题的真值：（4）()(())p q r p q r ∧∧⌝↔⌝∨⌝→ 解：p=1，q=1，r=0，()(110)1p q r ∧∧⌝⇔∧∧⌝⇔，(())((11)0)(00)1p q r ⌝∨⌝→⇔⌝∨⌝→⇔→⇔ ()(())111p q r p q r ∴∧∧⌝↔⌝∨⌝→⇔↔⇔19、用真值表判断下列公式的类型： （2）()p p q →⌝→⌝解：列出公式的真值表，如下所示：由真值表可以看出公式有3个成真赋值，故公式是非重言式的可满足式。
20、求下列公式的成真赋值： （4）()p q q ⌝∨→解：因为该公式是一个蕴含式，所以首先分析它的成假赋值，成假赋值的条件是：()10p q q ⌝∨⇔⎧⎨⇔⎩⇒0p q ⇔⎧⎨⇔⎩ 所以公式的成真赋值有：01，10，11。
习题二及答案：（P38）5、求下列公式的主析取范式，并求成真赋值： （2）()()p q q r ⌝→∧∧解：原式()p q q r ⇔∨∧∧q r ⇔∧()p p q r ⇔⌝∨∧∧()()p q r p q r ⇔⌝∧∧∨∧∧37m m ⇔∨，此即公式的主析取范式， 所以成真赋值为011，111。
*6、求下列公式的主合取范式，并求成假赋值： （2）()()p q p r ∧∨⌝∨解：原式()()p p r p q r ⇔∨⌝∨∧⌝∨∨()p q r ⇔⌝∨∨4M ⇔，此即公式的主合取范式，所以成假赋值为100。
离散数学及其应用习题答案
离散数学及其应用习题答案离散数学是一门研究离散结构的数学学科，它在计算机科学、信息科学、电子工程等领域中有着广泛的应用。
通过学习离散数学，我们可以培养出逻辑思维、抽象思维和解决问题的能力。
在学习离散数学的过程中，习题是不可或缺的一部分。
本文将回答一些离散数学中的常见习题，帮助读者更好地理解和应用离散数学的知识。
1. 集合论习题1.1 求解集合的交、并、差运算对于给定的集合A={1,2,3,4}和B={3,4,5,6}，求解A∩B、A∪B和A-B。
解答：A∩B={3,4}，A∪B={1,2,3,4,5,6}，A-B={1,2}。
1.2 判断集合关系对于给定的集合A={1,2,3,4}和B={3,4,5,6}，判断A是否是B的子集。
解答：A不是B的子集，因为A中的元素2不属于B。
2. 图论习题2.1 判断图的连通性给定一个无向图G，其顶点集合为V={1,2,3,4}，边集合为E={(1,2),(2,3),(3,4)}，判断图G是否连通。
解答：图G是连通的，因为任意两个顶点之间都存在一条路径。
2.2 求解最短路径给定一个有向图G，其顶点集合为V={A,B,C,D}，边集合为E={(A,B,2),(A,C,3),(B,D,4),(C,D,1)}，求解从顶点A到顶点D的最短路径。
解答：最短路径为A-C-D，路径长度为4。
3. 命题逻辑习题3.1 判断命题的真假给定命题P: "如果今天下雨，那么我就带伞"，命题Q: "我带了伞"，判断P→Q 的真假。
解答：由于P和Q都是真命题，且"真命题→真命题"为真命题，所以P→Q为真命题。
3.2 求解命题的合取范式给定命题P: "如果今天下雨，那么我就带伞"，命题Q: "我没有带伞"，将P∧Q 转化为合取范式。
解答：P∧Q的合取范式为"(¬P∨¬Q)"。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
习题一1.判断下列语句是否是命题，为什么？若是命题，判断是简单命题还是复合命题？(1)离散数学是计算机专业的一门必修课。
(2)李梅能歌善舞。
(3)这朵花真美丽！(4)３＋２＞６。
(5)只要我有时间，我就来看你。
(6)x＝５。
(7)尽管他有病，但他仍坚持工作。
(8)太阳系外有宇宙人。
(9)小王和小张是同桌。
(10)不存在最大的素数。
解在上述10个句子中，(3)是感叹句，因此它不是命题。
(6)虽然是陈述句，但它没有确定的值，因此它也不是命题。
其余语句都是可判断真假的陈述句，所以都是命题。
其中：(1)、(4) 、(8) 、(9) 、是简单命题，、(2) 、(5) 、(7)、(10) 是复合命题。
2.判断下列各式是否是命题公式，为什么？(1)(P→(P∨Q))。
(2)(⌝P→Q)→(Q→P)))。
(3)((⌝P→Q)→(Q→P))。
(4)(Q→R∧S)。
(5)(P∨QR)→S。
(6)((R→(Q→R)→(P→Q))。
解 (1)是命题公式。
(2)不是命题公式，因为括号不配对。
(3)是命题公式。
(4)是命题公式。
(5)不是命题公式，因为QR没有意义。
(6)不是命题公式，因为R→(Q→R)→(P→Q) 没有意义。
3.将下列命题符号化：(1)我们不能既划船又跑步。
(2)我去新华书店，仅当我有时间。
(3)如果天下雨，我就不去新华书店。
(4)除非天不下雨，我将去新华书店。
(5)张明或王平都可以做这件事。
(6)“2或4是素数，这是不对的”是不对的。
(7)只有休息好，才能工作好。
(8)只要努力学习，成绩就会好的。
(9)大雁北回，春天来了。
(10)小张是山东人或河北人。
解 (1)符号化为⌝(P ∧Q )，其中，P ：我们划船，Q ：我们跑步。
(2)符号化为Q →R ，其中，R ：我有时间，Q ：我去新华书店。
(3)符号化为P →⌝Q ，其中，P ：天下雨，Q ：我去新华书店。
(4)符号化为⌝P →Q ，其中，P ：天下雨，Q ：我去新华书店。
(5)符号化为P ∧Q ，其中，P ：张明可以做这件事，Q ：王平可以做这件事。
(6)符号化为⌝(⌝(P ∨Q ))，“2或4是素数，这是不对的”是不对的，其中，P ：2是素数，Q ：4是素数，。
(7)符号化为Q →P ，其中，P ：休息好，Q ：工作好。
(8)符号化为P →Q ，其中，P ：努力学习，Q ：成绩就会好的。
(9)符号化为P ↔Q ，其中，P ：大雁北回，Q ：春天来了。
(10)符号化为P ⊕Q ，其中，P ：小张是山东人，Q ：小张是河北人。
4.构造下列命题公式的真值表，并据此说明哪些是其成真赋值，哪些是其成假赋值？ (1)⌝(P ∨⌝Q )。
(2)P ∧(Q ∨R )。
(3)⌝(P ∨Q )↔(⌝P ∧⌝Q )。
(4)⌝P →(Q →P )。
解 (1)由真值表可知，公式⌝(P ∨⌝Q )的成真赋值为：01，成假赋值为00、10、11。
(2)由真值表可知，公式P ∧(Q ∨R )的成真赋值为：101、110、111，成假赋值为000、001、010、011、100。
(3)由真值表可知，公式⌝(P ∨Q )↔(⌝P ∧⌝Q )的成真赋值为：00、01、10、11，没有成假赋值。
(4)由真值表可知，公式⌝P →(Q →P )的成真赋值为：00、10、11，成假赋值为：01。
5.分别用真值表法和公式法判断下列命题公式的类型： (1)(P ∨Q )→(P ∧Q )。
(2)(P ∧Q )→(P ∨Q )。
(3)(⌝P ∨Q )∧⌝(Q ∨⌝R )∧⌝(R ∨⌝P ∨⌝Q )。
(4)(P ∧Q →R )→(P ∧⌝R ∧Q )。
(5)(Q →P )∧(⌝P ∧Q )。
(6)(⌝P ↔Q )↔⌝(P ↔Q )。
(7)(P ∧Q )∧⌝(P ∨Q)。
解 (1)真值表法：由真值表可知，公式(P ∨Q )→(P ∧Q )为可满足式。
公式法：因为(P ∨Q )→(P ∧Q )⇔⌝(P ∨Q )∨(P ∧Q )⇔(⌝P ∧⌝Q )∨(P ∧Q )，所以，公式(P ∨Q )→(P ∧Q )为可满足式。
(2)真值表法：由真值表可知，公式(P ∧Q )→(P ∨Q )为重言式。
公式法：因为(P ∧Q )→(P ∨Q )⇔⌝(P ∧Q )∨(P ∨Q )⇔⌝P ∨⌝Q ∨P ∨Q ⇔T ，所以，公式(P ∧Q )→(P ∨Q )为重言式。
(3)真值表法：由真值表可知，公式(⌝P ∨Q )∧⌝(Q ∨⌝R )∧⌝(R ∨⌝P ∨⌝Q )为矛盾式。
公式法：因为(⌝P ∨Q )∧⌝(Q ∨⌝R )∧⌝(R ∨⌝P ∨⌝Q )⇔(⌝P ∨Q )∧⌝Q ∧R ∧(⌝R ∧P ∧Q )⇔F ，所以，公式(⌝P ∨Q )∧⌝(Q ∨⌝R )∧⌝(R ∨⌝P ∨⌝Q )为矛盾式。
(4)真值表法：由真值表可知，公式(P ∧Q →R )→(P ∧⌝R ∧Q )为可满足式。
公式法：因为(P ∧Q →R )→(P ∧⌝R ∧Q )⇔⌝(⌝( P ∧Q )∨R )∨(P ∧⌝R ∧Q )⇔( P ∧Q ∧⌝R )∨(P ∧⌝R ∧Q )⇔( P ∧Q ∧⌝R )所以，公式(P ∧Q →R )→(P ∧⌝R ∧Q )为可满足式。
(5)真值表法：由真值表可知，公式(Q →P )∧(⌝P ∧Q )为可矛盾式。
公式法：因为(Q →P )∧(⌝P ∧Q )⇔(⌝Q ∨P )∧(⌝P ∧Q )⇔⌝(Q ∧⌝P )∧(⌝P ∧Q )⇔F ，所以，公式为可矛盾式。
(6)真值表法：由真值表可知，公式(⌝P ↔Q )↔⌝(P ↔Q )为永真式。
公式法：因为(⌝P ↔Q )↔⌝(P ↔Q )⇔((⌝P →Q )∧(Q →⌝P ))↔⌝((P ∧Q )∨(⌝P ∧⌝Q ))⇔((P ∨Q )∧(⌝P ∨⌝Q ))↔((⌝P ∨⌝Q )∧(P ∨Q ))⇔T所以，公式(⌝P ↔Q )↔⌝(P ↔Q )为永真式。
(7)真值表法：由真值表可知，公式(P ∧Q )∧⌝(P ∨Q )为矛盾式。
公式法：因为(P ∧Q )∧⌝(P ∨Q )⇔(P ∧Q )∧(⌝P ∧⌝Q )⇔F ，所以，公式(P ∧Q )∧⌝(P ∨Q )为矛盾式。
6.分别用真值表法和公式法证明下列各等价式： (1)(P ∨Q )∧⌝P ⇔⌝P ∧Q 。
(2)⌝(P ∨Q )∨(⌝P ∧Q )⇔⌝P 。
(3)(P ∧Q )∨⌝P ⇔⌝P ∨Q 。
(4)P →(Q ∧R )⇔(P →Q )∧(P →R )。
(5)(P →Q )∧(R →Q )⇔(P ∨R )→Q )。
(6)(P ∧Q ∧A →C )∧(A →P ∨Q ∨C )⇔(A ∧(P ↔Q ))→C 。
(7)⌝(P ↑Q )⇔⌝P ↓⌝Q 。
(8)⌝(P ↓Q )⇔⌝P ↑⌝Q。
证明 (1)真值表法：由真值表可知，(P ∨Q )∧⌝P ⇔⌝P ∧Q 。
公式法：(P∨Q )∧⌝P ⇔(P ∧⌝P )∨(Q ∧⌝P )⇔⌝P ∧Q 。
(2)真值表法：由真值表可知，⌝(P ∨Q )∨(⌝P ∧Q )⇔⌝P 。
公式法：⌝(P ∨Q )∨(⌝P ∧Q )⇔(⌝P ∧⌝Q )∨(⌝P ∧Q )⇔⌝P ∧(⌝Q ∨Q )⇔⌝P 。
(3)真值表法：由真值表可知，(P ∧Q )∨⌝P ⇔⌝P ∨Q 。
公式法：(P ∧Q )∨⌝P ⇔(P ∨⌝P )∧(Q ∨⌝P )⇔⌝P ∨Q 。
(4)真值表法：由真值表可知，P →(Q ∧R )⇔(P →Q )∧(P →R )。
公式法：P →(Q ∧R )⇔⌝P ∨(Q ∧R )⇔(⌝P ∨Q )∧(⌝P ∨R )⇔(P →Q )∧(P →R )。
(5)真值表法：由真值表可知，(P →Q )∧(R →Q )⇔(P ∨R )→Q )。
公式法：(P →Q )∧(R →Q )⇔(⌝P ∨Q )∧(⌝R ∨Q )⇔(⌝P ∧⌝R )∨Q⇔⌝(P ∨R )∨Q ⇔(P ∨R )→Q )。
(6)真值表法：由真值表可知，(P ∧Q ∧A →C )∧(A →P ∨Q ∨C )⇔(A ∧(P ↔Q ))→C 。
公式法：(P ∧Q ∧A →C )∧(A →P ∨Q ∨C )⇔(⌝P ∨⌝Q ∨⌝A ∨C )∧(⌝A ∨P ∨Q ∨C )⇔(⌝P ∨⌝Q ∨⌝A ∨C )∧(⌝A ∨P ∨Q ∨C ) ⇔((⌝P ∨⌝Q ∨⌝A )∧(⌝A ∨P ∨Q ))∨C ⇔⌝((P ∧Q ∧A )∨(A ∧⌝P ∧⌝Q ))∨C ⇔⌝( A ∧((P ∧Q )∨(⌝P ∧⌝Q )))∨C ⇔⌝( A ∧(P ↔Q ))∨C ⇔(A ∧(P ↔Q ))→C 。
(7)真值表法：由真值表可知，⌝(P ↑Q )⇔⌝P ↓⌝Q 。
公式法：⌝(P ↑Q )⇔⌝(⌝(P∧Q ))⇔⌝(⌝P ∨⌝Q ))⇔⌝P ↓⌝Q 。
(8)真值表法：由真值表可知，⌝(P ↓Q )⇔⌝P ↑⌝Q 。
公式法：⌝(P ↓Q )⇔⌝(⌝(P ∨Q ))⇔⌝(⌝P ∧⌝Q )⇔⌝P ↑⌝Q 。
7.设A 、B 、C 为任意的三个命题公式，试问下面的结论是否正确？ (1)若A ∨C ⇔B ∨C ，则A ⇔B 。
(2)若A ∧C ⇔B ∧C ，则A ⇔B 。
(3)若⌝A ⇔⌝B ，则A ⇔B 。
(4)若A →C ⇔B →C ，则A ⇔B 。
(5)若A ↔C ⇔B ↔C ，则A ⇔B 。
解 (1)不正确。
例如，设有一赋值：A ＝T ，B ＝F ，C ＝T ，则A ∨C ⇔B ∨C ，但A ⇔B 不成立。
(2)不正确。
例如，设有一赋值：A ＝T ，B ＝F ，C ＝F ，则A ∧C ⇔B ∧C ，但A ⇔B 不成立。
(3)正确。
因为⌝A ↔⌝B ⇔(⌝A →⌝B )∧(⌝B →⌝A )⇔(A ∨⌝B )∧(B ∨⌝A )⇔(B → A )∧(A →B )⇔ A ↔B ，所以，若⌝A ⇔⌝B ，则A ⇔B 。
(4)不正确。
例如，设有一赋值：A ＝T ，B ＝F ，C ＝T ，则A →C ⇔B →C ，但A ⇔B 不成立。
(5)正确。
因为，若A ↔C ⇔B ↔C ，则A ↔C 与B ↔C 等值。
当A ↔C 与B ↔C 都为真时，A 和C 等值且B 和C 等值，从而A 和B 等值，此时A ⇔B ；当A ↔C 与B ↔C 都为假时，A 和C 不等值且B 和C 也不等值，从而A 和B 等值，此时A ⇔B 。
总之有，若A ↔C ⇔B ↔C ，则A ⇔B 。
8.试给出下列命题公式的对偶式： (1)(P ∧Q )∨R 。
(2)T ∨(P ∧Q )。
(3)(P ∨Q )∧F 。
(4)⌝(P ∧Q )∧(⌝P ∨Q )。
解 (1)对偶式为(P ∨Q )∧R 。
(2)对偶式为F ∧(P ∨Q )。