对勾函数图像及其性质完整版
对勾函数绝对经典
对勾函数是一种类似于反比例函数的一般函数,形如f(x)=ax+ (接下来写作对勾函数f(x)二ax+二的图象与性质X繁华分享对勾函数是数学中一种常见而又特殊的函数。
它在高中教材上不出现,但考试总喜欢考的函数,所以也要注意它和了解它。
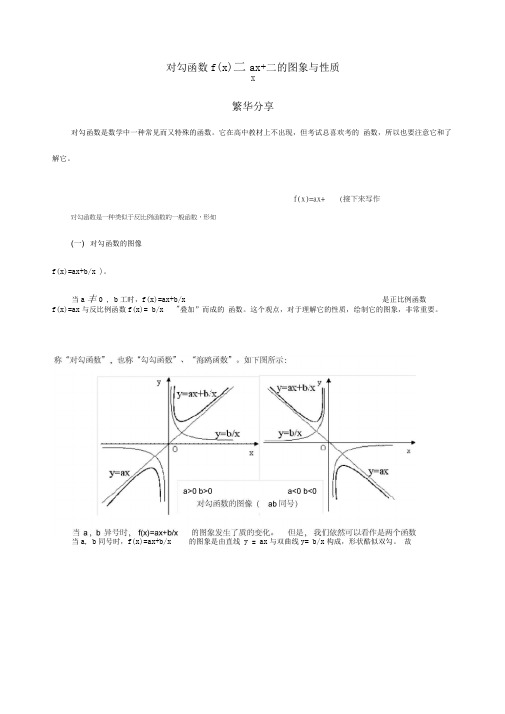
(一) 对勾函数的图像f(x)=ax+b/x )。
当a丰0 , b工时,f(x)=ax+b/x 是正比例函数f(x)=ax与反比例函数f(x)= b/x "叠加”而成的函数。
这个观点,对于理解它的性质,绘制它的图象,非常重要。
当a, b同号时,f(x)=ax+b/x 的图象是由直线y = ax与双曲线y= b/x构成,形状酷似双勾。
故加”而成。
(请自己在图上完成:他是如何叠加而成的。
ab异号)般地,我们认为对勾函数是反比例函数的一个延伸,即对勾函数也是双曲线的一种,只不过它的焦点和渐进线的位置有所改变罢了。
接下来,为了研究方便,我们规定a>0,b>0。
之后当a<0,b<0时,根据对称就很容易得出结论了。
(二)对勾函数的顶点对勾函数性质的研究离不开均值不等式。
利用均值不等式可以得到:当x>0时,g = 是2耐当且黯心扌时取等号),此时卞=卡。
当x<0时,f(£ = 3龙十g玉一2耳旺律且尽当= £时IR等号卜此时耳=-皆。
即对勾函数的定点坐标:ulr2,-2 vabA;(三)对勾函数的定义域、值域由(二)得到了对勾函数的顶点坐标,从而我们也就确定了对勾函数的定义域、值域等性质。
定义域:図£ = 0% 值域;{y|y >厶飯或v< -2VaS)(四)对勾函数的单调性对于函数f(x)= ax-1-单调增区间’fl U 卡卄);单调减2>(五)对勾函数的渐进线由图像我们不难得到:对于函它的渐进线有两離"Xiy = is;F =0;X(六)对勾函数的奇偶性对勾函数在定义域内是奇函数,利用对号函数以上性质,在解某些数学题时很简便,下面举例说明:1、求函数yx2 2x 4 .x22x 的最小值。
对勾函数绝对经典

对勾函数f(x)=ax+的图象与性质繁华分享对勾函数是数学中一种常见而又特殊的函数。
它在高中教材上不显现,但考试总喜爱考的函数,因此也要注意它和了解它。
(一)对勾函数的图像对勾函数是一种类似于反比例函数的一样函数,形如f(x)=ax+(接下来写作f(x)=ax+b/x)。
当a≠0,b≠0时,f(x)=ax+b/x是正比例函数f(x)=ax与反比例函数f(x)= b/x“叠加”而成的函数。
当a,b同号时,f(x)=ax+b/x的图象是由直线y=ax与双曲线y= b/x组成,形状酷似双勾。
故称“对勾函数”,也称“勾勾函数”。
如以下图所示:a>0 b>0 a<0 b<0对勾函数的图像(ab同号)当a,b异号时,f(x)=ax+b/x的图象发生了质的转变。
可是,咱们仍然能够看做是两个函数“叠加”而成。
(请自己在图上完成:他是如何叠加而成的。
)一样地,咱们以为对勾函数是反比例函数的一个延伸,即对勾函数也是双曲线的一种,只只是它的核心和渐进线的位置有所改变算了。
接下来,为了研究方便,咱们规定a>0,b>0。
以后当a<0,b<0时,依照对称就很容易患出结论了。
(二)对勾函数的极点对勾函数性质的研究离不开均值不等式。
利用均值不等式能够取得:当x>0时,。
对勾函数的图像(ab异号)当x<0时,。
即对勾函数的定点坐标:(一) 对勾函数的概念域、值域由(二)取得了对勾函数的极点坐标,从而咱们也就确信了对勾函数的概念域、值域等性质。
(二) 对勾函数的单调性(三) 对勾函数的渐进线由图像咱们不宝贵到:(四) 对勾函数的奇偶性对勾函数在概念域内是奇函数, 利用对勾函数以上性质,在解某些数学题时很简便,下面举例说明: 一、求函数324222++++=x x x x y 的最小值。
解:令322++=x x t ,那么22)1(2≥++=x t t t t t y 112+=+= 依照对勾函数t t y 1+=在(1,+∞)上是增函数及t 的取值范围,当2=t 时y 有最小值223。
对勾函数

对勾函数f(x)=ax+的图象与性质对勾函数是数学中一种常见而又特殊的函数。
它在高中教材上不出现,但考试总喜欢考的函数,所以也要注意它和了解它。
(一)对勾函数的图像对勾函数是一种类似于反比例函数的一般函数,形如f(x)=ax+(接下来写作f(x)=ax+b/x)。
当a≠0,b≠0时,f(x)=ax+b/x是正比例函数f(x)=ax与反比例函数f(x)= b/x “叠加”而成的函数。
这个观点,对于理解它的性质,绘制它的图象,非常重要。
当a,b同号时,f(x)=ax+b/x的图象是由直线y=ax与双曲线y= b/x构成,形状酷似双勾。
故称“对勾函数”,也称“勾勾函数”、“海鸥函数”。
如下图所示:a>0 b>0 a<0 b<0对勾函数的图像(ab同号)当a,b异号时,f(x)=ax+b/x的图象发生了质的变化。
但是,我们依然可以看作是两个函数“叠加”而成。
(请自己在图上完成:他是如何叠加而成的。
)对勾函数的图像(ab异号)一般地,我们认为对勾函数是反比例函数的一个延伸,即对勾函数也是双曲线的一种,只不过它的焦点和渐进线的位置有所改变罢了。
接下来,为了研究方便,我们规定a>0,b>0。
之后当a<0,b<0时,根据对称就很容易得出结论了。
(二)对勾函数的顶点对勾函数性质的研究离不开均值不等式。
利用均值不等式可以得到:当x>0时,。
当x<0时,。
即对勾函数的定点坐标:(三)对勾函数的定义域、值域由(二)得到了对勾函数的顶点坐标,从而我们也就确定了对勾函数的定义域、值域等性质。
(四)对勾函数的单调性(五)对勾函数的渐进线由图像我们不难得到:(六)对勾函数的奇偶性对勾函数在定义域内是奇函数,yXOy=ax。
对勾函数
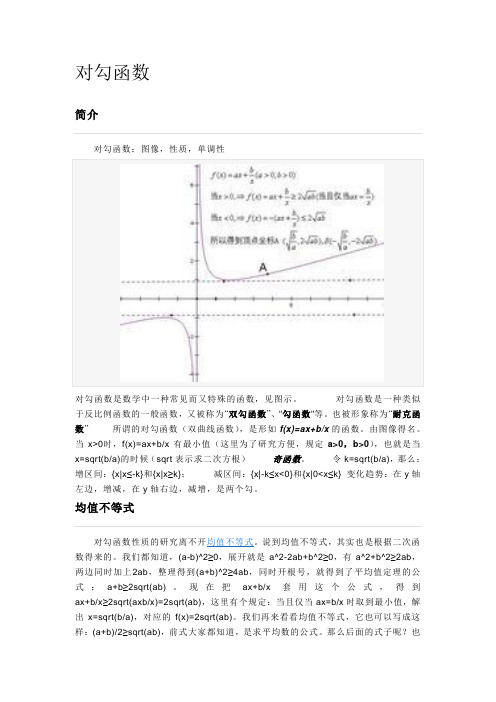
对勾函数简介对勾函数:图像,性质,单调性对勾函数是数学中一种常见而又特殊的函数,见图示。
对勾函数是一种类似于反比例函数的一般函数,又被称为“双勾函数”、"勾函数"等。
也被形象称为“耐克函数”所谓的对勾函数(双曲线函数),是形如f(x)=ax+b/x的函数。
由图像得名。
当x>0时,f(x)=ax+b/x有最小值(这里为了研究方便,规定a>0,b>0),也就是当x=sqrt(b/a)的时候(sqrt表示求二次方根)奇函数。
令k=sqrt(b/a),那么:增区间:{x|x≤-k}和{x|x≥k};减区间:{x|-k≤x<0}和{x|0<x≤k} 变化趋势:在y轴左边,增减,在y轴右边,减增,是两个勾。
均值不等式对勾函数性质的研究离不开均值不等式。
说到均值不等式,其实也是根据二次函数得来的。
我们都知道,(a-b)^2≥0,展开就是a^2-2ab+b^2≥0,有a^2+b^2≥2ab,两边同时加上2ab,整理得到(a+b)^2≥4ab,同时开根号,就得到了平均值定理的公式:a+b≥2sqrt(ab)。
现在把ax+b/x套用这个公式,得到ax+b/x≥2sqrt(axb/x)=2sqrt(ab),这里有个规定:当且仅当ax=b/x时取到最小值,解出x=sqrt(b/a),对应的f(x)=2sqrt(ab)。
我们再来看看均值不等式,它也可以写成这样:(a+b)/2≥sqrt(ab),前式大家都知道,是求平均数的公式。
那么后面的式子呢?也是平均数的公式,但不同的是,前面的称为算术平均数,而后面的则称为几何平均数,总结一下就是算术平均数绝对不会小于几何平均数。
这些知识点也是非常重要的。
导数求解其实用导数也可以研究对勾函数的性质。
不过首先要会负指数幂的换算,这也很简单,但要熟练掌握。
举几个例子:1/x=x^-1,4/x^2=4x^-2。
明白了吧,x为分母的时候可以转化成负指数幂。
对勾函数的图象及性质

对勾函数一、定义对勾函数是由两个幂函数相加得到的,对勾函数是一种类似于反比例函数的一般双曲函数,其标准形式为f(x)=ax+(其中ab>0)。
由于函数图像形似两个中心对称的对勾,因此得名“对勾函数”,又被称为“双勾函数”、“勾函数”、“对号函数”、“双飞燕函数”等。
在许多情况下,为了简化分析,常取a=b=1,即函数形式为f(x)=x+。
研究初等函数的一般路径,背景—概念—图象—性质—应用二、图象及性质图像特征:1、对勾函数的图像是分别以y 轴和直线y=ax 为渐近线的两支曲线。
2、图像上任意一点到两条渐近线的距离之积恰为渐近线夹角(0-180°)的正弦值与|b|的乘积。
3、函数图像整体呈两个“对勾”的形状,且关于原点呈中心对称。
定义域:,即除了x=0外,所有实数都是其定义域内的元素。
值域:。
单调性:函数在(−∞,−1)∪(1,+∞)上单调递增,在(1,0)∪(0,1)上单调递减。
奇偶性:对勾函数是奇函数,即满足f(−x)=−f(x)。
x 122严禁复制三、题型1、基础计算题给定对勾函数表达式,求函数在特定点的值或特定区间的最值。
2.、图像结合题根据对勾函数的图像,判断函数在哪些区间内满足特定条件(如大于某值、小于某值)。
利用图像分析函数与直线、其他曲线的交点情况。
3.、综合应用题求最值问题:利用对勾函数的性质,可以快速求解形如ax+(ab>0)的函数的最值问题。
不等式证明:在不等式证明中,对勾函数的性质也常被用来进行放缩或构造反例。
实际问题建模:在某些经济学问题中,如成本分析、收益最大化等,也可能涉及到对勾函数的应用。
4、参数变化分析:探讨参数a 和b 变化时,对勾函数图像和性质的变化规律。
5、复杂函数组合将对勾函数与其他函数(如二次函数、指数函数等)组合,分析新函数的性质和应用。
四、解题步骤1、对勾函数求最值问题的解题步骤(1)理解函数形式确认函数f(x)=ax+的形式,注意a 和b 都是正数且不相等。
完整版对勾函数详细解析总结计划

对勾函数的性质及应用一、对勾函数y ax b(a 0,b 0)的图像与性x质:1.定义域: ( ,0) (0, )2.值域: ( , 2 ab ] [ 2 ab , )3.奇偶性:奇函数,函数图像整体呈两个“对勾”的形状,且函数图像关于原点呈中心对称,即 f (x) f ( x)04. 图像在一、三象限,当 xb2 ab (当且仅当xb取等号),0 时,y axx a即 f ( x) 在x= b 时,取最小值2 aba由奇函数性质知:当 x<0 时,f (x)在 x=b时,取最大值2 ab a5. 单调性:增区间为(b,),(,b), 减区间是( 0,b),(b,0 )a a a a二、对勾函数的变形形式种类一:函数y ax b(a0, b 0) 的图像与性x质1. 定义域:(,0) (0, )2. 值域:(, 2 ab ] [ 2 ab , )3. 奇偶性:奇函数,函数图像整体呈两个“对勾”的形状 .4. 图像在二、四象限 , 当 x<0 时, f ( x) 在 x= b时,取最小值 2ab ;当 x 0 时,af ( x) 在 x=b时,取最大值 2 aba5. 单调性:增区间为( 0, b),(b ,0 )减区间是( b, ),(,b),aaaa种类二: 斜勾函数 yaxb( ab 0)x① a 0,b 0 作图以下1. 定义域: (,0) (0,) 2. 值域: R3. 奇偶性:奇函数4. 图像在二、四象限,无最大值也无最小值 .5. 单调性:增区间为( - ,0),(0,+ ).② a 0,b 0 作图以下:1. 定义域: (,0) (0,) 2. 值域: R3. 奇偶性:奇函数4. 图像在二、四象限,无最大值也无最小值.5. 单调性:减区间为( - ,0),(0,+ ).种类三: 函数 f ( x)ax2bx c(ac 0) 。
x此类函数可变形为 f ( x)axc c 上下平移获取b ,可由对勾函数 y axxx练习 1. 函数 f ( x)x2x 1的对称中心为x种类四: 函数 f (x ) xa (a 0, k 0)xk此类函数可变形为 f (x)( x ka ) k ,则 f ( x) 可由对勾函数 yxa左右平移,x kx上下平移获取练习 1. 作函数 f ( x)x1与 f ( x)x 3x xx 的草图222. 求函数 f (x)x1 在 (2, ) 上的最低点坐标2x 43. 求函数 f (x)xx 的单调区间及对称中心x1种类五 :函数 f (x)ax (a 0,b 0) 。
对勾函数的性质及应用(史上上最完整版)

对勾函数的性质及应用一、概念:【题型1】函数()(0,0)af x x a k =+>≠【例1】函数1()f x x =+的值域为【例2】函数3()x f x x +=+的值域为【题型2】函数()(0)ax bx cf x ac ++=>。
【例3】函数1()x x f x ++=的值域为【题型3】函数2()(0,0)axf x a b =≠>。
【例4】函数2()1xf x x =+的在区间[)2,+∞上的值域为 【解析】2x ≥,∴,函数15222≥+=【例5】如2214xa x +=-+,(1,2)x ∈,则实数a 的取值范围是(1,2)x ∈4y x x =+1144x x <+,7352a <-<【题型4】函数2()(0)ax bx cf x a ++=≠.【例6】已知1x >-,求函数710()1x x f x x ++=+的最小值。
,1x >-,7101x ++的最小值【例7】已知1x <,求函数299()x x f x +-=的最大值。
,1x <,2991x x +--的最大【题型5】函数2()(0)x mf x a +=≠ 【例8】求函数21()2x f x x x -=++在区间(1,)+∞上的最大值。
【例9】求函数2223()x x f x ++=在区间[0,)+∞上的最大值。
【例10】求函数()f x =的最小值。
类型九:函数2()0)f x a>。
【例12】求函数2()f x=的最小值。
【解析】由题可知,函数22()f x===2t=,则1()()f xg t tt==+,显然在[)2,+∞上单调递增,故min15()(2)222g t g==+=,此时0x=,故函数2()f x=的最小值为52。
【例13】求函数()f x=的值域.。
对勾函数绝对经典

对勾函数f(x)=ax+的图象与性质繁华分享对勾函数是数学中一种常见而又特殊的函数。
它在高中教材上不出现,但考试总喜欢考的函数,所以也要注意它和了解它。
(一) 对勾函数的图像对勾函数是一种类似于反比例函数的一般函数,形如f(x)=ax+(接下来写作f(x)=ax+b/x)。
当a≠0,b≠0时,f(x)=ax+b/x是正比例函数f(x)=ax与反比例函数f(x)= b/x “叠加”而成的函数。
这个观点,对于理解它的性质,绘制它的图象,非常重要。
当a,b同号时,f(x)=ax+b/x的图象是由直线y=ax与双曲线y= b/x构成,形状酷似双勾。
故称“对勾函数”,也称“勾勾函数”、“海鸥函数”。
如下图所示:a>0 b>0 a<0 b<0对勾函数的图像(ab同号)当a,b异号时,f(x)=ax+b/x的图象发生了质的变化。
但是,我们依然可以看作是两个函数“叠加”而成。
(请自己在图上完成:他是如何叠加而成的。
)一般地,我们认为对勾函数是反比例函数的一个延伸,即对勾函数也是双曲线的一种,只不过它的焦点和渐进线的位置有所改变罢了。
接下来,为了研究方便,我们规定a>0,b>0。
之后当a<0,b<0时,根据对称就很容易得出结论了。
(二)对勾函数的顶点对勾函数性质的研究离不开均值不等式。
利用均值不等式可以得到:当x>0时,。
当x<0时,。
即对勾函数的定点坐标:(三)对勾函数的定义域、值域由(二)得到了对勾函数的顶点坐标,从而我们也就确定了对勾函数的定义域、值域等性质。
(四)对勾函数的单调性对勾函数的图像(ab异号)(五) 对勾函数的渐进线由图像我们不难得到:(六) 对勾函数的奇偶性对勾函数在定义域内是奇函数,利用对号函数以上性质,在解某些数学题时很简便,下面举例说明: 1、求函数324222++++=x x x x y 的最小值。
解:令322++=x x t ,则22)1(2≥++=x ttt t t y 112+=+=根据对号函数t t y 1+=在(1,+∞)上是增函数及t 的取值范围,当2=t 时y 有最小值223。
