山东省济南市2018年中考数学一轮复习第一章数与式第二节整式与因式分解课件
山东潍坊市2018年中考数学复习 第1章 数与式 第2讲 整式及其运算

括号前面是“+”号,把括号和它前面的“+”号
去括号
去掉,括号里的各项都③ 不改变 符号;括号前 面是“-”号,把括号和它前面的“-”号去掉,
括号里的各项都④ 改变 符号
括号前面是“+”号,括到括号里的各项的符号都 添括号 ⑤ 不改变 ;括号前面是“-”号,括到括号里
的各项的符号都⑥ 改变
提示
整式加减的实质是合并同类项,若有括号,就要用去括号法则去掉括号, 然后再合并同类项.去、添括号时,括号前面是负号时,要特别注意括号 里面各项的符号的改变.
④ 单项式 和⑤ 多项式 统称为整式
所含字母⑥ 相同 ,并且相同字母的⑦ 指数 也相同的项,叫做同类项 把一个多项式中的同类项合并成一项叫做合并同类 项
考点3 整式的运算 6年2考 1.整式的加减
法则
内容
合并同类 在合并同类项时,只把同类项的① 系数 相加, 项 所得的和作为系数,字母与字母的② 指数 不变
公因式可以是单项式,也可以是多项式.公因式的确定方法:①取各项整数
系数的最大公约数;②取各项相同的字母;③取各项相同字母的最低次
数.(2)能用平方差公式进行因式分解的多项式应是二项式,两项都能写成
平方的形式,且符号相反.即用完全平方公式进行因式分解的多项式应符合
a2±2ab+b2=(a±b)2,左边是三项式,其中的两项都能写成平方的形式且符
先用一个多项式的每一项分别乘另一个多项式 的每一项,再把所得的积相加.如:(m+n)(a +b)=⑯ ma+mb+na+nb
乘法公式
平方差公式:(a+b)(a-b)=⑰ a2-b2 ; 完全平方公式:(a±b)2=⑱ a2±2ab+b2
考点4 因式分解 6年6考
概念
把一个多项式化成①__几个整式的乘积__的形式,叫做 因式分解.
中考数学一轮优化复习 第一部分 教材同步复习 第一章 数与式 第2讲 实数的大小比较与运算课件

12/10/2021 第6页
第六页,共十七页。
2.实数的四则运算法则 (1)加法:同号两数相加,取相同的符号,并把绝对值⑳____相_加_____;绝对值不 相等的异号两数相加,取○21 ____绝_对__值_____较大的加数的符号,并用较大数的绝对值 减去较小数的○22 __绝__对__值______;互为相反数的两个数相加得 0;一个数同 0 相加,仍
12/10/2021
第十七页,共十七页。
得这个数. (2)减法:减去一个数,等于加上这个数的○23 __相__反__数______,即 a-b=a+(-b).
12/10/2021 第7页
第七页,共十七页。
(3)乘法:两数相乘,同号得○24 ____正____,异号得○25 ____负____,并把绝对值相乘; |a|·|b|a,b同号,
第一(dìyī)部 分
教材同步(tóngbù)复习
第一章 数与式
第2讲 实数的大小比较与运算
12/10/2021
第一页,共十七页。
知识要点·归纳
知识点一 实数的大小比较
直接比较法 正数>0>负数 数轴法 在数轴上,右边的点所表示的数总比左边的点所表示的数大 两个正数比较大小,绝对值大的数比较大;两个负数比较大小, 绝对值法 绝对值大的数反而小,即 a<0,b<0,若|a|>|b|,则 a<b 平方 对任意正实数 a, b,有:a2>b⇔a> b(适用于含有根式的数的 比较法 大小比较或二次根式的估值)
【正解】原式=-9+1--1122+4 =-9+1-4+4 =-8.
12/10/2021 第 14 页
第十四页,共十七页。
2.(2018·张家界)计算:( 3-1)0+(-1)-2-4sin60°+ 12.
人教版中考数学一轮复习课件第1章 第2讲 整式与因式分解

2.(1)(2022泰州)下列计算正确的是( A ) A.3ab+2ab=5ab B.5y2-2y2=3 C.7a+a=7a2 D.m2n-2mn2=-mn2 (2)计算:2a2-(a2+2)=__a_2_-__2__.
3.整式的乘除
(1)幂的运算法则:
①am•an=am+n;
②(am)n=amn;
考点1 整式的运算 1.(2022广东)单项式3xy的系数为___3___. 2.(2022牡丹江)下列计算正确的是( B ) A.a+a=a2 B.a•a2=a3 C.(a2)4=a6 D.a3÷a-1=a2
3.先化简,再求值:(2a-b)2+(a-b)(a+b)-5a(a-2b),其中a=
1 2
1.(1)单项式-
2 5
a2b的系数是__-__25____,次数是___3___.多项式5x3-
3x2y2+2xy+1的次数是___4___.
(2)如果2x4y2n与-3xmy6是同类项,那么m+n=____7__.
2.整式的加减 运算法则:有括号先去括号,再合并同类项. (1)去括号法则(“+”不变,“-”整体变号): a+(b+c)=a+b+c; a-(b+c)=a-b-c. (2)合并同类项法则:把同类项的系数相加,字母连同它的的指数不变.
③(ab)m=ambm;abm=bamm(b≠0);
④am÷an=am-n(a≠0);
⑤a-m=
1 am
(a≠0);a0=1(a≠0).
3.(1)a3•a2=__a_5_; (2)(a3)2=__a_6_; (3)(-3a)3=__-__2_7_a_3__; (4)a6÷a2=__a_4_;
3.整式的乘除 (2)整式的乘除: 单项式乘多项式:a(b+c)=ab+ac; 多项式乘多项式:(a+b)(m+n)=am+an+bm+bn; 多项式除以单项式:(a+b)÷m=a÷m+b÷m. (3)乘法公式: 平方差公式:(a+b)(a-b)=a2-b2; 完全平方公式:(a±b)2=a2±2ab+b2.
2018中考数学专题复习 第二讲整式、因式分解 (共68张PPT)

【自主解答】原式=3a-2a2+2(a2-1)=3a-2a2+2a22=3a-2.
命题角度3:化简求值 【示范题5】(2017·眉山中考)先化简,再求 值:(a+3)2-2(3a+4),其中a=-2. 【思路点拨】原式利用完全平方公式化简,去括号合 并得到最简结果,把a的值代入计算即可求出值.
【自主解答】原式=a2+6a+9-6a-8=a2+1, 当a=-2时,原式=4+1=5.
2.(2017·潍坊中考)下列计算正确的是 ( )
A.a3×a2=a6
B.a3÷a=a3
C.a2+a2=a4
D.(a2)2=a4
【解析】选D.选项A是同底数幂的乘法,结果为a5,故选 项A错误;选项B是同底数幂的除法,结果为a2,故选项B 错误;选项C是合并同类项,结果为2a2,故选项C错误;选 项D是幂的乘方,底数不变,指数相乘,故选项D正确.
3.(2017·威海中考)下列运算正确的是 ( )
A.3x2+4x2=7x4
B.2x3·3x3=6x3
C.a÷a-2=a3
D. (-1a2b)3-1a6b3
2
6
【解析】选C. A.原式=7x2,不符合题意; B.原式=6x6,不符合题意; C.原式=a·a2=a3,符合题意; D.原式=- 1 a6b3,不符合题意.
()
A.-m
B.-1
C. 3
4
D.- 3
4
【解析】选D.6m6÷(-2m2)3=6m6÷(-8m6)= - 3 .
4
2.(2017·台州中考)下列计算正确的是 ( ) A.(a+2)(a-2)=a2-2 B.(a+1)(a-2)=a2+a-2 C.(a+b)2=a2+b2 D.(a-b)2=a2-2ab+b2
中考第一轮复习--第一章数与式
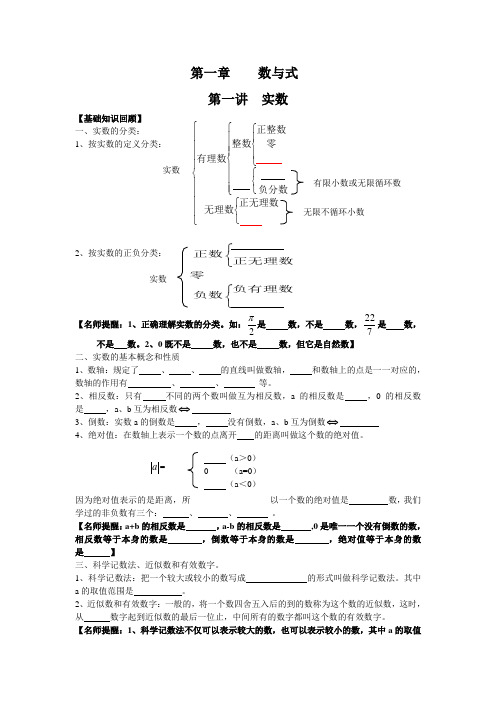
第一章 数与式第一讲 实数【基础知识回顾】 一、实数的分类: 1、按实数的定义分类: 实数 有限小数或无限循环数2、按实数的正负分类:实数【名师提醒:1、正确理解实数的分类。
如:2π是 数,不是 数,722是 数,不是 数。
2、0既不是 数,也不是 数,但它是自然数】二、实数的基本概念和性质1、数轴:规定了 、 、 的直线叫做数轴, 和数轴上的点是一一对应的,数轴的作用有 、 、 等。
2、相反数:只有 不同的两个数叫做互为相反数,a 的相反数是 ,0的相反数是 ,a 、b 互为相反数⇔3、倒数:实数a 的倒数是 , 没有倒数,a 、b 互为倒数⇔4、绝对值:在数轴上表示一个数的点离开 的距离叫做这个数的绝对值。
a =因为绝对值表示的是距离,所以一个数的绝对值是 数,我们学过的非负数有三个: 、 、 。
【名师提醒:a+b 的相反数是 ,a-b 的相反数是 ,0是唯一一个没有倒数的数,相反数等于本身的数是 ,倒数等于本身的数是 ,绝对值等于本身的数是 】三、科学记数法、近似数和有效数字。
1、科学记数法:把一个较大或较小的数写成 的形式叫做科学记数法。
其中a 的取值范围是 。
2、近似数和有效数字:一般的,将一个数四舍五入后的到的数称为这个数的近似数,这时,从 数字起到近似数的最后一位止,中间所有的数字都叫这个数的有效数字。
【名师提醒:1、科学记数法不仅可以表示较大的数,也可以表示较小的数,其中a 的取值⎪ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎧ ⎩ ⎨ ⎧ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎨ ⎧ ⎩ ⎨ ⎧ ⎪ ⎩ ⎪ ⎨ ⎧ 正无理数 无理数 负分数 零 正整数 整数 有理数 无限不循环小数 ⎧⎨⎩⎧⎨⎩正数正无理数零 负有理数负数 (a >0) (a <0) 0 (a=0)范围一样,n 的取值不同,当表示较大数时,n 的值是原整数数位减一,表示较小的数时,n 是负整数,它的绝对值等于原数中左起第一个非零数字前零的个数(含整数数位上的零)。
中考数学一轮复习课件整式及因式分解

(1)x2y+2xy+y= y(x+1)2 ;
(2)x3-xy2= x(x+y)(x-y) ;
(3)x3-4x2+4x= x(x-2)2 .
B
3n
6
y(x+1)2
x(一个多项式,把它因式分解后有一个因式为(x+1),请你写出一个符合条件的多项式: x2-1(答案不唯一) .
6ab
3m2+3mn
m2-6m+9
1-a2
-4x2yz
5a2-2b3
2x2-x-1
知识点4 因式分解
定义
把一个多项式表示成若干个整式的乘积的形式
基本方法
(1)提公因式法:ma+mb+mc=⑬ m(a+b+c) ;(2)公式法 a.a2-b2⑭ (a+b)(a-b) ; b.a2±2ab+b2⑮ (a±b)2
a(a+2)
(x+2)(x-2)
4a(x-y)(x+y)
2 022(x-1)2
6
1.(2023·毕节期末)代数式-7x的意义可以是( C )
A.-7与x的和
B.-7与x的差
C.-7与x的积
D.-7与x的商
A.x6
B.x6
C.x5
D.x9
A.3x4y5
B.-3x4y5
C.3x3y6
D.-3x3y6
a(a+4)
(2+x)(2-x)
(a+4)2
-3ma(a2-2a+4)
(x+2)(x-4)
2a(2a+b)(2a-b)
(x-y)(x-y-1)
2a·(a+1)2
命题点1 列代数式及求值
1.当x=-1时,代数式3x+1的值是( B )
A.-1
B.-2
C.4
D.-4
中考数学一轮复习PPT课件第3讲 整式及因式分解
第3讲┃整式及因式分解
回 归 教 材
完全平方公式大变身 把下列各式分解因式: (1)3ax2+6axy+3ay2;(2)-x2-4y2+4xy.
解
(1)3ax2+6axy+3ay2 =3a(x2+2xy+y2) =3a(x+y)2; (2)-x2-4y2+4xy =-(x2-4xy+4y2) =-[x2-2·x·2y+(2y)2] =-(x-2y)2.
2±2ab+b2 (a±b)2=a ________
(a+b)2-2ab = (1)a2+b2=____________ (a-b)2+2ab ____________ (2)(a-b)2=(a+b)2-4ab
第3讲┃整式及因式分解
考点4
因式分解的概念
因式分解:把一个多项式化为几个整式的积 ________的形式, 像这样的式子变形,叫做多项式的因式分解. 注意:(1)因式分解专指多项式的恒等变形; (2)因式分解的结果必须是几个整式的积的形式; (3)因式分解与整式乘法互为逆运算.
第3讲┃整式及因式分解
点析
如果三项中有两项能写成两数或式的平方,但符号不
是“+”号时,可以先提取“-”号,然后再用完全平方公 式分解因式.
第3讲┃整式及因式分解
中 考 预 测
分解因式: (1)x3-6x2+9x; (2)2x2-4x+2; (3)a3-a; (4)9ax2-6ax+a。
解
1.x(x-3)2 2.2(x-1)2 3.a(a+1)(a-1) 4.a(3x-1)2
第3讲┃整式及因式分解
(1)同类项必须符合两个条件:第一,所含字母相同; 第二,相同字母的指数相同.两者缺一不可。 (2)根据同类项概念——相同字母的指数相同列方程 (组)是解此类题的一般方法。
中考数学复习第一单元数与式第2课时代数式与整式课件95
【解析】由已知可得:根据第一列的奇数行的数的规律是 第几行就是那个数的平方,第一行的偶数列的数的规律, 与奇数行规律相同,∵45×45=2025,2025在第45行,向 右依次减小,故2017所在的位置是第45行,第9列,即2017 对应的有序数对为(45,9).
练习3
一列数a1,a2,a3,…满足条件:a1=
__a_m_-__n _(a≠0) 幂的乘方,底数不变,指数相乘,(am)n= 14__a_m_n _ 积的乘方,先给每一个因式分别乘方,再把所得 的幂相乘,(ab)n= 15 _a_n_b_n
乘法 运算
单项式乘以单项式:把它们的系数、同底数幂分别 相乘,其余字母同它的指数不变,作为积的因 式,如:ma2·ab2=16 __m_a_3_b2 单项式乘以多项式:用单项式去乘多项式的每一项 再把所得的积相加,如:m(a+b+c)= 17 _m_a_+__m__b_+__m_c__ 多项式乘以多项式:先用一个多项式的每一项乘另 一个多项式的每一项,再把所得的积相加, 如:(m+n)(a+b)= 18 _m_a_+__m__b_+__n_a_+__n_b
∵原式要化为三次二项式,
∴令2a-b=0,2a-1=0,
解得a=
1 2
,b=1,
即当a=
1 2
,b=1时,整式x3+2a(x2+xy)-bx2-xy+y2能
化简成一个三次二项式.
二 、数式规律探索
例 将自然数按以下规律排列:
第一列 第二列 第三列 第四列 第五列
第一行 1
4
5
16
17 …
第二行 2
练习2 是否存在实数a、b,使得整式 x3+2a(x2+xy)-bx2 _xy+y2能化简成一个三次二项式,若存在,请求出满足条
中考数学总复习——2.代数式和整式
7.【2019·厦门集美区二模·4 分】下列计算正确的是( C )
A.a8+a2=a10
B.a8·a2=a16
C.(a8)2=a16
D.a8÷a2=a4
8.【2019·福建·4 分】分解因式:x2-9=_(_x_-__3_)(_x_+__3_)__.
9.【2020·福州质检·4 分】若 m(m-2)=3,则(m-1)2 的值是 ____4______.
考点1 求代数式的值
例1【2020·漳州质检·4分】若a是方程x2+x-1=0的根, 则代数式2 020-a2-a的值是__2__0_1_9____.
考点2 整式的化简求值
例 2【2019·宁德质检·8 分】先化简,再求值:(x-3)2+x(2-x) -9,其中 x=- 3. 解:原式=x2-6x+9+2x-x2-9=-4x. ∵x=- 3, ∴原式=-4×(- 3)=4 3.
考点3整式的概念
例3【2020·厦门质检·4分】将单项式3m与m合并同类项, 结果是( B ) A.4 B.4m C.3m2 D.4m2
例 4【2020·厦门质检·4 分】若多项式 x2+2x+n 是完全平方式,
则常数 n 是( D )
A.-1
B.14
1 C.2
D.1
【点拨】本题考查完全平方式的概念,完全平方式必须满 足“a2+2ab+b2”或“a2-2ab+b2”的结构特征,解答 时容易出错.
考点4 整式的运算
例5【2020·三明质检·4分】下列运算正确的是( C )
A.(a2)3=a5
B.3a2+a=3a3
C.a5÷ a2=a3(a≠0) D.a(a+1)=a2+1
考点5 因式分解
例6【2020·宁德质检·4分】下列多项式能用完全平方公式
1中考数学第一轮复习精品讲解第一单元数与式(共126张PPT)
·新课标
第1讲 │归类示例
类型之二 实数的有关概念
命题角度: 1.数轴、相反数、倒数等概念 2.绝对值的概念及计算
填空题: (1)相反数等于它本身的数是_____0___. (2)倒数等于它本身的数是____±__1__. (3)平方等于它本身的数是___0_或__1__. (4)平方根等于它本身的数是____0____. (5)绝对值等于它本身的数是__非_负__数___.
7.数轴上的点A到原点的距离是6,则点A表示的数为( A )
A.6或-6
B.6
C.-6
D.3或-3
[解析] 数轴上到原点的距离是6的点有两个,分别位于原 点的左右两侧.
·新课标
第1讲 │ 考点随堂练
8.[2011·丽水]有四包真空小包装火腿,每包以标准克数(450 克)
为基数,超过的克数记作正数;不足的克数记作负数,以下数
第1讲 │归类示例
[解析] 指环的个数为5的倍数,而前面有8个,最后又有4个, 把四个选项中的数加上12,能被5整除的是2013,因为2013+12= 2025,故选D.
此类探究实数规律性问题的特点是给定一列数或等式或图形,进 行适当地计算,并观察、猜想、归纳、验证,利用从特殊到一般的数 学思想,分析特点,探索规律,总结结论.
有理数
负整数
实数
分数
正分数 有限小数或 负分数 无限循环小数
无理数
正负无无理理数数无限不循环小数
第1课时┃ 考点聚焦
2.按正负分类:
正有理数
正实数
正整数 正分数
实数
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解答代数式求值问题,一般有两种方法:直接代入求值和 整体代入求值.直接代入求值时,要注意代数式的符号问 题;整体代入求值时,关键是把要求的代数式转化为已知 代数式的形式.
1.(2017·重庆)若x=-3,y=1,则代数式2x-3y+1的 值为( A.-10 B ) B.-8 C .4 D.10
2.(2017·高新二模) 若a2=a+2,则2a2-2a+2 017的 2 021 . 值为 ______
)
4.(2015·济南)下列运算不正确的是( D A.a2·a=a3 C.(2a2)2=4a4 B.(a3)2=a6 D.a2 ÷a2 =a
考点三
整式运算
(5年5考)
命题角度❶
整式的化简
例3 (2015·济南)化简:(x+2)2+x(x+3).
【分析】 利用完全平方公式以及单项式乘以多项式运算法
则化简即可.
讲:
混淆幂的运算法则
在幂的运算中,最易出错的是混淆同底数幂的乘法与乘
方的运算法则.在应用时,牢记以下公式:am·an=am+n,
(am)n=amn,(ab)n=anbn.
练:链接变式训练4
3.(2014·济南)下列运算中,结果是a5的是( A A.a2·a3 C.(a2)3 B.a10÷a2 D.(-a)5 )
【自主解答】 原式=x2+4x+4+x2+3x=2x2+7x+4.
4.整式的除法
(1)单项式除以单项式:把系数、同底数幂分别相除后,作
为商的因式,只在被除式里含有的字母,则连同它的指数一
1 1 2 ac =(3÷ 3 3
起作为商的一个因式,如3a2b÷
=9abc-2.
)a2-1·bc-2
(2)多项式除以单项式:先把这个多项式的每一项分别除以
这个单项式,再把所得的商相加,如(4a3b+5ab2)÷3ab=
知识点三 整式的运算
1.幂的运算法则
m +n (1)同底数幂相乘:am·an= a____ .
am -n . (2)同底数幂相除:am÷an= ____ (3)幂的乘方:(am)n= ___ amn .
an bn . (4)积的乘方:(ab)n= ____ 1 (a≠0). (5)零指数幂:a0= ______
考点二
幂的运算
(5年4考) )
例2 (2016·济南)下列运算正确的是( A.a2+a=2a3 C.(-2a3)2=4a6 B.a2·a3=a6 D.a6 ÷a2 =a3
【分析】 根据合并同类项法则和幂的运算性质对各选项分 析即可.
【自主解答】A.a2与a不是同类项,不能合并,故本选项错误; B.原式=a2+3=a5,故本选项错误; C.原式=(-2)2·a3×2=4a6,故本选项正确; D.原式=a6-2=a4,故本选项错误.故选C.
4a3b÷3ab+5ab2÷3ab= 4 a2+ 5 b.
3 3
知识点四
因式分解
整式 的积的形式 1.因式分解:把一个多项式化成几个 _____ ,这种变形叫做因式分解.
因式分解 整式乘法
2.因式分解与整式乘法互为逆运算,即多项式
因式分解整式乘法整式的积.
3.因式分解的方法
(1)提公因式法:ma+mb+mc=m(a+(5年1考) )
(2013·济南)已知x2-2x-8=0,则3x2-6x-18的值为( A.54 B.6 C.-10 D.-18
【分析】 利用x2-2x与3x2-6x之间的倍数关系整体代入求值. 【自主解答】 ∵x2-2x-8=0,即x2-2x=8, ∴3x2-6x-18=3(x2-2x)-18=24-18=6.故选B.
(2)去括号法则
①括号前是“+”号,把括号和它前面的“+”号去掉后, 都不改变 ,如a+(b-c)=a+b-c, 原括号里各项的符号 _________ a+(b+c)=a+b+c.
②括号前是“-”号,把括号和它前面的“-”号去掉后, 都要改变 ,如a-(b-c)=a-b+c, 原括号里各项的符号 _________ a-(b+c)=a-b-c.
知识点二
整式的有关概念
乘积 数字因数 指数和 和
最高
指数 也相 2.同类项:所含字母相同,并且相同字母的 _____ 同的项叫做同类项.
确定代数式的同类项要严格按照定义中的两个条件,即字 母相同,指数一样.特别地,所有常数项都是同类项.
3.合并同类项:把同类项合并成一项叫做合并同类项. 系数 相加,字母 其法则是:合并同类项时,把同类项的 _____ 指数 不变. 和字母的 _____
3.整式的乘法
(1)单项式乘单项式:把它们的系数、相同字母的幂分别相
乘,其余字母连同它的指数不变,作为积的因式,如
3xy·4x2z=12x3yz.
(2)单项式乘多项式:根据分配律用单项式去乘多项式的每一
项,再把所得的积相加,如a×(b+c-d)=ab+ac-ad.
(3)多项式乘多项式:先用一个多项式的每一项乘另一个 多项式的每一项,再把所得积相加,如(a+b)(c+d)=ac +ad+bc+bd.
第二节 整式与因式分解
知识点一 代数式求值
运算符号 把数和字母连接而成的式子叫做 1.代数式:用 _________
代数式.特别地,单独一个数或字母也是代数式. 字母 ,按照 2.代数式的值:用具体数值代替代数式里的 _____ 代数中的运算关系,计算得出的结果.
在有些代数式的求值问题中,题目并没有直接给出字母的 值,而且通过已知条件很难求出该字母的值,这时需要考 虑整体代入,从而求出所给代数式的值.
(6)负指数幂:a-p=
1 ap
(a≠0,p是正整数).
要牢记幂的运算公式,区分开幂的乘方和同底数幂相乘的 运算法则.注意不同底数幂不能按照幂的运算法则运算, 需先转化为同底数幂再运算,如4n·2m=(22)n·2m= 22n·2m=22n+m.
2.整式的加减
(1)几个整式相加减,有括号的先去括号,然后再合并同类项.
确定公因式的一般方法:先取系数,取多项式中各项系数
的最大公因数;再取字母,取各项中的共同的字母;最后 取指数,取相同字母的指数中最小的数.
(a+b)(a-b) ; (2)公式法:①平方差公式:a2-b2= _____________ (a±b)2 ②完全平方公式:a2±2ab+b2= ________.
