线段与角测试卷精选
《线段与角度》的练习题

《线段与角度》的练习题线段与角度的练题
1. 线段练题:
a. 画一个长度为5cm的线段。
b. 根据给出的方向,画一个长度为8cm的线段。
c. 比较上面两个线段的长度。
2. 角度练题:
a. 画一个 90°的直角。
b. 画一个 45°的角度。
c. 比较上面两个角度的大小。
d. 画一个锐角。
e. 画一个钝角。
3. 混合练题:
a. 画一个以AB为边、90°为角度的直角三角形。
b. 如果一个直角三角形的直角边长为6cm,斜边长为10cm,求第三条边的长度。
c. 画一个以AC为边、45°为角度的等腰直角三角形。
d. 复以上练的内容,并回答以下问题:
- 直角三角形有几条直角边?
- 钝角的度数大于锐角的度数吗?
- 两个角度相等的直角形是什么角形?
- 直角处的两个线段称为什么?
4. 挑战题:
a. 画一个以AB为边、60°为角度的等边三角形。
b. 画一个以ABC为边、90°为角度的正方形。
c. 画一个以AD为边、120°为角度的正方形。
d. 在一个直角坐标系中画一个图形,其中包括不同角度和线段的组合。
以上是线段与角度的练习题,请按照题目要求完成。
线与角测试题

线与角测试题一、选择题1. 下列哪个选项不是线段的基本性质?A. 线段有两个端点B. 线段的长度可以无限延长C. 线段是直线的一部分D. 线段可以度量2. 直线AB和直线CD相交于点O,如果∠AOC = 30°,那么∠BOC的度数是多少?A. 30°B. 60°C. 120°D. 150°3. 在一个直角三角形中,如果一个锐角是30°,那么另一个锐角的度数是多少?A. 30°B. 45°C. 60°D. 90°4. 以下哪个选项描述的是一条射线?A. 直线B. 线段C. 从一点出发,无限延伸的线D. 两点之间的连线5. 如果一个角是直角的两倍,那么这个角的度数是多少?A. 120°B. 180°C. 240°D. 360°二、填空题6. 直线是无限延伸的,它没有______。
7. 如果两条直线相交,形成的角中有一个是锐角,那么其余的角都是______。
8. 平行线之间的距离是______的。
9. 一个角的度数为90°,这个角被称为______。
10. 在一个三角形中,如果两个角的度数分别是50°和60°,那么第三个角的度数是______。
三、简答题11. 解释什么是垂线,并给出垂线的基本性质。
12. 描述什么是对顶角,并解释为什么对顶角相等。
13. 如果一个三角形的内角和为180°,解释为什么这个性质适用于所有三角形。
四、计算题14. 在一个直角三角形中,已知一个角是30°,另一个角是60°,求斜边与较短直角边的比例。
15. 如果一个角的补角是120°,求这个角的度数。
五、应用题16. 在一个平面上,有两条平行线l1和l2,它们之间的距离是5cm。
如果从点A到l1的距离是3cm,求点A到l2的距离。
线段与角度练习题

线段与角度练习题一、线段练习题1. 在直角坐标系中,已知点A(-2, 3)和B(4, -1),求线段AB的长度。
解析:根据两点之间的距离公式,设AB的长度为d,有:d = √[(x2-x1)² + (y2-y1)²]= √[(4-(-2))² + (-1-3)²]= √[6² + (-4)²]= √[36 + 16]= √52= 2√13所以线段AB的长度为2√13。
2. 在平面内,已知线段CD的中点为E,且CE = 2m,DE = 4m。
求线段CD的长度。
解析:由线段中点定理得:CE² + DE² = CD²代入已知条件:2² + 4² = CD²4 + 16 = CD²20 = CD²CD = √20 = 2√5所以线段CD的长度为2√5。
二、角度练习题1. 已知角A的度数为30°,角A的补角的度数为多少?解析:角A的补角为90°减去角A的度数:补角度数 = 90° - 30° = 60°所以角A的补角的度数为60°。
2. 已知角B的度数为60°,角B的余角的度数为多少?解析:角B的余角为90°减去角B的度数:余角度数 = 90° - 60° = 30°所以角B的余角的度数为30°。
3. 在平面内,已知角C的度数为45°,角C的补角的度数为多少?解析:角C的补角为90°减去角C的度数:补角度数 = 90° - 45° = 45°所以角C的补角的度数为45°。
4. 在平面内,已知角D为直角,求角D的补角和余角的度数。
解析:直角的度数为90°,所以角D的补角为90° - 90° = 0°(零度)。
最新-(几1)《线段、角》基础测试+答案精品

1 2.(4分)已知线段 a、b(如图),画出线段 AB,设 AB=3a- b,并写出画法.
2
【答案】方法一:①量得 a= 1. 9 cm, b= 2. 6 cm; ②算 AB 的长, AB= 3×1. 9- 1 ×2. 6= 4. 4( cm); 2 ③画线段 AB= 4. 4 cm.
1 1.(4分)已知线段 a、 b(如图),作出线段 AB,使 AB= 3a- b,并写出作法.
2
5.读句作图填空(每空 1 分,共 10 分)
(1)作∠ AOB=60°. (2)作∠ AOB 的平分线 OC,则∠ BOC=∠ ____= 1 ∠ ____= ____°.
2 (3)作 OB 的反向延长线 OD,则∠ AOD=∠ ____-∠ AOB= _____°. (4)作∠ AOD 的平分线 OE,则∠ AOE=∠ ____= _____°,∠ COE= _____°.
(5)以 O 为顶点, OB 为一边作∠ AOB 的余角∠ BOF,则∠ EOF= ____°,射线 OC、
OB 将∠ ____三 等分.
六、解答题(每小题 5 分,共 15 分)
1.如图, M 是线段 AB 的中点,点 C 在线段 AB 上,且 AC= 4 cm,N 是 AC 的中 点, MN= 3 cm,求线段 CM 和 AB 的长.
( 1)画∠ AOB= 60°. ( 2)画∠ AOB 的平分线 OC,则∠ BOC=∠ ____= 1 ∠ ____ =____°.
2 ( 3)画 OB 的反向延长线 OD,则∠ AOD=∠ ____-∠ AOB= _____°. ( 4)画∠ AOD 的平分线 OE,则∠ AOE=∠ ____= _____°,∠ COE=_____°. ( 5)以 O 为顶点, OB 为一边作∠ AOB 的余角∠ BOF,则∠ EOF= ____°, 射
第四章线段和角单元测试题
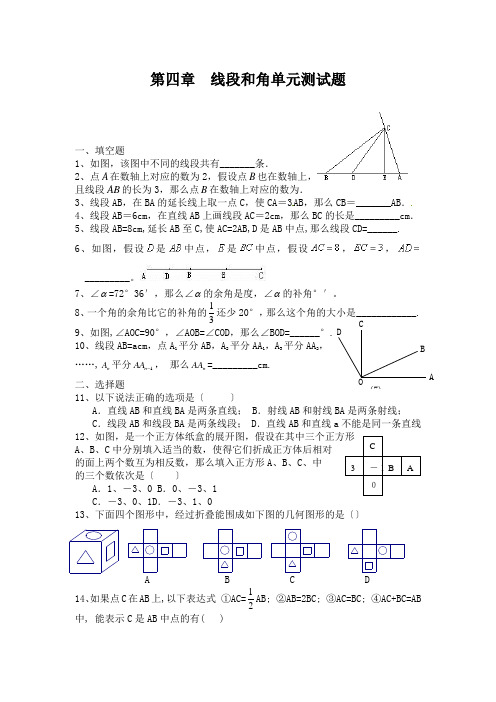
第四章 线段和角单元测试题一、填空题1、如图,该图中不同的线段共有_______条.2、点A 在数轴上对应的数为2,假设点B 也在数轴上, 且线段AB 的长为3,那么点B 在数轴上对应的数为.3、线段AB ,在BA 的延长线上取一点C ,使CA =3AB ,那么CB =_______AB .4、线段AB =6cm ,在直线AB 上画线段AC =2cm ,那么BC 的长是_________cm .5、线段AB=8cm,延长AB 至C,使AC=2AB,D 是AB 中点,那么线段CD=______.6、如图,假设是中点,是中点,假设,,_________。
7、∠α=72°36′,那么∠α的余角是度,∠α的补角°′。
8、一个角的余角比它的补角的13还少20°,那么这个角的大小是____________.9、如图,∠AOC=90°,∠AOB=∠COD ,那么∠BOD=______°.10、线段AB=acm ,点A 1平分AB ,A 2平分AA 1,A 3平分AA 2, ……,n A 平分1n AA -, 那么n AA =_________cm.二、选择题11、以下说法正确的选项是〔 〕A .直线AB 和直线BA 是两条直线; B .射线AB 和射线BA 是两条射线;C .线段AB 和线段BA 是两条线段;D .直线AB 和直线a 不能是同一条直线 12、如图,是一个正方体纸盒的展开图,假设在其中三个正方形A 、B 、C 中分别填入适当的数,使得它们折成正方体后相对的面上两个数互为相反数,那么填入正方形A 、B 、C 、中的三个数依次是〔 〕A .1、-3、0B .0、-3、1C .-3、0、1D .-3、1、013、下面四个图形中,经过折叠能围成如下图的几何图形的是〔〕14、如果点C 在AB 上,以下表达式 ①AC=12AB; ②AB=2BC; ③AC=BC; ④AC+BC=AB中, 能表示C 是AB 中点的有( )D C(7)AB AB C -1 0 315、线段AB ,延长AB 至C ,使AC=2BC ,反向延长AB 至D ,使AD=21BC , 那么线段AD 是线段AC 的〔 〕A .31B .72C .51D .4116、如图,∠1=︒15,∠AOC=︒90点B 、O 、D 在同一直线上,那么的度数为〔 〕A 75°B 15°C 105°D 165°17、在时刻8∶30时,时钟上的时针与分针间的夹角是〔〕 A 、75° B 、85° C 、70 ° D 、60°18、如上图所示,点O 为直线AB 上一点,∠AOC =∠DOE =90°, 那么图中互余角的对数为〔 〕A .2对B .3对C .4对D .5对19、两个角,它们的比是6:4,其差为36°,那么这两个角的关系是( )20、把一张报纸的一角斜折过去,使A 点落在E 点处,BC 为折痕, BD 是∠EBM 的平分线,那么∠CBD=〔 〕 A.85° B.80° C.75° D.90°三、解答题21、如图,平面上有四个点A 、B 、C 、D ,根据以下语句画图 (1)画直线AB ;作射线BC ;画线段CD ;(2)连接AD ,并将其反向延长至E ,使DE=2AD ;(3)找到一点F ,使点F 到A 、B 、C 、D 四点距离和最短 22、如图,假设CB=4㎝,DB=7㎝,且D 是AC 的中点,求线段DC 和AB 的长度.23、线段AB=14cm ,C 是AB 上一点,且AC=9cm ,O 为AB 中点,求线段OC 的长度。
初二数学线段和角度练习题

初二数学线段和角度练习题1. 直线段练习题(1) 请画出一条长度为5cm的直线段。
(2) 请画出一条长度为8cm的直线段,并在直线段上任意选择一点P。
(3) 在直线段AB上,现在已知A点的坐标是(2, 3),B点的坐标是(7, 1),请问直线段AB的长度是多少?2. 角度练习题(1) 请画出一个直角,并标注其内角、外角和相邻补角。
(2) 请画出一个钝角,并标注其内角、外角和对角。
(3) 请画出一个锐角,并标注其内角、外角和对角。
(4) 角ABC是一个直角,角ABD是一个钝角,角BCD是一个锐角。
请问角A和角D的关系是什么?3. 线段和角度的计算练习题(1) 如果直线段AB的长度是3cm,直线段AC的长度是5cm,直线段AD的长度是7cm,请问直线段BC的长度是多少?(2) 在三角形ABC中,已知∠ABC是一个锐角,∠ACB的度数是30°,边AB的长度是4cm,请问边AC的长度是多少?(3) 在直角三角形ABC中,已知∠BAC是一个直角,边AB的长度是5cm,边AC的长度是12cm,请问边BC的长度是多少?4. 实际问题运用练习题(1) 一辆汽车以每小时60km的速度行驶,行驶5个小时后停下来。
请问汽车总共行驶了多少千米?(2) 一张长方形的长是10cm,宽是6cm,请问长方形的周长是多少厘米?(3) 在一个直角三角形中,一条直角边的长度是3cm,斜边的长度是5cm,请问另一条直角边的长度是多少厘米?通过以上练习题,我们可以巩固对于初二数学中线段和角度的基础知识。
通过练习画线段、计算线段长度,以及练习画角度、确定角度的类型和计算角度的相关问题,我们可以提高自己的数学能力,加深对于数学概念的理解。
祝你在数学学习中取得优异的成绩!。
七年级数学上册-线段和角精选练习题
七年级数学上册-线段和角精选练习题线段和角精选练习题一.选择题(共22小题)1.如图是某个几何体的展开图,该几何体是()A.圆柱B.圆锥C.圆台D.四棱柱2.如图,线段AD上有两点B、C,则图中共有线段()A.三条B.四条C.五条D.六条3.下列语句:①不带“﹣”号的数都是正数;②如果a是正数,那么﹣a一定是负数;③射线AB和射线BA是同一条射线;④直线MN和直线NM是同一条直线,其中说法正确的有()A.1个B.2个C.3个D.4个4.如图,某同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长小,能正确解释这一现象的数学知识是()A.两点之间,直线最短B.两点确定一条直线C.两点之间,线段最短D.经过一点有无数条直线5.若数轴上点A、B分别表示数2、﹣2,则A、B两点之间的距离可表示为()A.2+(﹣2)B.2﹣(﹣2) C.(﹣2)+2 D.(﹣2)﹣26.如图,点C在线段AB上,点D是AC的中点,如果CB=CD,AB=10.5cm,那么BC的长为()A.A2.5cm B.3cm C.4.5cm D.6cm7.已知线段AB=8cm,在直线AB上画BC,使BC=2cm,则线段AC的长度是()A.6cm B.10cm C.6cm或10cm D.4cm或16cm8.如图,在直线l上顺次取A、B、C三点,使得AB=5cm,BC=3cm,如果O是线段AC的中点,那么线段OB长为()A.1cm B.1.5cm C.2cm D.4cm9.已知点A、B、P在一条直线上,则下列等式中,能判断点P是线段AB的中点的个数有()①AP=BP;②BP=AB;③AB=2AP;④AP+PB=AB.A.1个B.2个C.3个D.4个10.如图所示,某工厂有三个住宅区,A,B,C各区分别住有职工30人,15人,10人,且这三点在一条大道上(A,B,C三点在同一直线上),已知AB=300米,BC=600米.为了方便职工上下班,该厂的接送车打算在此路段只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在()A.点A B.点B C.AB之间D.BC之间11.若一个角为65°,则它的补角的度数为()A.25°B.35°C.115°D.125°12.如图,将一副三角尺按不同的位置摆放,下列方式中∠α与∠β互余的是()A.图①B.图②C.图③D.图④13.一副三角板按如图所示的方式摆放,且∠1比∠2大50°,则∠2的度数为()A.20°B.50°C.70°D.30°14.如图,在△ABC中,过点A作BC边上的高,正确的作法是()A.B.C.D.15.如图所示,已知∠AOC=∠BOD=70°,∠BOC=30°,则∠AOD的度数为()A.100°B.110°C.130°D.140°16.将一副直角三角尺如图放置,若∠BOC=160°,则∠AOD的大小为()A.15°B.20°C.25°D.30°17.一个角是这个角的余角的2倍,则这个角的度数是()A.30°B.45°C.60°D.75°32.如图,O,D,E三点在同一直线上,∠AOB=90°.(1)图中∠AOD的补角是,∠AOC的余角是;(2)如果OB平分∠COE,∠AOC=35°,请计算出∠BOD的度数.33.如图,已知∠AO B=155°,∠AOC=∠BOD=90°.(1)写出与∠COD互余的角;(2)求∠COD的度数;(3)图中是否有互补的角?若有,请写出来.34.如图,直线AB.CD相交于点0,OE平分∠BOC,∠COF=90°.(1)若∠BOE=70°,求∠AOF的度数;(2)若∠BOD:∠BOE=1:2,求∠AOF的度数.35.如图,点O是直线AB上任一点,射线OD和射线OE分别平分∠AOC和∠BOC.(1)填空:与∠AOE互补的角是;(2)若∠AOD=36°,求∠DOE的度数;(3)当∠AOD=x°时,请直接写出∠DOE的度数.36.已知,如图,∠AOC=90°,∠DOE=90°,∠AOB=56°,E,O,B三点在同一条直线上,OF平分∠DOE,求∠COF的度数.37.如图,∠AOB=120°,射线OD是∠AOB的角平分线,点C是∠AOB外部一点,且∠AOC=90°,点E是∠AOC内部一点,满足∠AOC=3∠AOE.(1)求∠DOE的度数;(2)请通过计算,找出图中所有与∠AOE互余的角.试题解析一.选择题(共22小题)1.如图是某个几何体的展开图,该几何体是()A.圆柱B.圆锥C.圆台D.四棱柱【分析】侧面为长方形,底边为2个圆形,故原几何体为圆柱.2.如图,线段AD上有两点B、C,则图中共有线段()A.三条B.四条C.五条D.六条【分析】由图知,线段有AB,BC,CD,AC,BD,AD.3.下列语句:①不带“﹣”号的数都是正数;②如果a是正数,那么﹣a一定是负数;③射线AB和射线BA是同一条射线;④直线MN和直线NM是同一条直线,其中说法正确的有()A.1个B.2个C.3个D.4个【分析】根据正数、负数、直线、射线的定义和表示方法对各小题分析判断后利用排除法求解.4.如图,某同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长小,能正确解释这一现象的数学知识是()A.两点之间,直线最短B.两点确定一条直线C.两点之间,线段最短D.经过一点有无数条直线【分析】根据线段的性质,可得答案.5.若数轴上点A、B分别表示数2、﹣2,则A、B两点之间的距离可表示为()A.2+(﹣2)B.2﹣(﹣2) C.(﹣2)+2 D.(﹣2)﹣2【分析】根据数轴上两点间距离的定义进行解答即可.6.如图,点C在线段AB上,点D是AC的中点,如果CB=CD,AB=10.5cm,那么BC的长为()A.A2.5cm B.3cm C.4.5cm D.6cm【分析】根据线段中点的性质,可得DA与CD的关系,根据线段的和差,可得关于BC的方程,根据解方程,可得答案.7.已知线段AB=8cm,在直线AB上画BC,使BC=2cm,则线段AC的长度是()A.6cm B.10cm C.6cm或10cm D.4cm或16cm【分析】由于点C的位置不确定,故应分点C在AB之间与点C在AB外两种情况进行讨论.8.如图,在直线l上顺次取A、B、C三点,使得AB=5cm,BC=3cm,如果O是线段AC的中点,那么线段OB长为()A.1cm B.1.5cm C.2cm D.4cm【分析】由已知条件可知,AB+BC=AC,又因为O是线段AC的中点,则OB=AB﹣AO,故OB可求.9.已知点A、B、P在一条直线上,则下列等式中,能判断点P是线段AB的中点的个数有()①AP=BP;②BP=AB;③AB=2AP;④AP+PB=AB.A.1个B.2个C.3个D.4个【分析】根据题意画出图形,根据中点的特点即可得出结论.10.如图所示,某工厂有三个住宅区,A,B,C各区分别住有职工30人,15人,10人,且这三点在一条大道上(A,B,C三点在同一直线上),已知AB=300米,BC=600米.为了方便职工上下班,该厂的接送车打算在此路段只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在()A.点A B.点B C.AB之间 D.BC之间【分析】此题为数学知识的应用,由题意设一个停靠点,为使所有的人步行到停靠点的路程之和最小,肯定要尽量缩短两地之间的里程,就用到两点间线段最短定理.11.若一个角为65°,则它的补角的度数为()A.25°B.35°C.115°D.125°【分析】根据互为补角的两个角的和等于180°列式进行计算即可得解.12.如图,将一副三角尺按不同的位置摆放,下列方式中∠α与∠β互余的是()A.图①B.图②C.图③D.图④【分析】根据平角的定义,同角的余角相等,等角的补角相等和邻补角的定义对各小题分析判断即可得解.13.一副三角板按如图所示的方式摆放,且∠1比∠2大50°,则∠2的度数为()A.20°B.50°C.70°D.30°【分析】根据图形得出∠1+∠2=90°,然后根据∠1的度数比∠2的度数大50°列出方程求解即可.14.如图,在△ABC中,过点A作BC边上的高,正确的作法是()A.B.C.D.【分析】从三角形的一个顶点向它的对边引垂线,从顶点到垂足之间的线段是三角形的高,据此作高.15.如图所示,已知∠AOC=∠BOD=70°,∠BOC=30°,则∠AOD的度数为()A.100°B.110°C.130°D.140°【分析】根据图形和题目中的条件,可以求得∠AOB的度数和∠COD的度数,从而可以求得∠AOD的度数.16.将一副直角三角尺如图放置,若∠BOC=160°,则∠AOD的大小为()A.15°B.20°C.25°D.30°【分析】依据∠COB=∠COD+∠AOB﹣∠AOD求解即可.17.一个角是这个角的余角的2倍,则这个角的度数是()A.30°B.45°C.60°D.75°【分析】先表示出这个角的余角为(90°﹣α),再列方程.18.如图,∠1和∠2都是∠α的余角,则下列关系不正确的是()A.∠1+∠α=∠90°B.∠2+∠α=90°C.∠1=∠2 D.∠1+∠2=90°【分析】根据互为余角的两个角的和等于90°和同角的余角相等解答.19.如图,两轮船同时从O点出发,一艘沿北偏西50°方向直线行驶,另一艘沿南偏东25°方向直线行驶,2小时后分别到达A,B点,则此时两轮船行进路线的夹角∠AOB的度数是()A.165°B.155°C.115°D.105°【分析】根据题意可得:∠1=50°,∠2=25°,再根据角的和差关系可得答案.20.如图,已知∠COB=2∠AOC,OD平分∠AOB,且∠COD=20°,则∠AOB=()A.40°B.60°C.120°D.135°【分析】设∠AOC=x,则∠BOC=2x,则∠AOD=1.5x,最后,依据∠AOD﹣∠AOC=∠COD列方程求解即可.21.如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°,则∠COE=()A.65°B.70°C.75°D.80°【分析】首先由角平分线定义求得∠COD的度数,然后根据∠COE=∠DOE﹣∠COD即可求得∠COE的度数.22.如图,O是直线AB上的一点,过点O任意作射线OC,OD平分∠AOC,OE平分∠BOC,则∠DOE()A.一定是钝角 B.一定是锐角 C.一定是直角 D.都有可能【分析】直接利用角平分线的性质得出∠AOD=∠DOC,∠BOE=∠COE,进而得出答案.二.填空题(共3小题)23.一个多边形有8条边,从其中的一个顶点出发,连接这个点和其他顶点,可以得到 6 个三角形.【分析】从n边形的一个顶点出发,连接这个点与其余各顶点,可以把一个多边形分割成(n﹣2)个三角形.24.如图所示,∠AOB是平角,∠AOC=30°,∠BOD=60°,OM,ON分别是∠AOC,∠BOD的平分线,∠MON等于135 度.【分析】根据平角和角平分线的定义求得.25.如图,点O在直线AB上,射线OD平分∠AOC,若∠AOD=20°,则∠COB的度数为140 度.【分析】根据角平分线的定义得到∠AOC=2∠AOD=40°,根据平角的定义计算即可.三.解答题(共12小题)26.如图,四边形ABCD,在四边形内找一点O,使得线段AO、BO、CO、DO的和最小.(画出即可,不写作法)【分析】要确定点O的位置,根据“两点之间,线段最短”只需要连接AC,BD,交点即为所求.27.如图,A、B是公路L两旁的两个村庄,若两村要在公路上合修一个汽车站,使它到A、B两村的距离和最小,试在L上标注出点P的位置,并说明理由.【分析】根据线段的性质:两点之间线段最短,即可得出答案.28.如图,C,D是线段AB上的两点,已知AC:CD:DB=1:2:3,MN分别是AC,BD的中点,且AB=36cm,求线段MN的长.【分析】根据比例设AC=xcm,CD=2xcm,DB=3xcm,然后根据AC的长度列方程求出x的值,再根据线段中点的定义表示出CM、DN,然后根据MN=CM+CD+DN求解即可.29.如图,线段AC=6cm,线段BC=15cm,点M是AC的中点,在CB上取一点N,使得CN:NB=1:2,求MN的长.【分析】因为点M是AC的中点,则有MC=AM=AC,又因为CN:NB=1:2,则有CN=BC,故MN=MC+NC 可求.30.已知:如图,∠AOB=∠AOC,∠COD=∠AOD=120°,求:∠COB的度数.【分析】直接利用周角的定义得出∠AOC=120°,进而利用已知得出答案.31.填空,完成下列说理过程如图,点A,O,B在同一条直线上,OD,OE分别平分∠AOC和∠BOC.(1)求∠DOE的度数;(2)如果∠COD=65°,求∠AOE的度数.【分析】(1)首先根据角平分线定义可得∠COD=∠AOC,∠COE=∠BOC,然后再根据角的和差关系可得答案;(2)首先计算出∠BOE的度数,再利用180°减去∠BOE的度数可得答案.32.如图,O,D,E三点在同一直线上,∠AOB=90°.(1)图中∠AOD的补角是∠AOE ,∠AOC的余角是∠BOC ;(2)如果OB平分∠COE,∠AOC=35°,请计算出∠BOD的度数.【分析】(1)根据互余和互补解答即可;(2)利用角平分线的定义和平角的定义解答即可.33.如图,已知∠AOB=155°,∠AOC=∠BOD=90°.(1)写出与∠COD互余的角;(2)求∠COD的度数;(3)图中是否有互补的角?若有,请写出来.【分析】根据余角和补角的概念进行计算即可.34.如图,直线AB.CD相交于点0,OE平分∠BOC,∠COF=90°.(1)若∠BOE=70°,求∠AOF的度数;(2)若∠BOD:∠BOE=1:2,求∠AOF的度数.【分析】(1)根据角平分线的定义求出∠BOC的度数,根据邻补角的性质求出∠AOC的度数,根据余角的概念计算即可;(2)根据角平分线的定义和邻补角的性质计算即可.35.如图,点O是直线AB上任一点,射线OD和射线OE分别平分∠AOC和∠BOC.(1)填空:与∠AOE互补的角是∠BOE、∠COE ;(2)若∠AOD=36°,求∠DOE的度数;(3)当∠AOD=x°时,请直接写出∠DOE的度数.【分析】(1)先求出∠BOE=∠COE,再由∠AOE+∠BOE=180°,即可得出结论;(2)先求出∠COD、∠COE,即可得出∠DOE=90°;(3)先求出∠AOC、COD,再求出∠BOC、∠COE,即可得出∠DOE=90°.36.已知,如图,∠AOC=90°,∠DOE=90°,∠AOB=56°,E,O,B三点在同一条直线上,OF平分∠DOE,求∠COF的度数.【分析】依据同角的余角相等,可得∠COD=∠AOB=56°,再根据OF平分∠DOE,∠DOE=90°,即可得到∠DOF=∠DOF=45°,最后依据∠COF=∠COD+∠DOF进行计算即可.37.如图,∠AOB=120°,射线OD是∠AOB的角平分线,点C是∠AOB外部一点,且∠AOC=90°,点E是∠AOC内部一点,满足∠AOC=3∠AOE.(1)求∠DOE的度数;(2)请通过计算,找出图中所有与∠AOE互余的角.【分析】(1)根据角平分线的性质可得∠BOD=∠AOD=∠AOB=60°,再计算出∠AOE的度数,然后可得∠DOE的度数;(2)根据余角定义进行分析即可.。
《线与角》单元测试卷
《线与角》单元测试卷姓名:班级:成绩:一、填空( 25 分)1.线段有个端点,射线有个端点,直线端点.2.周角 =度直角=度1 个周角 =个平角=个直角.3.两条直线订交成直角时,这两条直线,这两条直线的交点叫做.4.3 点整时,时针与分针所成的角度是度,是角;6 点整时,时针与分针所成的角度是度,是角;2 点整时,时针与分针所成的角度是度,是角.5、用一个放大 100 倍的放大镜看一个30°的角,看到的角的度数是(),一个角是 50°用放大 2 倍的放大镜来察看是()。
6、在一条直线上有 A、B、C 三点,以以下图.图中有条线段,有条射线7、下边的图形都是一副三角尺拼成的,拼成的每个角各是多少度?在相应的括号里填一填。
二、判断( 10 分)1.过两点只好画一条直线.()2.一个 20 度的角,透过放大 5 倍的放大镜看是 100 度.()3.用一副三角板能够拼出 105°的角.()4.十字路口的斑马线是平行线.()5.平角就是一条直线,周角就是一条射线.()三、选择题( 15 分)1.能够丈量出长度的是()A .直线B.射线C.线段2.如图中有()个锐角.A.1 B.2 C.33.角的大小与()相关.A .两边张开的大小B.两边的长短C.极点的地点4.以下几个角用一副三角尺就能够拼出的是()A.80 度B.120 度C.170 度5.图中()是周角.A.B.C.四、操作题( 29 分)1.过 c 点分别画直线 L 的垂线、平行线.( 8 分)4.画出一个 80 度的角。
( 4 分)五、解决问题( 21 分)2.量出图中角的度数,并标在图上(8 分)1、已知∠ 1=30°,求出∠ 2。
( 5 分)3.在点子图上分别画一个锐角、一个钝角、一个平角,在所画的角上标2、看图,求图中∠ 2 是多少度?( 5 分)出你所画的是哪个角.(9 分)3、求出∠ A 的度数。
初中数学线段和角的测试卷
初中数学线段和角的测试卷一、填空题。
1.线段是直的,有( )个端点;将线段向两个方向无限延长,就形成了( )线;从线段的一个端点向一个方向无限延长,就得到一条( )线。
2.从一点引出两条射线所组成的图形叫做( )。
这个点叫做它的( ),这两条射线叫做它的( )。
3.测量角的大小要用( ),直角的度数是( ),平角的度数是( ),周角的度数是( )。
4.把我们所认识的角的种类按度数从小到大排列。
( )角<( )角<( )角<( )角<( )角5.过一点可以画出( )条直线,过两点只能画出( )条直线;从一点出发可以画( )条射线。
6.1个周角=( )个平角=( )个直角;1个平角=( )个直角。
7.如果∠1和65°角正好组成一个直角,则∠1等于( );如果∠2和65°角正好组成一个平角,则∠2等于( )。
8.3时整时和( )时整时,时针和分针所成的角是直角;( )时整时,时针和分针所成的角是平角。
二、判断题。
(对的画“√”,错的画“✕”)1.直线总比射线长。
( )2.大于90°的角一定是钝角。
( )3.平角是一条直线。
( )4.任意两个锐角度数之和一定比钝角要大。
( )5.用放大镜去看90°的角,角的大小不会发生变化。
( )6.线段是直线上两点之间的部分。
( )7.过一点只能画出一条直线。
( )8.一条射线长6厘米。
( )9.过两点只能画一条直线。
( )10.两边越长,角的度数越大。
( )三、选择题。
(把正确答案的序号填在括号里)1.角的两条边是( )。
A.直线B.线段C.射线2.下面不能用三角板画出的角是( )的角。
A .15°B .70°C .105°3.丫丫画了一条长20厘米的( )。
A.直线B.射线C.线段四、分别画出90°、40°、125°的角。
五、下图中已知∠2=130°,求∠1、∠3、∠4的度数。
小学数学线段与角度练习题
小学数学线段与角度练习题【练习题一】线段的长度计算1. A、B两点的坐标分别是(2, 3)和(5, 1),请计算线段AB的长度。
【练习题二】线段的比较2. 下图是一张城市地图,A、B、C、D四个地点分别标在图上。
请根据图上刻度计算线段AB、BC和CD的长度,并回答以下问题:AB C Da) 线段AB的长度与线段BC的长度相比,哪个更长?b) 线段BC的长度与线段CD的长度相比,哪个更短?【练习题三】线段的延长与截取3. 下图中,线段AB的长度是5个单位,仅根据图上信息,回答以下问题:C/ |\/ B| \/ | \/____A|a) 如果将线段AB延长2个单位,得到的点是什么?b) 如果将线段AB截取3个单位并得到的点是C,则点C在原来线段AB的什么位置上?【练习题四】角度的测量4. 利用直尺和量角器测量以下角的度数:a) 直角b) 锐角c) 钝角【练习题五】角的比较5. 下图中,三个角分别为α、β和γ,请回答以下问题:B/ \/ \α γ/ \A_________Ca) 角α的度数与角γ的度数相比,哪个更大?b) 角α的度数与角β的度数相比,哪个更小?【练习题六】角的分类6. 根据以下信息,判断并分类角:a) 度数为90°,是哪种类型的角?b) 度数为180°,是哪种类型的角?c) 度数为30°,是哪种类型的角?d) 度数为0°,是哪种类型的角?【练习题七】角的补角与余角7. 两个角的和为90°时,这两个角互为补角;两个角的和为180°时,这两个角互为补角。
请分别找出以下角的补角和余角:a) 30°角的补角和余角分别是多少?b) 120°角的补角和余角分别是多少?c) 45°角的补角和余角分别是多少?【练习题八】角的相等关系8. 判断以下各组角是否相等:a) 60°角和120°角是否相等?b) 45°角和90°角是否相等?c) 钝角和锐角是否相等?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《线段角》单元测试卷
一、选择题
1、下列说法中正确的是()
A、两点之间的所有连线中,线段最短
B、射线就是直线
C、两条射线组成的图形叫做角
D、小于平角的角可分为锐角和钝角两类
2、下列说法正确的是()
A、过一点P只能作一条直线
B、直线AB和直线BA表示同一条直线
C、射线AB和射线BA表示同一条射线
D、射线a比直线b短
3、已知AB=10cm,在AB的延长线上取一点C,使AC=16cm,则线段AB的中点与AC的中点的距离为()
A、5cm
B、4cm
C、3cm
D、2cm
4、按下列线段长度,可以确定点A、B、C不在同一条直线上的是()
A、AB=8cm,BC=19cm,AC=27cm
B、AB=10cm,BC=9cm,AC=18cm
C、AB=11cm,BC=21cm,AC=10cm
D、AB=30cm,BC=12cm,AC=18cm
5、下列图形中,无端点的是()
A、角平分线
B、线段
C、射线
D、直线
6、以下给出的四个语句中,结论正确的有()
①如果线段AB=BC,则B是线段AC的中点;
②线段和射线都可看作直线上的一部分;
③大于直角的角是钝角;
④如图,∠ABD也可用∠B表示.
A、1个
B、2个
C、3个
D、4个
7、钟表在5点半时,它的时针和分针所成的锐角是()
A、15°
B、70°
C、75°
D、90°
8、钟表上12时15分钟时,时针与分针的夹角为()
A、90°
B、82.5°
C、67.5°
D、60°
9、已知∠A=40°,则∠A的补角等于()
A、50°
B、90°
C、140°
D、180°
10、下列说法中正确的是()
A、8时45分,时针与分针的夹角是30°
B、6时30分,时针与分针重合
C、3时30分,时针与分针的夹角是90°
D、3时整,时针与分针的夹角是90°
11. 下列图形中,能够相交的是( ).
12. 如果线段
AB=13cm,MA+MB=17 cm,那么下面说法中正确的是( ).
A .M 点在线段A
B 上. B .M 点在直线AB 上.
C .M 点在直线AB 外.
D .M 点可能在直线AB 上,也可能在直线AB 外.
13. 将一正方体纸盒沿下右图所示的线剪开,展开成平面图,其展开图的形状为( ).
14. 下列说法中,正确的个数有( ). (1)射线AB 和射线BA 是同一条射线 (2)延长射线MN 到C
(3)延长线段MN 到A 使NA==2MN (4)连结两点的线段叫做两点间的距离
A .1
B .2
C .3
D .4
15.如图,C 是线段AB 的中点,D 是CB 上一点,下列说法中错误的是( ).
A .CD=AC-BD
B .CD=
21BC C .CD=2
1AB-BD D .CD=AD-BC 16.如果线段AB=13cm,MA+MB=17 cm,那么下面说法中正确的是( ).
A .M 点在线段A
B 上. B .M 点在直线AB 上.
C .M 点在直线AB 外.
D .M 点可能在直线AB 上,也可能在直线AB 外.
17.下列四个图中,能用∠1、∠AOB 、∠O 三种方法表示同一个的是( )
18.如图是某一个多面体的平面展开图,那么这个多面体是 ( )
A 四棱柱
B 四棱锥
C 三棱柱
D 三棱锥。
