主成分分析(论文)
主成分分析讲解范文
主成分分析讲解范文下面我们来具体讲解主成分分析的步骤和原理：1.数据预处理在进行主成分分析之前，需要对原始数据进行预处理，包括去除噪声、处理缺失值和标准化等操作。
这些操作可以使得数据更加准确和可靠。
2.计算协方差矩阵协方差矩阵是衡量各个变量之间相关性的指标。
通常，我们会对数据进行标准化处理，使得各个变量具有相同的尺度。
然后，计算标准化后的数据的协方差矩阵。
3.计算特征值和特征向量通过对协方差矩阵进行特征分解，可以得到特征值和特征向量。
其中，特征值表示新坐标系中的投影方差，特征向量表示新坐标系的方向。
4.选择主成分根据特征值的大小，我们可以按照降序的方式选择主成分。
选取一部分较大的特征值所对应的特征向量，即可得到相应的主成分。
这些主成分是原始数据中最重要的成分。
5.生成投影数据通过将原始数据投影到选取的主成分上，即可得到降维后的数据。
每个样本在各个主成分上的投影即为新的特征值。
6.重构数据在需要恢复原始数据时，可以通过将降维后的数据乘以选取的主成分的转置矩阵，再加上原始数据的均值，即可得到近似恢复的原始数据。
主成分分析在实际应用中有很广泛的用途。
首先，它可以用于数据的降维，使得复杂的数据集可以在低维空间中进行可视化和分析。
其次，它可以用于数据的简化和压缩，减少数据存储和计算的成本。
此外，主成分分析还可以用于数据的特征提取和数据预处理，辅助其他机器学习和统计分析方法的应用。
然而，主成分分析也有一些限制和注意事项。
首先，主成分分析假设数据具有线性关系，对于非线性关系的数据可能失效。
其次，主成分分析对于离群值敏感，需要对离群值进行处理。
另外，主成分分析得到的主成分往往是原始数据中的线性组合，不易解释其具体含义。
总之，主成分分析是一种常用的降维数据分析方法，通过寻找新的投影空间，使得数据的方差最大化，实现数据的降维和简化。
它可以应用于数据可视化、数据压缩和特征提取等方面，是数据分析和机器学习中常用的工具之一、在应用主成分分析时，需要注意数据的预处理和对主成分的解释和理解。
主成分分析 毕业论文
主成分分析毕业论文主成分分析（Principal Component Analysis，简称PCA）是一种常用的多变量数据分析方法，广泛应用于统计学、机器学习、图像处理等领域。
它的主要目的是通过线性变换将原始数据转换为一组新的变量，这些新变量被称为主成分，它们能够最大程度地保留原始数据的信息。
PCA的基本思想是通过寻找数据中的主要方向，将高维数据降维到低维空间中。
在降维的过程中，PCA会按照数据中的方差大小对各个方向进行排序，将方差较大的方向作为主要方向。
这样做的好处是可以减少数据的维度，提高计算效率，同时保留了数据的主要特征。
PCA的数学原理比较复杂，但是在实际应用中，我们只需要掌握它的基本步骤和使用方法即可。
下面我将简要介绍一下PCA的具体步骤。
首先，我们需要对原始数据进行标准化处理，使得各个变量具有相同的尺度。
这是因为PCA是基于协方差矩阵进行计算的，如果各个变量的尺度不一致，会影响到计算结果的准确性。
接下来，我们需要计算协方差矩阵。
协方差矩阵反映了各个变量之间的相关性。
通过计算协方差矩阵，我们可以得到各个变量之间的相关性大小，从而确定主要方向。
然后，我们需要对协方差矩阵进行特征值分解。
特征值分解可以将协方差矩阵分解为特征值和特征向量。
特征值表示了各个主成分的方差大小，特征向量表示了各个主成分的方向。
接下来，我们将特征值按照大小进行排序，选择前k个特征值对应的特征向量作为主成分。
这样就得到了一组新的变量，它们是原始数据在主要方向上的投影。
最后，我们可以利用主成分对原始数据进行降维。
降维的过程就是将原始数据用主成分表示，可以将高维数据转换为低维数据，提取出数据的主要特征。
PCA在实际应用中有很多优点。
首先，它能够减少数据的维度，提高计算效率。
其次，它能够提取出数据的主要特征，降低了数据的噪声和冗余信息。
此外，PCA还可以用于数据的可视化，将高维数据转换为二维或三维空间，方便我们对数据进行观察和分析。
基于主成分分析法的水果成分含量分析（论文）
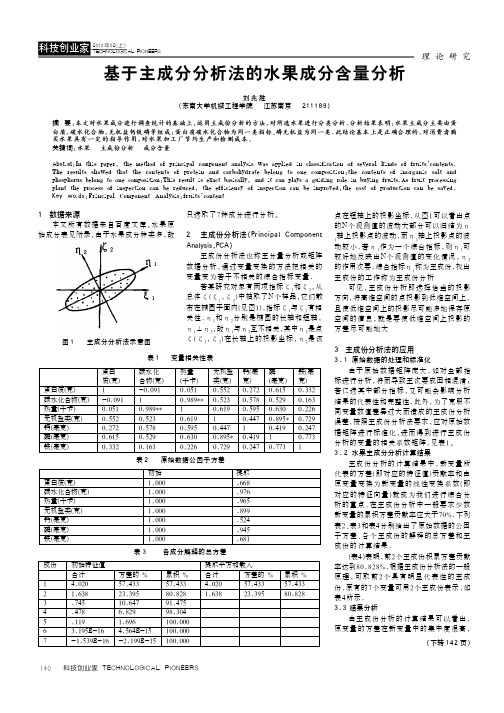
1 数据来源本文所有数据来自百度文库,水果原始成分表见附录,由于水果成分种类多,故只选取了7种成分进行分析。
2 主成份分析法(Principal Component Analysis,PCA)主成份分析法也称主分量分析或矩阵数据分析,通过变量变换的方法把相关的变量变为若干不相关的综合指标变量.若某研究对象有两项指标ζ1和ζ2,从总体ζ(ζ1,ζ2)中抽取了N个样品,它们散布在椭圆平面内(见图1),指标ζ1与ζ2有相关性.η1和η2分别是椭圆的长轴和短轴,η1⊥η2,故η1与η2互不相关.其中η1是点ζ(ζ1,ζ2)在长轴上的投影坐标,η2是该基于主成分分析法的水果成分含量分析刘兆胜(东南大学机械工程学院 江苏南京 211189)摘 要:本文对水果成分进行调查统计的基础上,运用主成份分析的方法,对所选水果进行分类分析.分析结果表明:水果主成分主要由蛋白质,碳水化合物,无机盐钙铁磷等组成;蛋白质碳水化合物为同一类指标、磷无机盐为同一类.此结论基本上是正确合理的,对消费者购买水果具有一定的指导作用,对水果加工厂节约生产和检测成本。
关键词:水果 主成份分析 成分含量Abstrat :In this paper, the method of principal component analysis was applied in classification of several kinds of fruits’contents.The results showed that the contents of protein and carbohydrate belong to one composition;the contents of inorganic salt and phosphorus belong to one composition;This result is exact basically, and it can plays a guiding role in buying fruits.As fruit processing plant the process of inspection can be reduced, the efficiency of inspection can be improved,the cost of production can be saved.Key words :Principal Component Analysis;fruits’content点在短轴上的投影坐标.从图1可以看出点的N个观测值的波动大部分可以归结为η1轴上投影点的波动,而η2轴上投影点的波动较小．若η1作为一个综台指标,则η1可较好地反映出N个观测值的变化情况,η2的作用次要．综合指标η1称为主成份,找出主成份的工作称为主成份分析可见,主成份分析即选择恰当的投影方向,将高维空间的点投影到低维空间上,且使低维空间上的投影尽可能多地保存原空间的信息,就是要使低维空间上投影的方差尽可能地大3 主成份分析法的应用3.1原始数据的处理和标准化由于原始数据矩阵庞大,如对全部指标进行分析,将而导致主次要成因相混淆;若仅选其中部分指标,又可能会影响分析结果的代表性和完整性.此外,为了克服不同变量数值差异过大而造成的主成份分析误差,按照主成份分析法要求,应对原始数据矩阵进行标准化,进而得到进行主成份分析的变量的相关系数矩阵,见表1。
关于主成分分析的常用改进方法论文
关于主成分分析的常用改进方法论文1. 核主成分分析（Kernel PCA）核主成分分析通过使用核技巧将线性PCA扩展到非线性情况。
它通过将数据从原始空间映射到一个高维特征空间，然后在高维空间中进行PCA，从而实现非线性降维。
核PCA可以更好地处理非线性关系，但计算复杂度较高。
2. 稀疏主成分分析（Sparse PCA）稀疏主成分分析是一种改进的PCA方法，旨在产生稀疏的主成分。
传统PCA生成的主成分是线性组合的数据特征，而稀疏PCA将主成分的系数限制在一定范围内，产生稀疏的解。
这样可以更好地捕捉数据的稀疏结构，提高降维效果。
3. 增量主成分分析（Incremental PCA）增量主成分分析是一种改进的PCA方法，用于处理大型数据集。
传统PCA需要一次性计算所有数据的协方差矩阵，如果数据量很大，计算复杂度就会很高。
增量PCA通过将数据分批进行处理，逐步计算主成分，从而减轻计算负担。
这样可以在处理大型数据集时实现更高效的降维。
4. 自适应主成分分析（Adaptive PCA）自适应主成分分析是一种改进的PCA方法，旨在处理具有时变性质的数据。
传统PCA假设数据的统计特性不会发生变化，但在现实世界中，许多数据集的统计特性会随着时间的推移而变化。
自适应PCA可以自动适应数据的变化，并更新主成分以适应新的数据分布。
5. 鲁棒主成分分析（Robust PCA）鲁棒主成分分析是一种改进的PCA方法，用于处理包含离群点或噪声的数据。
传统PCA对离群点和噪声十分敏感，可能导致降维结果出现严重偏差。
鲁棒PCA通过引入鲁棒估计方法，可以更好地处理异常值和噪声，提高降维结果的鲁棒性。
以上是常见的几种PCA的改进方法，每种方法都有其适用的场景和优缺点。
研究人员可以根据实际需求选择适合的方法，以实现更好的降维效果。
主成分分析方法范文
主成分分析方法范文在主成分分析中，我们将数据从一个高维空间映射到一个低维空间，同时保留数据的主要结构和方差信息。
这个低维空间的维度通常比原始数据的维度低，因此可以更方便地进行可视化和分析。
主成分分析的基本思想是通过线性组合来构建新的特征，使得投影后的数据具有最大的方差。
具体来说，假设我们有一个具有n个样本和m个特征的数据集，其中$n\geq m$。
我们的目标是找到k个正交的线性组合，将数据从m维空间映射到k维空间中。
这些线性组合被称为主成分，主成分的个数k通常比m小。
我们可以通过计算协方差矩阵来找到这些主成分，然后对协方差矩阵进行特征值分解，获得特征值和特征向量。
特征向量即为主成分，它们与特征值一起表示了数据的主要结构。
1.数据标准化：如果原始数据的特征具有不同的量纲或者度量单位，我们首先需要对数据进行标准化处理，使得每个特征的均值为0，方差为1、这样可以确保每个特征对结果的影响权重是相同的。
2.计算协方差矩阵：在将数据标准化后，我们计算标准化后的数据的协方差矩阵。
协方差矩阵的元素表示了数据中两个特征之间的相关性。
协方差矩阵是一个对称矩阵，对角线上的元素表示了每个特征的方差，非对角线上的元素表示了两个特征之间的协方差。
3.特征值分解：我们对协方差矩阵进行特征值分解，得到特征值和特征向量。
特征值代表了主成分的重要性，特征向量表示了主成分的方向。
4.选择主成分：我们按照特征值的大小对特征向量进行排序，选择k 个最大的特征向量作为主成分。
这些主成分按照重要性递减的顺序排列，第一个主成分解释了最大的方差，第二个主成分解释了次大的方差，以此类推。
5.获得映射矩阵：我们将选择的k个特征向量按列排列，构成映射矩阵，将原始数据投影到主成分空间中。
6.降维：最后，我们将原始数据乘以映射矩阵，得到降维后的数据。
这些降维后的数据具有较低的维度，但仍然能够保留原始数据的主要结构和方差信息。
在实际应用中，主成分分析也存在一些局限性。
主成分分析详解范文
主成分分析详解范文1.理论背景假设我们有一个n维的数据集，其中每个样本有m个特征。
我们的目标是找到一个k维的新数据集（k<m），使得新的数据集中每个样本的特征之间的相关性最小。
2.算法步骤（1）数据标准化：PCA对数据的尺度很敏感，因此首先需要对数据进行标准化，使得每个特征具有零均值和单位方差。
（2）计算协方差矩阵：协方差矩阵描述了数据中各特征之间的相关性。
通过计算协方差矩阵，可以得到原始数据的特征向量和特征值。
（3）特征值分解：将协方差矩阵分解成特征向量和特征值，特征向量可以看作是新数据空间的基向量，而特征值表示这些基向量的重要性。
（4）选择主成分：根据特征值的大小，选择前k个特征向量作为主成分。
（5）数据映射：将原始数据映射到主成分空间中，得到降维后的新数据。
3.主成分的物理解释主成分通常被认为是原始数据线性组合的结果。
第一个主成分是数据变化最大的方向，第二个主成分是和第一个主成分正交且变化次之大的方向，以此类推。
因此，主成分提供了原始数据的一个表示，其中每个主成分包含一部分原始数据的方差信息。
4.特征值与解释方差特征值表示每个主成分的重要性。
较大的特征值对应较重要的主成分。
通过特征值的比例，我们可以了解这些主成分对数据方差的解释程度。
通常，我们选择特征值之和的一部分来解释原始数据方差的比例（例如，90%）。
这样可以帮助我们确定保留多少个主成分，以在保持数据信息的同时降低数据维度。
5.应用场景主成分分析在许多领域都有广泛的应用，包括数据预处理，模式识别，图像处理等。
例如，在图像压缩中，我们可以使用PCA将图像从RGB颜色空间转换为YCbCr颜色空间，然后把Cb和Cr分量降维，从而减少图像的存储空间。
总的来说，主成分分析是一种常用的降维算法，通过找到数据中的主要特征，可以帮助我们减少数据的维度，简化计算和分析的复杂性，并在保持数据信息的同时减少噪声和冗余。
同时，PCA的应用还涉及到数据可视化、数据压缩和模式识别等领域，具有广泛的实际应用价值。
主成份分析因子分析毕业论文终稿
主成份分析因子分析毕业论文终稿学科分类号110 黑龙江科技大学本科学生毕业论文题目主成分与因子分析对黑龙江省城市经济发展水平的评价The principal components and factor analysisof urban economic development levelevaluation of heilongjiang province姓名学号院（系）理学院专业、年级数学与应用数学指导教师2014年6月12日摘要经济是指一个国家国民经济的总称。
我们要提高某地方人民的生活水平，要更好更快地发展某个地区，就必须充分了解这个地区现有的经济发展状况。
因此，现有的经济发展状况研究对将来的发展有着非常重要的指导意义。
主成分分析也称主分量分析，就是设法将原来指标重新组合成一组新的互相无关的几个综合指标来代替原来指标。
因子分析是主成分分析的推广和发展，它也是将具有错综复杂关系的变量综合为数量较少的几个因子，以再现原始变量与因子的相互关系，同时根据不同因子还可以对变量进行分类。
主成分分析与因子分析都是多元分析中处理降维的一种统计方法。
本文通过学习与查阅相关资料找到黑龙江省12个地级市的10个具有代表性指标，运用spss统计分析软件对这些指标进行主成分分析和因子分析得到特征值、方差贡献率及公共因子等相关数据。
并利用这些数据对12个市经济水平划分等级。
关键词主成分分析因子分析经济spss统计分析软件IAbstractEconomy refers to the floorboard of the national economy of a country. We will improve the level of a local people's life, to somewhere better and faster development, we must fully understand the current situation of economic development. Therefore, the existing research on the development of future economic development has a very important guiding significance.Principal component analysis (also called principal component analysis, is to try the original index combined into a new set of several comprehensive index instead of the original index has nothing to do with each other, at the same time, according to the actual need to recommend a few less comprehensive response as much as possible the original information of indicators. Is a generalization of the principal component analysis and factor analysis, it is also will have the intricate relationship between variables comprehensive to a small number of several factors, and to recreate the relationship of the original variables and factor, at the same time according to different factors can also categorize variables,. Principal component analysis and factor analysis is a multivariate analysis of a statistical method of dealing with the dimension reduction. In this article, through learning and access to relevant data found nine representative indexes of 12 cities in heilongjiang province, using the SPSS statistical analysis software to the indicators of principal component analysis and factor analysis of the characteristic value, the variance contribution rate and public factor and related data. And using the data of 13 cities economic grade level.Key words Principal component analysis Factor analysis Economic SPSS statistical analysis softwarII目录摘要 (I)Abstract (II)第1章绪论 (1)1.1 选题的背景和提出 (1) (1) (2)1.2 选题的意义和目的 (3) (3) (3)1.3 主成分分析和因子分析的发展及应用 (4) (4) (4)1.4 本文主要研究内容 (5)第2章主成分与因子分析 (6)2.1 主成分分析的内容 (6) (6) (6) (8)2.2 主成分分析的求解方法和数学模型 (8)2.3 主成分分析的基本步骤 (11)2.4 因子分析的内容 (13) (13) (13)III2.5 因子分析的求解方法和数学模型 (14) (14) (15) (16)2.6 计算步骤 (16)第3章主成分与因子分析在黑龙江省城市经济水平研究中的应用 (17)3.1主成分分析法 (18)3.2 因子分析法 (22)3.3 综合评价结果分析 (26)结论 (28)致谢 (29)参考文献 (30)IVContentsAbstract....................................................................................... 错误!未定义书签。
主成分分析论文
主成分分析论文简介主成分分析(Principal Component Analysis, PCA)是一种常用的数据分析和降维技术。
它是一种线性变换技术，通过寻找数据集中的主要分量来简化数据集。
主成分分析能够将高维度数据降维到低维度数据，并尽可能的保留原始数据的信息。
PCA的应用1.数据可视化：由于 PCA 能够将高维数据降至二维或三维空间，因此它能够帮助我们更好地理解数据集，并将其可视化展示。
2.数据压缩：PCA 通过降维的方式减少数据的冗余信息，并将其转化为更少的维度。
因此，PCA 可以作为数据压缩 techniq ，以减少数据集的存储和传输成本。
3.特征选取/提取：在机器学习中，选择最优的特征是一个非常重要的任务。
通过 PCA，我们可以将原始数据转化为一组新的、具有更好可表示性的特征，以提高模型的性能。
PCA的实现以下为 PCA 的实现步骤：1.数据预处理：去除均值，并进行归一化处理，使得每列数据的平均值为0。
2.计算数据的协方差矩阵：协方差矩阵反映了数据之间的相关程度。
3.特征值分解(Covariance Matrix Decomposition)：通过计算协方差矩阵的特征值和特征向量，来找到数据的主要成分。
4.选取主要成分：将特征值从大到小排序，并选取最大的k个特征值(也就是说，将数据降至k维)。
这些特征值所对应的特征向量便是 PCA 的主要成分。
5.将原始数据映射至新的低维度空间：使用所选的k个特征向量，将原始数据映射至新的低维度空间。
新的数据集将由选取特征向量所构成的矩阵和原始数据集相乘所得到。
PCA与其他降维方法的比较PCA和t-SNE的比较1.PCA 是一种线性方法，它假设数据之间具有线性关系。
而 t-SNE 则是一种非线性方法，它适用于非线性数据的降维。
2.PCA 可以更高效的计算，不同于 t-SNE 需要迭代多次。
当数据集的维度较高时，PCA 的运行速度优势更加明显。
3.PCA 是一种无监督 learning algorithm，而 t-SNE 则是一种有监督或半监督的算法。
主成分分析论文范文
主成分分析论文范文
PCA的基本思想是通过找到数据中变化最大的方向，将多维数据映射
到一个低维度的空间中。
在这个新的空间中，第一个主成分是原始数据中
方差最大的方向，第二个主成分是在第一个主成分之后方差最大的方向，
以此类推。
主成分具有不相关性，即它们之间的协方差为零。
PCA可以应用于很多领域，例如在图像处理中，可以使用PCA对图像
进行降噪和特征提取；在机器学习中，可以使用PCA进行特征选择和降维；在金融领域，可以使用PCA对资产组合进行优化等。
论文采用了一个跨行业的数据集，包含11家公司的股票价格数据和
11个与该公司相关的经济因素。
首先，论文对这些因素进行了主成分分析，并提取了前两个主成分。
然后，论文使用这两个主成分作为输入特征，建立了一个简单的线性回归模型来预测股票价格。
实验结果表明，使用主成分分析可以显著提高股票价格的预测准确性。
与传统的多元回归模型相比，使用主成分分析的模型具有更低的预测误差
和更好的稳定性。
此外，论文还进行了一些敏感性分析，结果显示主成分
分析的模型在不同的经济环境下都具有很好的适应性。
总的来说，这篇论文展示了主成分分析在股票价格预测中的应用，并
证明了其在提高预测准确性方面的有效性。
这些研究结果对于金融领域的
实践具有重要的意义，同时也为其他领域的数据分析和建模提供了启示。
以上是对一篇使用主成分分析进行股票价格预测研究的论文的综述。
这篇论文展示了主成分分析在实际问题中的应用，并证明了其在提高预测
准确性方面的有效性。
希望这篇论文可以对你了解主成分分析的应用和研
究方法有所帮助。
主成分分析论文
工业废水处理情况的主成分分析【摘要】工业废水的综合治理已成为当代环境工作亟待解决的重大问题之一。
工业废水的处理情况受工业废水达标排放量、化学需氧量排放量、氨氮排放量、废水治理设施数、废水治理费用等多因素的综合影响。
选取全国各主要城市的废水排放指标进行主成分分析。
研究结果表明：工业废水的达标排放量与工业废水处理情况成正相关；化学需氧量、氨氮排放量增加对于废水的排放起了重要作用。
工业废水处理设施数、废水治理费用越多，城市的废水处理情况越好。
【关键词】工业废水达标排放量；化学需氧量；氨氮排放量；主成分分析1问题的提出真正改变我国的环境质量，必须有效地治理各类污染源。
随着我国工业化和城市化的快速推进，废水种类和数量增加迅猛，对水体环境污染的压力加重，并威胁生态安全和居民健康。
从环境保护角度看，工业废水处理比城市污水处理更为复杂、更为重要。
随着“十二五”国家对节能减排工作的重视，积极引入市场机制，加大投资力度，污水处理能力快速增长，城镇污水处理设施的建设和运营对污染物减排的贡献率不断提升。
工业废水处理不能一概而论。
那么，工业废水处理情况与哪些问题密切相关呢？针对这些问题我们又能怎么处理呢？2相关研究成果工业污染的防治应从末端处理改变为源头控制，以达到节约资源、削减污染的目的30年来，工业污染控制的基本策略还是没有跳出末端处理的老框框。
“三同时”、“达标排放”指的就是建设工业内部的废水处理厂，达到工业废水排放标准。
这样的策略虽然可以起到一定的作用，但其费用效益比是很低的，而且不符合可持续发展的战略。
从工业生产的源头控制污染的产生，即通过实施清洁生产，包括改变产品设计、采用清洁原料、改革生产工艺、更新生产设备、循环使用物料、加强生产管理等，使资源的利用率尽量提高，污染物的产生量尽量减少，不仅可以获得环境效益，还可以因为降低成本而获得经济效益。
水污染防治应该实施工业、城市、点源、面源、内源、地面水、地下水同时控制的综合防治策略。
主成分分析讲解范文
主成分分析讲解范文PCA的基本原理是通过线性变换，将原始数据投影到一个新的坐标系统中。
在新的坐标系统中，数据的第一主成分是原始数据中方差最大的方向；第二主成分是与第一主成分正交的方向中方差最大的方向；以此类推，可以得到多个主成分。
通过选择合适的主成分个数，可以实现数据的降维。
首先，对原始数据进行标准化处理。
由于PCA是基于方差来进行计算的，所以数据的尺度对结果有很大的影响。
为了消除量纲的影响，需要对原始数据进行标准化处理，保证各个特征变量具有相同的尺度。
其次，计算协方差矩阵。
协方差矩阵是一个对称的矩阵，描述了数据集中各个特征变量之间的相关性。
它的对角线上的元素表示各个特征变量的方差，非对角线上的元素表示各个特征变量之间的协方差。
然后，求解特征值和特征向量。
将协方差矩阵进行特征值分解，得到特征值和对应的特征向量。
特征值表示了各个主成分方向上的方差，特征向量表示了原始数据在各个主成分方向上的投影。
接下来，选择主成分。
根据特征值的大小排序，选择前k个特征值对应的特征向量作为主成分。
一般可以根据特征值的累计贡献率来确定选择多少个主成分。
累计贡献率表示了选择前k个主成分能够保留的原始数据的信息量。
最后，进行数据重构。
通过将原始数据投影到选取的主成分上，可以得到降维后的数据。
数据重构可以通过将主成分乘以系数再相加的方式来实现。
总而言之，主成分分析是一种常用、有效的数据降维技术。
通过保留原始数据的主要信息，它可以将高维度的数据转化为低维度的数据，方便数据分析和数据可视化。
但需要根据具体情况来选择合适的主成分个数，并注意不同情况下PCA的限制。
主成分分析法2篇
主成分分析法2篇
第一篇：主成分分析法概述
主成分分析法（Principal Component Analysis，PCA）
是一种基于数学统计学的数据分析方法，主要应用于减少数据维度和探测相互关系。
该方法最初由卡尔·皮尔逊（Karl Pearson）在1901年提出，并在1933年由霍特（Hotelling）进一步完善。
主成分分析法的核心思想是将高维空间中的数据降维到
低维空间中，尽量保留原始数据的信息。
其中，主成分便是指数据在低维空间中的最大方差方向。
在PCA中，首先需要对原始数据进行中心化（也叫标准化），即将数据平移至坐标原点。
然后，通过数学模型寻找数据最大方差的方向，作为第一主成分。
随后，找到与第一主成分方向正交的第二主成分，再寻找与前两个主成分正交的第三主成分，依次类推，直到找到所有主成分。
主成分分析法可以用于多个方面，比如：1、数据降维——当原始数据拥有很多维度时，主成分分析法可以将数据降维到更低的维度，从而更轻松地对数据进行分析；2、数据可视化——通过只保留主成分来绘制散点图或者折线图，从而更加清晰地展示数据特征；3、数据预处理——主成分分析法可以
去除特定维度的噪声和冗余，使得后续算法更加稳定和可靠。
当然，在应用主成分分析法时需要遵循一些基本原则：1、要保证数据满足线性或近似线性；2、要进行数据中心化和标
准化；3、需要进行主成分选取和分析。
总之，主成分分析法是一种十分广泛应用的分析方法，它不仅可以用来降维和可视化，还可以在多个领域中发挥重要的作用。
主成分分析论文
利用主成分分析对我国某省物流产业发展的综合评价【摘要】现代物流的发展程度已经逐渐成为衡量一个区域或国家现代化程度和综合竞争力的 重要标志之一。
物流产业的实质体现为技术密集和劳动密集相结合 ,是具有第三产业特征的 跨地区、跨行业、跨部门特点的产业形式。
物流产业对经济增长,特别是区域经济增长和区域产业协作的推动 ,都有着不可替代的重大意义 ,在区域经济、 产业布局研究过程中 ,都不能忽 视物流产业在其中的基础保障作用。
本文在构建江苏省沿江地区物流产业发展综合指标体系 的基础上，运用多元统计分析中的主成分分析方法，对江苏省沿江地区 20 个地市的物流发 展现状进行了综合评价， 为江苏省各地市物流产业主管部门制定相应政策提供一定的理论依 据，旨在提高江苏省沿江地区整体物流发展水平。
【关键词】主成分分析 物流产业 综合评价一．研究背景经济的快速增长对物流业产生了巨大的需求 ,促使物流业以及与物流相关的交通运输、 仓储配送和邮电通信业等都有较快的发展。
同时,作为经济增长的 “加速器 ”物流业的快速发展将会改变国民经济增长方式 ,降低国民经济的运行成本 ,促进了经济的可持续发展。
物流对 于经济增长的影响以及物流业与经济增长之间的关系已经成为物流领域的一个研究重点。
本 文拟从主成分分析的角度出发，以江苏省数据为例来探讨哪些因素是物流发展的主要因素， 对江苏省物流产业发展现状进行综合评价， 从而为江苏省乃至全国的物流产业的发展提供一 定的启示。
二．主成分分析方法介绍主成分分析是把原来多个变量化为少数几个综合指标的一种统计分析方法， 来看，这是一种降维处理技术。
假定有 n 个地理样本，每个样本共有 p 个变量描述，这样就 构成了一个 n ×p 阶的数据矩阵：如何从这么多变量的数据中抓住主要的变量指标呢？要解决这一问题， 自然要在 p 维空 间中加以考察， 这是比较麻烦的。
为了克服这一困难，就需要进行降维处理，即用较少的几 个综合指标来代替原来较多的变量指标， 而且使这些较少的综合指标既能尽量多地反映原来 较多指标所反映的信息，同时它们之间又是彼此独立的。
如何运用主成分分析法进行毕业论文的研究
如何运用主成分分析法进行毕业论文的研究毕业论文是研究生阶段的重要成果之一，为了得到准确可靠的研究结果，研究者需要选择合适的研究方法和工具。
主成分分析（Principal Component Analysis，PCA）作为一种常用的多变量分析方法，在毕业论文的研究中具有广泛的应用价值。
本文将介绍如何运用主成分分析法进行毕业论文的研究，并探讨其优势和注意事项。
一、主成分分析的基本原理主成分分析是一种通过线性变换将多个相关变量转化为一组无关变量的统计方法。
通过寻找变量之间的线性关系，主成分分析能够将高维数据降维为低维数据，并尽可能保留原始数据的信息。
在毕业论文的研究中，主成分分析可以用于数据的降维、变量的选择和数据的可视化等方面，为研究者提供了更多的分析手段和思路。
二、如何应用主成分分析进行毕业论文的研究1. 数据预处理在进行主成分分析之前，需要对原始数据进行预处理。
这包括数据的清洗、缺失值的处理以及数据的标准化等。
清洗数据可以去除异常值和离群点，以减少其对主成分分析结果的影响。
处理缺失值可以采用插补方法，如均值插补或回归插补。
数据标准化可以使各个变量具有相同的尺度，以避免某些变量对主成分的贡献过大。
2. 提取主成分主成分分析的核心是提取主成分，即将原始变量通过线性组合得到一组新的变量。
这些新变量具有以下特点：相互之间无相关性、依次按照方差的大小排列、每个主成分都能够解释原始变量的一部分方差。
在提取主成分时，可以根据特征值和累计方差贡献率进行选择，通常选择特征值较大的主成分或累计方差贡献率达到一定阈值的主成分。
3. 解释和解读主成分提取主成分后，需要对主成分进行解释和解读。
通过查看主成分的载荷矩阵，可以了解原始变量对每个主成分的贡献程度。
载荷矩阵中的每个元素表示相应主成分与原始变量之间的相关系数，绝对值越大表示相关性越高。
通过解释主成分的含义，可以深入理解数据背后的规律和特征。
三、主成分分析的优势和注意事项1. 优势主成分分析在毕业论文的研究中具有以下优势：（1）降维：主成分分析可以将高维数据降为低维数据，减少变量的数量，便于统计分析和解释。
主成分分析法在论文中的运用分析
主成分分析法在论文中的运用分析主成分分析法是将多指标化为少数几个综合指标的一种统计方法。
它从原始变量中导出少数几个主分量，使它们尽可能多地保留原始变量的信息，且彼此互不相关。
它常被用来寻找判断某种事物或现象的综合指标，并且给综合指标所包含的信息以适当的解释，从而更加深刻地揭示事物的内在规律，因此在学术界得到了广泛应用。
本次作业拟分析主成分分析法在文章《基于主成分分析法的科技进步测评实证研究——以陕西省为例》、《基于主成分分析法的京津冀区域协调发展综合评价》中的具体应用，以此明晰主成分分析法的具体应用情形、运用过程与结果分析，进一步强化理论学习效果。
《基于主成分分析法的科技进步测评实证研究——以陕西省为例》1一文在建立科技进步评价指标体系的基础上，利用主成分分析法对包括陕西在内的全国内地30个省、市、区科技竞争力进行排序，分析陕西在科技发展水平方面与全国整体水平及其它发达省市的差距，为陕西制定有关科技政策提供依据。
文章首先建立了科技进步评价指标体系，立足于广义的科技进步建立了一套综合性的科技进步统计评价指标体系，涉及工业、农业、人才、环保、邮电等社会活动的许多面，不仅体现了科技投入、产出、成果转化，而且也反映了科技进步促进经济社会发展，整个指标体系为三阶层框架结构，其基本内容包括5个模块、13个子项、30个指标。
文章第二部分介绍了科技进步的综合测评方法——主成分分析法，详细介绍了期优点及主要步骤，将采用主成分分析法分析陕西科技发展水平与全国整体科技发展水平及其它发达省市科技发展水平的差距。
文章第三部分是基于主成分分析法的科技进步测评实证研究。
文章在SPSS14.0中输入正确数据后，对9个指标进行标准化处理，再利用SPSS中的factor命令对数据进行主成分分析，由于前两个主成分累计贡献率为93.949%≥85%，所以提取的主成分个数为两个，得出主成分系数矩阵。
把主成分系数矩阵中的每列系数矩阵除以其相应的特征根后，得到主成分函数的表达式F1与F2。
主成分分析论文 孟向前
部分上市公司财务绩效的主成分分析08数学1班孟向前 0807021036摘要为了全面地科学地评价我国2011年4月份部分上市公司的财务绩效状况，我们将借助SAS软件对其进行主成分分析分析。
选取6项经济指标，对上市公司的财务绩效进行综合分析，并提出了目前我国上市公司存在的问题并给出提高财务绩效的相关措施。
【关键词】财务绩效主成分分析上市公司存在问题相关措施1、研究意义上市公司的财务绩效是指上市公司在一定期间的盈利能力、资产质量、债务风险和经营增长四个方面的有关信息。
了解了不同上市公司的财务绩效，有利于投资者等信息使用者据以评价企业盈利能力、预测企业成长潜力、进而做出更加准确的相关经济决策。
2、相关研究成果由于主成分分析方法能浓缩信息，简化指标的结构,使分析问题的过程简单、直观、有效,故广泛应用于各个领域。
人们经常利用主成分分析方法综合评价企业或事业单位的经济效益、技术进步状况,并收到了良好的效果。
它的主演研究成果有：1．有时可通过因子负荷的结论，弄清变量间的某些关系。
2．多维数据的一种图形表示方法。
我们知道当维数大于3时便不能画出几何图形，多元统计研究的问题大都多于3个变量。
要把研究的问题用图形表示出来是不可能的。
然而，经过主成分分析后，我们可以选取前两个主成分或其中某两个主成分，根据主成分的得分，画出n个样品在二维平面上的分布况，由图形可直观地看出各样品在主分量中的地位，进而还可以对样本进行分类处理，可以由图形发现远离大多数样本点的离群点。
3．由主成分分析法构造回归模型。
即把各主成分作为新自变量代替原来自变量x做回归分析。
4．用主成分分析筛选回归变量。
回归变量的选择有着重的实际意义，为了使模型本身易于做结构分析、控制和预报，好从原始变量所构成的子集合中选择最佳变量，构成最佳变量集合。
用主成分分析筛选变量，可以用较少的计算量来选择量，获得选择最佳变量子集合的效果。
3、方法介绍3.1 主成分分析，又称主分量分析，是指将原始的多个变量，通过线性组合，提炼出较少几个彼此独立的新变量的一种多元统计分析方法。
主成分分析法(论文)
主成分分析法(论文)摘要：本文介绍主成分分析法（PCA）的基本原理、数学模型、以及应用领域，详细阐述了PCA在多变量统计分析、图像处理、模式识别等领域中的应用。
通过实例分析，展示了PCA在数据降维、去噪、特征提取等方面的应用优势。
最后，对PCA的优缺点进行了总结，展望了其未来的研究方向。
关键词：主成分分析；多变量统计分析；图像处理；模式识别1. 简介主成分分析法（PCA）是一种常用的数据分析方法，它是对多个相关性较高的变量进行线性组合，得到一组无关的新变量，这些新变量称为主成分。
主成分是原变量的线性组合，具有较强的统计意义，能够反映出原变量的主要信息，同时可以用较少的变量来描述原数据。
因此，PCA被广泛应用于多变量统计分析、图像处理、模式识别等领域。
2. 基本原理PCA的核心思想是将原始数据转化成一组线性不相关的主成分，即通过正交变换将原数据转化成具有更好的可解释性和更小的冗余性的形式。
这种变换的基本思路是将原始数据进行协方差矩阵分解，使得矩阵的特征向量可以表示出新的主成分，特征值可以表示出每个主成分的贡献率。
假设原数据为一个m维随机向量X，每一维的方差为σ1^2, σ2^2, ..., σm^2，协方差矩阵为C。
则PCA的目标是寻找一个线性变换矩阵W，使得变换后的数据Y=WX具有以下特征：- Y的各维度变量之间彼此独立- Y的第一维度变量拥有最大的方差，并且是C的最大特征值所对应的特征向量- Y的第二维度变量拥有次大的方差，并且是C中第二大特征值所对应的特征向量- 以此类推，Y的每一维度变量都是协方差矩阵C对应的特征向量3. 数学模型对于一个具有n个样本和m个特征的数据集，其中每一行表示一个样本，每一列表示一个特征，则PCA的数学模型可以表示为以下步骤：1. 标准化数据：对每个特征进行标准化处理，即将每个特征的均值设为0，方差为1，使得不同特征之间具有可比性。
2. 计算协方差矩阵：计算数据集的协方差矩阵C，即其中x为m维列向量，X为n*m的数据矩阵，XT为X的转置。
SPSS因子分析和主成分分析论文【范本模板】
基于因子分析的我国经济发展状况实证分析摘要：选取了2013年我国31个省、直辖市、自治区经济发展的10项指标作为研究对象,运用因子分析的方法,利用spss对数据进行计算，依据因子分析的结果对我国各省的经济发展做出综合评价，得出了这31各省份经济发展状况的综合排名，广东、江苏、山东、浙江、北京排在前5位，是中国各省、直辖市、自治区沿海经济发展较好的地区;甘肃、海南、青海、宁夏、西藏排在后5位，是西部地区经济发展较落后的地区，较为客观反映了中国各省、直辖市、自治区的综合经济实力，为中国各省、直辖市、自治区今后的经济发展提供了理论依据。
关键词：经济发展；因子分析；综合评价；主成分法一、引言我国地域辽阔,由于历史、地理位置及经济基础等原因，各地经济发展水平差异很大。
改革开放以来，特别是实施西部大开发、振兴东北地区等老工业基地、促进中部地区崛起、鼓励东部地区率先发展的区域发展总体战略以来，各地经济社会发展水平有了很大提高，人民生活也有了很大改善。
但区域发展不协调、发展差距拉大的趋势仍未根本改变。
本文从我国31 个省市自治区经济的发展视角入手，运用对应分析方法对我国各地区经济发展状况进行统计分析，用以说明我国各地区经济发展不协调的现状。
由于衡量各地区经济发展的指标有很多，故选取了比较有代表性的十个指标。
二、相关统计指标与数据的选取本文运用了因子分析的方法对我国31个省、直辖市、自治区的经济发展状况进行评价。
选取了10项经济指标：第一产业增加值（X1）；第二产业增加值（X2）；第三产业增加值（X3）;地方财政预算收入（X4)；地方财政预算支出（X5）；固定资产投资额（X6）；社会消费品零售总额（X7)；货物进出口总额(X8)；在岗职工平均工资（X9）;城乡居民储蓄年末余额（X10）.X2，X3，X4 反映的是经济总量中构成三大产业的不同增加值；X5,X6 反映的是地方财政预算收支；X7 反映的是居民的购买能力；X8反映的是对外贸易;X9，X10反映的是居民的收入与储蓄.本文数据资料来源于《中国统计年鉴》（2013年）,具体数据资料见表1。
主成分分析法范文
主成分分析法范文PCA的计算过程可以分为以下几个步骤：1.数据标准化：对原始数据进行标准化处理，将各个特征的尺度调整为相同的范围，防止一些特征的取值范围过大造成不必要的干扰。
2.计算协方差矩阵：对标准化后的数据计算其协方差矩阵。
协方差矩阵描述了数据之间的相关性，一般而言，协方差越大表示两个特征之间的相关性越强。
3.计算特征值和特征向量：对协方差矩阵进行特征值分解，得到特征值和特征向量。
4.选择主成分：按照特征值的大小，选择前几个特征值对应的特征向量作为主成分。
特征值越大表示该主成分保留了更多的数据方差。
5.数据投影：将原始数据投影到选择的主成分上，得到降维后的数据。
PCA的主要思想是通过找到一组新的坐标系，使得数据在新坐标系中的方差尽可能大。
由于协方差矩阵是对称矩阵，故存在若干正交的特征向量，这些特征向量称为主成分。
在选择主成分时，通常会根据特征值的大小进行排序，选取前几个特征值对应的特征向量。
降维是PCA的一个重要应用。
当数据维度较高时，往往存在冗余信息，而且高维数据的处理与可视化较为困难。
通过PCA可以将高维数据映射到低维空间中，保留主要特征的同时减少数据的维度，从而方便后续的分析和处理。
另外，PCA还可以用于特征选择。
在一些机器学习任务中，特征的数量往往远大于样本的数量，这样容易导致过拟合问题。
通过PCA可以将特征空间从原始的高维空间转换到低维空间，同时保留了原始数据的主要特征，将维度降低到一个较合适的范围。
此外，PCA还可以用于数据压缩。
通过PCA将高维数据映射到低维空间，可以实现对数据的压缩，减少存储空间和计算开销。
综上所述，主成分分析是一种常用的数据分析方法，可以通过降维、特征选择和数据压缩等手段来提取数据的主要特征，帮助解决高维数据分析中的问题。
在实际应用中，我们需要根据具体的问题和需求，合理选择PCA的使用方式和参数。
原创 数据分析课程设计--主成分分析论文
原创数据分析课程设计--主成分分析论文原创数据分析课程设计--主成分分析论文* * 大学数据分析课程设计论文题目：我国各省市自治区社会发展的综合状况指标分析学院: 专业: 姓名: 学号:我国各省市自治区社会发展的综合状况一个地区的全面发展必须使经济和社会协调发展。
为了全面衡量社会发展水平, 有必要选择一套能反映社会发展的有代表性的社会指标进行综合评价，对每个地区的社会发展水平进行测量分析, 我们根据各地区统计指标, 选择了有代表性的社会经济指标, 包括城镇居民可支配收入、农村居民可支配收入、在校学生数、学校数、卫生机构数、固定资产投资总额等方面数据进行综合考察，利用主成分分析方法对各地区综合发展状况进行评价。
论文中主要运用的方法是主成份分析法。
主成份分析法的目的是利用降维的思想，把多指标转化为少数几个综合指标。
分析出主成分后，对数据进行综合排名，能较直观的反应社会发展的综合状况，便于分析各省市自治区的社会发展情况和影响因素。
关键词：各省自治区社会发展综合状况指标主成分分析排名一、问题的提出………………………………………………… 4 二、基于主成份分析的社会发展综合状况指标的筛选2.1原理概述 (4)2.1.1主成分分析的一般数学模型.............................. 4 2.1.2主成分分析确定的一般原则.............................. 5 2.1.3主成分分析的基本步骤 (5)2.1.4主成分分析得到的主成分与原始变量之间的关系 (5)2.2 原始数据及来源......................................................... 6 2.3 对指标的主成分分析及筛选....................................... 7 2.3.1 操作过程 (7)2.3.2 实验结果输出 (8)2.3.3 实验结果分析……………………………………… 12 三、总结………………………………………………………… 14 参考文献..................................................................... 16 附录 (16)第一章问题的提出中国的经济和社会的发展如何让才能踏上一条内外和谐、全面增长的稳健之路，不但攸关中国自身的利益，也成为举世瞩目的焦点。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
高校人文社科科研综合实力评价研究
摘要
一、问题重述
高校人文社科科研综合实力评价研究
根据所给数据，并搜集更多相关数据，回答下面的问题
1.研究数据之间的内在关系；
2.设计几种方案对各省市科研实力进行综合评价并进行分类，论证方法的合
理性，给出合适的建议
二、条件假设
（1）假设高校人文社科科研指标在一定程度上会反映高校的人文社科科研综合实力
（2）假设资料所提供数据准确有效
三、符号约定x—同一葡萄酒样品的平均值
_
四、问题分析
3.主成分分析法
建立模型：基于主成分分析法研究高校人文社科科研综合实力
影响高校人文社科科研综合实力的成分有很多，例如投入的人年数，投入科研事业经费，课题总数等等。
常用于研究各变量对结果影响因素的方法有多元回归分析、主成分分析、因子分析、回归分类树等。
每种算法各有各的特点，本文尝试选取主成分分析法。
主成分分析：PCA 是将多指标重新组合成一组新的无相关的几个综合指标，是根据实际需要从中选取尽可能少的综合指标，以达到尽可能多地反应原指标信息的分析方法。
由于这种方法的第一主成分在所有的原始变量中方差最大，因而综合评价函数的方差总不会超过第一主成分的方差，所以该方法有一定的缺陷。
（1）题中共给影响高校人文社科科研综合能力的7种因素，分别是投入人年数、投入高级职称的人年数、投入科研事业费、课题总数等。
设各影响因素为
p 2,1,...,x x x ，它们的综合指标——主成分设为：p ,,...,,21<m z z z m 其中，则
⎪⎩⎪
⎨
⎧+++=+++=p p 2
211p 12121111 (x)
l x l x l z l x l x l z m m m m m z z z ,...,,21分别为原变量指标p 21,...,,x x x 的第一，第二，…,第m 个主成分。
（2）对原始数据进行标准化处理
由于原始数据的量纲不同，为了使不同量纲的数据能够进行运算，故对数据进行标准化处理。
设有随机变量x 1，x 2，…，x p ， 其样本均数记为1x ，2x ，…，
p x ，样本标准差记为S 1，S 2，…，S p 。
首先作标准化变换
（3）计算相关系数矩阵，对应的特征值p λλλ,...,,21（按从小到大排列）及其对应的特征向量
S
X
X x -=
⎥⎥⎥⎥⎥⎦
⎤⎢⎢⎢⎢⎢⎣⎡=pp p p p p r r r r r r r r r R ......................212222111211，其中∑∑∑----===n
k
j
kj n
k i ki j kj n
k i ki
ij x x x x
x x x x
r 2
21
1
()()
()(）
（4）计算主成分贡献率及累计贡献率 主成分i z 的贡献率为：
),...,2,1(1
p i p
k k
i
=∑=λ
λ
累计贡献率为：
),...,2,1(11
p i p
k k
i
k k
=∑∑==λ
λ
一般取累计贡献率达85%左右的特征值m λλλ,...,,21，对应第一、二，…,
)(p m m ≤个主成分。
（5）根据第一主成分的得分对高校人文社科科研综合实力进行评价
模型求解：
一般认为，在主成分分析法中，主成分的累计特征值占特征值总和的85%左右时，即可视为第一、二……主成分。
根据题中所给数据，在SPSS 中进行主成
提取方法：主成份分析。
根据表格结果可知，第一项的累计贡献率就达85.631%，故投入人年数即为影响高校人文社科科研综合实力的第一主成分。
该省投入人年数越高，则其省内所有高校人文社科科研综合实力越强。
仅按第一项因素排序，可得排名前三位的省份分别是：北京（6795.0）、江苏（5480.0）、湖北（4427.0），排名较落后的三位分别是：海南（163.0）、青海（159.0）、西藏（75.0）。