大学物理(1.3.2)--圆周运动与一般平面曲线运动
合集下载
大学物理学_第一章运动学
解 (1)因为
分离变量得
因为t＝0时，v＝ ， 所以
.代入，并整理得
再由dx=vdt，将v的表达式代入，并取积分 因为t=0时，x=0，所以C2=0.于是
(2)因为 所以有 分离变量，并取积分
因为x＝0时，v＝ ，所以
代入，并整理得
练习 质点沿x轴运动，其加速度和位置的关系为 a＝2+6x2，a的单位为ms-2，x的单位为 m. 质点在x ＝0处，速度为10 ms-1,试求质点在任何坐标处的 速度值．
大家好
大学物理学
绪论
a. 为什么要学？ b. 学什么？ c. 怎样学好？
一、为什么要学习大学物理？
1. 物理学是工程技术的重要支柱 2.物理学是一切自然科学的基础 3.物理学是创新思想的源泉
二、学什么？
物理学是研究物质运动规律及其相互作用的科学。 万物之理
“运动是物质的存在形式，物质的固有属性”。——《自然辩证法》
1.5 运动学中的两类问题
1、已知运动方程，求速度、加速度(用求导法 )
2、已知加速度(速度)，初始条件，求速度(运动方程)(用积分的 方法)
设初始条件为 ：t = 0 时，x=x0，v = v0
例1.3 已知一质点的运动方程为r＝3ti－ 4t2 j，式中r以m计， t以s计，求质点运动的轨道、速度、加速度.
点，运动方向为弧坐标轴正
方向。
a
设 t = 1s时质点运动至P O 点，在P点建立 和 坐标 轴，因已知运动规律为
S＝30t t2
R＝500m
R S
n
an
v
P
a
解：弧坐标 S = 30t t2
由速度公式
R S
n
a
分离变量得
因为t＝0时，v＝ ， 所以
.代入，并整理得
再由dx=vdt，将v的表达式代入，并取积分 因为t=0时，x=0，所以C2=0.于是
(2)因为 所以有 分离变量，并取积分
因为x＝0时，v＝ ，所以
代入，并整理得
练习 质点沿x轴运动，其加速度和位置的关系为 a＝2+6x2，a的单位为ms-2，x的单位为 m. 质点在x ＝0处，速度为10 ms-1,试求质点在任何坐标处的 速度值．
大家好
大学物理学
绪论
a. 为什么要学？ b. 学什么？ c. 怎样学好？
一、为什么要学习大学物理？
1. 物理学是工程技术的重要支柱 2.物理学是一切自然科学的基础 3.物理学是创新思想的源泉
二、学什么？
物理学是研究物质运动规律及其相互作用的科学。 万物之理
“运动是物质的存在形式，物质的固有属性”。——《自然辩证法》
1.5 运动学中的两类问题
1、已知运动方程，求速度、加速度(用求导法 )
2、已知加速度(速度)，初始条件，求速度(运动方程)(用积分的 方法)
设初始条件为 ：t = 0 时，x=x0，v = v0
例1.3 已知一质点的运动方程为r＝3ti－ 4t2 j，式中r以m计， t以s计，求质点运动的轨道、速度、加速度.
点，运动方向为弧坐标轴正
方向。
a
设 t = 1s时质点运动至P O 点，在P点建立 和 坐标 轴，因已知运动规律为
S＝30t t2
R＝500m
R S
n
an
v
P
a
解：弧坐标 S = 30t t2
由速度公式
R S
n
a
大学物理—曲线运动-PPT
度（绳子不可伸长）
θ l
x
h
0 车
解：人的速度为
0
dx dt
车前进的速率
车
dl dt
4
l 2 x2 h2
2l dl 2 dx x dt dt
车
x l
0
0x
x2 h2
d车
dt
0
x2 h2
dx dt
0
x
d dx
(
1 dx )
x2 h2 dt
d车
dt
2 0
(
1 x2 h2
x2 )
( x2 h2 )3
上海：v 398 (m / s), a 2.89 102 (m / s2 ) n
广州：v 428
(m /
s),
a n
3.10 102
(m / s2)
26
线量与角量之间的关系
例题2 一质点沿半径为R的圆周按规律 s v0t bt 2 / 2 运
动，v0、b都是正的常量。求：
（1） t 时刻质点的总加速度的大小； （2） t 为何值时，总加速度的大小为b ； （3）当总加速度大小为b 时，质点沿圆周运行了多少圈。
d. 运动物体的速率不变时，速度可以变化。
30
31
课后作业： 1-6，1-7，1-8
32
an
lim n
t0 t
lim
t0
t
n0
an
d
dt
n0
an
d
ds
ds dt n0
2
d
ds
n0
k d
ds
1 ds k d
an
2
n0
1
θ l
x
h
0 车
解：人的速度为
0
dx dt
车前进的速率
车
dl dt
4
l 2 x2 h2
2l dl 2 dx x dt dt
车
x l
0
0x
x2 h2
d车
dt
0
x2 h2
dx dt
0
x
d dx
(
1 dx )
x2 h2 dt
d车
dt
2 0
(
1 x2 h2
x2 )
( x2 h2 )3
上海：v 398 (m / s), a 2.89 102 (m / s2 ) n
广州：v 428
(m /
s),
a n
3.10 102
(m / s2)
26
线量与角量之间的关系
例题2 一质点沿半径为R的圆周按规律 s v0t bt 2 / 2 运
动，v0、b都是正的常量。求：
（1） t 时刻质点的总加速度的大小； （2） t 为何值时，总加速度的大小为b ； （3）当总加速度大小为b 时，质点沿圆周运行了多少圈。
d. 运动物体的速率不变时，速度可以变化。
30
31
课后作业： 1-6，1-7，1-8
32
an
lim n
t0 t
lim
t0
t
n0
an
d
dt
n0
an
d
ds
ds dt n0
2
d
ds
n0
k d
ds
1 ds k d
an
2
n0
1
大学物理-圆周运动
§1-6 圆周运动
圆周运动是曲线运动的一个重要特例 圆周运动中质点的速度的大小和方向都在改变
存在两个加速度
法向加速度（速度方向变化引起） 用 an 表示 切向加速度（速度大小变化引起） 用 at 表示
一．匀速率圆周运动
质点作匀速率圆周运动时，速
度大小不变，方向改变，只有 法向加速度用 an
a
a
lim v lim sv
解：v dS / dt b ct
a dv / dt c t
a b ct2 / R n
根据题意： at= an
c b ct2 / R
t Rb cc
三、一般曲线运动
总加速度
a
a
n
a
t
v2 R
e
n
dv
dt
e
t
用曲率半径 代替R
在曲线上某一点找到一个 和它内切的半径最大的圆， 这个圆的半径就定义为曲 率半径。
v vn vt
lim
vn
lim
v t
t t 0
t t 0
a a
n
t
法向加速度
an
v2 RΒιβλιοθήκη v2 v1or
v vt v2vn v1
切向加速度
at
lim vt t vt
t 0
t
dv dt
a t 大小
at
dv dt
a t 方向
v 当 v2 v1 时, a t 与 方向一致
v2 v1
o
r
v 当 v2 v1 时, a t 与 方向相反
总加速度
aa a
n
t
v2
e
dv
e
R n dt t
圆周运动是曲线运动的一个重要特例 圆周运动中质点的速度的大小和方向都在改变
存在两个加速度
法向加速度（速度方向变化引起） 用 an 表示 切向加速度（速度大小变化引起） 用 at 表示
一．匀速率圆周运动
质点作匀速率圆周运动时，速
度大小不变，方向改变，只有 法向加速度用 an
a
a
lim v lim sv
解：v dS / dt b ct
a dv / dt c t
a b ct2 / R n
根据题意： at= an
c b ct2 / R
t Rb cc
三、一般曲线运动
总加速度
a
a
n
a
t
v2 R
e
n
dv
dt
e
t
用曲率半径 代替R
在曲线上某一点找到一个 和它内切的半径最大的圆， 这个圆的半径就定义为曲 率半径。
v vn vt
lim
vn
lim
v t
t t 0
t t 0
a a
n
t
法向加速度
an
v2 RΒιβλιοθήκη v2 v1or
v vt v2vn v1
切向加速度
at
lim vt t vt
t 0
t
dv dt
a t 大小
at
dv dt
a t 方向
v 当 v2 v1 时, a t 与 方向一致
v2 v1
o
r
v 当 v2 v1 时, a t 与 方向相反
总加速度
aa a
n
t
v2
e
dv
e
R n dt t
大学物理 第一章(1)
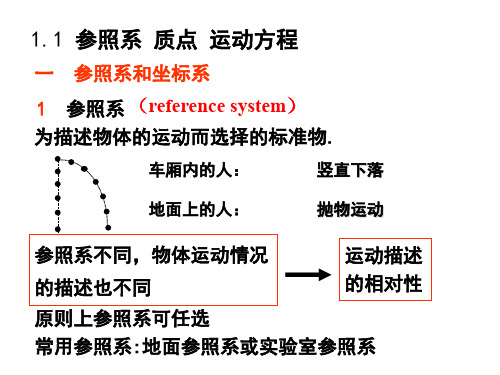
a
v2 R
n0
dv dt
t0
R―曲率半径
思考 求抛体运动过程中的曲率半径？
如B 点 at 0 , an g ,v B v 0cosθ
RB
v2
B an
(v 0cosθ)2
g
y v
B
思考
· a4 v
· a1
a·2
O
a3
O
x C
上图中分别是什么情形？ a4情形是否存在？
(2)物体各点运动情况相同
本课程力学部分,除刚体外,一般都可视为质点.
2 位置矢量（position vector of a particle）
表征某时刻质点位置的矢量, 简称位矢或矢径
r xi yj zk
r 位矢 的大小:
y
r r x2 y2 z2 r 位矢 的方向余弦:
a
ddtv
20
2
sin2ti
16
2
t 1s
cos 2tj
dt
t 1s
16 2 j (m / s2 )
x 5 sin2t
x2 y2
{
y 4 cos 2t
52 42 1
解题思路：
位移（求矢量差）
1 运动方程 轨道 方程（消去t）
：
an
v2 R
n0
（改变速度方向）
切向加速度(tangential acceleration)
：at
dv dt t0
v
aτ
（改变速度大小）
v2 dv a R n0 dt t0
大学物理 第一章 第一节 质点运动的描述
素，使问题简化但又不失客观真实性的一抽象思维方法；
质点、刚体、线性弹簧振子、理想气体、点电荷及光滑平
面、细绳、无阻尼振动、绝热过程等。
• 3、思考题: 地球可否看作质点？为什么?
6
※ 确定质点位置的方法
• 1、参考系：描述物体运动时被选作参考的其他物体或 物体系，称为“参考系” 或“参照系” 。
• 2、确定质点相对于参考系位置的方法
x
7
※ 运动(学)方程
用以确定在选定的参考系中质
z
z( t )
·P( t )
点相对坐标系的位置随时间变化 的数学表达式：
x x(t) , y y(t) , z z(t) , r r (t) , s f (t)
r( t )
·^z
x( t )^x 0
^y
x
y( t ) y
例如：
自然法
坐标法
※ 位移
1、位矢： 2、位移：
3、位移的大小：
4、位移的方向： 12
※ 速度
径向速度
速率 speed
v v
（速度的大小）
v
2 x
v
2 y
v
2 z
横向速度
dr 思考题： dt
d r 与 dr
是速率吗？ dt dt
有何区别？
13
※ 加速度
加速度的分量
14
加速度的大小
15
质点运动学的基本问题
两
速度的大小a 。
17
解：
y
h
0
小船只沿x方向运动,
简化为一维问题, 可
l
用标量处理。
x
x
18
例题2 一物体作直线运动，初速度为零，初加速度为a0 , 出发后经过时间间隔2秒，加速度均匀增加了a0 , 求经过 t 秒后物体的速度和离开出发点的距离。
大学物理课件-曲线运动
非匀速圆周运动
总结词：速度变化
详细描述：非匀速圆周运动是指物体在圆周运动过程中，速度大小或方向发生变化，导致向心加速度 大小和方向也随之变化的运动。非匀速圆周运动中，向心加速度的大小和方向均可能发生变化。
04
抛体运动
BIG DATA EMPOWERS TO CREATE A NEW
ERA
抛体运动的定义与特点
定义
抛体运动是指物体在不受其他外力的作 用下，只受重力作用而进行的曲线运动 。
VS
特点
抛体运动是加速度恒定的匀变速曲线运动 ，其轨迹是一条抛物线。
平抛运动
定义
平抛运动是指物体以一定的初速度沿水平方 向抛出，只在重力作用下的运动。
特点
平抛运动的轨迹是一条抛物线，速度方向时 刻变化，加速度方向始终竖直向下。
运动的分解
将一个复杂的运动分解为几个简单的运动，便于分析和研究。
运动的守恒定律
动量守恒定律
在封闭系统中，没有外力作用时，系统的总动量保持不变。
机械能守恒定律
在没有外力或外力做功为零时，系统的动能和势能之和保持不变。
03
圆周运动
BIG DATA EMPOWERS TO CREATE A NEW
ERA
摆动
物体在空间中做往复的圆 弧运动，如单摆、复摆等 ，加速度方向时刻改变。
曲线运动在生活中的应用
天体运动
行星绕太阳的公转、地球的自转等都是曲线运动的实例。
投掷项目
标枪、铁饼等投掷项目的运动轨迹为曲线，需要运动员掌握好出 手角度和速度。
车辆行驶
汽车在弯道行驶时，做曲线运动，需要驾驶员控制好车速和转向 角度。
圆周运动的定义与特点
总结词：基本概念
曲线运动知识点网络图
曲线运动知识点网络图1. 核心概念- 曲线运动定义- 物体在平面内沿曲线路径的运动- 曲线运动的条件- 合外力与速度方向不共线- 存在加速度分量2. 基本类型- 平面曲线运动- 圆周运动- 匀速圆周运动- 变速圆周运动- 抛体运动- 水平投射- 垂直投射- 斜投射- 空间曲线运动- 螺旋运动- 摆的运动3. 物理量描述- 位置- 直角坐标系- 极坐标系- 速度- 瞬时速度- 平均速度- 加速度- 瞬时加速度- 平均加速度- 力- 合外力- 向心力- 切向力4. 运动方程- 圆周运动方程- 角速度与周期- 线速度与角速度的关系- 抛体运动方程- 水平与竖直分量- 射程与初速度的关系- 螺旋运动方程- 螺旋线的参数方程5. 动力学分析- 牛顿运动定律- 第一定律（惯性定律）- 第二定律（加速度定律） - 第三定律（作用与反作用） - 能量守恒- 动能- 势能- 机械能守恒定律- 动量守恒- 动量的定义- 动量守恒条件6. 实际应用- 工程领域- 机械设计- 航空航天- 生物力学- 动物运动分析- 人体运动学- 体育竞技- 投掷项目- 赛车运动7. 解题技巧- 图形分析法- 速度-时间图- 加速度-时间图- 数学工具- 微分方程- 向量分析- 实验室测量- 光电门- 加速度计请注意，上述内容是一个文字描述的网络结构，您可以使用专业软件如Microsoft Word、Visio、MindManager或其他网络图绘制工具来创建一个视觉化的曲线运动知识点网络图。
在创建网络图时，您可以将每个主要概念作为节点，并通过连线表示它们之间的关系。
这样的视觉化工具可以帮助学生和研究人员更好地理解和记忆曲线运动的相关概念。
大学物理1-3 曲线运动
第1章 质点运动学
返回
12
南通大学
Nantong University
1-3 曲线运动
四
抛体运动
v
g
x
以抛射点为坐标原点。设t=0时，物体速度为 v0 y 任意时刻质点的加速度为： a g j v0 v v0 cos0 i (v0 sin 0 gt) j 速度：
o
v2 an n 法向加速度（由速度方向变化引起） R
dv at dt
v
切向加速度（由速度大小变化引起）
第1章 质点运动学
返回
v'
v n
v
v t
2
南通大学
Nantong University
1-3 曲线运动
变速圆周运动的加速度在“自然坐标系”中表示为：
即： v x v0 cos0
v y v0 sin0 gt
θ0 o
t 1 2 位矢： r r0 v dt v0 t cos 0 i ( v0 t sin 0 gt ) j 0 2
即： x v0 cos 0 t
y v0 sin 0 t
y p dy h ds
即： vdv g cos ds gdy 两边积分：
θ
v
v0
vdv g dy
y h
g
at
O
S
x
1 2 2 ( v v0 ) g ( h y ) 得： 2
2 v 2 v0 2 g ( h y )
与自由落体速度 公式相同！
A(t)
v
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
ω=ω0+αt
＝ 0
t
1 2
t
2
＝ 0＋0
t
1 2
t
2
四、一般曲线运动：
抛体运动和圆周运动都是曲线运动，分析曲线运动问题可以用直角坐标系 ，
也可以用自然坐标系。对于平面运动，质点在任一点的加速度为
法向加速度 an=v2/ρ
切向加速度 aτ=dv/dt
其中
1
f 2 f
4．加速度
a
a
an
dv dt
v2 r
n
P
图 1-13 法向加速度的推导
an , a 互相垂直，总加速度
大小： a an2 a2
方向：
arctg
an a
（ 是 a与a 的夹角），不再指向圆心。
n
a
an
a
P
二、圆周运动的角速度和角加速度
度，则这种运动称为匀速圆周运动（匀速率圆周运动）。
2）速度：
大小v ： v（速率）
方向：变化（沿该点切线方向）
3）加速度：
an
r 2
v2 r
at 0
在匀速圆周运动中，速度大小不变，但方向时刻变化，所以是变速运动， 存在加速度，这个加速度就是向心加速度，大小等于 v2/R，方向与速度垂直而 指 向 圆心。向心加速度只改变速度方向而不改变速度的大小。
3/2
为曲线的曲率半径(Radius of Curvature)，y=f(x)为曲线
运动的轨迹方程。
可分为四种情况： an=0，aτ=0，匀速直线运动； an=0，aτ≠0，变速直线运动； an≠0，aτ=0，匀速曲线运动； an≠0，aτ≠0，一般曲线运动。
4）运动公式 角位移 t
角位置 0 t
2．匀 变 速 率 圆 周 运 动
1）角加速度
物体沿着圆周运动时，其速度大小随时间变化，该物体做变速圆周运动，
速度大a小 和an 方 a向 都在变化，总的加速度为：
an
v2 r
r 2 ,——法向加速度，表示速度方 向 变 化 的快慢，改变速度方
图 1-14 合加速度的方向
与直线运动类似，描述曲线运动中质点位置变化也有平均、y瞬时速度和平均
瞬时加速度。只是在各物理量前加一个“角”字，以示区别。
1．角位置与角位移
B
角位置 θ，单位为弧度；角位移△θ，单位为弧度；
2．角速度
r
O
A x
图 1-15 圆周运动的角量表示
平均角速度
＝
t
向；
a
dv dtBiblioteka ——切向加速度，表示速度的大
小
变化的快慢，改变速度大小；
在变速圆周运动中，由于速度的大小和方向都在变化，所以加速度的方向
不再指向圆心。切向加速度在速度的方向上，用来改变速度的大小；法向加速度
与速度垂直，用来改变速度的方向。
2）运动公式
角加速度 α= const
角速度 角位移
角位置
a
dv dt
a a
rddvt
r
d dt
r
o
3add．nt法v向ddddt加tn速v度ddtnonrmal（ 速
d an
v
d dt
v
r 2
v2 r
度
的
方
向
变
化
引
起
的 —n—
d
难d点ds） P
v
3．角量与线量的关系
半径 r，角位移
弧长 s ： s r
lim lim 线速度 v：
v
t 0
s t
r t0 t
r
a r
an
v2 r
r 2
三、匀速率圆周运动和匀变速圆周运动
1． 匀 速 率 圆 周 运 动
1）定义：质点作圆周运动时，如果在任意相等的时间内通过相等的圆弧长
一、圆周运动的切向加速度和法向加速度
1．圆周运动的加速度
针
在自然坐标系中（只有在运动轨迹已知时才可以用），设其正方n向沿顺时
某时刻： 加速度：
asddsvt(t)
ddvt速 度 v：ddtv
v
s O
n
——速度的大小和方向均变化
图 1-12 自然坐标系
2．切向加速度 tangantial——速度的大小变化引起的
，——弧度/秒；
lim 瞬时角速度
＝
t 0
t
d dt
，
ω= const 匀角速圆周运动，即匀速圆周运动
ω≠const 变速圆周运动
3．角加速度
平均角加速度
＝
t
lim 瞬时角加速度
＝
t 0
t
d dt
d 2 dt 2
α= const 匀变速圆周运动
α≠const 非匀变速圆周运动