大学物理第二讲-圆周运动及其描述-质点运动学的基本问题
大学物理第二讲-圆周运动及其描述-质点运动学的基本问题
dy1 v1dt
同时B运动的路程为
ds v2dt
ds
P
dx
dy
y1(t dt) y1 (t )
y
且 ds dx2 dy2
o
x
L x 23
结合以上三式，得
dy1
v1dt
v1 v2
ds
v1 v2
dx2 dy2 v1 v2
1
dy dx
2
dx
dy1 v1 dx v2
a
aτ2 an2
(v0 kt)2 (kR)2 R
12
② 令 a = k ，即 a
解得 t v0 / k
(v0 kt)2 (kR)2 k R
③ 当a = k 时，t = v0 /k ，由此可求得质点历经的路 程长度为
s v0t kt2 / 2 v02 / 2k
y1(t dt) y1 (t )
ds P
dx
dy
v1
A
y
v2 x
Lx
22
由图中几何关系得
y1
y
(L
x) tan
y
(L
x)
dy dx
上式对x求导，得
dy1 dx
dy dx
dy dx
(L
x)
d2y dx2
(L
x)
d2y dx2
在dt时间内A向上运动的竖直距离为 y
③由运动方程
r 2ti (19 2t2 ) j
得分量方程 x 2t, y (19 2t2 )
力学中的圆周运动问题解析
力学中的圆周运动问题解析圆周运动是力学中的一个重要概念，涉及到物体在固定半径上做匀速或变速运动的情况。
本文将对圆周运动的基本原理、运动学和动力学等方面进行深入解析。
一、圆周运动的基本原理圆周运动是一种约束性运动，其基本原理可由以下两个关键要点来概括：1. 物体在圆周运动过程中会受到向心力的作用，向心力的大小与物体的质量和半径有关，表示为F = mω²r，其中m为物体的质量，ω为角速度，r为半径。
2. 物体在圆周运动过程中会产生向心加速度，向心加速度的大小与角速度的平方和半径有关，表示为a = ω²r。
二、圆周运动的运动学分析圆周运动的运动学分析主要包括角度、速度和加速度等方面的研究：1. 角度：圆周运动可以用角度来描述，物体在单位时间内所经过的角度称为角速度。
角速度的单位通常为弧度/秒，记作rad/s。
2. 速度：圆周运动的速度分为线速度和角速度。
线速度v表示物体在圆周轨道上的实际移动速度，其大小为v = ωr，其中r为圆周的半径。
角速度ω表示单位时间内物体角度的变化速率。
3. 加速度：圆周运动的加速度分为线加速度和角加速度。
线加速度a表示物体在圆周轨道上的实际加速度，其大小为a = ω²r。
角加速度α表示单位时间内角速度的变化速率。
三、圆周运动的动力学分析圆周运动的动力学分析主要涉及到向心力和转动惯量等方面的研究：1. 向心力：圆周运动身体所受的向心力与质量和半径的乘积成正比。
向心力的方向指向圆心，使物体沿着圆周轨道做匀速运动。
向心力的大小可通过F = mω²r来计算。
2. 转动惯量：圆周运动的物体具有转动惯量，其大小与物体的质量分布和转动轴的位置有关。
转动惯量的计算可通过I = mR²来求解，其中m为物体的质量，R为转动轴到物体质心的距离。
四、圆周运动的应用举例圆周运动在物理学和工程学等领域有着广泛的应用，以下是一些典型的应用场景：1. 机械振动：许多机械装置中都存在圆周运动，如发动机的曲轴、风力发电机的叶片等。
物理必修二圆周运动知识点总结
物理必修二圆周运动知识点总结一、圆周运动的基本概念定义：质点以某点为圆心，半径为r在圆周上运动，其轨迹是圆周或圆弧的运动称为圆周运动。
圆周运动是曲线运动的一种，因此它一定是变速运动。
分类：圆周运动可分为匀速圆周运动和变速圆周运动。
匀速圆周运动指的是线速度大小处处相等的圆周运动，尽管线速度大小不变，但由于方向时刻改变，因此匀速圆周运动仍然是变速运动。
二、描述圆周运动的物理量线速度：描述质点沿圆周运动的快慢的物理量，其方向是质点在圆周上某点的切线方向。
在匀速圆周运动中，线速度大小不变，但方向时刻改变。
角速度：描述质点绕圆心转动的快慢的物理量，是矢量，其方向用右手螺旋定则确定。
在匀速圆周运动中，角速度大小和方向都不变。
周期和频率：周期是质点完成一次圆周运动所需的时间，频率是周期的倒数，表示单位时间内完成圆周运动的次数。
在匀速圆周运动中，周期和频率都不变。
向心力：使质点沿圆周运动的力，方向始终指向圆心。
向心力的大小与线速度、角速度和半径有关，其作用是改变质点的速度方向，使质点能够持续沿圆周运动。
三、圆周运动的规律和应用牛顿第二定律在圆周运动中的应用：通过向心力表达式，可以推导出圆周运动的线速度、角速度、周期等物理量之间的关系。
圆周运动在日常生活和科技领域中的应用：例如电动机转子、车轮、皮带轮等的运动都是圆周运动。
此外，人造卫星、行星运动等天体运动也可以视为圆周运动。
四、离心运动做圆周运动的物体，由于惯性，总有沿着切线方向飞去的倾向。
一旦受力突然消失或合力不足以提供所需的向心力时，物体就会做离心运动。
以上是物理必修二中关于圆周运动的主要知识点总结。
这些知识点是理解和分析圆周运动的基础，对于后续学习物理的其他部分以及应用物理知识解决实际问题具有重要意义。
《大学物理》课程教学大纲
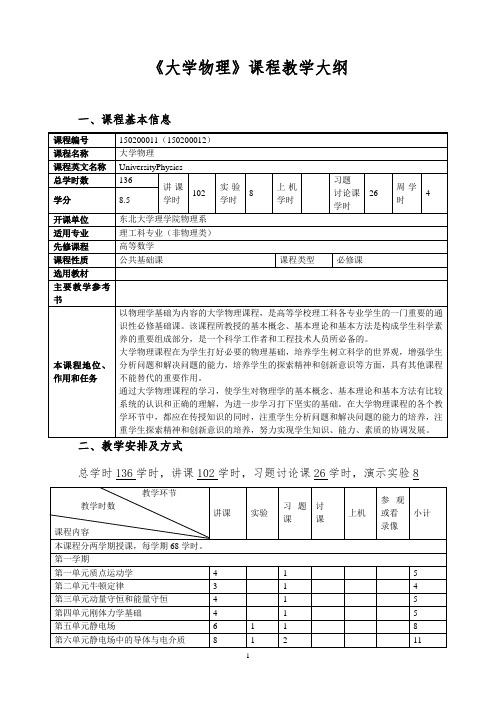
《大学物理》课程教学大纲一、课程基本信息总学时136学时，讲课102学时，习题讨论课26学时，演示实验8三、课程教学的有关说明1、本课程课内外学时比例：1:2；平均周学时：4。
2、本课程是公共基础课，分连续两个学期完成。
3、在教学中注意把传统教学手段和现代化教学手段相结合，充分利用现代化教学手段进行教学。
四、对于能力培养的基本要求通过大学物理课程教学,应注意培养学生以下能力：1.独立获取知识的能力——逐步掌握科学的学习方法，阅读并理解相当于大学物理水平的物理类教材、参考书和科技文献，不断地扩展知识面，增强独立思考的能力，更新知识结构；能够写出条理清晰的读书笔记、小结或小论文。
2.科学观察和思维的能力——运用物理学的基本理论和基本观点，通过观察、分析、综合、演绎、归纳、科学抽象、类比联想、实验等方法培养学生发现问题和提出问题的能力，并对所涉问题有一定深度的理解，判断研究结果的合理性。
3．分析问题和解决问题的能力——根据物理问题的特征、性质以及实际情况，抓住主要矛盾，进行合理的简化，建立相应的物理模型，并用物理语言和基本数学方法进行描述，运用所学的物理理论和研究方法进行分析、研究。
五、对于素质培养的基本要求通过大学物理课程教学,应注重培养学生以下素质：1.求实精神——通过大学物理课程教学，培养学生追求真理的勇气、严谨求实的科学态度和刻苦钻研的作风。
2.创新意识——通过学习物理学的研究方法、物理学的发展历史以及物理学家的成长经历等，引导学生树立科学的世界观，激发学生的求知热情、探索精神、创新欲望，以及敢于向旧观念挑战的精神。
3.科学美感——引导学生认识物理学所具有的明快简洁、均衡对称、奇异相对、和谐统一等美学特征，培养学生的科学审美观，使学生学会用美学的观点欣赏和发掘科学的内在规律，逐步增强认识和掌握自然科学规律的自主能力。
六、教学内容及基本要求模块1力学:第一单元质点运动学第一讲质点运动的描述，第二讲圆周运动与一般平面曲线运动，第三讲相对运动基本要求：1、质点运动的描述(1)掌握：位矢、位移、速度、加速度等物理量的定义及表达式，能够从已知的运动方程求导得到速度、加速度；同时能够从已知的速度或加速度积分得出运动方程。
大学物理第1章质点运动学的描述
t0
0 2 4
t 2s 4
2
t 2s
x/m
6
-6 -4 -2
例3 如图所示, A、B 两物体由一长为 l 的刚性 细杆相连, A、B 两物体可在光滑轨道上滑行.如物体 A以恒定的速率 v 向左滑行, 当 60 时, 物体B的 速率为多少？ 解 建立坐标系如图, 物体A 的速度
1. 5 arctan 56.3 1
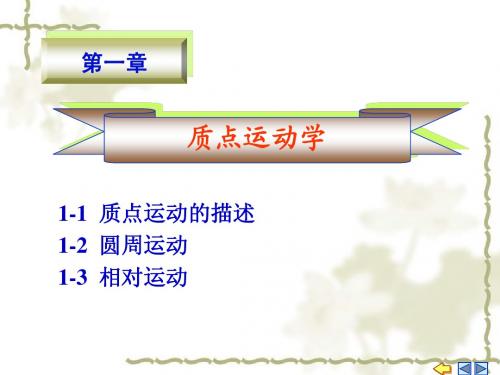
（2） 运动方程
x(t ) (1m s )t 2m
y(t ) ( m s )t 2m
1 4 2 2
1
由运动方程消去参数
1 -1 2 y ( m ) x x 3m 4
轨迹图
t 4s
6
t 可得轨迹方程为
y/m
三、位置变化的快慢——速度
速度是描写质点位置变化快慢和方向的物理量，是矢量。
速率是描写质点运动路程随时间变化快慢的物理量，是标量。 1 平均速度 在t 时间内, 质点从点 A 运动到点 B, 其位移为
B
y
r r (t t) r (t)
r (t t)
s r
质点是经过科学抽象而形成的理想化的物理模 型 . 目的是为了突出研究对象的主要性质 , 暂不考 虑一些次要的因素 .
二、位置矢量、运动方程、位移
1 位置矢量
确定质点P某一时刻在 坐标系里的位置的物理量称 . 位置矢量, 简称位矢 r
y
y j
r xi yj zk
j k 式中 i 、 、 分别为x、y、z
xA xB xB x A
yB y A
o
x
经过时间间隔 t 后, 质点位置矢量发生变化, 由 始点 A 指向终点 B 的有向线段 AB 称为点 A 到 B 的 位移矢量 r . 位移矢量也简称位移.
大学物理§1.2 圆周运动
a dv dt
gt v0 sin v0 g t 2v0 gt sin
2 2 2
g
o
P
(t )
☻ a an a
2 v ) 2 ( dv ) 2 dv 大小: a a a ( (对曲线运动) dt r dt 2 n 2
方向: arctg (
an a
)
Chapter 1. 质点运动学 主编：杨茂田
§1. 2 圆周运动
P. 14 / 21 .
如何直观反映加速度 a 是怎样随着速度的大小和方
向变化而变化
Chapter 1. 质点运动学 主编：杨茂田
§1. 2 圆周运动
P. 6 / 21 .
自然坐标系是建立在物体运动的轨迹上的，有两个坐
标轴，切向坐标轴和法向坐标轴。
☻切向坐标轴沿轨迹的切线
ˆ en
ˆ e
ˆ en
(运动)方向； 法向坐标轴
Chapter 1. 质点运动学 主编：杨茂田
§1. 2 圆周运动
P. 1 / 21 .
§1.2
圆周运动
Chapter 1. 质点运动学 主编：杨茂田
§1. 2 圆周运动
P. 2 / 21 .
一、圆周运动的角量描述
在极坐标系中可用一组角量描述：
☻角位置：极角 θ (rad)
☻角位置变动：角位移 △θ ( rad ) ☻角位置变动快慢：角速度 ω
2
x v0t cos
y v0t sin 1 gt 2 v x dx v0 cos dt dy v0 sin gt vy dt
2
y
v0
an
大学物理质点运动学总结
大学物理质点运动学总结质点运动学是物理学中的一个重要分支，研究物体在空间中的运动规律，对于理解物体的运动状态和运动规律具有重要意义。
在大学物理课程中，学习质点运动学是必不可少的一部分，下面我们来对大学物理质点运动学进行总结。
首先，我们要了解质点的基本概念。
质点是一个没有大小但有质量的物体，在运动学中，我们将物体视为质点来进行研究。
质点的运动状态可以用位置、速度和加速度来描述，这些是描述质点运动的基本物理量。
其次，我们要了解质点的运动规律。
根据牛顿运动定律，质点的运动状态受到力的影响，力是导致质点运动状态发生改变的原因。
根据牛顿第二定律，质点的加速度与作用在其上的合外力成正比，与质点的质量成反比。
这就是著名的F=ma公式，描述了质点的运动规律。
在质点运动学中，我们还需要了解匀速直线运动和变速直线运动。
在匀速直线运动中，质点在单位时间内位移相等，速度保持恒定；而在变速直线运动中，质点在单位时间内位移不等，速度不断发生变化。
这些运动规律对于我们理解质点的运动状态和运动规律具有重要意义。
此外，我们还需要了解曲线运动。
在曲线运动中，质点沿着曲线路径运动，速度和加速度的方向都会发生变化。
对于曲线运动，我们需要引入切线和法线的概念，以便更好地描述质点在曲线路径上的运动状态。
最后，我们需要了解相对运动。
在相对运动中，质点的运动状态是相对于其他物体或参考系来描述的。
相对运动涉及到相对速度和相对加速度的概念，通过这些概念，我们可以更好地描述质点在不同参考系下的运动状态。
总的来说，大学物理质点运动学是一个重要而复杂的学科，它涉及到质点的基本概念、运动规律、匀速直线运动、变速直线运动、曲线运动和相对运动等内容。
通过学习质点运动学，我们可以更好地理解物体的运动规律，为我们进一步学习和研究物理学奠定坚实的基础。
希望这篇总结对大家有所帮助，谢谢阅读！。
质点在匀速圆周运动中的力学分析
质点在匀速圆周运动中的力学分析在物理学中，圆周运动指的是物体沿着一个固定半径的圆形路径做匀速运动的情况。
质点是指在物理学中将物体抽象出的一个点，它没有质量和大小，但可以代表物体在空间中的位置。
在质点进行匀速圆周运动时，它所受到力的分析是十分关键的。
1. 圆周运动的基本概念质点在匀速圆周运动中，具有以下基本概念：- 半径（r）：指圆周上质点到圆心的距离。
- 角速度（ω）：指质点每单位时间绕圆心旋转的角度。
- 周期（T）：指质点完成一次绕圆运动所需要的时间。
2. 圆周运动中的向心力在质点进行匀速圆周运动时，质点受到一个向心力，使其沿着圆的路径运动。
向心力的大小可以通过以下公式计算：F = mω²r其中，F表示向心力的大小，m表示质点的质量，ω表示角速度，r 表示半径。
3. 圆周运动中的离心力在质点进行匀速圆周运动时，还存在一个离心力，它与向心力方向相反，试图将质点拉出圆的路径。
离心力的大小与向心力大小相等，但方向相反。
4. 圆周运动中的转动惯量转动惯量是物体对转动运动的惯性度量，对圆周运动也是十分重要的。
对于质点在圆周上的运动，它的转动惯量可以通过以下公式计算：I = mr²其中，I表示转动惯量，m表示质点的质量，r表示半径。
5. 圆周运动中的加速度质点在匀速圆周运动中，它的速度大小保持不变，但速度方向在不断改变，因此质点具有向心加速度。
向心加速度的大小可以通过以下公式计算：a = ω²r其中，a表示向心加速度的大小，ω表示角速度，r表示半径。
6. 圆周运动中的角加速度质点在匀速圆周运动中，它的角速度大小保持不变，但角速度的方向在不断改变，因此质点具有角加速度。
角加速度的大小可以通过以下公式计算：α = a / r其中，α表示角加速度的大小，a表示向心加速度的大小，r表示半径。
通过以上力学分析，可以看出质点在匀速圆周运动中受到向心力的作用，并且该向心力与质点的质量、角速度和半径之间有关。
圆周运动知识点总结
圆周运动知识点总结圆周运动是物体沿圆周路径运动的一种形式，它在物理学中占有重要地位。
以下是关于圆周运动的一些关键知识点：1. 圆周运动的基本概念：圆周运动是指物体沿圆周轨迹运动的过程，其中物体的速度方向时刻变化，始终指向圆心。
2. 圆周运动的类型：圆周运动可以分为匀速圆周运动和变速圆周运动。
匀速圆周运动是指物体以恒定速度沿圆周轨迹运动，而变速圆周运动则是指物体的速度大小或方向在运动过程中发生变化。
3. 圆周运动的描述：描述圆周运动时，通常使用线速度、角速度、周期、频率等物理量。
线速度是物体沿圆周轨迹的切线方向的速度，角速度是物体绕圆心转过的角度与时间的比值，周期是物体完成一次圆周运动所需的时间，频率是单位时间内物体完成圆周运动的次数。
4. 圆周运动的物理量关系：对于匀速圆周运动，线速度v、角速度ω、周期T和频率f之间的关系为v = ωr = 2πr/T = 2πf，其中r是圆周运动的半径。
5. 向心力：物体做圆周运动时，需要一个指向圆心的力来维持运动，这个力称为向心力。
向心力的大小与物体的质量、速度和半径有关，其公式为F_c = mω^2r = mv^2/r。
6. 向心加速度：物体做圆周运动时，由于速度方向时刻改变，会产生向心加速度，其大小为a_c = vω = ω^2r = v^2/r，方向始终指向圆心。
7. 圆周运动的实例：生活中的许多现象都涉及到圆周运动，如行星绕太阳的运动、车轮的旋转、钟摆的摆动等。
8. 圆周运动的动力学分析：在分析圆周运动时，需要考虑物体所受的所有力，包括向心力、摩擦力、重力等，并通过牛顿第二定律进行动力学分析。
9. 圆周运动的稳定性：圆周运动的稳定性与物体的质量和速度有关，质量越大、速度越小，圆周运动越稳定。
10. 圆周运动的实验研究：通过实验可以研究圆周运动的规律，例如使用旋转圆盘实验来测量角速度和线速度的关系，或者通过测量物体在圆周运动中的向心力来验证物理定律。
这些知识点为理解和分析圆周运动提供了基础，对于深入学习物理学中的动力学和运动学问题至关重要。
圆周运动的原理和计算知识点总结
圆周运动的原理和计算知识点总结圆周运动是物体绕固定轴线旋转的一种运动形式。
在日常生活中，我们经常接触到圆周运动，比如车轮的旋转、地球公转等。
了解圆周运动的原理和计算知识点，对于我们理解物体运动的规律和应用物理学等方面都很重要。
本文将从原理和计算两个方面来总结圆周运动的相关知识。
一、圆周运动的原理圆周运动的原理涉及到离心力和向心力的作用。
当物体做圆周运动时，存在一个向心力的作用，使得物体朝向轴线的方向运动。
这个向心力的大小和方向是什么呢？向心力的大小可以用公式F=mv²/r来表示，其中F是向心力的大小，m是物体的质量，v是物体的速度，r是物体离轴线的距离。
由该公式可知，向心力与物体的质量成正比，与速度的平方成正比，与离轴线的距离的倒数成正比。
向心力的方向指向轴线，与物体运动方向垂直。
当物体做圆周运动时，向心力的作用使得物体的运动轨迹成为圆形或弧形。
离心力则是指相对于旋转参考系的观察者而言，观察到物体运动的惯性力。
它指向远离轴线的方向，大小与向心力相等，但方向相反。
二、圆周运动的计算知识点在实际问题中，我们经常需要计算圆周运动的一些相关值，下面列举一些常见的计算知识点：1. 圆周运动的周期圆周运动的周期T是指物体完成一次完整运动所需的时间。
周期与物体的线速度和运动路径有关。
设物体沿圆周运动的线速度为v，半径为r，则圆周运动的周期T可以由公式T=2πr/v来计算得到。
2. 圆周运动的线速度圆周运动的线速度v是指物体在圆周运动过程中沿运动轨迹行走的距离与所用时间的比值。
线速度与物体的角速度和半径有关。
设物体的角速度为ω，半径为r，则圆周运动的线速度v可以由公式v=ωr来计算得到。
3. 圆周运动的角速度圆周运动的角速度ω是指物体在固定轴线上旋转的角度变化速率。
角速度与物体的线速度和半径有关。
设物体的线速度为v，半径为r，则圆周运动的角速度ω可以由公式ω=v/r来计算得到。
4. 圆周运动的加速度圆周运动的加速度是指物体在圆周运动过程中线速度的变化率。
质点的圆周运动
质点的圆周运动质点的圆周运动是物理学中常见的运动形式之一，用于描述质点在圆形轨道上运动的规律。
本文将介绍质点的圆周运动的特征和基本原理，以及相关的数学公式和应用。
一、质点的圆周运动特征质点的圆周运动具有以下几个特征：1. 运动路线为圆形轨道：质点在运动过程中沿着一个固定半径的圆形轨道运动，轨道的中心点为圆心。
2. 速度大小不变：质点在圆周运动过程中，以恒定的速率匀速运动，速度大小不发生变化。
3. 速度方向改变：尽管速度大小不变，但质点在圆周运动过程中，速度的方向会随着时间推移而改变。
4. 向心加速度存在：质点在圆周运动中会受到一个向心加速度的作用，该加速度指向圆心，使质点朝向圆心运动，而不是沿着切线方向。
二、质点的圆周运动基本原理质点的圆周运动可通过向心力来解释。
向心力是指质点在圆周运动中的一种向心的力量，它使得质点向圆心方向偏离直线运动，进而产生圆周运动。
向心力的大小可以通过以下公式进行计算：F = m * a其中，F表示向心力，m表示质点的质量，a表示向心加速度。
向心力的方向指向圆心，即与质点的运动方向相垂直。
三、质点的圆周运动数学表达在质点的圆周运动中，有一些关键的数学表达式可以用来描述运动的规律。
1. 周期：圆周运动的周期T是指质点从出发点绕圆周运动一周所需要的时间。
周期可以用以下公式计算：T = 2π * r / v其中，r表示圆周运动的半径，v表示质点的速度。
2. 角速度：圆周运动的角速度是指质点在圆周运动过程中角度的变化率，可以用以下公式计算：ω = 2π / T其中，ω表示角速度，T表示周期。
3. 向心加速度：圆周运动的向心加速度是指质点受到向心力作用而产生的加速度，可以用以下公式计算：a = v^2 / r其中，a表示向心加速度，v表示质点的速度，r表示圆周运动的半径。
四、质点的圆周运动应用质点的圆周运动在生活和科学研究中有着广泛的应用。
以下是一些常见的应用领域：1. 行星运动：行星围绕太阳的运动可以被视为质点的圆周运动。
圆周运动 参考系-概述说明以及解释
圆周运动参考系-概述说明以及解释1.引言1.1 概述在圆周运动中，物体围绕固定轴或点以特定的路径进行运动。
圆周运动是物体运动的一种普遍形式，广泛应用于日常生活、自然界和科学研究中。
圆周运动的基本特点是物体在运动过程中不断改变方向，但保持距离固定。
在圆周运动中，物体会沿着一个圆形轨道或弧线进行运动，同时遵循特定的速度和加速度规律。
圆周运动可以以直观、美学和实用的方式展示出来，例如地球围绕太阳的公转、行星围绕恒星的运动，或者钟表上指针的转动等。
在物理学中，圆周运动可以通过数学方法进行描述。
通过引入角度的概念，我们可以用角度来表示物体在圆周运动中所处的位置。
同时，线速度和角速度的概念也被引入，用于描述物体在圆周运动中的速度和旋转快慢。
而参考系则是指观察和描述物体运动时所选择的参考框架。
在圆周运动中，选择不同的参考系会对我们对运动的观察和描述产生影响。
不同的参考系可能导致不同的运动轨迹、速度和加速度的测量结果。
因此，对于准确理解和描述圆周运动，必须明确所选择的参考系。
本文旨在探讨圆周运动及其数学描述，并重点研究参考系对圆周运动的影响。
通过分析不同参考系下的运动特点和描述方法，旨在揭示圆周运动中的规律和规则，并深入探讨参考系对圆周运动的影响以及其在科学研究和实际应用中的重要性。
总之，圆周运动是一种常见且重要的物体运动形式，它在日常生活和科学研究中都具有重要的应用价值。
通过研究圆周运动的定义、基本概念、数学描述以及参考系对其影响的现象，我们可以更好地理解和应用圆周运动的规律，并为未来的研究提供新的思路和方向。
1.2文章结构文章结构（Article Structure）是指文章的整体组织和布局，它决定了文章的逻辑序列和篇章框架，使读者能够清晰地理解和吸收文章中的内容。
本文的文章结构主要分为引言、正文、参考系对圆周运动的影响、结论四个部分。
引言（Introduction）部分主要是对文章的研究对象进行概述，并说明文章的目的和意义。
大学物理圆周运动
圆周运动的分类
总结词
圆周运动可以根据不同的分类标准进行分类，如匀速圆周运动和变速圆周运动。
详细描述
匀速圆周运动是指物体在转动过程中角速度保持不变的运动，其特点是线速度的 大小不变，只有方向改变。变速圆周运动是指物体在转动过程中角速度发生变化 的运动，其特点是线速度的大小和方向都可能改变。
02
匀速圆周运动
ቤተ መጻሕፍቲ ባይዱ 匀速圆周运动的定义
总结词
匀速圆周运动是指物体沿着圆周路径做等速运动，即线速度大小恒定，方向时刻改变。
详细描述
匀速圆周运动是圆周运动的一种特殊形式，其特点是线速度的大小恒定，方向始终沿着圆周的切线方 向。匀速圆周运动中，物体的加速度大小恒定，方向始终指向圆心，即向心加速度的大小恒定，方向 始终与线速度垂直并指向圆心。
圆周运动的描述
总结词
圆周运动可以通过角速度、角加速度、转速等物理量进行描述。
详细描述
角速度是描述圆周运动快慢的物理量，单位为弧度/秒，其值等于物体转动一周所需的时间。角加速度是描述圆 周运动加速度的物理量，单位为弧度/秒²，表示物体转动过程中角速度的变化率。转速是描述圆周运动频率的物 理量，单位为转/分，表示物体每分钟转动的圈数。
03
非匀速圆周运动
非匀速圆周运动的定义
特点
加速度不指向圆心，存在 切向加速度和法向加速度 。
非匀速圆周运动
与匀速圆周运动相对，速 度大小或方向发生变化的 圆周运动。
切向加速度
改变速度大小，不改变速 度方向。
法向加速度
改变速度方向，不改变速 度大小。
非匀速圆周运动的描述
描述参数
线速度、角速度、周期、频率、向心加速 度等。
离心力的计算
2第二讲 圆周运动及其描述 质点运动学的基本问题
§1-3 圆周运动及其描述
Circular motion and the description
一、切向加速度与法向加速度 ⎧τˆ:切线方向单位矢量 ⎨ ˆ ⎩ n : 法线方向单位矢量 (曲线凹侧)
2
2
=b
20
得
t = v0 / b
s = v 0 t − bt /2
2
（3）当a = b 时，t = v0/b ，由此可求得质点 历经的弧长为 s
τ
n
= v /2 b
2 0
o
R
此时它已运行的圈数：
P
v n= = 2π R 4π Rb
21
s
2 0
例：在离水平高度为h的岸边，一人以匀速 率v0拉船，求船离岸边 x 远处时的速度。
v0 = v绳
l
h
o
r2
r1
Δr
X
x
解： ●忽略船高和滑轮高度，则
x = l −h
2
2
22
x = l −h
2
2
dx l dl v= = = 2 2 dt dt l −h
dl = −v0 dt
x + h dl x dt
2 2
dl dl 大小 : | |= v 0，l 变 小 ， 为 负 。 dt dt
θ O’ S
OR
aτ
an
12
四、角量与线量之间的矢量关系 1.角速度与线速度
Z R O′
v
v = ω R = ω r sin α = ω × r
v =ω×r
大学物理 圆周运动及其描述
0 t
v v0 at
比较知：两者数学形式完全相同,说明用角量描述,可把 平面圆周运动转化为一维运动形式，从而简化问题。
2 x x0 v0t at / 2 2 2 v v0 2a ( x x0 )
线量与角量之间的关系
3. 线量与角量之间的关系
R
2
a
的大小为
a at an
2
dv v dt R
2
2 2
1 at a的方向由它与法线方向 的夹角给出为 tan
讨论：下列情况时，质点各作什么运动？ at 等于0, an等于0, 质点做什么运动？
at 等于0, an不等于0 , 质点做什么运动？ at 不等于0, an等于0 , 质点做什么运动？ at 不等于0, an不等于0 , 质点做什么运动？
a
(v0 bt) (bR)
2
2
R
b
n
（2）令a = b ，即
τ
(v0 bt ) 2 (bR) 2 2 2 a aτ an R
s
o
R
线量与角量之间的关系
得 t v0 / b （3）当a = b 时，t = v0/b ，由此可求得质点历经
的弧长为
s v0t bt /2
(m/s ) (m/s ) (m/s )
2 2
2
a 2.89 10 a 3.10 10
n
2
2
线量与角量之间的关系
例题2 一质点沿半径为R的圆周按规律 运动，v0、b都是正的常量。求：
s v0t bt / 2
2
（1） t 时刻质点的总加速度的大小； （2） t 为何值时，总加速度的大小为b ； （3）当总加速度大小为b 时，质点沿圆周运行 了多少圈。 s
理解质点的匀速圆周运动
理解质点的匀速圆周运动质点的匀速圆周运动是物理学中重要的概念之一，它描述了质点在圆周轨道上以匀速旋转的运动方式。
本文将介绍质点的匀速圆周运动的基本概念、运动规律以及相关的物理量，并探讨质点的匀速圆周运动在实际生活中的应用。
一、基本概念1. 质点：在物理学中，质点是指形状极小、可以忽略其大小和形状的物体。
质点没有体积，只有质量。
2. 圆周运动：圆周运动是物体沿着圆周轨道运动的一种方式，质点在圆周运动中假设为质量点，并且旋转轨迹为圆形。
二、运动规律1. 角速度和角频率：在质点的匀速圆周运动中，角速度（ω）和角频率（ν）是描述旋转速度的物理量。
角速度表示单位时间内角度的改变量，角频率表示单位时间内圆周运动的周期数。
2. 周期和频率：质点的匀速圆周运动具有相等的周期（T）和频率（f），周期是一个圆周运动所需要的时间，频率是单位时间内圆周运动的周期数的倒数。
3. 线速度和圆周位移：质点在匀速圆周运动中，具有线速度（v）和圆周位移（s），线速度是质点沿圆周轨道的速度大小，圆周位移是质点在时间内沿圆周轨道的位移。
4. 向心加速度：质点在匀速圆周运动中，会受到向心力的作用，向心力的方向指向圆心。
这个向心力引起了质点的向心加速度（a_c），向心加速度与质点的线速度和圆周半径有关。
三、物理量之间的关系1. 角速度和线速度之间的关系：在质点的匀速圆周运动中，角速度和线速度之间的关系由公式v = rω 给出，其中 v 表示线速度，r 表示圆周半径，ω 表示角速度。
2. 角速度和周期之间的关系：角速度和周期之间的关系由公式ω =2π / T 给出，其中ω 表示角速度，T 表示周期。
3. 向心加速度和线速度之间的关系：向心加速度和线速度之间的关系由公式 a_c = v^2 / r 给出，其中 a_c 表示向心加速度，v 表示线速度，r 表示圆周半径。
四、实际应用质点的匀速圆周运动在我们的日常生活以及许多科学领域都有广泛的应用。
大学物理圆周运动
引言：大学物理中，圆周运动是一个重要的概念和题目，是建立在基础的运动学知识上的一个重要应用。
本文将详细介绍大学物理中的圆周运动（二），包括角速度、角加速度、牛顿定律在圆周运动中的应用以及相关的数学推导和实践应用。
概述：圆周运动是指物体在一个固定圆轨道上运动的情况。
在这种运动中，物体以一个恒定的速度绕着圆心旋转。
圆周运动是一种重要的运动形式，广泛应用于物理学、工程学和天文学等领域。
本文将着重介绍圆周运动中的角速度、角加速度以及相关的应用和推导。
正文：1.角速度的定义和计算1.1角速度的定义1.2圆周运动中的角速度计算方法1.3角速度与线速度的关系2.角加速度的定义和计算2.1角加速度的定义2.2圆周运动中的角加速度计算方法2.3角加速度与线加速度的关系3.牛顿定律在圆周运动中的应用3.1牛顿第一定律在圆周运动中的应用3.2牛顿第二定律在圆周运动中的应用3.3牛顿第三定律在圆周运动中的应用4.圆周运动相关的数学推导4.1圆周运动中的位移、速度和加速度的关系4.2圆周运动中的周期和频率的关系4.3圆周运动中的力学能量守恒定律5.圆周运动的实践应用5.1汽车在转弯时的圆周运动5.2行星围绕太阳的圆周运动5.3粒子加速器中的圆周运动总结：圆周运动是大学物理中一个重要的概念和题目，掌握相关的知识和应用对于深入理解物体的运动学特性和动力学规律具有重要意义。
本文通过对角速度、角加速度、牛顿定律在圆周运动中的应用以及相关的数学推导和实践应用的详细阐述，希望能够对读者加深对圆周运动的认识和理解，提高解题能力和应用能力。
在实践应用中，圆周运动的概念和方法也被广泛应用于各个领域，为相关领域的发展和进步做出了重要贡献。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
a
aτ2 an2
(v0 kt)2 (kR)2 R
12
② 令 a = k ，即 a
解得 t v0 / k
(v0 kt)2 (kR)2 k R
③ 当a = k 时，t = v0 /k ，由此可求得质点历经的路 程长度为
s v0t kt2 / 2 v02 / 2k
v v
ds
n d
S
o d
d d
d
2
a
a
an
dv
dt
v2
n
a an2 a2
dv dt
2
v2
2
a与 v方向的夹角：
arctan an
a
讨论
0 ,
2
a 0,
v
90 , a 0, v const
角加速度与线加速度
a dv d ( r )
dt dt
z
cR v
m
r
o
x
y
d r dr r v
dt
dt
8
a r v | r | r sin R 沿切线方向
r a 切向加速度 | v | v sin 90 =v
(t 0)
y
v0
l1
而 x l v v0
（三角形任意两边之差小于第三边）
h l2 v
l x
船速大于绳速
o
x2 x1
x
15
§1-5 质点运动学中的两类基本问题
第一类：
已知 r r (t), 求v, a, 用微分。
r 微分 v 微分 a
第二类：
已知 a及初始条件 v0、r0, 求v、r，用积分。
,
2
a 0,
v
a
S
an a
a
a
3
例：半径为R的滑轮可绕中心轴转动。绕于滑轮上的无形
变细绳其下端挂一重物。已知重物按 h = (1/2)a1t2 的规律 下降，求轮沿上任一点 P 的加速度（设绳与轮之间无相
对滑动） 。
解：由于绳无伸长且无相对滑动，故
P点的运动方程
y1(t dt) y1 (t )
ds P
dx
dy
v1
A
y
v2 x
Lx
22
由图中几何关系得
y1
y
(L
x) tan
y
(L
x)
dy dx
上式对x求导，得
dy1 dx
dy dx
dy dx
(L
x)
d2y dx2
(L
x)
d2y dx2
在dt时间内A向上运动的竖直距离为 y
1
dy dx
2
y
y1(t dt)
y1 (t )
代入第一个式子，得运动微分方程：
v1 v2
1
dy dx
2
(
L
x)
d2 dx
y
2
o
ds
P
dy dx
y
x Lx
求解上式即可得到B的运动轨迹方程。
将上式化为 1 u2 (L x) du
dx
v1 , u dy
L L
x
L L
x
dx
积分，并代入初始条件：t 0, x 0, y 0
解出B的轨迹方程：
y
L 2
1
1
1
x
1
L
1
1
1
x
1
L
L 1 2
25
2.B追上 A时，x =L，代入B的轨迹方程，得出B追上A时两者
dt
①根据两矢量相互垂直的条件
v r 4t 4t(19 2t2 ) 0 解得 t 3
②由 r 2ti (19 2t2 ) j r 4t2 (19 2t2 )2
20
r 4t2 (19 2t2 )2
求导，并令 dr 0 dt
解得 t 3
为正数。求:
S
① t 时刻质点的总加速度大小；
② t 为何值时，总加速度大小为k；
a
n an P
o
x
R
③ 当总加速度大小为k 时，质点运行的圈数。
解：设 t = 0 时质点位于 s = 0 的P点处。
①
dv d 2s a dt dt2 k
an
v2 R
(v0
kt)2 R
速度 v ds dt
s a1t
s0
1 2
a1t
2
a
R
a
an
P
加速度
an
v2 R
n
a12t 2 R
n
a
dv
dt
a1
a1
总加速度
a
an
a
a12t 2 R
n a1
4
三、圆周运动中的角量和线量
1.角位置（角坐标）
◎通常规定逆时针转动为正角位置。
o
x
◎角位置的单位常用弧度(rad，无量纲)表示。
v2
dx
24
分离变量，得 du dx
1 u2 L x
积分，并代入初始条件： t 0, x 0, u dy 0
dx
解得：
u
1 2
L
L
x
L
L
x
v1 , u dy
v2
dx
dy
1 2
dt dx dt dx
v
x
vdv a(x)dx
v0
x0
18
课堂练习
1.质点作任意曲线运动，试判断下列各式的对错：
dv a, d r v;
dt
dt
ds v, dt
dv dt
a ;
dv dt a ,
dr v; dt
dr v,
dv a.
dt
dt
解答：
a dv , dt
d dn ds d d
加速度 a dv dv v d dv v d n
dt dt
dt dt
dt
dv
dt
v
ds n dt
dv
dt
1
v2n a
an
a
dv
dt
an
v2
n
an
切向加速度 法向加速度
a S
a
v dr dr ds , dt dt dt
a
dv dt
dv dt
19
2.一质点作在平面上作曲线运动，其运动方程为
r 2ti (19 2t2 ) ja a(t)
求：①质点的位置矢量与速度矢量相互垂直的时刻; ②质点离原点最近的时刻；③质点的轨迹方程。
解：
v dr 2i 4tj
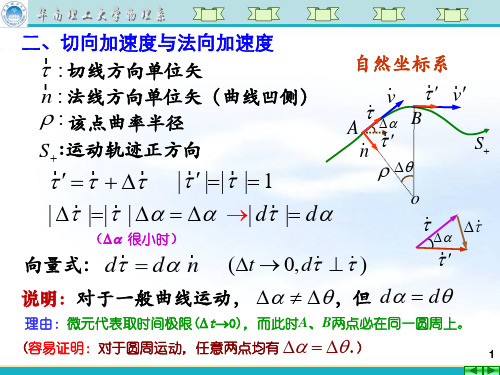
1. 求动物B的运动轨迹？2. 问动物B经多长时间能追上动物A？
解：1. 取B出发点为坐标原点O，A的出发点为(L, 0)。
时刻t，B位于P点，其坐标为x(t)、
y
y(t)，A的位置为y1(t) 。
t时刻B与A的连线与B轨迹在P点相切，
即
tan dy
dx
式中dx和dy是ds在x轴和y轴的投影。 B ds是B从t到(t+dt)时刻行经的路程。 o
o
y 12km, t 1.5h
ds
P
dy dx
y
x
Lx
26
dt dt
线加速度与角加速度
a
dv dt
R d
dt
R
an
v2 R
2R
a a2 an2 R 2 4
arctan an
a
d
dt
d d 2
dt dt2
7
五、角量与线量之间的向量关系
角速度与线速度
v R r sin r v r
（为常量）
（a为常量）
0 t v v0 at
0
0t
1 t2
2
s
s0
v0t
1 2
at
2
2 02 2 ( 0 ) v2 v02 2a(s s0 )
11
例：一质点沿半径为R的圆周按规律
s v0t kt2 / 2运动，其中v0、k
v
dt l2 h2 dt
x dt
v0 y
l0 hl
v
ox
设 t 0, l l0，则 l l0 v0t
x
dl dt
v0
14