《勾股定理的逆定理2》习题
勾股定理的逆定理练习题2024--2025学年苏科版八年级数学上册
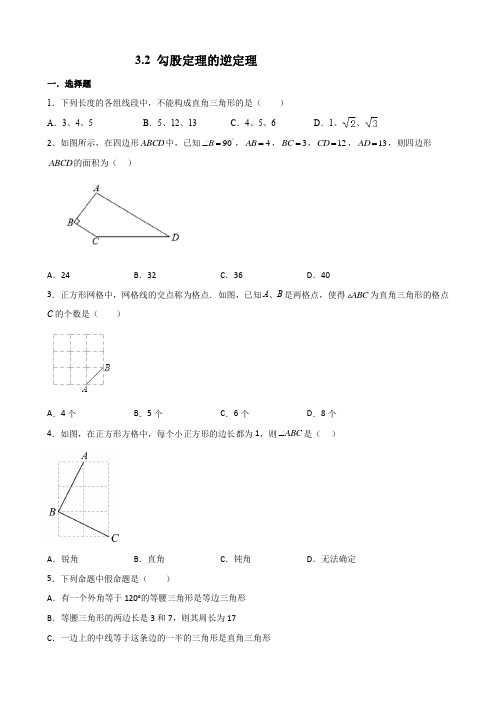
3.2 勾股定理的逆定理一.选择题1.下列长度的各组线段中,不能构成直角三角形的是( )A .3、4、5B .5、12、13C .4、5、6D .1、、2.如图所示,在四边形ABCD 中,已知90B ︒∠=,4AB =,3BC =,12CD =,13AD =,则四边形ABCD 的面积为( )A .24B .32C .36D .403.正方形网格中,网格线的交点称为格点.如图,已知A 、B 是两格点,使得ABC 为直角三角形的格点C 的个数是( )A .4个B .5个C .6个D .8个4.如图,在正方形方格中,每个小正方形的边长都为1,则ABC ∠是( )A .锐角B .直角C .钝角D .无法确定5.下列命题中假命题是( )A .有一个外角等于120°的等腰三角形是等边三角形B .等腰三角形的两边长是3和7,则其周长为17C .一边上的中线等于这条边的一半的三角形是直角三角形D.直角三角形的三条边的比是3:4:56.如图,在3×3的正方形网格中,每个小正方形的边长都为1,ABC的三个顶点均在格点上,则AB边上的高为()A.2105B.105C.1010D.310107.下列各组长度的线段①9,12,15;②7,24,25;③32,42,52;④3a,4a,5a(a>0)其中可以构成直角三角形的有()A.5组B.4组C.3组D.2组8若线段a、b、c能构成直角三角形,则它们的比为()A.5:11:13B.3:4:6C.7:24:25D.6:8:129.下列各组数中不能作为直角三角形的三边长的是()A.3,4,5B.6,8,10C.1.5,2,3D.5,12,1310.五根小木棒,其长度(单位:cm)分别为8,9,12,15,17,现将它们摆成两个直角三角形,其中正确的是()A.B.C.D.二.填空题1.如图,在四边形ABCD中,AB=BC=3,CD=,DA=5,∠B=90°,则∠BCD的度数.2.如图,在四边形ABCD中,∠A=90°,AD=AB=2,BC=,CD=.则∠ABC的度数为.3.已知:如图,四边形ABCD中,AB⊥BC,AB=1,BC=2,CD=2,AD=3,则四边形ABCD的面积为.4.一个三角形两条边长为3和4,当第三条边长为时,此三角形为直角三角形.5.在△ABC中,测得AB=6cm,AC=8cm,BC=10cm,则最长边上的高为.三.解答题1.如图,在四边形ABCD中,∠ABC=90°,AB=6,BC=8,CD=10,AD=10.(1)求四边形ABCD的面积.(2)求对角线BD的长.2.如图,在△ABC中,AB边上的垂直平分线DE与AB、AC分别交于点E和D,且CB2=AD2﹣CD2.(1)求证:∠C=90°;(2)若AC=4,BC=3,求CD的长.3.如图,在△ABC中,D是边BC的中点,E是边AC的中点,连接AD,BE.(1)若CD=8,CE=6,AB=20,求证:∠C=90°;(2)若∠C=90°,AD=13,AE=6,求△ABC的面积.4.如图,在△ABC中,D是边BC上一点,若AB=10,BD=6,AD=8,AC=17.(1)求∠ADB的度数.(2)求CD的长.5.如图,已知点C是线段BD上一点,∠B=∠D=90°,若AB=4,BC=3,CD=8,DE=6,AE2=125.(1)求AC、CE的长;(2)求证:∠ACE=90°.。
勾股定理的逆定理(2)

2m2n2 + n4 + 4m2n2
= m4 + 2m2n2 + n4
∴ a2 + c2 = b2
即: 三角形是直角三角形
科教园地
如果勾股定理的公式c2 = a2 + b2中的 a ,b ,c未知数,是第一个不定方程(即未知 数的个数多于方程的个数)也是最早得出完整解答的不定方程,它一方面引导到各式 各样的不定方程,另一方面也为不定方程的解题程序树立了一个范式。 法国人费尔马(Pierre de Fermat, 1601-1665)虽然学的是法律,从事的也是 律师的职业,但他对数学却有浓厚的兴趣,在业余时间常读数学书,并自己从事一些 数学研究。他在阅读希腊数学家丢番图(Diophontus)的《算术》一书中论述求解 x2 + y2 = z2 的一般解的问题时,在书的空白处,用笔写下这样的心得:“反过来说 不可能把一个立方数分拆为两个立方数的和,一个四方数分拆成两个四方数之和。更 一般地,任何大于二的方数不能分拆为同样方数的两个之和。我已发现了一个绝妙的 证明,但因为空白太小,写不下整个证明”。用数学语言来表达,费尔马的结论是: 当n≥3时, xn + yn = zn 没有正整数解。 1983年,史皮娄(Lucien Szpiro)提出史皮娄猜想,并证明由史皮娄猜想可以推出, 对于充分大的指数,费尔马大定理均成立。1985年,与塞尔(D.W.Masser)等人提 出一系列等价猜想,其中一个称为abc猜想,由它可推出史皮娄猜想。1987年,史皮 娄又提出一系列猜想,由它们也能推出史皮娄猜想。这些猜想似乎更容易下手,但至 今一个也没有证明。 1987年,塞尔由伽罗华表示出发提出一些更强的猜想,称为塞尔强(弱)猜想。 由它不仅可以推出费尔马大定理,还可推出许多其他猜想,但这条路最终也没有能走 通。 英国数学家维尔斯正是沿着这一道路,在经过漫长的7年探索,终于在1993年6月取 得突破。最终在一九九五年完全证明费尔马大定理。解开了困惑世间300多年的谜 .
勾股定理经典例题含答案(2)(K12教育文档)

勾股定理经典例题含答案(2)(word版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(勾股定理经典例题含答案(2)(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为勾股定理经典例题含答案(2)(word版可编辑修改)的全部内容。
勾股定理经典例题含答案11页勾股定理是一个基本的初等几何定理,直角三角形两直角边的平方和等于斜边的平方.如果直角三角形两直角边为a和b,斜边为c,那么a²+b²=c²,若a、b、c都是正整数,(a,b,c)叫做勾股数组。
勾股定理现约有500种证明方法,是数学定理中证明方法最多的定理之一.勾股定理是人类早期发现并证明的重要数学定理之一,用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一。
“勾三,股四,弦五”是勾股定理的一个最著名的例子。
远在公元前约三千年的古巴比伦人就知道和应用勾股定理,还知道许多勾股数组。
古埃及人也应用过勾股定理。
在中国,西周的商高提出了“勾三股四弦五”的勾股定理的特例.在西方,最早提出并证明此定理的为公元前6世纪古希腊的毕达哥拉斯,他用演绎法证明了直角三角形斜边平方等于两直角边平方之和。
类型一:勾股定理的直接用法1、在Rt△ABC中,∠C=90°(1)已知a=6, c=10,求b, (2)已知a=40,b=9,求c; (3)已知c=25,b=15,求a.思路点拨:写解的过程中,一定要先写上在哪个直角三角形中,注意勾股定理的变形使用。
解析:(1)在△ABC中,∠C=90°,a=6,c=10,b=(2) 在△ABC中,∠C=90°,a=40,b=9,c=(3)在△ABC中,∠C=90°,c=25,b=15,a=举一反三【变式】:如图∠B=∠ACD=90°,AD=13,CD=12,BC=3,则AB的长是多少?【答案】∵∠ACD=90°AD=13, CD=12∴AC2 =AD2-CD2=132-122=25∴AC=5又∵∠ABC=90°且BC=3∴由勾股定理可得AB2=AC2-BC2=52-32=16∴AB= 4∴AB的长是4.类型二:勾股定理的构造应用2、如图,已知:在中,,,。
17.2勾股定理逆定理(2)

下册
17.2 勾股定理的逆定理(2)
如果三角形的三边长a、b、c满足
2 a
+
2 b
=
2 c
那么这个三角形是直角三角形.
勾股定理
互逆命题
如果直角三角形两直角边分别为a,b, 斜边为c,那么 a2 + b2 = c2
练习:
1.将直角三角形的三边的长度扩大同样的倍数,则 得到的三角形是 ( A )
A. 是直角三角形;
B. 可能是锐角三角形;
C. 可能是钝角三角形; D. 不可能是直角三角形.
4. 已知∆ABC中BC=41, AC=40, AB=9, 则此三 ∠ A 是最大角. 直角 三角形, ______ 角形为_______ 5. 以∆ABC的三条边为边长向外作正方形, 依次 得到的面积是25, 144 , 169, 则这个三角形是 直角 三角形. ______
(4)全等三角形的对应角相等.
逆命题:对应角相等的两个三角形是全等三角形. 不成立
命题是真命题 ,它逆命题却不一定 是真命题. 感悟: 一个 原命题成立时 , 逆命题有时成立 , 有时不成立
D
A
C
B
小明想要检测雕塑底 座正面的 AD 边和BC边是 否分别垂直于底边AB,但他 随身只带了卷尺. 小明量得AD长是30厘 米,AB长是40厘米, BD长 是50厘米,AD边垂直于 AB边吗?为什么?
∵5²+12²=13² ∴这个三角形是直角三角形。
巩固练习
练习2 如图,在四边形ABCD中,AB=BC=CD=DA, ∠A=∠B=∠C=∠D=90°.点E是BC的中点,点F是CD 1 上一点,且 CF = CD .求证:∠AEF=90°. 4
18。2 勾股定理逆定理(二)勾股数[下学期] 新人教版
![18。2 勾股定理逆定理(二)勾股数[下学期] 新人教版](https://img.taocdn.com/s3/m/43744006bed5b9f3f90f1c71.png)
4
学海中学 何邦辉
问题: 判断由线段a、b、c组成的三 角形是不是直角三角形?
(1) a=8 b = 15 c =17 c =15
(2) a=13 b = 14
像8、15、17这样,能够成为直角三角形三 条边长的三个正整数,称为勾股数。
谈谈勾股数的特征:
(1)a、b、c三数都是正整数,且a <c ,b <c .
数海拾贝
• 从代数的角度看勾股数,就是考察方程 x + y = z 的正 整数解,古代中国人发现了”勾三股四弦五”,古希腊人找 到了这个方程的全部整数解. 17世纪,法国数学家费马提出猜想:当n≥3时,方程 n n n x + y = z 无正整数解,围绕着这个看似简单的费 马大定理,一批杰出的数学家,如欧拉,柯西,伽罗华, 还有维尔斯,他们前赴后继用了整整358年才最后完成这 项证明. 费马大定理被人比作数论中的“喜马拉雅山的顶峰”
(1)请你根据上述四组勾股数的规律,写出第 五组勾股数。 (2)试用数学等式描述上述勾股数组规律。 (3)请证明你所发现的规律。
1、下列数组中,不是勾股数的是( D ) A、3k、4k、5k(k为正整数)B、5、12、13
C、7、24、25
D、8、12、13
2、已知下列命题: (1) 如果a、b、c是一组勾股数,那么 ka、 kb、kc( k是正整数)仍是勾股数。 (2) 如果直角三角形的两边是3、4,那么斜 边必是5。 (3) 如果一个三角形的三边是12、25、21,那 么此三角形必是直角三角形。 (4) 2499、100、2501是一组勾股数组。
(2) 三数符合
a b c
2 2
2
今天,我们将沿着前人的足迹, 去寻找这些勾股数组的规律!
勾股定理练习题及答案(共6套)

勾股定理课时练(1)1.在直角三角形ABC 中,斜边AB=1,则AB 222AC BC ++的值是()A.2B.4C.6D.82.如图18-2-4所示,有一个形状为直角梯形的零件ABCD ,AD ∥BC ,斜腰DC 的长为10cm ,∠D=120°,则该零件另一腰AB 的长是______cm (结果不取近似值).3.直角三角形两直角边长分别为5和12,则它斜边上的高为_______.4.一根旗杆于离地面12m 处断裂,犹如装有铰链那样倒向地6.飞机在空中水平飞行上方4000米处,过了209.如图,在四边形CD=3,求AB 的长10.如图,一个牧童在小河的南的小屋B 的西8km 2m 的楼道上铺地毯,已知地毯平方米18元,请你帮助计算一下,铺完这个楼道至少需要多少元钱?12.甲、乙两位探险者到沙漠进行探险,没有了水,需要寻找水源.为了不致于走散,他们用两部对话机联系,已知对话机的有效距离为15千米.早晨8:00甲先出发,他以6千米/时的速度向东行走,1小时后乙出发,他以5千米/时的速度向北行进,上午10:00,甲、乙二人相距多远?还能保持联系吗? 第一课时答案:1.A ,提示:根据勾股定理得122=+AC BC ,所以AB222AC BC ++=1+1=2;2.4,提示:由勾股定理可得斜边的长为5m ,而3+4-5=2m ,所以他们少走了4步.3.1360,提示:设斜边的高为x ,根据勾股定理求斜边为1316951222==+,再利用面积法得,136011米,由勾所以飞机飞行的速度为CE=60.2⨯,由勾股定理,得CF=)(3416302222cm EF CE =+=+8.解:在直角三角形ABC 中,根据勾股定理,得在直角三角形CBD 中,根据勾股定理,得CD 2=BC 2+BD 2=25+122=169,所以CD=13. 9.解:延长BC 、AD 交于点E.(如图所示)第5题图第8题∵∠B=90°,∠A=60°,∴∠E=30°又∵CD=3,∴CE=6,∴BE=8, 设AB=x ,则AE=2x ,由勾股定理。
八年级数学《勾股定理的逆定理》练习题含答案
八年级数学《勾股定理的逆定理》练习题一、填空题1.如果三角形的三边长a 、b 、c 满足a 2+b 2=c 2,那么这个三角形是______三角形,我们把这个定理叫做勾股定理的______.2.在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论是第二个命题的题设,那么这两个命题叫做____________;如果把其中一个命题叫做原命题,那么另一个命题叫做它的____________.3.分别以下列四组数为一个三角形的边长:(1)6、8、10,(2)5、12、13,(3)8、15、17,(4)4、5、6,其中能构成直角三角形的有____________.(填序号)4.在△ABC 中,a 、b 、c 分别是∠A 、∠B 、∠C 的对边,①若a 2+b 2>c 2,则∠c 为____________;②若a 2+b 2=c 2,则∠c 为____________;③若a 2+b 2<c 2,则∠c 为____________.5.若△ABC 中,(b -a )(b +a )=c 2,则∠B =____________;6.如图,正方形网格中,每个小正方形的边长为1,则网格上的△ABC 是______三角形.7.若一个三角形的三边长分别为1、a 、8(其中a 为正整数),则以a -2、a 、a +2为边的三角形的面积为______.8.△ABC 的两边a ,b 分别为5,12,另一边c 为奇数,且a +b +c 是3的倍数,则c 应为______,此三角形为______.二、选择题9.下列线段不能组成直角三角形的是( ).(A)a =6,b =8,c =10 (B)3,2,1===c b a (C)43,1,45===c b a (D)6,3,2===c b a 10.下面各选项给出的是三角形中各边的长度的平方比,其中不是直角三角形的是( ).(A)1∶1∶2 (B)1∶3∶4 (C)9∶25∶26 (D)25∶144∶16911.已知三角形的三边长为n 、n +1、m (其中m 2=2n +1),则此三角形( ).(A)一定是等边三角形 (B)一定是等腰三角形 (C)一定是直角三角形 (D)形状无法确定综合、运用、诊断一、解答题12.如图,在△ABC 中,D 为BC 边上的一点,已知AB =13,AD =12,AC =15,BD =5,求CD 的长.13.已知:如图,四边形ABCD 中,AB ⊥BC ,AB =1,BC =2,CD =2,AD =3,求四边形ABCD 的面积.14.已知:如图,在正方形ABCD 中,F 为DC 的中点,E 为CB 的四等分点且CE =CB 41,求证:AF ⊥FE .15.在B 港有甲、乙两艘渔船,若甲船沿北偏东60°方向以每小时8海里的速度前进,乙船沿南偏东某个角度以每小时15海里的速度前进,2小时后,甲船到M 岛,乙船到P 岛,两岛相距34海里,你知道乙船是沿哪个方向航行的吗?拓展、探究、思考16.已知△ABC 中,a 2+b 2+c 2=10a +24b +26c -338,试判定△ABC 的形状,并说明你的理由.17.已知a 、b 、c 是△ABC 的三边,且a 2c 2-b 2c 2=a 4-b 4,试判断三角形的形状.18.观察下列各式:32+42=52,82+62=102,152+82=172,242+102=262,…,你有没有发现其中的规律?请用含n 的代数式表示此规律并证明,再根据规律写出接下来的式子.勾股定理的逆定理1.直角,逆定理.2.互逆命题,逆命题.3.(1)(2)(3).4.①锐角;②直角;③钝角.5.90°.6.直角.7.24.提示:7<a<9,∴a=8.8.13,直角三角形.提示:7<c<17.9.D.10.C.11.C.112.CD=9.13..514.提示:连结AE,设正方形的边长为4a,计算得出AF,EF,AE的长,由AF2+EF2=AE2得结论.15.南偏东30°.16.直角三角形.提示:原式变为(a-5)2+(b-12)2+(c-13)2=0.17.等腰三角形或直角三角形.提示:原式可变形为(a2-b2)(a2+b2-c2)=0.18.352+122=372,[(n+1)2-1]2+[2(n+1)]2=[(n+1)2+1]2.(n≥1且n为整数)。
17.2勾股定理的逆定理2—子龙
A B
CD 2 3 AC 2 19
D
在等腰△ABC中,AB=AC=13cm ,BC=10cm, 求△ABC的面积和AC边上的高.
AD 12
S ABC 60
120 A BE 13
A
A
E
两个直角三角形中,如果有一条公共边, 可利用勾股定理建立方程求解 C B C B .
已知:如图,四边形ABCD中,∠A =900,AB=3, BC=12 ,CD=13 , AD=4,求四边形ABCD的面积?
SABCD 6 30 36 SABCD 30 6 24
A 4 3 B
D
3 4 A 13 12 C
如图BE⊥AE, ∠A=∠EBC=60°,AB=4,BC= 2 3 CD= 3 ,DE=3,求证:AD⊥CD
D
3
90
3
C
60° A 4
2
E
2 3 2 3
2 3 60°
B
一个零件的形状如左图所示,按规定这个零件中 ∠A和∠DBC都应为直角。工人师傅量得这个零件各 边尺寸如右图所示,这个零件符合要求吗?此时四 边形ABCD的面积是多少? C C 13 D D 30 12 46 5 A B A3 B
SABCD 6 30 36
如图,在△ABC中,AB=AC,D点在CB延长线上, A 求证:AD2-AB2=BD· CD 证明:过A作AE⊥BC于E D 在Rt △ADE中, AD2=AE2+DE2 在Rt △ABE中, AB2=AE2+BE2 ∴ AD2-AB2=(AE2+DE2)-(AE2+BE2) = DE2- BE2 = (DE+BE)· ( DE- BE) = (DE+CE)· ( DE- BE) =BD· CD ∵AB=AC,∴BE=CE
2022-2023学年人教版八年级数学下册《17-2勾股定理的逆定理》同步练习题(附答案)
2022-2023学年人教版八年级数学下册《17.2勾股定理的逆定理》同步练习题(附答案)一.选择题1.下列几组数据中,不能作为直角三角形的三条边的是()A.1,2,B.3,4,5C.1,,D.4,12,13 2.在△ABC中,若AB=3,BC=5,AC=,则下列说法正确的是()A.△ABC是锐角三角形B.△ABC是直角三角形且∠C=90°C.△ABC是钝角三角形D.△ABC是直角三角形且∠B=90°3.如果将直角三角形的三条边长同时扩大10倍,那么得到的三角形是()A.锐角三角形B.钝角三角形C.直角三角形D.不能确定4.下列各组数中,是勾股数的是()A.7,8,9B.6,8,10C.5,12,14D.3,4,65.在△ABC中,若AC2﹣BC2=AB2,则()A.∠A=90°B.∠B=90°C.∠C=90°D.∠A=45°6.如图,一个梯子AB斜靠在一竖直的墙AO上,测得AO=2m.若梯子的顶端沿墙下滑0.5米,这时梯子的底端也恰好外移0.5米,则梯子的长度AB为()A.2.5m B.3m C.1.5m D.3.5m7.如图,在以下四个正方形网格中,各有一个三角形,不是直角三角形的是()A.B.C.D.8.如图,正方形网格中,每一小格的边长为1.网格内有△P AB,则∠P AB+∠PBA的度数是()A.30°B.45°C.50°D.60°二.填空题9.一个三角形的三边长为8cm、17cm、15cm,则其面积为cm2.10.如图,已知∠BAC=90°,BC=,AB=1,AD=CD=1,则∠BAD=.11.如图,长方体木箱的长、宽、高分别为12cm,4cm,3cm,则能放进木箱中的直木棒最长为cm.12.观察下列几组勾股数,并填空:①6,8,10,②8,15,17,③10,24,26,④12,35,37,则第⑤组勾股数为.13.如图,露在水面上的鱼线BC长为6m,钓鱼者想看看鱼钩上的情况,把鱼竿AC转动到AC'的位置,此时露在水面上的鱼线B'C'为8m,若BB'的长为2m,则钓鱼竿AC的长为m.14.在平静的湖面上,有一朵荷花高出水面半尺,忽然一阵强风吹来把荷花垂直拉到水里且荷花恰好落在水面.花在水平方向上离开原来的位置2尺远,则这个湖的水深是尺.15.如图是某公园的一角,有人为了抄近道而避开路的拐角∠ABC(∠ABC=90°),于是在草坪内走出了一条不该有的“捷径路AC”.已知AB=8米,BC=6米,他们踩坏了米的草坪,只为少走米的路.16.图是屋架设计图的一部分,点E、F分别为斜梁AB、AC的中点,D为横梁BC的中点,EM⊥BC于点M,FN⊥BC于点N,若AB=AC=6m,∠BAC=120°,则EM+AD+FN 等于m,四边形AEDC的周长为m.三.解答题17.如图是一块地的平面图,AD=4m,CD=3m,AB=13m,BC=12m,∠ADC=90°,求这块地的面积.18.为了绿化环境,我市某中学有一块四边形的=空地ABCD,如图所示,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,DA=4m,BC=12m,CD=13m(1)求出空地ABCD的面积.(2)若每种植1平方米草皮需要300元,问总共需投入多少元?19.“某市道路交通管理条例”规定:小汽车在城市道路上行驶速度不得超过60千米/时,如图,一辆小汽车在一条城市道路上直道行驶,某一时刻刚好行驶到路面对车速检测仪A 正前方24米的C处,过了1.5秒后到达B处(BC⊥AC),测得小汽车与车速检测仪间的距离AB为40米,判断这辆小汽车是否超速?若超速,则超速了多少?若没有超速,说明理由.20.如图,有一艘货船和一艘客船同时从港口A出发,客船与货船速度的比为4:3,出发1小时后,客船比货船多走了5海里.货船沿东偏南10°方向航行,2小时后货船到达B 处,客船到达C处,若此时两船相距50海里.(1)求两船的速度分别是多少?(2)求客船航行的方向.21.《西江月》中描述:平地秋千未起,踏板一尺离地,送行二步恰竿齐,五尺板高离地…;翻译成现代文为:如图,秋千OA静止的时候,踏板离地高一尺(AC=1尺)将它往前推进两步(EB=10尺),此时踏板升高离地五尺(BD=5尺),求秋千绳索OB的长度.22.位于沈阳的红河峡谷漂流项目深受欢迎,在景区游船放置区,工作人员把偏离的游船从点A拉回点B的位置(如图).在离水面高度为8m的岸上点C,工作人员用绳子拉船移动,开始时绳子AC的长为17m,工作人员以0.35米/秒的速度拉绳子,经过20秒后游船移动到点D的位置,问此时游船移动的距离AD的长是多少?23.如图,南北向MN为我国领海线,即MN以西为我国领海,以东为公海.上午9时50分,我国反走私艇A发现正东方有一走私艇C以16海里/时的速度偷偷向我领海开来,便立即通知正在MN线上巡逻的我国反走私艇B密切注意.(1)如图1,若反走私艇A和走私艇C的距离是10海里,A、B两艇的距离是6海里;反走私艇B测得距离C艇8海里,若走私艇C的速度不变,则再过多少小时它会进入我国领海?(2)如图2,若反走私艇A和走私艇C的距离是12海里,A、B两艇的距离是8海里,反走私艇B测得距离C艇10海里,发现走私艇C时,反走私艇B便立即沿领海线MN 对走私艇C进行拦截.若要使拦截成功,假设走私艇C的速度不变,那么反走私艇B的速度至少应为多少海里/时?(结果中若有根号,则保留根号).参考答案一.选择题1.解:A、12+()2=22,符合勾股定理的逆定理,故能作为直角三角形的三边长;B、32+42=52,符合勾股定理的逆定理,故能作为直角三角形的三边长;C、12+()2=()2,符合勾股定理的逆定理,故能作为直角三角形的三边长;D、42+122≠132,不符合勾股定理的逆定理,故不能作为直角三角形的三边长.故选:D.2.解:在△ABC中,AB=3,BC=5,AC=,∴AC2=34,AB2+BC2=9+25=34,∴AC2=AB2+BC2,∴△ABC是直角三角形,∠B=90°,故选:D.3.解:设原直角三角形的两直角边分别为a,b,斜边为c,则a2+b2=c2,∵三条边长同时扩大10倍为10a,10b,10c,∴(10a)2+(10b)2=100a2+100b2=100(a2+b2)=100c2,∴(10c)2=100c2,∴(10a)2+(10b)2=(10c)2,∴如果将直角三角形的三条边长同时扩大10倍,那么得到的三角形是直角三角形,故选:C.4.解:A、72+82≠92,故不是勾股数,故选项不符合题意;B、62+82=102,能构成直角三角形,都是整数,是勾股数,故选项符合题意;C、52+122≠142,故不是勾股数,故选项不符合题意;D、32+42≠62,故不是勾股数,故选项不符合题意.故选:B.5.解:∵AC2﹣BC2=AB2,∴AC2=BC2+AB2,∴∠B=90°.故选:B.6.解:设BO=xm,依题意得:AC=0.5m,BD=0.5m,AO=2m.在Rt△AOB中,根据勾股定理得:AB2=AO2+OB2=22+x2,在Rt△COD中,根据勾股定理得:CD2=CO2+OD2=(2﹣0.5)2+(x+0.5)2,∴22+x2=(2﹣0.5)2+(x+0.5)2,解得:x=1.5,∴AB==2.5(m),即梯子的长度AB为2.5m,故选:A.7.解:选项A如图:A、∵AC2=12+32=10,BC2=12+22=5,AB2=12+42=17,∴△ABC不是直角三角形,故本选项符合题意;选项B如图:B、∵AC2=22+42=20,BC2=12+22=5,AB2=32+42=25,∴△ABC是直角三角形,故本选项不符合题意;选项C如图:C、∵AB2=22+22=8,AC2=22+22=8,BC2=16,∴△ABC是直角三角形,故本选项不符合题意;选项D如图:D、∵AC2=12+32=10,BC2=12+32=10,AB2=22+42=20,∴△ABC是直角三角形,故本选项不符合题意.故选:A.8.解:延长AP到点C,连接BC,如右图所示,由图可得,∠CPB=∠P AB+∠PBA,PC==,BC==,PB==,∴BC2+PC2=PB2,CP=CB,∴△BCP是等腰直角三角形,∴∠CPB=45°,∴∠P AB+∠PBA=45°,故选:B.二.填空题9.解:∵82+152=172,∴此三角形是直角三角形,∴此直角三角形的面积为:×8×15=60(cm2).故答案为:60.10.解:∵∠BAC=90°,BC=,AB=1,∴AC==,∵AD=CD=1,12+12=()2,AD2+CD2=AC2,∴∠D=90°,∴∠DAC=45°,∴∠BAD=90°﹣45°=45°.故答案为:45°.11.解:∵侧面对角线BC2=32+42=52,∴CB=5cm,∵AC=12cm,∴AB==13(cm),∴空木箱能放的最大长度为13cm,故答案为:13.12.解:根据题目给出的前几组数的规律可得:这组数中的第一个数是2(n+2),第二个是:(n+1)(n+3),第三个数是:(n+2)2+1,故可得第⑤组勾股数是14,48,50.故答案为:14,48,50.13.解:设AB′=xm,∵AC′=AC,∴AB′2+B′C′2=AB2+BC2,∴x2+82=(x+2)2+62.解得x=6,∴AB=8m,∴AC===10(m),故答案为:10.14.解:若设湖水的深度x尺.则荷花的长是(x+0.5)米.在直角三角形中,根据勾股定理,得:(x+0.5)2=x2+22,解之得:x=3.75,∴湖水的深度为3.75尺.故答案为:3.75.15.解:在Rt△ABC中,∠ABC=90°,AB=8米,BC=6米,∴AC===10(米),∴BC+AB﹣AC=6+8﹣10=4(米),∴他们踩坏了10米的草坪,只为少走4米的路,故答案为:10,4.16.解:∵AB=AC=6m,∠BAC=120°,D为横梁BC的中点,∴∠B=∠C=30°,∠BAD=∠DAC=60°,∵点E、F分别为斜梁AB、AC的中点,EM⊥BC于点M,FN⊥BC于点N,∴AE=AD=AB=3m,FN=EM=BE=AB=1.5m,∴△AED是等边三角形,∴EM+AD+FN=3+1.5+1.5=6(m),∵AD=3m,AC=6m,∴DC==3(m),∴四边形AEDC的周长为:3+3+3+6=(12+3)m.故答案为:6,(12+3).三.解答题17.解:如图,连接AC,∵AD=4,CD=3,∠ADC=90°,∴AC==5,∴S△ACD=6,在△ABC中,∵AC=5,BC=12,AB=13,∴AC2+BC2=AB2,∴△ABC为直角三角形,且∠ACB=90°,∴Rt△ABC的面积=30,∴四边形ABCD的面积=30﹣6=24.18.解:(1)连接BD,在Rt△ABD中,BD2=AB2+AD2=32+42=52,在△CBD中,CD2=132,BC2=122,而122+52=132,即BC2+BD2=CD2,∴∠DBC=90°,则S四边形ABCD=S△BAD+S△DBC=•AD•AB+DB•BC=×4×3+×12×5=36(平方米);(2)需费用36×300=10800(元).19.解:小汽车已超速,理由如下:根据题意得:AC=24米,AB=40米,∠ACB=90°,在Rt△ACB中,根据勾股定理得:BC===32(米),∵小汽车1.5秒行驶32米,∴小汽车行驶速度为76.8千米/时,∵76.8>60,∴小汽车已超速,超速76.8﹣60=16.8(千米/时).20.解:(1)设两船的速度分别是4x海里/小时和3x海里/小时,依题意得4x﹣3x=5.解得x=5,∴4x=20,3x=15,∴两船的速度分别是20海里/小时和15海里/小时;(2)由题可得,AB=15×2=30,AC=20×2=40,BC=50,∴AB2+AC2=BC2,∴△ABC是直角三角形,且∠BAC=90°,又∵货船沿东偏南10°方向航行,∴客船航行的方向为北偏东10°方向.21.解:设OA=OB=x尺,∵EC=BD=5尺,AC=1尺,∴EA=EC﹣AC=5﹣1=4(尺),OE=OA﹣AE=(x﹣4)尺,在Rt△OEB中,OE=(x﹣4)尺,OB=x尺,EB=10尺,根据勾股定理得:x2=(x﹣4)2+102,整理得:8x=116,即2x=29,解得:x=14.5.则秋千绳索的长度为14.5尺.22.解:在Rt△ABC中,∠ABC=90°,BC=8m,AC=17m,∴AB===15(m),∵工作人员以0.35米/秒的速度拉绳子,经过20秒后游船移动到点D的位置,∴CD=17﹣0.35×20=10(m),∴BD===6(m),∴AD=AB﹣BD=9(m).答:此时游船移动的距离AD的长是9m.23.解:(1)由题意,AC=10海里,AB=6海里,BC=8海里,∴AB2+BC2=AC2,∴∠ABC=90°.由面积法得AC•BE=AB•BC,即10BE=6×8,∴BE=.在Rt△BEC中,CE==,∵艇C的速度为16海里/时,∴所求的时间为÷16=,答:再过小时艇C会进入我国领海.(2)由题意,AC=12海里,AB=8海里,BC=10海里,设CE=x,由勾股定理,得AB2﹣AE2=BC2﹣CE2,即82﹣(12﹣x)2=102﹣x2,解得x=,∴CE==7.5,再由勾股定理,得BE==(海里)设反走私艇B的速度为y海里/时,则=,解得y=.检验可知y=是方程的解,且适合题意.答:反走私艇B的速度至少应为海里/时.。
《勾股定理》典型练习题
《勾股定理》典型例题分析一、知识要点:1、勾股定理勾股定理:直角三角形两直角边的平方和等于斜边的平方。
也就是说:假如直角三角形的两直角边为a、b,斜边为c ,那么 a2 + b2= c2。
公式的变形:a2 = c2- b2, b2= c2-a2 。
2、勾股定理的逆定理假如三角形ABC的三边长分别是a,b,c,且满足a2 + b2= c2,那么三角形ABC 是直角三角形。
这个定理叫做勾股定理的逆定理.该定理在应用时,同学们要注意处理好如下几个要点:①已知的条件:某三角形的三条边的长度.②满足的条件:最大边的平方=最小边的平方+中间边的平方.③得到的结论:这个三角形是直角三角形,并且最大边的对角是直角.④假如不满足条件,就说明这个三角形不是直角三角形。
3、勾股数满足a2 + b2= c2的三个正整数,称为勾股数。
注意:①勾股数必须是正整数,不能是分数或小数。
②一组勾股数扩大相同的正整数倍后,仍是勾股数。
常见勾股数有:(3,4,5)(5,12,13) (6,8,10)(7,24,25)(8,15,17)(9,12,15)4、最短距离问题:主要使用的依据是两点之间线段最短。
二、考点剖析考点一:利用勾股定理求面积1、求阴影局部面积:(1)阴影局部是正方形;(2)阴影局部是长方形;(3)阴影局部是半圆.2. 如图,以Rt△ABC的三边为直径分别向外作三个半圆,试探索三个半圆的面积之间的关系.3、如下图,分别以直角三角形的三边向外作三个正三角形,其面积分别是S 1、S 2、S 3,则它们之间的关系是( )A. S 1- S 2= S 3B. S 1+ S 2= S 3C. S 2+S 3< S 1D. S 2- S 3=S 14、四边形ABCD 中,∠B=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD 的面积。
5、在直线上依次摆放着七个正方形(如图4所示)。
已知斜放置的三个正方形的面积分别是1、2、3,正放置的四个正方形的面积依次是、=_____________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《勾股定理的逆定理2》习题
课堂练习
1.小强在操场上向东走80m 后,又走了60m ,再走100m 回到原地.小强在操场上向东走了80m 后,又走60m 的方向是 .
2.如图,在操场上竖直立着一根长为2米的测影竿,早晨测得它的影长为4米,中午测得它的影长为1米,则A 、B 、C 三点能否构成直角三角形?为什么?
3.如图,在我国沿海有一艘不明国籍的轮船进入我国海域,我海军甲、乙两艘巡逻艇立即从相距13海里的A 、B 两个基地前去拦截,六分钟后同时到达C 地将其拦截.已知甲巡逻艇每小时航行120海里,乙巡逻艇每小时航行50海里,航向为北偏西40°,问:甲巡逻艇的航向? 课后练习
1.一根24米绳子,折成三边为三个连续偶数的三角形,则三边长分别为 ,此三角形的形状为 . 2.一根12米的电线杆AB ,用铁丝AC 、AD 固定,现已知用去铁丝AC =15米,AD =13米,又测得地面上B 、C 两点之间距离是9米,B 、D 两点之间距离是5米,则电线杆和地面是否垂直,为什么?
3.如图,小明的爸爸在鱼池边开了一块四边形土地种了一些蔬菜,爸爸让小明计算一下土地的面积,以便计算一下产量.小明找了一卷米尺,测得AB =4米,BC =3米,CD =13米,DA =12米,又已知∠B =90°.
参考答案: 课堂练习: 1.向正南或正北.
2.能,因为BC 2=BD 2+CD 2=20,AC 2=AD 2+CD 2=5,AB 2=25,所以BC 2+AC 2= AB 2; 3.由△ABC 是直角三角形,可知∠CAB +∠CBA =90°,所以有∠CAB =40°,航向为北偏东50°. 课后练习:
1.6米,8米,10米,直角三角形;
2.△ABC 、△ABD 是直角三角形,AB 和地面垂直.
N
A
B
3.提示:连结AC.AC2=AB2+BC2=25,AC2+AD2=CD2,因此∠CAB=90°,S四边形=S△ADC+S△ABC=36平方米.。
