弹性力学平面问题
合集下载
6-3弹性力学平面问题(极坐标)

可通过微分关系直接由直角坐标系下的几何方程得到。 同前分析,当 0 时,
所以
即
四. 极坐标系下的物理方程
因、方向正交,则物理方程与直角坐标系下具有相同形式。 即 当为平面应变问题时,E1E、1 。
五. 极坐标系下的相容方程
极坐标系下如果用应力函数表示相容方程,体力必须为零 或关于 ( , ) 有势。
x y
2
f x f y (1 ) x y 0
f f 1 f 1
2
五. 极坐标系下的应力边界条件
设边界S的外法线方向与 、 方向的方向余弦分别为 l1、 l2 ,其上作用的面力沿、方向的分量分别为f、f 。则其 应力边界条件与直角坐标系下具有相同形式。 即
2
2 1 1 2 2 2 2
二. 极坐标系下的平衡微分方程
1. 直角坐标与极坐标系下的应力分量关系
(1)极坐标系下的应力分量和体力分量
O
如图,根据应力状态的定义, 过P 点分别以 方向和 方向为法线的截面 上的应力 、、 , 作为在极坐 标系下的应力分量。 称为径向应力, y 称为环向向应力。 (2)应力分量的坐标转换
d 1 d 2 0 d d
2 2
f 0
1 u
(不计体力)
f f 1
2
应力分量 边界条件
应力分量 (不计体力)
( ) s l1 ( ) s l2 f ( ) s l1 ( ) s l2 f
应力边界条件
位移边界条件
所以
即
四. 极坐标系下的物理方程
因、方向正交,则物理方程与直角坐标系下具有相同形式。 即 当为平面应变问题时,E1E、1 。
五. 极坐标系下的相容方程
极坐标系下如果用应力函数表示相容方程,体力必须为零 或关于 ( , ) 有势。
x y
2
f x f y (1 ) x y 0
f f 1 f 1
2
五. 极坐标系下的应力边界条件
设边界S的外法线方向与 、 方向的方向余弦分别为 l1、 l2 ,其上作用的面力沿、方向的分量分别为f、f 。则其 应力边界条件与直角坐标系下具有相同形式。 即
2
2 1 1 2 2 2 2
二. 极坐标系下的平衡微分方程
1. 直角坐标与极坐标系下的应力分量关系
(1)极坐标系下的应力分量和体力分量
O
如图,根据应力状态的定义, 过P 点分别以 方向和 方向为法线的截面 上的应力 、、 , 作为在极坐 标系下的应力分量。 称为径向应力, y 称为环向向应力。 (2)应力分量的坐标转换
d 1 d 2 0 d d
2 2
f 0
1 u
(不计体力)
f f 1
2
应力分量 边界条件
应力分量 (不计体力)
( ) s l1 ( ) s l2 f ( ) s l1 ( ) s l2 f
应力边界条件
位移边界条件
6-1弹性力学平面问题(基本理论)

l2 cos( N , y) cos
v 0 x x l
x ( sin ) xy cos 0 y cos yx ( sin ) 0
例6-3
图示薄板,在y方向受均匀拉力作用, 证明在板中间突出部分(1 2 )的尖 点A处无应力存在。
(a) (b)
(2) x C ( x 2 y 2 ), y Cy 2, xy 2Cxy;
解:(1) 将式(a)代入平衡方程:
x xy Fbx 0 x y yx y Fby 0 x y
3xy 2 3xy 2 0
y y 0
y
xy
x y y 0 p( x) p0 l (2) BC段(x l): l1 1, l2 0
u |x l 0, v |x l 0
u y 0,
x l
y 0
0
(3) AC段(y x tan):
l1 cos( N , x) cos(90 ) sin
( x ) s l1 ( yx ) s l2 px ( xy ) s l1 ( y ) s l2 p y
px p y 0
x x h 0
xy x h
0
右侧面: x h l1 1, l2 0 px y, p y 0 代入应力边界条件公式,有
l O x a b
z p
y
l a , l b ——近似认为无限长
2. 受力特征
外力(体力、面力)平行于横截面作用,且沿长度 z 方 向不变化。
如水坝、滚柱、厚壁圆筒等。
水坝 3. 简化分析
(1)位移分量
v 0 x x l
x ( sin ) xy cos 0 y cos yx ( sin ) 0
例6-3
图示薄板,在y方向受均匀拉力作用, 证明在板中间突出部分(1 2 )的尖 点A处无应力存在。
(a) (b)
(2) x C ( x 2 y 2 ), y Cy 2, xy 2Cxy;
解:(1) 将式(a)代入平衡方程:
x xy Fbx 0 x y yx y Fby 0 x y
3xy 2 3xy 2 0
y y 0
y
xy
x y y 0 p( x) p0 l (2) BC段(x l): l1 1, l2 0
u |x l 0, v |x l 0
u y 0,
x l
y 0
0
(3) AC段(y x tan):
l1 cos( N , x) cos(90 ) sin
( x ) s l1 ( yx ) s l2 px ( xy ) s l1 ( y ) s l2 p y
px p y 0
x x h 0
xy x h
0
右侧面: x h l1 1, l2 0 px y, p y 0 代入应力边界条件公式,有
l O x a b
z p
y
l a , l b ——近似认为无限长
2. 受力特征
外力(体力、面力)平行于横截面作用,且沿长度 z 方 向不变化。
如水坝、滚柱、厚壁圆筒等。
水坝 3. 简化分析
(1)位移分量
03第三章 弹性力学中的平面问题

yx
yx y
dy
xy x dx
x
xy
Q
xy
c
dx
dy
x
x dx x
yx
y
x
o
力平衡
y y
?
1、力矩平衡:Mc=0
( xy dx dx dx) dy L xy dy L x 2 2 xy
z ( x y )
xy 2(1 ) xy
E
三、平面问题的方程组 平衡方程:
x yx f 0 x x y xy y f 0 y x y
?
几何方程:
u x v y y u v xy y x
P
p
S
x 若微平面的法线平行于某坐标轴,例如 Z轴,正应力表示为Z则可将剪应力 沿另两坐标轴分解, 得:zx、zy
o
y
应力正负规定
?
如果截面上的法线方向是沿坐标轴的正方向,则该截面 称为一个正面,截面上的应力以沿坐标轴正方向为正。
y
如果截面上的法线方向是沿坐 标轴的负方向,则该截面称为 一个负面,截面上的应力以沿 坐标轴负方向为正。
yx
y
x
xy
o
x
?
以均匀的单向拉伸为例。设P为轴向拉力,F0为横截面积,则法向 与拉伸轴成角的平面上的全应力大小为:
S
P
F0 cos
P cos 0 cos F0
该面的正应力 和平行于该面的剪应力 分别为
S cos 0 cos 2 S sin 0 sin cos
弹性力学-第二章 平面问题基本理论 (徐芝纶第五版)
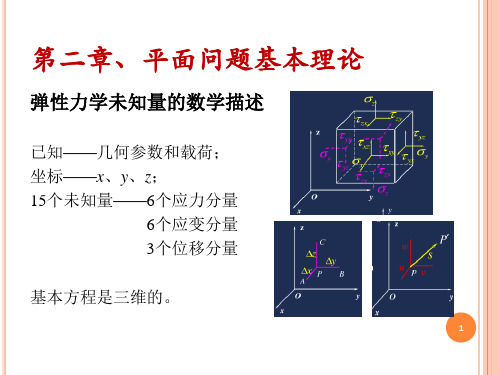
基本方程是二维的。
平面应力问题
平面应变问题
3
1.平面应力问题
支承板
z x
y
(2) 受力特性
外力(体力、面力)和约束,仅平行于 板面作用,沿z方向不变化。
(1) 几何特性
一个方向的尺寸比另两个 方向的尺寸小得多。
——平板
4
1.平面应力问题
(3) 应力特征
由于板面上不受力,有
sx =sx(x,y)
sy =sy(x,y)
53
54
55
56
习题
57
第二章 教学参考资料 (一)本章学习要求及重点
本章系统地介绍了平面问题的基本理论: 基本方程和边界条件,及两种基本解法。这 些内容在弹性力学中具有典型性和代表性。 因此,学好平面问题的基本理论,就可以方 便地学习其他各章。为此,我们要求学生深 入地理解本章的内容,掌握好以下几点:
)
f
y
0.
68
(2)用位移表示的应力边界条件
E
1
2
[l
(
u x
v
y
)m12
(
u y
v x
)]s
fx,
E
1
2
[m(
v y
u
x
)l12
(
u y
v x
)]s
fy.
(在s 上ss)
69
(3)位移边界条件
(u)s u , (v)s v.
(在Su上)
70
4、按应力求解平面问题(平面应力问题),
应力分量 σ x , σ y ,t x必y 须满足下列全部条件:
sx =sx(x,y) sy =sy(x,y) txy =txy(x,y) sz =sz (x,y) txz =tyz =0
平面应力问题
平面应变问题
3
1.平面应力问题
支承板
z x
y
(2) 受力特性
外力(体力、面力)和约束,仅平行于 板面作用,沿z方向不变化。
(1) 几何特性
一个方向的尺寸比另两个 方向的尺寸小得多。
——平板
4
1.平面应力问题
(3) 应力特征
由于板面上不受力,有
sx =sx(x,y)
sy =sy(x,y)
53
54
55
56
习题
57
第二章 教学参考资料 (一)本章学习要求及重点
本章系统地介绍了平面问题的基本理论: 基本方程和边界条件,及两种基本解法。这 些内容在弹性力学中具有典型性和代表性。 因此,学好平面问题的基本理论,就可以方 便地学习其他各章。为此,我们要求学生深 入地理解本章的内容,掌握好以下几点:
)
f
y
0.
68
(2)用位移表示的应力边界条件
E
1
2
[l
(
u x
v
y
)m12
(
u y
v x
)]s
fx,
E
1
2
[m(
v y
u
x
)l12
(
u y
v x
)]s
fy.
(在s 上ss)
69
(3)位移边界条件
(u)s u , (v)s v.
(在Su上)
70
4、按应力求解平面问题(平面应力问题),
应力分量 σ x , σ y ,t x必y 须满足下列全部条件:
sx =sx(x,y) sy =sy(x,y) txy =txy(x,y) sz =sz (x,y) txz =tyz =0
第七章_弹性力学平面问题的极坐标系解答讲解

在r = b边界(外径):
r= -qb,r=0
本问题仍为轴对称问题,且体力为零,
可采用前述的应力函数求解方程,也可按位移法求解。
1.按应力函数法求解
按应力函数求解前面已导出应力分量和位移表达式:
, ,
平面应力问题的位移:
法求解:
由基本方程 得
代入应力与位移之间关系式,对于平面应力问题,有
其中Brsin=By可略去。
将( r,)代入应力分量表达式
A、C、D由力的边界条件来定。
力的边界条件:在主要边界上,
在r = a:r= 0,r= 0, 2Aa+C/a-2D/a3= 0
在r = b:r= 0,r= 0, 2Ab+C/b-2D/b3= 0
在次要边界上,
在=0,环向方向的面力为零, 满足。
在= 0: 由于主要边界满足,则此式自然满足;
在= 0:
(3)
主要边界满足时,由(1)、(2)、(3)求出A、B、C,应力求出后,依次可求出应变和位移表达式,详细推导在徐芝纶(上册)P.91-92。
在徐芝纶(4-13)中I、K、H为刚体位移,I = u0、K = v0, H =。
可利用约束确定,如令r0=(a+b)/2,= 0处
应力分量表达代入几何方程的第一式并积分,得
——(b)
考虑位移单值性比较(a)和(b)式:
4Br-F=0B=F=0
轴对称问题的应力和位移解为:
, ,
,
A、C由两个力的边界条件确定。
对于无体力圆盘(或圆柱)的轴对称问题,
则根据圆盘(或圆柱)中心应力和
位移有限值,得
A=0
图示圆盘受力情况,得应力为r==2C= -q
然后,利用r = a时, ,得
r= -qb,r=0
本问题仍为轴对称问题,且体力为零,
可采用前述的应力函数求解方程,也可按位移法求解。
1.按应力函数法求解
按应力函数求解前面已导出应力分量和位移表达式:
, ,
平面应力问题的位移:
法求解:
由基本方程 得
代入应力与位移之间关系式,对于平面应力问题,有
其中Brsin=By可略去。
将( r,)代入应力分量表达式
A、C、D由力的边界条件来定。
力的边界条件:在主要边界上,
在r = a:r= 0,r= 0, 2Aa+C/a-2D/a3= 0
在r = b:r= 0,r= 0, 2Ab+C/b-2D/b3= 0
在次要边界上,
在=0,环向方向的面力为零, 满足。
在= 0: 由于主要边界满足,则此式自然满足;
在= 0:
(3)
主要边界满足时,由(1)、(2)、(3)求出A、B、C,应力求出后,依次可求出应变和位移表达式,详细推导在徐芝纶(上册)P.91-92。
在徐芝纶(4-13)中I、K、H为刚体位移,I = u0、K = v0, H =。
可利用约束确定,如令r0=(a+b)/2,= 0处
应力分量表达代入几何方程的第一式并积分,得
——(b)
考虑位移单值性比较(a)和(b)式:
4Br-F=0B=F=0
轴对称问题的应力和位移解为:
, ,
,
A、C由两个力的边界条件确定。
对于无体力圆盘(或圆柱)的轴对称问题,
则根据圆盘(或圆柱)中心应力和
位移有限值,得
A=0
图示圆盘受力情况,得应力为r==2C= -q
然后,利用r = a时, ,得
5第三章弹性力学平面问题的解析解法讲解

2 X Y 2 x y y 2 x 2 ( x y ) (1 )
(平面应力情形)
(3)边界条件:
l ( x ) s m( xy ) s X m( y ) s l ( xy ) s Y
x 2 y
2
y 2 x
2
xy
2 xy
(2-28)
(无体力情形)
(3) 再让 x , y , xy满足应力边界条件和位移单值条件 (多连体问题)。
第三章 弹性力学平面问题的 解析解法
第四节 第五节 逆解法与半逆解法—多项式解答 矩形梁的纯弯曲
(2)边界条件: 位移边界条件: 应力边界条件:
(1 )
u s u , vs v
(2)
E u v 1 u v l m X 2 y s 2 y x s 1 x (3 ) v u 1 v u E m l Y 2 1 y x s 2 x y s
4.
按应力求解平面问题的基本方程 说明:
(1)对位移边界问题,不易按应力 求解。
(1)平衡方程
x xy X 0 x y yx y Y 0 x y
(2)相容方程(形变协调方程)
(2)对应力边界问题,且为单连通 问题,满足上述方程的解是唯 一正确解。
(3)对多连通问题,满足上述方程 外,还需满足位移单值条件, 才是唯一正确解。
按应力求解平面问题(X = 常量、Y = 常量)的归结为: (1) 先由方程(2-27)求出应力函数: ( x ,7) 0 4 2 2 4 x x y y x , y , xy (2) 然后将 ( x , y ) 代入式(2-26)求出应力分量:
有限元2-弹性力学平面问题(24矩形单元,25六节点三角形单元)

u 1 1 2 3 4 u 2 1 2 3 4
u 3 1 2 3 4
u 4 1 2 3 4
有限单元法
土木工程学院
P-9/44
解方程组便可求得待定常数。将这些参数代回式 (2-4-4),经整理得:
(1,1)
有限单元法
土木工程学院
P-6/44
二、结点位移列阵和结点力列阵
每个结点2个位移分量,共8个位移分量, 设结点位移和结点力列阵分别为:
d u v u v u v u v
e
2 4 2 e T F X Y X Y X Y X Y 1 1 2 2 3 3 4 4 2 4 3
有限单元法
土木工程学院
P-18/44
第2章 弹性力学平面问题有限单元法
2.1 三角形单元 2.2 三角形单元中几个问题的讨论 2.3 平面问题有限元程序设计 2.4 矩形单元 2.5 六结点三角形单元 2.6 四结点四边形单元 2.7 八结点曲线四边形等参元 2.8 几个问题的补充
有限单元法
土木工程学院
3
1
2
(1 ,1 )
(1,1)
有限单元法
土木工程学院
P-11/44
如果引进参数: ξ0=ξiξ, η0=ηiη(i=1, 2, 3, 4), (ξi, ηi)是矩形单元4个结点的局部坐标。结点i(ξi, ηi)的 坐标值分别是 (-1,-1), (1,-1),(1,1), (-1,-1)。代入 上式,则可将上式简记成:
Ai Li A
Lj Aj A
Am Lm A
i
m
Aj
弹性力学平面问题总结

P
思考题
① 试证明微分体绕 z 轴的平均转动分量是
1 2 v x u . y
② 当应变为常量时,x=a, y=b, xy=c, 试 求对应的位移分量。
第二章 平面问题的基本理论
2-1 平面应力问题与平面应变问题 2-2 平衡微分方程 2-4 几何方程 刚体位移 2-5 物理方程
物理方程
物理方程描述应力分量和应变分量之间
z
x
y
z
x
y
xy
zx
zy
1 G 1 G 1 G
xy ,
xy
) E
0,
xy ,
zx ,
zx
zy .
zy
0.
物理方程
平面应力问题的物理方程:
x
y
1 E 1 E 2(1
x
y
, ,
y
x
) E
xy
xy .
此外, z
E
x
y
,
zx
zy
0.
平面应力问题,虽然 σz=0,但一般 εz≠0。
物理方程
平面应变问题: z
0,
(在V 中)
xy 存在。
故只有平面应力 σx , σy ,
平面应力问题
(2) 由于板为等厚度,外力、约束沿 z 向不变, 故应力 x , y , xy 仅为 f x , y 。
所以归纳为平面应力问题:
a.应力中只有平面应力 x , y , xy 存在;
b.且仅为 f x , y 。
几何方程
平面问题中的几何方程:
x
u , x
y
v , y
xy
v x
u . y
当弹性体的位移分量完全确定时,应变分 量即完全确定。反之,当应变分量完全确定时, 位移分量却不能完全确定。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
应力分量:
( z 0)
(非独立)
x , y , xy
应变分量:
——x,y的函数
x , y , xy
位移分量:
——x,y的函数
u u( x, y) v v( x, y)
第三章 弹性力学平面问题有限元法
平面应力问题的例子
§3.2
二、平面应变问题
弹性力学平面问题基础
第三章 弹性力学平面问题有限元法
§3.1
弹性力学基本概念
4)完全弹性假设 假设物体在外加因素去除后能完全恢复原来形状,没有剩余变形。 同时认为应力与应变呈线性关系,即服从虎克定律。 5)微小变形假设
假设物体在载荷作用下产生的位移远远小于物体的特征尺寸,
应变分量和转角均远小于1。 •上述5项假设中,前四个属于物理假设,符合前四个基本假设的称
0 x 1 0 y 1 xy 0 2
D
0 1 D E 2 1 0 ——平面应力弹性矩阵,对称方阵。 1 1 0 0 2 平面应变问题弹性矩阵可按如下办法得到。
• • •
这种平面问题模型下,所得到的结果能满足工程上的精度要求,
而分析计算工作量大大减少。
大量的固体力学问题都可以简化为平面问题。 平面问题包括:平面应力问题和平面应变问题。
第三章 弹性力学平面问题有限元法
§3.2
一、平面应力问题 •
弹性力学平面问题基础
平面应力问题的基本特征: 1)几何特征 物体在一个方向(z)的尺寸远远小于其它两个方向(x,y)的尺寸。 几何上为均匀薄板。 2)受力特征
§3.1
弹性力学基本概念
四、弹性力学中的基本量
• 弹性力学中用以描述研究对象状态的基本力学量包括:外力、应 力、应变、位移。 外力 1) 体积力(体力):物体内部单位体积上所受外力称为体力 (矢量)。如:重力、惯性力等。
2) 表面力(面力):物体表面单位面积上所受外力称为面力 (矢量)。如:静水压力、接触力等。
f x,f y为体力分量。
第三章
弹性力学平面问题有限元法
§3.2
四)平面问题边界条件
弹性力学平面问题基础
平面弹性体的边界分为位移边界
Su
和应力边界
St
通过前面的基本方程求解弹性力学 问题时,必须考虑上述边界上位移 的协调和力的平衡——边界条件。 边界条件描述如下: 1)位移边界条件
u u,v v
第三章
弹性力学平面问题有限元法
§3.1
•
弹性力学基本概念
弹性力学研究方法概述 1)研究弹性体内微分单元体的平衡,写出一组平衡微分方程; 2)由于平衡方程数少于未知应力数,必须考虑几何方面的关系:应 变分量和位移分量之间的微分方程。 3)再引入应力和应变之间的物理关系——广义虎克定律。 4)边界上单元体的内部应力和外部载荷之间的平衡,得到应力边界 条件;考虑边界位移约束得到位移边界条件。 上述基本方程和边界条件组成一个复杂的偏微分方程边值问题,
第三章
弹性力学平面问题有限元法
§3.1
一、弹性力学的任务 •
弹性力学基本概念
弹性力学是固体力学的分支学科,研究一般弹性体在外部因素 (力、温度变化等)作用下产生的应力、变形;并为机械零件、 工程结构的强度、刚度、稳定性分析提供理论工具。
• 弹性力学与材料力学和结构力学的比较:
1)基本任务相同 2)研究对象和范围有所区别 材料力学:研究杆状构件
结构力学:研究杆件系统
弹性力学:研究一般弹性体的一般行为。如二、三维实体,板壳 结构,应力集中体,无限、半无限体等。
第三章 弹性力学平面问题有限元法
§3.1
二、弹性力学的基本假设 •
弹性力学基本概念
为什么要作基本假设基本假设? 对实际研究对象根据所研究的层次和范围,进行科学抽象和假设, 突出主要矛盾,以建立可用的模型。
•平面应ห้องสมุดไป่ตู้问题的应力、应变、位移分量 由基本特征推出:
z zy zx 0 z 0
应变分量:
(非独立)
x , y , xy
——x,y的函数
应力分量:
x , y , xy
位移分量:
——x,y的函数
u u( x, y) v v( x, y)
将平面应力弹性矩阵中的弹性常数作如下变换: E 因此,对于平面问题的推导和编程, E 2 1 1 u 只按平面应力问题处理。
第三章 弹性力学平面问题有限元法
§3.2
三)平面问题的平衡方程
弹性力学平面问题基础
通过研究微分单元体平衡,得到下列平衡微分方程:
x xy fx 0 x y xy y fy 0 x y
为理想弹性体。第五个假设属于几何假设,符合该假设的理想弹性
体的问题称为线性弹性力学。
第三章
弹性力学平面问题有限元法
§3.1
三、弹性力学的研究方法
弹性力学基本概念
• 与材料力学研究方法的比较:
材料力学:除了引入“基本假设”,还根据不同对象引入补充假 设,如:直梁弯曲的“平面假设”,“纵向纤维无挤压”假设; 扭转理论中的“刚性平面”假设等。 弹性力学:除了必要的基本假设外,不再引入补充假设,而是严 格按照静力学、几何学、物理学三方面的条件建立基本方程和边 界条件,求得精确结果。因而弹性力学可以对材料力学的理论和 解答进行验证考核。
平面应变问题的例子
第三章
弹性力学平面问题有限元法
§3.2
弹性力学平面问题基础
三、平面问题基本方程和边界条件
•
平面应力和平面应变问题都归结为求解平面内的3个应力分量、3 个应变分量、2个位移分量。 要求解这些未知力学量,需要研究平面弹性体的平衡、几何、 物理关系得到足够的方程。
•
一)平面问题几何方程——应变~位移关系 u x x x x v y 0 y y xy u v xy y y x
可以确定弹性体中的位移场、应力场、应变场。
第三章 弹性力学平面问题有限元法
§3.1
弹性力学基本概念
• 弹性力学问题的求解策略
1)解析法—精确解 a. 应力解法 b. 位移解法 2)能量法(变分法)—近似解 3)数值法—近似解 a.有限差分法 b.有限元法 c.边界元法
第三章
弹性力学平面问题有限元法
1) 连续性假设
假设物体所占的空间被组成该物体的介质所充满,不留任何空隙。 不考虑介质的微观物质结构。物体内的物理量就能用空间坐标的连 续函数来描述。
2) 均匀性假设 认为物体由同一种材料组成,内部的物理性质处处完全相同。
3)各向同性假设
假设物体内每一点沿不同方向的物理性质相同,如弹性常数,导 热系数等。
几何方程对于平面应力和平面应变问题相同
0 u y v x
算子矩阵
第三章
弹性力学平面问题有限元法
§3.2
弹性力学平面问题基础
二)平面问题的物理方程——应力~应变关系
对于平面应力问题,应用虎克定律可导出应力与应变之间的关系。
x 1 y E 2 1 0 xy
•平面应变问题的基本特征: 1)几何特征
一个方向(z)尺寸远远大于其它两个方向(x,y)的尺寸,呈现为无 限长等截面柱体;或任何横截面可以看作对称面:z方向无位移。
2)受力特征
外力(体力、面力)平行于横截面作用,且沿纵向不变化。
平面应变问题的例子
第三章
弹性力学平面问题有限元法
§3.2
弹性力学平面问题基础
薄板上下两个面上无载荷作用; 周边侧面上受到平行于板面且沿板厚均匀分布的面力作用;
体力平行于板面且不沿板厚变化(x,y的函数)。
平 面 应 力 问 题 模 型
第三章
弹性力学平面问题有限元法
§3.2
•
弹性力学平面问题基础
平面应力问题的应力、应变、位移分量 由基本特征推出: z zx zy 0
x , y , z
3个剪应变: xy , yz , zx
第三章 弹性力学平面问题有限元法
§3.1
弹性力学基本概念
位移
弹性体受力变形后任意一点都产生位置的变化,形成一个位移
矢量,其在坐标轴上的投影(位移分量)用 u,v,w 表示。
• 一般情况下,各点的应力、应变、位移分量是其空间坐标的函数。
第三章
弹性力学平面问题有限元法
§3.2
弹性力学平面问题基础
•
弹性力学平面问题基础
任何实际变形体的力学问题都是空间问题(三维问题),所受的 外力一般都是空间力系。
•
在某些特殊情况下,比如物体具有特殊形状,受特殊的外力,特
殊的位移约束时,空间问题就可以简化成平面问题。此时,问题 的几何和力学量仅仅是二维坐标的函数。所求未知力学量只是二 维空间内的分量。
在弹性力学中体力、面力均为空间坐标的函数。
第三章
弹性力学平面问题有限元法
§3.1
弹性力学基本概念
应力
弹性体中某一点的应力状态用9个应力分量表示:
x , xy , xz
y , yz , yx
z , zx , zy
其中由于剪应力互等,只有6个独立分量。
应变
空间问题的一点应变分量包括: 3个正应变:
2)应力边界条件
在
Su 上
l,m为边界外法线方向余弦 t x,t y为边界上面力分量
l x m xy t x m y l xy t y
( z 0)
(非独立)
x , y , xy
应变分量:
——x,y的函数
x , y , xy
位移分量:
——x,y的函数
u u( x, y) v v( x, y)
第三章 弹性力学平面问题有限元法
平面应力问题的例子
§3.2
二、平面应变问题
弹性力学平面问题基础
第三章 弹性力学平面问题有限元法
§3.1
弹性力学基本概念
4)完全弹性假设 假设物体在外加因素去除后能完全恢复原来形状,没有剩余变形。 同时认为应力与应变呈线性关系,即服从虎克定律。 5)微小变形假设
假设物体在载荷作用下产生的位移远远小于物体的特征尺寸,
应变分量和转角均远小于1。 •上述5项假设中,前四个属于物理假设,符合前四个基本假设的称
0 x 1 0 y 1 xy 0 2
D
0 1 D E 2 1 0 ——平面应力弹性矩阵,对称方阵。 1 1 0 0 2 平面应变问题弹性矩阵可按如下办法得到。
• • •
这种平面问题模型下,所得到的结果能满足工程上的精度要求,
而分析计算工作量大大减少。
大量的固体力学问题都可以简化为平面问题。 平面问题包括:平面应力问题和平面应变问题。
第三章 弹性力学平面问题有限元法
§3.2
一、平面应力问题 •
弹性力学平面问题基础
平面应力问题的基本特征: 1)几何特征 物体在一个方向(z)的尺寸远远小于其它两个方向(x,y)的尺寸。 几何上为均匀薄板。 2)受力特征
§3.1
弹性力学基本概念
四、弹性力学中的基本量
• 弹性力学中用以描述研究对象状态的基本力学量包括:外力、应 力、应变、位移。 外力 1) 体积力(体力):物体内部单位体积上所受外力称为体力 (矢量)。如:重力、惯性力等。
2) 表面力(面力):物体表面单位面积上所受外力称为面力 (矢量)。如:静水压力、接触力等。
f x,f y为体力分量。
第三章
弹性力学平面问题有限元法
§3.2
四)平面问题边界条件
弹性力学平面问题基础
平面弹性体的边界分为位移边界
Su
和应力边界
St
通过前面的基本方程求解弹性力学 问题时,必须考虑上述边界上位移 的协调和力的平衡——边界条件。 边界条件描述如下: 1)位移边界条件
u u,v v
第三章
弹性力学平面问题有限元法
§3.1
•
弹性力学基本概念
弹性力学研究方法概述 1)研究弹性体内微分单元体的平衡,写出一组平衡微分方程; 2)由于平衡方程数少于未知应力数,必须考虑几何方面的关系:应 变分量和位移分量之间的微分方程。 3)再引入应力和应变之间的物理关系——广义虎克定律。 4)边界上单元体的内部应力和外部载荷之间的平衡,得到应力边界 条件;考虑边界位移约束得到位移边界条件。 上述基本方程和边界条件组成一个复杂的偏微分方程边值问题,
第三章
弹性力学平面问题有限元法
§3.1
一、弹性力学的任务 •
弹性力学基本概念
弹性力学是固体力学的分支学科,研究一般弹性体在外部因素 (力、温度变化等)作用下产生的应力、变形;并为机械零件、 工程结构的强度、刚度、稳定性分析提供理论工具。
• 弹性力学与材料力学和结构力学的比较:
1)基本任务相同 2)研究对象和范围有所区别 材料力学:研究杆状构件
结构力学:研究杆件系统
弹性力学:研究一般弹性体的一般行为。如二、三维实体,板壳 结构,应力集中体,无限、半无限体等。
第三章 弹性力学平面问题有限元法
§3.1
二、弹性力学的基本假设 •
弹性力学基本概念
为什么要作基本假设基本假设? 对实际研究对象根据所研究的层次和范围,进行科学抽象和假设, 突出主要矛盾,以建立可用的模型。
•平面应ห้องสมุดไป่ตู้问题的应力、应变、位移分量 由基本特征推出:
z zy zx 0 z 0
应变分量:
(非独立)
x , y , xy
——x,y的函数
应力分量:
x , y , xy
位移分量:
——x,y的函数
u u( x, y) v v( x, y)
将平面应力弹性矩阵中的弹性常数作如下变换: E 因此,对于平面问题的推导和编程, E 2 1 1 u 只按平面应力问题处理。
第三章 弹性力学平面问题有限元法
§3.2
三)平面问题的平衡方程
弹性力学平面问题基础
通过研究微分单元体平衡,得到下列平衡微分方程:
x xy fx 0 x y xy y fy 0 x y
为理想弹性体。第五个假设属于几何假设,符合该假设的理想弹性
体的问题称为线性弹性力学。
第三章
弹性力学平面问题有限元法
§3.1
三、弹性力学的研究方法
弹性力学基本概念
• 与材料力学研究方法的比较:
材料力学:除了引入“基本假设”,还根据不同对象引入补充假 设,如:直梁弯曲的“平面假设”,“纵向纤维无挤压”假设; 扭转理论中的“刚性平面”假设等。 弹性力学:除了必要的基本假设外,不再引入补充假设,而是严 格按照静力学、几何学、物理学三方面的条件建立基本方程和边 界条件,求得精确结果。因而弹性力学可以对材料力学的理论和 解答进行验证考核。
平面应变问题的例子
第三章
弹性力学平面问题有限元法
§3.2
弹性力学平面问题基础
三、平面问题基本方程和边界条件
•
平面应力和平面应变问题都归结为求解平面内的3个应力分量、3 个应变分量、2个位移分量。 要求解这些未知力学量,需要研究平面弹性体的平衡、几何、 物理关系得到足够的方程。
•
一)平面问题几何方程——应变~位移关系 u x x x x v y 0 y y xy u v xy y y x
可以确定弹性体中的位移场、应力场、应变场。
第三章 弹性力学平面问题有限元法
§3.1
弹性力学基本概念
• 弹性力学问题的求解策略
1)解析法—精确解 a. 应力解法 b. 位移解法 2)能量法(变分法)—近似解 3)数值法—近似解 a.有限差分法 b.有限元法 c.边界元法
第三章
弹性力学平面问题有限元法
1) 连续性假设
假设物体所占的空间被组成该物体的介质所充满,不留任何空隙。 不考虑介质的微观物质结构。物体内的物理量就能用空间坐标的连 续函数来描述。
2) 均匀性假设 认为物体由同一种材料组成,内部的物理性质处处完全相同。
3)各向同性假设
假设物体内每一点沿不同方向的物理性质相同,如弹性常数,导 热系数等。
几何方程对于平面应力和平面应变问题相同
0 u y v x
算子矩阵
第三章
弹性力学平面问题有限元法
§3.2
弹性力学平面问题基础
二)平面问题的物理方程——应力~应变关系
对于平面应力问题,应用虎克定律可导出应力与应变之间的关系。
x 1 y E 2 1 0 xy
•平面应变问题的基本特征: 1)几何特征
一个方向(z)尺寸远远大于其它两个方向(x,y)的尺寸,呈现为无 限长等截面柱体;或任何横截面可以看作对称面:z方向无位移。
2)受力特征
外力(体力、面力)平行于横截面作用,且沿纵向不变化。
平面应变问题的例子
第三章
弹性力学平面问题有限元法
§3.2
弹性力学平面问题基础
薄板上下两个面上无载荷作用; 周边侧面上受到平行于板面且沿板厚均匀分布的面力作用;
体力平行于板面且不沿板厚变化(x,y的函数)。
平 面 应 力 问 题 模 型
第三章
弹性力学平面问题有限元法
§3.2
•
弹性力学平面问题基础
平面应力问题的应力、应变、位移分量 由基本特征推出: z zx zy 0
x , y , z
3个剪应变: xy , yz , zx
第三章 弹性力学平面问题有限元法
§3.1
弹性力学基本概念
位移
弹性体受力变形后任意一点都产生位置的变化,形成一个位移
矢量,其在坐标轴上的投影(位移分量)用 u,v,w 表示。
• 一般情况下,各点的应力、应变、位移分量是其空间坐标的函数。
第三章
弹性力学平面问题有限元法
§3.2
弹性力学平面问题基础
•
弹性力学平面问题基础
任何实际变形体的力学问题都是空间问题(三维问题),所受的 外力一般都是空间力系。
•
在某些特殊情况下,比如物体具有特殊形状,受特殊的外力,特
殊的位移约束时,空间问题就可以简化成平面问题。此时,问题 的几何和力学量仅仅是二维坐标的函数。所求未知力学量只是二 维空间内的分量。
在弹性力学中体力、面力均为空间坐标的函数。
第三章
弹性力学平面问题有限元法
§3.1
弹性力学基本概念
应力
弹性体中某一点的应力状态用9个应力分量表示:
x , xy , xz
y , yz , yx
z , zx , zy
其中由于剪应力互等,只有6个独立分量。
应变
空间问题的一点应变分量包括: 3个正应变:
2)应力边界条件
在
Su 上
l,m为边界外法线方向余弦 t x,t y为边界上面力分量
l x m xy t x m y l xy t y
