第6章应力状态与强度理论.
应力状态分析与强度理论-习题与答案
（A）受力构件横截面上各点的应力情况
（B）受力构件各点横截面上的应力情况
（C）构件未受力之前，各质点之间的相互作用力状况
（D）受力构件内某一点在不同横截面上的应力情况
2、一实心均质钢球，当其外表面迅速均匀加热，则球心O点处的应力状态是（）
（A）单向拉伸应力状态（B）平面应力状态
（A）铸铁为塑性材料
（B）铸铁在三向压应力状态下产生塑性变形
（C）铸铁在单向压应力作用下产生弹性变形
（D）材料剥脱
7、混凝土立方试块在作单向压缩试验时，若在其上、下表面上涂有润滑剂，则试块破坏时将沿纵向裂开，其主要原因是（）
（A）最大压应力（B）最大剪应力
（C）最大伸长线应变（D）存在横向拉应力
8、一中空钢球，内径d＝20cm，内压p＝15Mpa，材料的许用应力 ＝160Mpa，则钢球壁厚t只少是（）
（A）t＝47㎜（B）t＝2.34㎜
（C）t＝4.68㎜（D）t＝9.38㎜
9、将沸水注入厚玻璃杯中，有时玻璃杯会发生破裂，这是因为（）
（A）热膨胀时，玻璃杯环向线应变达到极限应变，从内、外壁同时发生破裂
（B）玻璃材料抗拉能力弱，玻璃杯从外壁开始破裂
（C）玻璃材料抗拉能力弱，玻璃杯从内壁开始破裂
（D）水作用下，玻璃杯从杯底开始破裂
因圆柱与钢筒之间的空隙 ，而 > ，故圆柱受钢筒弹性约束。设柱与筒之间的作用力为p，则铝柱中各点处主应力为
钢筒中各点处主应力为
设铝柱和钢筒的径向应变分别为 ，变形协变条件为
即
于是
得
p＝2.74Mpa
故钢筒周向应力为
即
得
所以则其相当应力为
由于 <0.5
材料力学应力状态和强度理论
x 122.5MPa x 64.6MPa
σy 0
τ y 64.6
(122.5 , 64.6)
D1
B2
o
C
B1
(0 , - 64.6)
由 x ， x 定出 D1 点 由 y ， y 定出 D2 点 以 D1D2 为直径作应力圆。
D2
A1，A2 两点的横坐标分别代表 a 点的两个主应力
1 oA1 150MPa
1 x 136.5MPa
σ x 136.5MPa σy 0
τx0 τy0
2 3 0
D2 (0,0)
D1(136.5,0)
x 136.5MPa
b
σ1
σ x 136.5MPa τ x 0
σy 0
τy0
1 所在的主平面就是 x 平面 , 即梁的横截面 C 。
解析法求 a 点的主平面和主应力
解： x 100MPa, y 20MPa, x 40MPa, 300
20
300
100 40
x 100MPa, y 20MPa, x 40MPa, 300
x
2
y
x
2
y
cos
2
x
sin
2
x
2
y
sin
2
x
cos
2
300
100
(20) 2
100
(20) 2
cos( 600)
m
F
A
F
m
A
F
F
A
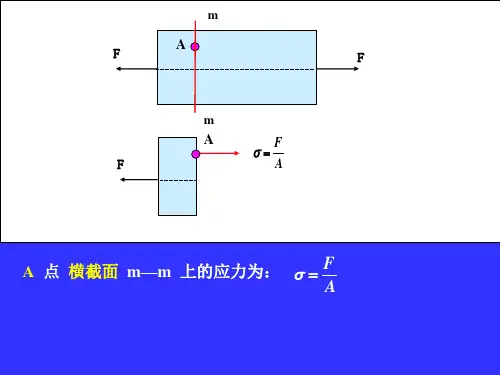
A 点 横截面 m—m 上的应力为： F
A
n
m
F
A
F
m
n
F
A
2
应力状态与强度理论
理论理论能很好的解释石料或混凝土等脆性材 料受轴向压缩时的断裂破坏。
3、最大剪应力理论（第三强度理论）：
理论认为最大剪应力是引起塑性屈服的主要 因素，只要最大剪应力τmax达到与材料性质 有关的某一极限值，材料就发生屈服。
单向拉伸下，当与轴线成45。的斜截面上的
τmax= s/2时
任意应力状态下
莫尔强度条件为：
1
Байду номын сангаас
t c
3
t
对于拉压强度不同的脆性材料，如铸铁、 岩石和土体等，在以压为主的应力状态下， 该理论与试验结果符合的较好。
综合以上强度理论所建立的强度条件， 可以写出统一的形式： σr≤[σ]
σr称为相当应力
r1 1
r2 1 2 3
r3 1 3
r4
1 2
理论理论能很好的解释石料或混凝土等脆性材 料受轴向压缩时，沿纵向发生的断裂破坏。
2、最大伸长线应变理论(第二强度理论)：
理论认为最大伸长线应变是引起断裂的主要因素。
拉断时伸长线应变的极限值为
断裂准则为：
1
1 E
1
2
11
b
E
3
1 2 3 b
第二强度理论的强度条件：
1 2 3
max
1 3
2
屈服准则： 1 3 s
2
2
1 3 s
第三强度理论建立的强度条件为：
1 3
在机械和钢结构设计中常用此理论。
4、形状改变比能理论(第四强度理论)：
第四强度理论认为： 形状改变比能是引起塑性屈服的主要因素。
单向拉伸时，
1
3E
s
2的形状改变比能。
应力状态的概念
应力状态与强度理论\应力状态的概念
应力状态的概念
1.1 一点处的应力状态
在工程中，只知道杆件横截面上的应力是不够的。例如，在铸 铁试件压缩时，沿与轴线大约成45°左右的斜截面发生破坏（如 图），这是由于在与轴线成45°的斜截面上存在最大切应力所引起 的。
目录
应力状态与强度理论\应力状态的概念
力的影响。
为了分析破坏现象以及解决复杂受力构件的强度问题，必须首
先研究通过受力构件内一点处所有截面上应力的变化规律。我们把
通过受力构件内一点处不同方位的截面上应力的大小和方向情况，
称为一点处的应力状态。
目录
应力状态与强度理论\应力状态的概念
1.2 应力状态的表示
为了研究受力构件内一点处的应力状态，可围绕该点取出一个 微小的正六面体，称为单元体，并分析单元体六个面上的应力。由 于单元体的边长无限小，可以认为在单元体的每个面上应力都是均 匀分布的；且在单元体内相互平行的截面上应力都是相同的。
力状态。例如从地层深处某点取出的单元体，它在三个方向都受到 压力的作用，处于空间应力状态（如图）。
目录
应力状态与强度理论\应力状态的概念 若平面应力状态的单元体中，正应力都等于零，仅有切应力作
用，称为纯剪切应力状态，例如图所示的应力状态。
目录
应力状态与强度理论\应力状态的概念 应力状态也可以按主应力的情况分类。若单元体的三个主应力
如果知道了单元体的三个互相垂直平面上的应力，则其他任意 截面上的应力都可以通过截面法求得（详见8.2.1），那末该点处的 应力状态就可以确定了。因此，可用单元体的三个互相垂直平面上 的应力来表示一点处的应力状态。
目录
应力状态与强度理论\应力状态的概念
第二篇第六章（第十章）应力状态与强度理论
第⼆篇第六章（第⼗章）应⼒状态与强度理论第⼗章应⼒状态与强度理论第⼀节概述前述讨论了构件横截⾯上的最⼤应⼒与材料的试验许⽤应⼒相⽐较⽽建⽴了只有正应⼒或只有剪应⼒作⽤时的强度条件。
但对于分析进⼀步的强度问题是远远不够的。
实际上，不但横截⾯上各点的应⼒⼤⼩⼀般不同，即使同⼀点在不同⽅向的截⾯上，应⼒也是不同的。
例.直杆轴向拉伸(压缩时)斜截⾯上的应⼒.上例说明构件在复杂受⼒情况下，最⼤应⼒并不都在横截⾯上，从⽽需要分析⼀点的应⼒状态。
⼀、⼀点的应⼒状态凡提到“应⼒”，必须指明作⽤在哪⼀点，哪个（⽅向）截⾯上。
因为不但受⼒构件内同⼀截⾯上不同点的应⼒⼀般是不同的。
即使通过同⼀点不同（⽅向）截⾯上应⼒也是不同的。
⼀点处的应⼒状态就是指通过⼀点不同截⾯上的应⼒情况的总和。
或者说我们把过构件内某点所有⽅位截⾯上应⼒情况的总体称为⼀点的应⼒状态。
下图为通过轴向拉伸构件内某点不同（⽅向）截⾯上的应⼒情况。
⽽本章就是要研究这些不同⽅位截⾯上应⼒随截⾯⽅向的变化规律。
并以此为基础建⽴复杂受⼒(既有正应⼒，⼜有剪应⼒)时的强度条件。
⼆、⼀点应⼒状态的描述1、微元法：在⼀般情况下，总是围绕所考察的点作⼀个三对⾯互相垂直的微正六⾯体，当各边边长充分⼩并趋于零时，六⾯体便趋于宏观上的“点”，这种六⾯体称为“微单元体”，简称“微元”。
当微元三对⾯上的应⼒已知时，就可以应⽤截⾯法和平衡条件，求得过该点任意⽅位⾯上的应⼒。
因此，通过微元及其三对互相垂直的⾯上的应⼒情况，可以描述⼀点的应⼒状态。
上图为轴向拉伸杆件内围绕m点截取的两种微元体。
根据材料的连续均匀假设以及整体平衡则局部平衡即微元体也平衡的原则，微元体（代表⼀个材料点）各微⾯上应⼒特点如下：（1）各微⾯上应⼒均匀分布；（2）相互平⾏的两个侧⾯上应⼒⼤⼩相等、⽅向相反；（3）互相垂直的两个侧⾯上剪应⼒服从剪切互等定律。
（在相互垂直的两个平⾯上，剪应⼒必然成对存在，且⼤⼩相等，两者都垂直于两个平⾯的交线，⽅向则共同指向或共同背离这⼀交线。
材料力学第06章 复杂应力状态分析及强度理论
2
s′
p
A πD
πD 2 F p 4 pD s A πD 4
n
D
（2）假想用一直径平面将圆筒截分为二,并取下半环为研究对象
s"
p
直径平面
FN
Ｏ
FN
d
y
D Fy 0 0 pl 2 sin d plD pD 2s l plD 0 s 2
理论分析表明，在复杂应力状态下（平面应力状态和空 间应力状态），一点处的最大正应力为 s max s 1 ，最小 正应力为 s min s 3 ，最大切应力的值为t s 1 s 3。
max
2
例题1 简支梁如图所示.已知 m-m 截面上A点的弯曲正应力和 切应力分别为s =-70MPa,t =50MPa.确定A点的主应力及主平面 的方位.
t xy
s x s y 0
txy
Mn t xy t WP
求极值应力
tyx
y O
s x s y 2 2 s 1 s x s y （ ）t xy 2 2 s 2
2 t xy t
x
s 1t ;s 2 0;s 3 t
s x s y 2 2 t max （ ）t xy t 2 t min
铸铁
在圆杆的扭转试验中，对于剪切强度低于拉伸强度的材料(例如低碳 钢)，破坏是从杆的最外层沿横截面发生剪断产生的(图c)，而对于 拉伸强度低于剪切强度的材料(例如铸铁)，其破坏是由杆的最外层 沿杆轴线约成450倾角的螺旋形曲面发生拉断而产生的(图d)
2
平面应力状态分析——图解法
一、应力圆（ Stress Circle）
2 2
材料力学——第6章(应力状态分析及强度理论)
t min
2t x tan 2 0 = s x s y
t max s max s min = R半 径 = 2 t min
s x s y 2 2 （ ） t x 2
25
[例6-4]求 ⑴图示单元体α =300 斜截面上的应力 ⑵主应力、主平面（单位：MPa）。
40
§6–1 应力状态概述
§6-2 平面应力状态分析
§6-3 三向应力状态分析 §6-4 广义胡克定律 §6-5 工程中常用的四种强度理论
1
拉压
扭转
弯曲
y
y
y
C
s max 压 s max 拉 s max
截面 应力 危险点
应力状态
C
o
FN
s=smax smax
MT
t max
M
t max
2
S平面
n
F
1
sx 面上的应力(s ，t )
tx
y x t n D( s , t C O B(sy ,ty) 2 O
面的法线
两面夹角 两半径夹角2 ； 且转向一致。 x
A(sx ,tx)
s
23
ty
sy s t
n
t D = DC sin[ 180 ( 2 0 2 )]
O
sx sy
图2
ty
px t
同理： t = p x sin p y cos
= s x cos t y sin sin t y cos s y sin cos
经简化 得
s x s y t = sin 2 t x cos 2 2
s
sx sy
材料力学第六章 应力状态理论和强度理论
单元体的各个面均为主平面，其上的主应力为： 单元体的各个面均为主平面，其上的主t
9
工程力学
Engineering mechanics
§6-1 应力状态理论的概念 和实例
3、三向应力状态（空间应力状态） 、三向应力状态（空间应力状态） 定义：三个主应力均不为零。 定义：三个主应力均不为零。 例如：导轨与滚轮接触点处，取导轨表面任一点 的单元体 的单元体， 例如：导轨与滚轮接触点处，取导轨表面任一点A的单元体， 它各侧面均受到压力作用，属于三向应力状态。 它各侧面均受到压力作用，属于三向应力状态。
工程力学
Engineering mechanics
第六章 应力状态理论 和强度理论
1
工程力学
Engineering mechanics
引
言
前面的分析结果表明， 前面的分析结果表明，在一般情况下杆件横截面上不同点 的应力是不相同的，过一点不同方向面上的应力也是不相同的。 的应力是不相同的，过一点不同方向面上的应力也是不相同的。 因此，当提及应力时，必须明确“哪一个面上哪一点” 因此，当提及应力时，必须明确“哪一个面上哪一点”的应力或 哪一点哪一个方向面上”的应力。 者“哪一点哪一个方向面上”的应力。 如果危险点既有正应力，又有切应力，应如何建立其强度 如果危险点既有正应力，又有切应力， 条件？ 条件？ 如何解释受力构件的破坏现象？ 如何解释受力构件的破坏现象？ 对组合变形杆应该如何进行强度计算？ 对组合变形杆应该如何进行强度计算？ 要全面了解危险点处各截面的应力情况。 要全面了解危险点处各截面的应力情况。
2
工程力学
Engineering mechanics
§6-1 应力状态理论的概念 和实例
一、一点的应力状态 定义：过受力体内一点所有方向面上应力的集合。 定义：过受力体内一点所有方向面上应力的集合。 一点的应力状态的四要素 四要素： 一点的应力状态的四要素： ）、应力作用点的坐标 （1）、应力作用点的坐标； ）、应力作用点的坐标； ）、过该点所截截面的方位 （2）、过该点所截截面的方位； ）、过该点所截截面的方位； ）、应力的大小 （3）、应力的大小； ）、应力的大小； ）、应力的类型 （4）、应力的类型。 ）、应力的类型。 二、研究应力状态的目的 对受到轴向拉伸（压缩）、扭转、弯曲等基本变形的杆件， 对受到轴向拉伸（压缩）、扭转、弯曲等基本变形的杆件， ）、扭转 其危险点处于单向应力状态或纯剪切应力状态，受力简单， 其危险点处于单向应力状态或纯剪切应力状态，受力简单，可直 接由相应的试验确定材料的极限应力，建立相应的强度条件。 接由相应的试验确定材料的极限应力，建立相应的强度条件。
应力状态分析和强度理论
03
弹性极限
材料在弹性范围内所能承受的最大应力状态，当超过这一极限时，材料会发生弹性变形。
01
屈服点
当物体受到一定的外力作用时，其内部应力状态会发生变化，当达到某一特定应力状态时，材料会发生屈服现象。
02
强度极限
材料所能承受的最大应力状态，当超过这一极限时，材料会发生断裂。
应力状态对材料强度的影响
形状改变比能准则
04
弹塑性材料的强度分析
屈服条件
屈服条件是描述材料在受力过程中开始进入屈服（即非弹性变形）的应力状态，是材料强度分析的重要依据。
根据不同的材料特性，存在多种屈服条件，如Mohr-Coulomb、Drucker-Prager等。
屈服条件通常以等式或不等式的形式表示，用于确定材料在复杂应力状态下的响应。
最大剪切应力准则
总结词
该准则以形状改变比能作为失效判据，当形状改变比能超过某一极限值时发生失效。
详细描述
形状改变比能准则基于材料在受力过程中吸收能量的能力。当材料在受力过程中吸收的能量超过某一极限值时，材料会发生屈服和塑性变形，导致失效。该准则适用于韧性材料的失效分析，尤其适用于复杂应力状态的失效判断。
高分子材料的强度分析
01
高分子材料的强度分析是工程应用中不可或缺的一环，主要涉及到对高分子材料在不同应力状态下的力学性能进行评估。
02
高分子材料的强度分析通常采用实验方法来获取材料的应力-应变曲线，并根据曲线确定材料的屈服极限、抗拉强度等力学性能指标。
03
高分子材料的强度分析还需要考虑温度、湿度等环境因素的影响，因为高分子材料对环境因素比较敏感。
02
强度理论
总结词
该理论认为最大拉应力是导致材料破坏的主要因素。
应力分析和强度理论
要点二
详细描述
在机械工程领域，应力分析用于研究 机械零件和结构在各种工况下的受力 情况，以及由此产生的内部应力分布 。强度理论则用于评估这些应力是否 在材料的承受范围内，以确定结构是 否安全可靠。
要点三
应用举例
在机械设计中，通过对发动机、传动 系统、轴承等关键部件进行应力分析 ，可以优化设计，提高其承载能力和 可靠性。
该理论认为最大拉应力是导致材料破坏的 主要因素，当最大拉应力达到材料的极限 抗拉强度时，材料发生断裂。
第二强度理论
总结词
最大剪应力理论
详细描述
该理论认为最大剪应力是导致材料破坏的主 要因素，当最大剪应力达到材料的极限抗剪 强度时，材料发生断裂。
第三强度理论
总结词
最大应变能密度理论
详细描述
该理论认为最大应变能密度是导致材料破坏 的主要因素，当最大应变能密度达到材料的
应力分析
目录
• 应力分析概述 • 应力分析方法 • 材料力学中的应力分析 • 强度理论 • 实际应用中的应力分析与强度理
论
01
应力分析概述
定义与目的
定义
应力分析是研究物体在受力状态下应 力分布、大小和方向的一种方法。
目的
评估物体的强度、刚度、稳定性以及 预测可能的破坏模式，为结构设计提 供依据。
平衡方程
根据力的平衡原理，物体内部的应力分布满足平衡方程。
应变与应力的关系
通过材料的力学性能试验，可以得到应变与应力的关系，即应力-应变曲线。
弹性力学基本方程
根据弹性力学的基本原理，建立物体内部的应力、应变和位移之间的关系。
02
应力分析方法
有限元法
总结词
有限元法是一种广泛应用于解决复杂工程问题的数值分析方法。
材料力学应力状态
2
y
2
x
y
2 xy
J12 4
J2
R2
sin
2 0
xy
R
c os 2 0
(
x
R
y
)
/
2
x
y
2
R cos(2
20 )
R sin(2 20 )
x
2
y
2
2
R2
x
2
y
2
2 xy
6.2 平面应力状态
H ( , )
B
O
yx
y E
2
R
2
C 2 0
( x y ) / 2 x
y
y yx n
40
30 z
( MPa )
80
x
z 30MPa (主应力) x 80MPa y 40MPa
(1)求主应力
xy 40MPa
~m ~m
ax in
x
y
2
x
2
y
2
2 xy
104.72 15.28
(MPa)
1 104 .72MPa 2 15.28MPa 3 30MPa
3
2
-30 O 15.28
( 3 1)( 3 2 )
2 n
(
n
2
2
3
)
2
2
3
(
n
2
2
3
)
2
2
3
0
n
2
2
3
2
2 n
2
2
3
2
O
c1
3 2
c2 c3
材料力学 第06章 强度理论
可见：由第三强度理论，图b所示应力状态比 图a所示的安全；而由第四强度理论，两者的危险 程度一样。 注意：图a所示应力状态实际上为拉扭和弯扭组 合加载对应的应力状态，其相当应力如下：
s r 3 s 2 4 2
s r 4 s 2 3 2
例 工字钢梁如图a所示。已知材料（Q235钢）的许 用应力为[s]=170MPa和[]= 100MPa。试按强度条 件选择工字钢号码。 (a) 200 kN 解：确定危险截面。 200 kN
1 2s s2 6E
因此：
1 2 2 2 s 1 s 2 s 2 s 3 s 1 s 3 s s 2
由此可得强度条件为：
ss 1 2 2 2 s 1 s 2 s 2 s 3 s 1 s 3 [s ] 2 n
s r4
1 2 2 2 s 1 s 2 s 2 s 3 s 1 s 3 2
§7-7 强度理论的应用
应用范围： a) 仅适用于常温、静载条件下的均匀、连续、各 向同性的材料； b) 不论塑性或脆性材料，在三向拉应力状态都 发生脆性断裂，宜采用第一强度理论； c) 对于脆性材料，在二向拉应力状态下宜采用第 一强度理论； d) 对塑性材料，除三向拉应力状态外都会发生 屈服，宜采用第三或第四强度理论； e) 不论塑性或脆性材料，在三向压应力状态都发 生屈服失效，宜采用第四强度理论。
假设形状改变能密度vd是引起材料塑性屈服的 因素，即：
vd vd u
vd u
所以：
可通过单拉试验来确定。
因为材料单拉屈服时有： s 1 s s s 2 s 3 0
材料力学第6章应力状态与强度理论
6.2 平 面 应 力 状 态 分析 6.3 三 向 应 力 状 态 分 析 6.4 广 义 胡 克 定 律 6.5 一般应力状态下的应变必能 6.6 工程中常用的四种强度理论
6.1 应 力 状 态 概 述
6.1.1、应力状态概念 （1）、铸铁与低碳钢的拉、压、扭试验现象 P M 低碳钢 铸铁拉伸
图c单元体的应变能为 : d: 畸变能密度 (Strain-Energy Density Corresponding to the Distortion)
1 2 2 2 ud s 1 s 2 s 2 s 3 s 3 s 1 6E —— 形状改变比能（歪形能） s 1 -s m
2t xy
s x s y
0 45
s x s y 2 2 t max （ ）t xy t 2 t min
s x s y tg21 0 1 0 2t xy
破坏分析
低碳钢: s s 240MPa;
t s 200MPa
低碳钢
灰口铸铁 : s Lb 98 ~ 280MPa
6.5.2 线弹性体的应变能
作用在弹性杆件上的力，其加力点的位移，随着杆件受力和 变形的增加而增加，这种情形下，力所作的功为变力功。
0
FP
FP
Δ Δ
O
对于材料满足胡克定律、又在小变形条件下工作的弹性杆件， 作用在杆件上的力与位移成线性关系。 这时，力所作的变力功为 1 W FP Δ 2
不考虑加载过程中的能量损耗，则外力功将转化为弹性变形能
s x s y 0
t
s
2
xy
应力状态及强度理论
应力张量是一个二阶对称张量， 包含六个独立的分量，可以用 来描述物体的应力状态。
主应力和应力张量可以通过计 算得到，它们是描述物体应力 状态的重要参数。
02
强度理论
第一强度理论
总结词
最大拉应力准则
详细描述
该理论认为材料达到破坏是由于最大拉应力达到极限值，不考虑剪切应力和压 力的影响。
第二强度理论
05
实际应用
航空航天领域
飞机结构强度分析
利用应力状态及强度理论，对飞 机各部件的受力状态进行详细分 析，确保飞机在各种工况下的结 构安全。
航天器材料选择
根据材料的应力-应变关系，选择 适合航天器发射和运行阶段的材 料，确保航天器的可靠性和寿命。
航空材料疲劳寿命
评估
通过应力状态及强度理论，评估 航空材料的疲劳寿命，预防因疲 劳引起的结构失效。
03
材料失效分析
弹性失效
总结词
材料在弹性阶段发生的失效。
详细描述
当材料受到的应力超过其弹性极限时 ，会发生弹性失效。这种失效通常表 现为突然断裂或大幅度变形，且材料 不具有恢复原状的能力。
塑性失效
总结词
材料在塑性阶段发生的失效。
详细描述
当材料受到的应力超过其屈服点后，会发生塑性失效。这种 失效表现为材料发生较大的塑性变形，无法保持其原始形状 和尺寸。
土木工程领域
桥梁承载能力分析
通过对桥梁的应力分布和承载能力的分析，确保桥梁在设计寿命 内的安全性和稳定性。
建筑结构抗震设计
利用强度理论，对建筑结构进行抗震设计，提高建筑物的抗震能 力，减少地震灾害的影响。
岩土工程稳定性分析
通过对岩土工程的应力状态和强度理论的分析，评估岩土工程的 稳定性和安全性。
材料力学第六章应力状态与强度理论
e
xy
x
b
a
a
f
y
yx
第6章
应力状态与强度理论
斜截面应力
由图 d 所示体元上各面上的力的平衡，参考法 线n和切线t方向可得：
(d)
e
xy dA cosa xdA cosa
b yx dA sina
adA
n
adA
f t
n 0
y dA sina
⇒
a dA x dA cos a cosa xy dA cos a sin a
x y
2
x y
2
因此，C点坐标为应力圆圆心坐标，并且
B1B2 2 x y 2 CD1 B1D1 xy 2 2
该线段长度等于应力圆半径。从而证明上述 圆确为应力圆。
2
2
第6章
应力状态与强度理论
由图b可见，A1、A2两点的横坐标为：
OA1 OC CA1
OA2 OC CA2
第6章
应力状态与强度理论
主应力
由此可得两个主应力值为：
应力圆
2
1
x y
2
x y 2 2 xy
x y 2 2 xy
⇒
其中dA为斜截面ef的面积。 由此可得，任一斜截面上的应力分量为：
a
x y
2
x y
2
cos 2a xy sin 2a
a
x y
2
sin 2a xy cos 2a
第6章
应力状态与强度理论
材料力学应力状态分析和强度理论
材料力学应力状态分析和强度理论材料力学是一门研究物质内部各个部分之间的相互作用关系的科学。
在材料力学中，应力状态分析和强度理论是非常重要的概念和方法，用来描述和分析材料的力学行为和变形性能。
材料的应力状态是指在外力作用下，物体内部各个部分所受到的力的分布情况。
应力有三个分量：法向应力、剪应力和旋转应力。
法向应力是垂直于物体表面的作用力，剪应力是平行于物体表面的作用力，旋转应力则是物体受到扭转力产生的应力分量。
应力状态的描述可以用应力矢量来表示。
应力状态分析的目的是确定材料内部各个部分的应力分布情况，进而推导出物体的变形和破坏行为。
常用的应力状态分析方法有平面应力问题、平面应变问题和三维应力问题。
平面应力问题是指在一个平面上的应变为零，而垂直于该平面的应力不为零；平面应变问题是指在一个平面上的变形为零，而垂直于该平面的应力不为零；三维应力问题则是指在空间中3个方向的应力都不为零。
强度理论是指根据材料的内部应力状态来评估其抗拉强度、抗压强度和抗剪强度等，以判断材料是否能够承受外力而不发生破坏。
常见的强度理论有最大正应力理论、最大剪应力理论和最大扭转应力理论。
最大正应力理论是指在材料的任何一个点，其法向应力都不能超过材料的抗拉强度；最大剪应力理论则是指剪应力不能超过材料的抗剪强度；最大扭转应力理论则是指旋转应力不能超过材料的极限扭转强度。
实际应用中，强度理论通常与材料的断裂理论结合起来，以评估材料的破坏行为。
材料断裂的主要原因是应力超过了材料的强度极限，从而导致材料的破坏。
为了提高材料的强度和抗拉性能，可以通过选择合适的材料、改变材料的结构和制造工艺等方法来实现。
综上所述，材料力学应力状态分析和强度理论是描述和分析材料力学行为和变形性能的重要理论和方法。
通过深入研究应力状态、应力分析和强度理论，可以为材料的设计和制造提供指导和支持，从而提高材料的强度和抗拉性能。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第六章应力状心《«皮理论§ 1 轨述卿?血oa?低或4i4A 伸技,* # <a1w4*戈aT7剪中有拉结论不仪横筑面上存及应力，蚪IG 荀上也存在 盒力；不仗要研丸横就面•！的应力，而且也 萎研丸斜就ft 上的虫力-应力的三个宣要:k 念应力的点的概念; 应力的面的概念; 应力状态的概念.lAr.n; aZ横截面上正应力分析和切应力分析S 的结果表明：同一面上不同点的应力各! 不相同，此即应力的点的概念・%单元体平衡分析结果表明：即使同一点不同方向面上的应力也是各不相同的，此即应力的面的概念应力状态的分类9T ；O aa O Q ! ______________T*A平面应力状态■・三向应力状态单向应力状炭纯3r 应力状态§2 平而曲力状盘的皮力分析i 盘力6■1»aTrr -<T H= « 工片=0 :J llz". cos a =yi■I.2 I - COS 2asn a-3 !(7皿-码(必砌<除(^了 丁 1^淞师上畑晶8何Mn 口瓦20^(d45in ff )sm (/ "02 2匚必-码(必zHakm a - r,(/MctKa)eos£e + r^(dE4sh ajsin df+cr JtMsn a )ccscza0 (7 ~<7J =———sin 加 + J cos 2a〕2场**^^*卑元体皮力如图所念，其切墓方耐=?-术+方向各平而 的血力乙知・互柑套直的二灣asab 柑be 的卄出戎分別易X 砂/ 粘成30°和-63角，战求此二科面ab 和1X 上的皮力•6-b cJ ■ ———-sin 2a + G cos2a2Q ij<:北此］砒V 细肘如厲删伽■ 2込（f +6 = 6+5 = 40MPa4二甸血劝狀去・1\ 佞*的个,4*上.AO 的和芳一 $it 。
二.苻罟规：由X 虽甸逵4f4f 林列Z7JL4｝命舟正t 总之为A 0O i.:粗力为止切应力後単丸体或Jt 易押用! 时什*砌样场知足,及之；iOM 九 iIftWAjJ化=b 工+6匚45血32b 0a Wa---- -------% Vi■分析轴初核伸杵件的最丸切宏力的作用而.说凹低琰攵： 竝什才发生血服的i 要虑B.AQt 饭担*Ab 真丄佟您一点卯是羊勺左力找4k6*6 €r -CT..= • +—— cos 2a -r,sn2£Z2 2<7 a<F. =—+ —COS2£C•予 1■ ■6 —6 - = -- ------ sin 2a + s cos 2tz 2T. = ^sin2«• 5 性載也氏耳ii 挣£41«1对*£妙45£出现旻•*支匕应力引邑4^・分析圖轴扭舁对最久切皮力的作用面，说明4<>铁国风=^ i 坏的i 要虑0.tfT - zr_ -二 ^rarsff% =-rsbi 2aC ■ <7—_ srla + r cos2«2山f^-rcos2<3fa - ±45"=11件檢S 比綽4ftW 比**h 王是^t<<A 皮力并黑逓("45'«戏irJ 棉/t 的.《比. 丐琅认为迄静雄也戒坏是由*丸A A 力nd (t M,应力圓-•应力0的方b。
- b?十°\ 十 _cos 2a - r, sin 2«2 2“宁*加十沁也二•应力B的&出衣q-s坐标察中p标走与微元垂直:的A, D面上应力对皮的点a丢d i连＜5〃交0症轴于G盘，Cp%srs cd为良i力0半程。
二特角对宏A J _______J H 向对皮 ---- 车銓it 黑?方向与许观而空戋ilui 方*)-枚;半&转过的角皮是郵面it 骑角度的两点面对应ba转向对应、二信九对应a鬪心兀严.());半径/ 岂玉)亏;对于图中斯=5：之年面应力状态，若要求*肉最a \ maxMP乳’^zv<85MPa,洪求J的取<4#tfi・ffl中A力的半住為；巴知疑彫札第1&上的ir 力F 尸120kZA^«M=10kZE ■烬电： 康*1・2. 3・4点直力欢杰轲单死体.幷卓岀$点的ij6"g be60mm.h«100mnn.2.计鼻各AiA-4=1AJJW ' VI =^i- = 500o 『 (r(]) = — s? UlCiifra<r, = a. = 0 <T , =-l(K)Wfu-"12/&50() xM]2点(it 于*t J IIJ =2盒，弘胡虹121(T, = 3()MA J<7^ = 0 f 73=-50MFa2/1 2x 60x1004 4,；3点_ 空2 _ 15*切P'x60x25x37.5•, = 100MP«]切成力等于举的截面为主平® 主平面上的正虫力称为主成力矽&0+ 9O'*) = fg2a^■ 6 5 匕巧・Sz ■—2 —■A~T~-2r.心“= --------- -b 厂J\i4T：主应力和宝丰面20,,O巧d(务&a （碍忑） ba7;/5 > 叭：61 £少・ pj 2?；创-:過礦f 心…6 =0 ' b严5&6MP<i 6 二0 6 二8・6 肘尸"(T, = 235MPa n^j s 0 r_ = l72・5MPn ran＜魏7" S 吳力的仲内飢-*充律•*上畝更应力bffl*. r -CT /V3 •戎库此点； 检/ 的X,衣力Ai 年區.I•才b goc 巩T 上窗 30" 4无Aj,eg30° =0 ；6 =—r/73 = -n-/3 <Tj 3/7 —6 = • b/3构件中#盘孙年面应力秋恚，两斜黴上的皮力如酌折［ 徐/ 示.武用废力0求主血力和墩丸七?康力Ic/3IfV)Ki n人龙力Q 上畳JK平面应力状态的儿种椅辣侑况a /■；%+空矜z2a -r.sin2a<r* ft仏二土乙nin平面底力状态的几种特珠情况S J ；%+空旦心 2a -r,sin 2a2 2乙= --(! +cos 2a)2C7, =66=6=0r s 冬 sin la25严±守 mn 厶d = -f sin 2a *» "a = COS 2a6*6 CT. ■rr. 亠.C6 =二工 + -- cos3« -T^sn2cf2 2 f7 —(TJ ■' sin 2a +r,cos2ttcr^ = — T —cos 2a - r, sin 2a■ 2r* = ^sin 2ff + 巧£os2<?仏=土J(牛尸*/ii*n I J§3空间应力状态的帆念r；6J9 6 %土” 26分析:SOWRji aOAm 单尢体如®示・求三个力和倉丸切皮力・O ZTM MlMP/r<T, = 80MP“xy 平Ji 丄角他itu*怎 6 = SQMPa2000^1•北京 fti丸*5£lMPa§4 应力占应支间的关纟cr -<7S = —€ = -1^ =7 —EE 0\ :I 八■泊松比・ 66 I6宀哙CjXz^S 遽良为20mE的伺直方养i手AH ®X ft力F-14kN0E用・[ /^吵“乙如.v=03 «1设・*的丈形以;(IA*体勾衬的康族^可以电: 4不计•比J K A才体•金而上的A皮力・S ==-竺0=-35J WP£/▼ A 20x20£八浪7& 5)1=0S-0.3(-35+<7： )=0 冬=*-血"』=0fT, ■ 0・3(・ 35 + trj - 0CT =C7. = -15MPa某点的应力状态如旳所示，吿5。
护巧不支忑）《犬列 匕饋X 关于5值的说注正确的走_—• A所以i 切戎力堆丸列，减戍丈术文.图示为荼点的应力状冬，其录大切皮力30 MPa.2001 <4glPu% = 2（）M 內 % =-2(WPacr,= 40MPa6 = 2()MPad 、= -2QMPa-_5-6 _ 40-(- 20) imx= 30MPdma x衙同#*♦纤的休应文Li=q （ig ）c"（i 十匂kJig ） J I 6?—£：, i-Gj +-c^"=1^（巧+匹+円录《此«坎裔^a ' ■" _5》几（1 •氏k 、（l r J 皿4 jyM （l+hF*&・^，T ）-*[d^«・|l—受扭a 赫,直&d=20mm,H 林的材料为钢 /^^；^«^=2OOGP3 v=0 3现测得m 牡表面上与轴規成45°方向 直护厂 的底主航=5.2x'IO 七武隶®*所‘h 吳的扱*色.EE©er, = r rr, =0 b 、=Y& = — k +rrE '卄 ——TEx;rx2'tT r =—Wp图b图CH 运bg + -b26 + -rTQ6=二^[c ； + <x ； + <r ； -2（Xcr|CTi 十 66 十56）] 2dSc图电元体的应变能为:Vv = £疔”£林十*占,=-^^1^（^.十 6 十（T J2ft:为体积改蛍能密啖・图C 单元体的应变能为匕,=7^ [（6 - CT J 十（6 - <7 J 十（6 - 6 ）'] O 上s 间&力状态下的应支能密度b 机-3（b|Fz+h3）柠为平禺应力・I %「5rr = — ^ [rx]a = < [a]化L 」第一强度理论r 景大按S 力理论丿很材甘发A 斷裂嵐坏的主矣因索是*丸主扯 金力0＞只姜0|达列单向拉伸时材料的技 友按限db 材料将*斷昱*t 坏・破坏条件 强度条件玄｛兀丽和耳・#*|***涉事**板冢§6强度理怡及其相当应力r 厶片］ Wp L 」 厂=竺＜［丁 %弟二强度理沦r景大伸長线应隻理论丿吳拉农坏对的找.应賈Cb-0』E对，材料将要发主斷裂破坏•玻坏条件&产云E-血+如］径度条件 5 -讥6+6)W H第三强度理论r最丸切应力理论丿@ .只要倉丸切应力T E*达月材料卑向曼力对的斥服枝限(r$所对应的核限切应力J- “2,材列将发生忌躲^ r剪餌丿戎坏.破坏条件r…企nnx J 2T =五二皿2强度条件5一5«[6弟四强度理论rufe-f理论丿形欢粽t比能是引建材**总眼咬坏的屋本虑a 筑麵金力媛盒Ti^倍弟坎&兰比*迖剖__ 单的畏力情况忌服阪时#n底的叔限彫状改支比危，材*4此会皮生4服破坏.破坏条件1+U6£ bz）"宀r+q-胡=罟（2 巧强度条件苗何一<7$+(6-内r+(6-6[簡于*会，果■it冷•十tt*6<b5=5-0（6 + 6）5 =5 _66严J扣-5）2 +（6 -5）2+（6西A丸，欽A J•就衣的赫岌24・*丫4| AAiCH第2tt血a冷! 支■■«1就・4•便卅^«“1揉«比廉a孰*于觸榔爸8寧时4、科丿4对皺i4丄•負铃人*・良4«总HILA■耐翼A丄會鼻友■良妁豪■«・・14 “MP"令己知妁铁构侔上危险点，处的皮力状志，為圈示.若件 匕费"钱血伸许雋A 力％ fa] * =30MPa.戎较«€女点吐的》度 少尹是皿全・i ：yCT, = 29.28A/Pwi CTj = 3d2MPa 、eZj = 0牛=M XMPm Y 卜卜 yiMPc< *结构上底险的皮力伙杰如®所示.其中a = 116.7M PSr T — 46.3MPa ・4t 的为创*许用皮力【a ]—160MPa<汎杭柚此rt*是否妥仝・JM 巧-bJ + G -6)'」(6-对kSI Jb 】+3X <b]29・2«MP43・72MH J(7C7^需'+4r' s[fr]149X)M 兀OftMPa)<7 6 » + • 2图杀为一距«戡®科缺#，•灵阿个橫*）力* «• 丿）从畢n*的b乩C三点处取出的堆"上.牌歸头出个*上曲直力・ a （2）it柱3出八乩C三A的直分n.B< （3）虚备A的单九*上，XJBUfcA出土平*的位■粗主ja力的才角.才（4） UM■將一a废《•,观朗（ABIu录）lUMT甘H逢崔& （：溥成处《^是為・£_J卜g*cr「I^kZz^对團示的绘剪初应力状态.试■報强度理论iti疑.剪切状念下的豪•废糸仲，幷纟出劳切许《皮力frj与拉伸许用直#^应力m丈间的美糸.旷才=『.巳=0t g\=-r _______________ \ _____ Z 5 <*««<<»-*<«<' <T, ^I<r］■=!>［巧一V同»**<«*H- 01I J Huq-丐<0]»・«皮■命J扣pF +(化-2[士M"0.250 r a+")<[nj[r] = 0.8[o-]［心）•嗣[d=Md6 尸・(6 -竹)*' W J5了< [rr]才子Utt*用[H=(O.K)*T]对子Ptt****；■―rHo.5〜0.6旧swuGyjr _________________________比•ttMZMftW样力2舛》1«・!由M性材料Mtt的《«)件崔启抚务《［* †力M« K*Y1:^M«R. 件的MK. iA 育Utter(的夫«■■Ritl FftWIKMflfAWWMimnwn^ nftnfl-ffKw.构仲杞交费a力ffWf.Vltfi■代輛n■性桂Bi 一C次■输W1J = £ ke pJ 十(S -6)'+q-q 円氏天* Ik科力狀冷下.N桂样料将粒主栈金附徉犬力狀奉札《性>4联笈宅・・《0«(«・故应進用«三•走废《逡・(K材料的・"：《式不仅*决于村料的力*行九《a勺新捡的紋力秋点・■ rtftitnu«布关・实««期・《性甘料在-定的•件丁向Rilh•金K«A, n>X4|. (2)不JLV)C. ri>(2) 邮正确ID. (})(2) 邮不JL确.fU Ait«AaA4†"■叭，时谊・&-丈(2) 丸狀左京MW找-丸•户宴■星■ <«>-. »««A •冰的弦度欲侑伙高; C •冰的富废孩钟纵零； D •冰的应力苓于$・5 =叭 一6 «伶仗水聲$11妬冰对会《*4»»4枝》11. * *内的冰*不2«^・这是8为（•丿•B •冰处于艺松4乐矗力状态;#构伸内扈•衣的底力戟$再工亀等审* f B JftJia 雜就爪.《|用其他呂令《友a 论4M •^相・倉方長相¥«•A •第一JB ・第二；C ・第三;<7门=(75 =(7-1X7(J 丹=CF^-CTy = aD •弟叭- 5)']"<T <T:5=q 孰 YJ +(6 -bj+(6a,=a<7, =<To 、・Q。