工学]机械振动噪声学习题课
机械振动基础课后习题解答_第3章习题
m
0
0 m
u1 u2
3k k
k 3k
u1 u2
2ku0
sin 0
t
K
2M
3k
2m
k
k
3k 2m
H11 ( )
3k 2m ()
H 21 ( )
k ()
u1(t) u2 (t)
H11 ( ) H21()
2ku0
sin
t
3k 为反共振频率 m
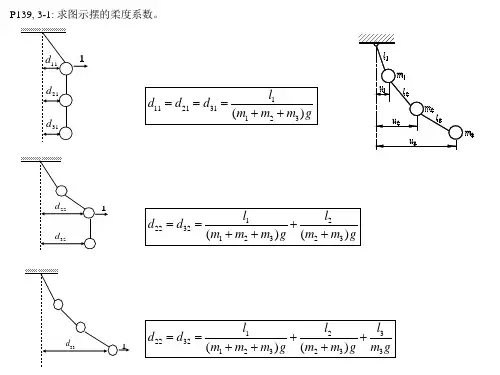
P140,3-9: 图示系统初始静止，求左端基础产生阶跃位移u0后系统的响应。
ml2 1 0 M 3 0 7 /16
K
l2k 16
9 9
9
13
| K 2M | 0
1 0.65
k m
2 2.62
k m
P139,3-3: 建立图示系统的运动微分方程，并求当ki k,i 1, 6, m1 m, m2 2m, m3 m时的固有 频率和固有振型。
m1
M
m2
u2
c
3c
2c
u2
k
3k
2k
u2
0
m u3 0 2c 2c u3 0 2k 2k u3 f0
1 0,2
k m
, 3
2k m
1 1 1
φ1
1 , φ2
0
, φ3
1
1
1/ 2
1
u1 1
u2
1
u3 1
1 0 1/ 2
1 q1
1
q2
1 q3
)d
u0 2
(1 cos1t)
q2
(t)
u0 2
(1
cos 2t )
机械振动前三节习题课ppt课件
A．振子在M、N两点受回复力相同 C
B．振子在M、N两点对平衡位置的位移相同
C．振子在M、N两点加速度大小相等
D．从M点到N点，振子先做匀加速运动，后 做匀减速运动
• 例题：一个做简谐运动的质点，先 后以相同的速度通过a、b两点历时 0.1s，再经过0.1s质点第二次（反向） 通过b点。若质点在这0.2s内经过的 路程是8cm，则此简谐运动的周期 为_____0_._4s，振幅为_______4_ cm。
思考：小球从高处自由落体，接 触弹簧压缩到最低点，在最低 点小球的加速度a与重力加速度 g的关系？
什么位置释放可以让它成为一个竖 直方向的弹簧振子？
经过2s它第二次经过M点;则质点第三
次经过M点所需要的时间是： CD
A、8s
B、4s
C、14s
D、(10/3)s
• 如图4所示，做简谐运动的质点，表示加速 度与位移的关系的图线是 （ ）
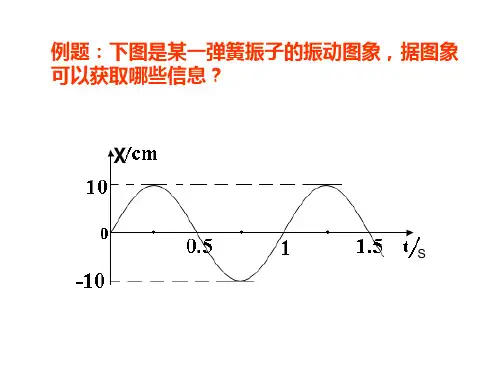
• 如下图是弹簧振子的振动图线，试回答下列问 题： （1）振动的振幅、周期、频率各是多少？
• （2）如果从O点算起，到图线上哪一点为止振 子完全成了一次全振动？从A点算起呢？
1 2
mg
由以上可以得出振幅为A时， 最大 回复力大小为0.5mg. k A 0.5mg ③
欲使物体在振动时不离开弹簧， 则最大
回复力可为mg，k A mg
④
由 ③ ④ 联立得：A 2A
小结：
解决此类问题, 首先在确定对称点; 然后利用对称点中速度大小相等、加速 度大小相等, 回复力大小相等; 最后根据 题目要求确定所求物理量．
练习1、弹簧振子在AA’之间做简 谐振动，O为平衡位置，在OA之 间有一点C，那么振子每次经过C 点时一定相同的物理量有：ACD
振动噪声课后习题答案
振动噪声课后习题答案振动噪声课后习题答案在学习振动噪声的课程中，习题是非常重要的一部分，通过解答习题可以帮助我们巩固所学知识，提高解决问题的能力。
下面是一些振动噪声课后习题的答案，希望能对大家的学习有所帮助。
1. 什么是振动噪声？振动噪声是指由于机械系统的振动引起的噪声。
当机械系统发生振动时，会产生声音，这种声音就是振动噪声。
振动噪声可以对人体健康和环境造成不良影响。
2. 振动噪声的主要来源有哪些？振动噪声的主要来源包括机械设备、交通工具、建筑物、电器设备等。
机械设备的运转会产生振动，交通工具在行驶过程中也会产生振动，建筑物和电器设备的使用也会引起振动噪声。
3. 如何评价振动噪声的强度？振动噪声的强度可以通过声级来评价。
声级是一种用于表示声音强度的单位，通常用分贝（dB）来表示。
振动噪声的强度越大，声级也就越高。
4. 振动噪声对人体健康有哪些影响？振动噪声对人体健康有很多不良影响。
长期暴露在高强度的振动噪声下会导致听力受损、心理压力增加、睡眠质量下降等问题。
此外，振动噪声还会引起头痛、胃痛、消化不良等身体不适。
5. 如何减少振动噪声的传播？减少振动噪声的传播可以采取多种措施。
首先，可以通过减少振动源的振动来降低振动噪声的产生。
其次，可以在振动源和传播路径之间设置隔振措施，如橡胶垫、减震器等。
此外，还可以通过改善建筑结构、增加隔音材料等方式来减少振动噪声的传播。
6. 如何评价振动噪声的影响？评价振动噪声的影响可以从两个方面来考虑。
一方面是对人体健康的影响，如对听力、心理状态、睡眠等的影响。
另一方面是对环境的影响，如对动植物的生长、生活质量等的影响。
7. 如何进行振动噪声的监测和控制？振动噪声的监测可以通过安装振动传感器等设备来实现。
控制振动噪声可以采取技术措施和管理措施相结合的方式。
技术措施包括减振、隔振等方法，管理措施包括制定噪声限制标准、加强监督检查等。
8. 振动噪声的治理需要政府和企业共同努力。
大学 机械振动 课后习题和答案(1~4章 总汇)
1.1 试举出振动设计、系统识别和环境预测的实例。
1.2 如果把双轴汽车的质量分别离散到前、后轴上去，在考虑悬架质量和非悬架质量两个离散质量的情况下，画出前轴或后轴垂直振动的振动模型简图，并指出在这种化简情况下，汽车振动有几个自由度?1.3 设有两个刚度分别为1k ，2k 的线性弹簧如图T —1.3所示，试证明：1)它们并联时的总刚度eq k 为：21k k k eq +=2)它们串联时的总刚度eq k 满足：21111k k k eq +=解：1)对系统施加力P ，则两个弹簧的变形相同为x ，但受力不同，分别为：1122P k xP k x=⎧⎨=⎩由力的平衡有：1212()P P P k k x =+=+故等效刚度为：12eq Pk k k x ==+2)对系统施加力P ，则两个弹簧的变形为： 1122Px k Px k ⎧=⎪⎪⎨⎪=⎪⎩，弹簧的总变形为：121211()x x x P k k =+=+故等效刚度为：122112111eq k k P k x k k k k ===++1.4 求图所示扭转系统的总刚度。
两个串联的轴的扭转刚度分别为1t k ，2t k 。
解：对系统施加扭矩T ，则两轴的转角为： 1122t t Tk T k θθ⎧=⎪⎪⎨⎪=⎪⎩系统的总转角为：121211()t t T k k θθθ=+=+，12111()eq t t k T k k θ==+故等效刚度为：12111eq t t k k k =+1.5 两只减振器的粘性阻尼系数分别为1c ，2c ，试计算总粘性阻尼系数eq c1)在两只减振器并联时，2)在两只减振器串联时。
解：1)对系统施加力P ，则两个减振器的速度同为x ，受力分别为：1122P c x P c x =⎧⎨=⎩ 由力的平衡有：1212()P P P c c x =+=+故等效刚度为：12eq P c c c x ==+ 2)对系统施加力P ，则两个减振器的速度为：1122P x c Px c ⎧=⎪⎪⎨⎪=⎪⎩，系统的总速度为：121211()x x x P c c =+=+ 故等效刚度为：1211eq P c x c c ==+1.6 一简谐运动，振幅为0.5cm，周期为0.15s，求最大速度和加速度。
机械振动与波习题课.ppt
x (t ) 解： y 2 cos600 330 x 2 cos2 (300t ) 1.1 1 . 1 m 所以，
r (2 k 1 ) 相消条件：r 2 1
A
r1 r2
C
B
2
k=0,1,2….
（1）
2 2 由几何关系有： r r 2 1
1
A
r1
C
所以
( r r )( r r ) 1 2 1 2 1
（2）写出距P点为b的Q点的振动方程 Y Y
l
b
b
O
P u
Q
X
O P
Q
X
l y A co s[ ( t ) ] O u
波动方程
原点的振动方程
u 原点的振动方程
y A cos( t ) O
x l y A cos[ ( t ) ] uu
x yA cos[ ( t ) ] u
2
0
2
0
y 0 . 5 cos( t ) 0 0
0 ,
3
2 2
t 2,v0 0
0 2
2.一平面简谐波沿X轴负向传播，波长为，P点处质点
的振动规律如图 （1）求出P处质点的振动方程
（2）求此波的波动方程
（3）若图中d=/2，求O处质点的振动方程
u 0 . 84 m / s
取
17 /3
O a u b X
/3
故得波动方程为
x y 0 . 1 c os[ 7 ( t ) ]( m ) 0 . 84 3
9. 题中图a表示一水平轻绳，左端D为振动器，右端固定 于B点。t0时刻振动器激起的简谐波传到O点。其波形如 图b所示。已知OB＝2.4m，u=0.8m/s. 求：（1）以t0为 计时零点，写出O点的谐振动方程；（2）取O 点为原 点，写出向右传播的波动方程；（3）若B 处有半波损 失，写出反射波的波动方程（不计能量损失）。 2 D O 解：（1）由 B u 2 2 y(cm) (a) 得 u 80 4 40 4
(完整版)机械振动课后习题和答案第二章习题和答案
2.1 弹簧下悬挂一物体，弹簧静伸长为δ。
设将物体向下拉，使弹簧有静伸长3δ，然后无初速度地释放，求此后的运动方程。
解：设物体质量为m ，弹簧刚度为k ，则：mg k δ=，即：n ω==取系统静平衡位置为原点0x =，系统运动方程为： δ⎧+=⎪=⎨⎪=⎩&&&00020mx kx x x （参考教材P14）解得：δω=()2cos n x t t2.2 弹簧不受力时长度为65cm ，下端挂上1kg 物体后弹簧长85cm 。
设用手托住物体使弹簧回到原长后无初速度地释放，试求物体的运动方程、振幅、周期及弹簧力的最大值。
解：由题可知：弹簧的静伸长0.850.650.2()m =-=V所以：7(/)n rad s ω=== 取系统的平衡位置为原点，得到：系统的运动微分方程为：20n x x ω+=&& 其中，初始条件：(0)0.2(0)0x x=-⎧⎨=⎩& （参考教材P14） 所以系统的响应为：()0.2cos ()n x t t m ω=- 弹簧力为：()()cos ()k n mg F kx t x t t N ω===-V因此：振幅为0.2m 、周期为2()7s π、弹簧力最大值为1N 。
2.3 重物1m 悬挂在刚度为k 的弹簧上并处于静平衡位置，另一重物2m 从高度为h 处自由落到1m 上而无弹跳，如图所示，求其后的运动。
解：取系统的上下运动x 为坐标，向上为正，静平衡位置为原点0x =，则当m 有x 位移时，系统有： 2121()2T E m m x =+& 212U kx =由()0T d E U +=可知：12()0m m x kx ++=&& 即：12/()n k m m ω=+系统的初始条件为：⎧=⎪⎨=-⎪+⎩&2020122m gx k m x gh m m （能量守恒得：221201()2m gh m m x =+&） 因此系统的响应为：01()cos sin n n x t A t A t ωω=+其中:ω⎧==⎪⎨==-⎪+⎩&200021122n m g A x k x m g ghk A k m m即：ωω=-2()(cos )n n m g x t t t k2.4 一质量为m 、转动惯量为I 的圆柱体作自由纯滚动，圆心受到一弹簧k 约束，如图所示，求系统的固有频率。
机械振动与机械波习题课
观察者
2
A
S
Vs
Vs
2u s
4u s 4u
2 2 2
2
0.25m / s
反射面 声源
(2) 若波源不动，反射面运动 ，观察者接收到的频率有：直 接从静止的波源来的声音和经 相向运动的反射面反射后的频 率，两者形成拍。
哈尔滨工程大学理学院
观察者
A
S V
机械振动与机械波习题课
第三章 机械振动与机械波
习题2、如图所示，原点O是波源，振 动方向垂直于纸面，波长是λ，AB为波 的反射平面，反射时无半波损失。O点 位于A点的正上方，AO = h，OX轴平 行于AB，求OX轴上干涉加强点的坐标。
O
h x
A
哈尔滨工程大学理学院
B
机械振动与机械波习题课
第三章 机械振动与机械波
解：沿ox轴传播的波与从AB面上P点反射 来的波在坐标x处相遇，两波的波程差为：
哈尔滨工程大学理学院
机械振动与机械波习题课
第三章 机械振动与机械波
二、典型习题
习题1、假想沿地球的南北极直径开凿 一条贯通地球的隧道,且将地球当作一 密度为ρ半径为r 的均匀球体。
(1)若不计阻力,试证明一物体由地面 落入此隧道后作简谐振动； (2)求此物体由地球表面落至地心所需 的时间。
哈尔滨工程大学理学院
u VR 2VR
(340 0.2) 4 2 0.2
3398Hz
/2
3 4
) cos(t
4
3
4
)
哈尔滨工程大学理学院
机械振动与机械波习题课
第三章 机械振动与机械波
习题4：一声源振动的频率为2040赫兹， V 以速度 向一反射面接近, 观察者在A处测 得拍音的频率 3 赫兹，声速为340米/ 秒 (1) 波源移动的速度？ 求:
机械振动_机械波课后习题
习题5 •机械振动5.1选择题(1) 一物体作简谐振动，振动方程为x=Acos(，t )，则该物体在t=0时刻2的动能与t二T/8(T为振动周期)时刻的动能之比为：(A) 1: 4 ( B) 1：2 (C) 1：1 (D) 2：1(2) 弹簧振子在光滑水平面上作简谐振动时，弹性力在半个周期内所作的功为(A)kA2(B) kA2/2(C) kA2//4(D)0(3)谐振动过程中，动能和势能相等的位置的位移等于(A)，4(C) 一3A2(B)冷(D) - 2A5.2填空题(1) 一质点在X轴上作简谐振动，振幅A = 4cm,周期T = 2s,其平衡位置取作坐标原点。
若t= 0时质点第一次通过x = —2cm处且向X轴负方向运动，则质点第二次通过x= —2cm处的时刻为___ So(2) —水平弹簧简谐振子的振动曲线如题 5.2(2图所示。
振子在位移为零，速度为—呱、加速度为零和弹性力为零的状态，对应于曲线上的______________ 点。
振子处在位移的绝对值为A、速度为零、加速度为--2A和弹性力为-KA的状态，则对应曲线上的_____________ 点。
题5.2(2)图(3) —质点沿x轴作简谐振动，振动范围的中心点为x轴的原点，已知周期为T，振幅为A。
(a) 若t=0时质点过x=0处且朝x轴正方向运动，则振动方程为x= __________________ 。
(b) 若t=0时质点过x=A/2处且朝x轴负方向运动，则振动方程为x= ________________ 。
5.3符合什么规律的运动才是谐振动？分别分析下列运动是不是谐振动：⑴拍皮球时球的运动；(2)如题5.3图所示，一小球在一个半径很大的光滑凹球面内滚动(设小球所经过的弧线很短).题5.3图题5.3图(b)5.4弹簧振子的振幅增大到原振幅的两倍时，其振动周期、振动能量、最大速度和最大加速度等物理量将如何变化？5.5单摆的周期受哪些因素影响？把某一单摆由赤道拿到北极去，它的周期是否变化？5.6简谐振动的速度和加速度在什么情况下是同号的？在什么情况下是异号的？加速度为正值时，振动质点的速率是否一定在增大？5.7质量为10 10：kg的小球与轻弹簧组成的系统，按x = 0.1cos(8t，空)(SI)的规律3作谐振动，求：(1) 振动的周期、振幅和初位相及速度与加速度的最大值；(2) 最大的回复力、振动能量、平均动能和平均势能，在哪些位置上动能与势能相等？⑶t2 =5S与t1 =1s两个时刻的位相差；5.8 一个沿x轴作简谐振动的弹簧振子，振幅为A，周期为T，其振动方程用余弦函数表示•如果t =0时质点的状态分别是:(1) x o = -A ；(2) 过平衡位置向正向运动；A(3) 过x二一处向负向运动；2A(4) 过x A处向正向运动.V2试求出相应的初位相，并写出振动方程.5.9 —质量为10 10^kg的物体作谐振动，振幅为24cm，周期为4.0s，当t =0时位移为24cm .求：(1) t =0.5s时，物体所在的位置及此时所受力的大小和方向；(2) 由起始位置运动到x = 12cm处所需的最短时间；(3) 在x =12cm处物体的总能量.5.10有一轻弹簧，下面悬挂质量为1.0g的物体时，伸长为4.9cm .用这个弹簧和一个质量为8.0g的小球构成弹簧振子，将小球由平衡位置向下拉开 1.0cm后，给予向上的初速度V。
机械振动课后习题答案
机械振动课后习题答案机械振动是力学中的一个重要分支，研究物体在受到外力作用后的振动特性。
在学习机械振动的过程中，课后习题是巩固知识、提高能力的重要途径。
本文将为大家提供一些机械振动课后习题的答案，希望能够帮助大家更好地理解和掌握这一知识。
1. 一个质量为m的弹簧振子在无阻尼情况下振动，其振动方程为mx'' + kx = 0，其中x为振子的位移，k为弹簧的劲度系数。
试求振动的周期。
解答：根据振动方程可知，振子的振动是简谐振动，其周期T与振子的质量m和弹簧的劲度系数k有关。
根据简谐振动的周期公式T = 2π√(m/k)，可得振动的周期为T = 2π√(m/k)。
2. 一个质量为m的弹簧振子在受到外力F(t)的作用下振动，其振动方程为mx''+ kx = F(t)，其中F(t) = F0cos(ωt)。
试求振动的解析解。
解答：根据振动方程可知，振子的振动是受迫振动，其解析解可以通过求解齐次方程和非齐次方程得到。
首先求解齐次方程mx'' + kx = 0的解xh(t)，得到振子在无外力作用下的自由振动解。
然后根据外力F(t)的形式，假设其特解为xp(t) = Acos(ωt + φ)，其中A为振幅，φ为相位差。
将特解xp(t)代入非齐次方程，求解得到A和φ的值。
最后，振动的解析解为x(t) = xh(t) + xp(t)。
3. 一个质量为m的弹簧振子在受到阻尼力和外力的作用下振动，其振动方程为mx'' + bx' + kx = F(t)，其中b为阻尼系数。
试求振动的稳定解。
解答：根据振动方程可知，振子的振动是受到阻尼力和外力的作用，其稳定解可以通过求解齐次方程和非齐次方程得到。
首先求解齐次方程mx'' + bx' + kx = 0的解xh(t)，得到振子在无外力和阻尼作用下的自由振动解。
然后根据外力F(t)的形式，假设其特解为xp(t) = Acos(ωt + φ)，其中A为振幅，φ为相位差。
《机械振动与噪声学》习题集与答案
《机械振动噪声学》习题集1－1 阐明下列概念，必要时可用插图。
(a) 振动；(b) 周期振动和周期；(c) 简谐振动。
振幅、频率和相位角。
1－2 一简谐运动，振幅为0.20 cm，周期为0.15 s，求最大的速度和加速度。
1－3 一加速度计指示结构谐振在82 Hz 时具有最大加速度50 g，求其振动的振幅。
1－4 一简谐振动频率为10 Hz，最大速度为4.57 m/s，求其振幅、周期和最大加速度。
1－5 证明两个同频率但不同相位角的简谐运动的合成仍是同频率的简谐运动。
即：A cos ωn t +B cos (ωn t + φ) =C cos (ωn t + φ' )，并讨论φ＝0、π/2 和π三种特例。
1－6 一台面以一定频率作垂直正弦运动，如要求台面上的物体保持与台面接触，则台面的最大振幅可有多大？1－7 计算两简谐运动x1 = X1 cos ω t和x2 = X2 cos (ω + ε ) t之和。
其中ε << ω。
如发生拍的现象，求其振幅和拍频。
1－8 将下列复数写成指数A e i θ形式：(a) 1 + i3(b) -2 (c) 3 / (3- i ) (d) 5 i (e) 3 / (3- i ) 2(f) (3+ i ) (3 + 4 i ) (g) (3- i ) (3 - 4 i ) (h) [ ( 2 i ) 2 + 3 i + 8 ]2－1 钢结构桌子的周期τ＝0.4 s，今在桌子上放W = 30 N 的重物，如图2－1所示。
已知周期的变化∆τ＝0.1 s。
求：( a ) 放重物后桌子的周期；( b )桌子的质量和刚度。
2－2 如图2－2所示，长度为L、质量为m 的均质刚性杆由两根刚度为k 的弹簧系住，求杆绕O点微幅振动的微分方程。
2－3 如图2－3所示，质量为m、半径为r的圆柱体，可沿水平面作纯滚动，它的圆心O 用刚度为k的弹簧相连，求系统的振动微分方程。
机械振动和波习题课_百度文库
2007-2008学年第二学期大学物理“振动和波”习题课1、一谐振动的余弦曲线如图,则A=ω=φ=2、一简谐振子的振动曲线如图所示,则以余弦函数表示该振动方程。
3、由曲线求振动方程。
24、一物体沿X 轴作简谐振动,振幅为0.12m ,周期为2s 。
当 t=0 时位移为0.06m ,且向X 轴正方向运动。
求:(1初相,(2在 x=-0.06m 处,且向X 轴负方向运动时,物体的速度和加速度,以及从这一位置回到平衡位置所需的时间。
5、一物体作简谐振动,其振幅为24cm ,周期为4s ,当t=0时,位移为-12cm 且向x 轴负方向运动,求1简谐振动方程; 2物体由起始位置运动到x=0处所需的最短时间。
6、一弹簧振子作简谐振动,当其偏离平衡位置的位移的大小为振幅的1/4时,其动能为振动总能量的A 1/4B 3/4C 1/16D 15/167、两个谐振动分别为cm cos(431051π+=t x ,cm cos(22106ϕ+=t x ;当ϕ2= 时,合振幅最大;当ϕ2= 时,合振幅最小,且写出它们的合振动方程。
8、沿X 轴正方向传播的平面简谐波、在 t=0 时刻的波形如图,问:(1原点O的初相及P点的初相各为多大?(2已知A及ω,写出波动方程。
9、一平面简谐波某时刻的波形如图,则OP之间的距离为多少厘米。
10、如图,某一点波源发射功率为40瓦,求球面波上单位面积通过的平均能流。
11、如图S1、S2为两平面简谐波相干波源,S2的位相比S1的位相超前π/4,λ=8m,r1=12m,r2=14m。
S1在P点引起的振幅为0.3m, S2在P点引起的振幅为0.2m,求P点的合振幅。
12、当机械波在媒质中传播时,一媒质质元的最大变形量发生在 (设振幅是A(A 媒质质元离开其平衡位置最大位移处.(B 媒质质元离开其平衡位置(2/2A 处.(C 媒质质元在其平衡位置处.(D 媒质质元离开其平衡位置A 21处.13、设沿弦线传播的一入射波的表达式为](2cos[1φλπ+-=xT t A y 波在x = L 处(B 点发生反射,反射点为固定端。
(完整版)大学机械振动课后习题和答案(1~4章总汇)
1.1 试举出振动设计、系统识别和环境预测的实例。
1.2 如果把双轴汽车的质量分别离散到前、后轴上去，在考虑悬架质量和非悬架质量两个离散质量的情况下，画出前轴或后轴垂直振动的振动模型简图，并指出在这种化简情况下，汽车振动有几个自由度?1.3 设有两个刚度分别为1k ，2k 的线性弹簧如图T —1.3所示，试证明：1)它们并联时的总刚度eq k 为：21k k k eq +=2)它们串联时的总刚度eq k 满足：21111k k k eq +=解：1)对系统施加力P ，则两个弹簧的变形相同为x ，但受力不同，分别为：1122P k xP k x=⎧⎨=⎩由力的平衡有：1212()P P P k k x =+=+故等效刚度为：12eq Pk k k x ==+2)对系统施加力P ，则两个弹簧的变形为： 1122Px k Px k ⎧=⎪⎪⎨⎪=⎪⎩，弹簧的总变形为：121211()x x x P k k =+=+故等效刚度为：122112111eq k k P k x k k k k ===++1.4 求图所示扭转系统的总刚度。
两个串联的轴的扭转刚度分别为1t k ，2t k 。
解：对系统施加扭矩T ，则两轴的转角为： 1122t t Tk T k θθ⎧=⎪⎪⎨⎪=⎪⎩系统的总转角为：121211()t t T k k θθθ=+=+，12111()eq t t k T k k θ==+故等效刚度为：12111eq t t k k k =+1.5 两只减振器的粘性阻尼系数分别为1c ，2c ，试计算总粘性阻尼系数eq c1)在两只减振器并联时，2)在两只减振器串联时。
解：1)对系统施加力P ，则两个减振器的速度同为x &，受力分别为：1122P c x P c x =⎧⎨=⎩&& 由力的平衡有：1212()P P P c c x =+=+&故等效刚度为：12eq P c c c x ==+& 2)对系统施加力P ，则两个减振器的速度为： 1122P x c P x c ⎧=⎪⎪⎨⎪=⎪⎩&&，系统的总速度为：121211()x x x P c c =+=+&&& 故等效刚度为：1211eq P c x c c ==+&1.6 一简谐运动，振幅为0.5cm，周期为0.15s，求最大速度和加速度。
机械振动基础课后习题解答_第2章习题
0.5
1
1
1
1 1/ 3
u1 (t ) u2 (t)
8 4
/ /
9 9
cos(
k 2m
)t
1/9 1/ 9
cos(
2k )t m
(3) 求结构的稳态响应
m1u1(t) k1(u1(t) u2 (t)) m2u2 (t) k1(u1(t) u2 (t)) k2 (u2 (t) v(t))
0 0
(K 2M)φ 0
1
1
2 2
k J
,
2
1
2k 2 J
1 1
φ1
1/
2
,
φ2
1/
2
P88,2-6: 不计刚杆质量，按图示坐标建立运动微分方程，并求出固有频率和固有振型。
系统动能：T
1 2
mu12
1 2
2mu22
系统势能：U
1 2
k (2u1
u2 )2
1 2
k (2u2
P87,2-1: 图示用于风洞试验的翼型剖面由拉伸弹簧k1和扭转弹簧k2支承着，剖面重心G到支承点 的距离为e, 剖面绕重心的转动惯量为J0,试建立系统运动微分方程。
动能：T
1 2
m(h e )2
1 2
J0 2
势能：U
1 2
k1h2
1 2
k2 2
m me
J0
me me2
h
k1
0
(e 0)
)
Re
2k k
k k
2
m
0
0 m
－1
i
f1
f2
eit
u* (t )
1
机械振动与噪声学答案
机械振动与噪声学答案1. 机械振动的基本概念及分类机械振动是指机械运动中出现的周期性变化，通常包括以下几个方面：•振幅：振动系统的最大偏移量，是振动的主要特征之一。
•周期：振动系统经过一个完整的振动过程所需的时间。
•频率：振动系统在单位时间内所完成的振动次数。
•相位：用来描述振动状态的相对时间位置，是一种相对概念，通常用弧度来表示。
•谐振：振动系统的固有频率与外界激励频率相等时产生的现象，通常会引起振幅的急剧增加。
•非谐振：振动系统的固有频率与外界激励频率不等时产生的现象，随着激励频率的不同，振幅和相位也会不同。
根据机械振动的性质和机械结构的不同，可以将机械振动分为以下几类：•自由振动：振动系统在没有外界干扰的情况下，按照固有频率自行振动的过程。
•强迫振动：振动系统受到外界周期性的激励，按照外界激励的频率发生振动，通常比自由振动更为复杂。
•阻尼振动：振动系统因为受到摩擦力的作用而逐渐减弱的振动过程。
•维持振动：振动系统受到外界持续的激励时能够保持稳定的振动状态。
2. 声波的基本概念及特性噪声是指那些会引起人类不适的声音，它的特点是声强大、频率广泛，通常会对人的身体产生负面影响。
声波是一种在空气、水、固体等介质中传播的机械波，声波的基本概念包括以下几个方面：•音量：声音的强度，是声波与人耳之间的相对力度比较。
它通常用分贝(dB)来表示。
•频率：声波的频率表示了声音的音高，是声波波形中的周期性变化。
•色调：不同频率的声波会产生不同的音色，通常用人耳可以感知的不同声音来描述。
•声速：声波在介质中传播的速度，通常用米/秒来表示。
•声源：产生声波的物体或者振动体。
•声波强度：单位时间内声波传播时单位面积上的能量。
噪声的基本特性包括以下几个方面：•声压级：噪声的声压级决定了噪声的强度，通常用分贝dB来表示。
•频谱特性：噪声的频率分布情况，不同的噪声具有不同的频率分布特性。
•时间特性：噪声的音量随时间的变化，通常用峰值、持续时间来描述。
机械振动和波习题及解答.
(1)波的波速、频率和波长； (2)绳子上各质点振动时的最大速度和最大加速度； (3)求=0.2m 处质点在=1s时的位相，它是原点在哪一时刻的位相?这一 位相所代表的运动状(SI)．
(1)写出=4.2 s时各波峰位置的坐标式，并求此时离原点最近一个波峰 的位置，该波峰何时通过原点? (2)画出=4.2 s时的波形曲线．
机械振动和波习题
4-4 质量为的小球与轻弹簧组成的系统，按的规律作谐振动，求： (1)振动的周期、振幅和初位相及速度与加速度的最大值； (2)最大的回复力、振动能量、平均动能和平均势能，在哪些位置上动 能与势能相等? (3)与两个时刻的位相差； 4-7 有一轻弹簧，下面悬挂质量为的物体时，伸长为．用这个弹簧和 一个质量为的小球构成弹簧振子，将小球由平衡位置向下拉开后 ，给 予向上的初速度，求振动周期和振动表达式． 4-8 图为两个谐振动的曲线，试分别写出其谐振动方程．
(3)因任一时刻同一波线上两点之间的位相差为
将，及代入上式，即得 ．
5-9 沿绳子传播的平面简谐波的波动方程为=0.05cos(10)，式中,以米
计，以秒计．求： (1)波的波速、频率和波长； (2)绳子上各质点振动时的最大速度和最大加速度； (3)求=0.2m 处质点在=1s时的位相，它是原点在哪一时刻的位相?这一 位相所代表的运动状态在=1.25s时刻到达哪一点? 解: (1)将题给方程与标准式
题图
5-17 一平面余弦波，沿直径为14cm的圆柱形管传播，波的强度为
18.0×10-3J·m-2·s-1，频率为300 Hz，波速为300m·s-1，求 ： (1)波的平均能量密度和最大能量密度? (2)两个相邻同相面之间有多少波的能量?
机械振动和波习题及解答
机械振动、机械波习题课
习题精讲
【例 3】(2012·新课标卷)一简谐横波沿 x 轴正向传播，t ＝0 时刻的波形如图 9-1-3(a)所示，x＝0.30m 处的质点的 振动图线如图 9-1-3(b)所示，该质点在 t＝0 时刻的运动方
向沿 y 轴__正__向____(填“正向”“负向”)．已知该波的波 长大于 0.30m，则该波的波长为__0__.8____m.
机械振动、机械波 习题课
课前回顾
课前回顾
课前回顾
课前回顾
课堂精练
1习．在题振精动讲过程中各物理量的变化
【例 1】(2012·北京卷)一个弹簧振子沿 x 轴做简谐运动， 取平衡位置 O 为 x 轴坐标原点．从某时刻开始计时，经 过四分之一周期，振子具有沿 x 轴正方向的最大加速 度．能正确反映振子位移 x 与时间 t 关系的图象是( )
下节课再见
习题精讲
一列简谐横波沿x轴正向传播，传到M点时波形如图所示，再经0.6s，N点开始振动，则该 波的振幅A和频率f为( D )
A．A=1m f=5Hz C．A=1m f=2.5 Hz
B．A=0.5m f=5Hz D．A=0.5m f=2.5 Hz
习题精讲
一列简谐横波沿x轴传播，周期为T，t=0时刻的波形如图所示.此时平衡位置位于x=3 m处 的质点正在向上运动，若a、b两质点平衡位置的坐标分别为xa=2.5 m, xb=5.5 m,则( ) A.当a质点处在波峰时，b质点恰在波谷 B.t=T/4时，a质点正在向y轴负方向运动 C.t=3T/4时，b质点正在向y轴负方向运动 D.在某一时刻，a、b两质点的位移和速度可能相同
习题精讲
一列简谐横波沿x轴传播，周期为T，t=0时刻的波形如图所示.此时平衡位置位于x=3 m处 的质点正在向上运动，若a、b两质点平衡位置的坐标分别为xa=2.5 m, xb=5.5 m,则( C ) A.当a质点处在波峰时，b质点恰在波谷 B.t=T/4时，a质点正在向y轴负方向运动 C.t=3T/4时，b质点正在向y轴负方向运动 D.在某一时刻，a、b两质点的位移和速度可能相同
机械振动与噪声学答案
x ( x0 )n sin n t
n
x0
n
cos n t
x0
x
0
xmax ( x0 )n 25 0.189
7000 9
x max 644.5 mm / s
速度振幅每周衰减 4n 210.8 mm / s
Free Vibration
3－7 图3－23所示带有库仑阻尼的系统中，质量 m = 9 kg，弹簧刚
Vibration equation of discrete system
2－14 图2－43是固定滑车力学模型。起吊物品质量为 m， 滑轮绕中心O的转动惯量为J0，假定绳索与滑轮间无滑动， 求系统的振动微分方程。
k2R R k1 x R R J J k1Rx k2 k1 R2 0
1 2
k r2 , 1, { [ -1, 1 ] }
J
3 k r2 J , 1, { [ 1, 1 ] }
J1
0
0 J2
12
k1
k2 k2r 2
r
2
k2
k2
r2 k3
r
2
12
0 0
Vibration equation of discrete system
2－17 如图2－46所示，系统中 k1 = k2 = k3 = k，m1 = m2 = m，r1 = r2 = r ，J1 = J2 = J。求系统的振动微分方程。
Vibration equation of discrete system
2－6 图2－36所示系统垂直放置，L2杆处于铅垂位置时系统 静平衡，求系统作微振动的微分方程。 [m1L12 m2L22 m3(L3 L4)2] L32c (L3 L4)2k m2gL2 0
机械振动与噪声培训课程
机械振动与噪声培训课程简介机械振动与噪声是机械工程中的重要研究领域。
振动和噪声不仅会影响机械设备的性能和寿命，还会对人的健康和环境造成不良影响。
因此，了解和掌握机械振动与噪声的原理和控制方法是每一个机械工程师都需要具备的基本知识和技能。
本文档为机械振动与噪声培训课程的详细介绍，旨在帮助学员了解振动与噪声的基本概念和原理，掌握振动与噪声的测量和分析方法，以及探讨振动和噪声控制的技术手段。
内容本课程将涵盖以下内容：1.振动与噪声基础知识–振动与噪声的定义和分类–振动与噪声的来源和传播途径–振动量化指标和评价标准2.振动的测量与分析方法–振动传感器的选择和应用–振动信号采集与处理技术–振动频谱分析和特征提取方法3.噪声的测量与分析方法–噪声传感器的选择和应用–噪声信号采集与处理技术–噪声频谱分析和特征提取方法4.机械振动与噪声控制技术–振动与噪声控制的基本原理–主动振动控制技术–被动振动控制技术–噪声隔离和减排技术5.案例分析与实践–振动与噪声问题实例分析–振动与噪声控制解决方案设计与实施–振动与噪声控制效果评估与改进学习目标通过参加本培训课程，学员将能够达到以下目标：•理解振动与噪声的基本概念和原理；•掌握机械振动与噪声的测量和分析方法；•熟悉振动与噪声控制的技术手段和方法；•能够在实际工程项目中应用振动与噪声控制技术。
教学方法本课程将采用以下教学方法：•授课讲解：通过系统的理论讲解，介绍振动与噪声的基本概念和原理。
•实例分析：通过实际案例分析，帮助学员理解和应用振动与噪声控制技术。
•实验演示：通过实验演示，展示振动与噪声的测量和分析方法。
•小组讨论：通过小组讨论，促进学员之间的交流和合作。
参与要求参加本培训课程的学员需具备以下要求：•具备机械工程相关背景知识；•熟悉基本的工程数学和物理知识；•熟悉基本的计算机操作和数据处理；•具备一定的英语阅读和理解能力。
结束语机械振动与噪声培训课程将为学员提供了掌握振动与噪声基础知识、掌握振动与噪声测量和分析方法、了解振动与噪声控制技术的机会。
11.8《机械振动》习题课
求两个简谐 运动的相位 差
写出两个简谐 运动的位移对 时间的函数关 系式
弹簧振子作简谐运动时，以下说法正确的是： 1.弹簧振子作简谐运动时，以下说法正确的是： A．振子通过平衡位置时，回复力一定为零 ．振子通过平衡位置时， B．振子做减速运动，加速度却在增大 ．振子做减速运动， C．振子向平衡位置运动时，加速度方向与速度方向相反 ．振子向平衡位置运动时， D．振子远离平衡位置运动时，加速度方向与速度方向相反 ．振子远离平衡位置运动时， 如图所示，是一弹簧振子，设向右方向为正， 为平衡位置 为平衡位置， 2.如图所示，是一弹簧振子，设向右方向为正，O为平衡位置， 则： A．A→O位移为负值，速度为正值 位移为负值， ． 位移为负值 B．O→B时，位移为正值，加速度为负值 ． 时 位移为正值， A O B C．B→O时 位移为负值， C．B→O时，位移为负值，速度为负值 D．O→A时，位移为负值，加速度为正值 ． 时 位移为负值， 一个弹簧振子在光滑的水平面上做简谐运动,其中有两个时刻 3.一个弹簧振子在光滑的水平面上做简谐运动 其中有两个时刻 弹簧振子的弹力大小相等,但方向相反 则这两个时刻振子的 弹簧振子的弹力大小相等 但方向相反,则这两个时刻振子的 但方向相反 A．速度一定大小相等 方向相反 ．速度一定大小相等,方向相反 B．加速度一定大小相等 方向相反 ．加速度一定大小相等,方向相反 C．位移一定大小相等 但方向不一定相反 ．位移一定大小相等,但方向不一定相反 D．以上三项都不一定大小相等方向相反 ．
简谐运动的周期性
【例1 【例1】一个在水平方向做简谐运动的弹簧振子的振动周期是 0.025s，当振子从平衡位置开始向右运动，在0.17s时刻，振 时刻， ，当振子从平衡位置开始向右运动， 时刻 子的运动情况是（ 子的运动情况是（ ） A．正在向左做减速运动 B．正在向右做加速运动 ． ． C．加速度正在减小 D．动能正在减少 ． ．
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2r 3
122.13
1 r 2 (2r)2
5-9
解：由P136式（5-27）
FT F0
1 2 r 2
1 r2 2 2 r 2
①若 FT / F0 1
则 1 2 r2 1 r2 2 2 r2
1 1 r 2 2
0 r2 2 r 2 即
2
n
对本题，
2 n
k
/m
800
(1
1 3n2
1)m(nl&&) n
k(nl)
0
(1
1 3n2
1 )m&x& n
kx&
0 meq
(1
1 3n2
1)m n
3-3解：(a)建立坐标，向下为正则有
[ 1 ml2 m(1 l)2 ]&& cl2& ka2 0
12
2
即
[ 1 ml2 m(1 l)2 ]&& cl2& ka2 0
m2 (l2&)2
1 2
m3[(l3
l4 )&]2
U
1 2
k[(l3
l4 )]2
mgl2 (1 cos)
V
t 0
c
(l3&)2
dt
T U V 常数
对之求时间的导数，得
[m1l12 m2l22 m3(l3 l4 )2]&& cl32& k(l3 l4 )2 m2gl2 0
2-9 解：
其解为 x Acosnt B sin nt
其中 n
k m1 m2
解的初始条件依题意为 x(0) x0 ; x(0) x0
x
x0 的求解：m2 下落至 m1 处，
1 2
m2V22
m2 ghV
2gh
.
碰撞过程利用动量守恒 m2v (m1 m2 ) x 0
.
x0
m2
m1 m2
m2 m1 m2
3 mR 2 2k (R a) 2 0
2
2-5 求如图所示系统的振动微分方程。
解：假定绳与轮之间无滑动
T
U
1 2
m(r&)2
1 2
J0&2
1 2
k (r )2
由 d (T U ) 0 dt
结合 x r
J0
1 2
Mr 2
可得
m
J0 r2
&x&
kx
0
2-6解：
T
1 2
m1(l1&)2
1 2
10 3
/
2500
10 3
/ 9.8
n 1.77 又 2 n
60
2n 2.5
n 30 23.9r / min
ka2 mgL mL2 2 2 ca2 2
tg 1
ca 2
ka2 mgL mL2 2
4-4解： m&x& cx& kx F0 cost
2 2
Td d
n
1 2
n
Td
2 1
2
1
2 1 0.04
6.41
rad
s
m
k
n2
3000 6.412
73kg
运动微分方程化为
&x& 2.56x& 41.09x 0.27 cos3t
1 11
ke k1 k2 k3
ke
(k1 k2 )k3 k1 k2 k3
2-12解：
T 1g1 (nl m)(nl)2&2 1g1 (l nl m)(l nl)2&2
23 l
23 l
1 (1 3n 3n2 )ml 2&2
6
U 1 k (nl)2 2
2
1 (1 3n 3n2)ml2&& k(nl)2 0 3
1 2r 2 1 r 2 2 2r 2
r 2 f
2 20
2.52 , 0.1
n k m 2.802105 /113
S X 0.21 x 0.21Y
Y
再设
x Xei( )
则仪器加速度为
&x& X e2 i(t) 0.21Y2ei(t) 0.032ei(t)
而
tg 1
mx cx kx 0 x 2 n x n2 x 0
代入已知m，c，k，得
n
1000 10
10 rad s
即 x 20x100x 0
1） 0
x(t) x0 sin(10t ) 可得 x(t) 0.01cos10t
初始条件 x0 0.01m, x0 0
2） 0.2
x(t) Rent sin(dt ) Re2 sin(10 1 0.22t )
由 x0 0.01， x0 0
可解得 A1 0.01，A 2 0.1
xt 0.01 0.1te10t
4-2 解：建立如右坐标
mL2&& c(a&)a k(a Acost)a mgL sin
mL2&& ca2& (ka2 mgL) akAcost
若设 co X cos(t )
则
X
0.27
0.0082(m)
41.09 32
2
2.5643
2
tg
1
2 n
2 n
2
tg 1 0.24
0.235(rad )
x 8.2cos(t 0.235)(mm)
5-7解：设基础运动
y Yei
则 y Y 2ei
依题意， Y 2 15.24
又位移传递率 S X Y
12
2
&&
3c m
&
3
k m
a l
2
0
n
3
k m
a l
2
fn
1
2
3
k m
a l
2
1
2
a l
3k m
3c m
2n
1
2n
3 c m
2m
2a
3c
c
3
k m
a l
2
cc
cc 3 l 3 m k
3-5解：建立x坐标，以 m1 m2 接触后的静平衡位置为坐标原点
(m1 m2 )x kx 0
机械振动噪声学 习题课
1 J&2
2
2-3解：
T 1 m(r)2 1 J2
2
2
平动 转动
J 1 mr 2 U 1 k(r)2
2-3
2
2
T+U=常数，
整理，得
3 m k 0
2
2-4
解：
T 1 m(R) 2 1 J2
2
2
U 1 (2k) [(R a)]2 2
J 1 mR2 2
由d (T U ) / dt 0可得
2gh
x0 等于 m2 导致弹簧伸长的负值。
x0
m2 g k
于是
x(t) m2g cos
k t m2 2gh m1 m2 sin
kt
k
m1 m2 m1 m2
k
m1 m2
m2g cos k t m2 2gh sin k t
k
m1 m2
m1 m2 k
m1 m2
3-6 解：依题意，系统运动微分方程为
R
x02
x0 n x0 n 1 2
2
,
tg 1
x0
d x0 n x0
代入 x0 , x0 后可得
R
1
1 2
x0
0.0102 (mm)
tg 1
1 2
1.369 (rad )
x(t) 0.0102e2t sin(9.798t 1.369)
3） 1 此时为临界阻尼状态
x(t) ( A1 A2t)ent ( A1 A2t)e10t