解三角不等式
三角不等式的证明方法

三角不等式的证明方法最近看到一道有意思的三角不等式问题:在锐角ΔABC中,证明:cosA+cosB+cosC−4cosAcosBcosC≥1这种三角形内角余弦的不等式有两种方法:一是化为边转换为齐次的代数不等式进行证明,二是利用三角形中内角相关恒等式或不等式进行证明。
下面来分别使用两种不同方法进行证明。
一、代数法利用余弦定理:cosA=b2+c2−a22bc我们可以得到:cosA+cosB+cosC−4cosAcosBcosC≥1∑cycb2+c2−a22bc−4∏cycb2+c2−a22bc−1≥0∑cyca2bc(b2+c2−a2)−∏cyc(b2+c2−a2)−2(abc)2≥0(a+b+c)(∑cyca3(a2−bc)−∑cycab(a3+b3))≥0∑cyca3(a−b)(a−c)≥0由Schur不等式知:原命题得证。
当然,此题也可以使用SOS方法进行配方证明,具体配凑比较麻烦,在此不做赘述。
二、三角法利用三角形中的恒等式:cosA+cosB+cosC=1+4sinA2sinB2sinC2,我们有:cosA+cosB+cosC−4cosAcosBcosC≥1sinA2sinB2sinC2≥cosAcosBcosC>0 sin2A2sin2B2sin2C2≥cos2Acos2Bcos2C下面证明只需要两个不等式:{cosAcosBcosC≤18cosAcosBcosC≤∏cyc(1−cosA)对于前者,由射影定理:a=bcosC+ccosB≥2bccosBcosCb=ccosA+acosC≥2cacosCcosAc=acosB+bcosA≥2abcosAcosB三式相乘,得:abc≥∏cyc2abcosAcosB=8abccosAcosBcosC即cosAcosBcosC≤18对于后者,注意到ΔABC是锐角三角形,有:{cosA>01−cosA>0又这个不等式左右都是乘积形式,故两边取对后移项,只需证明:∑cyc[lncosA−ln(1−cosA)]≤0⋯⋯(∗)考察函数f(x)=lncosx−ln(1−cosx),(0<x<π2)则f′(x)=tanx−2sinxcosx−1f″(x)=(cosx−1)(1cos2x−2cosx)+sinx(tanx−2sinx)(cosx−1)2=(cos x−1)(1−2cos2x)+sin2xcosx(1−2cosx)cos2x(cosx−1)2=(cosx−1)(1−2cos2x)+(1−cos2x)cosx(1−2cosx)cos2x(cosx−1)2=1−2cos2x+cosx(1+cosx)(1−2cosx)cos2x(cosx−1)=cos2x−cosx+1cos2x(cosx−1)<0故由Jensen不等式,有:f(A)+f(B)+f(C)3≤f(A+B+C3)=f(π3)=ln12−ln12=0即(*)式得证。
三角不等式公式大全

三角不等式公式大全三角不等式是初中数学中的一个重要概念,它是指任意两边之和大于第三边的三角形中的关系。
在几何学和代数学中,三角不等式都有着重要的应用。
下面将对三角不等式的相关公式进行大全总结,希望对大家有所帮助。
1. 一般三角不等式公式:对于任意三角形ABC,有以下不等式成立:AB + BC > AC。
AC + BC > AB。
AB + AC > BC。
这是最基本的三角不等式公式,它表明了三角形中任意两边之和大于第三边。
2. 余弦定理:在三角形ABC中,设三边分别为a、b、c,夹角A对应的边为a,夹角B对应的边为b,夹角C对应的边为c,则有余弦定理:c^2 = a^2 + b^2 2abcosC。
b^2 = a^2 + c^2 2accosB。
a^2 = b^2 + c^2 2bccosA。
余弦定理可以用来求解三角形的边长和角度大小,是三角形中常用的重要公式。
3. 正弦定理:在三角形ABC中,设三边分别为a、b、c,夹角A对应的边为a,夹角B对应的边为b,夹角C对应的边为c,则有正弦定理:a/sinA = b/sinB = c/sinC = 2R。
其中R为三角形外接圆半径。
正弦定理可以用来求解三角形的边长和角度大小,也是三角形中常用的重要公式。
4. 三角形面积公式:设三角形ABC的三边分别为a、b、c,三角形的面积S可以用以下公式表示:S = √[p(p-a)(p-b)(p-c)]其中p为半周长,即p=(a+b+c)/2。
三角形面积公式是计算三角形面积常用的公式,可以通过三边长度直接求解三角形的面积。
5. 海伦公式:海伦公式是用来计算任意三角形面积的公式,对于任意三角形ABC,设三边分别为a、b、c,半周长为p,则三角形的面积S可以用以下公式表示:S = √[p(p-a)(p-b)(p-c)]海伦公式是三角形面积公式的一种推广,适用于任意三角形的面积计算。
以上是关于三角不等式的相关公式大全总结,这些公式在解决三角形相关问题时都有着重要的应用价值。
求解三角不等式

求解三角不等式不等式是数学中一种常见的表达方式,用来表示两个或多个数的大小关系。
而三角不等式则是一类特殊的不等式,涉及三角函数的性质和大小关系。
三角不等式可以分为两种情况讨论:一种是涉及到正弦函数(sin)的不等式,另一种是涉及到余弦函数(cos)的不等式。
下面将详细讨论这两种情况。
一、涉及到正弦函数的不等式对于三角函数sin(x),我们知道它的取值范围是[-1, 1],即-1≤sin(x)≤1。
基于这一性质,我们可以得出一系列的三角不等式。
1. sin(x)≤1这是最基本的三角不等式之一。
由于sin(x)的取值范围不能超过1,所以当x为任意实数时,sin(x)≤1始终成立。
2. sin(x)≥-1与上一个不等式类似,sin(x)的取值范围不能小于-1,所以当x为任意实数时,sin(x)≥-1恒成立。
3. -1≤sin(x)≤1这是sin(x)函数的取值范围,也是最常见的三角不等式之一。
根据定义,对于任何实数x,都有-1≤sin(x)≤1。
4. sin(x)≥sin(y)当x > y时,sin(x) ≥ sin(y)。
这是由于对于角度而言,正弦函数是单调递增的。
5. sin(x)≤sin(y)当x < y时,sin(x)≤sin(y)。
同样地,因为正弦函数是单调递增的,当x < y时,sin(x) ≤ sin(y)。
二、涉及到余弦函数的不等式对于三角函数cos(x),也有类似的不等式规则。
1. cos(x)≤1余弦函数cos(x)的取值范围不能超过1,所以对于任意实数x,cos(x)≤1。
2. cos(x)≥-1同样地,余弦函数cos(x)的取值范围不能小于-1,所以对于任意实数x,cos(x)≥-1。
3. -1≤cos(x)≤1与正弦函数类似,余弦函数cos(x)的取值范围也是-1≤cos(x)≤1。
4. cos(x)≥cos(y)当x > y时,cos(x) ≥ cos(y)。
《三角不等式》 知识清单

《三角不等式》知识清单在数学的广阔天地中,三角不等式是一个非常重要的概念。
它不仅在数学理论中有着关键地位,还在实际应用中发挥着巨大作用。
接下来,让我们一同深入探索三角不等式的奥秘。
一、什么是三角不等式三角不等式是指在三角形中,任意两边长度之和大于第三边的长度。
用数学语言表述就是:对于一个三角形的三条边 a、b、c,有 a + b >c,a + c > b,b + c > a。
这看起来似乎很简单,但却是构建三角形的基本规则。
如果不满足这个条件,就无法构成一个有效的三角形。
二、三角不等式的证明证明三角不等式可以通过多种方法。
其中一种常见的方法是利用两点之间线段最短的原理。
假设存在三个点 A、B、C,如果要从点 A 到点 C,直接连接 A、C 两点的线段长度是最短的。
而如果先经过点 B 再到点 C,那么所经过的路径长度(即 AB + BC)必然大于直接连接 A、C 的线段长度,即AC。
同理可证其他两边的情况。
另一种证明方法可以通过代数运算。
假设三角形的三条边分别为a、b、c,并且 c 是最大边。
根据余弦定理:c²= a²+ b² 2ab cos C。
由于-1 ≤ cos C ≤ 1,所以 2ab cos C 的取值范围是-2ab, 2ab。
因此,c²= a²+b² 2ab cos C ≤ a² + b²+ 2ab =(a + b)²,即c ≤a + b。
三、三角不等式的推广三角不等式不仅仅局限于三角形的三条边,还可以推广到更多的情况。
例如,在平面直角坐标系中,对于两个点 A(x₁, y₁)和 B(x₂, y₂),它们之间的距离 d =√(x₂ x₁)²+(y₂ y₁)²。
如果有三个点 A、B、C,那么|AB| +|BC| ≥ |AC|,这也是三角不等式的一种推广形式。
在三维空间中,对于三个点 A(x₁, y₁, z₁)、B(x₂, y₂, z₂)、C(x₃, y₃, z₃),它们之间的距离分别为 d₁=√(x₂ x₁)²+(y₂ y₁)²+(z₂ z₁)²,d₂=√(x₃ x₂)²+(y₃ y₂)²+(z₃ z₂)²,d₃=√(x₃ x₁)²+(y₃ y₁)²+(z₃ z₁)²,同样有 d₁+ d₂ ≥ d₃。
高中数学中的三角函数利用三角函数性质解决三角方程与三角不等式的技巧

高中数学中的三角函数利用三角函数性质解决三角方程与三角不等式的技巧三角函数在高中数学中是一个重要的概念,它涉及到三角方程和三角不等式的解决方法。
通过运用三角函数的性质,我们可以更加灵活地解决这些问题。
本文将介绍一些利用三角函数性质解决三角方程与三角不等式的技巧。
一、三角方程1. 利用函数周期当我们遇到含有三角函数的方程时,可以利用函数的周期性来简化问题。
例如,对于形如sin(x) = a的方程,可以将其转化为sin(x) =sin(b)的形式,其中b = arcsin(a)。
由于sin函数的周期为2π,所以除了sin(b) = a本身的解外,还有无数个解,可以表示为x = b + 2πn,其中n为整数。
2. 利用函数对称性三角函数有一些对称性质,例如sin函数是奇函数,cos函数是偶函数。
当我们面对形如cos(x) = a的方程时,可以利用cos函数的偶性质将其转化为cos(x) = cos(b)的形式,其中b = arccos(a)。
同样地,由于cos函数的周期为2π,所以除了cos(b) = a本身的解外,还有无数个解,可以表示为x = ±b + 2πn,其中n为整数。
3. 利用三角函数的平方性质对于一些特殊的三角方程,我们可以利用三角函数的平方性质来解决。
例如,对于形如sin^2(x) = a^2的方程,我们可以将其转化为sin(x) = ±a的形式。
同样地,对于形如cos^2(x) = a^2的方程,我们可以将其转化为cos(x) = ±a的形式。
这样一来,我们就可以采用之前介绍的方法来求解方程。
二、三角不等式1. 利用三角函数的单调性三角函数在特定区间上是单调递增或递减的,可以利用这一性质来解决三角不等式。
例如,对于形如sin(x) > a的不等式,我们可以找到sin函数的单调递增区间,并找到满足条件的解。
2. 利用三角函数的周期性类似于解三角方程时的处理方法,我们可以利用三角函数的周期性来解决三角不等式。
解三角不等式专题
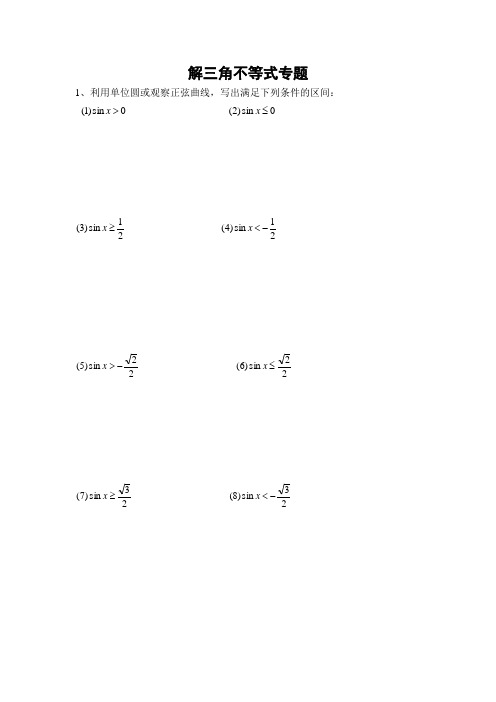
解三角不等式专题1、利用单位圆或观察正弦曲线,写出满足下列条件的区间:0sin )1(>x 0s i n)2(≤x21sin )3(≥x21s i n )4(-<x22sin )5(->x22s i n )6(≤x23sin )7(≥x23s i n )8(-<x2、利用单位圆或观察余弦曲线,写出满足下列条件的区间:0cos )1(≥x 0c o s )2(<x21cos )3(≥x21c o s )4(-<x22cos )5(->x22c o s )6(≤x23cos )7(>x23c o s )8(-≤x6、利用单位圆或根据正切函数的图象,写出满足下列条件的区间:0tan )1(>x 0t a n )2(≤x33tan )3(≥x 33t a n )4(-<x1tan )5(-≥x1t a n )6(<x3tan )7(>x3t a n )8(-≤x1、利用单位圆解不等式3tan α+3>0解:要使3tan α+3>0,即要tan α>-33 如图14,由正切线可知 k π-6π<α< k π+2π ,k ∈Z ∴ 不等式的解集为(k π-6π,k π+2π),k ∈Z2、求函数y=21cos sin -+x x 的定义域。
解:由⎪⎩⎪⎨⎧≥-≥021cos 0sin x x 得⎪⎩⎪⎨⎧≥≥21cos 0sin x x 如图15,则图中阴影部分(Ⅰ)和(Ⅱ)的公共部分即为不等式组的解.∴函数的定义域为{x | 2 k π≤x ≤2 k π+3π, k ∈Z }. 小提示:首先要把不等式变为基本型(最简单的三角不等式),对于三角不等式组应分别确定区域,取其公共部分。
3、求函数y=+lg(2sinx+)的定义域.分析:定义域即为使函数有意义的x 的值所组成的集合.解:要使函数y 有意义,必须根据上面说明的步骤在单位圆中画出符合条件的x 的范围,据阴影部分写出:+2k π<x ≤+2k π(k ∈Z).故所求函数的定义域为(-+2k π,+2k π](k ∈Z).。
三角方程与三角不等式的解法

三角方程与三角不等式的解法三角方程和三角不等式是在三角函数的基础上建立的方程和不等式,它们在数学中具有广泛的应用。
本文将介绍三角方程和三角不等式的解法,以帮助读者更好地理解和应用这些概念。
一、三角方程的解法三角方程是含有三角函数的方程,常见的三角方程类型包括:sinθ=a、cosθ=b、tanθ=c等。
下面将分别介绍几种常见三角方程的解法。
1. sinθ=a的解法:当a的取值范围在[-1,1]时,可以利用反三角函数来求解。
即令θ= arcsin(a) + 2kπ 或θ = π - arcsin(a) + k2π,其中k为整数。
2. cosθ=b的解法:当b的取值范围在[-1,1]时,可以利用反三角函数来求解。
即令θ= arccos(b) + 2kπ 或θ = -arccos(b) + k2π,其中k为整数。
3. tanθ=c的解法:当c没有限制时,可以利用反三角函数来求解。
即令θ = arctan(c) +kπ,其中k为整数。
二、三角不等式的解法三角不等式是关于三角函数的不等式,常见形式如:sinθ < a、cosθ > b、tanθ ≠ c等。
下面将介绍几种常见三角不等式的解法。
1. sinθ < a的解法:首先求解基本解,即sinθ = a的解法,然后根据sinθ的周期性,再根据周期性解得sinθ < a的解。
2. cosθ > b的解法:首先求解基本解,即cosθ = b的解法,然后根据cosθ的周期性,再根据周期性解得cosθ > b的解。
3. tanθ ≠ c的解法:tanθ ≠ c可以转化为tanθ < c或tanθ > c的形式,再利用反三角函数求解。
三、三角方程与三角不等式的应用三角方程与三角不等式在实际问题和计算中有广泛应用。
以下是几个例子:1. 三角方程的应用:在物理学和工程学领域中,三角方程常被用来描述交流电流、振动系统等的周期性和波动性质。
解三角形里的基本不等式

解三角形里的基本不等式三角形是数学中最基本的图形。
《解三角形里的基本不等式》是一个有益的数学主题。
这一主题研究三角形的基本不等式,帮助我们更好地理解三角形的结构,以及如何从结构中解释不等式。
首先,关于三角形的基本定义如下:三角形是由三条直线连接三个不同的点构成的图形,它们恰好有三个顶点和三条边。
它有三种不同类型:等腰三角形、直角三角形和斜角三角形。
其次,三角形的基本不等式是指对每个三角形,当其两个内角总度数等于180度,该不等式就成立,而不等式的特殊表示方式是:[等腰三角形]a +b = c[直角三角形]a^2 + b^2 = c^2[斜角三角形]a^2 + b^2 > c^2这种不等式可以用于计算三角形的面积,因为三角形的面积是由其顶点和边长来表示的。
对于等腰三角形,面积是由其两个半径相乘给出的,而对于直角三角形,面积是由其两个等腰边长乘以直角边长来表示的,而对于斜角三角形,面积则是由三角形的三条边长的海伦公式来表示的。
此外,三角形的基本不等式还可以用来进行根据图形来判断三角形的类型以及计算边长的长度。
如果两个内角的度数之和等于180度,则可以确定该三角形的类型。
同时,可以根据不等式求出三角形的边长,例如:已知两个内角的度数分别为60°和50°,则可以确定该三角形应该是等腰三角形,并可以利用不等式求出该三角形的边长:a+b=c,即a+b=70,这样就能确定三角形的边长了。
最后,三角形基本不等式也可以应用于其他数学领域,例如可以用来分析复杂几何图形的性质,从而解决其他科学问题。
另外,三角形的基本不等式也被用于航海和航空行业,以帮助航海家和飞行员判断他们的位置。
本文详细讨论了三角形里的基本不等式,包括它的定义、性质、不同类型的特征、在解三角形中的应用以及在其他领域的应用。
这项研究将有助于我们更好地理解三角形的结构,从而更好地解释它的基本不等式。
