2017-2018学年高中数学专题柱体、锥体、台体的表面积与体积课堂同步试题新人教A版

合集下载

人教A版高中数学必修二1.3.1柱体、锥体、台体的表面积与体积同步练习A卷

人教A版高中数学必修二 1.3.1柱体、锥体、台体的表面积与体积同步练习A卷姓名:________ 班级:________ 成绩:________一、单选题 (共6题；共12分)1. （2分）(2018·银川模拟) 圆锥的底面半径为a，侧面展开图是半圆面，那么此圆锥的侧面积是（）A . 2B . 4C .D . 32. （2分）(2018·普陀模拟) 如图所示的几何体，其表面积为，下部圆柱的底面直径与该圆柱的高相等，上部圆锥的母线长为，则该几何体的主视图的面积为（）A . 4B . 6C . 8D . 103. （2分）三棱锥P-ABC中，PA⊥底面ABC，PA=3，底面ABC是边长为2的正三角形，则三棱锥P-ABC的体积等于（）A . 3B .C . 2D . 44. （2分）如果一个几何体的三视图如图所示（单位长度：cm），则此几何体的表面积是（）A . 24 cmB . 21 cmC . （24+4 ）cm2D . （20+4 ）cm25. （2分） (2016高一下·定州期末) 图为一个几何体的三视图，尺寸如图所示，则该几何体的体积为（）A .B .C .D .6. （2分） (2017高三下·凯里开学考) 某四棱台的三视图如图所示，则该四棱台的体积是（）A . 4B .C .D . 6二、填空题 (共4题；共8分)7. （1分）已知一个正三棱柱的所有棱长均相等，其侧（左）视图如图所示，则此三棱柱的表面积为________．8. （1分）(2017·东台模拟) 三棱锥S﹣ABC中，面SAB，SBC，SAC都是以S为直角顶点的等腰直角三角形，且AB=BC=CA=2，则三棱锥S﹣ABC的表面积是________．9. （5分）已知球半径与一圆锥及一圆柱底半径相等，球直径与它们的高相等，圆锥、球、圆柱体积之比为．10. （1分） (2018高三下·滨海模拟) 一个几何体的三视图如图所示，则该几何体的体积为________．三、解答题 (共3题；共30分)11. （10分）(2017·舒城模拟) 如图所示的多面体是由一个直平行六面体被平面AEFG所截后得到的，其中∠BAE=∠GAD=45°，AB=2AD=2，∠BAD=60°．（1）求证：BD⊥平面ADG；（2）求此多面体的全面积．12. （10分）(2012·湖北) 如图1，∠ACB=45°，BC=3，过动点A作AD⊥BC，垂足D在线段BC上且异于点B，连接AB，沿AD将△ABD折起，使∠BDC=90°（如图2所示），（1）当BD的长为多少时，三棱锥A﹣BCD的体积最大；（2）当三棱锥A﹣BCD的体积最大时，设点E，M分别为棱BC，AC的中点，试在棱CD上确定一点N，使得EN⊥BM，并求EN与平面BMN所成角的大小．13. （10分）如图所示，在三棱柱ABC﹣A1B1C1中，底面△ABC是边长为6的等边三角形，点A1在底面△ABC内的射影为△ABC的中心O，D，E分别为A1B1 ， BC的中点．（1）求证：DE∥平面ACC1A1；（2）若AA1=4 ，求四棱锥A1﹣CBB1C1的表面积．参考答案一、单选题 (共6题；共12分)1-1、2-1、3-1、4-1、5-1、6-1、二、填空题 (共4题；共8分)7-1、8-1、9-1、10-1、三、解答题 (共3题；共30分)11-1、11-2、12-1、12-2、13-1、13-2、。

柱、锥、台的表面积与体积习题(有答案)

第一章空间立体几何初步 1.3 空间几何体的表面积与体积 1.3.1 柱、锥、台的表面积与体积测试题知识点1 柱、锥、台的表面积1．已知正六棱柱的高为h ，底面边长为a ，则它的表面积为( ) A ．33a 2＋6ah B.3a 2＋6hC ．43a 2＋6ah D.323a 2＋6ah2．矩形的边长分别为1和2，分别以这两边所在直线为轴旋转，所形成几何体的侧面积之比为( ) A ．1∶2 B ．1∶1 C ．1∶4 D ．1∶33．一个几何体的三视图如图所示，该几何体的表面积是( )A ．372B ．360C ．292D ．2804．一个圆柱的侧面展开图是一个正方形，则这个圆柱的表面积与侧面积之比为( )A.1＋2π2πB.1＋4π4πC.1＋2ππD.1＋4π2π5．一个圆柱和一个圆锥的轴截面分别是边长为a 的正方形和正三角形，则它们的表面积之比为________．6．如图所示的圆台的上、下底半径和高的比为1∶4∶4，母线长为10，则圆台的侧面积为________．7．已知一圆锥的侧面展开图为半圆，且面积为S ，则圆锥的底面面积是________．8.如图，一个正方体的棱长为2，以相对两个面的中心连线为轴，钻一个直径为1的圆柱形孔，所得几何体的表面积为多少？9．圆台的上、下底面半径分别是10 cm 和20 cm ，它的侧面展开图扇环的圆心角是180°，那么圆台的表面积是多少？(结果保留π)10.一个圆锥的底面半径为2 cm ，高为6 cm ，在其中有一个高为x cm 的内接圆柱． (1)求圆锥的侧面积；(2)当x 为何值时，圆柱侧面积最大？求出最大值．知识点2 柱、锥、台的体积11．圆台上、下底面面积分别是π、4π，侧面积是6π，这个圆台的体积是( ) A.233π B ．2 3C.736πD.733π 12．(2014·课标全国卷Ⅱ)如图，网格纸上正方形小格的边长为1(表示1 cm)，图中粗线画出的是某零件的三视图，该零件由一个底面半径为3 cm ，高为6 cm 的圆柱体毛坯切削得到，则切削掉部分的体积与原来毛坯体积的比值为( )A.1727B.59C.1027D.13 13．(2014·日照高一检测)某几何体的三视图如图，则它的体积是( )A ．8－2π3B ．8－π3C ．8－2π D.2π314．(2014·江苏高考)设甲、乙两个圆柱的底面积分别为S 1，S 2，体积分别为V 1，V 2.若它们的侧面积相等，且S 1S 2＝94，则V 1V 2的值是________．15．半径为2的半圆卷成一个圆锥，则它的体积为________．16．一个三棱柱的底面是边长为3的正三角形，侧棱垂直于底面，它的三视图如图，AA 1＝3. (1)请画出它的直观图；(2)求这个三棱柱的表面积和体积．17．如图，△ABC 的三边长分别是AC ＝3，BC ＝4，AB ＝5，作CD ⊥AB ，垂足为D.以AB 所在直线为轴，将此三角形旋转一周，求所得旋转体的表面积和体积．【参考答案】1A 【解析】柱体的表面积是侧面积加上底面积，据正六棱柱的性质，得其表面积为S侧＋2S 底＝33a 2＋6ah.2B 【解析】以边长为1的边所在直线为轴旋转形成的几何体的侧面积S 1＝2π×2×1＝4π，以2所在边为轴旋转形成的几何体的侧面积S 2＝2π×1×2＝4π，故S 1∶S 2＝1∶1，选B.3B 【解析】该几何体由两个长方体组合而成，其表面积等于下面长方体的全面积与上面长方体的四个侧面积之和．S ＝2(10×8＋10×2＋8×2)＋2(6×8＋8×2)＝360.故选B.4A 【解析】设圆柱的底面半径为r ，高为h ，则有h ＝2πr ，所以表面积与侧面积的比为2π(r 2＋rh)∶2πrh ＝(r ＋h)∶h ＝(2π＋1)∶2π.52∶1 【解析】S 圆柱＝2·π⎝⎛⎭⎫a 22＋2π·⎝⎛⎭⎫a 2·a ＝32πa 2， S 圆锥＝π⎝⎛⎭⎫a 22＋π·a 2·a ＝34πa 2，∴S 圆柱∶S 圆锥＝2∶1.6 100π【解析】设圆台的上底半径为r，则下底半径为4r，高为4r.由母线长为10可知10＝（3r）2＋（4r）2＝5r，∴r＝2.故圆台的上、下底半径和高分别为2，8，8.所以圆台的侧面积为π(2＋8)×10＝100π.7 S2【解析】如图，设圆锥底面半径为r，母线长为l，由题意得⎩⎨⎧π2l2＝S，πl＝2πr.解得r＝S2π，所以底面积为πr2＝π×S2π＝S2.8 【解】几何体的表面积为：S＝6×22－π×(0.5)2×2＋2π×0.5×2＝24－0.5π＋2π＝24＋1.5π.9 【解】如下图所示，设圆台的上底面周长为c cm，上、下底面半径分别为r1 cm，r2 cm，则r1＝10，r2＝20.因为扇环的圆心角是180°，所以c＝π·SA.又c＝2π·10＝20π，所以SA＝20.同理SB＝40.所以AB＝SB－SA＝20.S表面积＝S侧＋S上底＋S下底＝π(r1＋r2)·AB＋πr21＋πr22＝π(10＋20)×20＋π×102＋π×202＝1 100π(cm2)．答：圆台的表面积为1 100πcm2.10 【解】(1)圆锥的母线长为62＋22＝210 cm，∴圆锥的侧面积S＝π×2×210＝410πcm2.(2)画出轴截面如图所示：设圆柱的半径为r .由题意知：r2＝6－x6，∴r＝6－x3，∴圆柱的侧面积S ＝2πrx ＝2π3(－x 2＋6x)，∴当x ＝3 cm 时，S 最大＝6πcm 2.11D 【解析】 S 1＝π，S 2＝4π，∴r ＝1，R ＝2，S 侧＝6π＝π(r ＋R)l ， ∴l ＝2，∴h ＝ 3.∴V ＝13π(1＋4＋2)×3＝733π.故选D.12C 【解析】由三视图可知几何体是如图所示的两个圆柱的组合体．其中左面圆柱的高为4 cm ，底面半径为2 cm ，右面圆柱的高为2 cm ，底面半径为3 cm ，则组合体的体积V 1＝π×22×4＋π×32×2＝16π＋18π＝34π(cm 3)，原毛坯体积V 2＝π×32×6＝54π(cm 3)，则所求比值为54π－34π54π＝1027.13A 【解析】由三视图可知，该几何体是一个正四棱柱挖去一个圆锥，正四棱柱的体积为2×2×2＝8，圆锥的体积为13π×2＝2π3，所以该几何体的体积为8－2π3，选A.14.32【解析】设两个圆柱的底面半径和高分别为r 1，r 2和h 1，h 2，由S 1S 2＝94，得πr 21πr 22＝94，则r 1r 2＝32.由圆柱的侧面积相等，得2πr 1h 1＝2πr 2h 2，即r 1h 1＝r 2h 2，则h 1h 2＝23，所以V 1V 2＝πr 21h 1πr 22h 2＝32.1533π 【解析】由题意可知该圆锥的侧面展开图为半圆，如图所示，设圆锥底面半径为r ，高为h ，则⎩⎪⎨⎪⎧2πr ＝2π，h 2＋r 2＝4， ∴⎩⎪⎨⎪⎧r ＝1，h ＝ 3.∴它的体积为13×π×12×3＝33π.16【解】 (1)直观图如图所示．(2)由题意可知，S △ABC ＝12×3×332＝934.S 侧＝3AC ×AA 1＝3×3×3＝27.故这个三棱柱的表面积为27＋2×934＝27＋932.这个三棱柱的体积为934×3＝2734.17【解】在△ABC 中，由AC ＝3，BC ＝4，AB ＝5，知AC 2＋BC 2＝AB 2，∴AC ⊥BC.∴CD ＝125，记为r ＝125，那么△ABC 以AB 为轴旋转所得旋转体是两个同底的圆锥，且底半径r ＝125，母线长分别是AC ＝3，BC ＝4，∴S 表面积＝πr ·(AC ＋BC)＝π×125×(3＋4)＝845π.V ＝13πr 2(AD ＋BD)＝13πr 2·AB ＝13π×⎝⎛⎭⎫1252×5＝485π.所以，所求旋转体的表面积是845π，体积是485π.。

高一柱体、椎体、台体的表面积和体积练习题

柱体、椎体、台体的表面积和体积练习一、知识回顾（1）棱柱、棱锥、棱台的表面积 = 侧面积 + ______________；（2）圆柱：r 为底面半径，l 为母线长则侧面积为_______________；表面积为_______________. 圆锥：r 为底面半径，l 为母线长则侧面积为_______________；表面积为_______________.圆台：r ’、r 分别为上、下底面半径，l 为母线长则侧面积为____________；表面积为_____________.（3）柱体体积公式：________________________；（S 为底面积，h 为高）锥体体积公式：________________________；（S 为底面积，h 为高）台体体积公式：________________________；（S ’、S 分别为上、下底面面积，h 为高）二、典型练习1．一个圆柱的侧面展开图是一个正方形，这个圆柱的全面积与侧面积的比是（）.（A ）122ππ+ （B ）144ππ+ （C ）12ππ+ （D ）142ππ+2．在棱长为 1 的正方体上，分别用过共顶点的三条棱中点的平面截该正方体，则截去与8个顶点相关的8个三棱锥后，剩下的几何体的体积是（）.（A ）32 （B ）43 （C ）54 （D ）653. 正四棱台的上、下底面边长分别是方程01892=+-x x的两根，其侧面积等于两底面积的和，则其斜高与高分别为 A ．25与2 B.2与23C.5与4D.2与34.棱台的上、下底面面积分别为4和9，则这个棱台的高和截得棱台的原棱锥的高的比是A ．21 B.31 C.32 D.435.一个四棱锥和一个三棱锥恰好可以拼接成一个三棱柱．这个四棱锥的底面为正方形，且底面边长与各侧棱长相等，这个三棱锥的底面边长与各侧棱长也都相等．设四棱锥、三棱锥、三棱柱的高分别为1h ，2h ，h ，则12::h h h =（）Ａ．Ｂ．2:22:Ｄ．26、若一个圆锥的侧面展开图是面积为2π的半圆面，则该圆锥的体积为__________．7、一个高为2的圆柱，底面周长为2π.该圆柱的表面积为__________．8. 若等腰直角三角形的直角边长为2，则以一直角边所在直线为轴旋转一周所成的几何体体积是_______9、若一个圆锥的轴截面是边长为3,3,2的三角形，则该圆锥的侧面积是_______10.已知四棱椎P ABCD-的底面是边长为6 的正方形，侧棱PA⊥底面ABCD，且8PA=，则该四棱椎的体积是_________11、若圆锥的侧面积为2π，底面积为π，则该圆锥的体积为 .13. 三棱锥P—ABC中，PA⊥底面ABC，PA=3，底面ABC是边长为2的正三角形，则三棱锥P—ABC的体积等于______.14、如图，在三棱柱A1B1C1－ABC中，D，E，F分别是AB，AC，AA1的中点，设三棱锥F－ADE的体积为V1，三棱柱A1B1C1－ABC的体积为V2，则V1∶V2＝__________.15、如图，在长方体ABCD－A1B1C1D1中，AB＝AD＝3 cm，AA1＝2 cm，则四棱锥A－BB1D1D的体积为__________cm16、如图，正三棱锥O－ABC的底面边长为2，高为1，求该三棱锥的体积及表面积．17、由8个面围成的几何体，每一个面都是正三角形，并且有四个顶点A、B、C、D在同一个平面内，ABCD 是边长为30cm的正方形，求出此几何体的表面积和体积.。

专题1-3-1 柱体、锥体、台体的表面积与体积-2017-2018学年高一数学必修2 含解析精品

一、选择题1．若圆锥的底面半径为2，高为5，则圆锥的侧面积为A ．3πB ．12πC ．5πD ．6π 【答案】D【解析】圆锥的母线长l =22r h +=3，∴圆锥的侧面积S =πrl =π×2×3=6π，故选D ．2．已知长方体的表面积是24，所有棱长的和是24，则长方体的体对角线的长是A ．14B ．4C ．32D ．23 【答案】D 3．如图为某几何体的三视图,则该几何体的表面积为俯视图侧视图正视图12222A ．202π+B ．203π+C ．242π+D ．243π+【答案】B【解析】由三视图可知,该几何体是一个组合体,左边是底面半径为1、高为2的半圆柱,右边是棱长为2的正方体,所以该几何体的表面积为2115222π12π1222⨯⨯+⨯⨯⨯+⨯⨯⨯=203π+. 4．一个几何体的三视图如图所示,则该几何体的体积为A ．83B ．43C ．89 D ．49 【答案】A5．若一圆柱与圆锥的高相等，且轴截面面积也相等，那么圆柱与圆锥的体积之比为A ．1B ．12C ．32D ．34【答案】D【解析】设圆柱与圆锥的底面半径分别为R ，r ，高都是h ，由题设，2R ·h ＝12×2r ·h ，∴r ＝2R ，V 圆柱＝πR 2h ，V 圆锥＝13πr 2h ＝43πR 2h ，∴34V V =圆柱圆锥，选D ． 6．某四棱台的三视图如图所示，则该四棱台的体积是A ．4B ．143C ．163D ．6【答案】B【解析】由三视图知：四棱台的上底面是边长为1的正方形，下底面是边长为2的正方形，高为2，所以该四棱台的体积是()22221141122233V =⨯+⨯+⨯=，故选B ． 7．正方体的八个顶点中有四个恰为正四面体的顶点，则正方体的全面积与正四面体的全面积之比为A ．2B ．3C ．62D ．233【答案】B8．如图，在多面体ABCDEF 中，已知底面ABCD 是边长为3的正方形，EF AB ∥，32EF =，且EF 与底面ABCD 的距离为2，则该多面体的体积是A ．92B ．5C ．6D ．152【答案】D9．某几何体的三视图如图所示，则该几何体的体积是A ．3(2)π2+ B ．3 (4)π3+ C ．3(2)π6+ D ．3(2)π3+【答案】C10．《九章算术》中，将底面是直角三角形的直三棱柱称之为“堑堵”，已知某“堑堵”的三视图如图所示，俯视图中虚线平分矩形的面积，则该“堑堵”的表面积为A ．224+B ．2C ．244+D ．246+ 【答案】D【解析】由题意及三视图可知，该棱柱底面为等腰直角三角形，其斜边上的高为1，则斜边长为2 ，直角边长为2，则其表面积为1222222226422S =⨯⨯⨯+⨯+⨯⨯=+.二、填空题11．正四棱柱的体对角线长为6，侧面对角线长为33，则它的侧面积是________. 【答案】362 【解析】设正四棱柱的底面边长为a ，侧棱长为b ，则222227236a b a b ⎧+=⎪⎨+=⎪⎩，解得a =3，32b =，则侧面积为4362ab =．12．已知圆锥的母线长为4，侧面展开图的中心角为π2，那么它的体积为________. 【答案】15π3【解析】设底面圆的半径为r ，ππ12412r r ∴=⋅∴=，，因此圆锥的高224115h =-=，23π13π15V r h ∴==． 13．一个几何体的三视图如图所示，则该几何体的体积为________.【答案】π4+ 【解析】由三视图可知，该几何体为半个圆柱加一个长方体的组合体，故其体积为21π12212π42V =⨯⨯+⨯⨯=+. 14．圆台的一个底面周长是另一个底面周长的3倍，母线长为3，圆台的侧面积为84π，则圆台较小底面的半径为________.【答案】7三、解答题15．已知ABCD －A 1B 1C 1D 1是棱长为a 的正方体，E 、F 分别为棱AA 1与CC 1的中点，求四棱锥A 1－EBFD 1的体积. 【答案】36a . 【解析】如图所示，所以1111111122311 (34346)A EBFD A EBF A EFD F A EB F A ED a a a V V V V V a a -----=+=+=+=． 16．已知一个圆锥的底面半径为R ，高为H ，在其中有一个高为x 的内接圆柱．（1）求圆柱的侧面积；（2）x 为何值时，圆柱的侧面积最大？【答案】（1）()22π2π0R S Rx x x H H =⋅<-<圆柱侧；（2）2H x =时，圆柱的侧面积最大.【名师点睛】立体几何中求某些量的最值时，也可采用代数方法．其方法是：首先根据题意合理选取变量x ，用其把所要求最值的量表示出来，然后采用代数方法求其最值，同时应注意变量x 的几何意义．。

2017-2018学年高中数学必修2课时达标检测五柱体、锥

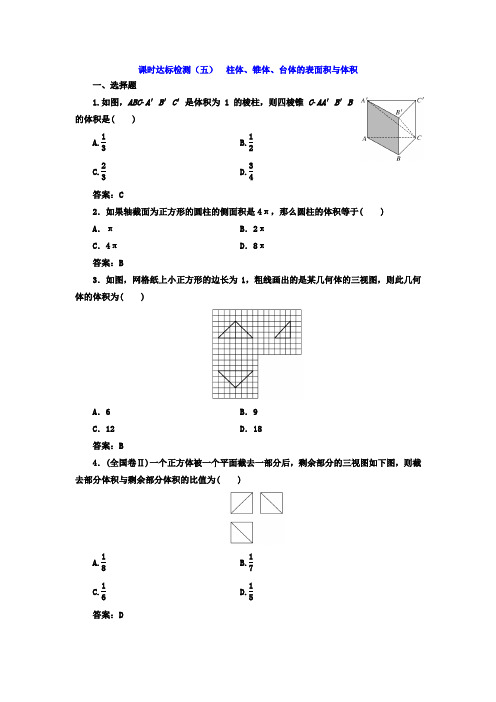
课时达标检测（五）柱体、锥体、台体的表面积与体积一、选择题1.如图，ABC A ′B ′C ′是体积为1的棱柱，则四棱锥C AA ′B ′B的体积是( )A.13B.12C.23D.34答案：C2．如果轴截面为正方形的圆柱的侧面积是4π，那么圆柱的体积等于( )A ．πB ．2πC ．4πD ．8π 答案：B3．如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为( )A ．6B ．9C ．12D ．18答案：B4．(全国卷Ⅱ)一个正方体被一个平面截去一部分后，剩余部分的三视图如下图，则截去部分体积与剩余部分体积的比值为( )A.18B.17C.16D.15答案：D5.一个四棱锥的侧棱长都相等，底面是正方形，其正视图如图所示，则该四棱锥的侧面积和体积分别是( )A ．45，8B ．45，83C ．4(5＋1)，83D ．8,8答案：B二、填空题6．一个六棱锥的体积为23，其底面是边长为2的正六边形，侧棱长都相等，则该六棱锥的侧面积为________．答案：127．(浙江高考)某几何体的三视图如图所示(单位：cm)，则该几何体的表面积是________cm 2，体积是________cm 3.答案：72 328．一个正四棱台，其上、下底面均为正方形，边长分别为8 cm 和18 cm ，侧棱长为13 cm ，则其表面积为________ cm 2.答案：1 012三、解答题9．如图是某几何体的三视图，请你指出这个几何体的结构特征，并求出它的表面积与体积．(单位：cm)解：由三视图知该几何体是一个组合体，下半部是长方体，上半部是半圆柱，其轴截面的大小与长方体的上底面大小一致．长方体的长、宽、高分别是8,4,6，圆柱的高是8，底面半径是2，∴表面积为S ＝8×4＋2×8×6＋2×4×6＋2×12×π×22＋12×2π×2×8＝176＋20π(cm 2)，体积为V ＝8×4×6＋12×π×22×8＝192＋16π(cm 3)，故该几何体的表面积为(176＋20π)cm 2，体积为(192＋16π)cm 3.10．已知正三棱锥V ABC 的正视图、俯视图如图所示，其中VA ＝4，AC ＝23，求该三棱锥的表面积．解：由正视图与俯视图可得正三棱锥的直观图如图所示，且VA ＝VB ＝VC ＝4，AB ＝BC ＝AC ＝2 3.取BC 的中点D ，连接VD ，则VD ⊥BC ，有VD ＝ VB 2－BD 2＝ 42－32＝13，则S △VBC ＝12×VD ×BC ＝12×13×23＝39， S △ABC ＝12×(23)2×32＝33，所以，三棱锥V ABC 的表面积为3S △VBC ＋S △ABC ＝339＋33＝3(39＋3)．。

广东省深圳市乐而思教育2017-2018学年高一数学必修2同步练习：柱体、锥体、台体的表面(体)积(含答案)

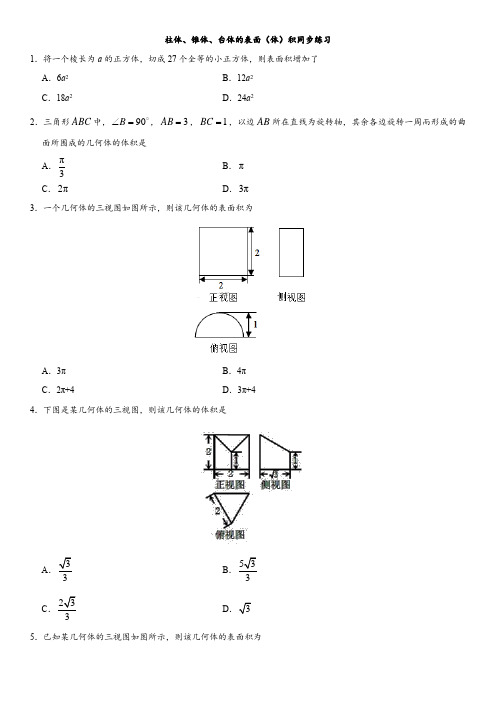
柱体、锥体、台体的表面（体）积同步练习1．将一个棱长为a 的正方体，切成27个全等的小正方体，则表面积增加了 A ．6a 2 B ．12a 2 C ．18a 2D ．24a 22．三角形ABC 中，90B ∠=，3AB =，1BC =，以边AB 所在直线为旋转轴，其余各边旋转一周而形成的曲面所围成的几何体的体积是 A ．π3B ．πC ．2πD ．3π3．一个几何体的三视图如图所示，则该几何体的表面积为A ．3πB ．4πC ．2π+4D ．3π+44．下图是某几何体的三视图，则该几何体的体积是A BCD 5．已知某几何体的三视图如图所示，则该几何体的表面积为A．73B．172C．13 D6．正六棱柱的高为5 cm，最长的对角线为13 cm，则它的侧面积为__________．7．已知圆柱的底面半径为1，母线长与底面的直径相等，则该圆柱的表面积为__________．8．已知正四棱锥的侧面积是底面积的2倍，高是3，求它的全面积．9．一个几何体的三视图如图所示，则其表面积是A．20B．18C．14+D．14+10．《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有委米依垣内角，下周八尺，高五尺，问：积及为米几何？”其意思为：“在屋内墙角处堆放米（如图，米堆为一个圆锥的四分之一），米堆底部的弧长为8尺，米堆的高为5尺，米堆的体积和堆放的米各为多少？”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放的米有A ．14斛B ．22斛C ．36斛D ．66斛11．一个几何体的三视图如图所示，已知这个几何体的体积为，则h =ABC ．D ．12．设一个圆锥与一个圆柱的底面半径和高都对应相等，它们的侧面积分别为1S ，2S ，则必有A ．12S S <B ．12S S =C ．12S S >D ．以上情况均有可能13．如图，正方体ABCD A B C D ''''-的棱长为a ，连接A C A D A B ''''，，，BD BC C D ''，，，得到一个三棱锥A BC D ''-．求：（1）三棱锥A BC D ''-的表面积与正方体表面积的比值；（2）三棱锥A BC D ''-的体积．14．如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分后所得，则该几何体的体积为A ．90πB ．63πC ．42πD ．36π15．某几何体的三视图如图所示（单位：cm ），则该几何体的体积（单位：cm 3）是A ．12π+ B ．32π+ C ．312π+D ．332π+16．某三棱锥的三视图如图所示，则该三棱锥的体积为A ．60B ．30C ．20D ．1017．下图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为A ．20πB ．24πC ．28πD ．32π18．已知某三棱锥的三视图如图所示，则该三棱锥的体积为.19．某几何体的三视图如图所示（单位：cm），则该几何体的表面积是______cm2,体积是______cm3.20．由一个长方体和两个圆柱体构成的几何体的三视图如图，则该几何体的体积为.参考答案6．【答案】180 cm 2【解析】设正六棱柱底面边长为a ，则底面上最长对角线长2a ，∴=13，∴a =6，侧面积S =6a ×5=180(cm 2)． 7．【答案】6π【解析】因为圆柱的表面积为22π2π,1,2r rl r l +==，所以圆柱的表面积为6π. 8．【答案】36.【解析】如图，高PO =3，PE 是斜高，∵S 侧=2S 底，∴4×12×BC ×PE =2BC 2，∴BC =PE . 在Rt △POE 中，PO =3，OE =12BC =12PE .∴229()2PE PE +=，∴PE =.∴S 底=BC 2=PE 2=()2=12，S 侧=2S 底=2×12=24. ∴S 全=S 底＋S 侧=12＋24=36.13．【答案】（1（2【解析】（1）∵ABCD A B C D ''''-是正方体，∴三棱锥A BC D ''-的表面积为．而正方体的表面积为26a ， ∴三棱锥A BC D ''-的表面积与正方体表面积的比值为（2）三棱锥,,,A ABD C BCD D A D C B A B C ''''''''----是完全一样的，18.19．【答案】80 40【解析】由三视图可知该组合体是一个长方体上面放置了一个小正方体，则22262244242280S =⨯+⨯+⨯⨯-⨯=表面积，3244240V =+⨯⨯=．20．【答案】π22+【解析】由三视图可知,长方体的长、宽、高分别为2,1,1,圆柱的高为1,底面圆半径为1,所以2π1π21121242V ⨯=⨯⨯+⨯⨯=+.。

高中数学1.3.1柱体、锥体、台体的表面积与体积精品课堂同步练习试题

1.3.1 柱体、锥体、台体的表面积与体积一、选择题1、圆锥母线长为1,侧面展开图的圆心角为240︒，该圆锥体积为（）A B 、881π C D 、1081π 2、长方体的高等于h ，底面积等于a ，过相对侧棱的截面面积等于b ，则此长方体的侧面积等于（）A 、B 、C 、D 3、圆台上、下底面面积为π、4π，侧面积为6π，则该圆台的体积为（）AB 、CD 4、三棱台111ABC A B C -中，11:1:2AB A B =，则三棱锥1A ABC -，11B A B C -，111C A B C -的体积之比为（） A 、1:1:1 B 、1:1:2 C 、1:2:4 D 、1:4:4二、填空题5、将一个圆心角为65π，半径为5的扇形卷成一个圆锥的侧面，则此圆锥的体积为______________6、面积为2的菱形，绕其一边旋转一周所得几何体的表面积是_______________7、已知正方体的棱长为a ，以正方体的六个面的中心为顶点的多面体的体积为_______________8、已知圆锥的底面半径为4，母线长为6，一只蚂蚁从底面圆周上一点A 出发，在侧面上绕圆锥爬行一周，又回到A 点，则蚂蚁经过的最短路程为_______________三、解答题9、棱长为4cm的正方体，若在它的各个面的中心位置上，各打一个直径为2cm，深为1cm的圆柱形的孔，求打孔后几何体的表面积10、倒圆锥形容器的轴截面是正三角形，内盛水的深度为6cm，水面距离容器口距离为1cm，现放入一个棱长为4cm的正方体实心铁块，让正方体一个面与水平面平行，问容器中的水是否会溢出？。

高中数学柱体、锥体、台体的表面积与体积(练习)(解析版)

1.3.1 柱体、锥体、台体的表面积与体积（练习）(建议用时：40分钟)一、选择题1．已知某长方体同一顶点上的三条棱长分别为1,2,3，则该长方体的表面积为( ) A ．22 B ．20 C ．10 D ．11【答案】A [所求长方体的表面积S ＝2×(1×2)＋2×(1×3)＋2×(2×3)＝22.]2．已知高为3的直棱柱ABC -A 1B 1C 1的底面是边长为1的正三角形，则三棱锥B 1-ABC 的体积为( ) A.14 B.12 C.36 D.34【答案】D [由题意，锥体的高为BB 1，底面为S △ABC ＝34，所以V ＝13Sh ＝13×34×3＝34.] 3．体积为52的圆台，一个底面积是另一个底面积的9倍，那么截得这个圆台的圆锥的体积是( ) A ．54 B ．54π C ．58 D ．58π【答案】A [设上底面半径为r ，则由题意求得下底面半径为3r ，设圆台高为h 1，则52＝13πh 1(r 2＋9r 2＋3r ·r )，∴πr 2h 1＝12.令原圆锥的高为h ，由相似知识得r 3r ＝h －h 1h ，∴h ＝32h 1，∴V 原圆锥＝13π(3r )2×h ＝3πr 2×32h 1＝92×12＝54.]4．若一个圆锥的轴截面是等边三角形，其面积为3，则这个圆锥的表面积是( ) A ．3π B ．33π C ．6π D ．9π【答案】A [根据轴截面面积是3，可得圆锥的母线长为2，底面半径为1，所以S ＝πr 2＋πrl ＝π＋2π＝3π.]5．分别以一个锐角为30°的直角三角形的最短直角边、较长直角边、斜边所在的直线为轴旋转一周，所形成的几何体的体积之比是( )A ．1∶2∶ 3B ．6∶23∶ 3C ．6∶23∶3D ．3∶23∶6【答案】C [设Rt △ABC 中，∠BAC ＝30°，BC ＝1，则AB ＝2，AC ＝3，求得斜边上的高CD ＝32，基础篇旋转所得几何体的体积分别为V 1＝13π(3)2×1＝π，V 2＝13π×12×3＝33π，V 3＝13π⎝⎛⎭⎫322×2＝12π.V 1∶V 2∶V 3＝1∶33∶12＝6∶23∶3.] 二、填空题6．侧面都是直角三角形的正三棱锥，底面边长为a ，则该三棱锥的表面积为__________．【答案】3＋34a 2 [∵底面边长为a ，则斜高为a 2，故S 侧＝3×12a ×a 2＝34a 2，而S 底＝34a 2，故S 表＝3＋34a 2.] 7．圆台的一个底面周长是另一个底面周长的3倍，母线长为3，圆台的侧面积为84π，则圆台较小的底面半径为________．【答案】7 [设圆台较小的底面半径为r ，因为圆台的一个底面周长是另一个底面周长的3倍，母线长l ＝3，圆台的侧面积为84π，所以S 侧面积＝π(r ＋3r )l ＝84π，解得r ＝7.]8．过圆锥的高的三等分点作平行于底面的截面，它们把圆锥的侧面分成的三部分的面积之比为________．【答案】1∶3∶5 [如图，由题意知O 1A 1∶O 2A 2∶OA ＝1∶2∶3，以O 1A 1，O 2A 2，OA 为底面半径的圆锥的侧面积之比为1∶4∶9.故圆锥被截面分成的三部分侧面的面积之比为1∶(4－1)∶(9－4)＝1∶3∶5.] 三、解答题9．将一个圆形纸片沿半径剪开为两个扇形，其圆心角之比为3∶4，再将它们卷成两个圆锥侧面，求这两个圆锥的体积之比．【答案】设圆的半径为r ，则两个圆锥的母线长为r .由已知可得两个圆锥的底面半径分别为2πr ×372π＝37r ，2πr ×472π＝47r ，所以两圆锥的体积之比为 13π×⎝⎛⎭⎫37r 2×r 2－⎝⎛⎭⎫37r 213π×⎝⎛⎭⎫47r 2×r 2－⎝⎛⎭⎫47r 2＝333088.10．若E ，F 是三棱柱ABC -A 1B 1C 1侧棱BB 1和CC 1上的点，且B 1E ＝CF ，三棱柱的体积为m ，求四棱锥A -BEFC 的体积.【答案】如图所示，连接AB 1，AC 1.因为B 1E ＝CF ，所以梯形BEFC 的面积等于梯形B 1EFC 1的面积．又四棱锥A -BEFC 的高与四棱锥A -B 1EFC 1的高相等，所以V A -BEFC ＝VA -B 1EFC 1＝12VA -BB 1C 1C . 又VA -A 1B 1C 1＝13S △A 1B 1C 1·h ，VABC -A 1B 1C 1＝S △A 1B 1C 1·h ＝m ，所以VA -A 1B 1C 1＝m 3，所以VA -BB 1C 1C ＝VABC -A 1B 1C 1－VA -A 1B 1C 1＝23m ，所以V A -BEFC ＝12×23m ＝m3，即四棱锥A -BEFC 的体积是m3.1．圆柱的一个底面积是S ，侧面展开图是一个正方形，那么这个圆柱的侧面积是( ) A ．4πSB ．2πSC ．πSD.233πS【答案】A [底面半径是Sπ，所以正方形的边长是2πSπ＝2πS ，故圆柱的侧面积是(2πS )2＝4πS .] 2．如图1-3-5，三棱台ABC -A 1B 1C 1中，AB ∶A 1B 1＝1∶2，则三棱锥A 1-ABC ，B -A 1B 1C ，C -A 1B 1C 1的体积之比为( )图1-3-5提升篇A ．1∶1∶1B ．1∶1∶2C ．1∶2∶4D ．1∶4∶4【答案】C [设棱台的高为h ，S △ABC ＝S ，则S △A 1B 1C 1＝4S ，∴VA 1-ABC ＝13S △ABC ·h ＝13Sh ，VC -A 1B 1C 1＝13S △A 1B 1C 1·h ＝43Sh .又V 台＝13h (S ＋4S ＋2S )＝73Sh ，∴VB -A 1B 1C ＝V 台－VA 1-ABC －VC -A 1B 1C 1＝73Sh －Sh 3－4Sh 3＝23Sh ，∴体积比为1∶2∶4.]3．一个圆锥形容器和一个圆柱形容器，它们的轴截面尺寸如图1-3-6所示，两容器内所盛液体的体积正好相等，且液面高度h 正好相同，则h ＝________.图1-3-6【答案】32a [设圆锥形容器的液面的半径为R ，则液体的体积为13πR 2h ，圆柱形容器内的液体体积为π⎝⎛⎭⎫a 22h . 根据题意，有13πR 2h ＝π⎝⎛⎭⎫a 22h ，解得R ＝32a . 再根据圆锥形容器的轴截面与内盛液体轴截面是相似三角形，得32a a ＝ha ，所以h ＝32a .] 4．用一张正方形的纸把一个棱长为1的正方体礼品盒完全包住，不将纸撕开，则所需纸的最小面积是________.【答案】8 [如图①为棱长为1的正方体礼品盒，先把正方体的表面按图所示方式展成平面图形，再把平面图形尽可能拼成面积较小的正方体，如图②所示，由图知正方形的边长为22，其面积为8.]5．已知一个三棱台的上、下底面分别是边长为20 cm 和30 cm 的正三角形，侧面是全等的等腰梯形，且侧面面积等于上、下底面面积之和，求棱台的高和体积．【答案】如图所示，在三棱台ABC -A ′B ′C ′中，O ′，O 分别为上、下底面的中心，D ，D ′分别是BC ，B ′C ′的中点，连接OO ′，A ′D ′，AD ，DD ′，则DD ′是等腰梯形BCC ′B ′的高，记为h 0，所以S 侧＝3×12×(20＋30)h 0＝75h 0.上、下底面面积之和为S 上＋S 下＝34×(202＋302)＝3253(cm 2)．由S 侧＝S 上＋S 下，得75h 0＝3253，所以h 0＝1333(cm)．又O ′D ′＝13×32×20＝1033(cm)，OD ＝13×32×30＝53(cm)，记棱台的高为h ，则h ＝O ′O＝h 20－(OD －O ′D ′)2＝⎝⎛⎭⎫13332－⎝⎛⎭⎫53－10332＝43(cm)，由棱台的体积公式，可得棱台的体积 V ＝h3(S 上＋S 下＋S 上S 下)＝433×(3253＋34×20×30) ＝1 900(cm 3)．。

高中数学必修2-1.3.1《柱体、锥体、台体的表面积与体积》同步练习

1.3.1《柱体、锥体、台体的表面积与体积》同步练习(1)一、选择题1．轴截面是正三角形的圆锥称作等边圆锥，则等边圆锥的侧面积是底面积的( ) A ．4倍 B ．3倍 C ．2倍 D ．2倍[答案] D[解析] 由已知得l ＝2r ，S 侧S 底＝πrl πr 2＝lr ＝2，故选D.2．长方体的高为1，底面积为2，垂直于底的对角面的面积是5，则长方体的侧面积等于( )A ．27B ．4 3C ．6D ．3[答案] C[解析] 设长方体的长、宽、高分别为a 、b 、c ，则c ＝1，ab ＝2，a 2＋b 2·c ＝5， ∴a ＝2，b ＝1，故S 侧＝2(ac ＋bc )＝6.3．已知一个圆柱的侧面展开图是一个正方形，这个圆柱的全面积与侧面积的比是( ) A ．1＋2π2πB ．1＋4π4πC ．1＋2ππD ．1＋4π2π[答案] A[解析] 设圆柱的底面半径为r ，高为h ，则由题设知h ＝2πr ，∴S 全＝2πr 2＋2πr ·h ＝2πr 2(1＋2π)又S 侧＝h 2＝4π2r 2，∴S 全S 侧＝1＋2π2π.4．将一个棱长为a 的正方体，切成27个全等的小正方体，则表面积增加了( ) A ．6a 2 B ．12a 2 C ．18a 2 D ．24a 2[答案] B[解析] 原来正方体表面积为S 1＝6a 2，切割成27个全等的小正方体后，每个小正方体的棱长为13a ，其表面积为6×⎝⎛⎭⎫13a 2＝23a 2，总表面积S 2＝27×23a 2＝18a 2，∴增加了S 2－S 1＝12a 2.5．某四棱锥的三视图如图所示，该四棱锥的表面积是( )A ．32B ．16＋16 2C ．48D ．16＋32 2[答案] B[解析] 易知此四棱锥为正四棱锥，底面边长为4，高为2，则斜高为22，故S 侧＝4×12×4×22＝162，S 底＝4×4＝16，所以S 表＝16＋16 2.6．某几何体的三视图如图所示，则该几何体的表面积为( )A ．180B ．200C ．220D ．240[答案] D[分析] 根据三视图可以确定此几何体为四棱柱，再由数量关系分别去确定侧面积与底面面积，相加为该几何体的表面积．[解析] 几何体为直四棱柱，其高为10，底面是上底为2，下底为8，高为4，腰为5的等腰梯形，故两个底面面积的和为12×(2＋8)×4×2＝40，四个侧面面积的和为(2＋8＋5×2)×10＝200，所以直四棱柱的表面积为S ＝40＋200＝240.[易错警示] 本题在求解过程中易错误将3作为等腰梯形的腰长，从而误求结果为200.二、填空题7．已知圆柱OO ′的母线l ＝4 cm ，全面积为42π cm 2，则圆柱OO ′的底面半径r ＝ ________cm.[答案] 3[解析] 圆柱OO ′的侧面积为2πrl ＝8πr (cm 2)，两底面积为2×πr 2＝2πr 2(cm 2)， ∴2πr 2＋8πr ＝42π，解得r ＝3或r ＝－7(舍去)， ∴圆柱的底面半径为3 cm.8．一个几何体的三视图如图所示，其中俯视图为正三角形，则该几何体的表面积为________．[答案] 24＋2 3[解析] 该几何体是三棱柱，且两个底面是边长为2的正三角形，侧面是全等的矩形，且矩形的长是4，宽是2，所以该几何体的表面积为2×(12×2×3)＋3×(4×2)＝24＋2 3.9．如图所示，一圆柱内挖去一个圆锥，圆锥的顶点是圆柱底面的圆心，圆锥的底面是圆柱的另一个底面．圆柱的母线长为6，底面半径为2，则该组合体的表面积等于________．[答案] (410＋28)π[解析] 挖去的圆锥的母线长为62＋22＝210，则圆锥的侧面积等于410π.圆柱的侧面积为2π×2×6＝24π，圆柱的一个底面面积为π×22＝4π，所以组合体的表面积为410π＋24π＋4π＝(410＋28)π.三、解答题10．已知圆台的上、下底面半径分别是2,5，且侧面积等于两底面面积之和，求该圆台的母线长．[答案]297[解析] 设圆台的母线长为l ，则圆台的上底面面积为S 上＝π×22＝4π，圆台的下底面面积为S 下＝π×52＝25π，所以圆台的底面面积为S ＝S 上＋S 下＝29π.又圆台的侧面积S 侧＝π(2＋5)l ＝7πl ，则7πl ＝29π，解得l ＝297，即该圆台的母线长为297.11．如图在底面半径为2，母线长为4的圆锥中内接一个高为3的圆柱，求圆柱的表面积．[解析] 设圆锥的底面半径为R ，圆柱的底面半径为r ，表面积为S . 则R ＝OC ＝2，AC ＝4， AO ＝42－22＝2 3.如图所示易知△AEB ∽△AOC ，∴AE AO ＝EB OC ，即323＝r2，∴r ＝1， S 底＝2πr 2＝2π，S 侧＝2πr ·h ＝23π. ∴S ＝S 底＋S 侧＝2π＋23π＝(2＋23)π.12．已知某几何体的三视图如图，求该几何体的表面积．(单位：cm)[解析] 几何体的直观图如图．这是底面边长为4，高为2的同底的正四棱柱与正四棱锥的组合体，易求棱锥的斜高h ′＝22，其表面积S ＝42＋4×4×2＋(12×4×22)×4＝48＋16 2 cm 2.1.3.1《柱体、锥体、台体的表面积与体积》同步练习(2)一、选择题1．长方体三个面的面积分别为2、6和9，则长方体的体积是( ) A ．63 B ．36 C ．11 D ．12[答案] A[解析] 设长方体长、宽、高分别为a 、b 、c ，则ab ＝2，ac ＝6，bc ＝9，相乘得(abc )2＝108，∴V ＝abc ＝6 3.2．圆台的体积为7π，上、下底面的半径分别为1和2，则圆台的高为( ) A ．3 B ．4 C ．5 D ．6 [答案] A[解析] 由题意，V ＝13(π＋2π＋4π)h ＝7π，∴h ＝3.3．一个空间几何体的正视图、侧视图、俯视图为全等的等腰直角三角形，直角边长为1，则这个几何体的体积为( )A ．1B ．12C ．13D ．16[答案] D[解析] 由三视图知，该几何体是三棱锥．体积V ＝13×12×1×1×1＝16.4．在△ABC 中，AB ＝2，BC ＝3，∠ABC ＝120°，若使△ABC 绕直线BC 旋转一周，则所形成的几何体的体积是( )A ．6πB ．5πC ．4πD ．3π[答案] D[解析] 如图过A 作AD 垂直BC 于点D ，此几何体为一个大圆锥挖去一个小圆锥V ＝13π×(3)2×4－13π×(3)2×1＝3π.故选D.5．某四棱台的三视图如图所示，则该四棱台的体积是( )A ．4B ．143C ．163D ．6[答案] B[分析] 根据三视图可知此几何体为棱台，分别确定棱台的底面面积和高即可求得体积．[解析] 由四棱台的三视图可知，台体上底面积S 1＝1×1＝1，下底面积S 2＝2×2＝4，高h ＝2，代入台体的体积公式V ＝13(S 1＋S 1S 2＋S 2)h ＝13×(1＋1×4＋4)×2＝143.6．如图(1)所示，一只装了水的密封瓶子，其内部可以看成是由半径为1 cm 和半径为3 cm 的两个圆柱组成的简单几何体．当这个几何体如图(2)水平放置时，液面高度为20 cm ，当这个几何体如图(3)水平放置时，液面高度为28 cm ，则这个简单几何体的总高度为( )A ．29 cmB ．30 cmC ．32 cmD ．48 cm[答案] A[解析] 图(2)和图(3)中，瓶子上部没有液体的部分容积相等，设这个简单几何体的总高度为h ，则有π×12(h －20)＝π×32(h －28)，解得h ＝29(cm)．二、填空题7．已知圆锥SO 的高为4，体积为4π，则底面半径r ＝________. [答案]3[解析] 设底面半径为r ，则13πr 2×4＝4π，解得r ＝3，即底面半径为 3.8．如图，在三棱柱A 1B 1C 1－ABC 中，D ，E ，F 分别是AB ，AC ，AA 1的中点．设三棱锥F －ADE 的体积为V 1，三棱柱A 1B 1C 1－ABC 的体积为V 2，则V 1∶V 2＝________.[答案] 1 24[分析] 找到棱锥的底、高与棱柱的底、高之间的关系，从而可以得出它们的体积之比． [解析] 设三棱柱A 1B 1C 1－ABC 的高为h ，底面三角形ABC 的面积为S ，则V 1＝13×14S ×12h ＝124Sh ＝124V 2，即V 1 V 2＝1 24. 9．设甲、乙两个圆柱的底面积分别为S 1、S 2，体积分别为V 1、V 2，若它们的的侧面积相等且S 1 S 2＝9 4，则V 1 V 2＝________.[答案] 3 2[解析] 设甲圆柱底面半径r 1，高h 1，乙圆柱底面半径r 2，高h 2，S 1S 2＝πr 21πr 22＝94，∴r 1r 2＝32，又侧面积相等得2πr 1h 1＝2πr 2h 2，∴h 1h 2＝23.因此V 1V 2＝πr 21h 122h 2＝32.三、解答题10．已知圆台的高为3，在轴截面中，母线AA 1与底面圆直径AB 的夹角为60°，轴截面中的一条对角线垂直于腰，求圆台的体积．[解析] 如图所示，作轴截面A 1ABB 1，设圆台的上、下底面半径和母线长分别为r ，R ，l ，高为h .作A 1D ⊥AB 于点D ，则A 1D ＝3.又∵∠A 1AB ＝60°，∴AD ＝A 1D ·1tan60°，即R －r ＝3×33，∴R －r ＝ 3. 又∵∠BA 1A ＝90°，∴∠BA 1D ＝60°. ∴BD ＝A 1D ·tan60°，即R ＋r ＝3×3， ∴R ＋r ＝33，∴R ＝23，r ＝3，而h ＝3， ∴V 圆台＝13πh (R 2＋Rr ＋r 2)＝13π×3×[(23)2＋23×3＋(3)2] ＝21π.所以圆台的体积为21π.11．已知△ABC 的三边长分别是AC ＝3，BC ＝4，AB ＝5，以AB 所在直线为轴，将此三角形旋转一周，求所得旋转体的表面积和体积．[分析] 应用锥体的侧面积和体积的计算公式求解．解题流程：△ABC 的特征――→AC ⊥BC 旋转体是两个同底圆锥――→底面半径为CD 求表面积――→高BD ，AD 求体积[解析] 如图，在△ABC 中，过C 作CD ⊥AB ，垂足为D . 由AC ＝3，BC ＝4，AB ＝5，知AC 2＋BC 2＝AB 2，则AC ⊥BC . 所以BC ·AC ＝AB ·CD ，所以CD ＝125，记为r ＝125，那么△ABC 以AB 为轴旋转所得旋转体是两个同底的圆锥，且底面半径r ＝125，母线长分别是AC ＝3，BC ＝4，所以S 表面积＝πr ·(AC ＋BC )＝π×125×(3＋4)＝845π，V ＝13πr 2(AD ＋BD )＝13πr 2·AB＝13π×(125)2×5＝485π. [特别提醒] 求旋转体的有关问题常需要画出其轴截面，将空间问题转化为平面问题来解决．对于与旋转体有关的组合体问题，要弄清楚它是由哪些简单几何体组成的，然后根据条件分清各个简单几何体底面半径及母线长，再分别代入公式求各自的表面积或体积．12．若某几何体的三视图(单位：cm)如图所示，求此几何体的体积．[解析] 该空间几何体的上部分是底面边长为4，高为2的正四棱柱，体积为16×2＝32；下部分是上底面边长为4，下底面边长为8，高为3的正四棱台，体积为13×(16＋4×8＋64)×3＝112.故该空间几何体的体积为144.。

高中数学必修二同步练习专题1.3.1 柱体、锥体、台体的表面积与体积(原卷版)

一、选择题1．已知圆柱的高等于1，侧面积等于4π，则这个圆柱的体积等于A．πB．2πC．3πD．4π2．已知长方体的表面积是24，所有棱长的和是24，则长方体的体对角线的长是A．14B．4C．32D．233．《九章算术》中，将底面是直角三角形的直三棱柱称之为“堑堵”，已知某“堑堵”的三视图如图所示，则该“堑堵”的表面积为A．4 B．642C．4+42D．24．一个几何体的三视图如图所示,则该几何体的体积为A ．83B ．43 C ．89D ．495．某圆台上、下底面半径和母线的比为1：4：5，高为8，那么它的侧面积为 A ．50πB ．100πC ．150πD ．200π6．某四棱台的三视图如图所示，则该四棱台的体积是A ．4B ．143C ．163D ．67．已知一个底面是菱形、侧面是矩形的四棱柱，侧棱长为5，菱形的对角线的长分别是9和15，则这个棱柱的侧面积是 A ．3034B ．6034C ．3034135+D ．1358．如图，在多面体ABCDEF 中，已知底面ABCD 是边长为3的正方形，EF AB ∥，32EF =，且EF 与底面ABCD 的距离为2，则该多面体的体积是A ．92B ．5C ．6D ．1529．某几何体的三视图如图所示，则该几何体的体积是A ．3(2)π+B ．3(4)π+ C ．3(2)π+D ．3(2)π+ 10．甲、乙两个几何体的三视图如图所示（单位相同），记甲、乙两个几何体的体积分别为1V ，2V ，则A ．122V V >B ．122V V =C ．12163V V -=D ．12173V V -=二、填空题11．正四棱柱的体对角线长为6，侧面对角线长为33________.12．已知圆锥和圆柱的底面半径均为R ，高均为3R ，则圆锥和圆柱的表面积之比是______． 13．一个几何体的三视图如图所示，则该几何体的体积为________.14．如图，已知圆锥的高是底面半径的2倍，侧面积为π，若正方形ABCD内接于底面圆O，则四棱锥的侧面积为__________．P ABCD三、解答题15．如图，已知几何体的三视图(单位：cm).（1）画出这个几何体的直观图(不要求写画法).（2）求这个几何体的表面积及体积.16．已知一个圆锥的底面半径为R，高为H，在其中有一个高为x的内接圆柱．（1）求圆柱的侧面积；（2）x为何值时，圆柱的侧面积最大？。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

柱体、锥体、台体的表面积与体积
高考频度：★★★★★ 难易程度：★★★☆☆
典例在线
如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的表面积为
A ．18+
B ．54+
C ．90
D ．81
【参考答案】B
【试题解析】由三视图知该几何体是一个斜四棱柱，所以该几何体的表面积为
2362332354S =⨯⨯+⨯⨯+⨯⨯=+B ．
【解题必备】1．（1）柱体的侧面展开图是矩形，解决其侧面积问题时，先求出相应的底面周长和高，再代入侧面积公式求解即可.
（2）牢记公式：2S S S =+棱柱表面积棱柱侧面积棱柱底面面积，2π()S =r r l +圆柱表面积，
()V =Sh S h 柱体为底面面积，为高.
2．（1）求解棱锥的表面积和体积时，注意高、斜高、底面边心距所成的直角三角形的应用.
（2）求解圆锥的表面积和体积时，注意扇形的有关知识和圆锥的轴截面是等腰三角形的应用.
（3）求三棱锥的体积时，注意等积变换法的应用，即通过选择合适的底面来求几何体体积的一种方法.
（4）牢记公式：S =S +S 棱锥表面积棱锥侧面积底面积，π()S =r r l +圆锥表面积，
1()3
V =Sh S h 锥体为底面面积，为高.
3．（1）求解正棱台的表面积和体积时，注意两个直角梯形的应用：高、侧棱、上下底面外接圆半径所成的直角梯形和高、斜高、上下底面边心距所成的直角梯形.求解时，一般把基本量转化到这两个直角梯形中求解.
（2）求解圆台的表面积和体积时，注意轴截面是等腰梯形的运用.
（3）不管是棱台还是圆台，还台为锥是常用的解题思路.
（4）牢记公式：S =S +S +S 棱台表面积棱台侧面积上底面面积下底面面积，22
)S =r r r l rl π''+++圆台表面积（， 1
()(,)3
V =S S h S S h ''+台体分别为上、下底面面积，为高 . 学霸推荐
1．若圆锥的侧面积为2π，底面面积为π，则该圆锥的体积为______．
2．有一个正四棱台形状的油槽，可以装油190L ，假如它的两底面边长分别等于60cm 和40cm ，求该油槽的深度？
2．【解析】由题意有22401600(cm )上S ==，22603600(cm )下S ==，
则117600()(16003600)333下上V h S S h h =
=+=，故76001900003
h =，则75cm h =. 答：该油槽的深度为75 cm.。