第六章 基本立体的投影
第6章 基本立体的投影视图

r' 1'
b'
a'
br
1s
a
1"
c' (c") b" c
a" R
SB
B A
C 第二点
S IC
A
返回
s'
s"
1'
b' e’ a' b
s e
a
S 1"
c'
(c")b"
cy
y
a" IC
B E A
第二点
返回
三棱锥表面上取点2
s'
s"
2'
2"
S
b'
a' c' (c") b"
a"
b c
s
B S
2'
2 C
A
a
位置的母线称为素线,母线上的各点绕轴线旋转时,
形成回转面上垂直于轴线的纬圆。
返回
返回
曲面立体的投影特性
1、圆柱的投影特性 2、圆锥的投影特性 3、球的投影特性
返回
1.圆柱体
(1) 圆柱体的组成 由圆柱面和两底平面组成。
(2) 圆柱面的形成 圆柱面是由直线AA1绕与
它平行的轴线OO1旋转而成。 这条运动的直线AA1称为
母线。母线上的各点绕轴线 旋转时,形成回转面上垂直 于轴线的纬圆。
基本体是构成复杂物体的基本单元,一般也称基本体 为简单形体。本章主要介绍基本体的投影以及基本体截切、 相交产生的交线的求作方法。
按立体表面的性质不同,将立体分为平面立体和曲面立体。 平面立体—表面是由平面围成的立体。(例如) 曲面立体—表面由曲面或曲面和平面围成的立体。(例如)
基本立体的投影及其表面取点

作图。
(a)
图3.5 正三棱锥表面取点
(b)
方法一:过M点在△SAB上作AB的辅助平行线ⅠM,即1’m’‖a’b’,再作1m‖ab,求出m, 再根据m、m求出m″(如图3.5a)所示;
方法二:过锥顶S和点M作一辅助线SⅡ,然后求出点M的水平投影m(如图3.5b)。 可见性判断:同棱柱。
2.圆锥 (1) 圆锥的形成 如图3.8a可知,圆锥的表面由圆锥曲面和底面圆组成。圆锥面可以看成是一直线OA绕与 其相交的轴线OO1旋转而成。圆锥面上通过锥顶S的任一直线都是圆锥面的素线。
(a) (c)
(b) 图3.8 圆锥的投影
(2)投影分析 由图3.8b可知,底面平行于H面的圆锥,其正面投影和侧面投影
(3)画法 首先画出圆柱在各个投影位置上的轴线和底圆的对称中心线,其 次画出投影为圆的圆的视图——俯视图,最后根据圆柱高及投影的 外形轮廓素线画出其余两个视图。注意:绘制回转体投影时,必须 画出轴线和对称中心线。根据国家标准的规定,轴线和对称中心线 应采用细点画线画出,且要超出轮廓线2~5 mm,如图3.6c所示。 (4)圆柱表面上取点 轴线处于特殊位置的圆柱,其圆柱面在与轴线垂直的投影面上的
1.2曲面立体的投影及其表面上取点 表面均为曲面,或由曲面和平面共同围成的基本立体称为曲面立体。常见的曲面立体多为
回转体。回转体是由一母线(直线或曲线)绕以固定的轴线ห้องสมุดไป่ตู้回转运动所形成。常见的回 转体包括圆柱、圆锥、圆环和球等。
1.圆柱 (1)圆柱的形成 圆柱体表面是由圆柱面和上下两圆形底面所组成。圆柱面可以看成是由直线AA1绕与它平 行的轴线OO1旋转而成的回转面,如图3.6a所示。直线AA1为母线,它在圆柱面上任一位 置称为素线。
组合体的三面投影图

四、组合体的尺寸标注
组合体尺寸标注的基本方法 形体分析法 在标注组合体尺寸时,首先要确定尺寸基准(即尺寸标注的起点)。 三个基准:长度方向、宽度方向、高度方向
可作为尺寸基准的要素 重要的基面,对称面,回转面的轴线等。
左右对称中心线: 长度方向尺寸基准
底面:高度方向尺 寸基准
前后对称中心线: 宽度方向尺寸基准
读图——也称看图。
根据所画出的多面正投影图,运用投影规律和画图规则,综合多面正投影 图表达的信息,想象出组合体的 空间形状。
画图——运用正投影法表达组合体;
读图——画图的逆过程。
几个投影联系起来读 图—特征投影
2. 先局部后整体,逐步读图 培养构思能力—整体构思
a"
a'
b"
b'
c'
c"
d" d'
Ф36
45° 90 98 Ф22
12
40
42
48
2)标注定形尺寸 底板:长98,宽42,高12 圆筒:外直径Ф36,高度40
内径Ф22,高度48 肋板:长90,宽14,倾角45°
Ф36
45° 90 98 Ф22
12
40
42
48
(3)标注定位尺寸
各基本体之间的相对 位置尺寸.
(4)标注总体尺寸
(有时可以是某基本 体的定形尺寸)
本章小结
在对组合体的组合方式进 行分析的基础上,运用形 体分析法画组合体的三面 图、尺寸标注,读图。
组合体由基本体按一定的相对位置以叠加 和切割两种方式混合组成的。
一、组合体的三面图 1. 组合体三面图的形成
在工程制图中,通常将物体在投影面体系 中的正投影称为视图 。
第六章 组合体的视图及尺寸标注
第六章组合体的视图及尺寸标注由基本立体组合而成的立体称为组合体。
本章将学习组合体三视图的投影特性,组合体画图和读图和基本方法以及组合体的尺寸标注。
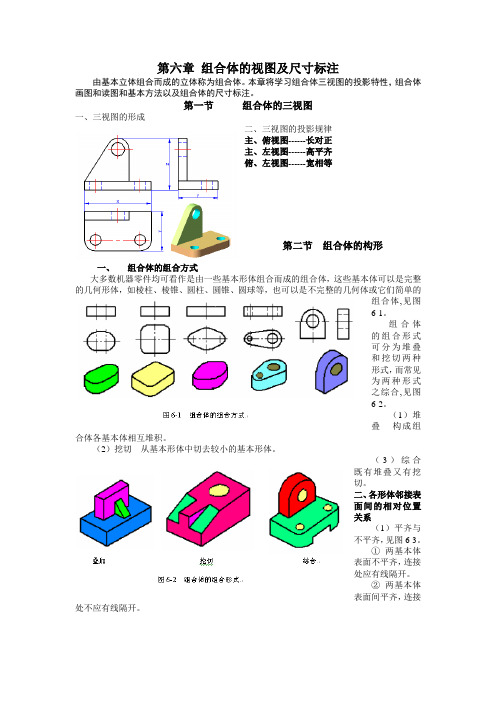
第一节组合体的三视图一、三视图的形成二、三视图的投影规律主、俯视图------长对正主、左视图------高平齐俯、左视图------宽相等第二节组合体的构形一、组合体的组合方式大多数机器零件均可看作是由一些基本形体组合而成的组合体,这些基本体可以是完整的几何形体,如棱柱、棱锥、圆柱、圆锥、圆球等,也可以是不完整的几何体或它们简单的组合体,见图6-1。
组合体的组合形式可分为堆叠和挖切两种形式,而常见为两种形式之综合,见图6-2。
(1)堆叠构成组合体各基本体相互堆积。
(2)挖切从基本形体中切去较小的基本形体。
(3)综合既有堆叠又有挖切。
二、各形体邻接表面间的相对位置关系(1)平齐与不平齐,见图6-3。
①两基本体表面不平齐,连接处应有线隔开。
②两基本体表面间平齐,连接处不应有线隔开。
(2)相交当两基本体表面相交时,其相交处交线一定要画出来,如图6-4所示,(3)相切当两基本体表面相切时,其相切处是圆滑过渡,应不画线,如图6-5所示,图中底板前端平面与圆弧面相切其平面上的棱线末端应画至切点为止。
切点位置由投影关系确定,相切处无线。
第三节组合体视图的画法一、形体分析画组合体视图之前,应对组合体进行形体分析,了解组合体的各基本体的形状、组合形式、相对位置以及在某个方向上是否对称,以便对组合体的整体形状有个概念,为画图做准备。
(a) 轴承座(b) 形体分析图6-6 画组合体视图从图6-6中可以看出,该组合体由四棱柱底板、空心圆柱体、等腰梯形柱的支承板、直角梯形柱和四棱柱叠合的肋板组成。
支承板与空心圆柱体外表面相切,叠放在底板上,它与底板后面平齐。
肋板叠放在底板上,其上与圆筒外面相结合,后面与支承板紧靠,两侧面与圆柱面相交。
整个组合体左右对称。
注意:画图时不要把组合体看成是由各零散的基本体“拼接”而成。
工程图学A教学大纲

《工程图学A》教学大纲课程编码:08297003-04课程名称:工程图学(A)英文名称:Mechanical Drawing(A)开课学期:1-2学时/学分:110/ 6.5课程类型:学科基础课开课专业:机械类专业本科生选用教材:侯洪生主编《机械工程图学》科学出版社2001年9月第一版林玉祥主编《机械工程图学习题集》科学出版社2001年9月第一版主要参考书:1、焦永和主编《机械制图》,北京理工大学出版社2000年版2、焦永和主编《机械制图习题集》,北京理工大学出版社2000年版3、孙兰凤主编《工程制图》,高等教育出版社2004年版4、曾维川主编《工程制图习题集》,高等教育出版社2004年版执笔人:侯洪生一、课程性质、目的与任务工程图学课程是研究绘制和阅读工程图样的一门技术基础课,它既有系统的理论又有较强的实践性和技术性。
在现代工业生产中,设计制造机器和进行工程建设都离不开工程图样。
在使用机器设备时,也要通过阅读图样了解机器的结构和性能。
因此,工程图样是人类用来表达和交流设计思想的重要工具,是工程技术部门的一项重要技术文件,是工程界的共同语言。
每个工程技术人员必须把握这种语言,否则就无法从事技术工作。
本课程为培养学生的绘图、读图和空间想象能力打下必要的基础。
同时,它又是学生学习后续课程和完成课程设计和毕业不可缺少的基础知识。
二、教学基本要求1.学习投影法(主要是正投影法)的基本理论及其应用;2.学习、贯彻制图国家标准和有关的基本规定,培养查阅有关设计资料和标准的能力;3.培养绘制(徒手绘图、尺规绘图和运算机绘图)和阅读机械图样的技能;4.培养空间想象能力和图解空间几何问题的初步能力;5.培养零、部件构型表达能力;6.培养学生认真负责的工作态度和严谨细致的工作作风,使学生的动手能力、工程意识、创新能力、设计概念等得以全面提高。
此外,还必须重视自学能力、分析问题和解决问题的能力以及审美能力的培养。
三、各章节内容及学时分配绪论(0.5学时)教学目的与要求通过本部分的学习,要求学生了解图学发展史和图样在生产实践中的作用。
第六章建筑形体的图示方法

标注建筑形体尺寸时,要考虑的两个问题: ★应标注那些尺寸? ★尺寸应标注在投影图的什么位置?
一、尺寸的类型 定形尺寸(长、宽、高) 定位尺寸(相对于基准) 总体尺寸(总长、总宽、总高)
二、标注尺寸的步骤
定形尺寸 定位尺寸 总体尺寸 三、尺寸配置
一、尺寸的类型
定形尺寸——确定各基本形体的形状和大小的尺寸。
以上六个投影图称为形体的基本视图, 六个投影图的展开方法如图所示。
六个投影面的展开
底面图 正立面图
平面图
视图的配置
仰视图(底面图)
基本视图的 配置
右视图
主视图 左视图
后视图(背立面图)
俯视图(平面图)
★ 六个基本视图按如图位置布局时,不需标注视图的名称。
视图的配置
在实际工作中,当在同一张图纸上绘制同一个物体的若干个视图时, 为了合理地利用图纸可根据需要重新配置视图的位置。
2×φ 10
66
10
底板的尺 寸标注
44
24
52
★ 定位尺寸——确定各基本形体间的相对位置尺寸。 ★ 总体尺寸——组合体的总长、总宽、总高尺寸。
组合体是由基本体组成的,熟悉基本体的尺寸注法是组合体尺 寸标注的基础。
二、标注尺寸的步骤
标注尺寸的步骤和方法:
① 形体分析 ② 标注各基本形体的定形尺寸; ③ 选择长宽高三个方向的尺寸基准,标注各形体的定位尺寸; ④ 标注总体尺寸; ⑤ 对尺寸作适当的调整,检查是否正确、完整等。
用几个相互平行的剖切平面,阶状剖开形体,所 得的剖视图称阶梯剖视图。
(1)不应画出剖切平面转折处的界线
阶梯剖
1-1剖面图
1
1
1
1 1
(3)剖切起止点和转折出均应画上剖切位置线,并在 转角外侧加注与该符号相同的编号。
第六章 立体化学
解
Cl
>
CBr3
>
CHCl2 C6H5
>
COCl CH2CH3
>
COOH
>
CONH2
>
CHO
>
CH2OH
>
>
24
A. 三维结构:
(a>b>c>d)
25
OH
C2H5 H CH3
R
方法:站在最小基团d的对面,然后按先后次序观察 其他三个基团。从最大的a经b到c,若是顺时针的, 则为“R”;反之,标记为“S”。(a>b>c>d)
六、环状化合物的立体异构
有两个碳原子各连有一个取代基,就有顺反异构。 如环上有手性碳原子,则有对映异构现象。 环状化合物手性碳原子的判断: 看要考察的碳原子所在的环左右 是否具有对称性,若无对称性则 相当于两个不一样的官能团,则 该碳原子是手性碳原子。如有所 示结构中:
几个*?几 个光学异 构体?
HOOC
HOOC NO2
COOH O 2N
2,2‘-二羧基-6,6’-二硝基联苯分子的一对对映体
基团的阻转能力大小:
I>Br>Cl>CH3>NO2>COOH>NH2>OCH3>OH>F>H
结论:联苯型化合物只要同一苯环上所连的基团不同, 分子就具有手性。
50
指出下列化合物有无光活性
CHO Br (1) CN Br (2) N CH3 H2N N C2H5 C2H5 CH3 HOOC (3) CONH2 CH2 CH
(5)
CH3 CH
CH Cl
(6)
工程图学第六章
6-2(4) 并补全曲面立体表面上点、线的其它 投影。
6-2(5) 并补全曲面立体表面上点、线的其它 投影。
6-2(6) 并补全曲面立体表面上点、线的其它 投影。
6-2(7) 并补全曲面立体表面上点、线的其它 投影。
6-2(8) 并补全曲面立体表面上点、线的其它 投影。
6-2(9) 并补全曲面立体表面上点、线的其它 投影。
第六章 基本立体的投影
6-1(1)完成立体的三面投影,并补全立体表面 上点、线的其它投影。
6-1(2)完成立体的三面投影,并补全立体表面 上点、线的其它投影。
△的其它投影。
6-1(4)完成立体的三面投影,并补全立体表面 上点、线的其它投影。
6-1(5)完成立体的三面投影,并补全立体表面 上点、线的其它投影。
6-1(6)完成立体的三面投影,并补全立体表面 上点、线的其它投影。
6-2(1) 并补全曲面立体表面上点、线的其它 投影。
ΔY
ΔY
6-2(2) 并补全曲面立体表面上点、线的其它 投影。
6-2(3) 并补全曲面立体表面上点、线的其它 投影。
6-2(10) 并补全曲面立体表面上点、线的其它 投影。
6-2(11) 并补全曲面立体表面上点、线的其它 投影。
6-2(12) 并补全曲面立体表面上点、线的其它 投影。
机械工程图学-基本立体的投影(圆球)
3-36/143
3.3 基本回转体的投影—3.3.3 圆球的投影
作业
《机械工程图学基础教程习题集》 P45~ P48
ቤተ መጻሕፍቲ ባይዱ
Wang chenggang
3-37/143
3.3 基本回转体的投影—3.3.3 圆球的投影
作业
《机械工程图学基础教程习题集》 P45~ P48
Wang chenggang
3-38/143
图3-38 求作正垂面P与圆球截交线的投影(续)
Wang chenggang
3-27/143
3.3 基本回转体的投影—3.3.3 圆球的投影
在截交线的积聚性投影 a′b′的适当位置选取位于同 一纬圆上的点I、J,用辅助 平面法可由i′(j′)求出其 水平投影i、j和侧面投影i″、 j″。
图3-38 求作正垂面P与圆球截交线的投影(续)
3-3/143
3.3 基本回转体的投影—3.3.2 圆锥的投影
作业
。
《机械工程图学基础教程习题集》 P39~ P44
Wang chenggang
3-4/143
3.3 基本回转体的投影—3.3.2 圆锥的投影
作业
。
《机械工程图学基础教程习题集》 P39~ P44
Wang chenggang
3-5/143
由于截平面与圆锥轴线相对位置的不同,可形成五种截交线。
圆、椭圆、 抛物线、双 曲线、三角 形(与圆锥 面的截交线 为两条相交 的直线)。
Wang chenggang
3-2/143
3.3 基本回转体的投影—3.3.2 圆锥的投影
作业
《机械工程图学基础教程习题集》 P41~ P44
Wang chenggang
《建筑工程制图与识图》(第二版)课件 第6章
6.2.2 平面体的正等轴测图的画法
2.特征面法
适用于柱体的绘制轴测图的方法。当柱体的 某—端面较为复杂且能够反映柱体的形状特 征时,可先画出该面的正等测图,然后再 “扩展”成立体,这种方法被称为特征面法。 图6-5就是用特征面法作出的组合体正等测图。
图6-5 特征面坐标法画的轴测图
6.2.2 平面体的正等轴测图的画法
◦ (3)从底面的四个顶点引 竖直线,并截取棱柱高度10, 连接各顶点,即得四棱柱的 正等测图,如图6-3(c)。注 意,在一般情况下,画轴测 图时都不画出不可见的线条。
图6-3 坐标法画基础的轴测图
6.2.2 平面体的正等轴测图的画法
坐标法作图步骤:
◦ (4)棱台底面与棱柱顶面 重合。棱台的侧棱是一般线, 其轴测投影的方向和伸缩系 数都未知,可先画出它们的 2个端点,然后连成斜线。 作棱台顶面的4个顶点,可 先画出它们在棱柱顶面(平 行于H面)上的次投影,再竖 高度。为此,从棱柱顶面的 4个顶点起,分别沿X方向量 取5,Y方向量取5,并各引 直线相应平行于X和Y,得小 四棱柱底面的4个交点,如 图6-3(d)所示。
图6-2 正等测图的轴间角和轴向变化率
6.2 正等轴测投影
正等轴测投影(isometric projection )的 轴间角和轴向伸缩系数 平面体的正等轴测图的画法 圆柱的正等轴测投影画法
6.2.1正等轴测投影(isometric projection ) 的轴间角和轴向伸缩系数
当物体的三个坐标轴和轴测投影面P的倾角相等时,物体在P平面上的正 投影即为物体的正等测图。轴间角相等,如图6-2(a)所示, ∠XOY=∠YOZ=∠XOZ=120。通常OZ轴总是竖直放置,而OX,OY轴的方向 可以互换。
