八年级数学周周测
周考初二数学试卷及答案

一、选择题(每题3分,共30分)1. 下列数中,是负数的是:A. -5B. 0C. 5D. -5.52. 如果a < b,那么下列不等式中正确的是:A. a + 3 < b + 3B. a - 3 > b - 3C. a + 3 > b + 3D. a - 3 < b - 33. 下列方程中,解为x = 2的是:A. 2x + 1 = 5B. 3x - 2 = 5C. 4x + 3 = 7D. 5x - 4 = 94. 一个等腰三角形的底边长为6cm,腰长为8cm,那么这个三角形的周长是:A. 20cmB. 22cmC. 24cmD. 26cm5. 下列函数中,y随x增大而减小的是:A. y = 2x + 3B. y = -x + 5C. y = 3x - 2D. y = -3x + 16. 一个长方形的长是10cm,宽是6cm,那么这个长方形的面积是:A. 60cm²B. 100cm²C. 120cm²D. 150cm²7. 下列数中,是质数的是:A. 18B. 19C. 20D. 218. 如果a² = 16,那么a的值是:A. 4B. -4C. 2D. -29. 下列图形中,是轴对称图形的是:A. 正方形B. 等腰三角形C. 平行四边形D. 梯形10. 下列分数中,是最简分数的是:A. 4/6B. 8/12C. 9/15D. 10/20二、填空题(每题3分,共30分)11. 5的平方根是__________,-3的立方根是__________。
12. 若a = 3,b = -2,则a - b的值是__________。
13. 下列数中,是偶数的是__________。
14. 一个直角三角形的两个锐角分别是30°和60°,那么这个三角形的斜边与直角边的比是__________。
15. 下列数中,是奇数的是__________。
八年级数学下册周周测五作业新版华东师大版

11.下列命题:①一组对边平行,另一组对边相等的四边形是平行四边形;② 对角线互相平分的四边形是平行四边形;③在四边形ABCD中,AB=AD,BC= DC,那么四边形ABCD是平行四边形;④一组对边相等,一组对角相等的四边形 是平行四边形.其中正确的命题是 _②___ (填序号).
12.如图,已知等边△ABC的边长为8,P是△ABC内一点,PD∥AC, PE∥AB,PF∥BC,点D,E,F分别在AB,BC,AC上,则PD+PE+PF=__8__.
7.如图,在▱ABCD中,E,F分别是AD,BC边的中点,G,H是对角线BD上 的两点,且BG=DH,则下列结论中不正确的是 ( A )
A.GF⊥FH B.GF=EH C.EF与AC互相平分 D.EG=FH
8.已知在正方形网格中,每个小方格的边长都相等,A,B两点在小方格的顶 点上,位置如图,则以A,B为顶点的网格平行四边形的个数为 ( D )
解:(1)∵四边形 ABCD 是平行四边形,∴AD=BC,∠A=∠C.在△ADE 与△
AD=CB, CBF 中, ∠A=∠C, ∴△是平行四边形.理由:∵四边形 ABCD 是平行四边形,∴AB
∥CD,AB=CD.∵AE=CF,∴DF=EB,∴四边形 DEBF 是平行四边形
16.(18分)如图,在▱ABCD中,AB>BC,∠BAD与∠ADC的平分线交于点E, ∠ABC与∠BCD的平分线交于点F.连结EF.
(1)延长DE交AB于点M,则图中与线段EM一定相等的线段有哪几条?说明理由; (不再另外添加字母和辅助线)
(2)EF,BC与AB之间有怎样的数量关系?为什么? (3)如果将条件“AB>BC”改为“AB<BC”,其他条件不变,EF,BC与AB的 关系又如何?请画出图形并证明你的结论.
第8周——2022-2023学年人教版数学八年级上册周周测(含答案)
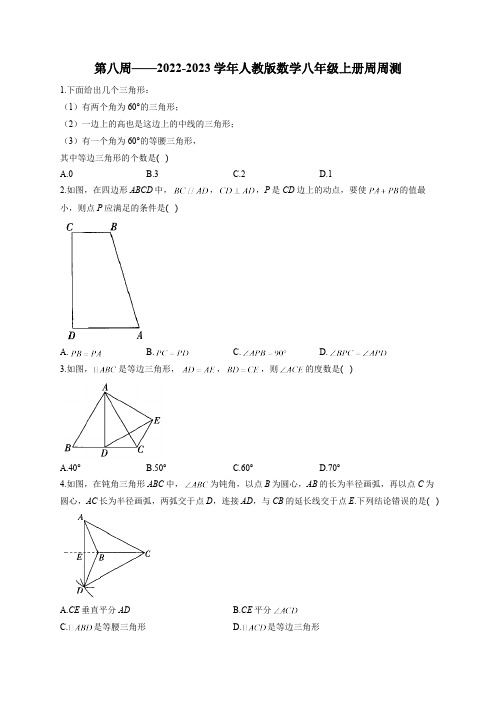
第八周——2022-2023学年人教版数学八年级上册周周测1.下面给出几个三角形:(1)有两个角为60°的三角形;(2)一边上的高也是这边上的中线的三角形;(3)有一个角为60°的等腰三角形,其中等边三角形的个数是( )A.0B.3C.2D.12.如图,在四边形ABCD中,,,P是CD边上的动点,要使的值最小,则点P应满足的条件是( )A. B. C. D.3.如图,是等边三角形,,,则的度数是( )A.40°B.50°C.60°D.70°4.如图,在钝角三角形ABC中,为钝角,以点B为圆心,AB的长为半径画弧,再以点C为圆心,AC长为半径画弧,两弧交于点D,连接AD,与CB的延长线交于点E.下列结论错误的是( )A.CE垂直平分ADB.CE平分C.是等腰三角形D.是等边三角形5.如图,牧童在A处放牛,其家在B处,A、B到河岸的距离分别为AC的长和BD的长,且,若点A到河岸CD的中点的距离为500米,则牧童从A处把牛牵到河边饮水再回家,最短距离是( )A.750米B.1000米C.1500米D.2000米6.如图,在等边中,BD平分交AC于点D,过点D作于点E,且,则AB的长为( )A.3B.4.5C.6D.7.57.如图,CD是的角平分线,的面积为12,BC的长为6,点E,F分别是CD,AC上的动点,则的最小值是( )A.6B.4C.3D.28.如图,等边三角形ABC的边长为4,AD是BC边上的中线,F是AD上的动点,E是AC边上一点.若,则取得最小值时,的度数为( )A.15°B.22.5°C.30°D.45°9.如图,在等边中,BD为AC边上的中线,CE为的平分线,BD、CE交于点M,则___________°.10.如图,在等边中,,点O在AC上,且,点P是AB上一动点,连接OP,将线段OP绕点O逆时针旋转60°得到线段OD.要使点D恰好落在BC上,则AP的长是____________.11.如图,直线m是中BC边的垂直平分线,点P是直线m上的动点.若,,,则的周长的最小值是_____________.12.如图,A,B,C是平面内三点.(1)按要求作图:①作射线BC,过点B作直线l,使A,C两点在直线l两旁;②点P为直线l上任意一点,点Q为射线BC上任意一点,连接线段AP,PQ.(2)在(1)所作图形中,若点A到直线l的距离为2,点A到直线BC的距离为5,点A,B之间的距离为8,点A,C之间的距离为6,求的最小值,并写出其依据.答案以及解析1.答案:C解析:易知(1)有两个角为60°的三角形的三个内角都是60°,(3)有一个角是60°的等腰三角形是等边三角形,所以(1)(3)为等边三角形,故等边三角形的个数是2.2.答案:D解析:如图所示,作点A关于CD的对称点,连接,交CD于点P,连接AP,则的最小值为的长,点P即为所求.点与点A关于CD对称,,,,故D符合题意.由图可知,选项A和选项B不成立,而C只有在时才成立,故选项C不一定成立.故选D.3.答案:C解析:是等边三角形,,,在和中,,,,故选C.4.答案:D解析:由题意可得,,直线CB是AD的垂直平分线,即CE垂直平分AD,故A选项结论正确;CE垂直平分AD,,,,即CE平分,故B选项结论正确;,是等腰三角形,故C选项结论正确;AD与AC不一定相等,不一定是等边三角形,故D选项结论错误.故选D.5.答案:B解析:作A关于CD的对称点,连接交CD于P,则,,,在和中,,,,,P为CD的中点,米,米.6.答案:C解析:是等边三角形,,,,,,,BD平分,,.7.答案:B解析:如图,作点A关于CD的对称点H.CD是的角平分线,点H一定在BC上.过H作于F,交CD于E,此时的值最小,的最小值.过A作于G.的面积为12,BC的长为6,,CD垂直平分AH,,,,的最小值是4,故选B.8.答案:C解析:如图,连接交于点是等边三角形的中线,,此时的值最小.是的中点.是等边三角形,平分,.,.故选C.9.答案:60解析:是等边三角形,,BD为AC边上的中线,CE为的平分线,,,.10.答案:6解析:,,.在和中,,,,.11.答案:10解析:直线m垂直平分BC,B、C两点关于直线m对称,如图,设直线m交AB于D,连接CD,则.当P和D重合时,的值最小,最小值等于AB的长,的周长的最小值是.12.答案:(1)(作法不唯一)如图所示,射线BC,直线l,线段AP,PQ即为所求.(2)如图,过点A作于点Q,交直线l于点P,此时的值最小.因为点A到直线BC的距离为5,所以的最小值为5,依据是垂线段最短.。
八年级数学下册周周测三检测内容:17-1~17-3作业新版华东师大版

解:(1)观察图象得方案一与方案二相交于点(30,1200),∴员工生产 30 件产品时,
两种方案付给的报酬一样多 (2)设方案二的函数图象表达式为 y=kx+b,将点(0,600),
二、填空题(每小题 4 分,共 32 分)
7.在下列 4 个等式中:①y=x+1;②y=-2x;③y2=x;④y=x2 中,y 是 x
的函数的是
①②④ (填序号).
8.在直线 y=-2x+5 上到 x 轴的距离等于 3 的点的坐标是 (1,3)或(4,-3) .
9.已知一次函数 y=(m+2)x+3 的图象经过第一、二、四象限,则 m 的取值范围 是______m_<_-__2___.
(1)求 y 与 x 的函数关系式;
(2)当弹簧长度为 20 cm 时,求所挂物体的质量.
解:(1)把 x=2,y=19 代入 y=kx+15 中,得 19=2k+15,解得 k=2,所以 y 与 x 的函数关系式为 y=2x+15(x≥0)
(2)把 y=20 代入 y=2x+15 中,得 20=2x+15,解得 x=2.5.所挂物体的质量
2 ( B)
6.如图①,在矩形 MNPQ 中,动点 R 从点 N 出发,沿 N→P→Q→M 方向运动 至点 M 处停止.设点 R 运动的路程为 x,△MNR 的面积为 y,若 y 关于 x 的函数图象 如图②所示,则当 x=9 时,点 R 应运动到( D )
A.M 处 B.N 处 C.P 处 D.Q 处
2
∴y=1 x.∵y=1 x 过点(3,n),∴n=3
八年级周周考

周周考数学试题(八年级)45分钟)一、选择题(40分)1、若一直角三角形的两边长为5和12,则第三边长为( )A 13B 15C 13或15D 13或1192、下列各组数中,不是勾股数的是( )A 3、4、5B 5、12、13C 8、15、17D 5525、、3、在Rt △ABC 中∠C=90°,AC=BC,则AC:BC:AB=( )A 1:1:2B 1:1:2C 1:2:1D 1:2:14、如图在Rt △ABC 中∠C=90°,AB=13cm,过Rt △ABC 的两直角边作两个正方形,则这两个正方形的面积和为( )A 169cm 2B 196cm 2C 200cm 2D 160cm 2二、填空题 (40分)1、在Rt △ABC 中∠A=90°,BC=2.5cm,AB=2cm,则AC=_________2、如图阴影部分是一个正方形,则这个正方形的面积为_______12133、如图是由边长为1m 的正方形地砖铺设的地面示意图,小明沿图中所示的折线A B C 所走的路程为________(结果保留根号)A BCABC4、在等腰直角三角形中,一直角边长为8,则斜边长为________;在等腰直角三角形中,斜边长为10,则它的一直角边长为_______.三、解答题(20分)1、在△ABC中∠C=90°,BC=a,AC=b,AB=c,若a:b=5:12,c=130cm,求△ABC的面积。
2、直角三角形的周长为24,斜边长为10,求三角形的面积。
八年级数学周测试卷答案

一、选择题(每题2分,共20分)1. 下列数中,不是有理数的是()A. 3.14B. -5/7C. √2D. 0答案:C2. 若a > b,那么下列不等式中正确的是()A. a + 1 > b + 1B. a - 1 < b - 1C. a - 2 < b - 2D. a + 2 > b + 2答案:A3. 已知函数y = 2x - 3,若x = 4,则y的值为()A. 5B. 7C. 9D. 11答案:C4. 在直角坐标系中,点P(2, -3)关于y轴的对称点坐标为()A. (2, 3)B. (-2, -3)C. (-2, 3)D. (2, -3)答案:B5. 下列各式中,能被3整除的是()A. 123B. 456C. 789D. 0答案:A6. 若a、b、c是三角形的三边,且a + b = c,那么这个三角形是()A. 等腰三角形B. 直角三角形C. 等边三角形D. 梯形答案:B7. 下列各式中,正确的是()A. 3^2 = 9B. 5^2 = 25C. 7^2 = 49D. 9^2 = 81答案:C8. 已知一次函数y = kx + b,若k > 0,b > 0,那么函数的图像在()A. 第一、二象限B. 第一、三象限C. 第二、四象限D. 第三、四象限答案:B9. 在梯形ABCD中,AD平行于BC,且AD = 4cm,BC = 6cm,AB = 3cm,CD = 5cm,那么梯形的高为()A. 2cmB. 3cmC. 4cmD. 5cm答案:A10. 下列各式中,正确的是()A. (a + b)^2 = a^2 + 2ab + b^2B. (a - b)^2 = a^2 - 2ab + b^2C. (a + b)^2 = a^2 - 2ab + b^2D. (a - b)^2 = a^2 + 2ab + b^2答案:B二、填空题(每题2分,共20分)11. 有理数a的相反数是_________。
八年级数学下册周周测试卷

一、选择题(每题3分,共30分)1. 若一个数的平方根是2,则这个数是()A. 4B. -4C. 8D. -82. 下列各组数中,互为相反数的是()A. 3和-5B. 0和0C. -3和3D. 5和-53. 下列图形中,对称轴最多的是()A. 等边三角形B. 等腰三角形C. 长方形D. 正方形4. 若a、b、c是三角形的三边,且a+b>c,则下列不等式中一定成立的是()A. a+c>bB. b+c>aC. a-b>cD. a-b<c5. 下列函数中,自变量x的取值范围是全体实数的是()A. y=2x+1B. y=x²-1C. y=√xD. y=1/x6. 下列各式中,正确的是()A. (a+b)²=a²+2ab+b²B. (a-b)²=a²-2ab+b²C. (a+b)³=a³+3a²b+3ab²+b³D. (a-b)³=a³-3a²b+3ab²-b³7. 下列方程中,解为x=2的是()A. 2x-3=5B. 3x+2=7C. x+3=8D. 2x+1=58. 下列图形中,中心对称图形是()A. 等边三角形B. 等腰三角形C. 长方形D. 正方形9. 下列各式中,正确的是()A. 3x+4y=5B. 2x-3y=6C. 4x+5y=10D. 5x-6y=1210. 下列各式中,正确的是()A. a²+b²=c²B. a²-c²=b²C. b²-c²=a²D. a²+b²=c²+2ab二、填空题(每题3分,共30分)11. 已知a=-2,则a²的值是________。
12. 下列数中,负数的倒数是________。
人教版数学八年级上册周周测(含解析)第4周

第四周1.如图,OA OBC∠等于( )∠=︒,30∠=︒,则OBD=,OC OD=,若45OA.75°B.105°C.90°D.120°2.如图,已知AC DB=,添加下列四个条件:①A D∠=∠;②ABD DCA∠=∠;③ACB DBC∠=∠;④ABC DCB∠=∠中的一个,其中能使ABC DCB≌的有( )A.1个B.2个C.3个D.4个3.如图是作ABC的作图痕迹,则此作图的已知条件是( )A.已知两边及夹角B.已知三边C.已知两角及夹边D.已知两边及一边对角4.要测量圆形工件的外径,工人师傅设计了如图所示的卡钳,点O为卡钳两柄交点,且有===,如果圆形工件恰好通过卡钳AB,则此工件的外径必是CD之长了,其中的OA OB OC OD依据是全等三角形的判定条件( )A.SSSB.SASC.ASAD.AAS5.如图所示,AC 和BD 相交于点O ,AO DO =,AB AC ⊥,CD BD ⊥,那么AB 与CD 的关系是( )A.一定相等B.可能相等也可能不相等C.一定不相等D.增加条件后,它们相等6.如图,D 是AB 上的一点,DF 交AC 于点,,//E DE EF FC AB =.若4,3AB CF ==,则BD 的长是( )A.0.5B.1C.1.5D.27.如图,点B ,C ,E 在同一条直线上,60B E ACF ∠=∠=∠=︒,AB CE =,则与BC 相等的线段是( )A.ACB.AFC.CFD.EF8.在ABC 中,AB AC =,AB BC >,点D 在边BC 上,2CD BD =,点E ,F 在线段AD 上,12BAC ∠=∠=∠,若ABC 的面积为18,则ACF 与BDE 的面积之和是( )A.6B.8C.9D.129.如图所示,已知AF DC≌,则需添加的条件是=,BC EF,若要用“ASA”去证ABC DEF______________.10.如图所示,在ABC中,50∠的度数是B C=,则EDF=,BE CD∠=∠=︒,BD CF____________.11.如图,Rt ABC中,90BAC=,分别过点B、C作过点A的直线的垂线BD、∠=︒,AB ACCE,垂足分别为DE,若4BD=,2CE=,则DE=___________.12.如图①,ABC中,H是高AD和高BE的交点,且AD BD=.(1)请你猜想BH和AC的数量关系,并说明理由;(2)若将图①中的BAC∠改成钝角,请你在图②中画出该题的图形,此时(1)中的结论还成立吗?答案以及解析1.答案:B解析:在AOC 与BOD 中,OA OB O O OC OD =⎧⎪∠=∠⎨⎪=⎩,(SAS)AOC BOD ∴≌,30D C ∴∠=∠=︒,1804530105OBD ∴∠=︒-︒-︒=︒,故选B.2.答案:A解析:已知AC DB =,由题图知BC CB =,则添加条件③,可以使得(SAS)ABC DCB ≅,故选A.3.答案:C解析:观察题图可知:已知线段AB ,CAB α∠=,CBA β∠=,故选C.4.答案:B解析:如图,连接AB 、CD ,在ABO 和DCO 中,OA OD AOB DOC OB OC =⎧⎪∠=∠⎨⎪=⎩,(SAS)ABO DCO ∴≅,AB CD ∴=.故选B.5.答案:A解析:AB AC ⊥,CD BD ⊥,90A D ∴∠=∠=︒.在OAB 和ODC 中,A D OA ODAOB DOC ∠=∠⎧⎪=⎨⎪∠=∠⎩,(ASA)OAB ODC ∴≅,AB CD ∴=,故选A.6.答案:B解析:,/,/FC AB A FCE ADE F ∴∠=∠∠=∠.在ADE △和CFE △中,,,,A FCE ADE F DE FE ∠=∠⎧⎪∠=∠⎨⎪=⎩, 3.4ADE CFE AD CF AB ∴∴===≌△△,1BD AB AD ∴=-=.7.答案:D 解析:ACE B BAC ACF ECF ∠=∠+∠=∠+∠,60B E ACF ∠=∠=∠=︒,BAC ECF ∴∠=∠.在ABC 和CEF 中,B E AB CEBAC ECF ∠=∠⎧⎪=⎨⎪∠=∠⎩,(ASA)ABC CEF ∴≅,BC EF ∴=.故选D. 8.答案:A解析:12BAC ∠=∠=∠,1BAE ABE ∠=∠+∠,BAC BAE CAF ∠=∠+∠,2FCA CAF ∠=∠+∠,ABE CAF ∴∠=∠,BAE FCA ∠=∠.在ABE 和CAF 中,ABE CAF AB ACBAE ACF ∠=∠⎧⎪=⎨⎪∠=∠⎩,(ASA)ABE CAF ∴≅,ACF ∴的面积ABE =的面积,ACF ∴与BDE 的面积之和ABE =与BDE 的面积之和ABD =的面积.ABC 的面积为18,2CD BD =,ABD ∴的面积为11863⨯=,ACF ∴与BDE 的面积之和ABD =的面积6=. 9.答案:A D ∠=∠解析:需添加A D ∠=∠,理由:AF CD =,AF FC CD FC ∴+=+,AC DF ∴=.BC EF ,BCA EFD ∴∠=∠.在ABC 和DEF 中,A D AC DF BCA EFD ∠=∠⎧⎪=⎨⎪∠=∠⎩,(ASA)ABC DEF ∴≅. 10.答案:50°解析:在BDE 与CFD 中,50BD CF B C BE CD =⎧⎪∠=∠=︒⎨⎪=⎩,(SAS)BDE CFD ∴≅,BDE CFD ∴∠=∠,()180()180()18018050EDF BDE CDF CFD CDF C ∴∠=︒-∠+∠=︒-∠+∠=︒-︒-∠=︒.11.答案:6解析:90BAC ∠=︒,90BAD CAE ∴∠+∠=︒,BD DE ⊥,90BDA ∴∠=︒,90BAD DBA ∴∠+∠=︒,DBA CAE ∴∠=∠,CE DE ⊥,90AEC ∴∠=︒,在BDA 和AEC 中,90ABD CAE BDA AEC AB AC ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩,(AAS)BDA AEC ∴≅,2AD CE ∴==,4AE BD ==,246DE AD AE ∴=+=+=.12.答案:(1)BH AC =. 理由:AD 和BE 是ABC 的高,90BDH ADC ∴∠=∠=︒,90DBH C CAD C ∠+∠=∠+∠=︒,DBH DAC ∴∠=∠,在BDH 和ADC 中,DBH DAC BD ADBDH ADC ∠=∠⎧⎪=⎨⎪∠=∠⎩, (ASA)BDH ADC ∴≅,BH AC ∴=.(2)成立.如图,AD 和BE 是ABC 的高,90BDH ADC BEC ∴∠=∠=∠=︒,90DBH H DBH C ∴∠+∠=∠+∠=︒,H C ∴∠=∠, 在BDH 和ADC 中,H C BDH ADC BD AD ∠=∠⎧⎪∠=∠⎨⎪=⎩,(AAS)BDH ADC ∴≅,BH AC ∴=.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
八年级数学周周测
1.计算(-a)3·(a2)3·(-a)2的结果正确的是( )
A.a11B.-a11C.-a10D.a13
2.下列计算正确的是( )
A.x2(m+1)÷x m+1=x2B.(xy)8÷(xy)4=(xy)2
C.x10÷(x7÷x2)=x5D.x4n÷x2n·x2n=1
3.若(ax+2y)(x-y)展开式中,不含xy项,则a的值为( ) A.-2 B.0 C.1 D.2
4.若x+y=1,xy=-2,则(2-x)(2-y)的值为( )
A.-2 B.0 C.2 D.4
5.一个长方体的长、宽、高分别是3x-4、2x-1和x,则它的体积是( )
A.6x3-5x2+4x B.6x3-11x2+4x
C.6x3-4x2D.6x3-4x2+x+4
6.观察下列多项式的乘法计算:
(1)(x+3)(x+4)=x2+7x+12;(2)(x+3)(x-4)=x2-x-12;(3)(x-3)(x+4)=x2+x-12;(4)(x-3)(x-4)=x2-7x+12
根据你发现的规律,若(x+p)(x+q)=x2-8x+15,则p+q的值为( ) A.-8 B.-2 C.2 D.8
7.如图,甲、乙、丙、丁四位同学给出了四
种表示该长方形面积的多项式:
①(2a+b)(m+n);②2a(m+n)+b(m+
n);
③m(2a+b)+n(2a+b);④2am+2an+bm+
bn,
你认为其中正确的有( )
A.①②B.③④C.①②③D.①②③④
8.计算:
(1)(-3ab2c3)2=________;(2)a3b2·(-ab3)3=________;
(3)(-x 3y 2)(7xy 2-9x 2y)=_______________.
9.若3m =81,3n =9,则m +n =________.
10.若a 5·(a m )3=a 4m ,则m =________.
11.计算:(1)(a 2)3·a 3-(3a 3)3+(5a 7)·a 2; (2)(-4x 2y)·(-x 2y 2)·(12y)3
(3)(-3ab)(2a 2b +ab -1); (4)(m -23)(m +16);
12.若多项式x 2+ax +8和多项式x 2-3x +b 相乘的积中不含x 3项且含x 项的系数是-3,求a 和b 的值.
13.如图,长为10 cm ,宽为6 cm 的长方形,在4个角剪去4个边长为x cm 的小正方形,按折痕做一个有底无盖的长方体盒子,求盒子的体积.
14化简求值:(3x +2y)(4x -5y)-11(x +y)(x -y)+5xy ,其中x =312,
y =-212。
