2016大连市一模考试25题答案解析(最新4种方法)
2016年大连市区25题汇编
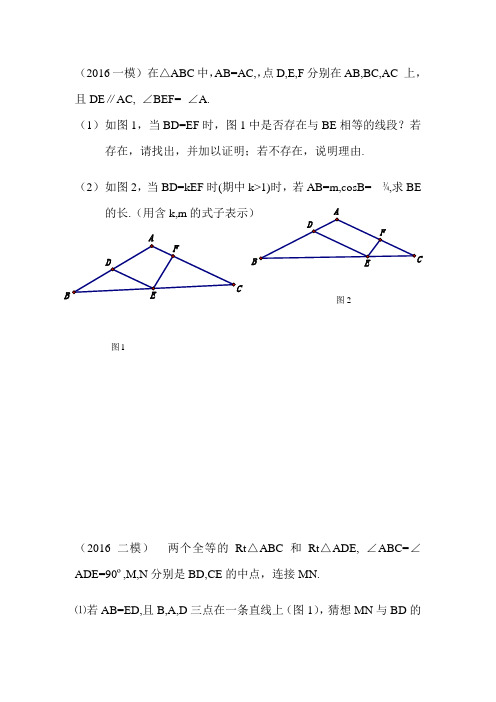
ABB图2(2016一模) 在△ABC 中,AB=AC,,点D,E,F 分别在AB,BC,AC 上,且DE ∥AC, ∠BEF= ∠A.(1) 如图1,当BD=EF 时,图1中是否存在与BE 相等的线段?若存在,请找出,并加以证明;若不存在,说明理由.(2) 如图2,当BD=kEF 时(期中k>1)时,若AB=m,cosB= ¾,求BE的长.(用含k,m(2016二模) 两个全等的Rt △ABC 和Rt △ADE, ∠ABC=∠ADE=90º,M,N 分别是BD,CE 的中点,连接MN.⑴若AB=ED,且B,A,D 三点在一条直线上(图1),猜想MN 与BD 的图1关系,并加以证明;⑵若AB=AD ,sin∠BAD=, 且B,A,D三点不在一条直线上(图2)求MNBD的值CB(甘井子1模)如图1,在四边形ABCD中,AD∥BC, ∠D=90º,以AB为边向四边形外作Rt△ABE,使得∠BAE=90°,AB=m AE.F为线段AD上一点,AF=n FD.过点F作直线MN⊥BC于点G,过点E作EH ⊥MN于点H⑴①请先用直尺和圆规在图2中补全m=1,n=1时的图形(不写作法,保留作图痕迹);②再猜想并验证CD,EH和AD的关系.⑵在图一中,猜想并验证m≠1,n≠1时,线段CD,EH和AD的关系..EBEE(甘井子2模)在△ADB 和△AEC 中,AD=AE, ∠DAE=α, ∠AEC=∠ADB=90°,BD=KCE,延长ED 交BC 于点F.⑴如图1,当k=1时,是否存在与BF 相等的线段?若存在,请找出,并加以证明;若不存在,说明理由.⑵如图2,当k ≠1时,猜想并证明EC,ED,EF 的数量关系(用含k, α的式子表示.CAAA(高新园区一模)在△ABC 中,∠BAC 为锐角,AB>AC,AD 平分∠BAC 交BC 于点D ,.⑴如图1,若△ABC 是等腰直角三角形(∠C=90°),直接写出线段AC,CD,AB 之间的数量关系.⑵BC 的垂直平分线交AD 延长线于点E ,交BC 于点F.① 如图2,若∠ABE=60°,猜想AC,CE,AB 之间的数量关系,并证明② 如图3,,若∠ABE=α(0<α<90°),猜想AC,CE,AB 之间的数量关系,并证明(用含α的式子表示).(普兰店一模)如图,在Rt △ABC 中,∠ACB=90°.DD⑴分别以AB,AC 为边向外作等边三角形ABD 和等边三角形ACE,连接DE 交AB 于点F,若∠BAC=30°,求证:DF=DE.⑵分别以AB,AC 为边向外作等腰三角形ABD 和等腰三角形ACE,且∠ADB=∠AEC=2∠BAC=2α,用含α的锐角三角函数表示EF 与DF 的数量关系.如图,在Rt △ABC 中,∠BAC=90°,∠BAC=α,将△ABC 旋转一个角度后得到△AED,CE 交AB 于点N,交BD 于点M ⑴求证:M 为BD 中点;⑵若CN=CA=m ,求BD 的长(用含m, α的式子表示)A DMDCB如图,在△ABC 中,过A 点作DE ∥BC ,点P 在线段AC 上,∠FPM=∠B,且两边分别交AB,DE 于点F,M.⑴如图1,若AC=BC, ∠ACB=90°,猜想PF 与PM 的数量关系并证明;⑵如图2,若AB=m,BC=n,求PFPM的值.MBA CDEF P。
大连市2016年初中毕业升学考试卷及答案

大连市2016年初中毕业升学考试试测(一)数 学注意事项:1.请在答题卡上作答,在试卷上作答无效。
2.本试卷共五大题,26小题,满分150分。
考试时间l20分钟。
一、选择题(本题共8小题。
每小题3分,共24分。
在每小题给出的四个选项中,只有一个选项正确) 1.43-的相反数为( ) A .34 B .43 C .43- D .34-2.据大连市公安局统计,2016年全市约有410 000人换领第二代居民身份证,将410 000用科学记数法表示应为( )A .0.41×106B .41×104C .4.1×106D .4.1×1053.如图,点A 、B 、C 都在⊙0上,若∠ACB=29°,则∠AOB 的度数为( )A .14.5°B .29°C .58°D .61° 4.不等式62-<x 的解集为( )A .3-<xB .3->xC .3>xD .3<x 5.在平面直角坐标系中,下列函数的图象经过原点的是( )A .12+-=x yB .x y 2-=C .xy 2-= D . 12+-=x y 6.如图,正方形ABCD 的对角线AC 、BD 相交于点0,OA=3,则此正方形的面积为( )A .23B .12C .18D .367.一个不透明的口袋中有三个完全相同的小球,把它们分别标号为1,2,3.随机摸出一个小球,然后放回,再随机摸出一个小球.两次摸出的小球标号的和为5的概率 是( )A .61 B .92 C .31 D .21 8.如图,按照三视图确定该几何体的全面积为(图中尺寸单位:cm)A .128πcm 2B .160πcm 2C .176πcm 2D .192πcm 2二、填空题(本题共8小题,每小题3分,共24分)9.因式分解:x 3-x=___________________. 10.方程2123=-x x的解是______________. 11.某校男子足球队队员的年龄分布如下表所示,则这些队员年龄的中位数 是___________岁.12.如图,△ABC 中,AB=AC ,将△ABC 绕点A 逆时针旋转60°后得到△ADE ,若AB=1,则CE 的长为 _______________.13.如图,平行线AB 、CD 被直线EF 所截,过点E 作EG ⊥EF ,与直线CD 相交于点G .若∠AEF=39°,则14.如图,菱形ABCD 的对角线BD 与x 轴平行,点B 、C 的坐标分别是(0,1)、(2,0),点A 、D 在函数xky =(x>0)的图象上.则k 的值为____________.15.在平面直角坐标系中,点A 、B 的坐标分别是(-3,1)、(-1,-2),将线段AB 沿某一方向平移后,得到点A 的对应点A ′的坐标为(-1,O),则点B 的对应点B ′的坐标为________________.16.某飞机模型的机翼形状如图所示,其中AB ∥DC ,∠BAE=90°,根据图中的数据计算CD 的长为_____________cm(精确到1 cm).(参考数据:⋅≈≈≈75.037tan ,80.037cos ,60.037sin o ) 三、解答题(本题共4小题,其中17、18、19题各9分,20题12分,共39分) 17.计算:.64|35|)52(30-+-+-18.先化简,再求值:)1)(1()2(-+--a a a a ,其中21-=a 19.如图,△ABC 中,AB=AC ,点D 在AB 上,过点D 作BC 的平行线,与AC 相交于点E ,点F 在BC 上,EF=EC . 求证:四边形DBFE 是平行四边形.20.某校1200名学生参加了全区组织的“经典诵读”活动,该校随机选取部分学生,对他们在三、四两个月的诵读时间进行调查,下面是根据调查数据制作的统计图表的一部分.根据以上信息,解答下列问题:(1)本次调查的学生数为_____________人;(2)图表中的a、b、c的值分别为__________,__________,__________ ;(3)在被调查的学生中,四月份日人均诵读时间在l<x≤1.5范围内的人数比三月份在此范围的人数多______________ 人;(4)试估计该校学生四月份日人均诵读时间在1小时以上的人数.四、解答题(本题共3小题。
大连市2016年中考一模化学答案

大连市2016年初中毕业升学考试试测(一)化学参考答案及评分标准说明:只有52题、55题的化学方程式有0.5分。
58题若出现评分点之外的规范性错误,不论几处,只扣1分。
一、选择题(本题共15小题,每小题1分,共15分)33.D 34.C 35.A 36.B 37.B 38.C 39.C 40.A 41.B 42.D 43.B 44.D 45.A46.D 47.C二、填空题(本题共5小题,每空1分,共25分)48.(1)①肥皂水②煮沸(或蒸馏)(2)①吸附②沉降(或沉淀)49.(1)①碳②二氧化硫(或二氧化氮)③使用脱硫煤(其他合理答案均可)(2)①碳、氢②液化石油气50.(1)①铝②钢铁(2)①铁的硬度比铝的大②铝的熔点较低(3)①氧气、水蒸气②涂油(其他合理答案均可)51.(1)升高温度(2)蒸发结晶(3)4:5 (4)=52.(1)CaCO3CaO+CO2↑分解反应(2)Na2CO3+Ca(0H)2==CaCO3↓+2NaOH 复分解反应(3)4P+5O22P2O5化合反应三、简答题(本题共5小题,共24分)53.金刚石、石墨均由碳原子构成,但碳原子的排列方式不同(1分),C60由C60分子构成,1个C60分子由60个碳原子构成(1分),因此物理性质存在明显差异。
在参加化学反应时C60分子会分解成碳原子(1分),因而它们的化学性质相似。
54.(1)铜有良好的导热性,冷的铜线圈会吸收热量(1分),能使石蜡的温度降低到着火点以下(1分)。
(2)热的铜线圈能让石蜡燃烧产生的热量不易散失(1分),火焰更集中,并能提高石蜡的温度使其燃烧更旺(1分)。
2KCl+3O2↑②B ③C(或D、CD)55.(每空1分)(1)①2KClO3MnO2△(2)①CaCO3+2HCl==CaCl2+H2O+CO2↑②A ③燃着木条在集气瓶口熄灭56.(1)Fe 203+3H2SO4==Fe2(SO4)3+3H2O(1分) 2Cu+O2+2H2SO42CuSO4+2H2O(1分)(2)CuSO4、FeSO4、H2SO4(1分)向滤液中加入过量铁粉,过滤(1分),所得滤渣中加入适量稀硫酸,再过滤出铜,滤液合并为硫酸亚铁溶液(1分)。
2016年辽宁省大连市中考数学模拟试卷含答案解析

2016年辽宁省大连市中考数学模拟试卷一、选择题(共8小题,每小题3分,满分24分)1.分别取正整数5的绝对值、倒数、相反数、算术平方根,得到的数值仍为正整数的是()A.绝对值B.倒数 C.相反数D.算术平方根2.我国是一个严重缺水的国家,淡水资源总量为28000亿立方米,人均淡水资源低于世界平均水平,因此,珍惜水、保护水是我们每一位公民的责任,其中数据28000用科学记数法表示为()A.28×103B.2.8×104C.0.28×105 D.2.8×1053.如图,在⊙O中,直径CD⊥弦AB,则下列结论中正确的是()A.AC=AB B.∠C=∠BOD C.∠C=∠B D.∠A=∠BOD4.不等式|x﹣1|<1的解集是()A.x>2 B.x<0 C.1<x<2 D.0<x<25.在平面直角坐标系中,抛物线y=﹣(x+1)2﹣的顶点是()A.(﹣1,﹣) B.(﹣1,)C.(1,﹣)D.(1,)6.如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠1=124°,∠2=88°,则∠3的度数为()A.26°B.36°C.46°D.56°7.一枚质地均匀的正方体骰子的六个面分别刻有1到6的点数,将这枚骰子掷两次,其点数之和是7的概率为()A.B.C.D.8.《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺,问”积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有()A.14 B.22斛C.36斛D.66斛二、填空题(本题共8小题,每小题3分,满分24分)9.因式分解:2a2﹣4a=.名队员年龄的众数是.11.若二次根式有意义,则x的取值范围是.12.如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=1,△A′B′C可以由△ABC绕点C 顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为.13.如图,△ABC与△DEF位似,位似中心为点O,且△ABC的面积等于△DEF面积的,则AB:DE=.14.如图,点A是反比例函数图象上y=一点,过点A作AB⊥y轴于点B,点C、D在x轴上,且BC∥AD,四边形ABCD的面积为3,则k=.15.在平面直角坐标系中,有平行四边形ABCD,点A坐标为(2,0),点C(5,﹣3),点B(4,1),则D点坐标为.16.如图,一艘潜艇在海面下500m深的点A处,测得正前方俯角为31°方向上的海底有黑匣子发出信号,潜艇在同一深度保持直线航行500m,在点B处测得海底黑匣子位于正前方俯角36.9°的方向上,海底黑匣子C所在点距海面的深度为m.(精确到1,m.参考数据:sin36.9°≈0.60,cos36.9°≈0.80,tan36.9°≈0.75,sin31°≈0.51,cos31°≈0.87,tan31°≈0.60)三、解答题(本题共4小题,其中17、18、19题各9分,20题12,共39分)17.计算:20160﹣|﹣2|﹣()﹣1+6tan30°.18.先化简,再求值:,其中.19.如图,在正方形ABCD内有一点P满足AP=AB,PB=PC,连接AC、PD.求证:△APB ≌△DPC.20.我市某校九年级实行小组合作学习,为了解学生课堂发言情况,随机抽取该年级部分学生,对他们每天在课堂上发言的次数进行调查和统计,统计表如下,并绘制了两幅不完整的A B1:5.(1)A组的人数是多少?本次调查的样本容量是多少?(2)求出C组的人数并补全直方图;(3)该校七年级共有250人,请估计全年级每天在课堂上发言次数不少于15次的人数.四、解答题(本题共3小题,其中21、22题各9分,23题10,共28分)21.一学校为了绿化校园环境,向某园林公司购买了一批树苗,园林公司规定:如果购买树苗不超过60棵,每棵售价120元;如果购买树苗超过60棵,每增加1棵,所出售的这批树苗每棵售价均降低0.5元,但每棵树苗最低售价不得少于100元,该校最终向园林公司支付树苗款8800元,请问该校共购买了多少棵树苗?22.如图,已知一次函数的图象y=kx+b与反比例函数y=﹣的图象交于A,B两点,且点A的横坐标和点B的纵坐标都是﹣2,求:(1)一次函数的解析式;(2)△AOB的面积;(3)直接写出一次函数的函数值大于反比例函数的函数值时x的取值范围.23.如图,O为等腰三角形ABC内一点,⊙O与△ABC的底边BC交于M,N两点,与底边上的高AD交于点G,且与AB,AC 分别相切于E,F两点.(1)证明:EF∥BC;(2)若AG等于⊙O的半径,且AE=MN=2,求四边形EBCF的面积.五、解答题(本题共3小题,其中24题11分,25、26题各12分,共35分)24.如图1,在△ABC中.∠C=90°,AC>BC,正方形CDEF的顶点D在边AC上,点F 在射线CB上设CD=x,正方形CDEF与△ABC重叠部分的面积为S,S关于x的函数图象如图2所示(其中0<x≤m,m<x≤2,2<x≤n时,函数的解析式不同).(1)填空:m的值为;(2)求S关于x的函数解析式,并写出x的取值范围;(3)S的值能否为?若能,直接写出此时x的值;若不能,说明理由.25.如图,已知:在矩形ABCD中,O为AC的中点,直线l经过点B,且直线l绕着点B 旋转,AM⊥l于点M,CN⊥l于点N,连接OM,ON(1)当直线l经过点D时,如图1,则OM、ON的数量关系为;(2)当直线l与线段CD交于点F时,如图2(1)中的结论是否仍然成立?若成立,请加以证明;若不成立,请说明理由;(3)当直线l与线段DC的延长线交于点P时,请在图3中作出符合条件的图形,并判断(1)中的结论是否仍然成立?不必说明理由.26.在平面直角坐标系xOy中,抛物线C:y=ax2.(1)若直线l1:y=x﹣1与抛物线C有且只有1个交点,求抛物线C的解析式.(2)如图1,在(1)的条件下,在y轴上有一点A(0,4),过点A作直线l2与抛物线C 有两个交点M、N(N位于第一象限),过点N作x轴的垂线,垂足为H.试探究:是否存在l2,使△MON∽△NHO?若存在,求出l2的解析式;若不存在,说明理由.(3)如图2,E、F为抛物线C(y=ax2)上两动点,始终满足OE⊥OF,连接EF,则直线EF是否恒过一定点G?若存在点G,直接写出G点坐标(用含a的坐标表示),若不存在,给予证明.(参考结论:若直线l:y=kx+b上有两点(x1,y1)、(x2,y2),则斜率k=;当两直线l1、l2的斜率乘积k1•k2=﹣1时,l1⊥l2)2016年辽宁省大连市中考数学模拟试卷参考答案与试题解析一、选择题(共8小题,每小题3分,满分24分)1.分别取正整数5的绝对值、倒数、相反数、算术平方根,得到的数值仍为正整数的是()A.绝对值B.倒数 C.相反数D.算术平方根【考点】算术平方根;相反数;绝对值;倒数.【分析】利用绝对值的代数意义,倒数,相反数,算术平方根定义判断即可.【解答】解:正整数5的绝对值为5;倒数为;相反数为﹣5;算术平方根为,得到的数值仍为正整数的是绝对值,故选A.2.我国是一个严重缺水的国家,淡水资源总量为28000亿立方米,人均淡水资源低于世界平均水平,因此,珍惜水、保护水是我们每一位公民的责任,其中数据28000用科学记数法表示为()A.28×103B.2.8×104C.0.28×105 D.2.8×105【考点】科学记数法—表示较大的数.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.【解答】解:将28000用科学记数法表示为2.8×104.故选B.3.如图,在⊙O中,直径CD⊥弦AB,则下列结论中正确的是()A.AC=AB B.∠C=∠BOD C.∠C=∠B D.∠A=∠BOD【考点】垂径定理;圆周角定理.【分析】根据垂径定理得出=,=,根据以上结论判断即可.【解答】解:A、根据垂径定理不能推出AC=AB,故A选项错误;B、∵直径CD⊥弦AB,∴=,∵对的圆周角是∠C,对的圆心角是∠BOD,∴∠BOD=2∠C,故B选项正确;C、不能推出∠C=∠B,故C选项错误;D、不能推出∠A=∠BOD,故D选项错误;故选:B4.不等式|x﹣1|<1的解集是()A.x>2 B.x<0 C.1<x<2 D.0<x<2【考点】解一元一次不等式.【分析】根据绝对值性质分x﹣1>0、x﹣1<0,去绝对值符号后解相应不等式可得x的范围.【解答】解:①当x﹣1≥0,即x≥1时,原式可化为:x﹣1<1,解得:x<2,∴1≤x<2;②当x﹣1<0,即x<1时,原式可化为:1﹣x<1,解得:x>0,∴0<x<1,综上,该不等式的解集是0<x<2,故选:D.5.在平面直角坐标系中,抛物线y=﹣(x+1)2﹣的顶点是()A.(﹣1,﹣) B.(﹣1,)C.(1,﹣)D.(1,)【考点】二次函数的性质.【分析】结合抛物线的解析式和二次函数的性质即可得出该抛物线顶点坐标.【解答】解:∵抛物线的解析式为y=﹣(x+1)2﹣,∴该抛物线的顶点坐标为(﹣1,﹣).故选A.6.如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠1=124°,∠2=88°,则∠3的度数为()A.26°B.36°C.46°D.56°【考点】平行线的性质.【分析】如图,首先运用平行线的性质求出∠AOB的大小,然后借助平角的定义求出∠3即可解决问题.【解答】解:如图,∵直线l4∥l1,∴∠1+∠AOB=180°,而∠1=124°,∴∠AOB=56°,∴∠3=180°﹣∠2﹣∠AOB=180°﹣88°﹣56°=36°,故选B.7.一枚质地均匀的正方体骰子的六个面分别刻有1到6的点数,将这枚骰子掷两次,其点数之和是7的概率为()A.B.C.D.【考点】列表法与树状图法.【分析】画树状图展示所有36种等可能的结果数,再找出点数之和是7的结果数,然后根据概率公式求解.【解答】解:画树状图为:共有36种等可能的结果数,其点数之和是7的结果数为6,所以其点数之和是7的概率==.故选C.8.《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺,问”积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有()A.14 B.22斛C.36斛D.66斛【考点】圆锥的计算;弧长的计算.【分析】根据米堆的底部的弧度即底面圆周的四分之一为8尺,可求出圆锥的底面半径,从而计算出米堆的体积,用体积除以每斛的体积即可求得斛数.【解答】解:设米堆所在圆锥的底面半径为r尺,则×2πr=8,解得:r=,所以米堆的体积为V=××πr2×5=≈35.56,所以米堆的斛数是≈22,故选B.二、填空题(本题共8小题,每小题3分,满分24分)9.因式分解:2a2﹣4a=2a(a﹣2).【考点】因式分解-提公因式法.【分析】原题中的公因式是2a,用提公因式法来分解因式.【解答】解:原式=2a(a﹣2).故答案为:2a(a﹣2).名队员年龄的众数是岁.【考点】众数.【分析】众数可由这组数据中出现频数最大数据写出;【解答】解:这组数据中14岁出现频数最大,所以这组数据的众数为14岁;故答案为:14岁.11.若二次根式有意义,则x的取值范围是x≥.【考点】二次根式有意义的条件.【分析】根据二次根式中的被开方数是非负数,可得出x的取值范围.【解答】解:∵二次根式有意义,∴2x﹣1≥0,解得:x≥.故答案为:x≥.12.如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=1,△A′B′C可以由△ABC绕点C 顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为3.【考点】旋转的性质.【分析】利用直角三角形的性质得出AB=2,再利用旋转的性质以及三角形外角的性质得出AB′=1,进而得出答案.【解答】解:∵在Rt△ABC中,∠ACB=90°,∠B=60°,BC=1,∴∠CAB=30°,故AB=2,∵△A′B′C由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,∴AB=A′B′=2,AC=A′C,∴∠CAA′=∠A′=30°,∴∠ACB′=∠B′AC=30°,∴AB′=B′C=1,∴AA′=1+2=3,故答案为3.13.如图,△ABC与△DEF位似,位似中心为点O,且△ABC的面积等于△DEF面积的,则AB:DE=2:3.【考点】位似变换.【分析】由△ABC经过位似变换得到△DEF,点O是位似中心,根据位似图形的性质,即可得AB∥DE,即可求得△ABC的面积:△DEF面积=,得到AB:DE═2:3.【解答】解:∵△ABC与△DEF位似,位似中心为点O,∴△ABC∽△DEF,∴△ABC的面积:△DEF面积=()2=,∴AB:DE=2:3,故答案为:2:3.14.如图,点A是反比例函数图象上y=一点,过点A作AB⊥y轴于点B,点C、D在x 轴上,且BC∥AD,四边形ABCD的面积为3,则k=﹣3.【考点】反比例函数系数k的几何意义;反比例函数图象上点的坐标特征;平行四边形的判定.【分析】设点A的坐标为(m,n),先证明四边形ABCD为平行四边形,再根据平行四边形的面积公式结合点A的坐标,即可得出k的值.【解答】解:设点A的坐标为(m,n),∵AB⊥y轴,CD⊥y轴,∴AB∥CD,又∵BC∥AD,∴四边形ABCD为平行四边形.=AB•OB=﹣m•n=3,S平行四边形ABCD∴k=mn=﹣3.故答案为:﹣3.15.在平面直角坐标系中,有平行四边形ABCD,点A坐标为(2,0),点C(5,﹣3),点B(4,1),则D点坐标为(3,﹣4).【考点】平行四边形的性质;坐标与图形性质.【分析】设点D的坐标为(x,y),然后根据平行四边形的中心对称性和中点公式列出方程,然后计算即可得解.【解答】解:设点D的坐标为(x,y),∵四边形ABCD是平行四边形,点A(2,0),点C(5,﹣3),点B(4,1),∴x+4=2+5,y+1=0+(﹣3),解得:x=3,y=﹣4,∴点D的坐标是(3,﹣4).故答案为:(3,﹣4).16.如图,一艘潜艇在海面下500m深的点A处,测得正前方俯角为31°方向上的海底有黑匣子发出信号,潜艇在同一深度保持直线航行500m,在点B处测得海底黑匣子位于正前方俯角36.9°的方向上,海底黑匣子C所在点距海面的深度为2000m.(精确到1,m.参考数据:sin36.9°≈0.60,cos36.9°≈0.80,tan36.9°≈0.75,sin31°≈0.51,cos31°≈0.87,tan31°≈0.60)【考点】解直角三角形的应用-仰角俯角问题.【分析】作CD ⊥AB 于D ,设CD=xm ,利用正切的定义用x 表示出AD 、BD ,根据题意列出方程,解方程求出x 的值,计算即可.【解答】解:作CD ⊥AB 于D ,设CD=xm ,则AD==xm ,BD==xm ,由题意得,AD ﹣BD=500m ,即x ﹣x=500,解得,x=1500m ,1500+500=2000m ,故答案为:2000.三、解答题(本题共4小题,其中17、18、19题各9分,20题12,共39分)17.计算:20160﹣|﹣2|﹣()﹣1+6tan30°.【考点】实数的运算;零指数幂;负整数指数幂;特殊角的三角函数值.【分析】原式利用零指数幂、负整数指数幂法则,绝对值的代数意义,以及特殊角的三角函数值计算即可得到结果.【解答】解:原式=1﹣2﹣2+6×=1﹣2﹣2+2=﹣1.18.先化简,再求值:,其中.【考点】分式的化简求值.【分析】先根据分式混合运算的法则把原式进行化简,再把a=代入进行计算即可.【解答】解法一解:原式===当时,原式=.解法二:原式===当时,原式=.19.如图,在正方形ABCD内有一点P满足AP=AB,PB=PC,连接AC、PD.求证:△APB ≌△DPC.【考点】正方形的性质;全等三角形的判定.【分析】由正方形的性质和已知条件易证∠ABC﹣∠PBC=∠DCB﹣∠PCB,即∠ABP=∠DCP,因此可证得两三角形全等.【解答】证明:∵四边形ABCD是正方形,∴∠ABC=∠DCB=90°,∵PB=PC,∴∠PBC=∠PCB.∴∠ABC﹣∠PBC=∠DCB﹣∠PCB,∴即∠ABP=∠DCP.又∵AB=DC,PB=PC,∴在△APB和△DPC中,∴△APB≌△DPC.20.我市某校九年级实行小组合作学习,为了解学生课堂发言情况,随机抽取该年级部分学生,对他们每天在课堂上发言的次数进行调查和统计,统计表如下,并绘制了两幅不完整的A B1:5.(1)A组的人数是多少?本次调查的样本容量是多少?(2)求出C组的人数并补全直方图;(3)该校七年级共有250人,请估计全年级每天在课堂上发言次数不少于15次的人数.【考点】扇形统计图;总体、个体、样本、样本容量;用样本估计总体;频数(率)分布直方图.【分析】(1)根据B组有10人,A组发言人数:B发言人数=1:5,可以求得A组的人数,由扇形统计图可知A组占4%,从而可以求得调查的总人数;(2)根据(1)中求得的总人数可以求得C组的人数,从而可以将条形统计图补充完整;(3)根据扇形统计图可以估计全年级每天在课堂上发言次数不少于15次的人数.【解答】解:(1)∵B组有10人,A组发言人数:B发言人数=1:5,∴A组发言人数为:10÷5=2(人),∴本次调查的样本容量为:2÷4%=50,即A组有2人,本次调查的样本容量是50;(2)c组的人数有:50×40%=20(人),补全的直方图如右图所示,(3)全年级每天发言次数不少于15次的发言的人数有:250×(1﹣4%﹣40%﹣20%)=90(人),即全年级每天在课堂上发言次数不少于15次的有90人.四、解答题(本题共3小题,其中21、22题各9分,23题10,共28分)21.一学校为了绿化校园环境,向某园林公司购买了一批树苗,园林公司规定:如果购买树苗不超过60棵,每棵售价120元;如果购买树苗超过60棵,每增加1棵,所出售的这批树苗每棵售价均降低0.5元,但每棵树苗最低售价不得少于100元,该校最终向园林公司支付树苗款8800元,请问该校共购买了多少棵树苗?【考点】一元二次方程的应用.【分析】根据设该校共购买了x棵树苗,由题意得:x[120﹣0.5(x﹣60)]=8800,进而得出即可.【解答】解:因为60棵树苗售价为120元×60=7200元<8800元,所以该校购买树苗超过60棵,设该校共购买了x棵树苗,由题意得:x[120﹣0.5(x﹣60)]=8800,解得:x1=220,x2=80.当x=220时,120﹣0.5×=40<100,∴x=220(不合题意,舍去);当x=80时,120﹣0.5×(80﹣60)=110>100,∴x=80.答:该校共购买了80棵树苗.22.如图,已知一次函数的图象y=kx+b与反比例函数y=﹣的图象交于A,B两点,且点A的横坐标和点B的纵坐标都是﹣2,求:(1)一次函数的解析式;(2)△AOB的面积;(3)直接写出一次函数的函数值大于反比例函数的函数值时x的取值范围.【考点】反比例函数与一次函数的交点问题.【分析】(1)由点A、B的横纵坐标结合反比例函数解析式即可得出点A、B的坐标,再由点A、B的坐标利用待定系数法即可得出直线AB的解析式;(2)设直线AB与y轴交于C,找出点C的坐标,利用三角形的面积公式结合A、B点的横坐标即可得出结论;(3)观察函数图象,根据图象的上下关系即可找出不等式的解集.【解答】解:(1)令反比例函数y=﹣中x=﹣2,则y=4,∴点A的坐标为(﹣2,4);反比例函数y=﹣中y=﹣2,则﹣2=﹣,解得:x=4,∴点B的坐标为(4,﹣2).∵一次函数过A、B两点,∴,解得:,∴一次函数的解析式为y=﹣x+2.(2)设直线AB与y轴交于C,令为y=﹣x+2中x=0,则y=2,∴点C的坐标为(0,2),∴S△AOB=OC•(x B﹣x A)=×2×[4﹣(﹣2)]=6.(3)观察函数图象发现:当x<﹣2或0<x<4时,一次函数图象在反比例函数图象上方,∴一次函数的函数值大于反比例函数的函数值时x的取值范围为x<﹣2或0<x<4.23.如图,O为等腰三角形ABC内一点,⊙O与△ABC的底边BC交于M,N两点,与底边上的高AD交于点G,且与AB,AC 分别相切于E,F两点.(1)证明:EF∥BC;(2)若AG等于⊙O的半径,且AE=MN=2,求四边形EBCF的面积.【考点】切线的性质;等腰三角形的性质.【分析】(1)利用等腰三角形的性质先判断AD是∠CAB的平分线,再根据切线长定理得到AE=AF,接着利用等腰三角形的性质判断AD⊥EF,然后根据平行线的判定可得到结论;(2)先证明AD是EF的垂直平分线得到O在AD上;连结OE,OM,再根据切线的性质得到OE⊥AE,接着证明△ABC和△AEF都是等边三角形,则根据等边三角形的性质和含30度的直角三角形三边的关系计算出OE、AO,再利用勾股定理计算出OD,然后根据等边三角形的面积公式,利用四边形EBCF的面积=S△ABC﹣S△AEF进行计算即可.【解答】(1)证明:∵△ABC是等腰三角形,AD⊥BC,∴AD是∠CAB的平分线,又∵☉O分别与AB,AC相切于点E,F,∴AE=AF,∴AD⊥EF,∴EF∥BC;(2)解:由(1)知,AE=AF,AD⊥EF,∴AD是EF的垂直平分线,∴O在AD上;连结OE,OM,∵AB为切线,∴OE⊥AE,∴AG=OG=OE,即AO=2OE,∴∠OAE=30°,∴∠EAF=60°,∴△ABC和△AEF都是等边三角形,∴AE=2,∴OE=AE=2,AO=2OE=4,∵OM=OE=2,DM=MN=,∴OD==1,∴AD=AO+OD=5,∴BD=AD=,∴AB=2BD=,∴四边形EBCF的面积=S△ABC﹣S△AEF=•()2﹣×(2)2=.五、解答题(本题共3小题,其中24题11分,25、26题各12分,共35分)24.如图1,在△ABC中.∠C=90°,AC>BC,正方形CDEF的顶点D在边AC上,点F 在射线CB上设CD=x,正方形CDEF与△ABC重叠部分的面积为S,S关于x的函数图象如图2所示(其中0<x≤m,m<x≤2,2<x≤n时,函数的解析式不同).(1)填空:m的值为;(2)求S关于x的函数解析式,并写出x的取值范围;(3)S的值能否为?若能,直接写出此时x的值;若不能,说明理由.【考点】四边形综合题.【分析】(1)当0<x≤m时,结合图形可知S=x2,把点(m,)代入可求得m的值;(2)结合图形的变换可知当m<x≤2时,点F运动到点B,可求得BC,当x=m时,可得△BEF∽△BAC,利用相似三角形的性质可求得AC的长,当m<x≤2,设AB分别交DE、EF于点P、Q两点,可用x分别表示出PE和QE,S=S﹣S△PEQ,可得到S与x正方形CDEF的关系式,当2<x≤n时,设AB交DE于点H,可用x表示出AP和PH,则有S=S△ABC ﹣S△APH,可得到S与x的关系式,从而可求得函数解析式;(3)利用(2)中所求得关系式,分别令S=,解相应的方程进行判断即可.【解答】解:(1)当0<x≤m时,如图1,则可知点F从C点运动到点E运动到AB上,∴S=x2,∵点(m,)在函数图象上,∴m2=,解得m=或m=﹣(舍去),故答案为:;(2)当<x≤2时,可知点F从E点在AB上运动到B点,∴BC=2,在图1中,由EF∥AC,∴△BEF∽△BAC,∴=,且CF=EF=,BF=BC﹣CF=2﹣=,∴=,解得AC=6,①当0<x≤时,由(1)可知S=x2;②当<x≤2时,设AB分别交DE、EF于点P、Q两点,如图2,当CD=CF=DE=EF=x时,BF=2﹣x,AD=6﹣x,∵EF∥AC,∴=,即=,∴FQ=3(2﹣x),∴QE=EF﹣FQ=x﹣3(2﹣x)=4x﹣6,同理可得=,即=,∴PD=(6﹣x),∴PE=DE﹣PD=x﹣(6﹣x)=(4x﹣6),∴S△PEQ=PE•PQ=×(4x﹣6)•(4x﹣6)=(4x﹣6)2,﹣S△PEQ=x2﹣(4x﹣6)2=﹣x2+8x﹣6;∴S=S正方形CDEF③当2<x≤6时,即点F从B点运动到使A、D重合,设AB交DE于点H,如图3,当CD=x时,则AD=6﹣x,同理可得=,即=,∴DH=(6﹣x),∴S△ADH=DH•AD=×(6﹣x)•(6﹣x)=(6﹣x)2,且S△ABC=AC•BC=6,∴S=S△ABC﹣S△APH=6﹣(6﹣x)2=﹣x2+2x;综上可知S=,且0<x≤6;(3)若S=,则有三种情况,①当x2=时,则x=±,当x=﹣时显然不满足条件,当x=时,>,也不满足条件;②当﹣x2+8x﹣6=时,整理可得10x2﹣48x+75=0,该方程判别式△=482﹣4×10×75<0,即该方程无实数解;③当﹣x2+2x=时,整理可得x2﹣12x+39=0,该方程判别式△=122﹣4×39<0,即该方程无实数解;综上可知S的值不能为.25.如图,已知:在矩形ABCD中,O为AC的中点,直线l经过点B,且直线l绕着点B 旋转,AM⊥l于点M,CN⊥l于点N,连接OM,ON(1)当直线l经过点D时,如图1,则OM、ON的数量关系为OM=ON;(2)当直线l与线段CD交于点F时,如图2(1)中的结论是否仍然成立?若成立,请加以证明;若不成立,请说明理由;(3)当直线l与线段DC的延长线交于点P时,请在图3中作出符合条件的图形,并判断(1)中的结论是否仍然成立?不必说明理由.【考点】四边形综合题.【分析】(1)OM=ON;易证△AOM≌△CON,所以OM=ON;(2)结论仍然成立.如答图2,作辅助线,证明△AEO≌△CNO,得点O为Rt△MEN斜边上的中点,所以OM=ON结论成立;(3)结论仍然成立.与(2)同理.【解答】解:(1)OM=ON;如题图1,∵O为AC的中点,∴OA=OB,∵AM⊥l于点M,CN⊥l于点N,∴∠AMO=∠CNO=90°,在△AMO和△CNO中,,∴△AMO≌△CNO(AAS)∴OM=ON;(2)答:(1)中的结论仍然成立.理由如下:如答图2,延长NO,交AM于点E,∵AM⊥l于点M,CN⊥l于点N,∴AM∥CN,∴∠OAE=∠OCN.∵矩形ABCD,点O为对角线AC中点,∴OA=OC.在△AEO和△CNO中,∴△AEO≌△CNO(ASA)∴OE=ON,∵Rt△MEN,点O为EN的中点∴OM=ON(直角三角形斜边上的中线等于斜边的一半).(3)答:(1)中的结论仍然成立.理由如下:如答图3,延长NO,交MA的延长线于点E.与(2)同理,可以证明OM=ON.26.在平面直角坐标系xOy中,抛物线C:y=ax2.(1)若直线l1:y=x﹣1与抛物线C有且只有1个交点,求抛物线C的解析式.(2)如图1,在(1)的条件下,在y轴上有一点A(0,4),过点A作直线l2与抛物线C 有两个交点M、N(N位于第一象限),过点N作x轴的垂线,垂足为H.试探究:是否存在l2,使△MON∽△NHO?若存在,求出l2的解析式;若不存在,说明理由.(3)如图2,E、F为抛物线C(y=ax2)上两动点,始终满足OE⊥OF,连接EF,则直线EF是否恒过一定点G?若存在点G,直接写出G点坐标(用含a的坐标表示),若不存在,给予证明.(参考结论:若直线l:y=kx+b上有两点(x1,y1)、(x2,y2),则斜率k=;当两直线l1、l2的斜率乘积k1•k2=﹣1时,l1⊥l2)【考点】二次函数综合题.【分析】(1)首先将l1和抛物线C的解析式联立得:ax2﹣x+1=0,由直线l1:y=x﹣1与抛物线C有且只有1个交点,可得△=0,继而求得a的值,即求得抛物线C的解析式;(2)首先设l 2解析式为y=kx +b ,然后与抛物线C 解析式联立,再设点M (x 1,kx 1+4),N (x 2,kx 2+4),分别表示出OM ,ON 的斜率,然后求得k 1k 2=﹣1,即可证得OM ⊥ON ,则可求得l 2的解析式;(3)与(2)类似,可以由k 1k 2=﹣1,求得G 点坐标.【解答】解:(1)将l 1和抛物线C 的解析式联立得:ax 2﹣x +1=0, ∵y=x ﹣1与抛物线C 有且只有1个交点,∴△=1﹣4a=0,解得a=,∴C 的解析式为y=x 2;(2)假设存在l 2,设l 2解析式为y=kx +b ,与抛物线C 解析式联立得: x 2﹣kx ﹣4=0,设点M (x 1,kx 1+4),N (x 2,kx 2+4),则直线OM 、ON 的斜率分别为k 1=,k 2=,∴k 1k 2=k 2++,∵x 1+x 2=4k ,x 1•x 2=﹣16,∴k 1k 2=k 2++=﹣1,∴OM ⊥ON 恒成立,∠MON=∠NHO=90°,要想使△MON ∽△NHO 成立,只需再令∠MNO=∠NOH 即可, 即MN ⊥x 轴,∴存在l 2符合题意,l 2解析式为y=4;(3)存在定点G ,假设存在l ,设l 解析式为y=kx +b ,与抛物线C 解析式联立得:ax 2﹣kx ﹣b=0,设点M (x 1,kx 1+b ),N (x 2,kx 2+b ),则直线OM 、ON 的斜率分别为k 1=,k 2=,∴k 1k 2=k 2++,∵x 1+x 2=,x 1•x 2=﹣,OE ⊥OF ,∴k1k2=k2++=﹣ab=﹣1,∴b=,∴点G坐标为(0,).2016年8月8日。
2016大连市第一次模拟考试--理综参考答案

大连市2016年高三第一次模拟考试参考答案和评分标准生物29.(每空2分,共10分)(1)类囊体薄膜无水乙醇(或:丙酮)(2)先增多后减少(类似答案可酌情给分) b(3)番茄叶片气孔导度下降,胞间CO2浓度却升高(类似答案可酌情给分)30.(除注明外,每空2分,共9分)(1)蛋白质(或:糖蛋白)(1分)腺苷(2)促甲状腺激素释放(1分。
答出:“促性腺激素释放”或“促肾上腺皮质激素释放”给分,其余情况不给分)肾小管和集合管(只答:“肾小管”或“集合管”或“子宫”给分)(3)胰岛A(1分)(4)激素(一经靶细胞接受并)起作用后就被灭活了(类似答案可酌情给分)31.(除注明外,每空1分,共9分)(1)标志重捕法种群密度(2)春夏小于(3)二、三(少答、错答均不给分,2分)捕食、竞争(2分,少答给1分错答不给分)(4)反馈(或:负反馈)32.(除注明外,每空2分,共11分)(1)X 大翅 X A X a、X a Y(少答、错答、顺序颠倒均不给分)(2)♀大翅与♂大翅(答出:“♀小翅与♂大翅”也可给分,“♀、♂”答成“雌、雄”给分,其余答案不给分)♀大翅:♂大翅:♂小翅=2:1:1(3分)(答出:“♀大翅:♂小翅=1:1”也可给分,“♀、♂”答成“雌、雄”给分,其余答案不给分)39.(除注明外,每空2分,共15分)(1)酵母菌可在有氧条件下大量繁殖液泡显微镜(硫酸酸化)重铬酸钾(2)好氧(或:需氧。
1分)缺少碳源(3)缺氧、呈酸性(2分。
少答给1分,错答不给分)(4)(醋酸发酵前后的)pH(答:酸碱度给分)40.(除注明外,每空2分,共15分)(1)卵子(或:卵细胞。
1分)早期胚胎培养氨基酸、核苷酸(少答给1分,错答不给分)(2)内细胞团体积小、细胞核大、核仁明显(少答、错答均不给分)(3)生殖隔离受精 4大连市2016年高三第一次模拟考试参考答案和评分标准化学一、选择题二、非选择题26.(14分)(1)HgO + 2e- + H2O = Hg + 2OH-(2分)(2)Hg2+ + S2-= HgS↓(2分)(3)水解生成的胶体具有吸附作用,可加快HgS微粒的沉降(2分)(4)使反应物充分混合,提高反应速率(2分) NH3(1分)(5)2LiH2PO4 + Fe2O3 + C = 2LiFePO4 + 2H2O + CO↑(2分) N A×1023(1分)(6)Fe(2分)27.(14分)(1)2CaCO3(s) + O2 (g)+ 2SO2(g) + 4H2O(l)⇋2[CaSO4· 2H2O](s)+2CO2(g)△H = (2分)(2)ad (2分)(3)①2×10-5(2分)② <(2分)> (2分)③ = (2分)该反应的平衡常数表达式为K = 1/c(SO2),温度不变,平衡常数不变,所以浓度相等。
大连市2016年高三第一次模拟考试英语

大连市2016年高三第一次模拟考试参考答案和评分标准英语听力(1.5×20=30)1—5CABBC 6—10CAACB 11—15 BACCA 16—20 BACBB阅读理解(2×20=40)21—25BCACC 26—30BABDD 31—35 ABABD36—40 DGBEC完形填空(1.5×20=30)41—45 ACCBD 46—50BBACB 51—55DDBCA 56—60CADAD语法填空(1.5×10=15)61. whether 62. larger 63. his 64. of 65. an66.To make 67. which/that 68. announcement 69. written 70. will help短文改错(1×10=10)In a general, most houseparents are annoying for boy students living indormitories. I didn’t begin tountildropped wasblaming me, he asked me houseparent ofanxiously Afterhimselfkeeping书面表达(25分)依据高考作文评分标准One possible version:Dear Sir or Madam,I’m writing to ask for some informatio n about the books I bought on your website.The purchase was made on March12th. As is shown in Shipment Details, the delivery number is HU186GB0092. The books were sent out on March13th and are supposed to have arrived within 15 days. But today, unfortunat ely, I’m still waiting.I don’t think your delivery is satisfying, for I can’t find more information about shipment after March 18th. I’d like to point out I’ve provided right address and already paid for the books. Please deal with this matter immediately and let me know the latest information.Your earliest reply will be highly appreciated.Sincerely Yours,Li Hua听力录音稿第一部分听力(共两节,共20小题;每小题1.5分,满分30分)听力原文:Text 1M: I hope you don’t mind but I want very much to watch the game this coming Sunday.W: I certainly do, but there’s not much I can do about it, is there?Text 2M: Are you looking for someone?W: Yes, I need to speak to Neil. He isn’t in this office.M: He is talking to the boss at the moment.Text 3W: What was the play about?M: Well, this woman met this man…W: Oh, love story as usual!M: Actually they were brother and sister, but they hadn’t seen each other since they were babies because their parents broke up and took one child each.Text 4W: This is a beautiful park. Shall we come again tomorrow?M: Don’t we have to go shopping?W: We can do that in the afternoon, and come here in the morning.M: OK. And let’s bring Joe and Linda with us.Text 5W: I want one pound of pork and three pounds of chicken.M: The pork is $3.48 a pound and the chicken is $5.25 a pound.W: OK, I think that will be all for me today.Text 6M: I will buy a car this year.W: That’s really good news.M: I don’t know which brand I should go for, though.W: Are you looking for some advice?M: If you have any good idea s, please don’t keep them to yourself.W: Well, I’ve always been partial to Ferrari’s cars, they have everything you’d ever need.M: No, they have everything you need, not me. I’m a family man now, remember?W: Yeah, but imagine how great it would be to have a fast car to escape from your wife and kids when they bother you too much!M: That sounds tempting, but let’s be serious here. I need something that has a lot of room, and I want it to be safe.W: Maybe V olvo would be your thing.M: That’s good advice.But I’m not sure V olvo is within the price range I’m aiming for.W: Then I’d suggest a Fiat.Text 7W: Good morning, Sales and Marketing, may I help you?M: Hello, I’m interested in the job you’ve advertised for a marketing assistant.W: Certainly, sir. Can I take your name?M: My name’s Sam Blunt.W: Well, Mr. Blunt, what would you like to know?M: First of all, about the duties.W: Well, you have to carry out market research. You will mainly be responsible for collecting the information and writing reports.M: Oh, sounds interesting. Will there be opportunities to travel?W: Not at first, but after you’ve been with the company for about six months, you’ll be expected to attend meetings in the branches in different cities.M: OK, that’s fine, thank you. I’ve already sent my application form in, so I’m looking forward to hearing from you.W: Thank you for your interest, Mr. Blunt, and if you have any more questions, please call me any time. M: I will do. Thank you very much. Bye.W: Bye, Mr. Blunt.Text 8W: So, I was just hanging out in Sydney last weekend.M: I love Sydney. I mean if it wasn’t so expensive, I’d totally be there.W: Me, too, exactly. You know, there are so many things to do and… (The man’s cell phone rings.)M: Oh, hold on. Hello, yeah, hey! How’s it going? No, no! I mean, I… I can’t visit you tonight! I don’t think I can. Really? I’ll call you back. All right! OK, bye! I am sorry, what were you saying?W: You know, I just have to say, I … I’m sorry, I hate it when people do that. I think th at it is so rude.When we’re having a conversation, and your phone rings, and you just… You know, you are so involved in your conversation and I am left hanging.M: Yeah, I mean…W: I think it’s rude.M: I am sorry, I mean, when people call you, don’t you feel like… um… it could be something important.I should at least check.W: I actually… don’t have a cell phone.Text 9W: Are you ready to go to the concert?M: Yes. Should we go there by bus so that we aren’t late?W: Actually, why don’t we go there by b ike? We could get stuck in traffic if we travel by bus in rush hour.M: That’s true. Cycling is good for our environment, too. Let me just get my helmet then.W: Is your helmet comfortable?M: Not really, but I liked the design, so I got it.W: Maybe you s hould think about getting a round helmet; they’re better.M: I’ll think about it.W: Is that your new bicycle?M: Yes, my father gave it to me for my birthday. Do you like it?W: It’s the latest 10 speed cycling mountain bike. These are really expensive!M: Nothing but the best from my dad. I like everything about it except for the brakes. They are a bit sticky.W: I can fix those for you. Is there anything else wrong with it?M: Well, my saddle is too low for me. Do you know how to change the height?W: Th at’s easy. It’s important to have the saddle high enough so that your legs can extend fully when you are on your bicycle.Text 10Have you ever heard the old saying, “Never judge a book by its cover”? This is a good rule to follow when trying to judge the intelligence of others. Some people have minds that shine only in certain situations. A young man with an unusual gift in creative writing may find himself speechless in the presence of a pretty girl. He searches awkwardly for words and does not talk smoot hly. But don’t makethe mistake of thinking him stupid. With a pen and paper, he can express himself very well.Other people may fool you into overvaluing their intelligence by putting up a good appearance. A student who listens attentively and takes notes in class is bound to make a favorable impression on his teachers. But when it comes to exams, he may score near the bottom of the class. The main idea is you can’t judge someone by their appearances. The only way to determine a person’s intelligence is to get to know him. Then you can observe how he reacts to different situations. The more situations you observe, the more accurate your judgment is likely to be. So take your time. Don’t judge the book by its cover.。
辽宁省大连市2016届高三第一次模拟考试 理综物理 Word版含答案
辽宁省大连市2016届高三第一次模拟考试理科综合物理部分二、选择题:本题共8小题,每小题6分。
其中14-18题在给出的四个选项中,只有一个选项正确,19-21题在给出的四个选项中,只有多个选项正确,全部选对的得6分,选对但不全的得3分,有选错或不答的得0分。
14.矩形线圈abcd在匀强磁场中逆时针匀速转动时线圈中产生如右图所示的交流电,取沿a→b→c→d→a方向为电流正方向,则对应t1时刻线圈的位置应为下图中的15.如图所示,一竖直放置的大圆环,在其水平直径上的A、B两端系着一根不可伸长的柔软细绳,绳上套有一光滑小铁环。
现将大圆环在竖直平面内绕O点顺时针缓缓转过一个微小角度,则关于轻绳对A、B两点拉力F1、F2的变化情况,下列说法正确的是A. F A变小, F B变小B. F A变大, F B变大C. F A变大,F B变小D. F A变小,F B变大16.如图所示,打置于光滑水平面上的物块在水平恒力F的作用下由静止开始运动,其速度错误!未找到引用源。
、动能Ex及拉力功率P随时间t或位移x的变化图象可能正确的是17.如图所示,在正方形的顶点A 和B 上分别固定有电量为+q 和-q 的点电荷,过正方形中心O 并与正方形所在平面垂直的直线上有P 、Q 两点,设P 、Q 两点的场强大小分别为E P 和E Q , P 、Q 两点的电势分别为P ϕ和Q ϕ,则下列判断正确的是A. P ϕ>Q ϕB. P ϕ<Q ϕC. P ϕ>Q ϕ且电场强度方向相同D. P ϕ<Q ϕ且电场强度方向不同18. 如图所示,半径为R 的光滑圆环竖直放置,N 为圆环的最低点。
在环上套有两个小球A 和B ,A 、B 之间用一根长为R 3的轻杆相连,使小球能在环上自由滑动。
已知A 球质量为4m ,B 球质量为m ,重力加速度为g ,现将杆从图示的水平位置由静止释放,则当A 球滑倒N 点时,轻杆对B A. mgRB. 1.2 mgRC. 1.4 mgRD. 1.6 mgR19. 如图所示,A 、B 、C 、D 、E 为楼梯台阶边缘上的五个点,它们在同一竖直面内,且各级台阶都相同。
2016年辽宁省大连市中考物理一模试卷
2016年辽宁省大连市中考物理一模试卷一、选择题(本题共11小题,每小题2分,共28分)注意:第1~11题中,每题只有一个选项正确.1.(2分)小明骑自行车上学,他看到路边的小树向后运动,则他选择的参照物是()A.地面B.路边的房屋C.所骑的自行车D.远处的高山2.(2分)家庭电路中,空气开关的主要作用是()A.保持电路的电压不变B.可以节省电能C.保证用电器功率不变D.当电路中电流过大时自动切断电路3.(2分)一盒草莓放在冰箱冷藏室里,冷藏室里就有草莓的清香,这表明()A.分子间存在引力 B.分子在不停地运动C.分子间有间隙D.温度越低,分子运动越剧烈4.(2分)把毛皮摩擦过的橡胶棒靠近轻质小球时,小球被吸引,则这个小球()A.一定不带电B.一定带负电C.一定带正电D.可能不带电5.(2分)正确电器设备中,将机械能转化为电能的是()A.发电机B.电动机C.电磁继电器D.电热水器6.(2分)电视机、电烙铁和电风扇上都标有“220V 60W”的字样,它们都在额定电压下工作相同的时间,则()A.电视机消耗的电能最多B.电流通过电风扇做的功最多C.电风扇消耗的电能全部转化为机械能D.电流通过电烙铁产生的热量最多7.(2分)一艘轮船从长江驶入大海,下列分析正确的是()A.浮力变小,船体上浮一些B.浮力变大,船体下沉一些C.浮力不变,船体下沉一些D.浮力不变,船体上浮一些8.(2分)汽车的安全带指示灯,会提醒驾驶员系好安全带.当安全带系好时,相当于闭合开关S,指示灯L不亮;安全带未系好时,相当于断开开关S,指示灯L亮.下列符合要求的电路图是()A.B.C.D.9.(2分)做“凸透镜成像”实验时,把蜡烛放在二倍焦距之外,移动光屏找到像.若将蜡烛向凸透镜移动s1的距离(此时物距仍然大于二倍焦距),移动光屏重新找到像,光屏移动的距离为s2.则下列说法正确的是()A.光屏远离透镜移动,光屏上的像变小B.光屏远离透镜移动,且s2<s1C.光屏靠近透镜移动,光屏上的像变大D.光屏靠近透镜移动,且s2=s110.(2分)如图所示,电源电压恒为20V,电压表量程是“0~15V”,电流表量程是“0~0.6A”,滑动变阻器的规格是“100Ω 1A”,灯泡标有“12V 6W”字样.闭合开关S,若两表的示数均不超过量程,灯泡两端的电压不超过额定电压,不考虑灯丝电阻的变化.下列说法正确的是()A.电压表的示数变化范围是3V~15VB.电压表的示数变化范围是0.1A~0.5AC.电路中的最大功率是20WD.滑动变阻器连入电路阻值的变化范围是16Ω~72Ω11.(2分)如图所示,小球从高处下落到竖直旋转的轻弹簧上并压缩弹簧.从小球接触弹簧到将弹簧压缩到最短的过程中,下列说法正确的是()A.小球的速度逐渐变小B.小球的机械能保持不变C.小球所受的合力先变小后变大D.小球所受的弹力先变大后变小二、注意:第12~14小题中,每小题至少有两个选项正确.12.(2分)在探究“水沸腾时温度变化的特点”实验中,下列说法正确的是()A.记录加热时间越大越好B.在烧杯上盖上带孔的盖可以缩短加热时间C.水沸腾前气泡在上升过程中体积逐渐变小D.水沸腾时气泡在上升过程中体积逐渐变大13.(2分)水平地面上有一木箱,小明用水平推力推木箱,木箱的速度v随时间t的变化图象如图所示.则()A.0~1,木箱所受的推力小于静摩擦力B.1~3s,木箱所受的摩擦力逐渐减小C.3~5s,木箱所受的推力等于摩擦力D.5~6s,木箱所受的推力小于摩擦力14.(2分)在如图所示的电路中,电源电压不变.闭合开关s,将滑动变阻器的滑片P从a滑到b的过程中,不计温度对灯丝电阻的影响.则下列说法正确的是()A.电路的总电阻先变大后变小B.电流表A1的示数逐渐减小C.灯L先变暗后变亮D.电流表A1示数的变化量大于A2示数的变化量二、填空题(本题共10小题,每小题2分,共20分)15.(2分)笛子是通过从吹孔向管内灌气引起空气柱而发声的,演奏时,通过分别开闭六个音孔,笛子就能发出(填“音调”、“响度”或“音色”)不同的声音.16.(2分)在用天平测物体质量时,应先估测物体的质量,再按照质量(选填“由小到大”或“由大到小”)的顺序往右盘添加砝码;若测得体积是10cm3的物体的质量是43g,则该物体的密度是kg/m3.17.(2分)某凸透镜的焦距是10cm,把蜡烛放在距离凸透镜16cm的位置,在光屏上成一个倒立、的像.小明站在平面镜前2m,他在平面镜中成的像距离平面镜m.18.(2分)某同学练习爬杆,当他从竿的顶端滑下时,感到后很热,说明手的内能(选填“变大”、“不变”或“变小”),这是通过的方法改变手的内能的.19.(2分)氢弹是利用原子核(选填“裂变”或“聚变”)在瞬间释放出巨大能量的一种武器;自然界中能量的形式有很多,其中“水能”属于(选填“可再生”或“不可再生”)能源.20.(2分)在探究液体吸收热量的多少与哪些因素有关时,小明猜想可能与液体的质量、升高的温度以及种类有关.为了探究“液体吸收热量的多少与液体种类是否有关”,选取了相同的水、酒精、色拉油,用规格相同的加热器同时开始加热,使三者升高相同的温度.实验测得水的加热时间最长,色拉油的加热时间最短,由此可得出的探究结论是.21.(2分)如图所示,图中的条形磁铁置于水平桌面上,电磁铁与其在同一水平面上,左端固定并保持水平.闭合开关S,条形磁铁所受摩擦力的方向;将滑动变阻器的滑片P由中点向b端移动,电磁铁的磁性将.22.(2分)如图所示,实心圆柱体甲、乙旋转在水平桌面上,现沿水平虚线切去部分后,使甲、乙剩余的高度均为h.甲、乙剩余部分对桌面的压力相等,则甲、乙物体的密度ρ甲ρ乙;切除前甲、乙对桌面的压强p甲p乙.(都选填“>”、“=”或“<”)23.(2分)如图所示,请画出光从空气斜射向玻璃的反射光线和折射光线.24.(2分)如图所示,一个人在缓慢下降的吊桥上行走,某时刻人走在吊桥的中间,钢丝绳对吊桥的拉力为F,A点是人对吊桥压力的作用点,O点是支点.请画出此时人对吊桥的压力F1的示意图和钢丝绳拉力的力臂l.三、计算题(本题共3小题,共20分)25.(5分)某野外考察队员使用酒精炉烧水,将1kg的水从20℃加热到100℃,完全燃烧了22.4g的酒精.水的比热容是4.2×103J/(kg•℃),酒精的热值是3.0×107J/kg.试求:(1)水吸收的热量是多少?(2)酒精完全燃烧放出的热量是多少?(3)该酒精炉的效率是多少?26.(7分)我国第一艘航空母舰“辽宁号”某次进行军事演习时,航母的总质量是6×107kg.航母以54km/h的速度匀速直线行驶0.5h,发动机的牵引力是3.6×108N.若行驶过程中航母的总质量不变,g取10N/kg.试求:(1)航母所受的浮力是多少?(2)发动机牵引力做的功是多少?(3)发动机牵引力做功的功率是多少?27.(8分)图甲是用来焊接塑料管的热熔器,两个塑料管接头部分在热熔器中熔化,再被紧压、冷却,结合为一体.热熔器内部电路如图乙所示,R1和R2均为电热丝,电源电压为220V,R1的阻值为171.6Ω.S2、S2都闭合时,为加热状态;S1闭合、S2断开时,为保温状态,保温功率220W.试求:(1)保温状态时,电路中的电流是多少?R2的阻值是多少?(2)加热状态时,加热功率是多少?(3)某次加热熔接塑料管时,塑料管需要吸收9×104J的热量,热熔器的效率为90%,热熔器的加热时间是多少?四、简答题(本题共2小题,共6分)28.(3分)2015年12月底,大连地区突然降温,沿海海城出现“海浩”奇观.“海浩”是指当海面上方的气温突然降到﹣10℃以下时,海面上呈现出好像“白茫茫云雾”的现象,如图所示.请解释这一现象.29.(3分)一个玻璃瓶中装有一定量的水,盖紧瓶盖,放在水平桌面上.在玻璃瓶上开一个很小的孔a,水就从小孔中流出,如图所示.一段时间后水不再流出.请分析说明水能流出和不再流出的原因.五、综合题(本题共3小题,共16分)30.(5分)某同学在探究“并联电路的干路电流与各支路电流关系”实验中,所用的实验器材有:阻值不同的电阻若干,可调电压的稳压电源、电流表、开关各一个,导线若干.(1)用笔画线,将图的电路连接完整.要求电流表测量干路电流.(2)该同学计划做三次实验,做三次实验的目的是:.(3)有甲、乙两种实验方案:甲方案:任意选两个电阻,改变电源电压做实验;乙方案:电源电压不变,选取比值不同的三个电阻做实验.选择方案更好.(4)实验中,电流表用“0~0.6A”的量程完成了第一次实验.第二次实验在“试触”时,发现干路电流为2A,则电流表用“0~3A”的量程完成了第二次实验.那么第一次实验是否需要将电流表改成“0~3A”的量程重新进行?.31.(5分)光通过透明物质时,光的强度会减弱,透过光的强度与入射光的强度之比是该物质的透光率.某同学猜想液体的透光率与液体的密度和深度有关.为了探究“液体透光率与液体深度是否有关”,实验器材有:足量的水,玻璃容器、光源、光屏各一个.实验装置如图13所示,实验中通过往玻璃容器中加减液体改变液体的深度,通过观察光屏上的光点的亮度判断透光率的大小.(1)实验时,光屏上的亮点越亮,说明液体的透光率.(2)画出记录实验数据的表格,表中要有必要的信息.(3)如果用能测出光的强度的传感器进行该实验,通过测量入射和透过光的强度计算出液体的透光率.但是这样测出的透光率会与该液体的真实透光率有差异,产生这种差异的最主要原因是.32.(6分)某同学知道接触面的粗糙程度一定时,压力越大,滑动摩擦力越大.为了进一步探究“接触面粗糙程度一定时,滑动摩擦力与压力的关系”,所用的器材有:水平桌面一个;规格不同的甲(量程是2.5N、分度值是0.05N),乙(量程是5N、分度值是0.1N)两个弹簧测力计,重力为4N的大木块一个,重力为2N 的钩码5个.(1)该同学通过实验操作选取了一个弹簧测力计进行实验,请简单说明如何通过实验操作选取合适的弹簧测力计.(2)经过正确操作,记录的实验数据如表:①将表格中的数据填写完整.②在方格纸上画出摩擦力f与压力F1的关系图象.(3)根据图象得出的探究结论是:.2016年辽宁省大连市中考物理一模试卷参考答案与试题解析一、选择题(本题共11小题,每小题2分,共28分)注意:第1~11题中,每题只有一个选项正确.1.(2分)小明骑自行车上学,他看到路边的小树向后运动,则他选择的参照物是()A.地面B.路边的房屋C.所骑的自行车D.远处的高山【解答】解:以自行车为参照物,小树的位置发生了变化,自行车向前行驶,小树则向后运动,故C正确;以地面、路边的房屋和远处的高山为参照物,小树的位置没有发生变化,小树是静止的,故ABD错误.故选C.2.(2分)家庭电路中,空气开关的主要作用是()A.保持电路的电压不变B.可以节省电能C.保证用电器功率不变D.当电路中电流过大时自动切断电路【解答】解:家庭电路中空气开关的作用是保护电路,当电路中发生短路或总功率过大导致电流过大时会引起空气开关跳闸.故选D.3.(2分)一盒草莓放在冰箱冷藏室里,冷藏室里就有草莓的清香,这表明()A.分子间存在引力 B.分子在不停地运动C.分子间有间隙D.温度越低,分子运动越剧烈【解答】解:草莓放在冰箱冷藏室里,冷藏室里就有草莓的清香,是草莓的香味分子扩散到冰箱中,说明分子在永不停息地做无规则运动,且温度越高分子无规则运动越剧烈,故B正确,ACD错误.故选B.4.(2分)把毛皮摩擦过的橡胶棒靠近轻质小球时,小球被吸引,则这个小球()A.一定不带电B.一定带负电C.一定带正电D.可能不带电【解答】解:毛皮摩擦过的橡胶棒带负电,小球被吸引,小球可能带正电也有可能不带电.故选D.5.(2分)正确电器设备中,将机械能转化为电能的是()A.发电机B.电动机C.电磁继电器D.电热水器【解答】解:A、发电机是利用电磁感应现象的原理制成的,即消耗机械能,产生电能,所以是将机械能转化为电能的过程,故A正确;B、电动机是利用电流工作的,工作过程中将电能转化为机械能.故B错误;C、电磁继电器内部有一个电磁铁,是利用电流的磁效应工作的,故C错误;D、电热水器是电能转化为内能的用电器.故D错误;故选A.6.(2分)电视机、电烙铁和电风扇上都标有“220V 60W”的字样,它们都在额定电压下工作相同的时间,则()A.电视机消耗的电能最多B.电流通过电风扇做的功最多C.电风扇消耗的电能全部转化为机械能D.电流通过电烙铁产生的热量最多【解答】解:各用电器的额定功率相同,在额定电压下它们的实际功率相等.AB.由W=Pt可知,工作相同时间时,消耗的电能相同,电流通过用电器做的功相同,故AB错误;C.电风扇工作时消耗电能大部分转化为机械能,产生很少的热量,故C错误;D.电烙铁工作时消耗的电能全部转化为热量,电流通过电烙铁产生的热量最多,故D正确.故选D.7.(2分)一艘轮船从长江驶入大海,下列分析正确的是()A.浮力变小,船体上浮一些B.浮力变大,船体下沉一些C.浮力不变,船体下沉一些D.浮力不变,船体上浮一些【解答】解:当轮船由从长江驶入大海后始终处于漂浮状态,则船受到的浮力:F浮=G,因为船受到的重力不变,所以船受到的浮力不变;又因为F浮=ρ水V排g,ρ海水>ρ江水,所以排开海水的体积小于排开江水的体积,即:船浸入水中的体积变小,船上浮一些.故选D.8.(2分)汽车的安全带指示灯,会提醒驾驶员系好安全带.当安全带系好时,相当于闭合开关S,指示灯L不亮;安全带未系好时,相当于断开开关S,指示灯L亮.下列符合要求的电路图是()A.B.C.D.【解答】解:由于闭合开关S指示灯L不亮;断开开关S指示灯L亮,所以灯泡的亮与L不亮是利用对用电器短路来实现的,则指示灯应与S并联;但电路不会出现短路,即电路中必须串联一个保护电阻;结合选项可知C符合题意,ABD不符合.故选C.9.(2分)做“凸透镜成像”实验时,把蜡烛放在二倍焦距之外,移动光屏找到像.若将蜡烛向凸透镜移动s1的距离(此时物距仍然大于二倍焦距),移动光屏重新找到像,光屏移动的距离为s2.则下列说法正确的是()A.光屏远离透镜移动,光屏上的像变小B.光屏远离透镜移动,且s2<s1C.光屏靠近透镜移动,光屏上的像变大D.光屏靠近透镜移动,且s2=s1【解答】解:在“凸透镜成像”实验时,把蜡烛放在二倍焦距之外,移动光屏找到像,此时u>2f,成倒立、缩小的实像,2f>v>f,若将蜡烛向凸透镜移动s1的距离(此时物距仍然大于二倍焦距),移动光屏重新找到像,光屏移动的距离为s2,在这种情况下,物体移动的距离大于像移动的距离,即s2<s1,故B正确.故选B.10.(2分)如图所示,电源电压恒为20V,电压表量程是“0~15V”,电流表量程是“0~0.6A”,滑动变阻器的规格是“100Ω 1A”,灯泡标有“12V 6W”字样.闭合开关S,若两表的示数均不超过量程,灯泡两端的电压不超过额定电压,不考虑灯丝电阻的变化.下列说法正确的是()A.电压表的示数变化范围是3V~15VB.电压表的示数变化范围是0.1A~0.5AC.电路中的最大功率是20WD.滑动变阻器连入电路阻值的变化范围是16Ω~72Ω【解答】解:由电路图可知,滑动变阻器R与灯泡L串联,电压表测滑动变阻器R两端的电压,电流表测电路中的电流.(1)由P=UI可得,灯的额定电流:I L===0.5A,由I=可得,灯泡的电阻:R L===24Ω,因串联电路中各处的电流相等,且灯泡的额定电流为0.5A,电流表的量程为0~0.6A,滑动变阻器允许通过的最大电流为1A,=0.5A,所以,电路中的最大电流为I大此时滑动变阻器接入电路中的电阻最小,电路的总功率最大,电压表的示数最小,因串联电路中总电压等于各分电压之和,所以,电压表的最小示数:U滑小=U﹣U L=20V﹣12V=8V,滑动变阻器接入电路中的最小阻值:R滑小===16Ω,该电路的最大功率:P大=UI大=20V×0.5A=10W,故C错误;=15V时,电路中的电流最小,滑动变阻器接入电路中(2)当电压表的示数U滑大的电阻最大,则电压表的示数变化范围为8V~15V,故A错误;此时灯泡两端的电压:U L小=U﹣U滑大=20V﹣15V=5V,电路中的最小电流:I小===A≈0.21A,所以,电流表示数变化范围0.21A~0.5A,故B错误;滑动变阻器接入电路中的最大阻值:R滑大===72Ω,所以,滑动变阻器连入电路的阻值变化范围16Ω~72Ω,故D正确.故选D.11.(2分)如图所示,小球从高处下落到竖直旋转的轻弹簧上并压缩弹簧.从小球接触弹簧到将弹簧压缩到最短的过程中,下列说法正确的是()A.小球的速度逐渐变小B.小球的机械能保持不变C.小球所受的合力先变小后变大D.小球所受的弹力先变大后变小【解答】解:A、小球接触弹簧向下运动过程中,受到弹簧向上弹力的作用,但刚开始弹力小于重力,合力的方向仍然向下,小球做加速运动,故A错误;B、小球接触弹簧向下运动过程中,小球的速度减小,小球的动能减小,小球的能转化为弹簧的弹性势能,同时小球的高度变低,所以重力势能减小,因此小球的机械能减小,故B错误;C、小球在向下运动过程中,受到重力与弹簧弹力作用,在此过程中,向下的重力大小保持不变,刚开始弹力小于重力,合力的方向仍然向下,当弹簧被压缩到一定程度时,弹力等于重力时,合力为零,弹簧继续被压缩,弹力大于重力时,合力方向向上,小球所受的合力先变小后变大,故C正确;D、在向下运动过程中,弹簧被小球压缩,向上的弹力逐渐增大,故D错误.故选C.二、注意:第12~14小题中,每小题至少有两个选项正确.12.(2分)在探究“水沸腾时温度变化的特点”实验中,下列说法正确的是()A.记录加热时间越大越好B.在烧杯上盖上带孔的盖可以缩短加热时间C.水沸腾前气泡在上升过程中体积逐渐变小D.水沸腾时气泡在上升过程中体积逐渐变大【解答】解:A、水加热时间的影响因素:水的多少、水的初温、烧杯是否加盖、火焰的大小,并不是加热时间越长越好,故A错误;B、烧杯上加盖是为了减少蒸发,减慢热量的散失,缩短加热的时间,故B正确;C、水沸腾前,下层的水温度高于上层水温度,气泡上升过程中,气泡内的水蒸气遇冷液化成小水珠,气泡越来越小,故C正确.D、水沸腾时,整个容器内水温相同,气泡上升过程中,不断有水变为水蒸气进入气泡,气泡越来越大,故D正确.故选BCD.13.(2分)水平地面上有一木箱,小明用水平推力推木箱,木箱的速度v随时间t的变化图象如图所示.则()A.0~1,木箱所受的推力小于静摩擦力B.1~3s,木箱所受的摩擦力逐渐减小C.3~5s,木箱所受的推力等于摩擦力D.5~6s,木箱所受的推力小于摩擦力【解答】解:A、由图可知,0一ls,木箱静止,处于平衡状态,所以,推力等于木箱受到的静摩擦力,木箱所受到的合力为零.故A错误;B、由图可知,1~3s,木箱做匀加速直线运动,但木箱对地面的压力不变,接触面的粗糙程度不变,所以,木箱所受的摩擦力大小不变.故B错误;C、由图可知,3~5s,木箱做匀速直线运动,处于平衡状态,木箱所受的推力与摩擦力是一对平衡力,大小相等.故C正确;D、由图可知,5~6s,木箱做匀减速直线运动,处于非平衡状态,所以,木箱所受的推力小于摩擦力.故D正确.故选CD.14.(2分)在如图所示的电路中,电源电压不变.闭合开关s,将滑动变阻器的滑片P从a滑到b的过程中,不计温度对灯丝电阻的影响.则下列说法正确的是()A.电路的总电阻先变大后变小B.电流表A1的示数逐渐减小C.灯L先变暗后变亮D.电流表A1示数的变化量大于A2示数的变化量【解答】解:由图知,变阻器的左半部分与有半部分并联,电流表A1、A2分别测量左边和右边的电流,设变阻器的总电阻为R,则并联后的总电阻:R总====+,当R=时,R有最大值,为.总A、由分析知,滑片在中点时,电阻最大,所以将滑动变阻器的滑片P从a滑到b的过程中,电路的总电阻先变大后变小,A说法正确;B、将滑动变阻器的滑片P从a滑到中点的过程中,变阻器并联部分总电阻变大,电路的总电阻变大,由欧姆定律知电路中总电流变小,灯泡两端电压增大,并联部分分得电压减小,而左半部分电阻变大,所以A1变小;当滑片由中点向b端滑动时,并联部分总电阻减小,分得电压减小,而左半部分电阻增大,所以左半部分电流变小,即A1示数变小.故B说法正确;C、灯泡在干路中,将滑动变阻器的滑片P从a滑到b的过程中,变阻器的电阻先变大后变小,所以灯泡先变暗后变亮,C说法正确;D、左右两半部分的电压相同,电阻的变化量相同,所以两边的电流变化量相同,D说法错误.故选ABC.二、填空题(本题共10小题,每小题2分,共20分)15.(2分)笛子是通过从吹孔向管内灌气引起空气柱振动而发声的,演奏时,通过分别开闭六个音孔,笛子就能发出音调(填“音调”、“响度”或“音色”)不同的声音.【解答】解:吹笛子是笛子内的空气柱振动而发声;演奏时,用手分别按住不同的笛孔,空气柱的长度不同,质量不同,振动频率不同,音调不同.故答案为:振动;音调.16.(2分)在用天平测物体质量时,应先估测物体的质量,再按照质量由大到小(选填“由小到大”或“由大到小”)的顺序往右盘添加砝码;若测得体积是10cm3的物体的质量是43g,则该物体的密度是 4.3×103kg/m3.【解答】解:称量物体时,应先加质量大的砝码,后加质量小的砝码,这样可以节省测量时间.该物体的密度ρ===4.3g/cm3=4.3×103kg/m3.故答案为:由大到小;4.3×103.17.(2分)某凸透镜的焦距是10cm,把蜡烛放在距离凸透镜16cm的位置,在光屏上成一个倒立、放大的像.小明站在平面镜前2m,他在平面镜中成的像距离平面镜2m.【解答】解:已知凸透镜的焦距f=10cm,物体放在凸透镜前16cm的位置,f<u <2f,所以在凸透镜后的光屏上出现一个倒立、放大的实像;平面镜成像,像和物体到平面镜的距离相等,小明距平面镜的距离为2m,所以他所成像到平面镜的距离也为2m.故答案为:放大;2.18.(2分)某同学练习爬杆,当他从竿的顶端滑下时,感到后很热,说明手的内能变大(选填“变大”、“不变”或“变小”),这是通过做功的方法改变手的内能的.【解答】解:练习爬杆的同学从竿的顶端滑下时,克服摩擦做功,机械能转化为内能,使手的内能增大、温度升高,这是通过做功的方法使手的内能发生改变的.故答案为:变大;做功.19.(2分)氢弹是利用原子核聚变(选填“裂变”或“聚变”)在瞬间释放出巨大能量的一种武器;自然界中能量的形式有很多,其中“水能”属于可再生(选填“可再生”或“不可再生”)能源.【解答】解:据上面的分析可知,氢弹是利用轻核聚变制成的武器;水能和风能可以从自然界源源不断获得,它们是可再生能源.故答案为:聚变;可再生.20.(2分)在探究液体吸收热量的多少与哪些因素有关时,小明猜想可能与液体的质量、升高的温度以及种类有关.为了探究“液体吸收热量的多少与液体种类是否有关”,选取了相同质量的水、酒精、色拉油,用规格相同的加热器同时开始加热,使三者升高相同的温度.实验测得水的加热时间最长,色拉油的加热时间最短,由此可得出的探究结论是液体吸收热量的多少与液体种类有关.【解答】解:要探究液体吸收热量的多少与液体种类的关系,需要选择相同的加热器、相同的容器、质量相同的不同液体,使三者升高相同的温度,比较所用时间.实验测得水的加热时间最长,酒精的加热时间居中,色拉油的加热时间最短,说明不同液体吸收热量的多少与液体的种类有关.故答案为:质量;液体吸收热量的多少与液体种类有关.21.(2分)如图所示,图中的条形磁铁置于水平桌面上,电磁铁与其在同一水平面上,左端固定并保持水平.闭合开关S,条形磁铁所受摩擦力的方向水平向左;将滑动变阻器的滑片P由中点向b端移动,电磁铁的磁性将减弱.。
2016年辽宁省大连市高考数学一模试卷(文科)
2016年辽宁省大连市高考数学一模试卷(文科)一、选择题(每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.)1.(5分)集合A={x|﹣1<x<3},集合B={x|﹣1<x<2},则A∩B=()A.(1,2) B.(﹣1,2)C.(1,3) D.(﹣1,3)2.(5分)设复数z1,z2在复平面内对应的点关于虚轴对称,且z1=2+i,则z2=()A.2+i B.﹣2+i C.2﹣i D.﹣2﹣i3.(5分)已知向量=(2,﹣1),=(0,1),则|+2|=()A.2 B.C.2 D.44.(5分)已知函数,则=()A.4 B.C.﹣4 D.5.(5分)某集团为了解新产品的销售情况,销售部在3月1日至3月5日连续五天对某个大型批发市场中该产品一天的销售量及其价格进行了调査,其中该产品的价格(元)与销售量y(万件)的统计资料如表所示:已知销售量y(万件)与价格x(元)之间具有线性相关关系,其回归直线方程为:=x+40.若该集团将产品定价为10.2元,预测该批发市场的日销售量约为()A.7.66万件B.7.86万件C.8.06万件D.7.36万件6.(5分)已知tanα=2,α为第一象限角,则sin2α的值为()A.B.C.D.7.(5分)如图,在长方体ABCD﹣A1B1C1D1中,点P是棱CD上一点,则三棱锥P﹣A1B1A的左视图可能为()A.B.C.D.8.(5分)将函数f(x)=sin(2x+φ)的图象向右平移个单位后的图象关于y轴对称,则函数f(x)在上的最小值为()A.B.C.D.9.(5分)见如图程序框图,若输入a=110011,则输出结果是()A.51 B.49 C.47 D.4510.(5分)已知双曲线C:的右焦点为F,以F为圆心和双曲线的渐近线相切的圆与双曲线的一个交点为M,且MF与双曲线的实轴垂直,则双曲线C的离心率为()A.B.C.D.211.(5分)在△ABC中,a,b,c分别是角A,B,C的对边,且满足acosA=bcosB,那么△ABC的形状一定是()A.等腰三角形B.直角三角形C.等腰或直角三角形D.等腰直角三角形12.(5分)已知函数f(x)是定义在R上的奇函数,且在区间[0,+∞)上是增函数,则不等式<f(1)的解集为()A.(0,)B.(0,e) C.(,e)D.(e,+∞)二、填空题(每小题5分,共20分)13.(5分)若x,y满足约束条件,则z=2x+y的最大值为.14.(5分)在椭圆+=1上有两个动点M、N,K(2,0)为定点,若=0,则的最小值为.15.(5分)已知正三棱柱ABC﹣A1B1C1的所有顶点都在半径为1的球面上,当正三棱锥的体积最大时,该正三棱锥的高为.16.(5分)设G是一个非空集合,*是定义在G上的一个运算,如果满足下述四个条件(1)对于∀a,b∈G,都有a*b∈G;(2)对于∀a,b,c∈G,都有(a*b)*c=a*(b*c);(3)对于∀a∈G,∃e∈G,使得a*e=e*a=a;(4)对于∀a∈G,∃a′∈G,使得a*a′=a′*a=e则称G关于运算*构成一个群.现给出下列集合和运箅①G是整数集合,*为加法;②G是奇数集合,*为乘法;③G是平面向量集合,*为数量积运算;④G是非零复数集合,*为乘法,其中G关于运算*构成群的序号是(将你认为正确的序号都填上).三、解答题(本题共5小题,共70分,解答应写出文字说明、证明过程或演算步骤)17.(12分)已知等差数列{a n}的前n项和为S n,且S4=4(a3+1),3a3=5a4,数列{b n}是等比数列,且b1b2=b3,2b1=a5.(Ⅰ)求数列{a n},{b n}的通项公式;(Ⅱ)求数列{|a n|}的前n项和T n.18.(12分)某小学为迎接校运动会的到来,在三年级招募了16名男志愿者和14名女志愿者.调查发现,男、女志愿者中分别各有10人和6人喜欢运动,其他人员不喜欢运动.(Ⅰ)根据以上数据完成以下2×2列联表:(Ⅱ)判断性别与喜欢运动是否有关,并说明理由.(Ⅲ)如果喜欢运动的女志愿者中恰有4人懂得医疗救护,现从喜欢运动的女志愿者中抽取2名负责医疗救护工作,求抽出的2名志愿者都懂得医疗救护的概率.附:临界值表(部分):19.(12分)已知等腰梯形ABCD(如图(1)所示),其中AB∥CD,E,F分別为AB和CD的中点,且AB=EF=2,CD=6,M为BC中点.现将梯形ABCD沿着EF所在直线折起,使平面EFCB⊥平面EFDA(如图(2)所示),N是线段CD上一动点,且CN=ND.(1)求证:MN∥平面EFDA;(2)求三棱锥A﹣MNF的体积.20.(12分)已知动点P在抛物线x2=2y上,过点P作x轴的垂线,垂足为H,动点Q满足=.(1)求动点Q的轨迹E的方程;(2)点M(﹣4,4),过点N(4,5)且斜率为k的直线交轨迹E于A、B两点,设直线MA、MB的斜率分别为k1、k2,求k1•k2的值.21.(12分)已知函数f(x)=lnx﹣ax.(Ⅰ)若函数f(x)在(1,+∞)上单调递减,求实数a的取值范围;(Ⅱ)当a=1时,函数有两个零点x1,x2,且x1<x2.求证:x1+x2>1.选做题(请考生在22、23、24三题中任选一题作答,如果多做.则按所做的第一题记分.作答时.用2B铅笔在答题卡上把所选题目对应的标号涂黑.)[选修4-1:几何证明选讲]22.(10分)已知四边形ABCD为⊙O的内接四边形,且BC=CD,其对角线AC 与BD相交于点M.过点B作⊙O的切线交DC的延长线于点P.(1)求证:AB•MD=AD•BM;(2)若CP•MD=CB•BM,求证:AB=BC.[选修4-4:坐标系与参数方程]23.在平面直角坐标系中,已知直线l的参数方程为(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ2cos2θ+3ρ2sin2θ=12,点F的极坐标为(2,π),且F在直线l上.(Ⅰ)若直线l与曲线C交于A、B两点,求|FA|•丨FB丨的值;(Ⅱ)求曲线C内接矩形周长的最大值.[选修4-5:不等式选讲]24.已知∃x0∈R使得关于x的不等式|x﹣1|﹣|x﹣2|≥t成立.(Ⅰ)求满足条件的实数t集合T;(Ⅱ)若m>1,n>1,且对于∀t∈T,不等式log3m•log3n≥t恒成立,试求m+n 的最小值.2016年辽宁省大连市高考数学一模试卷(文科)参考答案与试题解析一、选择题(每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.)1.(5分)集合A={x|﹣1<x<3},集合B={x|﹣1<x<2},则A∩B=()A.(1,2) B.(﹣1,2)C.(1,3) D.(﹣1,3)【解答】解:集合A={x|﹣1<x<3}=(﹣1,3),集合B={x|﹣1<x<2}=(﹣1,2),则A∩B=(﹣1,2),故选:B.2.(5分)设复数z1,z2在复平面内对应的点关于虚轴对称,且z1=2+i,则z2=()A.2+i B.﹣2+i C.2﹣i D.﹣2﹣i【解答】解:∵z1=2+i,∴z1在复平面内对应点的坐标为(2,1),由复数z1,z2在复平面内对应的点关于虚轴对称,可知z2在复平面内对应的点的坐标为(﹣2,1),∴z2=﹣2+i,选:B.3.(5分)已知向量=(2,﹣1),=(0,1),则|+2|=()A.2 B.C.2 D.4【解答】解:向量=(2,﹣1),=(0,1),则|+2|=|(2,1)|=.故选:B.4.(5分)已知函数,则=()A.4 B.C.﹣4 D.【解答】解:f()=log5=﹣2,=f(﹣2)=,故选:B.5.(5分)某集团为了解新产品的销售情况,销售部在3月1日至3月5日连续五天对某个大型批发市场中该产品一天的销售量及其价格进行了调査,其中该产品的价格(元)与销售量y(万件)的统计资料如表所示:已知销售量y(万件)与价格x(元)之间具有线性相关关系,其回归直线方程为:=x+40.若该集团将产品定价为10.2元,预测该批发市场的日销售量约为()A.7.66万件B.7.86万件C.8.06万件D.7.36万件【解答】解:==10,=8,∴8=10+40,解得=﹣3.2.∴回归直线方程为=﹣3.2x+40.当x=10.2时,=﹣3.2×10.2+40=7.36.故选D.6.(5分)已知tanα=2,α为第一象限角,则sin2α的值为()A.B.C.D.【解答】解:由tanα=2=,α为第一象限角,sin2α+cos2α=1,∴,,所以,故选:C.7.(5分)如图,在长方体ABCD﹣A1B1C1D1中,点P是棱CD上一点,则三棱锥P﹣A1B1A的左视图可能为()A.B.C.D.【解答】解:在长方体ABCD﹣A1B1C1D1中,三棱锥P﹣A1B1A的左视图中,B1、A1、A的射影分别是C1、D1、D.故选D.8.(5分)将函数f(x)=sin(2x+φ)的图象向右平移个单位后的图象关于y轴对称,则函数f(x)在上的最小值为()A.B.C.D.【解答】解:∵由题,又∵图象关于y轴对称,∴依题,∴结合范围|φ|<,解得.这样,又∵x∈,∴,∴可得:,故选:D.9.(5分)见如图程序框图,若输入a=110011,则输出结果是()A.51 B.49 C.47 D.45【解答】解:第一次执行循环体后,t=1,b=1,i=2,不满足退出循环的条件,第二次执行循环体后,t=1,b=3,i=3,不满足退出循环的条件,第三次执行循环体后,t=0,b=3,i=4,不满足退出循环的条件,第四次执行循环体后,t=0,b=3,i=5,不满足退出循环的条件,第五次执行循环体后,t=1,b=19,i=6,不满足退出循环的条件,第六次执行循环体后,t=1,b=51,i=7,满足退出循环的条件,故输出b值为51,故选:A.10.(5分)已知双曲线C:的右焦点为F,以F为圆心和双曲线的渐近线相切的圆与双曲线的一个交点为M,且MF与双曲线的实轴垂直,则双曲线C的离心率为()A.B.C.D.2【解答】解:设F(c,0),渐近线方程为y=x,可得F到渐近线的距离为=b,即有圆F的半径为b,令x=c,可得y=±b=±,由题意可得=b,即a=b,c==a,即离心率e==,故选C.11.(5分)在△ABC中,a,b,c分别是角A,B,C的对边,且满足acosA=bcosB,那么△ABC的形状一定是()A.等腰三角形B.直角三角形C.等腰或直角三角形D.等腰直角三角形【解答】解:根据正弦定理可知∵bcosB=acosA,∴sinBcosB=sinAcosA∴sin2A=sin2B∴A=B,或2A+2B=180°即A+B=90°,即有△ABC为等腰或直角三角形.故选C.12.(5分)已知函数f(x)是定义在R上的奇函数,且在区间[0,+∞)上是增函数,则不等式<f(1)的解集为()A.(0,)B.(0,e) C.(,e)D.(e,+∞)【解答】解:f(x)为定义在R上的奇函数;∴=f(lnx)+f(lnx)=2f(lnx);∴由得,|f(lnx)|<f(1);∴﹣f(1)<f(lnx)<f(1);即f(﹣1)<f(lnx)<f(1);又f(x)在[0,+∞)上是增函数,∴f(x)在(﹣∞,0]上为增函数;∴f(x)在R上为增函数;∴﹣1<lnx<1;∴;∴原不等式的解集为.故选:C.二、填空题(每小题5分,共20分)13.(5分)若x,y满足约束条件,则z=2x+y的最大值为4.【解答】解:画出满足条件的平面区域,如图示:,显然直线z=2x+y过(2,0)时,z最大,z的最大值是4.14.(5分)在椭圆+=1上有两个动点M、N,K(2,0)为定点,若=0,则的最小值为.【解答】解:M在椭圆+=1上,可设M(6cosα,3sinα)(0≤α<2π),则=•(﹣)=2﹣=2,由K(2,0),可得2=||2=(6cosα﹣2)2+(3sinα)2=27cos2α﹣24cosα+13=27(cosα﹣)2+,当cosα=时,2取得最小值,故答案为:.15.(5分)已知正三棱柱ABC﹣A1B1C1的所有顶点都在半径为1的球面上,当正三棱锥的体积最大时,该正三棱锥的高为.【解答】解:设正三棱柱的底面边长为a,则底面中心O到A的距离为OA==.∴棱柱的高h=2=2.•h===∴正三棱柱的体积V=S△ABC≤1.当且仅当即a=时取等号.此时h=2=2=.故答案为:.16.(5分)设G是一个非空集合,*是定义在G上的一个运算,如果满足下述四个条件(1)对于∀a,b∈G,都有a*b∈G;(2)对于∀a,b,c∈G,都有(a*b)*c=a*(b*c);(3)对于∀a∈G,∃e∈G,使得a*e=e*a=a;(4)对于∀a∈G,∃a′∈G,使得a*a′=a′*a=e则称G关于运算*构成一个群.现给出下列集合和运箅①G是整数集合,*为加法;②G是奇数集合,*为乘法;③G是平面向量集合,*为数量积运算;④G是非零复数集合,*为乘法,其中G关于运算*构成群的序号是①④(将你认为正确的序号都填上).【解答】解:①若G是整数集合,则(i)两个整数相加仍为整数;(ⅱ)整数加法满足结合律;(iii)∃0∈G,∀a ∈G,则)0+a=a+0=a;(iv)∀a∈G,在整数集合中存在唯一一个b=﹣a,使a+(﹣a)=(﹣a)+a=0;故整数集合关于运算*构成一个群;②G是奇数集合,*为乘法,则e=1,不满足(iv);③G是平面向量集合,*为数量积运算,则不满足(i)a*b∈G;④G是非零复数集合,*为乘法,则(i)两个非零复数相乘仍为非零复数;(ⅱ)非零复数相乘符合结合律;(iii)∃1∈G,∀a∈G,则)1×a=a×1=a;(iv)∀a∈G,在G中存在唯一一个,使a×=×a=1.故答案为:①④.三、解答题(本题共5小题,共70分,解答应写出文字说明、证明过程或演算步骤)17.(12分)已知等差数列{a n}的前n项和为S n,且S4=4(a3+1),3a3=5a4,数列{b n}是等比数列,且b1b2=b3,2b1=a5.(Ⅰ)求数列{a n},{b n}的通项公式;(Ⅱ)求数列{|a n|}的前n项和T n.【解答】解:(I)令等差数列{a n}的公差为d,∵S4=4(a3+1),3a3=5a4,∴,解得,则a n=11﹣2n;令数列{b n}的公比为q,∵b1b2=b3,2b1=a5,∴,解得,则;(2)通过(I)知,,于是.18.(12分)某小学为迎接校运动会的到来,在三年级招募了16名男志愿者和14名女志愿者.调查发现,男、女志愿者中分别各有10人和6人喜欢运动,其他人员不喜欢运动.(Ⅰ)根据以上数据完成以下2×2列联表:(Ⅱ)判断性别与喜欢运动是否有关,并说明理由.(Ⅲ)如果喜欢运动的女志愿者中恰有4人懂得医疗救护,现从喜欢运动的女志愿者中抽取2名负责医疗救护工作,求抽出的2名志愿者都懂得医疗救护的概率.附:临界值表(部分):【解答】解:(Ⅰ)由已知得(4分)(Ⅱ)假设:是否喜欢运动与性别无关,由已知数据可求得:χ2=≈1.1575<3.841.(7分)因此,我们认为喜欢运动与性别无关.(8分)(Ⅲ)喜欢运动的女志愿者有6人,设分别为A、B、C、D、E、F,其中A、B、C、D懂得医疗救护,则从这6人中任取2人有AB,AC,AD,AE,AF,BC,BD,BE,BF,CD,CE,CF,DE,DF,EF,共15种取法,其中两人都懂得医疗救护的有AB,AC,AD,BC,BD,CD,共6种.(10分)设“抽出的志愿者中2人都能胜任医疗救护工作”为事件A,则P(A)==.(12分)19.(12分)已知等腰梯形ABCD(如图(1)所示),其中AB∥CD,E,F分別为AB和CD的中点,且AB=EF=2,CD=6,M为BC中点.现将梯形ABCD沿着EF所在直线折起,使平面EFCB⊥平面EFDA(如图(2)所示),N是线段CD上一动点,且CN=ND.(1)求证:MN∥平面EFDA;(2)求三棱锥A﹣MNF的体积.【解答】证明:(1)过点M作MP⊥EF于点P,过点N作NQ⊥FD于点Q,连接PQ由题意,得平面EFCB⊥平面EFDA,又MP⊥EF,∴MP⊥平面EFDA,由EF⊥CF,EF⊥DF,CF∩DF=F,得EF⊥平面CFD,又NQ⊂平面CFD,∴NQ⊥EF,而NQ⊥FD,∴NQ⊥平面EFDA,∴MP∥NQ,又CN=ND,∴,,即MP∥NQ且MP=NQ,∴四边形MNQP为平行四边形.∴MN∥PQ,又∵MN⊄平面EFDA,PQ⊂平面EFDA,∴MN∥平面EFDA;解:(2)延长DA,CB相交于一点H.则H∈CB,H∈DA,又∵CB⊂平面FEBC,DA⊂平面FEAD,∴H∈平面FEBC,H∈平面FEAD,即H∈EF,∴DA,FE,CB交于一点H,∴,又由平面几何知识得:则,于是.20.(12分)已知动点P在抛物线x2=2y上,过点P作x轴的垂线,垂足为H,动点Q满足=.(1)求动点Q的轨迹E的方程;(2)点M(﹣4,4),过点N(4,5)且斜率为k的直线交轨迹E于A、B两点,设直线MA、MB的斜率分别为k1、k2,求k1•k2的值.【解答】解:(1)设点Q(x,y),由,则点P(x,2y),将点P(x,2y)代入x2=2y得x2=4y.∴动点Q的轨迹E的方程为x2=4y.(2)设过点N的直线方程为y=k(x﹣4)+5,A(x1,y1),B(x2,y2).联立,得x2﹣4kx+16x﹣20=0,则.∵,∴=.21.(12分)已知函数f(x)=lnx﹣ax.(Ⅰ)若函数f(x)在(1,+∞)上单调递减,求实数a的取值范围;(Ⅱ)当a=1时,函数有两个零点x1,x2,且x1<x2.求证:x1+x2>1.【解答】解:(I)因为f(x)=lnx﹣ax,则,若函数f(x)=lnx﹣ax在(1,+∞)上单调递减,则1﹣ax≤0在(1,+∞)上恒成立,即当x>1时恒成立,所以a≥1.(5分)(II)证明:根据题意,,因为x1,x2是函数的两个零点,所以,.两式相减,可得,(7分)即,故.那么,.令,其中0<t<1,则.构造函数,(10分)则.因为0<t<1,所以h'(t)>0恒成立,故h(t)<h(1),即.可知,故x1+x2>1.(12分)选做题(请考生在22、23、24三题中任选一题作答,如果多做.则按所做的第一题记分.作答时.用2B铅笔在答题卡上把所选题目对应的标号涂黑.)[选修4-1:几何证明选讲]22.(10分)已知四边形ABCD为⊙O的内接四边形,且BC=CD,其对角线AC 与BD相交于点M.过点B作⊙O的切线交DC的延长线于点P.(1)求证:AB•MD=AD•BM;(2)若CP•MD=CB•BM,求证:AB=BC.【解答】证明:(1)由BC=CD可知,∠BAC=∠DAC,由角分线定理可知,=,即AB•MD=AD•BM得证.﹣﹣﹣﹣﹣﹣﹣(4分)(2)由CP•MD=CB•BM,可知=,又因为BC=CD,所以=所以PB∥AC.所以∠PBC=∠BCA又因为∠PBC=∠BAC所以∠BAC=∠BCA所以AB=BC﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(10分)[选修4-4:坐标系与参数方程]23.在平面直角坐标系中,已知直线l的参数方程为(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ2cos2θ+3ρ2sin2θ=12,点F的极坐标为(2,π),且F在直线l上.(Ⅰ)若直线l与曲线C交于A、B两点,求|FA|•丨FB丨的值;(Ⅱ)求曲线C内接矩形周长的最大值.【解答】解:(I)点F的极坐标为所以直角坐标为∴,∴曲线C的极坐标方程为ρ2cos2θ+3ρ2sin2θ=12,所以直角坐标方程为x2+3y2=12﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(3分)将直线AB的参数方程是(t为参数)代入曲线C直角坐标方程中可得t2﹣2t﹣2=0所以|FA|•|FB|=2﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(6分)(Ⅱ)设椭圆C的内接矩形在第一象限的顶点为,由对称性可得椭圆C的内接矩形的周长为=﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(9分)当时,即时椭圆C的内接矩形的周长取得最大值16.﹣﹣﹣﹣﹣﹣﹣﹣﹣(10分)[选修4-5:不等式选讲]24.已知∃x0∈R使得关于x的不等式|x﹣1|﹣|x﹣2|≥t成立.(Ⅰ)求满足条件的实数t集合T;(Ⅱ)若m>1,n>1,且对于∀t∈T,不等式log3m•log3n≥t恒成立,试求m+n 的最小值.【解答】解:(I)令f(x)=|x﹣1|﹣|x﹣2|≥|x﹣1﹣x+2|=1≥t,∴T=(﹣∞,1];(Ⅱ)由(I)知,对于∀t∈T,不等式•≥t恒成立,只需•≥t max,所以•≥1,又因为m>1,n>1,所以>0,>0,又1≤•≤=(=时取“=”),所以≥4,所以≥2,mn≥9,所以m+n≥2≥6,即m+n的最小值为6(此时m=n=3).。
辽宁省大连市2016届九年级中考模拟考试数学试题解析(解析版)
辽宁省大连市2016届九年级中考模拟考试数学试题一、选择题:本题共8小题,每小题3分,共24分,在每小题给出的四个选项中,只有一个选项是正确1.﹣34的相反数是()A.43B.﹣34C.﹣43D.34【答案】D【解析】试题分析:根据互为相反数的两个数的和为0,求出答案即可.【解答】解:因为34+(﹣34)=0,所以﹣34的相反数是34,故选D.考点:相反数2.据大连市公安局统计,2016年全市约有410000人换二代居民身份证,将410000用科学记数法表示应为()A.0.41×104B.41×104C.4.1×106D.4.1×105【答案】D【解析】试题分析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.将410000用科学记数法表示为:4.1×105.故选:D.考点:科学记数法—表示较大的数3.如图,点A、B、C都在⊙O上,若∠ACB=29°,则∠AOB的度数为()A.14.5°B.29° C.58° D.61°【答案】C【解析】试题分析:由∠ACB=29°,∠ACB与∠AOB是同弧所对的圆周角与圆心角,根据圆周角定理即可得∠AOB=2∠ACB=58°.故选C.考点:圆周角定理4.不等式2x<﹣6的解集为()A.x<﹣3 B.x>﹣3 C.x>3 D.x<3【答案】A【解析】试题分析:利用不等式的基本性质解答不等式2x<﹣6的解集为:x<﹣3.故选A.考点:解一元一次不等式5.在平面直角坐标系中,下列函数的图象经过原点的是()A.y=﹣2x+1 B.y=﹣2x C.y=﹣2xD.y=﹣x2+1【答案】B【解析】试题分析: A、y=-2x+1与坐标轴有两个交点,但是不经过原点,故此选项错误;B、y=-2x,经过原点,故此选项正确;C、y=-2x,图象分布在第二、四象限,故此选项错误;D、y=-x2+1,图象与y轴交于(0,1),不经过原点,故此选项错误.故选:B.考点:1、二次函数的图象;2、一次函数的图象;3、正比例函数的图象6.如图,正方形ABCD的对角线AC、BD相交于点O,OA=3,则此正方形的面积为()A.B.12 C.18 D.36【答案】C考点:正方形的性质7.一个不透明的口袋中有三个完全相同的小球,把它们分别标号为1,2,3,随机摸出一个小球,然后放回,再随机摸出一个小球,两次摸出的小球标号的和为5的概率是()A.16B.29C.13D.12【答案】B【解析】试题分析:根据题意,画树状图如下:共有9种等可能结果,其中两次摸出的小球标号的和为5的有2种,因此两次摸出的小球标号的和为5的概率是29.故选:B.考点:列表法与树状图法8.如图,按照三视图确定该几何体的全面积为(图中尺寸单位:cm)()A.128πcm2B.160πcm2C.176πcm2D.192πcm2【答案】D【解析】试题分析:首先根据几何体的主视图和左视图是相同的矩形,俯视图是圆,可得该几何体为圆柱,且圆柱的高为20cm,底面直径为8cm,因此圆柱的表面积为2×π×42+2π×4×20=32π+160π=192πcm2.故选D.考点:由三视图判断几何体二、填空题:本题共8小题,每小题3分,共24分9.因式分解:x3﹣x= .【答案】x(x+1)(x﹣1)【解析】试题分析:原式提取x,再利用平方差公式分解即可得x3-x=x(x2﹣1)=x(x+1)(x﹣1).考点:提公因式法与公式法的综合运用10.方程3221xx=-的解是.【答案】x=2【解析】试题分析:观察可得最简公分母是(2x﹣1),方程两边乘最简公分母,可以把分式方程转化为整式方程:3x=2(2x﹣1),解得:x=2.检验:把x=2代入(2x﹣1)=3≠0,即x=2是原分式方程的解,故原方程的解为:x=2.考点:解分式方程11.某校男子足球队队员的年龄分布如表所示:则这些队员年龄的中位数是 岁. 【答案】15 【解析】试题分析:先求出总人数2+6+8+3+3=22人,再根据中位数的定义进行解得这些队员年龄的中位数是15152=15. 考点:中位数12.如图,△ABC 中,AB=AC ,将△ABC 绕点A 逆时针旋转60°后得到△ADE ,若AB=1,则CE 的长为 .【答案】1 【解析】试题分析:由旋转的性质得:AC=AE ,∠CAE=60°,由等边三角形的判定得到△ACE 是等边三角形,由等边三角形的性质即可得到CE=AB=1.考点:1、旋转的性质,2、等边三角形的判定和性质13.如图,平行线AB 、CD 被直线EF 所截,过点E 作EG ⊥EF ,与直线CD 相交于点G ,若∠AEF=39°,则∠EGF 的度数为 °.【答案】51 【解析】试题分析:根据垂直的定义得到∠FEG=90°,根据平行线的性质得到∠EFG=∠AEF=39°,根据三角形的内角和即可得到∠EGF=51°.考点: 1、平行线的性质,2、垂直定义14.如图,菱形ABCD的对角线BD与x轴平行,点B、C的坐标分别是(0,1)、(2,0),点A、D在函数y=kx(x>0)的图象上,则k的值为.【答案】4【解析】试题分析:连结AC,如图,根据菱形的性质得AC与BD互相垂直平分,再利用BD∥x轴得到AC⊥x轴,则可写出A点坐标(2,2),然后根据反比例函数图象上点的坐标特征求k =2×2=4.考点:1、反比例函数图象上点的坐标特征;2、菱形的性质15.在平面直角坐标系中,点A、B的坐标分别是(﹣3,1)、(﹣1,﹣2),将线段AB沿某一方向平移后,得到点A的对应点A′的坐标为(﹣1,0),则点B的对应点B′的坐标为.【答案】(1,﹣3)【解析】试题分析:由A(﹣3,1)的对应点A′的坐标为(﹣1,0),根据点A、A′的坐标确定出平移规律:横坐标加2,纵坐标减1,然后根据规律由点B(﹣1,﹣2)的对应点为B′(1,﹣3).考点:坐标与图形变化﹣平移16.某飞机模型的机翼形状如图所示,其中AB∥DC,∠BAE=90°,根据图中的数据计算CD的长为cm (精确到1cm)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)【答案】22 【解析】试题分析:作DM ⊥AB 于M ,在Rt △BCN 中,由三角函数求出BC ≈83.3(cm ),BN ≈66.7(cm ),求出AN=AB+BN=34+37.5=71.5cm ,证出△ADM 是等腰直角三角形,得出AM=DM=50cm ,即可得出CD =MN=AN ﹣AM=71.5﹣50≈22(cm ).考点:1、解直角三角形的应用,2、三角函数,3、等腰直角三角形的判定与性质三、解答题:本题共4小题,17、18、19各9分,20题12分.17.(9分)计算:02()|3|5-+-【答案】 【解析】试题分析:原式利用零指数幂法则,绝对值的代数意义,以及立方根定义计算即可得到结果.试题解析:02()|3|5-+-=1+3 4=考点:1、实数的运算;2、零指数幂18.(9分)先化简,再求值:a(a﹣2)﹣(a+1)(a﹣1),其中a=﹣12.【答案】-2a+1,2【解析】试题分析:原式利用单项式乘以多项式,平方差公式计算,去括号合并得到最简结果,把a的值代入计算即可求出值.试题解析:原式=a2﹣2a﹣a2+1=﹣2a+1,当a=-12时,原式=1+1=2考点:整式的混合运算—化简求值19.(9分)如图,△ABC中,AB=AC,点D在AB上,过点D作BC的平行线,与AC相交于点E,点F在BC 上,EF=EC.求证:四边形DBFE是平行四边形.【答案】证明见解析【解析】试题分析:由等腰三角形的性质证出∠B=∠EFC,得出AB∥EF,由DE∥BC,即可得出四边形DBFE是平行四边形.试题解析:∵AB=AC,∴∠B=∠C,∵EF=EC,∴∠EFC=∠C,∴∠B=∠EFC,∴AB∥EF,又∵DE∥BC,∴四边形DBFE是平行四边形.考点:1、平行四边形的判定,2、等腰三角形的性质,3、平行线的判定20.(12分)某校1200名学生参加了全区组织的“经典诵读”活动,该校随机选取部分学生,对他们在三、四两个月的诵读时间进行调查,下面是根据调查数据制作的统计图表的一部分.根据以上信息,解答下列问题:(1)本次调查的学生数为人;(2)图表中的a、b、c的值分别为,,;(3)在被调查的学生中,四月份日人均诵读时间在1<x≤1.5范围内的人数比三月份在此范围的人数多人;(4)试估计该校学生四月份人均诵读时间在1小时以上的人数.四月日人均诵读时间的统计表三月日人均诵读时间的频数分布直方图【答案】(1)100;(2)6,4,4%;(3)44;(4)768【解析】试题分析:(1)由统计表可以得到本次调查的学生数;(2)由统计图和统计表可以分别求得a、b、c的值;(3)由统计图和统计表可以求得四月份日人均诵读时间在1<x≤1.5范围内的人数比三月份在此范围的人数多多少人;(4)根据统计表可以求得该校学生四月份人均诵读时间在1小时以上的人数.考点:1、频数分布直方图,2、频数分布表,3、用样本估计总体四、解答题:本题共3小题,其中21、22题各9分,23题10分21.(8分)如图用一段长为30m的篱笆,围成一个一边靠墙的矩形花圃,若花圃面积为108m2,墙的长度不限,求矩形花圃的长和宽.【答案】矩形的长为18m,宽为6m或长12m,宽为9米【解析】试题分析:设所围矩形的长为x米,则宽为12(30﹣x)米,根据矩形面积的计算方法列出方程求解.试题解析:设矩形与墙平行的一边长为xm,则另一边长为12(30﹣x)m.根据题意,得12(30﹣x)x=108,解方程,得x=18或x=12(舍去).当x=18时,12(30﹣x)=6.当x=12时,12(30﹣x)=9.答:矩形的长为18m,宽为6m或长12m,宽为9米.考点:一元二次方程的应用22.(8分)如图,直线y=kx+b与双曲线y=3x相交于点A,B,与x轴相交于点C,矩形DEFG的端点D在直线AB上,E,F在x轴上,点G在双曲线上,若DE=32,CE=2,点A的横坐标是1.(1)求点A,G的坐标;(2)求直线AB的解析式.【答案】(1)(2,32)(2)y=34x+94.【解析】试题分析:(1)由矩形的性质结合DE=32,可知点G的纵坐标为32,分别令双曲线y=32中x=1、y=32,即可求出点A、G的坐标;(2)分别令直线y=kx+b中y=0、y=32,求出点C、E的横坐标,结合线段CE=2即可得出关于k的一元一次方程,解方程即可得出k值,将k值和点A的坐标代入到直线y=kx+b中得出关于b的一元一次方程,解方程即可得出结论.试题解析:(1)∵DE=32,且四边形DEFG为矩形,∴GF=DE=32.令双曲线y=3x中x=1,则y=31=3,∴点A的坐标为(1,3);令双曲线y=3x中y=32,则32=3x,解得:x=2,∴点G的坐标为(2,32).(2)令直线y=kx+b中y=32,则32=kx+b,解得:x=32bk-,即点D的坐标为(32bk-,32),点E的坐标为(32bk-,0);令直线y=kx+b中y=0,则0=kx+b,解得:x=﹣bk,即点C的坐标为(﹣bk,0).∵CE=32bk-﹣(﹣bk)=2,∴32=2k,解得:k=34,∴直线AB的解析式为y=34x+b,∵点A(1,3)在直线AB上,∴3=34+b,解得:b=94,∴直线AB的解析式为y=34x+94.考点:反比例函数与一次函数的交点问题23.(10分)如图,⊙O是△ABC的外接圆,AD是⊙O的直径,AD与BC相交于点M,且BM=MC,过点D作BC的平行线,分别与AB、AC的延长线相交于点E、F;(1)求证:EF与⊙O相切;(2)若CE的长.【答案】(1)证明见解析(2【解析】试题分析:(1)根据垂径定理证得AD⊥BC,然后根据平行线的性质证得AD⊥EF,即可证得结论;(2)连接OB,根据勾股定理求得OB和OM,由BC∥EF,证得△ABC∽△AEF,根据相似三角形的性质求得EF的长,解直角三角形ACM求得∠CAM=30°,进而求得CN的长和∠FCN=∠CAM=30°,解直角三角形求得NF,得出EN,然后根据勾股定理即可求得.试题解析:(1)∵AD是⊙O的直径,AD与BC相交于点M,且BM=MC,∴AD⊥BC,∵EF∥BC,∴AD⊥EF,∴EF与⊙O相切;(2)连接OB,在△OBM中,BM2+OM2=OB+(OB=OB2,∴∵BC∥EF,∴△ABC∽△AEF∴AM BC AD EF=,∴EF=AD BCAM⋅==,∵tan∠CAM=MCAM==,∴∠CAM=30°,作CN⊥EF,∵AD⊥EF,∴CN∥AD,∴∠FCN=∠CAM=30°,∵BC∥EF,∴四边形MDNC是矩形,∴∴EN=EF﹣∴考点:1、切线的判定,2、垂径定理的应用,3、平行线的性质,4、三角形相似的判定和性质,5、解直角三角形五、解答题:本题共3小题,其中24题11分,25、26题各12分24.(11分)如图1,两个全等的△ABC和△DEF中,∠ACB=∠DFE=90°,AB=DE,其中点B和点D重合,点F在BC上,将△DEF沿射线BC平移,设平移的距离为x,平移后的图形与△ABC重合部分的面积为y,y 关于x的函数图象如图2所示(其中0≤x≤m,m<x≤3,3<x≤4时,函数的解析式不同)(1)填空:BC的长为;(2)求y关于x的函数关系式,并写出x的取值范围.【答案】(1)4(2)22211(02) 1212(23)3816(34)x x xy x xx x x⎧-++⎪⎪⎪=-+⎨⎪⎪-+⎪⎩≤≤<≤<≤【解析】试题分析:(1)通过图2观察可知y=0时x=4,即D点从B运动到C平移的距离为4;(2)当△DEF在平移过程中,与△ABC的重合部分有三种情况,将三种图形分别画出,通过作辅助线构造相似三角形,通过相似三角形对应边的关系,将各边用x表示出来,即可以列出y与x的函数关系式.试题解析:(1)由图2得当x=4时,y=0,说明此时△DEF与△ABC无重合部分,则点D从B到C运动的距离为4,即BC=4;故答案为:4.(2)当DE经过点A时(如图1),BD=3,CD=1,∵△ABC≌△DEF.∴∠EDF=∠BAC.∵∠ACD=∠BCA∴△ADC∽△BAC.∴AC DC BC AC=,即14ACAC=.AC=2∴n=2当0≤x≤2时(如图2),设ED、EF与AB分别相交于点M,G,作MN⊥BC,垂足为N.则∠MNB=90°=∠EFD=∠C.∵∠MDN=∠EDF.∴△DMN∽△DEF.∴MN DN EF DF=, 即42MN DN =. ∴MN=2DN .设DN=n ,则MN=2n .同理△BMN ∽△BAC . ∴MN BN AC BC=. 即224n BN =, ∴BN=4n ,即x+n=4n .∴n=13x . ∴S △BDM =12•BD•MN=2121233x x x ⋅= 同理△BGF ∽△BAC ∴GF BF AC BC=, 即224GF x +=. ∴GF=1(2)2x +, ∴y=BGF BDM S S ﹣=221111(2)(2)122312x x x x x +⋅+-=-++. 当2<x ≤3时(如图3),由①知,BDM S =13x 2. ∴y=ABC BDM S S ﹣ =22111244233x x ⨯⨯-=-+ 当3<x ≤4时(如图4),设DE与AB相交于点H.同理△DHC∽△DEF.∴HC DC EF DF=,即4 42 HC x-=∴HC=24﹣x.∴y=11(4)2(4)22DC HC x x⋅=-⋅-=x2﹣8x+16∴22211(02)1212(23)3816(34)x x xy x xx x x⎧-++⎪⎪⎪=-+⎨⎪⎪-+⎪⎩≤≤<≤<≤.考点:1、平移的性质,2、相似三角形性质25.(12分)阅读下面材料:小明遇到这样一个问题:如图1,△ABC中,∠A=90°,∠B=30°,点D,E分别在AB,BC上,且∠CDE=90°.当BE=2AD时,图1中是否存在与CD相等的线段?若存在,请找出并加以证明,若不存在,说明理由.小明通过探究发现,过点E作AB的垂线EF,垂足为F,能得到一对全等三角形(如图2),从而将解决问题.请回答:(1)小明发现的与CD相等的线段是.(2)证明小明发现的结论;参考小明思考问题的方法,解决下面的问题:(3)如图3,△ABC中,AB=AC,∠BAC=90°,点D在BC上,BD=2DC,点E在AD上,且∠BEC=135°,求BE CE的值.【答案】(1)DE(2)证明见解析(3【解析】试题分析:(1)直接写出答案;(2)先判断出∠ADC=ADC=∠FEDFED,在判断出FE=AD,即可判断出△FEDFED≌△ADCADC即可;(3)先判断出∠FBE=FBE=∠GECGEC,进而得出△BFEBFE∽△EGC,得出BE BF FECE EG GC==,再判断出FE=2EG,即可得出结论.试题解析:(1)DE;故答案为:DE;(2)证明:作EF⊥AB,垂足为F.则∠BFE=∠DFE=90°═∠A═∠CDE.∵∠ADC+∠CDE=∠ADE=∠DFE+∠FED,∴∠ADC=∠FED.∵∠BFE=90°,∠B=30°,∴BE=2FE.∵BE=2AD,∴FE=AD.在△FED和△ADC中,FED ADCDFE CAD FE AD∠=∠⎧⎪∠=∠⎨⎪=⎩∴△FED≌△ADC.∴DE=CD(3)如图3,过点E作BC的平行线,与AB、AC分别相交于点F、G.∵AB=AC,∠BAC=90°,∴∠ABC=∠ACB=45°.∵FG∥BC,∴∠AFG=∠ABC=∠ACB=∠AGF=45°,∠BFE=135°=∠EGC.∴AF=AG.BF=GC.∵∠GEC+∠CEB=∠GEB=∠EFB+∠FBE,∴∠FBE=∠GEC∴△BFE∽△EGC.∴BE BF FE CE EG GC==,∵FG∥BC,∴△AFE∽△ABD,△AFG∽△ADC,∴FE AEBD AD=,AE EGAD DC=∴FE EG BD DC=∵BD=2DC,∴FE=2EG,∴2BF EG EG BF=,∴BFEG=,∴BE BF CE EG==考点:1、同角的余角相等,2、全等三角形的判定和性质,3、相似三角形的判定和性质26.(12分)在平面直角坐标系xOy中,抛物线y=ax2+bx经过点A(﹣3,4),直线l与x轴相交于点B,与∠AOB的平分线相交于点C,直线l的解析式为y=kx﹣5k(k≠0),BC=OB.(1)若点C在此抛物线上,求抛物线的解析式;(2)在(1)的条件下,过点A 作y 轴的平行线,与直线l 相交于点D ,设P 为抛物线上的一个动点,连接PA 、PD ,当PAD COB 2S S 3=时,求点P 的坐标.【答案】(1)y=23x 2+23x ;(2)(﹣1,0)或(﹣5,403) 【解析】试题分析:(1)如图,先求出B 点坐标,则可得到OA=OB=5,再证明AO ∥CB ,加上OB=BC=5,则可判断四边形AOBC 为平行四边形,所以AC ∥OB ,AC=OB=5,于是得到C (2,4),然后利用待定系数法求抛物线解析式;(2)如图,先确定直线l 的解析式为y=﹣43x+203,再确定D 点坐标,则可求出AD 的长,设P (t ,23t 2+23t ),利用三角形面积公式和PAD COB 2SS 3=得到12•203•|t+3|=23•12•5•4,然后解绝对值方程求出t 的值,从而可确定点P 的坐标.试题解析:(1)如图,A (﹣3,4),∴,当y=0时,kx ﹣5k=0,解得x=5,则B (5,0),∵BC=BO=5,∴∠BOC=∠BCO ,∵OC 平分∠AOB ,∴∠AOC=∠BOC ,∴∠AOC=∠BCO ,∴AO ∥CB ,而OA=BC=5,∴四边形AOBC 为平行四边形,∴AC ∥OB ,AC=OB=5,∴C (2,4),把A (﹣3,4),C (2,4)代入y=ax 2+bx 得934424a b a b -=⎧⎨+=⎩, 解得a=23,b=23, ∴抛物线的解析式为y=23x 2+23x ; (2)如图,把C (2,4)代入y=kx ﹣5k 得2k ﹣5k=4,解得k=﹣43, ∴直线l 的解析式为y=﹣43x+203,当x=﹣2时,y=﹣43x+203=323,则D (﹣3,323),∴AD=323﹣4=203,设P (t ,23t 2+23t ), ∵PAD COB 2S S 3=, ∴12•203•|t+3|=23•12•5•4,解得t=﹣1或t=﹣5,∴点P 的坐标为(﹣1,0)或(﹣5,403).考点:二次函数的综合题。
