高考数学备考常用公式大全

合集下载

高中高考数学公式大全

高中高考数学公式大全1.代数公式- 二次方程根公式：若ax^2+bx+c=0 (a≠0)，则 x=(-b±√(b^2-4ac))/(2a)。

-二次三项全解公式：若知二次三项完全分解为(x-a)(x-b)(x-c)=0，则x=a,b,c。

- 余弦和公式：cos(A±B)=cosAcosB∓sinAsinB。

- 余弦差公式：cos(A-B)=cosAcosB+sinAsinB。

- 正弦和公式：sin(A±B) = sinAcosB±cosAsinB。

- 正弦差公式：sin(A-B) = sinAcosB-cosAsinB。

- 二项式定理：(a+b)^n = C(n,0)a^n b^0+C(n,1)a^(n-1)b+C(n,2)a^n^(n-2)b^2+…+C(n,n)na^0 b^n。

2.几何公式-长方形面积公式：面积=长×宽。

-正方形面积公式：面积=边长×边长。

-圆面积公式：面积=πr^2-平行四边形面积公式：面积=底边×高。

-梯形面积公式：面积=(上底+下底)×高÷2-三角形面积公式：面积=底边×高÷2- 三角形余弦定理：c^2 = a^2 + b^2 - 2abcosC。

- 三角形正弦定理：sinA/a = sinB/b = sinC/c。

- 三角形正弦面积公式：面积 = (1/2)abSinC。

-三角形内切圆半径公式：r=面积/半周长。

3.数列和数列项公式-等差数列通项公式：an = a1 + (n-1)d。

-等差数列前n项和公式：Sn = (n/2)(a1 + an)。

-等差数列等差公式：dn = an+1 - an。

-等差数列求和公式：Sn=(2a1+(n-1)d)n/2-等比数列通项公式：an = a1 * q^(n-1)。

-等比数列前n项和公式：Sn=a1(1-q^n)/(1-q)。

高考数学试卷中要用的公式

一、代数部分：1. 一元一次方程：ax + b = 0，解为 x = -b/a（a ≠ 0）。

2. 一元二次方程：ax^2 + bx + c = 0，解为 x = [-b ± √(b^2 - 4ac)] / 2a。

3. 平方差公式：a^2 - b^2 = (a + b)(a - b)。

4. 完全平方公式：a^2 + 2ab + b^2 = (a + b)^2，a^2 - 2ab + b^2 = (a -b)^2。

5. 立方公式：a^3 + b^3 = (a + b)(a^2 - ab + b^2)，a^3 - b^3 = (a -b)(a^2 + ab + b^2)。

6. 二项式定理：(a + b)^n = C(n, 0)a^n b^0 + C(n, 1)a^(n-1) b^1 + ... + C(n, n-1)a^1 b^(n-1) + C(n, n)a^0 b^n。

7. 多项式除法：将多项式P(x)除以单项式x - a，商为Q(x)，余数为R(x)，满足P(x) = (x - a)Q(x) + R(x)。

8. 指数运算法则：a^m a^n = a^(m+n)，(a^m)^n = a^(mn)，a^m / a^n = a^(m-n)（a ≠ 0，m，n为正整数）。

9. 对数运算法则：log_a(xy) = log_a(x) + log_a(y)，log_a(x/y) = log_a(x) - log_a(y)，log_a(x^n) = n log_a(x)。

二、几何部分：1. 三角形面积公式：S = (1/2) 底高。

2. 圆的周长公式：C = 2πr，圆的面积公式：S = πr^2。

3. 矩形面积公式：S = 长宽。

4. 平行四边形面积公式：S = 底高。

5. 梯形面积公式：S = (上底 + 下底) 高 / 2。

6. 圆锥体积公式：V = (1/3) πr^2h。

7. 球体积公式：V = (4/3) πr^3。

2024年数学高考必备详细公式

在2024年的数学高考中，学生需要记忆和熟练运用的数学公式非常多。

以下是一些数学高考必备的详细公式。

1.代数公式：- 二次方程公式：若ax²+bx+c=0，其中a≠0，那么它的解为x=(-b±√(b²-4ac))/(2a)。

-勾股定理：在直角三角形中，a²+b²=c²，其中a、b为直角边，c为斜边。

-平方差公式：(a+b)(a-b)=a²-b²。

- 一次函数的解析式：y=kx+b，其中k为斜率，b为y轴截距。

-等差数列求和公式：Sn=(n/2)(a₁+an)，其中Sn为前n项和，a₁为首项，an为末项。

-高斯公式：1+2+3+...+n=n(n+1)/2- 二项式定理：(a+b)^n=C(n,0)a^n + C(n,1)a^(n-1)b +C(n,2)a^(n-2)b² + ... + C(n,n-1)ab^(n-1) + C(n,n)b^n，其中C(n,k)表示从n个元素中选择k个元素的组合数。

2.几何公式：-两点间距离公式：设平面上有两点A(x₁,y₁)和B(x₂,y₂)，则AB的距离为√((x₂-x₁)²+(y₂-y₁)²)。

-直线的斜率公式：设直线上有两点A(x₁,y₁)和B(x₂,y₂)，则该直线的斜率为k=(y₂-y₁)/(x₂-x₁)。

-直线方程：(x-x₁)/(x₂-x₁)=(y-y₁)/(y₂-y₁)。

-圆的面积公式：A=πr²，其中A表示圆的面积，r表示半径。

-梯形面积公式：A=(上底+下底)×高/2，其中A表示梯形的面积，上底和下底分别为两个平行边的长度，高为两平行边的距离。

- 三角形的面积公式：设三角形的底边为a，高为h，则三角形的面积A=ah/2-正多边形的内角和公式：内角和=(n-2)×180°，其中n为正多边形的边数。

「高考数学公式定理大全」

「高考数学公式定理大全」1.初等代数- 分式性质：$\frac{a}{b}+\frac{c}{d}=\frac{ad+bc}{bd}$- 因式分解：差平方公式 $a^2 - b^2 = (a+b)(a-b)$，和差平方公式 $a^2+b^2=(a+b)^2-2ab$- 二次根式：$(\sqrt{a}\pm\sqrt{b})^2=a+b\pm 2\sqrt{ab}$，$(\sqrt{a}+\sqrt{b})(\sqrt{a}-\sqrt{b})=a-b$- 二次方程：$ax^2+bx+c=0$，求根公式 $x = \frac{-b\pm\sqrt{b^2-4ac}}{2a}$- 一次不等式：若$a>b$，则$ca>cb$($c>0$)，若反号方向，不等号方向互换即可2.平面向量- 向量表示：$\vec{AB}=(x_2-x_1,y_2-y_1)$- 向量运算：加法 $\vec{a}+\vec{b}=(a_1+b_1,a_2+b_2)$，数乘$k\cdot \vec{a}=(ka_1,ka_2)$- 向量模长：$，\vec{AB}，=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$ - 向量共线：若$\vec{a}=k\cdot \vec{b}$，则$\vec{a}$与$\vec{b}$共线- 向量垂直：若$\vec{a}\cdot \vec{b}=0$，则$\vec{a}$和$\vec{b}$垂直，其中$\vec{a}\cdot \vec{b}=a_1b_1+a_2b_2$3.空间几何- 距离公式：点P(x,y,z)到平面Ax+By+Cz+D=0的距离为 $d=\frac{，Ax+By+Cz+D，}{\sqrt{A^2+B^2+C^2}}$- 点到直线的距离：点P(x0,y0,z0)到直线Ax+By+Cz+D=0的距离为$d=\frac{，Ax_0+By_0+Cz_0+D，}{\sqrt{A^2+B^2+C^2}}$- 两直线关系：平行条件为$\frac{A_1}{A_2}=\frac{B_1}{B_2}=\frac{C_1}{C_2}$，垂直条件为$A_1A_2+B_1B_2+C_1C_2=0$4.三角函数- 基本关系：正弦定理 $\frac{a}{\sin A}=\frac{b}{\sinB}=\frac{c}{\sin C}=2R$，余弦定理 $a^2=b^2+c^2-2bc\cos A$ - 解三角形：已知三边a、b、c或三边两角及夹边等情况下，先确定角的类型，然后利用$S=\frac{1}{2}ab\sin C$公式计算面积，最后利用相关定理计算其他需要的长度或角度。

高考数学公式大全

高考数学公式大全一、代数公式：1.二次方程的求根公式：对于二次方程 $ax^2 + bx + c = 0$，其根可以由以下公式求得：$x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$2.平方差公式：$(a+b)^2 = a^2 + 2ab + b^2$$(a-b)^2 = a^2 - 2ab + b^2$3.一元二次方程求解公式：对于一元二次方程 $ax^2 + bx + c = 0$，其根可以由以下公式求得：$x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$4.一次函数方程的解法：对于一次函数方程 $y = kx + b$，其中 $k$ 为斜率，$b$ 为$y$ 轴截距，可以通过解方程 $kx + b = 0$ 求得直线与 $x$ 轴的交点和方程的解。

5.倍角公式：$\sin{2\theta} = 2\sin{\theta}\cos{\theta}$$\cos{2\theta} = \cos^2{\theta} - \sin^2{\theta} =2\cos^2{\theta} - 1 = 1 - 2\sin^2{\theta}$$\tan{2\theta} = \frac{2\tan{\theta}}{1-\tan^2{\theta}}$$\cot{2\theta} = \frac{\cot^2{\theta}-1}{2\cot{\theta}}$ 6.三角函数关系：$\sin^2{\theta} + \cos^2{\theta} = 1$$\tan{\theta} = \frac{\sin{\theta}}{\cos{\theta}}$$\cot{\theta} = \frac{\cos{\theta}}{\sin{\theta}}$$\sin{(\pi - \theta)} = \sin{\theta}$$\cos{(\pi - \theta)} = -\cos{\theta}$$\tan{(\pi - \theta)} = -\tan{\theta}$二、几何公式：1.圆的周长和面积：圆的半径为$r$，则其周长$C$和面积$A$分别为：$C = 2\pi r$$A = \pi r^2$2.直角三角形的勾股定理：直角三角形的两直角边分别为$a$和$b$，斜边长度为$c$，则满足勾股定理：$a^2+b^2=c^2$3.三角形的面积公式：设三角形的底为$b$，高为$h$，则其面积$S$可以用以下公式计算：$S = \frac{1}{2}bh$4.向量的模长和方向角公式：设二维向量 $\boldsymbol{a} = (x,y)$，其中 $x$ 为横坐标，$y$ 为纵坐标，其模长 $，\boldsymbol{a}，$ 和方向角 $\theta$（与$x$ 轴的夹角）计算公式如下：$，\boldsymbol{a}， = \sqrt{x^2 + y^2}$$\theta = \arctan{\frac{y}{x}}$5.相似三角形的性质：设 $\triangle ABC$ 和 $\triangle A'B'C'$ 是相似三角形，则它们对应边长之间的比例关系为：$\frac{AB}{A'B'} = \frac{BC}{B'C'} = \frac{AC}{A'C'}$6.空间几何平行、垂直关系判定公式：设直线 $l_1$ 和 $l_2$ 在空间中，其方向向量分别为$\boldsymbol{a}$ 和 $\boldsymbol{b}$，则有以下关系：$l_1 \perp l_2 \iff \boldsymbol{a} \cdot \boldsymbol{b} = 0$三、概率统计公式：1.排列公式：$A_n^m = \frac{n!}{(n-m)!}$2.组合公式：$C_n^m = \frac{n!}{m!(n-m)!}$3.二项式定理：$(a+b)^n = C_n^0 a^n b^0 + C_n^1 a^{n-1} b^1 + \cdots +C_n^n a^0 b^n$4.期望值公式：离散型随机变量$X$的期望值可以由以下公式计算：$E(X) = \sum{x \cdot P(X=x)}$连续型随机变量$X$的期望值可以由以下公式计算：$E(X) = \int{xf(x)dx}$其中，$P(X=x)$为离散型随机变量$X$取值为$x$的概率，$f(x)$为连续型随机变量$X$的概率密度函数。

高考数学必背必记公式

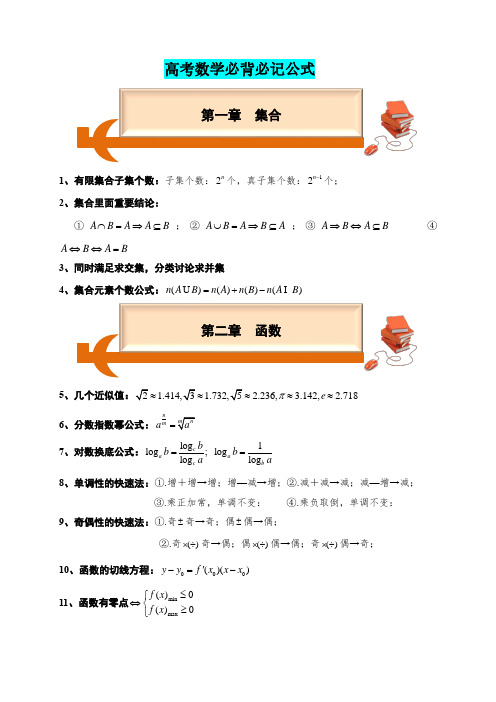
高考数学必背必记公式1、有限集合子集个数：子集个数：2n 个，真子集个数：12n −个；2、集合里面重要结论：①A B A A B ⋂=⇒⊆；②A B A B A ⋃=⇒⊆；③A B A B ⇒⇔⊆ ④A B A B ⇔⇔=3、同时满足求交集，分类讨论求并集4、集合元素个数公式：()()()()n A B n A n B n A B =+−U I5、几个近似值：2 1.414,3 1.732,5 2.236, 3.142, 2.718e π≈≈≈≈≈6、分数指数幂公式：n m n ma a = 7、对数换底公式：log 1log ;log log log c a a c b b b b a a ==8、单调性的快速法：①.增＋增→增；增—减→增；②.减＋减→减；减—增→减；③.乘正加常，单调不变： ④.乘负取倒，单调不变：9、奇偶性的快速法：①.奇±奇→奇；偶±偶→偶；②.奇()⨯÷奇→偶；偶()⨯÷偶→偶；奇()⨯÷偶→奇；10、函数的切线方程：000()()y y f x x x '−=−11、函数有零点min max ()0()0f x f x ≤⎧⇔⎨≥⎩第一章集合第二章函数12、函数无零点max min ()0()0f x f x ⇔≤≥或13、函数周期性：()()f a x f b x +=+的周期Tb a =−； 14、函数对称性：()()f a x f b x +=−的对称轴2a bx +=； 15、抽象函数对数型：若()()()f xy f x f y =+，则()log a f x x =； 16、抽象函数指数型：若()()()f x y f x f y +=，则()x f x a =； 17、抽象函数正比型：若()()()f x y f x f y +=+，则()f x kx =； 18、抽象函数一次型：若()f x c '=，则()f x cx b =+； 19、抽象函数导数型：若()()f x f x '=，则()x f x ke =或()0f x =;20、两个重要不等式：1ln(1)1(0)ln 1x x e x x x e x x x ⎧≥+⇒+≤≤−==⎨≤−⎩当且仅当时“”成立21、洛必达法则：()()()()limlim x ax a f x f x g x g x →→'='(当()0()0f x g x ∞→∞或时使用) 22、恒成立问题：max min(1)()()(2)()()a f x a f x a f x a f x ≥⇔≥<⇔<23、证明()()f x g x >思路：思路1：(1)()()()()0h x f x g x h x =−⇔>（常规首选方法）思路2：min max ()()f x g x >（思路1无法完成）24、等差数列通项公式：1(1)n a a n d =+− 25、等差数列通项公式：11()(1)22n n n a a n n S na d +−==+ 26、等比数列通项公式：11n n a a q −=27、等比数列通项公式：11(1)11n n n a a qa q S q q+−==−−第三章数列28、等差数列的性质：若m n p q +=+，则m n p q a a a a +=+ 29、等比数列的性质：若m n p q +=+，则m n p q a a a a = 30、等差中项：若,,a A b 成等差数列，则2A a b =+ 31、等比中项：若,,a G b 成等比数列，则2G ab = 32、裂项相消法1：若111(1)1n n nn −++=，则有1111n n T n n =−=++ 33、裂项相消法2：若1111(2)22n n n n −++⎛⎫= ⎪⎝⎭，则有1111(1)2212n T n n =+−−++ 34、裂项相消法3：若111111n nnn a a d a a ++=−⎛⎫⎪⎝⎭，则有11111()nn T d a a +=− 35、裂项相消法4：若1111(21)(21)22121n n n n −+−−+⎛⎫= ⎪⎝⎭，则有11(1)221n T n =−+ 36、错位相减法求和通式：1112()1(1)1n n n n dq b b a b q a b T q q q −=+−−−−37、三角函数的定义：正弦：sin y r α=；余弦：cos x r α=；正切：tan yxα=；其中：22r x y =+38、诱导公式：π倍加减名不变，符号只需看象限；半π加减名要变，符号还是看象限。

高考数学必背公式整理

高考数学必背公式整理一、平面几何公式1. 直线的一般方程：Ax + By + C = 02. 两点间的距离公式：AB = √[(x2 - x1)² + (y2 - y1)²]3. 点到直线的距离公式：d = |Ax0 + By0 + C| / √(A² + B²)4. 两直线夹角的余弦公式：cosθ = (A₁A₂ + B₁B₂) / (√(A₁² + B₁²) √(A₂² + B₂²))5. 两直线平行的条件：A₁ / A₂ = B₁ / B₂ ≠ C₁ / C₂6. 两直线垂直的条件：A₁A₂ + B₁B₂ = 07. 两直线交点的坐标：x = (B₁C₂ - B₂C₁) / (A₁B₂ - A₂B₁)，y = (A₂C₁ - A₁C₂) / (A₁B₂ - A₂B₁)二、立体几何公式1. 体积公式：长方体的体积 V = lwh，正方体的体积V = a³，圆柱的体积V = πr²h，圆锥的体积V = (1/3)πr²h，球体的体积 V = (4/3)πr³2. 表面积公式：长方体的表面积 S = 2lw + 2lh + 2wh，正方体的表面积 S = 6a²，圆柱的表面积S = 2πrh + 2πr²，圆锥的表面积S = πrl + πr²，球体的表面积S = 4πr²三、三角函数公式1. 余弦定理：c² = a² + b² - 2abcosC2. 正弦定理：a / sinA = b / sinB = c / sinC3. 三角恒等式：sin²θ + cos²θ = 1，1 + tan²θ = sec²θ，1 + cot²θ = csc²θ四、导数公式1. 基本导数：(xⁿ)' = nxⁿ⁻¹，(sinx)' = cosx，(cosx)' = -sinx，(tanx)' = sec²x，(cotx)' = -csc²x，(lnx)' = 1/x，(ex)' = ex2. 乘法法则：(uv)' = u'v + uv'3. 除法法则：(u/v)' = (u'v - uv') / v²4. 链式法则：(f(g(x)))' = f'(g(x)) * g'(x)五、积分公式1. 基本积分：∫xⁿdx = (xⁿ⁺¹) / (n⁺¹)，∫sinxdx = -cosx，∫cosxdx = sinx，∫sec²xdx = tanx，∫csc²xdx = -cotx，∫1/xdx = ln|x|，∫exdx = ex2. 乘法法则：∫uvdx = ∫u'vdx + ∫uv'dx3. 替换法则：∫f(g(x))g'(x)dx = ∫f(u)du六、概率统计公式1. 排列公式：Aₙₙ = n! / (n - m)!2. 组合公式：Cₙₙ = n! / (m!(n - m)!)3. 二项式定理：(a + b)ⁿ = Cⁿ₀aⁿb⁰ + Cⁿ₁aⁿ⁻¹b¹ + ... + Cⁿₙa⁰bⁿ4. 期望公式：E(X) = Σ(xP(x))5. 方差公式：Var(X) = Σ(x²P(x)) - [E(X)]²以上是高考数学中常用的必背公式。

高考数学必背公式整理

高考数学必背公式整理高考数学必背公式整理高考数学中，公式的掌握是非常重要的，因为它们不仅可以帮助我们快速解题，还可以帮助我们理解和应用数学知识。

下面是一份高考数学必背公式整理，包括代数、几何和概率三个方面的公式。

一、代数公式1. 二项式展开公式：(a+b)^2 = a^2 + 2ab + b^2(a-b)^2 = a^2 - 2ab + b^2(a+b)(a-b) = a^2 - b^22. 平方差公式：a^2 - b^2 = (a+b)(a-b)3. 一次二次因式分解：ax^2 + bx + c = a(x-x1)(x-x2)，其中x1、x2为二次方程的根4. 关于指数和对数的常用公式：log(a*b) = loga + logblog(a/b) = loga - logblog(a^n) = nlogaa^x * a^y = a^(x+y)a^x / a^y = a^(x-y)a^-x = 1/a^xloga a^x = x二、几何公式1. 三角函数相关公式：sin^2θ + cos^2θ = 11 + tan^2θ = sec^2θ1 + cot^2θ = csc^2θ2. 三角函数和角度的关系：sin(-θ) = -sinθcos(-θ) = cosθtan(-θ) = -tanθsin(π/2-θ) = cosθcos(π/2-θ) = sinθtan(π/2-θ) = cotθ3. 直角三角形中的三角函数：sinθ = 对边/斜边cosθ = 邻边/斜边tanθ = 对边/邻边4. 圆相关公式：圆的周长：C = 2πr圆的面积：A = πr^2圆的弧长：L = 2πr * (θ/360°)扇形面积：A = 1/2 r^2 θ三、概率公式1. 基本概率公式：P(A) = n(A)/n(S)，其中P(A)表示事件A发生的概率，n(A)表示事件A的样本空间，n(S)表示样本空间的元素个数2. 条件概率公式：P(A|B) = P(A∩B)/P(B)，其中P(A|B)表示在事件B已经发生的情况下事件A发生的概率，P(A∩B)表示事件A和事件B同时发生的概率，P(B)表示事件B发生的概率3. 乘法公式：P(A∩B) = P(A) * P(B|A)，其中P(A∩B)表示事件A和事件B同时发生的概率，P(A)表示事件A发生的概率，P(B|A)表示在事件A已经发生的情况下事件B发生的概率4. 加法公式：P(A∪B) = P(A) + P(B) - P(A∩B)，其中P(A∪B)表示事件A和事件B至少有一个发生的概率，P(A)表示事件A发生的概率，P(B)表示事件B发生的概率，P(A∩B)表示事件A和事件B同时发生的概率以上是一些高考数学必背公式的整理。

高考必记数学公式汇总

高考必记数学公式汇总1. 一元一次方程：ax + b = 0-解的公式：x=-b/a2. 一元二次方程：ax^2 + bx + c = 0- 解的公式：x = (-b ± √(b^2 - 4ac)) / (2a)3.三角函数：- 正弦定理：a/sinA = b/sinB = c/sinC- 余弦定理：c^2 = a^2 + b^2 - 2abcosC- 正切定理：tanA = a/b4.平面几何：-点到直线的距离：d=，Ax+By+C，/√(A^2+B^2)-平行线的性质：两条直线的斜率相等-垂直线的性质：两条直线的斜率的乘积等于-15.统计与概率：-高斯分布：P(x)=(1/(√(2π)σ))*e^(-((x-μ)^2/(2σ^2))) - 期望值计算：E(x) = ∑(xi * P(xi))- 方差计算：Var(x) = ∑((xi - E(x))^2 * P(xi))6.矩阵：-矩阵乘法：若A是一个mxn的矩阵，B是一个nxp的矩阵，那么它们的乘积C是一个mxp的矩阵，其中C的第i行第j列元素为A的第i行与B的第j列的乘积之和。

7.三角函数补充：- 反正弦函数：sin^(-1)(x)- 反余弦函数：cos^(-1)(x)- 反正切函数：tan^(-1)(x)8.指数与对数函数：-指数函数的性质：a^m*a^n=a^(m+n)- 对数函数的性质：log(a) * log(b) = log(a*b)9.数列与数学归纳法：-等差数列通项公式：an = a1 + (n-1)d-等差数列求和公式：Sn = (n/2)(a1 + an)-等比数列通项公式：an = a1 * r^(n-1)-等比数列求和公式：Sn=a1*(1-r^n)/(1-r)10.导数与微分：- 基本导数公式：(常数)' = 0，(x^n)' = nx^(n-1)，(e^x)' = e^x，(sinx)' = cosx，(cosx)' = -sinx-链式法则：(f(g(x)))'=f'(g(x))*g'(x)11.不等式与绝对值：-绝对值不等式性质：，a*b，=，a，*，b，a+b，≤，a，+，b- 一次不等式：ax + b > 0 (a ≠ 0)- 二次不等式：ax^2 + bx + c > 0 (a ≠ 0)这些是高考中常见的一些数学公式，掌握并熟练运用它们可以帮助你在数学考试中提高得分。

数学高考常用公式

数学高考常用公式1. 一次函数的标准方程：y = kx + b2. 一次函数的斜截式方程：y = mx + n3. 二次函数的标准方程：y = ax^2 + bx + c4. 二次函数的顶点坐标公式：x = -b / (2a), y = c - (b^2 / 4a)5. 二次函数的轴对称线方程：x = -b / (2a)6. 三角函数的和差化简公式：sin(A + B) = sinAcosB + cosAsinB, cos(A + B) = cosAcosB - sinAsinB7. 三角函数的倍角化简公式：sin2A = 2sinAcosA, cos2A = cos^2A - sin^2A = 2cos^2A - 1 = 1 - 2sin^2A8. 三角函数的半角化简公式：sin(A / 2) = ±√[ (1 - cosA) / 2 ], cos(A / 2) = ±√[ (1 + cosA) / 2 ]9. 两角和的正弦公式：sin(A + B) = sinAcosB + cosAsinB10. 两角和的余弦公式：cos(A + B) = cosAcosB - sinAsinB11. 两角差的正弦公式：sin(A - B) = sinAcosB - cosAsinB12. 两角差的余弦公式：cos(A - B) = cosAcosB + sinAsinB13. 正弦定理：a / sinA = b / sinB = c / sinC14. 余弦定理：c^2 = a^2 + b^2 - 2abcosC15. 面积公式：S = 1/2ab sinC16. 等差数列前n项和公式：Sn = (n / 2)(a1 + an)17. 等差数列通项公式：an = a1 + (n - 1)d18. 等比数列前n项和公式：Sn = a1(1 - q^n) / (1 - q)19. 等比数列通项公式：an = a1q^(n - 1)20. 圆的周长公式：C = 2πr21. 圆的面积公式：S = πr^2。

实用高考数学公式大全

实用高考数学公式大全一、函数和方程1. 一次函数表达式：y = kx + b2.一次函数斜率：k=(y2-y1)/(x2-x1)3. 二次函数表达式：y = ax² + bx + c（a ≠ 0）4.二次函数顶点坐标：(x,y)=(-b/2a,-Δ/4a)5.二次函数与x轴交点坐标：x1,2=(-b±√Δ)/2a6. 幂函数表达式：y = ax^m（a ≠ 0, m 是常数）7. 对数函数表达式：y = loga(x)（a > 0, a ≠ 1）8.指数函数表达式：y=a^x（a>0,a≠1）9. 三角函数表达式：sinθ, cosθ, tanθ, cotθ, secθ, cscθ10. 三角函数相关公式：sin²θ + cos²θ = 1，tanθ = sinθ / cosθ，cotθ = 1 / tanθ，secθ = 1 / cosθ，cscθ = 1 / sinθ二、几何与三角1.直角三角形性质：勾股定理：a²+b²=c²，勾股数：a²=b₁²+b₂²2.同位角性质：对内角和为180°，对内角的条件：余角，补角，同旁内角3.等腰三角形性质：底角相等（底边上的两个角度相等）4.等边三角形性质：三个内角均为60°5.相似三角形性质：对应角相等，对应边成比例6.正多边形性质：内角和公式：(n-2)×180°/n（n为边数）7.圆的性质：圆周率π，周长公式：C=2πr，面积公式：S=πr²8.直线与平面的相交性质：同位角相等，对内角相等，对对内角和为180°三、概率与统计1.总体平均数公式（期望值）：E(x)=∑(x*P(x))，其中x是取值，P(x)是取值概率2.组合计数公式：C(n,m)=n!/(m!*(n-m)!)3.排列计数公式：A(n,m)=n!/(n-m)!4.随机事件的概率公式：P(AUB)=P(A)+P(B)-P(A∩B)，P(A')=1-P(A)5.条件概率公式：P(A，B)=P(A∩B)/P(B)，P(B，A)=P(A∩B)/P(A)6.伯努利概型公式：P(A)=C(n,k)*p^k*q^(n-k)，其中n是试验次数，k是成功次数，p是成功概率，q是失败概率以上是一些基础的高考数学公式，希望对你的复习有所帮助。

新高考数学必背公式

一、代数部分平方差公式：公式：a² - b² = (a + b)(a - b)全平方公式：公式：a²± 2ab + b² = (a ± b)²立方和与立方差公式：立方和公式：a³ + b³ = (a + b)(a² - ab + b²)立方差公式：a³ - b³ = (a - b)(a² + ab + b²)因式分解公式：a² - b² = (a + b)(a - b)，a³ + b³ = (a + b)(a² - ab + b²)，等等。

集合运算性质：并集：A∪B=B∪A，A∪A=A，A∪∅=∅∪A=A交集：A∩B=B∩A，A∩A=A，A∩∅=∅∩A=∅德·摩根定律：(A∩B)=(A)∪(B)(A∪B)=(A)∩(B)不等式性质：如果a<b，c<d，那么a+c<b+d如果a<b，c>0，那么ac<bc如果a<b，c<0，那么ac>bc基本不等式：a+b≥2（a,b∈R+），当且仅当a=b时等号成立柯西不等式：二维柯西不等式：(a+b)(c+d)≥(ac+bd)，当且仅当ad=bc时成立伯努利不等式：对于实数x>-1，n≥1时，有(1+x)n≤1+nx成立，当且仅当n=0,1，或x=0时，等号成立。

二、三角函数部分正弦、余弦、正切的定义：sin = 对边/斜边cosθ = 邻边/斜边tanθ = 对边/邻边三角函数的和差公式：sin(α + β) = sinαcosβ + cosαsinβcos(α + β) = cosαcosβ - sinαsinβtan(α + β) = (tanα + tanβ) / (1 - tanαtanβ)三角函数的倍角公式：sin2α = 2sinαcosαcos2α = cos²α - sin²αtan2α = 2tanα / (1 - tan²α)三、几何部分圆的周长和面积公式：周长：C = 2πr面积：S = π*r²三角形的面积公式：S = 1/2 * 底 * 高平行四边形的面积公式：S = 底 * 高四、微积分部分导数的定义：(x) = lim(Δx→0) [f(x + Δx) - f(x)] / Δx 积分的基本公式：∫f(x)dx = f(x) + C（C为常数）。

高考数学公式总结大全

高考数学公式总结大全高考数学公式总结大全高考数学公式在备考中起到了至关重要的作用。

熟练掌握数学公式，能够为我们解题提供方便和效率。

下面是一份高考数学公式总结大全，供广大考生参考使用。

一、代数公式1. 二项式定理：$$(a+b)^n=\sum_{k=0}^{n}C_n^k \cdot a^{n-k} \cdot b^k$$2. 一元二次方程解的公式：$$x = \frac{-b \pm \sqrt{b^2-4ac}}{2a}$$3. 二次根式：$$\sqrt{mn}=\sqrt{m}\sqrt{n}, \;\left(\frac{m}{n}\right)^{\frac{1}{2}}=\frac{\sqrt{m}}{\sqrt{n}} $$4. 分式：$$\frac{a}{b} \cdot \frac{c}{d} = \frac{ac}{bd}, \;\frac{\frac{a}{b}}{\frac{c}{d}} = \frac{ad}{bc}$$5. 指数幂：$$a^m \cdot a^n = a^{m+n}, \; \frac{a^m}{a^n} =a^{m-n}, \; (a^m)^n = a^{mn}$$6. 对数换底公式：$$\log_a{x}=\frac{\log_b{x}}{\log_b{a}}$$7. 三角函数：$$\sin{2x} = 2\sin{x}\cos{x}, \; \cos{2x} =\cos^2{x}-\sin^2{x}, \; \tan{x} = \frac{\sin{x}}{\cos{x}}$$8. 三角三倍角公式：$$\sin{3x} = 3\sin{x}-4\sin^3{x}, \; \cos{3x} = 4\cos^3{x}-3\cos{x}, \; \tan{3x} = \frac{3\tan{x}-\tan^3{x}}{1-3\tan^2{x}}$$9. 三角和差公式：$$\sin{(a \pm b)} = \sin{a}\cos{b} \pm\cos{a}\sin{b}, \; \cos{(a \pm b)} = \cos{a}\cos{b} \mp\sin{a}\sin{b}$$10. 对数运算：$$\log_a{(mn)} = \log_a{m}+\log_a{n}, \;\log_a{\left(\frac{m}{n}\right)} = \log_a{m}-\log_a{n}$$二、几何公式1. 三角形面积公式：$$S = \frac{1}{2}bh, \; S =\frac{1}{2}ab\sin{C}, \; S = \sqrt{s(s-a)(s-b)(s-c)}$$2. 三角形周长公式：$$C = a+b+c$$3. 三角形中位线定理：三条中线交于同一点，且该点距离三个顶点的距离分别为各边长度的一半。

高考必考数学重点公式

高考必考数学重点公式高中数学基本公式大全有了此书,高分无忧一、基本公式必考公式1、抛物线：y = ax + bx + c1就是y等于ax 的平方加上 bx再加上 c2a > 0时开口向上 ,a < 0时开口向下 ,c = 0时抛物线经过原点 ,b = 0时抛物线对称轴为y轴;3还有顶点式y = ax+h + k4就是y等于a乘以x+h的平方+k5-h是顶点坐标的x ,k是顶点坐标的y6一般用于求最大值与最小值7抛物线标准方程:y^2=2px ,它表示抛物线的焦点在x的正半轴上,焦点坐标为p/2,0 准线方程为x=-p/29由于抛物线的焦点可在任意半轴,故共有标准方程y^2=2px y^2=-2px x^2=2py x^2=-2py2、圆：体积=4/3pir^31 面积=pir^22周长=2pir3圆的标准方程 x-a2+y-b2=r2 注：a,b是圆心坐标4圆的一般方程 x2+y2+Dx+Ey+F=0 注：D2+E2-4F>03、椭圆周长计算公式1椭圆周长公式：L=2πb+4a-b2椭圆周长定理：椭圆的周长等于该椭圆短半轴长为半径的圆周长2πb加上四倍的该椭圆长半轴长a与短半轴长b的差;3椭圆面积计算公式：椭圆面积公式： S=πab椭圆面积定理：椭圆的面积等于圆周率π乘该椭圆长半轴长a与短半轴长b的乘积;以上椭圆周长、面积公式中虽然没有出现椭圆周率T,但这两个公式都是通过椭圆周率T推导演变而来;常数为体,公式为用;椭圆形物体体积计算公式椭圆的长半径短半径PAI高4、三角函数：1两角和公式sinA+B=sinAcosB+cosAsinB sinA-B=sinAcosB-sinBcosAcosA+B=cosAcosB-sinAsinB cosA-B=cosAcosB+sinAsinBtanA+B=tanA+tanB/1-tanAtanB tanA-B=tanA-tanB/1+tanAtanBcotA+B=cotAcotB-1/cotB+cotA cotA-B=cotAcotB+1/cotB-cotA2倍角公式tan2A=2tanA/1-tan2A cot2A=cot2A-1/2cotacos2a=cos2a-sin2a=2cos2a-1=1-2sin2asinα+sinα+2π/n+sinα+2π2/n+sinα+2π3/n+……+sinα+2πn-1/n=0 cosα+cosα+2π/n+cosα+2π2/n+cosα+2π3/n+……+cosα+2πn-1/n=0 以及sin^2α+sin^2α-2π/3+sin^2α+2π/3=3/2tanAtanBtanA+B+tanA+tanB-tanA+B=03半角公式sinA/2=√1-cosA/2 sinA/2=-√1-cosA/2cosA/2=√1+cosA/2 cosA/2=-√1+cosA/2tanA/2=√1-cosA/1+cosA tanA/2=-√1-cosA/1+cosAcotA/2=√1+cosA/1-cosA cotA/2=-√1+cosA/1-cosA4和差化积2sinAcosB=sinA+B+sinA-B 2cosAsinB=sinA+B-sinA-B2cosAcosB=cosA+B-sinA-B -2sinAsinB=cosA+B-cosA-BsinA+sinB=2sinA+B/2cosA-B/2 cosA+cosB=2cosA+B/2sinA-B/2tanA+tanB=sinA+B/cosAcosB tanA-tanB=sinA-B/cosAcosBcotA+cotBsinA+B/sinAsinB -cotA+cotBsinA+B/sinAsinB5某些数列前n项和1+2+3+4+5+6+7+8+9+…+n=nn+1/2 1+3+5+7+9+11+13+15+…+2n-1=n22+4+6+8+10+12+14+…+2n=nn+11^2+2^2+3^2+4^2+5^2+6^2+7^2+8^2+…+n^2=nn+12n+1/61^3+2^3+3^3+4^3+5^3+6^3+…n^3=nn+1/2^212+23+34+45+56+67+…+nn+1=nn+1n+2/36正弦定理 a/sinA=b/sinB=c/sinC=2R 注：其中 R 表示三角形的外接圆半径7余弦定理 b2=a2+c2-2accosB 注：角B是边a和边c的夹角8乘法与因式分 a2-b2=a+ba-b a3+b3=a+ba2-ab+b2 a3-b3=a-ba2+ab+b29三角不等式 |a+b|≤|a|+|b| |a-b|≤|a|+|b| |a|≤b<=>-b≤a≤b|a-b|≥|a|-|b| -|a|≤a≤|a|5、一元二次方程1一元二次方程的解-b+√b2-4ac/2a -b-√b2-4ac/2a2根与系数的关系 x1+x2=-b/a x1x2=c/a 注：韦达定理3判别式 b2-4a=0 注：方程有相等的两实根 , b2-4ac>0 注：方程有两个不相等的个实根 ,b2-4ac<0 注：方程有共轭复数根二、公式表达式1、圆的标准方程 x-a2+y-b2=r2 注：a,b是圆心坐标2、圆的一般方程 x2+y2+Dx+Ey+F=0 注：D2+E2-4F>03、抛物线标准方程 y2=2px y2=-2px x2=2py x2=-2py4、直棱柱侧面积 S=ch 斜棱柱侧面积 S=c'h5、正棱锥侧面积 S=1/2ch' 正棱台侧面积 S=1/2c+c'h'6、圆台侧面积 S=1/2c+c'l=piR+rl 球的表面积 S=4pir27、圆柱侧面积 S=ch=2pih 圆锥侧面积 S=1/2cl=pirl8、弧长公式 l=ar a是圆心角的弧度数r >0 扇形面积公式 s=1/2lr9、锥体体积公式 V=1/3SH 圆锥体体积公式 V=1/3pir2h10、斜棱柱体积 V=S'L 注：其中,S'是直截面面积, L是侧棱长11、柱体体积公式 V=sh 圆柱体 V=pir2h12、图形周长面积体积公式13、长方形的周长=长+宽×214、正方形的周长=边长×415、长方形的面积=长×宽16、正方形的面积=边长×边长17、三角形的面积已知三角形底a,高h,则S＝ah/2已知三角形三边a,b,c,半周长p,则S＝√pp - ap - bp - c 海伦公式p=a+b+c/2 和：a+b+ca+b-c1/4已知三角形两边a,b,这两边夹角C,则S＝absinC/2设三角形三边分别为a、b、c,内切圆半径为r则三角形面积=a+b+cr/2设三角形三边分别为a、b、c,外接圆半径为r则三角形面积=abc/4r已知三角形三边a、b、c,则S＝√{1/4c^2a^2-c^2+a^2-b^2/2^2} “三斜求积”南宋秦九韶18、 | a b 1 |S△=1/2 | c d 1 || e f 1 || a b 1 || c d 1 | 为三阶行列式,此三角形ABC在平面直角坐标系内Aa,b,Bc,d, Ce,f,这里ABC| e f 1 |选区取最好按逆时针顺序从右上角开始取,因为这样取得出的结果一般都为正值,如果不按这个规则取,可能会得到负值,但不要紧,只要取绝对值就可以了,不会影响三角形面积的大小19、秦九韶三角形中线面积公式:S=√Ma+Mb+McMb+Mc-MaMc+Ma-MbMa+Mb-Mc/3 其中Ma,Mb,Mc为三角形的中线长.20、平行四边形的面积=底×高21、梯形的面积=上底+下底×高÷222、直径=半径×2 半径=直径÷223、圆的周长=圆周率×直径=24、圆周率×半径×225、圆的面积=圆周率×半径×半径26、长方体的表面积=长×宽+长×高＋宽×高×227、长方体的体积 =长×宽×高28、正方体的表面积=棱长×棱长×629、正方体的体积=棱长×棱长×棱长30、圆柱的侧面积=底面圆的周长×高31、圆柱的表面积=上下底面面积+侧面积32、圆柱的体积=底面积×高33、圆锥的体积=底面积×高÷334、长方体正方体、圆柱体的体积=底面积×高三、平面图形名称符号周长C和面积S正方形 a—边长 C＝4aS＝a2长方形 a和b－边长 C＝2a+bS＝ab三角形 a,b,c－三边长h－a边上的高s－周长的一半A,B,C－内角其中s＝a+b+c/2 S＝ah/2＝ab/2sinC＝ss-as-bs-c1/2＝a2sinBsinC/2sinA1 过两点有且只有一条直线2 两点之间线段最短3 同角或等角的补角相等4 同角或等角的余角相等5 过一点有且只有一条直线和已知直线垂直6 直线外一点与直线上各点连接的所有线段中,垂线段最短7 平行公理经过直线外一点,有且只有一条直线与这条直线平行8 如果两条直线都和第三条直线平行,这两条直线也互相平行9 同位角相等,两直线平行10 内错角相等,两直线平行11 同旁内角互补,两直线平行12两直线平行,同位角相等13 两直线平行,内错角相等14 两直线平行,同旁内角互补15 定理三角形两边的和大于第三边16 推论三角形两边的差小于第三边17 三角形内角和定理三角形三个内角的和等于180°18 推论1 直角三角形的两个锐角互余19 推论2 三角形的一个外角等于和它不相邻的两个内角的和20 推论3 三角形的一个外角大于任何一个和它不相邻的内角21 全等三角形的对应边、对应角相等22边角边公理sas 有两边和它们的夹角对应相等的两个三角形全等23 角边角公理 asa有两角和它们的夹边对应相等的两个三角形全等24 推论aas 有两角和其中一角的对边对应相等的两个三角形全等25 边边边公理sss 有三边对应相等的两个三角形全等26 斜边、直角边公理hl 有斜边和一条直角边对应相等的两个直角三角形全等27 定理1 在角的平分线上的点到这个角的两边的距离相等28 定理2 到一个角的两边的距离相同的点,在这个角的平分线上29 角的平分线是到角的两边距离相等的所有点的集合30 等腰三角形的性质定理等腰三角形的两个底角相等即等边对等角31 推论1 等腰三角形顶角的平分线平分底边并且垂直于底边32 等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合33 推论3 等边三角形的各角都相等,并且每一个角都等于60°34 等腰三角形的判定定理如果一个三角形有两个角相等,那么这两个角所对的边也相等等角对等边35 推论1 三个角都相等的三角形是等边三角形36 推论 2 有一个角等于60°的等腰三角形是等边三角形37 在直角三角形中,如果一个锐角等于30°那么它所对的直角边等于斜边的一半38 直角三角形斜边上的中线等于斜边上的一半39 定理线段垂直平分线上的点和这条线段两个端点的距离相等40 逆定理和一条线段两个端点距离相等的点,在这条线段的垂直平分线上41 线段的垂直平分线可看作和线段两端点距离相等的所有点的集合42 定理1 关于某条直线对称的两个图形是全等形43 定理 2 如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线 44定理3 两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上45逆定理如果两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称46勾股定理直角三角形两直角边a、b的平方和、等于斜边c的平方,即a^2+b^2=c^247勾股定理的逆定理如果三角形的三边长a、b、c有关系a^2+b^2=c^2 ,那么这个三角形是直角三角形48定理四边形的内角和等于360°49四边形的外角和等于360°50多边形内角和定理 n边形的内角的和等于n-2×180°51推论任意多边的外角和等于360°52平行四边形性质定理1 平行四边形的对角相等53平行四边形性质定理2 平行四边形的对边相等54推论夹在两条平行线间的平行线段相等55平行四边形性质定理3 平行四边形的对角线互相平分56平行四边形判定定理1 两组对角分别相等的四边形是平行四边形57平行四边形判定定理2 两组对边分别相等的四边形是平行四边形58平行四边形判定定理3 对角线互相平分的四边形是平行四边形59平行四边形判定定理4 一组对边平行相等的四边形是平行四边形60矩形性质定理1 矩形的四个角都是直角61矩形性质定理2 矩形的对角线相等62矩形判定定理1 有三个角是直角的四边形是矩形63矩形判定定理2 对角线相等的平行四边形是矩形64菱形性质定理1 菱形的四条边都相等65菱形性质定理2 菱形的对角线互相垂直,并且每一条对角线平分一组对角66菱形面积=对角线乘积的一半,即s=a×b÷267菱形判定定理1 四边都相等的四边形是菱形68菱形判定定理2 对角线互相垂直的平行四边形是菱形69正方形性质定理1 正方形的四个角都是直角,四条边都相等70正方形性质定理2正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角71定理1 关于中心对称的两个图形是全等的72定理2 关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分73逆定理如果两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点对称74等腰梯形性质定理等腰梯形在同一底上的两个角相等75等腰梯形的两条对角线相等76等腰梯形判定定理在同一底上的两个角相等的梯形是等腰梯形77对角线相等的梯形是等腰梯形78平行线等分线段定理如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等79 推论1 经过梯形一腰的中点与底平行的直线,必平分另一腰80 推论2 经过三角形一边的中点与另一边平行的直线,必平分第三边81 三角形中位线定理三角形的中位线平行于第三边,并且等于它的一半82 梯形中位线定理梯形的中位线平行于两底,并且等于两底和的一半 l=a+b ÷2 s=l×h83 1比例的基本性质如果a:b=c:d,那么ad=bc 如果ad=bc,那么a:b=c:d84 2合比性质如果a／b=c／d,那么a±b／b=c±d／d85 3等比性质如果a／b=c／d=…=m／nb+d+…+n≠0,那么 a+c+…+m／b+d+…+n=a／b86 平行线分线段成比例定理三条平行线截两条直线,所得的对应线段成比例87 推论平行于三角形一边的直线截其他两边或两边的延长线,所得的对应线段成比例88 定理如果一条直线截三角形的两边或两边的延长线所得的对应线段成比例,那么这条直线平行于三角形的第三边89 平行于三角形的一边,并且和其他两边相交的直线,所截得的三角形的三边与原三角形三边对应成比例90 定理平行于三角形一边的直线和其他两边或两边的延长线相交,所构成的三角形与原三角形相似91 相似三角形判定定理1 两角对应相等,两三角形相似asa92 直角三角形被斜边上的高分成的两个直角三角形和原三角形相似93 判定定理2 两边对应成比例且夹角相等,两三角形相似sas94 判定定理3 三边对应成比例,两三角形相似sss95 定理如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似96 性质定理1 相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比97 性质定理2 相似三角形周长的比等于相似比98 性质定理3 相似三角形面积的比等于相似比的平方99 任意锐角的正弦值等于它的余角的余弦值,任意锐角的余弦值等于它的余角的正弦值100任意锐角的正切值等于它的余角的余切值,任意锐角的余切值等于它的余角的正切值101圆是定点的距离等于定长的点的集合102圆的内部可以看作是圆心的距离小于半径的点的集合103圆的外部可以看作是圆心的距离大于半径的点的集合104同圆或等圆的半径相等105到定点的距离等于定长的点的轨迹,是以定点为圆心,定长为半径的圆106和已知线段两个端点的距离相等的点的轨迹,是着条线段的垂直平分线107到已知角的两边距离相等的点的轨迹,是这个角的平分线108到两条平行线距离相等的点的轨迹,是和这两条平行线平行且距离相等的一条直线109定理不在同一直线上的三点确定一个圆;110垂径定理垂直于弦的直径平分这条弦并且平分弦所对的两条弧111推论1 ①平分弦不是直径的直径垂直于弦,并且平分弦所对的两条弧②弦的垂直平分线经过圆心,并且平分弦所对的两条弧③平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧112推论2 圆的两条平行弦所夹的弧相等113圆是以圆心为对称中心的中心对称图形114定理在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等115推论在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两弦的弦心距中有一组量相等那么它们所对应的其余各组量都相等116定理一条弧所对的圆周角等于它所对的圆心角的一半117推论1 同弧或等弧所对的圆周角相等；同圆或等圆中,相等的圆周角所对的弧也相等118推论2 半圆或直径所对的圆周角是直角；90°的圆周角所对的弦是直径 119推论3 如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形120定理圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角121①直线l和⊙o相交 d＜r②直线l和⊙o相切 d=r③直线l和⊙o相离 d＞r122切线的判定定理经过半径的外端并且垂直于这条半径的直线是圆的切线 123切线的性质定理圆的切线垂直于经过切点的半径124推论1 经过圆心且垂直于切线的直线必经过切点125推论2 经过切点且垂直于切线的直线必经过圆心126切线长定理从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角127圆的外切四边形的两组对边的和相等128弦切角定理弦切角等于它所夹的弧对的圆周角129推论如果两个弦切角所夹的弧相等,那么这两个弦切角也相等130相交弦定理圆内的两条相交弦,被交点分成的两条线段长的积相等131推论如果弦与直径垂直相交,那么弦的一半是它分直径所成的两条线段的比例中项132切割线定理从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项133推论从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等134如果两个圆相切,那么切点一定在连心线上135①两圆外离 d＞r+r ②两圆外切 d=r+r③两圆相交 r-r＜d＜r+rr＞r④两圆内切 d=r-rr＞r ⑤两圆内含d＜r-rr＞r136定理相交两圆的连心线垂直平分两圆的公共弦137定理把圆分成nn≥3:⑴依次连结各分点所得的多边形是这个圆的内接正n边形⑵经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形138定理任何正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆139正n边形的每个内角都等于n-2×180°／n140定理正n边形的半径和边心距把正n边形分成2n个全等的直角三角形141正n边形的面积sn=pnrn／2 p表示正n边形的周长142正三角形面积√3a／4 a表示边长143如果在一个顶点周围有k个正n边形的角,由于这些角的和应为360°,因此k×n-2180°／n=360°化为n-2k-2=4144弧长计算公式：l=nπr／180145扇形面积公式：s扇形=nπr2／360=lr／2146内公切线长= d-r-r 外公切线长= d-r+r147等腰三角形的两个底脚相等148等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合 149如果一个三角形的两个角相等,那么这两个角所对的边也相等150三条边都相等的三角形叫做等边三角形。

高考必备数学公式大全

高考必备数学公式大全一、集合。

1. 集合的基本运算。

- 交集：A∩ B={xx∈ A且x∈ B}- 并集：A∪ B ={xx∈ A或x∈ B}- 补集：∁_UA={xx∈ U且x∉ A}（U为全集）2. 集合元素个数公式。

- n(A∪ B)=n(A)+n(B)-n(A∩ B)二、函数。

1. 函数的定义域。

- 分式函数y = (f(x))/(g(x))，定义域为g(x)≠0的x的取值范围。

- 偶次根式函数y=sqrt[n]{f(x)}（n为偶数），定义域为f(x)≥slant0的x的取值范围。

2. 函数的单调性。

- 设x_1,x_2∈[a,b]且x_1，对于函数y = f(x)- 若f(x_1)，则y = f(x)在[a,b]上是增函数，f^′(x)≥slant0（可导函数时）。

- 若f(x_1)>f(x_2)，则y = f(x)在[a,b]上是减函数，f^′(x)≤slant0（可导函数时）。

3. 函数的奇偶性。

- 对于函数y = f(x)，定义域关于原点对称。

- 若f(-x)=f(x)，则y = f(x)是偶函数，其图象关于y轴对称。

- 若f(-x)= - f(x)，则y = f(x)是奇函数，其图象关于原点对称。

4. 一次函数y=kx + b（k≠0）- 斜率k=frac{y_2-y_1}{x_2-x_1}，截距为b。

5. 二次函数y = ax^2+bx + c(a≠0)- 对称轴x =-(b)/(2a)。

- 顶点坐标(-(b)/(2a),frac{4ac - b^2}{4a})。

- 当a>0时，函数开口向上，在x =-(b)/(2a)处取得最小值frac{4ac -b^2}{4a}；当a<0时，函数开口向下，在x =-(b)/(2a)处取得最大值frac{4ac -b^2}{4a}。

6. 指数函数y = a^x(a>0,a≠1)- 性质：当a > 1时，函数在R上单调递增；当0 < a < 1时，函数在R上单调递减。

高考数学公式大全

高考数学公式大全高考数学公式大全包括以下内容：一、几何几率：1. 几何比：S：边长或半径；C：周长或圆周长；A：面积或圆面积；P：面积比。

S:C = A:P； C/A = S/P2. 三角函数公式：sin A = a/ c；cos A = b/c；tan A =a/b；倍角公式：sin 2A = 2 sin A cos A；cos 2A =cos²A -sin ²A；tan 2A=2 tan A/(1-tan²A)二、微积分公式：1. 二次函数的对称性：y=ax²+bx+c的图象关于直线 y= ( -b/2a ) 的对称，即(-b/2a, 0)为图象的中心；2. 微分：基本微分公式：d(f+g)/dx = df/dx + dg/dx ; d(fg)/dx = fdg/dx + gdf/dx ;d(f-g)/dx = df/dx - dg/dx ;3. 极限：极限的定义：当x变化无限接近于某个值a时，当x=a时，函数y=f(x)的值可以通过极限符号来表示：limx→af(x) = L。

4. 微积分法则：幂级数法则：∫xn·dx=（xn+1）/ (n+1) + C ；指数函数法则：∫eax·dx=eax/ a + C；三、统计数学：1. 众数：一个数据集中出现次数最多的数据值；2. 概率：事件A发生的可能性/所有可能发生的事件可能性之和；3. 正态分布：用来估计一组数据的分布情况，常用的正态分布公式为：f(x)= (1/sqrt(2π)) e^[-0.5(x-μ)²/σ²] ;4. 方差：用来衡量样本数据的离散程度，表示各个样本数据和平均数之间的平均距离，可以用方差公式表示：σ² = ∑[(xi-μ)²/ n]，其中xi为样本数据，μ为样本平均数，n为样本个数。

高考数学必背公式整理(衡水中学高中数学组)

高考数学必背公式整理一、平面几何公式1. 直线方程- 一般式：Ax + By + C = 0- 斜截式：y = kx + b- 截距式：x/a + y/b = 1- 两点式：(y-y₁)/(x-x₁) = (y₂-y₁)/(x₂-x₁)2. 圆的方程- 标准方程：(x-a)² + (y-b)² = r²- 一般方程：x² + y² + Dx + Ey + F = 0 - 中心半径方程：(x-h)² + (y-k)² = r²3. 直角三角形- 勾股定理：a² + b² = c²- 正弦定理：a/sinA = b/sinB = c/sinC - 余弦定理：c² = a² + b² - 2abcosC- 正切定理：tanA = b/a4. 圆锥曲线- 椭圆：x²/a² + y²/b² = 1- 双曲线：x²/a² - y²/b² = 1- 抛物线：y² = 2px二、空间几何公式1. 空间中的直线- 参数方程：x = x₁ + at, y = y₁ + bt, z = z₁ + ct - 对称式：(x-x₁)/l = (y-y₁)/m = (z-z₁)/n2. 空间中的平面- 一般方程：Ax + By + Cz + D = 0- 点法式：A(x-x₁) + B(y-y₁) + C(z-z₁) = 0- 三点式：[ABCD] = 03. 空间中的球面- 标准方程：(x-a)² + (y-b)² + (z-c)² = r²- 一般方程：x² + y² + z² + Dx + Ey + Fz + G = 0 - 中心半径方程：(x-h)² + (y-k)² + (z-l)² = r²4. 空间向量- 点积：a·b = |a| |b| cosθ- 叉积：a×b = |a| |b| sinθn- 混合积：[a,b,c] = a·(b×c)三、解析几何公式1. 直线和平面- 平面方程：Ax + By + Cz + D = 0- 直线方程：(x-x₁)/l = (y-y₁)/m = (z-z₁)/n- 点到直线距离：d = |Ax₀ + By₀ + Cz₀ + D|/√(A² + B² + C²) - 点到平面距离：d = |Ax₀ + By₀ + Cz₀ + D|/√(A² + B² + C²)2. 点、向量和运算- 点积：a·b = |a| |b| cosθ- 叉积：a×b = |a| |b| sinθn3. 曲线和曲面- 曲线斜率：y‘ = f'(x) = dy/dx- 曲面切面：z = f(x, y)- 曲线弧长：L = ∫√(1 + (dy/dx)²)dx四、数列与级数公式1. 数列- 等差数列通项公式：aₙ = a₁ + (n-1)d- 等比数列通项公式：aₙ = a₁qⁿ⁻¹- 通项公式求和：Sₙ = (a₁+aₙ)n/22. 级数- 等差级数求和：Sₙ = n(a₁+aₙ)/2- 等比级数求和：Sₙ = a₁(1-qⁿ)/(1-q)3. 数学归纳法- 数学归纳法证明- 数学归纳法应用五、概率统计公式1. 概率- 事件概率：P(A) = n(A)/n(Ω)- 加法公式：P(A∪B) = P(A) + P(B) - 条件概率：P(A|B) = P(A∩B)/P(B)2. 统计- 样本均值：μ = Σxᵢ/n- 样本方差：σ²= Σ(xᵢ-μ)²/n- 标准差：σ = √σ²3. 随机变量- 期望：E(X) = ΣxᵢP(X=xᵢ)- 方差：Var(X) = E(X²) - [E(X)]²- 协方差：Cov(X,Y) = E((X-E(X))(Y-E(Y)))六、函数与导数公式1. 基本函数- 幂函数：f(x) = xⁿ- 指数函数：f(x) = aⁿ- 对数函数：f(x) = logₐx- 三角函数：f(x) = sinx, cosx, tanx2. 函数性质- 奇函数和偶函数- 单调性和极值- 函数图像和性态3. 导数与微分- 导数定义：f'(x) = lim(h→0)(f(x+h)-f(x))/h - 函数求导：(xⁿ)’ = nxⁿ⁻¹- 链式法则：(f(g(x)))’ = f’(g(x))·g’(x)- 微分运算：dy = f’(x)dx七、积分公式1. 不定积分- 基本积分公式 - 定积分计算 - 变限积分求导2. 定积分- 定积分性质 - 定积分应用 - 变限积分求导3. 微分方程- 微分方程定解 - 微分方程解法 - 微分方程应用八、高等代数公式1. 行列式- 二阶行列式 - 三阶行列式 - 克拉默法则2. 矩阵运算- 矩阵相加- 矩阵相乘- 矩阵转置3. 线性方程组- 高斯消元法- 矩阵法解方程组- 克拉默法则以上是高考数学必背公式的整理，希望同学们能够认真学习并灵活运用这些公式，提高数学应用能力，取得优异的成绩。

高考数学公式总结大全

高考数学公式总结大全数学在高考中占据着非常重要的地位，而数学公式更是考试中必不可少的部分。

掌握好数学公式，对于高考取得好成绩至关重要。

因此，我将在这里为大家总结一些高考数学中常用的公式，希望能够帮助大家更好地备战高考。

一、代数部分。

1. 二次函数的顶点坐标公式：对于二次函数y=ax^2+bx+c，其顶点坐标为，(-b/2a, -Δ/4a)，其中Δ=b^2-4ac。

2. 二次方程求根公式：对于一元二次方程ax^2+bx+c=0，其根的公式为，x1,2=(-b±√Δ)/2a，其中Δ=b^2-4ac。

3. 等差数列前n项和公式：对于等差数列an=a1+(n-1)d，其前n项和Sn=(a1+an)n/2。

4. 等比数列前n项和公式：对于等比数列an=a1q^(n-1)，其前n项和Sn=a1(1-q^n)/(1-q)。

5. 二项式定理：(a+b)^n = C0n a^n + C1n a^(n-1)b + C2n a^(n-2)b^2 + ... + Cnn b^n。

二、几何部分。

1. 直角三角形斜边长公式：对于直角三角形，斜边长c的计算公式为，c=√(a^2+b^2)。

2. 圆的面积和周长公式：圆的面积公式为，S=πr^2，周长公式为，C=2πr。

3. 三角形面积公式：对于三角形，其面积S可以通过海伦公式计算，S=√[p(p-a)(p-b)(p-c)]，其中p为半周长，a、b、c为三边长。

4. 直线斜率公式：直线斜率的计算公式为，k=(y2-y1)/(x2-x1)。

5. 圆锥、圆柱、圆球体积公式：圆锥体积V=1/3πr^2h，圆柱体积V=πr^2h，圆球体积V=4/3πr^3。

三、概率与统计部分。

1. 事件的概率公式：对于事件A发生的概率P(A)的计算公式为，P(A)=n/N，其中n为A发生的次数，N为总次数。

2. 期望值公式：对于随机变量X的期望值E(X)的计算公式为，E(X)=∑(xP(x))，即所有可能取值的乘积再求和。

高中数学必背公式大全高考必考数学公式

高中数学必背公式大全高考必考数学公式1.二次方程的根与系数之间的关系：设二次方程 ax^2 + bx + c = 0（a ≠ 0）的根为 x1 和 x2，那么有以下关系式：x1+x2=-b/ax1*x2=c/a2.一元二次不等式的求解：设二次不等式 ax^2 + bx + c > 0（a ≠ 0）的解集为 S，那么有以下关系式：a>0时，S={x，x<x1或x>x2}a<0时，S={x，x1<x<x2}3.二次函数的顶点坐标：设二次函数 y = ax^2 + bx + c 的顶点坐标为 (h, k)那么有 h = -b/2a，k = f(h) = (4ac - b^2)/4a4.一次函数的斜率与函数图像的关系：设一次函数 y = mx + c 的斜率为 m，那么有以下关系式：m>0时，函数图像上升；m<0时，函数图像下降；m=0时，函数图像水平。

5.三角函数和三角公式：sin(A + B) = sinA * cosB + cosA * sinBcos(A + B) = cosA * cosB - sinA * sinBtan(A + B) = (tanA + tanB) / (1 - tanA * tanB)sin^2A + cos^2A = 1sin²θ + cos²θ = 16.幂函数的性质：若 a > 0 且a ≠ 1，则函数 y = ax^n （n 是整数）的性质如下：n>0时，函数图像单调递增；n<0时，函数图像单调递减；n为偶数时，函数图像关于y轴对称；n为奇数时，函数图像关于原点对称。

7.对数函数的性质：若 a > 0 且a ≠ 1，则函数 y = log_a(x) 的性质如下：a>1时，函数图像单调递增；0<a<1时，函数图像单调递减；函数图像过点(1,0)，且以x轴为渐近线；log_a(a^b) = b8.指数函数的性质：若a>0且a≠1，则函数y=a^x的性质如下：a>1时，函数图像单调递增；0<a<1时，函数图像单调递减；函数图像过点(0,1)，且a^0=1a^m*a^n=a^(m+n)9.排列组合公式：将n个物体排成一列，有以下公式：排列公式：从n个物体中任选m个物体的排列数为A(n,m)=n!/(n-m)!组合公式：从n个物体中任选m个物体的组合数为C(n,m)=n!/(m!*(n-m)!)10.三角函数的和差化积：sin(A + B) = sinA * cosB + cosA * sinBsin(A - B) = sinA * cosB - cosA * sinBcos(A + B) = cosA * cosB - sinA * sinBcos(A - B) = cosA * cosB + sinA * sinBtan(A + B) = (tanA + tanB) / (1 - tanA * tanB)tan(A - B) = (tanA - tanB) / (1 + tanA * tanB)这些公式是高中数学中的常用公式，掌握并熟练运用它们对于高考数学考试非常重要。

高中高考数学公式大全

高中高考数学公式大全1.代数公式：- 二次方程的根公式：对于二次方程ax²+bx+c=0，其根的公式为x=(-b±√(b²-4ac))/2a；- 韦达定理：对于三次方程ax³+bx²+cx+d=0，其根之和为-S₁/a，其根之积为S₃/a；-分式的倒数：若x是不等于0的实数，则x的倒数为1/x；- 二项式定理：(a+b)ⁿ的展开式为aⁿ+naⁿ⁻¹b+...+bⁿ；2.几何公式：-直角三角形的勾股定理：若a、b、c分别为直角三角形的两条直角边和斜边的长度，则a²+b²=c²；- 正弦定理：在三角形ABC中，a/sinA=b/sinB=c/sinC，其中a、b、c分别是三角形中对应的边，A、B、C分别是相对的角；- 余弦定理：在三角形ABC中，c²=a²+b²-2abcosC，其中a、b、c分别是三角形中对应的边，C是夹角；-长方形面积公式：长方形的面积等于长乘以宽；-圆的面积公式：圆的面积等于πr²，其中r为圆的半径；3.数列公式：-等差数列通项公式：如果数列{an}是等差数列，公差为d，首项为a₁，则其通项公式为an=a₁+(n-1)d；-等差数列前n项和公式：如果数列{an}是等差数列，公差为d，首项为a₁，前n项和为Sn，则其公式为Sn=(a₁+an)n/2；-等比数列通项公式：如果数列{an}是等比数列，公比为q，首项为a₁，则其通项公式为an=a₁qⁿ⁻¹；-等比数列前n项和公式：如果数列{an}是等比数列，公比为q≠1，首项为a₁，前n项和为Sn，则其公式为Sn=a₁(qⁿ-1)/(q-1)；4.概率公式：-事件A的概率：P(A)=A事件发生的可能性/所有可能性；-互斥事件的概率：P(A或B)=P(A)+P(B)；-相关事件的概率：P(A且B)=P(A)×P(B，A)，其中P(B，A)为在事件A发生的条件下事件B发生的概率；5.导数公式：-基本函数的导数：-常数函数的导数为0；- 幂函数f(x)=xⁿ的导数为f'(x)=nxⁿ⁻¹；-指数函数f(x)=eˣ的导数为f'(x)=eˣ；- 对数函数f(x)=ln(x)的导数为f'(x)=1/x；-基本运算法则：-f(x)=u(x)±v(x)的导数为f'(x)=u'(x)±v'(x)；-f(x)=c·u(x)的导数为f'(x)=c·u'(x)，其中c为常数；-f(x)=u(x)·v(x)的导数为f'(x)=u'(x)·v(x)+u(x)·v'(x)；-f(x)=u(x)/v(x)的导数为f'(x)=(u'(x)·v(x)-u(x)·v'(x))/v²(x)；这仅仅是高中高考数学公式的部分内容，还有很多其他的公式。