专题八 动点问题人教版八年级数学上册
人教八上动点问题
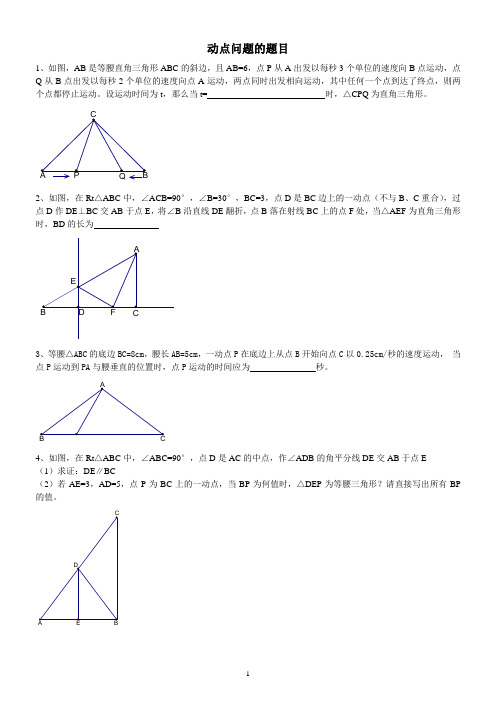
动点问题的题目1、如图,AB是等腰直角三角形ABC的斜边,且AB=6,点P从A出发以每秒3个单位的速度向B点运动,点Q从B点出发以每秒2个单位的速度向点A运动,两点同时出发相向运动,其中任何一个点到达了终点,则两个点都停止运动。
设运动时间为t,那么当t= 时,△CPQ为直角三角形。
2、如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=3,点D是BC边上的一动点(不与B、C重合),过点D作DE⊥BC交AB于点E,将∠B沿直线DE翻折,点B落在射线BC上的点F处,当△AEF为直角三角形时,BD的长为3、等腰△ABC的底边BC=8cm,腰长AB=5cm,一动点P在底边上从点B开始向点C以0.25cm/秒的速度运动,当点P运动到PA与腰垂直的位置时,点P运动的时间应为秒。
4、如图,在Rt△ABC中,∠ABC=90°,点D是AC的中点,作∠ADB的角平分线DE交AB于点E(1)求证:DE∥BC(2)若AE=3,AD=5,点P为BC上的一动点,当BP为何值时,△DEP为等腰三角形?请直接写出所有BP 的值。
备用图A C B 备用图A C B A C B yP1 A Ox P5、如图,△ABC 中,∠C=Rt ∠,AB=10cm ,BC=6cm ,若动点P 从点A 开始,沿射线AB 一直运动下去,且速度为每秒1cm ,设运动的时间为t 秒(1)求线段AC 的长和斜边AB 上的高(2)点P 出发2秒后,求△ACP 的面积(3)问t 为何值时,△BCP 为等腰三角形?6、如图,动点P 从(0.,3)出发,沿所示方向运动,每当碰到长方形的边时反弹,反弹时反射角等于入射角,当点P 第2014次碰到长方形的边时,点P 的坐标为7、如图,将边长为1的正三角形OAP 沿x 轴正方向连续翻转2014次,点P 依次落在点P 1,P 2,P 3,……P 2014,的位置,则点P 2014的横坐标为8、如图,将边长为1的正方形OAPB 沿x 轴正方向连续翻转2014次,点P 依次落在点P 1,P 2,P 3…P 2014的位置,则P 2014的坐标为9、已知,如图:在平面直角坐标系中,O 为坐标原点,四边形OABC 是矩形,点A 、C 的坐标分别为A (10,0)、C (0,4),点D 是OA 的中点,点P 在BC 边上运动,当△ODP 是腰长为5的等腰三角形时,点P 的坐标为 。
人教版初二上册第一学期数学期末复习《一次函数的应用—动点问题》(附练习及答案)

1用函数知识求解动点问题,需要将问题给合几何图形的性质,建立函数模型求解,解要符合题意,要注意数与形结合。
2.以一次函数为背景的问题,要充分运用方程、转化、函数以及数形结合等思想研究解决,注意自变量的取值范围例题1:如图,直线1l 的解析表达式为33y x =-+,且1l 与x 轴交于点D ,直线2l 经过点A B ,,直线1l ,2l 交于点C .(1)求点D 的坐标;(2)求直线2l 的解析表达式;(3)求ADC △的面积;(4)在直线2l 上存在异于点C 的另一点P ,使得ADP △与ADC △的面积相等,请直接..写出点P 的坐标.例题2:如图,在平面直角坐标系内,已知点A (0,6)、点B (8,0),动点P 从点A 开始在线段AO 上以每秒1个单位长度的速度向点O 移动,同时动点Q 从点B 开始在线段BA 上以每秒2个单位长度的速度向点A 移动,设点P 、Q 移动的时间为t 秒.(1) 求直线AB 的解析式;(2) 当t 为何值时,△APQ 的面积为524个平方单位?当堂巩固:如图,直线6y kx =+与轴、y 轴分别交于点E 、F ,点E 的坐标为(-8,0),点A 的坐标为(-6,0)。
(1)求k 的值;(2)若点P (x ,y )是第二象限内的直线上的一个动点,在点P 的运动过程中,试写出△OPA 的面积S 与的函数关系式,并写出自变量的取值范围;(3)探究:当点P 运动到什么位置时,△OPA 的面积为278,并说明理由。
课后检测: 1、如果一次函数y=-+1的图象与轴、y 轴分别交于点A 点、B 点,点M 在轴上,并且使以点A 、B 、M 为顶点的三角形是等腰三角形,那么这样的点M 有( )。
A .3个B .4个C .5个D .7个2、直线与y=-1与两坐标轴分别交于A 、B 两点,点C 在坐标轴上,若△ABC 为等腰三角形,则满足条件的点C 最多有( ).A .4个B .5个C .6个D .7个4、如图,在平面直角坐标系xOy 中,直线1y x =+与334y x =-+交于点A ,分别交x 轴于点B 和点C ,点D 是直线AC 上的一个动点.(1)求点A B C ,,的坐标.(2)当CBD △为等腰三角形时,求点D 的坐标.5、如图:直线3+=kx y 与轴、y 轴分别交于A 、B 两点,43=OA OB ,点C(,y)是直线y =+3上与A 、B 不重合的动点。
人教版初中八年级数学上册专题三角形全等之动点问题习题及答案

三角形全等之动点问题(习题)➢ 例题示范例1:已知:如图,正方形ABCD 的边长为4,动点P 从点A 出发以每秒2个单位的速度沿AB -BC -CD 方向运动,到达点D 时停止运动.连接AP ,DP .设点P 运动的时间为t 秒,求当t 为何值时,△ADP 的面积为6.【思路分析】1.研究背景图形,标注四边形ABCD 是边长为4的正方形,四条边都相等,四个角均为90°. 2.分析运动过程,分段①分析运动过程:动点P 的起点、终点、状态转折点,以及对应的时间范围.0≤t ≤6DC(2/s) P :②根据状态转折点分为三段:02t ≤≤,24t <≤,46t <≤,需要对每一段分别进行分析. 3.表达线段长,建等式①当02t ≤≤时,即点P 在线段AB 上,PDCBA此时AP =2t ,AD =4,12ADP S AD AP =⋅⋅△,即16422t =⋅⋅,32t =,符合题意.②当24t <≤时,即点P 在线段BC 上,P DC BAA BCDABCDP DCB A此时1144822ADP S AD AB =⋅⋅=⨯⨯=△,不符合题意,舍去.③当46t <≤时,即点P 在线段CD 上,PAB CD此时DP =12-2t ,AD =4,12ADP S AD DP =⋅⋅△,即164(122)2t =⋅⋅-,92t =,符合题意. 综上,当t 的值为32或92时,△ADP 的面积为6.➢ 巩固练习1. 已知:如图,在等边三角形ABC 中,AB =6,D 为BC 边上一点,AP且BD=4.动点P从点C出发以每秒1个单位的速度沿CA向点A运动,连接AD,BP.设点P运动时间为t秒,求当t为何值时,△BPA≌△ADC.2.如图,正方形ABCD的边长为8,动点P从点A出发以每秒1个单位的速度沿AB向点B运动(点P不与点A,B重合),动点Q从点B出发以每秒2个单位的速度沿BC向点C运动,点P,Q同时出发,当点Q停止运动,点P也随之停止.连接AQ,交BD于点E,连接PE.设点P运动时间为x秒,求当x为何值时,△PBE≌△QBE.3.已知:如图,在等边三角形ABC中,AB=10 cm,点D为边AB上一点,AD=6 cm.点P在线段BC上以每秒2 cm的速度由点B向点C运动,同时点Q在线段CA上由点C向点A运动.设CQBEPA DA点P运动时间为t秒,若某一时刻△BPD与△CQP全等,求此时t的值及点Q 的运动速度.4.已知:如图,在△ABC中,AB=AC=12,BC=9,点D为AB的中点.(1)如果点P在线段BC上以每秒3个单位的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.①若点Q的运动速度与点P的运动速度相等,则经过1秒后,△BPD与△CQP是否全等?请说明理由;②若点Q的运动速度与点P的运动速度不相等,则当点Q的运动速度为多少时,能够使△BPD与△CQP全等?(2)若点Q以(1)②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,则经过多长时间,点P与点Q 第一次在△ABC的哪条边上相遇?5.已知:如图,在矩形ABCD中,AB=4,AD=6.延长BC到E,使CE=2,连接DE,动点F从点B出发,以每秒2个单位的速度沿BC-CD-DA向终点A运动.设点F的运动时间为t秒.(1)请用含t的式子表达△ABF的面积S.(2)是否存在某个t值,使得△ABF和△DCE全等?若存在,求出所有符合条件的t值;若不存在,请说明理由.➢思考小结1.动点问题的处理方法:①______________________;②______________________,________;③______________________,________.2.分析运动过程包括4个方面(四要素):①起点、________、__________;②_________________________;③根据_____________分段;④所求目标.3.当研究目标多变或问题情形复杂时,我们往往将问题拆解成几个较为简单的问题来进行考虑,动点问题也是如此.具体分析动点问题时,往往会先研究背景图形,再分析运动过程、分段,为最后表达线段长,建等式做好准备.因为动点运动方向的改变不仅会改变线段长的表达,还可能改变和动点相关的图形的形状,所以要先分段,然后逐段分析,表达线段长,建等式.【参考答案】1.当t为4秒时,△BPA≌△ADC2.当x为83秒时,△PBE≌△QBE3. ①当t 为52秒时,△BPD ≌△CPQ ,此时Q 的速度为85cm/s . ②当t 为3秒时,△BPD ≌△CQP ,此时Q 的速度为2cm/s . 4. (1)①全等②Q 的速度为4cm/s 时,能够使△BPD 与△CQP 全等 (2)经过24秒,点P 与点Q 第一次在BC 边上相遇. 5.(1)034351258432t s t t s t s t <=<=<<=-+≤≤,,,(2)t 为1秒或7秒时,△ABF 与△DCE 全等。
人教版_人教版八年级数学关于动点问题的分析

动面问题博项训练之阳早格格创做1、如图,正在曲角坐标系中,O是本面,A,B,C三面的坐标分别为A (18,0),B(18,6),C(8,6),四边形OABC是梯形,面P,Q共时从本面出收,分别做匀速疏通,其中面P沿OA背末面A疏通,速度为每秒1个单位,面Q沿OC,CB背末面B疏通,当那二面有一面到达自己的末面时,另一面也停止疏通.(1)供曲线OC的剖析式.(2)设从出提倡,疏通了t秒.如果面Q的速度为每秒2个单位,试写出面Q的坐标,并写出此时t的与值范畴.(3)设从出提倡,疏通了t秒.当P,Q二面疏通的路途之战恰佳等于梯形OABC的周少的一半,那时,曲线PQ是可把梯形的里积也分成相等的二部分?如有大概,哀供出t的值;如没有成能,请道明缘由.2、如图1所示,正在△ABC中,面O正在AC边上疏通,过O做曲线MN∥BC接∠BCA内角仄分线于E面,中角仄分线于F面.试商量:当面O 疏通到那边时,四边形AECF是矩形?3、如图2所示,正在曲角坐标系中,四边形OABC为曲角梯形,OA∥BC,BC=14cm,A面坐标为(16,0),C面坐标为(0,2).面P、Q分别从C、A共时出收,面P以2cm/s的速度由C背B疏通,面Q以4cm/s的速度由A背O疏通,当面Q停止疏通时,面P也停止疏通,设疏通时间为ts(0≤t≤4).(1)供当t为几时,四边形PQAB为仄止四边形.(2)供当t为几时,PQ地圆曲线将梯形OABC分成安排二部分的里积比为1:2,供出此时曲线PQ的函数闭系式.坚韧普及:1. 如图,正在曲角梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,AB=8cm,BC=26cm,动面P从A启初沿AD边背D以1cm/s的速度疏通;动面Q从面C启初沿CB边背B以3cm/s的速度疏通.P、Q分别从面A、C共时出收,当其中一面到达端面时,其余一面也随之停止疏通,设疏通时间为ts.(1)当t为何值时,四边形PQCD为仄止四边形?(2)当t为何值时,四边形PQCD为等腰梯形?(3)当t为何值时,四边形PQCD为曲角梯形?2. 如图,△ABC中,面O为AC边上的一个动面,过面O做曲线MN∥BC,设MN接∠BCA的中角仄分线CF于面F,接∠ACB内角仄分线CE于E.(1)试道明EO=FO;(2)当面O疏通到那边时,四边形AECF是矩形并道明您的论断;(3)若AC边上存留面O,使四边形AECF是正圆形,预测△ABC的形状并道明您的论断.3. 如图,曲角梯形ABCD中,AD∥BC,∠ABC=90°,已知AD=AB=3,BC=4,动面P从B面出收,沿线段BC背面C做匀速疏通;动面Q从面D 出收,沿线段DA背面A做匀速疏通.过Q面笔曲于AD的射线接AC于面M,接BC于面N.P、Q二面共时出收,速度皆为每秒1个单位少度.当Q面疏通到A面,P、Q二面共时停止疏通.设面Q疏通的时间为t 秒.(1)供NC,MC的少(用t的代数式表示);(2)当t为何值时,四边形PCDQ形成仄止四边形;(3)是可存留某一时刻,使射线QN恰佳将△ABC的里积战周少共时仄分?若存留,供出此时t的值;若没有存留,请道明缘由;(4)商量:t为何值时,△PMC为等腰三角形.4. 如图,正在矩形ABCD中,BC=20cm,P,Q,M,N分别从A,B,C,D 出收沿AD,BC,CB,DA目标正在矩形的边上共时疏通,当有一个面先到达地圆疏通边的另一个端面时,疏通即停止.已知正在相共时间内,若BQ=xcm(x≠0),则AP=2xcm,CM=3xcm,DN=x2cm.(1)当x为何值时,以PQ,MN为二边,以矩形的边(AD或者BC)的一部分为第三边形成一个三角形;(2)当x为何值时,以P,Q,M,N为顶面的四边形是仄止四边形;(3)以P,Q,M,N为顶面的四边形是可为等腰梯形?如果能,供x的值;如果没有克没有及,请道明缘由.5. 如图,正在梯形ABCD中,AD∥BC,∠B=90°,AB=14cm,AD=15cm,BC=21cm,面M从面A启初,沿边AD背面D疏通,速度为1cm/s;面N 从面C启初,沿边CB背面B疏通,速度为2cm/s、面M、N分别从面A、C出收,当其中一面到达端面时,另一面也随之停止疏通,设疏通时间为t 秒.(1)当t为何值时,四边形MNCD是仄止四边形?(2)当t为何值时,四边形MNCD是等腰梯形?6. 如图,正在曲角梯形ABCD中,AD∥BC,∠C=90°,BC=16,DC=12,AD=21,动面P从面D出收,沿射线DA的目标以每秒2个单位少的速度疏通,动面Q从面C出收,正在线段CB上以每秒1个单位少的速度背面B疏通,P、Q分别从面D、C共时出收,当面Q疏通到面B时,面P随之停止疏通,设疏通时间为t(s).(1)设△BPQ的里积为S,供S与t之间的函数闭系;(2)当t为何值时,以B、P、Q三面为顶面的三角形是等腰三角形?7. 曲线y=- 34x+6与坐标轴分别接于A、B二面,动面P、Q共时从O面出收,共时到达A面,疏通停止.面Q沿线段OA疏通,速度为每秒1个单位少度,面P沿门路O⇒B⇒A疏通.(1)间接写出A、B二面的坐标;(2)设面Q的疏通时间为t(秒),△OPQ的里积为S,供出S与t之间的函数闭系式;(3)当S= 485时,供出面P的坐标,并间接写出以面O、P、Q为顶面的仄止四边形的第四个顶面M的坐标.。
人教版八年级上册数学期末动点问题压轴题专题训练(含答案)

人教版八年级上册数学期末动点问题压轴题专题训练1.如图,△ABC是等边三角形,点D是边BC上一个动点(点D不与点B,C重合),连接AD,点E在边AC的延长线上,且DA=DE.(1)求证:△BAD=△EDC:(2)用等式表示线段CD,CE,AB之间的数量关系,并证明.2.如图,已知△ ABC是边长为10cm的等边三角形,点F为AC的中点,动点D,E同时从A,B两点出发,分别沿AB,BC匀速运动,其中点D运动的速度是1cm/s,点E运动的速度是2cm/s,设运动时为t 秒.(1)当t为何值时,△ AFD与△ CFE全等;(2)当t为何值时,△ BDE为直角三角形.3.已知△ABC为等边三角形,点D为直线BC上的一动点(点D不与B、C重合),以AD为边作等边△ADE(顶点A、D、E按逆时针方向排列),连接CE.(1)如图1,当点D在边BC上时,求证:△BD=CE,△AC=CE+CD;(2)如图2,当点D在边BC的延长线上且其他条件不变时,结论AC=CE+CD是否成立?若不成立,请写出AC、CE、CD之间存在的数量关系,并说明理由.4.在等边△ABC中,(1)如图1,P,Q是BC边上两点,AP=AQ,△BAP=20°,求△AQB的度数;(2)点P,Q是BC边上的两个动点(不与B,C重合),点P在点Q的左侧,且AP=AQ,点Q关于直线AC的对称点为M,连接AM,PM.△依题意将图2补全;△求证:P A=PM.5.如图,在三角形ABC中,D是射线BC上一动点.(1)如图1,点D在BC边上(不与点B,C重合),△ 按要求作图:分别过点D作DE BA∥交边AB于点F;∥交边AC于点E,作DF CA△ 在△的条件下,判断△EDF与△A的数量关系,并说明理由;(2)如图2,若点D在BC的延长线上,DF CA∥,△EDF=△A,试判断DE与BA的位置关系,并说明理由.6.如图1,等腰Rt△ABC中,△BAC=90°,AB=AC,D,E分别是AC和BC上的动点,BD△AE,垂足为F.(1)求证△CAE=△ABD;(2)连接DE,满足△AEB=△DEC,求证:BD=DE+AE;(3)点G在BD的延长线上,连接EG,满足△AEB=△GEC,试写出AE,EG,BG之间的数量关系,并证明.7.已知:如图,ABC是边长为6cm的等边三角形,动点P,Q同时从A,B两点出发,分别沿AB,BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P,Q两点停止运动,设点P的运动时间为()s t,解答下列各问题:(1)ABC的面积为多少?△是等边三角形?(2)当t为何值时,PBQ△是直角三角形时,求t的值.(3)当PBQA a,将点A向右平移b个单位得到点B,其中a,b满足8.如图△所示,点A的坐标为(0,)+-=.a b50(2)如图△,坐标轴上有两个动点P ,Q ,点P 从A 点出发沿y 轴负方向以每秒1个单位长度的速度运动,点Q 从O 点出发以每秒2个单位长度的速度沿x 轴正方向运动,点P 、Q 同时出发,点P 到达O 点时整个运动结束.设运动时间为t 秒,问t 为何值时,使得12OBP BOQ S S =△△?并求出此时点P 和点Q 的坐标; (3)如图△所示,点F 为x 轴上一点,作△BOF 的平分线OG ,且OG △FB ,垂足为G ,△AOB 的平分线OE 与射线FB 交于点E ,求△E 的度数.9.如图,在平面直角坐标系中,点A ,B 的坐标分别为(a ,0),(b ,0),且a ,b 满足()23-20a b ++=.现同时将点A ,B 分别向左平移2个单位,再向上平移2个单位,得到点A ,B 的对应点C ,D ,连接AC ,BD ,CD .(1)直接写出A ,B 两点的坐标为:A ___________, B ___________.(2)若点P 是线段AC 上的一个动点,Q 是线段CD 的中点,连接PQ ,PO ,当点P 在线段AC 上移动时(不与点A ,C 重合),请找出PQD ∠,OPQ ∠,POB ∠的数量关系,并证明你的结论.(3)在坐标轴上是否存在点M ,使三角形MAD 的面积与三角形ACD 的面积相等?若存在,请求出点M 的坐标;若不存在,试说明理由.10.已知:直线AD BC ∥,动点P 在直线EF 上运动,探究ADP ,DPC ∠,BCP ∠之间的关系.(1)【问题发现】若25ADP ∠=︒,35BCP ∠=︒,求DPC ∠的度数.(2)【结论猜想】当点P 在线段AB 上时,猜想ADP ,DPC ∠,BCP ∠三个角之间的数量关系,并说明理(3)【拓展延伸】若点P 在射线AE 上或者在射线BF 上时(不包括端点),试着探究ADP ,DPC ∠,BCP ∠之间的关系是否会发生变化,请挑选一种情形画出图形,写出结论,并说明理由.11.ABC 中,70C ∠=︒,点D ,E 分别是ABC 边AC ,BC 上的点,点P 是一动点,令1PDA ∠=∠,2PEB ∠=∠,DPE α∠=∠.初探:(1)如图1,若点P 在线段AB 上,且60α∠=︒,则12∠+∠=_____________; (2)如图2,若点P 在线段AB 上运动,则△1,△2,α∠之间的关系为_____________; (3)如图3,若点P 在线段AB 的延长线上运动,则△1,△2,α∠之间的关系为_____________; 再探:(4)如图4,若点P 运动到ABC 的内部,写出此时△1,△2,α∠之间的关系,并说明理由.12.如图,AB 、CD 被AC 所截,AB CD ∥,△CAB =108°,点P 为直线AB 上一动点(不与点A 重合),连CP ,作△ACP 和△DCP 的平分线分别交直线AB 于点E 、F .(1)当点P 在点A 的右侧时△若△ACP =36°,则此时CP 是否平分△ECF ,请说明理由. △求△ECF 的度数.(2)在点P 运动过程中,直接写出△APC 与△AFC 之间的数量关系.(1)求证:AB CD ∥;(2)如图2,若3ABE EBF ∠=∠,120BFD ∠=︒,试求CDFBDF∠∠的值;(3)如图3,若H 是直线CD 上一动点(不与D 重合),BI 平分HBD ∠,则EBI ∠与BHD ∠的数量关系为______.14.如图1,在△ABC 中,BO AC ⊥于点O ,3,1AO BO OC ===,过点A 作AH BC ⊥于点H ,交BO 于点P .(1)求线段OP 的长度;(2)连接OH ,求证:点O 到△AHC 的两边距离相等;(3)如图2,若点D 为AB 的中点,点M 为线段BO 延长线上一动点,连接MD ,过点D 作DN DM ⊥交线段OA 延长线于N 点,则BDM ADN S S ∆∆-的值是否发生改变,如改变,求出该值的变化范围;若不改变,求该式子的值.15.在ABC 中,BAC ABC ∠>∠,三个内角的平分线交于点O .(1)填空:如图1,若80BCA ∠=︒,则BOA ∠的大小为________度;(3)如图2,CO 的延长线交AB 于点E ,点M 是AB 边上的一动点(不与点E 重合),过点M 作MN CE ⊥于点N ,请探索AMN ∠、ABC ∠、BAC ∠三者之间的数量关系.16.如图1,CE 平分ACD ∠,AE 平分BAC ∠,90EAC ACE ∠+∠=︒(1)请判断AB 与CD 的位置关系并说明理由;(2)如图2,在(1)的结论下,当90E ∠=︒保持不变,移动直角顶点E ,使MCE ECD ∠=∠,当直角顶点E 点移动时,问BAE ∠与MCD ∠是否存在确定的数量关系?(3)如图3,在(1)的结论下,P 为线段AC 上一定点,点Q 为直线CD 上一动点,当点Q 在射线CD 上运动时(点C 除外),CPQ CQP ∠+∠与BAC ∠有何数量关系?17.如图,在△ABC 中,D 为AB 的中点,AB =AC =10cm ,BC =8cm ,动点P 从点B 出发,沿BC 方向以每秒3cm 的速度向点C 运动;同时动点Q 从点C 出发,沿CA 方向以每秒3cm 的速度向点A 运动,运动时间是t 秒.(1)在运动过程中,当点C 位于线段PQ 的垂直平分线上时,求出t 的值;(2)在运动过程中,是否存在某一时刻t ,使△BPD 和△CQP 全等,若存在,求出t 的值.若不存在,请说明理由.18.如图,△ABC是边长是12cm的等边三角形,动点P,Q同时从A,B两点出发,分别沿AB,BC方向匀速移动,其中点P运动的速度是1cm/s,点Q运动的速度是2cm/s,当点Q到达点C时,P、Q两点都停止运动,设运动时间为t(s),解答下列问题:(1)当点Q到达点C时,PQ与AB的位置关系如何?请说明理由.(2)在点P与点Q的运动过程中,△BPQ是否能成为等边三角形?若能,请求出t,若不能,请说明理由.(3)则当t为何值时,△BPQ是直角三角形?2,0,以线段OA为边在第四象限内作等边AOB,点C 19.如图,在平面直角坐标系中,点A的坐标为()OC>,连接BC,以线段BC为边在第四象限内作等边CBD,连接DA.为x轴正半轴上一动点()2(1)求证:OBC ABD≌;(2)是否存在点C,使得ACD△为直角三角形.若存在,请求出点C的坐标;若不存在,请说明理由;(3)是否存在点C,使得ACD△为等腰三角形.若存在,请求出AC的长;若不存在,请说明理由.B-(0,4)点4(6,)A -.(1)如图1,动点P 从点B 出发,以每秒2个单位长度的速度沿BA 方向运动,同时动点Q 从点O 出发,以每秒3个单位长度的速度沿y 轴向上运动,当点P 运动到点A 时,P 、Q 同时停止运动,设点P 运动时间为t 秒.用含t 的式子表示P ,Q 两点的坐标.(2)如图2,点D 为线段OA (端点除外)上某一点,当点D 在线段上运动时,过点D 作直线EF 交x 轴正半轴于E ,交直线AB 于F ,,EOD AFD ∠∠的平分线相交于点N ,若ODF α∠=,请用含α的式子表示ONF ∠的大小,并说明理由.答案1. (2)AB =CD +CE 2.(1)103t =(2)t =2或53.(2)AC+CD =CE ,4.(1)80°5.(1);△△EDF =△A , (2)DE BA ∥,6. (3)BG =AE +EG ,7.(1)2cm (2)3 (3)2或48.(1)(0,2)A ,(3,2)B (2)65t =,点0,54P ⎛⎫ ⎪⎝⎭,12,05Q ⎛⎫ ⎪⎝⎭ (3)△E =45°9.(1)(−3,0);(2,0)(2)△DQP +△QPO +△BOP =360°; (3)(0,163)或(0,−43)或(−8,0)或(2,0)10.(1)60°;(2)△DPC =△ADP +△PCB(3)△PCB =△DPC +△ADP ;或△ADP =△DPC +△PCB11.(1)130︒;(2)1270α∠+∠=︒+∠; (3)1270α∠-∠=︒+∠; (4)12430α∠+∠=︒-∠,12.(1)△平分,;△36°(2)当点P 在点E 的右侧时,2APC AFC ∠=∠;当点P 、点E 在点A 的左侧,点F 在点A 的右侧时,2180AFC APC ∠+∠=︒;当点P 、点E 、点F 均在点A 的左侧时, 2180AFC APC ∠-∠=︒.13. (2)4(3)△BHD =2△EBI 或△EBI =90°-12△BHD14.(1)OP =1;(3)不变,9415.(1)130(3)2360AMN ABC BAC ∠=∠-∠+︒或2AMN BAC ABC ∠=∠-∠16.(1)平行,(2)存在,1902BAE MCD ∠+∠=︒(3)BAC PQC QPC ∠=∠+∠17.(1)43t = (2)当1t =时,△BPD △△CQP18.(1)PQ 与AB 垂直,(2)能,当4s t =时,△BPQ 是等边三角形(3) 2.4s t =或6s t =,△BPQ 是直角三角形19. (2)C (4,0)(3)不存在,20.(1)P (2t ,-4),Q (0,3t ); (2)12ONF α∠=,。
人教版八年级上册数学期末复习8专题八 动点问题

3. 如图①,等边三角形ABC中,D是AB边上的动点,以CD为 一边,向上作等边三角形EDC,连接AE. (1)△DBC和△EAC全等吗?请说明你的理由; (2)试说明AE∥BC; (3)如图②,当点D运动到边BA的延长线上时,仍向上作等边 三角形EDC,请问是否仍有AE∥BC?证明你的猜想.
(1)解:△DBC和△EAC全等.理由如下:
(3)BD⊥MF. 理由如下:∵∠BAC=90°,ME⊥BC, ∴∠ABC+∠ACB=∠AME+∠ACB=90°, ∴∠ABC=∠AME, ∵BD平分∠ABC,MF平分∠AME, ∴∠ABD=∠AMF, ∵∠AMF+∠F=90°, ∴∠ABD+∠F=90°, ∴BD⊥MF.
谢谢!
3
解得a=15 ,
4
综上所述,a的值为3或 15 .
4
2.如图,在△ABC中,AB=BC=AC=12 cm,现有两点M, N分别从点A,B同时出发,沿三角形的边运动,已知点M的 速度为1 cm/s,点N的速度为2 cm/s.当点N第一次到达A点时, M,N同时停止运动. (1)点M,N运动几秒后,M,N两点重合? (2)点M,N运动几秒后,可得到等边三角形AMN? (3)当点M,N在BC边上运动时,能否得到以 MN为底边的等腰三角形AMN?如果能, 请求出此时M,N运动的时间.
解:(1)设点M、N运动t秒后,M、N两点重合,则2t-t=12, ∴t=12, 即点M、N运动12秒后,M、N两点重合.
(2)点M、N运动x秒后,可得到等边三角形AMN, 则x=12-2x,∴x=4, 即点M、N运动4秒后,可得到等边三角形AMN.
(3)当点M、N在BC边上运动时,能得到以MN为底边的 等腰三角形, 设此时M、N运动的时间为m秒, ∵△AMN是等腰三角形 ∴∠1=∠2 , ∴∠3=180°-∠1=180°-∠2=∠4 ∵△ABC是等边三角形 ∴∠C=∠B,AC=AB , ∴△AMC≌△ANB ∴CM=BN 即m-12=12×3-2m. ∴m=16, 即M、N运动的时间为16秒时,得到以MN为底边的等腰△AMN.
(完整版)初二动点问题(含答案)

动态问题一、所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题.关键:动中求静.数学思想:分类思想数形结合思想转化思想类型:1.利用图形想到三角形全等,相似及三角函数2.分析题目,了解有几个动点,动点的路程,速度(动点怎么动)3.结合图形和题目,得出已知或能间接求出的数据4.分情况讨论,把每种可能情况列出来,不要漏5.动点一般在中考都是压轴题,步骤不重要,重要的是思路6.动点类题目一般都有好几问,前一问大都是后一问的提示,就像几何探究类题一样,如果后面的题难了,可以反过去看看前面问题的结论二、例题:1、如图1,梯形ABCD中,AD∥BC,∠B=90°,AB=14cm,AD=18cm,BC=21cm,点P从A开始沿AD边以1cm/秒的速度移动,点Q从C开始沿CB向点B以2 cm/秒的速度移动,如果P,Q分别从A,C同时出发,设移动时间为t秒。
当t= 时,四边形是平行四边形;当t= 时,四边形是等腰梯形.2、如图2,正方形ABCD的边长为4,点M在边DC上,且DM=1,N为对角线AC上任意一点,则DN+MN的最小值为3、如图,在Rt ABC △中,9060ACB B ∠=∠=°,°,2BC =.点O 是AC 的中点,过点O 的直线l 从与AC 重合的位置开始,绕点O 作逆时针旋转,交AB 边于点D .过点C 作CE AB ∥交直线l 于点E ,设直线l 的旋转角为α.(1)①当α= 度时,四边形EDBC 是等腰梯形,此时AD 的长为 ;②当α= 度时,四边形EDBC 是直角梯形,此时AD 的长为 ;(2)当90α=°时,判断四边形EDBC 是否为菱形,并说明理由.4、在△ABC 中,∠ACB=90°,AC=BC ,直线MN 经过点C ,且AD ⊥MN 于D ,BE ⊥MN 于E.(1)当直线MN 绕点C 旋转到图1的位置时,求证:①△ADC ≌△CEB ;②DE=AD +BE ; (2)当直线MN 绕点C 旋转到图2的位置时,求证:DE=AD-BE ;(3)当直线MN 绕点C 旋转到图3的位置时,试问DE 、AD 、BE 具有怎样的等量关系?请写出这个等量关系,并加以证明.OE CDα lC B AE D 图1 N M A B C D E M N 图2A CB E D N M 图35、数学课上,张老师出示了问题:如图1,四边形ABCD 是正方形,点E 是边BC 的中点.90AEF ∠=,且EF 交正方形外角DCG ∠的平行线CF 于点F ,求证:AE =EF .经过思考,小明展示了一种正确的解题思路:取AB 的中点M ,连接ME ,则AM =EC ,易证AME ECF △≌△,所以AE EF =.在此基础上,同学们作了进一步的研究:(1)小颖提出:如图2,如果把“点E 是边BC 的中点”改为“点E 是边BC 上(除B ,C 外)的任意一点”,其它条件不变,那么结论“AE =EF ”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由; (2)小华提出:如图3,点E 是BC 的延长线上(除C 点外)的任意一点,其他条件不变,结论“AE =EF ”仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.6、如图, 射线MB 上,MB=9,A 是射线MB 外一点,AB=5且A 到射线MB 的距离为3,动点P 从M 沿射线MB 方向以1个单位/秒的速度移动,设P 的运动时间为t. 求(1)△ PAB 为等腰三角形的t 值;(2)△ PAB 为直角三角形的t 值;(3) 若AB=5且∠ABM=45 °,其他条件不变,直接写出△ PAB 为直角三角形的t 值A D F C G EB 图1 A D FG E B 图3A D FC G E B 图28、如图,已知ABC △中,10AB AC ==厘米,8BC =厘米,点D 为AB 的中点.(1)如果点P 在线段BC 上以3cm/s 的速度由B 点向C 点运动,同时,点Q 在线段CA 上由C 点向A 点运动①若点Q 的运动速度与点P 的运动速度相等,经过1秒后,BPD △与CQP △是否全等,请说明理由; ②若点Q 的运动速度与点P 的运动速度不相等,当点Q 的运动速度为多少时,能够使BPD △与CQP △全等?(2)若点Q 以②中的运动速度从点C 出发,点P 以原来的运动速度从点B 同时出发,都逆时针沿ABC △三边运动,求经过多长时间点P 与点Q 第一次在ABC △的哪条边上相遇?。
初中数学人教版八年级上册三角形全等之动点问题(习题及答案)

初中数学人教版八年级上册实用资料三角形全等之动点问题(习题)➢ 例题示范例1:已知:如图,正方形ABCD 的边长为4,动点P 从点A 出发以每秒2个单位的速度沿AB -BC -CD 方向运动,到达点D 时停止运动.连接AP ,DP .设点P 运动的时间为t 秒,求当t 为何值时,△ADP 的面积为6.【思路分析】1.研究背景图形,标注四边形ABCD 是边长为4的正方形,四条边都相等,四个角均为90°. 2.分析运动过程,分段①分析运动过程:动点P 的起点、终点、状态转折点,以及对应的时间范围.0≤t ≤62s2sDC(2/s) P :②根据状态转折点分为三段:02t ≤≤,24t <≤,46t <≤,需要对每一段分别进行分析. 3.表达线段长,建等式①当02t ≤≤时,即点P 在线段AB 上,PDCB A此时AP =2t ,AD =4,12ADP S AD AP =⋅⋅△,即16422t =⋅⋅,32t =,符合题意.PDC B A AB CDABCD②当24t <≤时,即点P 在线段BC 上,P DCB A此时1144822ADP S AD AB =⋅⋅=⨯⨯=△,不符合题意,舍去.③当46t <≤时,即点P 在线段CD 上,PAB CD此时DP =12-2t ,AD =4,12ADP S AD DP =⋅⋅△,即164(122)2t =⋅⋅-,92t =,符合题意. 综上,当t 的值为32或92时,△ADP 的面积为6.➢巩固练习1.已知:如图,在等边三角形ABC中,AB=6,D为BC边上一点,且BD=4.动点P从点C出发以每秒1个单位的速度沿CA向点A运动,连接AD,BP.设点P运动时间为t秒,求当t为何值时,△BPA≌△ADC.2.如图,正方形ABCD的边长为8,动点P从点A出发以每秒1个单位的速度沿AB向点B运动(点P不与点A,B重合),动点Q从点B出发以每秒2个单位的速度沿BC向点C运动,点P,Q同时出发,当点Q停止运动,点P也随之停止.连接AQ,交BD于点E,连接PE.设点P运动时间为x秒,求当x为何值时,△PBE≌△QBE.3.已知:如图,在等边三角形ABC中,AB=10 cm,点D为边ABAPB D CCQBEPA DA上一点,AD=6 cm.点P在线段BC上以每秒2 cm的速度由点B向点C运动,同时点Q在线段CA上由点C向点A运动.设点P运动时间为t秒,若某一时刻△BPD与△CQP全等,求此时t的值及点Q的运动速度.4.已知:如图,在△ABC中,AB=AC=12,BC=9,点D为AB的中点.(1)如果点P在线段BC上以每秒3个单位的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.①若点Q的运动速度与点P的运动速度相等,则经过1秒后,△BPD与△CQP是否全等?请说明理由;②若点Q的运动速度与点P的运动速度不相等,则当点Q的运动速度为多少时,能够使△BPD与△CQP全等?(2)若点Q以(1)②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,则经过多长时间,点P与点Q 第一次在△ABC的哪条边上相遇?5.已知:如图,在矩形ABCD中,AB=4,AD=6.延长BC到E,使CE=2,连接DE,动点F从点B出发,以每秒2个单位的速度沿BC-CD-DA向终点A运动.设点F的运动时间为t秒.(1)请用含t的式子表达△ABF的面积S.(2)是否存在某个t值,使得△ABF和△DCE全等?若存在,求出所有符合条件的t值;若不存在,请说明理由.➢思考小结1.动点问题的处理方法:①______________________;②______________________,________;③______________________,________.2.分析运动过程包括4个方面(四要素):①起点、________、__________;②_________________________;③根据_____________分段;④所求目标.3.当研究目标多变或问题情形复杂时,我们往往将问题拆解成几个较为简单的问题来进行考虑,动点问题也是如此.具体分析动点问题时,往往会先研究背景图形,再分析运动过程、分段,为最后表达线段长,建等式做好准备.因为动点运动方向的改变不仅会改变线段长的表达,还可能改变和动点相关的图形的形状,所以要先分段,然后逐段分析,表达线段长,建等式.【参考答案】1.当t为4秒时,△BPA≌△ADC2.当x为83秒时,△PBE≌△QBE3. ①当t 为52秒时,△BPD ≌△CPQ ,此时Q 的速度为85cm/s . ②当t 为3秒时,△BPD ≌△CQP ,此时Q 的速度为2cm/s . 4. (1)①全等②Q 的速度为4cm/s 时,能够使△BPD 与△CQP 全等 (2)经过24秒,点P 与点Q 第一次在BC 边上相遇. 5.(1)034351258432t s t t s t s t <=<=<<=-+≤≤,,,(2)t 为1秒或7秒时,△ABF 与△DCE 全等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1. 如图,已知 E 为等腰三角形 ABC 的底边 BC
上一动点,过点 E 作 EF⊥BC 交直线 AB 于点 D,
交 CA 的延长线于点 F,问:
(1)∠F 与∠ADF 的关系怎样?说明理由;
解:(1)∠F=∠ADF. 理由如下. ∵△ABC为等腰三角形, ∴AB=AC,∴∠B=∠C. ∵EF⊥BC, ∴∠B+∠BDE=90°,∠C+∠F=90°. ∴∠BDE=∠F. ∵∠ADF=∠BDE,∴∠ADF=∠F.
解:(1)PC=BC-BP=6-2t.
(2)若点 P,Q 的运动速度不相等,当△BPD 与 △CQP 全等时,求 a 的值.
(2)∵点P,Q的运动速度不相等, ∴BP≠CQ. ∵△BPD≌△CPQ,∠B=∠C,∴BP= PC,BD=CQ.
3. 如图,在等边三角形 ABC 中,AB=AC=BC=10 厘米,DC=4 厘米.如果点 M 在线段 CB 上以 3 厘米/秒的速度由点 C 向点 B 运动,点 N 在线 段 BA 上以同样的速度由点 B 向点 A 点运动,
(2)M,N 同时运动几秒后,可得等边三角形
AMN?
(2)设点M,N运动t秒后, 可得到等边三角形AMN, 如图所示. AM=t×1=t,AN=AB-BN=10-2t. ∵△AMN是等边三角形, ∴t=10-2t. 解得t= . ∴点M,N运动 秒后,可得到等边三角形AMN.
谢谢!
●
1.情节是叙事性文学作品内容构成的 要素之 一,是叙 事作品 中表现 人物之 间相互 关系的 一系列 生活事 件的发 展过程 。
且它们同时出发.
(1)经过 2 秒后,△BMN 和 △CDM 是否全等?请说明
理由.
解:(1)△BMN≌△CDM.理由如下. ∵vN=vM=3厘米/秒,且t=2秒, ∴CM=2×3=6(厘米),BN=2×3=6(厘米), ∴BN=CM. BM=BC-CM=10-6=4(厘米), ∵CD=4厘米, ∴BM=CD. ∵△ABC为等边三角形, ∴∠B=∠C=60°. 在△BMN和△CDM中,
2. 如图,在△ABC 中,∠B=∠C,AB=8,BC=6,点 D 为 AB 的中点,点 P 在线段 BC 上以每秒 2 个单 位的速度由点 B 向点 C 运动,同时点 Q 在线段 CA 上以每秒 a 个单位的速度由点 C 向点 A 运动, 设运动时间为 t(单位:秒)(0≤t≤3).
(1)用含 t 的代数式表示线段 PC 的长;
●
2.它由一系列展示人物性格,反映人物 与人物 、人物 与环境 之间相 互关系 的具体 事件构 成。
●
3.把握好故事情节,是欣赏小说的基础,也是整 体感知 小说的 起点。 命题者 在为小 说命题 时,也必 定以情 节为出 发点,从整体 上设置 理解小 说内容 的试题 。通常 从情节 梳理、 情节作 用两方 面设题 考查。
(2)若 E 在 BC 的延长线上,其余条件不变,
上题的结论是否成立?若不成立,说明理由;
若成立,画出图形并给予证明.
(2)成立. 证明:如图,∵AB=AC,∴∠B=∠ACB. ∵∠ACB=∠ECF,∴∠B=∠ECF. ∵EF⊥BC, ∴∠B+∠BDE=90°,∠ECF+∠F=90°. ∴∠BDE=∠F,即∠ADF=∠F.
●
9.自信让我们充满激情。有了自信, 我们才 能怀着 坚定的 信心和 希望, 开始伟 大而光 荣的事 业。自 信的人 有勇气 交往与 表达, 有信心 尝试与 坚持, 能够展 现优势 与才华 ,激发 潜能与 活力, 获得更 多的实 践机会 与创造 可能。
感谢观看,欢迎指导!
●
4.根据结构来梳理。按照情节的开端 、发展 、高潮 和结局 来划分 文章层 次,进而 梳理情 节。
●
5.根据场景来梳理。一般一个场景可 以梳理 为一个 情节。 小说中 的场景 就是不 同时间 人物活 动的场 所。
●
6.根据线索来梳理。抓住线索是把握 小说故 事发展 的关键 。线索 有单线 和双线 两种。 双线一 般分明 线和暗 线。高 考考查 的小说 往往较 简单,线 索也一 般是单 线式。
●
7.阅历之所以会对读书所得产生深浅 有别的 影响, 原因在 于阅读 并非是 对作品 的简单 再现, 而是一 个积极 主动的 再创造 过程, 人生的 经历与 生活的 经验都 会参与 进来。
●
8.少年时阅历不够丰富,洞察力、理 解力有 所欠缺 ,所以 在读书 时往往 容易只 看其中 一点或 几点, 对书中 蕴含的 丰富意 义难以 全面把 握。
∴△BMN≌△CDM(SAS).
(2)若△BMN 是一个直角三角形,则两点的运
动时间为多少?
(2)设运动时间为t秒, △BMN是直角三角形有两种情况: ①当∠NMB=90°时.∵∠B=60°, ∴∠BNM=90°-∠B=90°-60°=30°. ∴BN=2BM. ∴3t=2×(10-3t).解得t= . ② 当∠BNM=90°时.∵∠B=60°, ∴∠BMN=90°-∠B=90°-60°=30°. ∴BM=2BN. ∴10-3t=2×3t. 解得t= . 综上所述,当运动时间为 秒或 秒时, △BMN是直角三角形.
4. 如图所示,在△ABC 中,AB=AC=BC=10 厘米, M,N 分别从点 A,B 同时出发,沿三角形的 边运动.已知点 M 的速度是 1 厘米/秒,点 N 的速度是 2 厘米/秒,当点 N 第一次到达点 B 时,M,N 同时停止运动.
(1)M,N 同时运动几秒后,M,N 两点重合?
解:(1)设点M,N运动x秒后,M,N两 点重合.x×1+10=2x. 解得x=10. 即M,N同时运动10秒后,M,N两点重合.
