实验一利用相关函数辨识脉冲响应
利用相关分析法辨识脉冲响应实验报告

实验一 利用相关分析法辨识脉冲响应1 实验方案设计1.1 生成输入数据和噪声用M 序列作为辨识的输入信号,噪声采用标准正态分布的白噪声。
生成白噪声时,首先利用乘同余法生成U[0,1]均匀分布的随机数,再利用U[0,1]均匀分布的随机数生成标准正态分布的白噪声。
1.2 过程仿真模拟过程传递函数)(s G ,获得输出数据y(k)。
)(s G 采取串联传递函数仿真,21211111)(T s T s T T K s G ++=,用M 序列作为辨识的输入信号。
1.3 计算互相关函数∑++=-=pp N r N i pMz i z k i u rN k R )1(1)()(1)(其中r 为周期数,1+=p N i 表示计算互相关函数所用的数据是从第二个周期开始的,目的是等过程仿真数据进入平稳状态。
1.4 计算脉冲响应估计值、脉冲响应理论值、脉冲响应估计误差脉冲响应估计值[])1()()1()(ˆ2--∆+=p Mz Mzp pN R k Rta N N k g脉冲响应理论值[]21//210)(T t k T t k e e T T Kk g ∆-∆---=脉冲响应估计误差()()∑∑==-=ppN k N k g k g k gk g12012)()(ˆ)(δ1.5 计算噪信比信噪比()()22)()(v k v y k y --=η2 编程说明M 序列中,M 序列循环周期取63126=-=p N ,时钟节拍t ∆=1Sec ,幅度1=a ,特征多项式为1)(56⊕⊕=s s s F 。
白噪声循环周期为32768215=。
)(s G 采样时间0T 设为1Sec ,Sec 2.6 Sec,3.8 ,12021===T T K3 源程序清单3.1 均匀分布随机数生成函数function sita=U(N)%生成N 个[0 1]均匀分布随机数 A=179; x0=11; M=2^15; for k=1:N x2=A*x0;x1=mod(x2,M); v1=x1/(M+1); v(:,k)=v1; x0=x1; end sita=v; end3.2 正态分布白噪声生成函数function v=noise(aipi)%生成正态分布N(0,sigma) sigma=1; %标准差 for k=1:length(aipi) ksai=0; for i=1:12temp=mod(i+k,length(aipi))+1; ksai=ksai+aipi(temp);endv(k)=sigma*(ksai-6);endend3.3 M序列生成函数function [Np r M]=createM(n,a)%生成长度为n的M序列,周期为Np,周期数为rx=[1 1 1 1 1 1]; %初始化初态for i=1:ny=x;x(2:6)=y(1:5);x(1)=xor(y(5),y(6));U(i)=y(6);endM=U*a;lenx=length(x);Np=2^lenx-1;r=n/Np;end3.4 过程仿真函数function y=createy(u,K,T1,T2,T0)n=length(u);K1=K/(T1*T2);E1=exp(-T0/T1);E2=exp(-T0/T2);x(1)=0;y(1)=0;for k=2:nx(k)=E1*x(k-1)+T1*K1*(1-E1)*u(k-1)...+T1*K1*(T1*(E1-1)+T0)*(u(k)-u(k-1))/T0;y(k)=E2*y(k-1)+T2*(1-E2)*x(k-1)...+T2*(T2*(E1-1)+T0)*(x(k)-x(k-1))/T0;u(k-1)=u(k);x(k-1)=x(k);y(k-1)=y(k);endend3.5 相关函数计算函数function R_Mz=RMz(Np,r,u,z)r=r-1;y=zeros(1,Np);for k=1:Npy(k)=0;for i=Np+1:(r+1)*Npy(k)=y(k)+u(i-k)*z(i);endy(k)=y(k)/(r*Np);endR_Mz=y;end3.5 主函数function [og yita]=main(time)% 脉冲响应估计误差og% 噪信比yitaN=time*63;K=120; T1=8.3; T2=6.2; T0=1; a=1;sita=U(N); %生成[0 1]均匀分布随机数v=noise(sita); %利用aipi生成正态分布白噪声[Np r u]=createM(N,a); %生成长度为N的M序列y=createy(u,K,T1,T2,T0); %利用M序列驱动,生成yz=y+v;R_Mz=RMz(Np,r,u,z); %计算相关函数% 计算脉冲响应估计值g_k=zeros(1,Np);for k=1:Npg_k(1,k)=(R_Mz(1,k)-R_Mz(Np-1))*Np/((Np+1)*a*a*T0);end% 计算脉冲响应理论值Eg=zeros(1,Np);for k=1:NpEg(1,k)=K/(T1-T2)*(exp(-k*T0/T1)-exp(-k*T0/T2));end% 计算脉冲响应估计误差og=sqrt(norm(Eg-g_k)^2/norm(Eg)^2);ov=fangcha(v); %计算噪声方差oy=fangcha(y); %计算信号方差yita=sqrt(oy/ov); %计算信噪比End3.5 画图函数1%mainPlot.mfigure(1)[og yita]=main(n);y1(n)=og;endy1=y1(4:40);plot([4:40],y1);xlabel('周期数');ylabel('脉冲响应估计误差');figure(2)for n=4:40[og yita]=main(n);y2(n)=yita;endy2=y2(4:40);plot([4:40],y2);xlabel('周期数');ylabel('噪信比');3.5 画图函数2%mainPlot2.mN=252;K=120; T1=8.3; T2=6.2; T0=1; a=1;sita=U(N); %生成[0 1]均匀分布随机数v=noise(sita); %利用aipi生成正态分布白噪声[Np r u]=createM(N,a); %生成长度为N的M序列y=createy(u,K,T1,T2,T0); %利用M序列驱动,生成yz=y+v;R_Mz=RMz(Np,r,u,z); %计算相关函数% 计算脉冲响应估计值g_k=zeros(1,Np);for k=1:Npg_k(1,k)=(R_Mz(1,k)-R_Mz(Np-1))*Np/((Np+1)*a*a*T0);end% 计算脉冲响应理论值Eg=zeros(1,Np);for k=1:NpEg(1,k)=K/(T1-T2)*(exp(-k*T0/T1)-exp(-k*T0/T2));endfigure(1)plot([1:252],y,[1:252],z);Legend('不含噪声的输出序列','含噪声的输出序列');plot([1:63],g_k,[1:63],Eg);Legend('脉冲响应估计值','脉冲响应理论值');4 数据记录表1脉冲响应估计值与脉冲响应理论值的比较t 1 2 3 4 5 6 7脉冲响应估计值0.79 0.92 1.02 1.04 1.05 1.01 0.92 脉冲响应理论值 2.03 3.52 4.59 5.32 5.77 6.02 6.11 t 8 9 10 11 12 13 14脉冲响应估计值0.87 0.80 0.74 0.65 0.57 0.50 0.42 脉冲响应理论值 6.07 5.94 5.74 5.49 5.21 4.91 4.60 t 15 16 17 18 19 20 21脉冲响应估计值0.33 0.23 0.17 0.10 0.05 -0.01 -0.06 脉冲响应理论值 4.29 3.99 3.69 3.40 3.12 2.86 2.62 t 22 23 24 25 26 27 28脉冲响应估计值-0.10 -0.16 -0.19 -0.22 -0.25 -0.29 -0.28 脉冲响应理论值 2.39 2.18 1.98 1.80 1.63 1.48 1.33 t 29 30 31 32 33 34 35脉冲响应估计值-0.30 -0.31 -0.32 -0.36 -0.37 -0.39 -0.41 脉冲响应理论值 1.20 1.09 0.98 0.88 0.79 0.71 0.64 t 36 37 38 39 40 41 42脉冲响应估计值-0.44 -0.46 -0.47 -0.46 -0.49 -0.51 -0.52 脉冲响应理论值0.58 0.52 0.46 0.41 0.37 0.33 0.30 t 43 44 45 46 47 48 49脉冲响应估计值-0.53 -0.54 -0.55 -0.55 -0.56 -0.54 -0.56 脉冲响应理论值0.27 0.24 0.21 0.19 0.17 0.15 0.13 t 50 51 52 53 54 55 56脉冲响应估计值-0.57 -0.57 -0.56 -0.57 -0.57 -0.56 -0.55 脉冲响应理论值0.12 0.11 0.10 0.09 0.08 0.07 0.06 t 57 58 59 60 61 62 63脉冲响应估计值-0.53 -0.52 -0.53 -0.52 -0.53 0.00 0.61 脉冲响应理论值0.05 0.05 0.04 0.04 0.03 0.03 0.035 曲线打印图1 信噪比随着周期数增大的变化图2 脉冲响应计算误差随着周期数增大的变化图3 加入噪声前后的输出序列比较图4 脉冲响应理论值与估计值的比较6 结果分析6.1 信噪比脉冲响应计算误差随周期的变化随着周期数的增加,信噪比减小,说明噪声随着周期数的增加变得更强烈,而计算误差的减小表示周期数的增加使得不确定因素的影响减小,使得计算结果与实际更接近。
基于相关分析法的脉冲响应辨识实验设计

基于相关分析法的脉冲响应辨识实验设计刘恒;孙晋;邰凡彬;张易晨【摘要】In combination with the knowledge points of the curriculum and by using the 555 timer,dual D flip-flop, NAND gate and operational amplifier,the m sequence signal generation is realized.The two-order identification system is designed through the operationalamplifier,capacitors and resistors.The Multisim software simulation verifies the correctness of the circuit design.The Matlab software is used to simulate the identification of impulse response with the correlation analysis,and the effectiveness of the algorithm is verified.The identification circuit with the correlation analysis is constructed by using the level lifting circuit,STM32F103 SCM and TFT screen.The experimental test shows that the six-order m sequence signal can correctly stimulate the two-order system,and the hardware circuit can realize the identification of the impulse response curve and identify the error of 2%.This experiment canbe used as a practical training experiment for the principle and application of the SCM,Digital Signal Processing course and electronic design contest for college students.%结合课程知识点,采用555定时器、双D触发器、与非门、运算放大器实现m序列信号产生,二阶辨识系统通过运算放大器、电容、电阻设计,M ultisim软件仿真验证了电路设计的正确性.利用M atlab软件对相关分析法辨识脉冲响应进行了仿真,验证了算法的有效性.利用电平抬升电路和ST M 32F103单片机、T FT屏构建了相关分析法辨识电路.实验测试表明:6阶m序列信号能正确激励二阶系统,硬件电路能实现脉冲响应曲线的辨识,辨识存在2% 的误差.本实验可作为单片机原理及应用和数字信号处理课程综合设计和大学生电子设计竞赛实训实验.【期刊名称】《实验技术与管理》【年(卷),期】2018(035)005【总页数】7页(P53-59)【关键词】m序列信号;相关分析法;系统辨识;脉冲响应【作者】刘恒;孙晋;邰凡彬;张易晨【作者单位】南京信息工程大学电子与信息工程学院,江苏南京 210044;南京信息工程大学电子与信息工程学院,江苏南京 210044;南京信息工程大学电子与信息工程学院,江苏南京 210044;南京信息工程大学电子与信息工程学院,江苏南京210044【正文语种】中文【中图分类】TN911.71;G642.423系统辨识是控制领域的一个十分重要分支。
脉冲响应函数分析,请高手解答

脉冲响应函数分析,请⾼⼿解答脉冲响应函数分析,请⾼⼿解答对两个时间序列A和B进⾏脉冲响应函数分析,在内⽣变量框⾥输⼊的次序不同,通过得出的脉冲响应图的结果怎么会完全不⼀样?输⼊A B 时得出的是A对B的⼀次冲击有很⼤响应,B对A的⼀次冲击没有什么响应;输⼊B A 时得出的是A对B的⼀次冲击没什么响应,B对A的⼀次冲击有很⼤响应。
哪位⾼⼿能解释⼀下这是什么原因?乔分解将所有影响的公共因素强加到你的V AR模型中的第⼀个变量中去,也就是说结果与你V AR模型中指定的变量秩序有关,你改变了秩序很正常的解决办法:定义脉冲时在IMPUSE DEFINITION项⽬中分解⽅法选择⼴义脉冲结果就不会因为模型中变量指定秩序改变⽽改变了,也就是说结果与变量秩序⽆关。
⾼⼈,能否详细解释⼀下geralized Impulses和adjusted这两种脉冲响应的应⽤有什么不同?在哪种情况下应该使⽤geralized Impulses,在哪种情况下⼜应该使⽤adjusted?不胜感激。
adjusted实际上是运⽤乔分解时,当是⼩样本时,在估计残差的协⽅差估计时进⾏了修正也就是说它实际上是修正过的乔分解,它进⾏脉冲时同样存在乔分解的问题:脉冲与秩序有关⽽⼴义脉冲分解法其结果与秩序⽆关,它是为了避免乔分解结果与秩序有关⽽采⽤的另外⼀种分解⽅法,对样本⽆什么要求,只要你建⽴的V AR/SV AR模型稳定即可!请问只有对平稳序列才能建⽴V AR模型吗?看了⼀些教材,好像说法不⼀。
如果有序列LnY和LnX,它们是⾮平稳序列,但是⼀阶差分后平稳,此时能否对原序列进⾏V AR分析以及脉冲响应和⽅差分解分析?如果只有平稳序列才能进⾏V AR预测的话,对于取了差分之后的序列,应该如何解释经济含义呢?如GDP/、能源消费量等。
1、只有平稳才能建V AR模型,但有特例,就是涉及到⼀些变量是如增长率,于种种原因,如数据太少,或其他原因,ADF检验没通过,但也可以算作平稳,视情况⽽定。
脉冲响应函数

脉冲响应函数
脉冲响应函数是指一种数学函数,可以用来描述系统如何响应一个脉冲输入,以及该输入如何影响系统的输出。
当任意一个脉冲输入被应用到一个系统时,脉冲响应函数可以用来表示该系统的输出。
脉冲响应函数有多种形式,其中最常见的形式是双曲正弦(hyperbolic sine)函数。
此外,还有一些其他的脉冲响应函数,包括幂函数、双指数函数和正弦函数。
脉冲响应函数在工程领域中有着广泛的应用,其中最常见的应用是滤波,即使用脉冲响应函数来消除信号中的噪声或者干扰。
与滤波相关的另一个应用是控制,即使用脉冲响应函数来控制信号的频率或者其他参数。
脉冲响应函数也可以用于信号检测,即使用脉冲响应函数来计算信号的频率、相位或者其他参数。
此外,脉冲响应函数还被广泛应用于信号处理,包括消除信号中的噪声和干扰,以及改变信号的频率或其他参数。
总之,脉冲响应函数是一种数学函数,可以用来描述系统如何响应一个脉冲输入,以及该输入如何影响系统的输出。
脉冲响应函数在工程领域中有着广泛的应用,包括滤波、控制、信号检测和信号处理等。
系统辨识实验报告30288
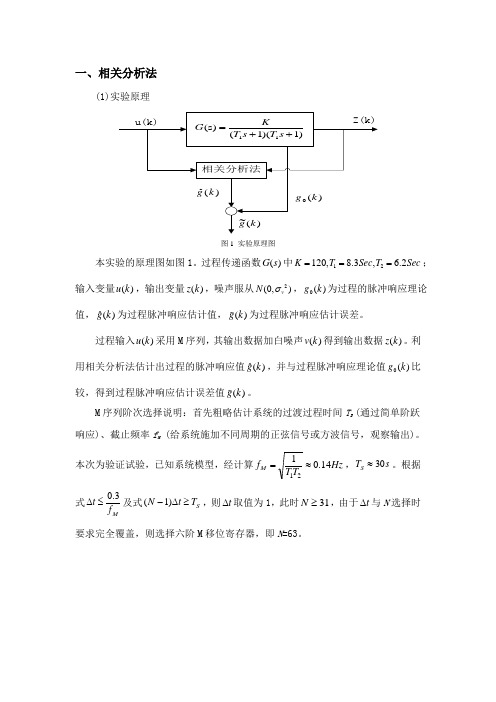
一、相关分析法(1)实验原理图1 实验原理图本实验的原理图如图1。
过程传递函数()G s 中12120,8.3, 6.2K T Sec T Sec ===;输入变量()u k ,输出变量()z k ,噪声服从2(0,)v N σ,0()g k 为过程的脉冲响应理论值,ˆ()gk 为过程脉冲响应估计值,()g k 为过程脉冲响应估计误差。
过程输入()u k 采用M 序列,其输出数据加白噪声()v k 得到输出数据()z k 。
利用相关分析法估计出过程的脉冲响应值ˆ()gk ,并与过程脉冲响应理论值0()g k 比较,得到过程脉冲响应估计误差值()g k 。
M 序列阶次选择说明:首先粗略估计系统的过渡过程时间T S (通过简单阶跃响应)、截止频率f M (给系统施加不同周期的正弦信号或方波信号,观察输出)。
本次为验证试验,已知系统模型,经计算Hz T T f M 14.0121≈=,s T S 30≈。
根据式Mf t 3.0≤∆及式S T t N ≥∆-)1(,则t ∆取值为1,此时31≥N ,由于t ∆与N 选择时要求完全覆盖,则选择六阶M 移位寄存器,即N =63。
(2)编程说明图2 程序流程图(3)分步说明 ① 生成M 序列:M 序列的循环周期63126=-=N ,时钟节拍1t Sec ∆=,幅度1a =,移位寄存器中第5、6位的内容按“模二相加”,反馈到第一位作为输入。
其中初始数据设为{1,0,1,0,0,0}。
程序如下:② 生成白噪声序列: 程序如下:③ 过程仿真得到输出数据:如图2所示的过程传递函数串联,可以写成形如121211()1/1/K Gs TT s T s T =++,其中112KK TT =。
图2 过程仿真方框图程序如下:④ 计算脉冲响应估计值:互相关函数采用公式)()(1)(10k i y i x Nr k R N r i xy +⋅⋅=∑-⋅=,互相关函数所用的数据是从第二个周期开始的,其中r 为周期数,取1-3之间。
实验一 利用相关辨识法辨识脉冲响应
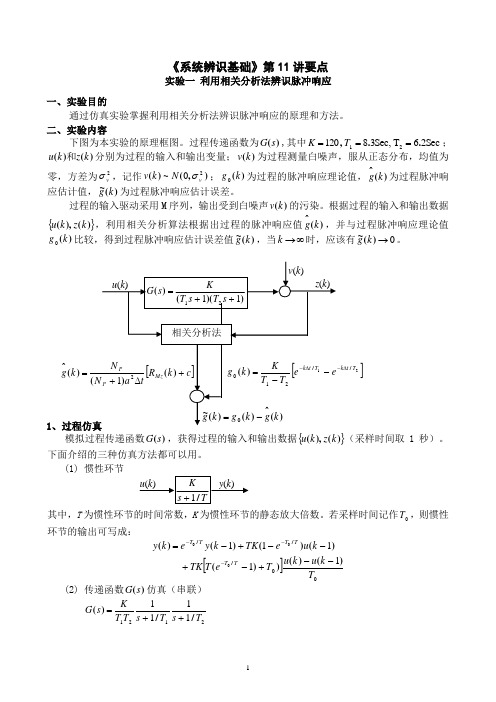
《系统辨识基础》第11讲要点实验一 利用相关分析法辨识脉冲响应一、实验目的通过仿真实验掌握利用相关分析法辨识脉冲响应的原理和方法。
二、实验内容下图为本实验的原理框图。
过程传递函数为)(s G ,其中Sec 26T Sec,3812021..,===T K ;)()(k z k u 和分别为过程的输入和输出变量;)(k v 为过程测量白噪声,服从正态分布,均值为零,方差为2v σ,记作),(~)(20v N k v σ;)(k g 0为过程的脉冲响应理论值,)(ˆk g 为过程脉冲响应估计值,)(~k g为过程脉冲响应估计误差。
过程的输入驱动采用M 序列,输出受到白噪声)(k v 的污染。
根据过程的输入和输出数据{})(),(k z k u ,利用相关分析算法根据出过程的脉冲响应值)(ˆk g ,并与过程脉冲响应理论值)(k g 0比较,得到过程脉冲响应估计误差值)(~k g,当∞→k 时,应该有0→)(~k g 。
1模拟过程传递函数)(s G ,获得过程的输入和输出数据{})(),(k z k u (采样时间取1秒)。
下面介绍的三种仿真方法都可以用。
(1) 惯性环节 其中,T 为惯性环节的时间常数,K为惯性环节的静态放大倍数。
若采样时间记作0T ,则惯性环节的输出可写成:[]011111000T k u k u T e T TK k u e TK k y e k y T T T T T T )()())()()()()(///--+-+--+-=---(2) 传递函数)(s G 仿真(串联)21211111T s T s T T K s G //)(++=k g =)(ˆ]2T t k /∆令211T T KK =,则)(s G 的表达框图为:编程语句可写成:[][][][]};);()();()();()(;/)()(*)(**)(*)(*)(*)(;/)()(*)(***)(*)(**)(*)({);;(;)(;)();/();/();*/(k y k y k x k x k u k u T k x k x T E T T k x E T k y E k y T k u k u T E T K T k u E K T k x E k x k k k y x T T E T T E T T K K =-=-=---+-+--+-=--+-+--+-=++<===-=-==11111111111112521for 0000EXP EXP 002222220011111111202101211(3) 传递函数)(s G 仿真(并联) ⎪⎪⎭⎫ ⎝⎛+-+-=21211111T s T s T T K s G //)(令211T T KK -=,则)(s G 的表达框图为:编程语句可写成:[][][][][]};);()();()();()()()(*)(;/)()(*)(**)(*)(*)(*)(;/)()(*)(**)(*)(*)(*)({);;(;)(;)(;)();/();/();/(k x k x k x k x k u k u k x k x K k y T k u k u T E T T k u E T k x E k x T k u k u T E T T k u E T k x E k x k k k y x x T T E T T E T T K K 2211211002222222200111111112120210121111111111111112521for 000000EXP EXP =-=-=--=--+-+--+-=--+-+--+-=++<==-=-=-=-=(4) 传递函数)(s G 仿真(双线性变换) ● Pade 逼近 因有s T s T sT sT ez sT 0000Pade 2221210-+=-+==//,则有110112--+-=z z T s ,条件是k T P k ∀≤,.500,其中k P 为传递函数的极点。
脉冲响应函数
脉冲响应函数
脉冲响应函数是一种动态控制系统的重要工具,它对动态控制系统的响应性能有重要影响。
下面就脉冲响应函数进行详细介绍:
一、什么是脉冲响应函数
脉冲响应函数又称冲动响应函数,是指控制系统中给定脉冲输入后,控制系统的输出变化情况,以此来反映控制系统的动态性能。
二、脉冲响应函数对控制系统的重要影响
脉冲响应函数可以准确地反映控制系统的动态特性,可以清楚地表示出系统的调节能力、阻尼情况以及振荡频率等,反映了控制系统是否满足要求。
三、研究脉冲响应函数的方法
(1)模拟方法:模拟技术是研究脉冲响应函数最常用的方法,可以在发生器上给定某一脉冲信号,然后可以测量控制系统的输出信号在时间上的变化,从而形成脉冲响应函数。
(2)数学模型方法:建立控制系统模型,然后用数学方法研究脉冲传
播率,推导出脉冲响应函数。
(3)曲线拟合方法:此方法是以正弦或者多项式拟合的形式表示脉冲响应函数,通过曲线拟合可以得到脉冲响应函数的表示式。
四、研究中的关键要点
(1)建立正确的模型。
(2)优化脉冲响应函数特性。
(3)正确掌握脉冲响应函数在控制系统中的影响。
(4)选择合理的收敛算法来进行脉冲响应函数的计算。
五、总结
脉冲响应函数是控制系统中一种重要的性能指标,能够有助于我们了解一个控制系统的动态行为特点,为控制系统的改进及调试提供有用的参考。
研究脉冲响应函数的主要方法有模拟方法、数学模型方法和曲线拟合方法。
此外,研究脉冲响应函数时,还需要重点关注正确建立模型、优化脉冲响应函数特性、正确掌握脉冲响应函数在控制系统中的影响以及使用合理的收敛算法。
第六章脉冲响应函数(骆建波)
第6章 脉冲响应函数的辨识一、辨识问题的提法假定被辨识的过程是线性系统,可以将作用在系统上的一切随机干扰和噪声,用一个作用于系统输出的等效随机干扰源)t (v 来代替。
输入信号)(u t 是过程的运行操作信号,是可以直接观测的确定性变量;)(y u t 是过程的实际输出,是不能被观测到的;y(t)是过程的观测输出,其中混有随机噪声)t (v 。
辨识问题:在已知输入、输出的观测量)(u t 、y(t)以及f t (f t 可以根据脉冲响应过渡历程时间的先验知识作粗略估计)的情况下,要求估计出脉冲响应函数)(g t 。
本章介绍两种辨识脉冲响应函数的常用方法:相关分析法和最小二乘法。
二、用相关分析法辨识脉冲响应函数假定噪声)t (v 是一个零均值平稳随机过程,并与)(u t 不相关,且过程是线性时不变的、因果性的系统,过程的未知脉冲响应函数为)(g t ,则过程的输入、输出和脉冲响应函数之间的基本关系如下:⎰∞-=0)()()(y λλλd u t g t u⎰+-=ft t v d u t g t 0)()()()(y λλλ把变量t 用τ+t 代换,得⎰++-+=+ft t v d t u g t 0)()()()(y τλλτλτ由此可求得y(t)的相关函数:)()()()(0uy τλτλτuv t uu R d t R g R f+-=⎰由于已经假设)t (v 与输入信号)(u t 不相关,因此对应的相关系数0)(uv =τR ,于是过程g(t))(u t y(t))(y u t )t (v ++λλλτd t R g R ft uu )()()(0uy -=⎰这就是维纳-霍夫(Wiener-Holf)方程。
在实际中脉冲响应函数也应为脉冲响应序列。
可得到离散型Wiener-Holf 方程:∑-=∆-=10)()()(N i uu uy t i k R i g k R式中t ∆为)(g t 的采样周期,f t t N =∆;∑-+=-=100)()(1)(M i i i uu i u k i u M k R∑-+=-=100)()(1)(M i i i uy i y k i u Mk RM 为足够大的整数,0i 为计算起点。
脉冲响应函数
3-2 脉冲响应函数对于线性定常系统,其传递函数)(s Φ为)()()(s R s C s =Φ式中)(s R 是输入量的拉氏变换式,)(s C 是输出量的拉氏变换式。
系统输出可以写成)(s Φ与)(s R 的乘积,即)()()(s R s s C Φ= (3-1) 下面讨论,当初始条件等于零时,系统对单位脉冲输入量的响应。
因为单位脉冲函数的拉氏变换等于1,所以系统输出量的拉氏变换恰恰是它的传递函数,即)()(s s C Φ= (3-2) 由方程(3-2)可见,输出量的拉氏反变换就是系统的脉冲响应函数,用)(t k 表示,即1()[()]k t s -=Φ脉冲响应函数)(t k ,是在初始条件等于零的情况下,线性系统对单位脉冲输入信号的响应。
可见,线性定常系统的传递函数与脉冲响应函数,就系统动态特性来说,二者所包含的信息是相同的。
所以,如果以脉冲函数作为系统的输入量,并测出系统的响应,就可以获得有关系统动态特性的全部信息。
在具体实践中,与系统的时间常数相比,持续时间短得很多的脉动输入信号就可以看成是脉冲信号。
设脉冲输入信号的幅度为11t ,宽度为1t ,现研究一阶系统对这种脉动信号的响应。
如果输入脉动信号的持续时间t )0(1t t <<,与系统的时间常数T 相比足够小,那么系统的响应将近似于单位脉冲响应。
为了确定1t 是否足够小,可以用幅度为12t ,持续时间(宽度)为21t 的脉动输入信号来进行试验。
如果系统对幅度为11t ,宽度为1t 的脉动输入信号的响应,与系统对幅度为12t ,宽度为21t 的脉动输入信号的响应相比,两者基本上相同,那么1t 就可以认为是足够小了。
图3-3(a)表示一阶系统脉动输入信号的响应曲线;图3-3(c)表示一阶系统对脉冲输入信号的响应曲线。
应当指出,如果脉动输入信号T t 1.01<(图3-3(b)所示),则系统的响应将非常接近于系统对单位脉冲信号的响应。
传递函数辨识(2):脉冲响应两点法和三点法
传递函数辨识(2):脉冲响应两点法和三点法丁锋;徐玲;刘喜梅【摘要】本工作利用系统的脉冲响应观测数据,提出了辨识一阶系统、二阶系统传递函数参数的两点法、三点法等,以及确定传递函数参数的差分方程法和面积法.所提出的方法能够避免直接求解超越方程,且原理简单,实现方便.%By means of the system impulse response data,this paper presents two-point methods and three-point methods for identifying the parameters of first-order systems and second-order systems,which are described by transfer functions,and presents the difference equation method and the area method for identifying transfer functions.The proposed algebraic methods of determining the parameters of the transfer functions have simple mechanism and ease to understand,and avoid solving some transcendental equations.【期刊名称】《青岛科技大学学报(自然科学版)》【年(卷),期】2018(039)002【总页数】15页(P1-15)【关键词】传递函数;参数估计;系统辨识;阶跃响应;脉冲响应【作者】丁锋;徐玲;刘喜梅【作者单位】青岛科技大学自动化与电子工程学院,山东青岛266042;江南大学物联网工程学院,江苏无锡214122;江南大学物联网工程学院,江苏无锡214122;青岛科技大学自动化与电子工程学院,山东青岛266042【正文语种】中文【中图分类】TP273传递函数是一种参数模型。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北京工商大学
《系统辨识》课程
实验报告
(2014-2015 1学期)
课程名称:系统辨识
题目:利用相关分析法辨识脉冲响应
专业班级:控制工程
学生姓名:
指导教师:刘刘
成绩:
2015年1月18日
一、实验目的
通过仿真实验掌握利用相关分析法辨识脉冲响应的原理和方法。
二、实验内容
图1为本实验的原理框图。
过程传递函数为)
(s
G,其中
Sec
2
6
T
Sec,
3
8
120
2
1
.
.
,=
=
=T
K;)
(
)
(k
z
k
u和分别为过程的输入和输出变量;)
(k
v
为过程测量白噪声,服从正态分布,均值为零,方差为2
v
σ,记作)
,
(
~
)
(2
v
N
k
vσ;
)
(k
g
为过程的脉冲响应理论值,)
(
ˆ
k
g为过程脉冲响应估计值,)
(~k
g为过程脉冲响应估计误差。
过程的输入驱动采用M序列,输出受到白噪声)
(k
v的污染。
根据过程的输入和输出数据{})(
),
(k
z
k
u,利用相关分析算法根据输出过程的脉冲响应值)
(
ˆ
k
g,并与过程脉冲响应理论值)
(k
g
比较,得到过程脉冲响应估计误差值)
(~k
g,当∞
→
k
时,应该有0
→
)
(~k
g。
图1 相关分析法辨识脉冲响应原理框图
三、实验要求
进行方案设计,模拟过程传递函数,获得输出数据,用M序列作为辨识的输入信号,噪声采用标准正态分布的白噪声,计算互相关函数,不同λ值的脉冲响应估计值、脉冲响应理论值和脉冲响应估计误差,计算信噪比,画出实验流程图,用MATLAB编程实现。
四、实验原理
相关分析法
v(k)
u(k) z(k)
)1
)(
1
(
)
(
2
1
+
+
=
s
T
s
T
K
s
G
y(k)
1、采用串联传递函数)
(s
G仿真
2
1
2
1
1
1
1
1
T
s
T
s
T
T
K
s
G
/
/
)
(
+
+
=
令
2
1
1T
T
K
K=,则)
(s
G的表达框图为:
2、一个单输入单输出线性定常系统的动态特性可用它的脉冲响应函数g(σ)来描述。
这样,只要记录x(t)、y(t)的值,并计算它们的互相关函数,即可求得脉冲响应函数g(τ)。
而在系统有正常输入的情形下,辨识脉冲响应的原理图如下图所示。
()()()
y t g x t d
σσσ
∞
=-
⎰
则
000
()
11
lim()()(){lim()()}
T T
T T
x t
y t x t dt g x t x t dt d
T T
τ
τσστσ
∞
→∞→∞
-
-=--
⎰⎰⎰
上式两端同乘,进而取时间均值,有
()()()
xy x
R g R d
τστσσ
∞
=-
-
⎰
则
这就是著名的维纳霍夫积分方程。
()
()(),()()
()()()()
()
()
x x
xy x
xy
x t
R k R k
R g R d kg
R
g
k
τδττσδτσ
τστσστ
τ
τ
∞
=-=-
-
=-=
=
⎰
如果输入是,这时的自相关函数为
则根据维纳霍夫积分方程可得
或者
白噪声
1
1
/1T
s
K
+
u(k) x(k)
2
1
1
T
s/
+
y(k)
五、实验框图
六、实验代码
function ex2
clc;
clear all;
close all;
%创建M序列
Np=63;%循环周期
delta_T = 1;%时钟节拍
a=1;%幅度
M(1)=1;
M(2)=0;
M(3)=0;
M(4)=1;
M(5)=1;
M(6)=0;%初始化M序列
M_XuLie(Np) = 0;
for n = 1 : Np
temp = xor(M(6), M(5));
if(temp == 0)
M_XuLie(n) = a;
else
M_XuLie(n) = -a;
end
M(6) = M(5);
M(5) = M(4);
M(4) = M(3);
M(3) = M(2);
M(2) = M(1);
M(1) = temp;
end
%生成M序列完毕
r=3;%周期数
u=repmat(M_XuLie,1,r+1);%将M序列赋给输入,作为输入信号%第一步,从u(k)得到x(k),y(k)
K = 120;
T0 = 1; % 采样时间
T1 = 8.3;
T2 = 6.2;
K1=K/(T1*T2);
%初始化X(k),Y(k)为0
K2=1
x(63)=0;
y(63)=0
for k = 2 : 63*4
%取得x(k)序列
x(k)=exp(-T0/T1)*x(k-1)+T1*K1*(1-exp(-T0/T1))*u(k-1)+T1*K1... *(T1*(exp(-T0/T1)-1)+T0)*(u(k)-u(k-1))/T0
%取得y(k)序列
y(k)=exp(-T0/T2)*y(k-1)+T2*K2*(1-exp(-T0/T2))*x(k-1)+T2*K2... *(T2*(exp(-T0/T2)-1)+T0)*(x(k)-x(k-1))/T0
end
%获取没有白噪声时候输出完毕
%作图
figure(1);
plot(u,'r');
hold on;
plot(x,'k');
plot(y,'b');
legend('u(k)','x(k)','y(k)');
%第二步,将白噪声添加入输出信号
%产生白噪声信号v
fangcha = 0.5;%随意指定的方差
v = fangcha * randn(1,63*4);
%信号叠加,输出实际信号z(k)
z = y + v;
figure(2);
%打印无白噪声污染信号
plot(y,'b');
hold on;
%打印白噪声信号
plot(v,'m');
%打印白噪声污染后的信号
plot(z,'k');
legend('y(k)','v(k)','z(k)');
%计算Rmz(k)
for k = 1 : Np
Rmz(k)=0;%初始化为0
for i = (Np + 1) : ((r+1)*Np)
Rmz(k)=Rmz(k) + u(i-k)*z(i);
end
Rmz(k)=Rmz(k)/(r*Np);
end
%计算c
c=-Rmz(Np - 1);
%计算脉冲响应估计值g1
g1=Np*(Rmz+c)/((Np+1)*a^2*delta_T);
%计算理论脉冲g0
for k = 1: Np
g0(k)=K/(T1-T2)*(exp(-k*delta_T/T1)-exp(-k*delta_T/T2));
end
%计算脉冲响应估计误差delta_g
delta_g=sqrt(sum((g0-g1).^2)/sum(g0.^2));
figure(3);
plot(g0,'k');
hold on;
plot(g1,'r');
%axis([0,100,0,10]);
legend('脉冲响应理论值g0(k)','脉冲响应估计值g1');
七、实验结果
1、输入u(k),中间输入x(k),无干扰输入(k)
2、白噪声标准差为1.5时,理想输出y(k),带干扰的输出z(k),干扰v(k)
3、输入白噪声标准差为1.5,周期数r为3时,脉冲响应理论值与估计值:
脉冲响应估计误差: 0.0467
八、实验结论
1、根据维纳-霍夫积分方程,只要记录x(t)、y(t)的值,并计算它们的互相关函数,即可求得脉冲响应函数;
2、通过仿真,看到白噪声方差越大,实际输出结果的偏差也就越大;
3、周期数越大脉冲响应的估计值与理论值越接近,同时会增大数据量。
可以证明当k很大时,误差趋于0。
