北师大版九年级数学上册《图形的位似》
合集下载
北师大版九年级数学上册《位似图形》
的图形.
A
B
D
A'
B'
D' C
C'
O
探究
对于上面的问题,还有其他方法吗?如果在四边形外任选一个点O,分别在
OA、OB、OC、OD的反向延长线上取A' ,B' 、C' 、D' ,使得
OA' OB' OC' OD' 1 OA OB OC OD 2
呢?如果点O取在四边形ABCD内部呢?
分别画出这时得到的图形.
B'
B
观察对应点之间的坐标 的变化,你有什么发现?
A′(2,1) B′(2,0) A (6,3) B (6,0)
在平面直角坐标系中,有两点A(6,3),B(6,0),以 原点O为位似中心,位似比为1:3,把线段AB缩小.
A′(2,1),B′(2,0) y
A〞(-2,-1),B〞(-2,0) A (6,3), B (6,0),
C'
O
D' B'
A'
A B
C
D
A
D
BO
C
位似变换的步骤
①确定位似中心,位似中心的位置可随意选择; ②确定原图形的关键点,如四边形有四个关键点, 即它的四个顶点; ③确定位似比,根据位似比的取值,可以判断是 将一个图形放大还是缩小; ④符合要求的图形不唯一,因为所作的图形与所 确定的位似中心的位置有关,并且同一个位似中心的 两侧各有一个符合要求的图形。
A'
B〞
o
B'
A〞
A
观察对应点之间的坐 标
的变化,你有什x么发现?
B
课件北师大版九年级数学上册 图形的位似精美PPT课件

画法二:△ABC与△DEF异侧
解:画射线OA,OB,OC;
A
沿着射线OA,OB,OC反方向上分别取点D,E,F, 如(1)果两两个个位相似似形多一边定形是任相意似一形组;对应顶点P,P̍ 所在的直线都过同一点O,且OP ̍ =k· OP (k≠0),那么这样的两个多边形叫做位似多边形,点O叫做位似中心.
在射线OA,OB,OC上反分向别延取长点线D上,E分,F别,使取O点DD=,E2,FO,A使,OEA = 2OBD,,OOFB== 22OOCE;,
顺序连接D,E,F,使△DEF 用问橡题皮 :筋下放面大两图个形多的边方形法相放似大,图将形两:个图形的顶点相连,观察发现连接的直线相交于点O.
(解1):两画个射位线似O形A一,O定B,是O相C;似形;
。
。
。。
。
。
。
。
。
O
。
。
• 1.若△ABC与△A’B’C’的相似比为:
1:2,则OA:OA’=( 1:2 A’)。
A
B
B’
O
C
C’
性质:位似图形上任意一对对应点到位似中心的距离 之比等于相似比.
归纳
画位似图形的关键是画出图形中顶点
的对应点,画图的方法大致有两种:一是每
对对应点都在位似中心的同侧,二是每对对
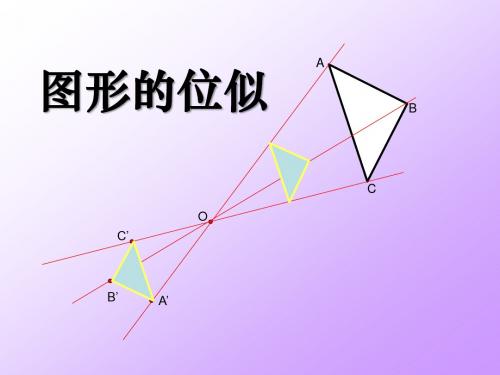
探索与思考☞ 观察下列图形的特点
A
B
C
P
D
特征: (1)是相似图形 (2)每组对应点所在的直线都经过同一个点
问题:下面两个多边形相似,将两个图形的顶点相连,
观察发现连接的直线相交于点O. OA' ,OB' ,OC' ,OD' ,OE'
OA OB OC OD OE 有什么关系?
数学北师大版九年级上册位似图形

概念与性质 2. 位似图形的性质
从第 (1),(2)图中,我们可以看到,△OAB∽△O A′B′, OA OB AB 则 = = . OA′ OB′ A′ B′
性质:位似图形上任意一对对应点到位似中心 的距离之比等于位似比.
若△ABC与△A’B’C’的相似比为:1:2,则OA: 1:2 OA’=( )。
A’ A B O C B’
C’
作出下列位似图形的位似中心:
O
点O即为所求
课堂小结
位似图形的概念:
回味无穷
如果两个图形不仅形状相 似,而且每组对应顶点所在的直 线都经过同一个点,对应边互相 平行,那么这样的两个图形叫 做位似图形,这个点叫做位似中 心,这时的相似比又称为位似比 .
位似图形的性质: 位似图形上的任意一对对应点 到位似中心的距离之比等于位似比
如果两个图形不仅是相似图形,而且对应顶 点的连线相交于一点,对应边平行,像这样的两 个图形叫位似图形.
这个点叫做位似中心, 这时的相似比又叫位似比。 特征:
1、位似图形一定是相似形,反之不一定。 2、判断位似图形时要注意首先它们必须是相似形, 其次每一对对应点所在直线都经过同一点。
1. 判断下列各对图形是不是位似图形.
(1)正五边形ABCDE与正五边 形A′B′C′D′E′; 是
(2)等边三角形ABC与等 边三角形A′B′C′. 是
思考:是否相似图形都是位似图形?
不一定
判断下面的正方形是不是位似图形?
A D
不是
E (1) B C F G
显然,位似图形是相似图形的特殊情形.相似 图形不一定是位似图形,可位似图形一定是相 似图形 思考:位似图形有何性质?
O O O
北师大版九年级数学上册第4章 位似图形

A'B'所在的位置,请把四边形A'B'C'D'其余部分补画上.
例7
如图,在的正方形网格中,每个小正方形的边长
均为,点和点在格点上,是格点三角形(顶点在网格线
交点上).
(1)画出以点为位似中心的位似图形,点的对应点分别为
点、和;
3:1
(2)与的周长之比为______.
本节课我们学习了位似图形,主要知识有:
不仅能解决实际问题,而且是我们后续知识学习的一个基础。
这节课我们将继续学习图形的变换。
自主探究
1.请同学们阅读课本113-114页内容.
2.请同学们阅读课本114页做一做,并完成做一做的内容.
3.请同学们在完成上面任务后思考以下问题:
位似图形具有什么性质?
①位似图形的对应顶点的连线经过位似中心;
②位似图形的对应边互相平行(或在同一条直线上);
③位似图形的对应顶点到位似中心(在不重合的情况下)的距离之比等于
相似比
小组讨论
小组展示
越展越优秀
提疑惑:你有什么疑惑?
教师讲评
知识点 1:位似图形的概念
一般地,如果两个相似多边形任意一组对应顶点 P,P'所在的直线都经过同一点O,且有
OP'=k·
1.什么是位似多边形?
一般地,如果两个相似多边形任意一组对应顶点 P,P'所在的直线都
经过同一点 O,且有 OP'=k·
OP(k≠0),那么这样的两个多边形叫做
位似多边形.
2.位似多边形的性质有哪些?
①位似图形的对应顶点的连线经过位似中心;
②位似图形的对应边互相平行(或在同一条直线上);
③位似图形的对应顶点到位似中心(在不重合的情况下)的距离之比
例7
如图,在的正方形网格中,每个小正方形的边长
均为,点和点在格点上,是格点三角形(顶点在网格线
交点上).
(1)画出以点为位似中心的位似图形,点的对应点分别为
点、和;
3:1
(2)与的周长之比为______.
本节课我们学习了位似图形,主要知识有:
不仅能解决实际问题,而且是我们后续知识学习的一个基础。
这节课我们将继续学习图形的变换。
自主探究
1.请同学们阅读课本113-114页内容.
2.请同学们阅读课本114页做一做,并完成做一做的内容.
3.请同学们在完成上面任务后思考以下问题:
位似图形具有什么性质?
①位似图形的对应顶点的连线经过位似中心;
②位似图形的对应边互相平行(或在同一条直线上);
③位似图形的对应顶点到位似中心(在不重合的情况下)的距离之比等于
相似比
小组讨论
小组展示
越展越优秀
提疑惑:你有什么疑惑?
教师讲评
知识点 1:位似图形的概念
一般地,如果两个相似多边形任意一组对应顶点 P,P'所在的直线都经过同一点O,且有
OP'=k·
1.什么是位似多边形?
一般地,如果两个相似多边形任意一组对应顶点 P,P'所在的直线都
经过同一点 O,且有 OP'=k·
OP(k≠0),那么这样的两个多边形叫做
位似多边形.
2.位似多边形的性质有哪些?
①位似图形的对应顶点的连线经过位似中心;
②位似图形的对应边互相平行(或在同一条直线上);
③位似图形的对应顶点到位似中心(在不重合的情况下)的距离之比
图形的位似 北师大版数学九年级上册

坐标和相似比之间关系.
教师板演区 学生展示区
新知讲解
探究:如图,在平面直角坐标系中,△OAB三个顶点的坐标分别为 O(0,0),A(3,0),B(2,3).
将点O,A,B 的横坐标、纵坐标都乘 -2,得到三个点,以这三个点为顶点的三角 形与△OAB位似吗?如果位似,指出位似 中心和相似比.
解:将点O,A,B 的横坐标、纵 坐标都乘-2,以所得三个点为顶点的 三角形△OA’’B’’ 与△OAB 也位 似,位似中心是原点,相似比是2 ∶1. 两个三角形位于位似中心的两侧.
新知讲解
探究:如图,在平面直角坐标系中,△OAB三个顶点的坐标分别为 O(0,0),A(3,0),B(2,3).
将点O,A,B 的横坐标、纵坐标都乘 2,得到三个点,以这三个点为顶点的三角 形与△OAB位似吗?如果位似,指出位似 中心和相似比.
解:将点O,A,B 的横坐标、纵 坐标都乘2,以所得三个点为顶点的三 角形△OA’B’ 与△OAB 位似,位似 中心是原点,相似比是2 ∶1.两个三 角形位于位似中心的同侧.
新知讲解
例:在平面直角坐标系中,四边形OABC 的顶点坐标分别为O(0, 0),A(6,0),B(3,6),C(-3,3). 以原点O 为位似中心,画出四边形 OABC 的位似图形,使它与四边形OABC 的相似比是2:3.
以原点O为位似中心,与四边形 OABC 相似比为2:3的位似图形有两个, 它们关于原点成中心对称.
D
A
B
C
D
课堂练习
2.如图,在平面直角坐标系中,正方形ABCD与正方形BEFG 是以原点O为位似中心的位似图形,且相似比为,点A,B,E 在 x 轴上,若正方形BEFG的边长为6,则C 点坐标为( )
北师大版九年级数学上册教学课件:4.8图形的位似 (共46张PPT)

拓展点一
拓展点二
解:(1)如图:
(2)C(-6,-2),D(-4,2).
拓展点一
拓展点二
(3)∵DE=4,OE=2,OF=2,EF=4,CF=6, ∴S△OCD=S 梯形 CDEF-S△ODE-S△OCF =2(DE+CF)· EF-2DE· OE-2CF· OF,
1 1 1 =2×(4+6)×4-2×4×2-2×6×2=10. 1 1 1
分析:两个位似图形的主要特征是:每对位似对应点与位似中心 共线;不经过位似中心的对应线段平行.则位似中心就是两对对应 点的延长线的交点.
拓展点一
拓展点二
解: ①当两个位似图形在位似中心同旁时,连接 CF 并延长交 x 轴于点 O'. 位似中心就是点 O',设直线 CF 的表达式为 y=kx+b,将 C(4,2),F(1,1)代入,得
知识点一
知识点二
知识点三
例3 如图,矩形OABC的顶点O是坐标原点,边OA在x轴上,边OC 在y轴上.若矩形OA1B1C1与矩形OABC关于点O位似,且矩形 1 OA1B1C1的面积等于矩形OABC面积的 4 ,则点B1的坐标是( ) A.(3,2) B.(-2,-3) C.(2,3)或(-2,-3) D.(3,2)或(-3,-2)
=
������������' ������������
=
������������' ������������
= 2;
1
顺次连接 A'B',B'C',C'D',D'A',得到所要画的四边形 A'B'C'D'.
知识点一
图形的位似课件北师大版数学九年级上册

E
内
E' O C'
部
A' B'
A
B
知识精讲
2. 位似图形的性质
(1)对应点所在的直线经过位似中心;
(2)任意一组对应点到位似中心的距离之比等于相似比;
(3)对应边平行或在同一条直线上.
D
′ ′′
=
.
D'
O
C'
E'
A'
D
C
E
B'
B
①
A
′ ′′
=
.
C
E
D'C'
E'
A A'OB' B
②
知识精讲
3. 位似图形的画法(将一个图形放大或缩小)
(1)确定位似中心和图形上的关键点;
(2)连接位似中心与关键点并延长所得线段;
(3)根据相似比确定位似图形上的关键点;
A'
(4)顺次连接位似图形上的关键点,得到位似图形.
A
画一个△A′B ′C ′,使它与∆位似,且相似比为2.
C'
C
O
B
′
分析: 设 = .
由矩形的周长
矩形与矩形′ ′ ′是位似图形
=
′ ′
D'
D
A
C'
C
B
用表示的长
用表示AB ′ , ′的长
B'
典例精讲
【例题3】如图,矩形与矩形′ ′ ′是
位似图形,为位似中心.已知矩形的周长为
24,′ = 4,′ = 2,求, 的长.
内
E' O C'
部
A' B'
A
B
知识精讲
2. 位似图形的性质
(1)对应点所在的直线经过位似中心;
(2)任意一组对应点到位似中心的距离之比等于相似比;
(3)对应边平行或在同一条直线上.
D
′ ′′
=
.
D'
O
C'
E'
A'
D
C
E
B'
B
①
A
′ ′′
=
.
C
E
D'C'
E'
A A'OB' B
②
知识精讲
3. 位似图形的画法(将一个图形放大或缩小)
(1)确定位似中心和图形上的关键点;
(2)连接位似中心与关键点并延长所得线段;
(3)根据相似比确定位似图形上的关键点;
A'
(4)顺次连接位似图形上的关键点,得到位似图形.
A
画一个△A′B ′C ′,使它与∆位似,且相似比为2.
C'
C
O
B
′
分析: 设 = .
由矩形的周长
矩形与矩形′ ′ ′是位似图形
=
′ ′
D'
D
A
C'
C
B
用表示的长
用表示AB ′ , ′的长
B'
典例精讲
【例题3】如图,矩形与矩形′ ′ ′是
位似图形,为位似中心.已知矩形的周长为
24,′ = 4,′ = 2,求, 的长.
图形的位似第1课时课件北师大版九年级数学上册

位似多边形
任意一组对应顶点 P ,P'所在
OP'= k ·OP ( k ≠0)
,点 O 叫做
课时学业质量评价
位似中心
,那么这样的两个
.
第1课时
位似图形
知识梳理
课时学业质量评价
1. 如图,已知△ ABC 与△ DEF 位似,位似中心点为 O ,且△ ABC 与△
DEF 的周长之比是4∶3,则 AO ∶ DO 的值为(
C. 16
B. 12
1
2
3
4
D. 20
5
6
C
)
第1课时
位似图形
知识梳理
课时学业质量评价
3. 如图,六边形 ABCDEF 与六边形 A1 B1 C1 D1 E1 F1是位似图形,点 O
为位似中心, OD = OD1,则 A1 B1∶ AB 为(
A. 2∶3
D
第3题图
C. 1∶2
B. 3∶2
1
2
3
B
)
第1题图
A. 4∶7
B. 4∶3
C. 3∶4
1
2
3
4
5
D. 16∶9
6
第1课时
位似图形
课时学业质量评价
知识梳理
2. 如图,△ ABC 与△ A1 B1 C1位似, A1, B1, C1分别为 OA , OB , OC
的中点,若△ A1 B1 C1面积是4,则△ ABC 的面积为(
A. 4
第2题图
点D,E,F,则△DEF与△ABC位似,且类
似比为 2.
图5
探究新知
做一做
用以下方法可以近似地把一个不规则图形放大:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在下列每个图形中,位似图形的对
应线段AB与A′B′是否平行?BC与
观察--思考
用点光源将△ABC投影到与其平 行的幕墙上得到△A′B′C′
改变点光源O的位置, 你有什么发现?
O
A C
B
A′ C′
B′
观察--思考
用点光源将△ABC投影到与其平行 的幕墙上 得到△A′B′C′
改变点光源O的位置, 你有什么发现?
A C
O B
① △ABC ∽△A′B′C′ ②对应点的连线相交于一点 ③对应边互相平行
y
3.⑴如图,已知A(2,0),
写出B、C的坐标。
CF ′
⑵将A、B、C的横坐标和
纵组成坐△标A都′B乘′C2,′写所出得A′各、点B′、BE ′
C′的坐标,画出△A′B′C′
C
B
⑶以O为位似中心,
按比例尺2:1,把
△ABC放大为△DEF O A AD′
x
典例分析
1、下列说法错误的是( )
A、位似图形一定是相似图形 B、相似图形不一定是位似图形 C、位似图形上任意一对对应点到位似中心的距 离之比等于位似比 D、位似图形中每组对应点所在的直线必相互平 行
得图1;
(2)以点Q为位似中心,按相似比1:2将图形缩小,
得图2。
图1与图2的相似比是(
),面积的比是(
)。
P 。Q
小结:
1.以前我们学习了平移、对称、旋转变 换,它们的特点是什么?
2. 位似变换的特点是什么?
观察与思考☞
下列图形中,每个图中的
四边形ABCD和四边形A′B′C′D′都是相似图形.分
已知点O和ΔABC
分别在OA、OB、OC的反向延长线上取点A2、
B2、C2,使
OA 2
OA
OB 2
OB
OC 2
OC
2 ,画ΔA2B2C2.
A2
B
C2
CO
A B2
合作交流
A1
A2
A
.
C
O
B
B1
C1 B
CO A
C2 B2
(1)ΔABC与ΔA1B1C1及ΔABC与ΔA2B2C2是否 分别相似?为什么?
C
F
O E B
F
O
D
B
将三角形ABC放大一倍。
A' . A
O.
B
C
B’
C’
将黄色五角星缩 小为原来的一半
。
。
。。
。
。
。
。
。
O
。
。
位似图形特征: 1、位似图形一定是相似形,反之 不一定。 2、判断位似图形时要注意首先它 们必须是相似形,其次每一对对应 点所在直线都经过同一点。
---试一试--- 你发现了什么?
典例分析
2、如图,△ABC与 △ABC是位似图形,点O
是位似中心,若 OA 2AA,S△ABC 8 ,则
S△ABC
C1 .
C
A
A1
O B B1
典例分析
3、如图,以O为位似中心,将四边形ABCD 放大为原来的2倍.
C' D'
C D
. O
A
B
A'
B'
典例分析
4、如图在6×6的方格中画出等腰梯形ABCD 的位似图形,位似中心为点A,所画图形与 原等腰梯形ABCD的位似比为2:1.
A′ C′
B′
下面两副图是相似形吗?认真观察 看它们还有什么特征?
B
A C E O
M
D F
N
探索活动
已知点O和ΔABC
(1)画射线OA、OB、OC,分别在OA、OB、OC
上取点A1、B1 、C1,使
OA 1
OB 1
OC 1
2
OA OB OC
画ΔA1B1C1.
A1
A
C1
.
C
O
B
B1
探索活动
如图,D,E分别AB,AC上的点.
(1)如果DE∥BC,那么∆ADE和 ∆ABC是位似图形吗?为什么? B
A DE
C
(2)如果∆ADE和 ∆ABC是位似图形,那么 DE∥BC吗?为什么?
解:(2) DE∥BC.理由是:
∆ADE和 ∆ABC是位似图形, ∆ADE∽ ∆ABC
∠ADE=∠B
DE∥BC.
∆ABC是位似图形吗?为什么? B
C
解:(1) ∆ADE和 ∆ABC是位似图形.理由是:
因为DE∥BC,所以∠ADE和=∠B, ∠AED =∠C.所以∆ADE∽ ∆ABC.
又因为 点A是∆ADE和 ∆ABC的公共点,点D 和点B是对应点,点E和点C是对应点,直线 BD与CE交于点A,所以∆ΔABC与ΔA1B1C1及ΔABC与ΔA2B2C2在 位置上还有什么特点?
A1 A
.
C
O
B
B1
C1 B
CO A
A2 C2
B2
1. 在上图中,两个多边形不仅相似,而且 对应顶点的连线交于一点,像这样的两个图形
叫做位似形,这个点叫做位似中 心. (对应边互相平行)
A1
A
.
C
O
B
C1 B
CO A
B1
2.位似形有哪些性质呢?:
A2 C2
B2
(1)两个位似形一定是相似形; (2)对应顶点所在的直线都经过同一点; (3)对应顶点到位似中心的距离之比等于相似比.
---试一试---
请你总结一下:这个问题 有几种解法?
2.如图,已知点O和△ABC
1
以O为位似中心,将△ABC缩小为原来的 2
A
A
D
C
E
第五步:过G点作GD⊥BC于点D.四边形 DEFG即为所求作的正方形DEFG.
典例分析
根据以上作图步骤,回答以下问题:
(1)上述所求作的四边形DEFG是正方形吗?为 什么?
(2)在△ABC中,如果BC=10,高AQ=6,求上
述正方形DEFG的边长.
A
G
F
G1 F1
B D1 E1 D
EC
(1)以点P为位似中心,按相似比2:1将图形放大,
什么位置关系? 位置不一样,位似中心就不一样.
(2)在各图中,任取一对对应点,度量这两个点到位
似中心的距离.它们的比与位似比有什么关系?再换一对
对应点试一试.
相等.
位似图形的对应点和位似中心在 同一条直线上,它们到位似中心的 距离之比等于相似比.
如图,D,E分别AB,AC上的点.
A
(1)如果DE∥BC,那么∆ADE和 D E
别观察这五个图,你发现每个图中的两个四边形
各对应点的连线有什么特征?
如果两个相似图形的每组对应点 所在的直线都交于一点,那么这样 的两个图形叫做位似图形, 这个 交点叫做位似中心, 这时两个相 似图形的相似比又叫做它们的位 似比.
观察下图中的五个图,回答下列问题:
(1)在各图中,位似图形的位似中心与这两个图形有
DC
A
B
典例分析
5、在给定的锐角△ABC中,求作一个正方 形DEFG,使D、E落在BC上,F、G分别落 在AC、AB边上,作法如下:
第一步:画出一个有3个顶点落在△ABC两边上 的正方形D1E1F1G1; 第二步:连结BF1,并延长交AC于点F; 第三步:过F点作FE⊥BC交AB于点E;
第四步:过F点作FG∥BC交AB于点G;
