高考数学葵花宝典
刘有珍数量资料《葵花宝典》
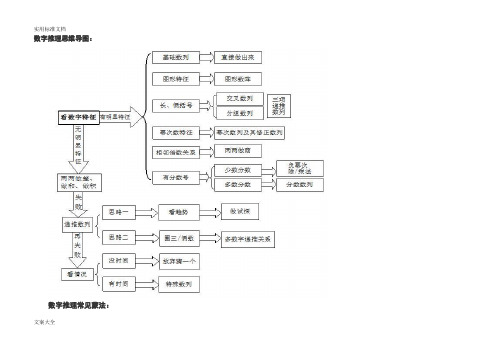
数字推理思维导图:数字推理常见蒙法:文案大全1)根据数字变化趋势蒙 2)根据数字属性蒙(奇偶属性,质数属性,合数属性) 3)根据选项大小蒙,优大原则4)根据选项变化蒙,选最不可思议的选项 5)蒙“1”法题型例题方法技巧及注意事项基础数列等差数列1,4,7,10,13,16,.......基础数列属于工具数列,虽然这部分内容不会直接出现在考试题目当中,但是它是我们在做题中的中间过程,必须熟练掌握。
等比数列1,3,9,27,81,243,......质数数列2,3,5,7,11,13,17,19,......合数数列4,6,8,9,10,12,14,15,16,......周期数列1,2,5,1,2,5,......直接递推数列和:1,2,3,5,8,13,......差:23,14,9,5,4,1,3,......积:2,3,6,18,108,......商:243,27,9,3,3,1,3,......多级数列二级数列二级等差数列:2,3,6,11,()A.15B.18C.17D.16做一次差:1,3,5 方法:逐差法。
常见错误:1.做差计算错误;2.做差时“左减右”和“右减左”混乱。
注:二级数列加括号,数列长度不会少于5项。
二级等比数列:1,2,5,14,41,()A.122B.126C.131D.143做一次差:1,3,9,27二级等比数列可以被看作递推倍数数列。
三级数列三级等差数列:12,14,19,29,46,()A.62B.68C.72D.76做一次差:2,5,10,17做两次差:3,5,7方法:两次逐差法常见错误:1.做差计算错误;2.做差时“左减右”和“右减左”混乱。
注:三级数列加括号,数列长度不会少于6项。
商和多级数列做商多级数列:1,1,2,6,24,()A.48B.96C.120D.122特征:数字之间存在明显的倍数关系。
做商之后得到的数列是基础数列。
文案大全做商一次:1,2,3,4,5做和多级数列:2,1,5,7,17,31,()A.59B.61C.65D.69做和一次:3,6,12,24,48两两做和之后得到的数列是基础数列。
葵花宝典——教你如何获取高考高分秘笈

葵花宝典——教你如何获取高考高分秘笈葵花宝典——教你如何获取高考高分秘笈葵花宝典——教你如何获取高考高分秘笈拿到试卷后,首先要听清监考老师的说明,看清试卷对考生的要求,答题说明和相关规定及注意事项,答卷之前要认真填好卷头,在指定位置把自己姓名、考号等认真填好,在做题时1审题要有一定的程序:(1)考生拿到试卷后,先看该试卷是不是本堂考试的试卷,再清点试卷页码是否齐全,检查试卷有无破损或漏印、重印、字迹模糊不清等情况。
如果发现问题,要及时报告监考人员处理,然后根据监考人员指令,在试卷规定的地方写上本人姓名和考号,第ⅱ卷还要在卷面右上角的座位号栏里填写自己的座位号。
在开考铃响之前如有时间,可浏览试卷,大致估计哪些题熟悉易做,哪些题生疏难做。
答题一定要在开考铃响了之后开始。
如提前答题将以(2)仔细阅读答题说明。
每份试卷前面都有关于本卷考试答题须知之类的要求,如哪类考生答哪部分题;哪些题是选答题,哪些题是必答题;哪些题可直接做在考卷上,哪些题要答在另一份考卷上;总共有几页,有几题等等,这些情况在作答前都必须搞清楚。
每年高考,都有考生在这方面出问题,或漏看了两题,或漏答了一页,也有多答题的情况,或将该答在另一份考卷上的答在了这一份考卷上。
(3)看清题目要求。
比如做选择题,就要看清是选正确的还是选不正确的,是选单项还是选多项。
考试中作文卷经常出现看错文体要求的情况,比如1996年高考,要求写一段说明文字介绍漫画,有些(4)看清题目本身。
数理化等学科要看清符号,英语要看清单词,语文要看清字词。
上海市有一年高考作文题叫《父辈》,不少考生写成了《父亲》。
一字之差,离题万里。
要确实弄清楚每道题的题意,搞清楚题目给予的条件和要求。
因为考试要求可能与自己的答题习惯有所不同。
要特别注意题目的隐含条件。
考生应从题目的文字叙述,或从给出的示意图中去挖掘隐含条件,才能准确地解决问题。
要记住课题,在头脑中保持课题清晰、完整的印象。
高等代数葵花宝典

例 1.7. 设 A 是 n 阶正定矩阵,求证 |A| ≤ a11a22 · · · ann,等号成立当且仅当 A 是 对角矩阵。
习题课上多了,自己也有一些体会。 讲课跟做题是不一样的,你必须脑子里时刻 清楚自己在讲什么,接下来要讲什么,然后把它们用平缓的节奏一遍讲正确。 你讲的 语气速度快了,或者思维有了跳跃,学生一下跟不上,那么你后面的内容他们听起 来都很茫然。 当我一时不知道说什么好的时候,我会面色如常地擦擦黑板,换换粉 笔,整理一下自己的思路,绝不轻易开口。 因为如果你不小心说错了话,那比没说要 糟糕一百倍:接下来你要用十句话来挽救你的错误,学生很可能就被绕晕了。 即使是 “嗯”、“啊”、“那么”这些口头禅,也会暴露你的思路的紊乱。高深莫测永远是 Hold 局面的不二法宝。 我曾经开玩笑地给学生说,我讲课有一个优点,就是从来没有口头 禅。 结果大家都笑了。 我不解,然后大家异口同声的告诉我:老师,你讲课有一个口 头禅,就是“很显然”(囧)。希望我在这个文档里没有再犯这个错误 :P。
证明. 首先做合同变换把 A 化成标准形
( A ∼ Er
0
) 0, 0
这时 B 仍然是半正定的(虽然 B 也发生了变化),所以不妨从一开始就假设 A 就是如
上的标准形,并设
( B = B11
B21
) B12 , B22
B12 = B2′ 1,
我们要在保持 A 的形状的前提下把 B 化成标准形。
设正交矩阵 Q 使得
目录
第零章 第一章 第二章 第三章 第四章 第五章 第六章 第七章 第八章
番外话 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 将打洞进行到底 . . . . . . . . . . . . . . . . . . . . . . . . . . 2 Jordan 标准形总结 . . . . . . . . . . . . . . . . . . . . . . . . 7 秩不等式 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12 交结数:刻画相似程度的不变量 . . . . . . . . . . . . . . . . 16 同时上三角化 . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19 覆盖定理 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23 有理标准形和交换的矩阵 . . . . . . . . . . . . . . . . . . . . 25 解题的艺术 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30
葵花宝典——初中数学解题思维方法篇

初中数学解题方法小结1.配方法它的应用非常广泛,在因式分解、化简根式、解方程、证明等式和不等式、求函数的极值和解析式等方面都经常用到它。
2.因式分解法因式分解在代数、几何、三角函数等的解题中起着重要的作用。
因式分解的方法有许多,除中学课本上介绍的提取公因式法、公式法、分组分解法、十字相乘法等外,还有如利用拆项添项、求根分解、换元、待定系数等等。
3.换元法(等量代换)所谓换元法,就是在一个比较复杂的数学式子中,用新的变元去代替原式的一个部分或改造原来的式子,使它简化,使问题易于解决。
换元法是数学中一个非常重要而且应用十分广泛的解题方法4.判别式法与韦达定理方程思想b²-4ac与0的大小关系例如:求函数的解析式,先设方程,再代入坐标求系数值6. 构造法(数形结合法)在解题时,我们常常会采用这样的方法,通过对条件和结论的分析,构造辅助元素,它可以是一个图形、一个方程(组)、一个等式、一个函数、一个等价命题等,架起一座连接条件和结论的桥梁,从而使问题得以解决,这种解题的数学方法,我们称为构造法。
例如:如图,C 为线段BD 上一动点,分别过点B 、D 作AB ⊥BD ,ED ⊥BD ,连接AC 、EC .已知AB =5,DE =1,BD =8,设CD =x .(1)用含x 的代数式表示AC +CE 的长;并求AC +CE 的最小值;(2)若x +y =12,x >0,y >0请仿照(1)中的规律,运用构图法求出代数式9422+++y x 的最小值.7. 反证法反证法可以分为归谬反证法(结论的反面只有一种)与穷举反证法(结论的反面不只一种)。
8. 等(面或体)积法9. 几何变换法在数学问题的研究中,常常运用变换法,把复杂性问题转化为简单性的问题而得到解决。
几何变换包括:(1)平移;(2)旋转;(3)对称。
10. 归纳法归纳法是指通过前几个式子或图形的规律归纳出通项公式。
11. 数学分析法数学分析法是指根据某些技术问题之间的内在联系,运用数学模型来分析其相互之间关系的一种方法。
葵花宝典2.0

导数-----------By 墨(如有错误欢迎指正)一.参变分离1. 注意分离后的函数是否严格单调2. 注意定义域上是否取遍3. 严格单调且定义域取遍用端点效应 二.端点效应比较适用于恒成立问题,那么区间的端点也一定满足恒成立要求 1. 优先论证函数严格单调2. 在区间左右端至少能找一点满足题干3. 不到万不得已不要取无穷远端注:一旦定义域完全为开区间,要么丢失此法,要么洛必达开始论述,要么证明函数严格单调并证函数值大于(小于)端点值 【例1】方法1:参变分离 方法2:端点效应解: (我们可以看到函数要非负一定要增,也可能又增又减出现极小值) (这就是函数增的一个条件)(这就是函数值非负的必要条件,我们仅考虑的是函数严格递增的条件) (现在我们论证一下函数是否在此条件下单调增)显然我们应有此方法成立的充要条件是函数严格单调,我们考虑的端点并不是整个定义域的增减趋势,但是从0开始函数值一定要单调增,否则恒成立失效。
于是才有导函数在0处也非负,我们就得到a 的一个大致范围,通过这个大致范围作为已知条件验证其充分性。
【注】:充分性验证时一旦出现导函数有小于0的情况,表示函数不单调,则在必要性的条件下研究函数的最值。
【思考1】的取值范围,求有,a x f x ax e ax x f x0)(,01)1()(≥∀++-=φ 20,0)(0)('22)('202)0(')('0)('0,0)(0)0(0,0)(≤∀≥∴≥-+=∴≤≥+-+=≤∴≥-=-+=≥∀≥=∀≥----a x x f a e e x f a e e a e e xf a a f a e e x f x f x x f f x x f xx x x x x x x 是恒成立的充分必要条件充分性:恒成立的必要条件为又恒成立φΘφφΘ的取值范围恒成立,求,使得,其中a x f x ax e e x f x x 0)(0)(≥∀--=-φ三:极值点偏移我们分析一下二次函数:我们把1).构造:判断函数单调性确定两对称点的区间,分析法(传统艺能,不在论述))()()(,.2)2()()(,2.1)()(),(,),(2020210021212121xx f x f x G x x x x x f x f x F x x x x f x f x x x x x f -=--=+=≠∃构造与构造与已知函数2) 对数均值不等式2222ln ln 112b 0b a ba b a b a ab ba a ++--+ππππππ,则若)1()(02)11(2211)('0)(,ln 21)()1(ln 211ln ln ln 12ln ln 12ln ln 0=∴≥-=-+=--=-⇔∴=-⇔--⇔+--⇔+--f t f x xx t f t f t t t t f t t t t ba t baa b b a b a b a abb a b a b a abba b a b a ab b a φφφφφφφφφππφφ恒成立只需证则令原式令①左边:要证不妨设证明:021********2),()()(,)(x x x x x f x f x x x x c bx ax x f =+=≠∃++=我们有是二次函数的对称轴,使得,称为极值点右偏。
高考状元们的“葵花宝典”

高考状元们的“葵花宝典”状元是怎样炼成的?不上补习班,还能在30余万考生中夺魁,状元们究竟有何绝技?仅仅是勤奋,必定不够。
宝典中,状元们高效的学习、良好的心态是如何养成的,我们将一一揭秘他们的这些独门绝技!法宝1不上补习班状元们的最“可怕”之处在于——都不上补习班,学习还能那么高效谈及经验,每一位状元必总结“效率高”。
状元们的更“可怕”之处在于,都不上补习班!那么,他们究竟有何绝妙的高招提高效率?以下几招,我们可以偷学:杭州市理科状元王忻恬、杭州中考状元徐恩迪:口袋里始终揣着一本宝典——里头记着英语单词、化学方程式、物理公式等,每到吃饭排队时、等公交车时,必拿出来读读看看记记。
其实,这招是从著名数学家苏步青处偷学的。
苏老曾说,“我的时间有限,‘没有整匹布’,我挤时间的办法就是充分利用‘零布头’,把1分钟2分钟的时间都利用起来,这样‘零布头’也能派上用场。
”全省理科状元李清扬:他山之石,可以攻玉。
与同学交换和共享各自的复习笔记,受益良多。
全省理科状元张琛:基础最重要,对基础知识点做细致、系统的梳理。
怪题难题,统统不做。
没有基础,一切只是空中楼阁。
全省文科钟隽仪:动作快,做作业不拖拉。
这个好习惯,小学一年级开始,就得培养。
全省文科王子君:遇到难题,和同学一起研讨解决。
集思广益,同学的解法更能开拓思路。
全省文科状元姜动:上课45分钟,并非分分钟全神贯注,但在重要环节,肯定听得极认真。
最主要的是,知道自己在做什么,知道做什么才最有效果。
为了达到目的才做,达不到就不做。
会判断哪些作业对自己有用,有用的才做。
如果做了还是不明白,就找别的题目继续加强。
杭州市文科状元喻鹏阳:上课很专注,跟着老师的思路转。
若是有不懂,当场发问。
杭州中考状元蔡梦如:选择最高效率的时间段学习,比如,晚上七八点。
还比如,课上的时间最宝贵,一定得把握。
晚上周末的其他时间段,可看电视、玩电脑(打CS)。
不过,一定要见好就收。
法宝2一本纠错秘笈状元们人手一册纠错本,里面收集的是——哪里出错了,为什么错了,如何解决问题每一位状元,都有一本纠错秘笈。
数学葵花宝典
2012数学葵花宝典昨天的一切已经不可改变,但今天的努力可以改变昨天的轨迹,做好今天的每一件事,做对今天的每一道题,定能描绘出自己辉煌的人生前景,让我们一起共同努力吧! 一、集合1.对于集合,一定要抓住集合的代表元素,及元素的“确定性、互异性、无序性”。
如:(1)已知R 是实数集,{21,M x N yy x ⎧⎫=<==⎨⎬⎩⎭,则RN CM ⋂=____________(2)已知集合{}b a a a b a +=⎭⎬⎫⎩⎨⎧,,0,,12,则20102011b a += .2.进行集合的交、并、补运算时,不要忘记集合本身和空集∅的特殊情况。
空集是任何集合的子集,是任何非空集合的真子集。
如:(1)集合{}{}2|230|1A x x x B x ax =--===,,若B A ⊂,则实数a 的值构成的集合为(2)已知集合}023|{2=+-=x x x A ,}0)5()1(2|{22=-+++=a x a x x B , ①若}2{=B A ,求实数a 的值;②若A B A = ,求实数a 的取值范围.3.注意下列性质:(1)集合{}12n a a a ,,……,的所有子集的个数是2n ,真子集的个数是2n -1 (2)若A B A B A A B B ⊆⇔== ,;(3)德摩根定律:()()()()()()U U U U U U A B A B A B A B C C C C C C == , 注重借助于数轴和文氏图解集合问题如:(1)设全集}5,4,3,2,1{=U ,若}2{=B A ,}4{)(=B A C U ,}5,1{)()(=B C A C U U ,则A =________B =________(2)已知集合}90{},06{2<-<=<--=m x x B x x x A ,①若B B A = ,求实数 m 的取值范围;②若φ=B A ,求实数m 的取值范围.4.你会用补集思想解决问题吗?(排除法、间接法) 如:(1)已知关于x 的不等式250ax x a-<-的解集为M ,若3M ∈且5M ∉,求实数a 的取值范围。
《高考数学葵花宝典》
目录1.常见函数的图像…………………………………………………………1-72.常用的放缩公式…………………………………………………………8-93.恰当运用放缩法,巧证导数不等式…………………………10-124.对数平均值不等式链的证明与应用…………………………13-275.活跃在各类考试中的对数平均不等式………………………28-316.均值不等式几何解释的探究 (32)7.高三数学一轮复习感悟总结及二轮复习策略……………33-40图像图像1常用的放缩公式对数放缩1.放缩成一次函数()ln1x x+≤ln x x≤2.放缩成双撇函数()ln1x x<>()ln01x x><<()11ln,012x x xx⎛⎫>-<<⎪⎝⎭()11ln,12x x xx⎛⎫<->⎪⎝⎭3.放缩成二次函数2ln x x x≤-()()21ln1,102x x x x+≤--<<()()21ln1,02x x x x+≥->4.放缩成反比例函数1ln1xx≥-()1ln11xx+≥+()()21ln,11xx xx->>+()()21ln,011xx xx-<<<+()()2ln1,101xx xx+<-<<+()()2ln1,01xx xx+>>+指数放缩1.放缩成一次函数1xe x≥+x e ex≥x e x>2.放缩成反比例函数()1,01xe xx≤≤-()1,0xe xx<-<3.放缩成二次函数()211,02xe x x x≥++>2311126xe x x x≥+++指对数放缩()()ln112xe x x x-≥+--=三角函数放缩tan sin,02x x x xπ⎛⎫>><<⎪⎝⎭21sin2x x x≥-22111cos1sin22x x x-≤≤-以直线1y x=-为切线的函数lny x=11xy e-=-2y x x=-11yx=-lny x x=对数平均值不等式链a b>>若,则2211ln ln2ab a b a ba ba b a ba b-+<=<<<<+-+裂项放缩分式放缩姐妹不等式,即()0,0b b m a b m a a m +<>>>+;()0,0b b m b a m a a m+>>>>+; 记忆口诀:“小者小,大者大”;解释:看字母b ,b 小,则不等式的符号是小于号,反之大于号。
2013年高考数学宝典(高一到高三所有知识点总结大全)
2013年高考数学宝典(高一到高三所有知识点总结大全)祝你成功1、高一数学必修1123412n x A x B A B A B A n A ∈∉⎧⎪⎪⎨⎪⎪⎩∈⇒∈⊆()元素与集合的关系:属于()和不属于()()集合中元素的特性:确定性、互异性、无序性集合与元素()集合的分类:按集合中元素的个数多少分为:有限集、无限集、空集()集合的表示方法:列举法、描述法(自然语言描述、特征性质描述)、图示法、区间法子集:若 ,则,即是的子集。
、若集合中有个元素,则集合的子集有个, 注关系集合集合与集合{}00(2-1)23,,,,.4/n A A A B C A B B C A C A B A B x B x A A B A B A B A B A B x x A x B A A A A A B B A A B ⎧⎪⎧⎪⎪⎪⊆⎪⎪⎨⎪⊆⊆⊆⎨⎪⎪⎪⎩⎪⎪⊆≠∈∉⎪⊆⊇⇔=⎪⎩⋂=∈∈⋂=⋂∅=∅⋂=⋂⋂⊆真子集有个。
、任何一个集合是它本身的子集,即 、对于集合如果,且那么、空集是任何集合的(真)子集。
真子集:若且(即至少存在但),则是的真子集。
集合相等:且 定义:且交集性质:,,,运算{}{},/()()()-()/()()()()()()U U U U U U U U A A B B A B A B A B x x A x B A A A A A A B B A A B A A B B A B A B Card A B Card A Card B Card A B C A x x U x A A C A A C A A U C C A A C A B C A C B ⎧⎪⎨⋂⊆⊆⇔⋂⎪⎩⎧⋃=∈∈⎪⎨⋃=⋃∅=⋃=⋃⋃⊇⋃⊇⊆⇔⋃⎪⎩⋃=+⋂=∈∉=⋂=∅⋃==⋂=⋃,定义:或并集性质:,,,,, 定义:且补集性质:,,,, ()()()U U U C A B C A C B ⎧⎪⎪⎪⎪⎪⎪⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎧⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⋃=⋂⎪⎪⎩⎩⎩⎩2\函数,,,A B A x B y f B A B x y x f y y x y →映射定义:设,是两个非空的集合,如果按某一个确定的对应关系,使对于集合中的任意一个元素, 在集合中都有唯一确定的元素与之对应,那么就称对应:为从集合到集合的一个映射传统定义:如果在某变化中有两个变量并且对于在某个范围内的每一个确定的值,定义 按照某个对应关系都有唯一确定的值和它对应。
《高考备考之葵花宝典》及疏议
《高考备考之葵花宝典》及疏议作者:王建锋前言面对高三学生,班主任最多的工作就是苦口婆心的劝诫他们,如何备考、如何学习、如何调试心理、如何应对考试。
渐渐的,悟出点道理来,于是就想针对高考、针对高三写一点经验心得,一可以让我从重复的工作中解脱出来,二可以让更多的高三学生受益。
第一章高考备考原则第一条集中精力原则:没有攻不克的考试,只有改不了的习惯[疏议] 只要是在纸张上做题,有标准答案的考试,就属于世界上最简单的那一类事——你不需要如父母一样为了生计而奔波操劳,你更不需要如警察叔叔一样与罪犯分子斗智斗勇,你唯一要做的就仅仅是集中精力。
但是,我们已经习惯于把自己当成多任务操作系统:吃饭的时候看电视,看电视的时候想学习,学习的时候想着玩,玩的时候想作业……殊不知,就因为这样,我们饭吃不香、电视看不爽、学习成绩差,玩的没有心情。
面临高考,我们只有改掉同时想/做几件事的习惯,把精力完全集中在课本和规范得不能再规范的试题上,才可能在有限的时间里获得无穷的可能。
第二条正确原则:正确的做事比做正确的事更重要。
[疏议] 这一条包括几个方面一是高三学生相比高一高二的学弟学妹来说,最大的优点在于知道学习了,大都将主要精力放到了学习上了,他们开始做正确的事了,此时如何正确的做事显的就更为重要了。
面对高考,如何才能更好的学习,如何才能在高考中取胜。
这是高考必胜者首先要思考的问题。
二是永远不要一开始就把精力放在弱科的提升上。
要先将自己学好的科目学好,学到最好,只少是年级前几名。
这样,就算你有一本弱科,也可用他来补,毕竟高考要的是总分。
更重要是强科效应将使你充满战胜所有高考的信心和力量。
三是永远不要放弃对弱科基础知识的学习与掌握,因为每一科中都有所谓的送分题。
如果你的弱科太多,那你一定考不上。
四、永远不要拿自己学不好和不可能的事情来折磨自己打击自己。
面对那些数学基础很差的文科学生,当他们发现数学又没有考好而痛不欲生时,我总是将他们批的体无完肤。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高考数学葵花宝典1.德摩根公式 ();()U U U U U U C A B C A C B C A B C A C B ==.2.U U A B A A B B A B C B C A =⇔=⇔⊆⇔⊆U A C B ⇔=ΦU C A B R ⇔=3.()()card AB cardA cardB card A B =+-()()card A B C cardA cardB cardC card A B =++-()()()()card A B card B C card C A card A B C ---+.4.二次函数的解析式的三种形式 ①一般式2()(0)f x ax bx c a =++≠;② 顶点式 2()()(0)f x a x h k a =-+≠;③零点式12()()()(0)f x a x x x x a =--≠.5.设[]2121,,x x b a x x ≠∈⋅那么[]1212()()()0x x f x f x -->⇔[]1212()()0(),f x f x f x a b x x ->⇔-在上是增函数;[]1212()()()0x x f x f x --<⇔[]1212()()0(),f x f x f x a b x x -<⇔-在上是减函数.设函数)(x f y =在某个区间内可导,如果0)(>'x f ,则)(x f 为增函数;如果0)(<'x f ,则)(x f 为减函数.6.函数()y f x =的图象的对称性:①函数()y f x =的图象关于直线x a =对称()()f a x f a x ⇔+=-(2)()f a x f x ⇔-=.②函数()y f x =的图象关于直线2a bx +=对称()()f a mx f b mx ⇔+=-()()f a b mx f mx ⇔+-=. 7.两个函数图象的对称性:①函数()y f x =与函数()y f x =-的图象关于直线0x =(即y 轴)对称.②函数()y f mx a =-与函数()y f b mx =-的图象关于直线2a b x m+=对称.③函数)(x f y =和)(1x f y -=的图象关于直线y=x 对称. 8.分数指数幂mn a =(0,,a m n N *>∈,且1n >).1m n m na a -=(0,,a m n N *>∈,且1n >).9.log (0,1,0)ba Nb a N a a N =⇔=>≠>.10.对数的换底公式 log log log m am N N a=.推论 loglog mn a anb b m=. 11.11,1,2n n n s n a s s n -=⎧=⎨-≥⎩( 数列{}n a 的前n 项的和为12n n s a a a =+++). 12.等差数列的通项公式*11(1)()n a a n d dn a d n N =+-=+-∈;其前n 项和公式 1()2n nn a a s +=1(1)2n n na d -=+211()22d n a d n =+-.13.等比数列的通项公式1*11()n n n a a a qq n N q-==⋅∈; 其前n 项的和公式11(1),11,1n n a q q s qna q ⎧-≠⎪=-⎨⎪=⎩或11,11,1n n a a qq q s na q -⎧≠⎪-=⎨⎪=⎩. 14.等比差数列{}n a :11,(0)n n a qa d a b q +=+=≠的通项公式为1(1),1(),11n n n b n d q a bq d b q d q q -+-=⎧⎪=+--⎨≠⎪-⎩;其前n 项和公式为(1),11(),1111n n nb n n d q s d q db n q q q q +-=⎧⎪=-⎨-+≠⎪---⎩. 15.分期付款(按揭贷款) 每次还款(1)(1)1nn ab b x b +=+-元(贷款a 元,n 次还清,每期利率为b ).16.同角三角函数的基本关系式 22sin cos 1θθ+=,tan θ=θθcos sin ,tan 1cot θθ⋅=.18.和角与差角公式sin()sin cos cos sin αβαβαβ±=±; cos()cos cos sin sin αβαβαβ±=;tan tan tan(),tan tan tan()(1tan tan )1tan tan αβαβαβαβαβαβ±±=±=±.,(1tan )(1tan )24A B k kZ A B ππ+=+∈⇔++= A+B+C=tanA+tanB+tanC=tanA tanB tanC π⇔sin cos a b αα+)αϕ+(辅助角ϕ所在象限由点(,)a b 的象限决定,tan b aϕ=). 19.二倍角公式sin 2sin cos ααα=.2222cos 2cos sin 2cos 112sin ααααα=-=-=-(记住降幂公式).22tan tan 21tan ααα=-.20.三角函数的周期公式 函数sin()y x ωϕ=+,x ∈R 及函数cos()y x ωϕ=+,x ∈R(A,ω,ϕ为常数,且A ≠0,ω>0)的周期2T πω=;函数tan()y x ωϕ=+,,2x k k Zππ≠+∈(A,ω,ϕ为常数,且A ≠0,ω>0)的周期T πω=.21.正弦定理 2sin sin sin a b cR A B C ===.22.余弦定理2222cos a b c bc A =+-;2222cos b c a ca B =+-; 2222cos c a b ab C =+-. 26.向量的平行与垂直 设a =11(,)x y ,b =22(,)x y ,且b ≠0,则a b⇔b =λa 12210x y x y ⇔-=.a⊥b(a ≠0)⇔a ·b=012120x x y y ⇔+=.27.线段的定比分公式 设111(,)P x y ,222(,)P x y ,(,)P x y 是线段12P P 的分点,λ是实数,且12PP PP λ=,则121211x x x y y y λλλλ+⎧=⎪⎪+⎨+⎪=⎪+⎩⇔121OP OP OP λλ+=+⇔12(1)OP tOP t OP =+-(11t λ=+).28.三角形的重心坐标公式 △ABC 三个顶点的坐标分别为11A(x ,y )、22B(x ,y )、33C(x ,y ),则△ABC的重心的坐标是123123(,)33x x x y y y G ++++.29.点的平移公式 ''''x x h x x h y y k y y k ⎧⎧=+=-⎪⎪⇔⎨⎨=+=-⎪⎪⎩⎩''OP OP PP ⇔=+ (图形F 上的任意一点P(x ,y)在平移后图形'F 上的对应点为'''(,)P x y ,且'PP 的坐标为(,)h k ).30.常用不等式: (1),a b R∈⇒222a b ab +≥(当且仅当a =b 时取“=”号).(2),a b R+∈⇒2a b+≥当且仅当a =b 时取“=”号). (3)3333(0,0,0).a b c abc a b c ++≥>>>(4)b a b a b a +≤+≤- 31.极值定理 已知y x ,都是正数,则有(1)如果积xy 是定值p ,那么当y x =时和y x +有最小值p 2;(2)如果和y x +是定值s ,那么当y x =时积xy 有最大值241s .32.一元二次不等式20(0)ax bx c ++><或2(0,40)a b ac ≠∆=->,如果a 与2ax bx c ++同号,则其解集在两根之外;如果a 与2ax bx c ++异号,则其解集在两根之间.简言之:同号两根之外,异号两根之间. 121212()()0()x x x x x x x x x <<⇔--<<; 121212,()()0()x x x x x x x x x x <>⇔--><或.33.含有绝对值的不等式 当a> 0时,有22x a x a a x a <⇔<⇔-<<.22x a x a x a >⇔>⇔>或x a <-.35.指数不等式与对数不等式 (1)当1a >时,()()()()f x g x a a f x g x >⇔>; ()0log ()log ()()0()()a a f x f x g x g x f x g x >⎧⎪>⇔>⎨⎪>⎩.(2)当01a <<时,()()()()f x g x a a f x g x >⇔<;()0log ()log ()()0()()a a f x f x g x g x f x g x >⎧⎪>⇔>⎨⎪<⎩36.斜率公式2121y y k x x -=-(111(,)P x y 、222(,)P x y ).37.直线的四种方程 (1)点斜式 11()y y k x x -=- (直线l 过点111(,)P x y ,且斜率为k ).(2)斜截式y kx b =+(b 为直线l 在y 轴上的截距).(3)两点式 112121y y x x y y x x --=--(12y y ≠)(111(,)P x y 、222(,)P x y (12x x ≠)).(4)一般式 0Ax By C ++=(其中A 、B 不同时为0).38.两条直线的平行和垂直 (1)若111:l y k x b =+,222:l y k x b =+①121212,l l k k b b ⇔=≠;②12121l l k k ⊥⇔=-.(2)若1111:0l A x B y C ++=,2222:0l A x B y C ++=,且A 1、A 2、B 1、B 2都不为零,①11112222A B C ll A B C ⇔=≠;②1212120l l A A B B ⊥⇔+=; 39.夹角公式 2121tan ||1k k k k α-=+.(111:l y k x b =+,222:l y k x b =+,121k k ≠-) 12211212tan A B A B A A B B α-=+(1111:0l A x B y C ++=,2222:0l A x B y C ++=,12120A A B B +≠). 直线12l l ⊥时,直线l 1与l 2的夹角是2π.40.点到直线的距离d =(点00(,)P x y ,直线l :0Ax By C ++=).41. 圆的四种方程(1)圆的标准方程 222()()x a y b r -+-=.(2)圆的一般方程220x y Dx Ey F ++++=(224D E F +->0).(3)圆的参数方程 cos sin x a r y b r θθ=+⎧⎨=+⎩.(4)圆的直径式方程 1212()()()()0x x x x y y y y --+--=(圆的直径的端点是11(,)A x y 、22(,)B x y ).42.椭圆22221(0)x y a b a b +=>>的参数方程是cos sin x a y b θθ=⎧⎨=⎩(了解). 43.椭圆22221(0)x y a b a b +=>>焦半径公式 )(21c a x e PF +=,)(22x c a e PF -=. 44.双曲线22221(0,0)x y a b a b -=>>的焦半径公式21|()|a PF e x c =+,22|()|a PF e x c=-. 45.抛物线px y 22=上的动点可设为P ),2(2y py 或或)2,2(2pt pt P P (,)x y ,其中 22y px=.47.直线与圆锥曲线相交的弦长公式AB =1212|||AB x x y y ==-=-(弦端点A),(),,(2211y x B y x ,由方程⎩⎨⎧=+=0)y ,x (F b kx y 消去y 得到02=++c bx ax ,注意0∆>,α为直线AB 的倾斜角,k 为直线的斜率). 48.曲线的两类对称问题:曲线(,)0F x y =关于点00(,)P x y 成中心对称的曲线是00(2-,2)0F x x y y -=.50.共线向量定理 对空间任意两个向量a 、b (b ≠0 ),a ∥b ⇔存在实数λ使a =λb . 51.对空间任一点O 和不共线的三点A 、B 、C ,满足OP xOA yOB zOC =++,则四点P 、A 、B 、C 是共面⇔1x y z ++=;P 是ABC ∆的重心13x y z ⇔===。
