MATLAB空间面板数据模型操作简介
利用MATLAB对状态空间模型进行分析

实验2 利用MATLAB 对状态空间模型进行分析2.1 实验设备 同实验1。
2.2 实验目的1、根据状态空间模型分析系统由初始状态和外部激励所引起的响应;2、通过编程、上机调试,掌握系统运动的分析方法。
2.3 实验原理说明给定系统的状态空间模型:)()()()()()(t t t t t t Du Cx y Bu Ax x+=+=& (2.1)设系统的初始时刻,初始状态为,则系统状态方程的解为)0(x 00=t ∫∫−−+=+=tt t tt t e e eee t 0)(0d )()0(d )()0()(ττττττBu x Bu x x A A A A A (2.2)输出为)(d )()0()(0)(t e e t tt t Du Bu C x C y A A ++=∫−τττ (2.3))(t x 包括两部分,第一部分是由系统自由运动引起的,是初始状态对系统运动的影响;第二部分是由控制输入引起的,反映了输入对系统状态的影响。
输出由三部分组成。
第一部分是当外部输入等于零时,由初始状态引起的,故为系统的零输入响应;第二部分是当初始状态为零时,由外部输入引起的,故为系统的外部输入响应;第三部分是系统输入的直接传输部分。
)(t y )(0t x )(0t x MATLAB 函数:函数initial(A,B,C,D,x0)可以得到系统输出对初始状态x0的时间响应; 函数step(A,B,C,D)给出了系统的单位阶跃响应曲线; 函数impulse(A,B,C,D) 给出了系统的单位脉冲响应曲线;函数 [y,T,x]=lsim(sys,u,t,x0) 给出了一个状态空间模型对任意输入的响应,其中的sys 表示贮存在计算机内的状态空间模型,它可以由函数sys=ss(A,B,C,D)得到,x0是初始状态。
u 2.4 实验步骤1、构建系统的状态空间模型,采用MATLA 的m-文件编程;2、求取系统的状态和输出响应;3、在MATLA 界面下调试程序,并检查是否运行正确。
MATLAB使用技巧大全

MATLAB使用技巧大全在科学计算和数据分析领域,MATLAB被广泛使用。
作为一种强大的软件工具,它提供了许多方便和高效的功能,帮助用户解决各种问题。
本文将介绍一些MATLAB的使用技巧,希望能够帮助读者更好地利用这个工具。
1. 向量和矩阵操作MATLAB中向量和矩阵的操作是非常常见的。
我们可以使用内置函数来创建向量和矩阵,如zeros、ones、eye等。
一些常用的操作包括:转置、矩阵相乘、元素相乘、矩阵求逆等。
此外,还可以使用索引和切片来访问和修改矩阵中的元素。
MATLAB还提供了一些特殊的矩阵函数,如diag、tril、triu等,用于生成特定类型的矩阵。
2. 图形绘制MATLAB提供了强大的绘图功能,可以生成各种类型的图形,如线图、散点图、柱状图、饼图等。
我们可以使用plot函数来绘制线图,scatter函数来绘制散点图,bar函数来绘制柱状图等。
此外,还可以对图形进行自定义,包括添加标题、坐标轴标签、图例等。
另外,MATLAB还支持三维和曲面绘图,用于可视化复杂的数据和函数关系。
3. 数据统计与分析MATLAB提供了许多用于数据统计和分析的函数。
例如,mean函数用于计算平均值,std函数用于计算标准差,median函数用于计算中位数等。
此外,MATLAB还提供了常见的统计分布函数,如正态分布、指数分布等。
通过这些函数,我们可以对数据进行描述统计和概率分析,从而更好地理解数据的特性和分布。
4. 信号处理MATLAB在信号处理领域也有广泛的应用。
它提供了许多用于信号处理的函数和工具箱,可以进行滤波、频谱分析、傅里叶变换等操作。
例如,我们可以使用fft函数进行快速傅里叶变换,使用filter函数进行滤波操作,使用spectrogram函数绘制频谱图等。
这些功能对于处理和分析信号具有重要意义,如音频处理、图像处理等。
5. 优化与求解MATLAB还提供了强大的优化和求解功能,可以用于解决复杂的数学问题。
MATLAB-空间计量模型详细步骤
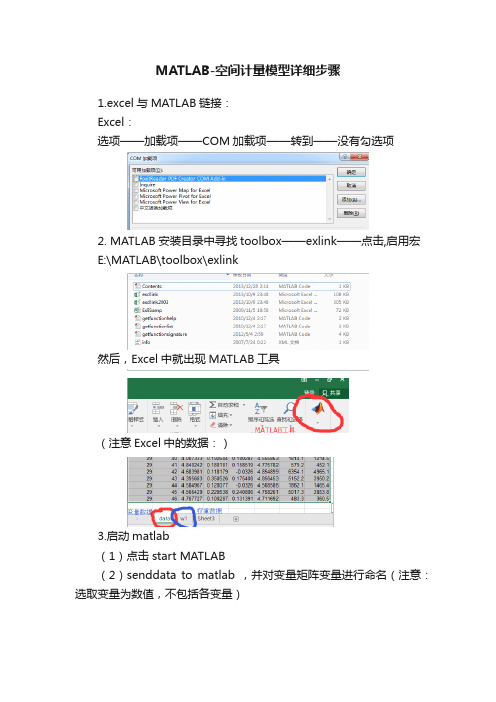
MATLAB-空间计量模型详细步骤1.excel与MATLAB链接:Excel:选项——加载项——COM加载项——转到——没有勾选项2. MATLAB安装目录中寻找toolbox——exlink——点击,启用宏E:\MATLAB\toolbox\exlink然后,Excel中就出现MATLAB工具(注意Excel中的数据:)3.启动matlab(1)点击start MATLAB(2)senddata to matlab ,并对变量矩阵变量进行命名(注意:选取变量为数值,不包括各变量)(data表中数据进行命名)(空间权重进行命名)(3)导入MATLAB中的两个矩阵变量就可以看见4.将elhorst和jplv7两个程序文件夹复制到MATLAB安装目录的toolbox文件夹5.设置路径:6.输入程序,得出结果T=30;N=46;W=norm(W1);y=A(:,3);x=A(:,[4,6]);xconstant=ones(N*T,1); [nobs K]=size(x);results=ols(y,[xconstant x]);vnames=strvcat('logcit','intercept','logp','logy');prt_reg(results,vnames,1);sige=results.sige*((nobs-K)/nobs);loglikols=-nobs/2*log(2*pi*sige)-1/(2*sige)*results.resid'*results.resid % The (robust)LM tests developed by ElhorstLMsarsem_panel(results,W,y,[xconstant x]); % (Robust) LM tests 解释附录:静态面板空间计量经济学一、OLS静态面板编程1、普通面板编程T=30;N=46;W=normw(W1);y=A(:,3);x=A(:,[4,6]);xconstant=ones(N*T,1);[nobs K]=size(x);results=ols(y,[xconstant x]);vnames=strvcat('logcit','intercept','logp','logy');prt_reg(results,vnames,1);sige=results.sige*((nobs-K)/nobs);loglikols=-nobs/2*log(2*pi*sige)-1/(2*sige)*results.resid'*results.resid % The (robust)LM tests developed by ElhorstLMsarsem_panel(results,W,y,[xconstant x]); % (Robust) LM tests2、空间固定OLS (spatial-fixed effects)T=30;N=46;W=normw(W1);y=A(:,3);x=A(:,[4,6]);xconstant=ones(N*T,1);[nobs K]=size(x);model=1;[ywith,xwith,meanny,meannx,meanty,meantx]=demean(y,x, N,T,model );results=ols(ywith,xwith);vnames=strvcat('logcit','logp','logy'); % should be changed if x is changedprt_reg(results,vnames);sfe=meanny-meannx*results.beta; % including the constant term yme = y - mean(y);et=ones(T,1);error=y-kron(et,sfe)-x*results.beta;rsqr1 = error'*error;rsqr2 = yme'*yme;FE_rsqr2 = 1.0 - rsqr1/rsqr2 % r-squared including fixed effectssige=results.sige*((nobs-K)/nobs);logliksfe=-nobs/2*log(2*pi*sige)-1/(2*sige)*results.resid'*results.residLMsarsem_panel(results,W,ywith,xwith); % (Robust) LM tests3、时期固定OLS(time-period fixed effects)T=30;N=46;W=normw(W1);y=A(:,3);x=A(:,[4,6]);xconstant=ones(N*T,1);[nobs K]=size(x);model=2;[ywith,xwith,meanny,meannx,meanty,meantx]=demean(y,x, N,T,model );results=ols(ywith,xwith);vnames=strvcat('logcit','logp','logy'); % should be changed if x is changedprt_reg(results,vnames);tfe=meanty-meantx*results.beta; % including the constant termyme = y - mean(y);en=ones(N,1);error=y-kron(tfe,en)-x*results.beta;rsqr1 = error'*error;rsqr2 = yme'*yme;FE_rsqr2 = 1.0 - rsqr1/rsqr2 % r-squared including fixed effectssige=results.sige*((nobs-K)/nobs);logliktfe=-nobs/2*log(2*pi*sige)-1/(2*sige)*results.resid'*results.residLMsarsem_panel(results,W,ywith,xwith); % (Robust) LM tests4、空间与时间双固定模型T=30;N=46;W=normw(W1);y=A(:,3);x=A(:,[4,6]);xconstant=ones(N*T,1);[nobs K]=size(x);model=3;[ywith,xwith,meanny,meannx,meanty,meantx]=demean(y,x, N,T,model );results=ols(ywith,xwith);vnames=strvcat('logcit','logp','logy'); % should be changed if x is changedprt_reg(results,vnames)en=ones(N,1);et=ones(T,1);intercept=mean(y)-mean(x)*results.beta;sfe=meanny-meannx*results.beta-kron(en,intercept);tfe=meanty-meantx*results.beta-kron(et,intercept);yme = y - mean(y);ent=ones(N*T,1);error=y-kron(tfe,en)-kron(et,sfe)-x*results.beta-kron(ent,intercept); rsqr1 = error'*error;rsqr2 = yme'*yme;FE_rsqr2 = 1.0 - rsqr1/rsqr2 % r-squared including fixed effects sige=results.sige*((nobs-K)/nobs);loglikstfe=-nobs/2*log(2*pi*sige)-1/(2*sige)*results.resid'*results.residLMsarsem_panel(results,W,ywith,xwith); % (Robust) LM tests二、静态面板SAR模型1、无固定效应(No fixed effects)T=30;N=46;W=normw(W1);y=A(:,[3]);x=A(:,[4,6]);for t=1:Tt1=(t-1)*N+1;t2=t*N;wx(t1:t2,:)=W*x(t1:t2,:);endxconstant=ones(N*T,1);[nobs K]=size(x);info.lflag=0;info.model=0;info.fe=0;results=sar_panel_FE(y,[xconstant x],W,T,info); vnames=strvcat('logcit','intercept','logp','logy');prt_spnew(results,vnames,1)% Print out effects estimatesspat_model=0;direct_indirect_effects_estimates(results,W,spat_model); panel_effects_sar(results,vnames,W);2、空间固定效应(Spatial fixed effects)T=30;N=46;W=normw(W1);y=A(:,[3]);x=A(:,[4,6]);for t=1:Tt1=(t-1)*N+1;t2=t*N;wx(t1:t2,:)=W*x(t1:t2,:);endxconstant=ones(N*T,1);[nobs K]=size(x);info.lflag=0;info.model=1;info.fe=0;results=sar_panel_FE(y,x,W,T,info);vnames=strvcat('logcit','logp','logy');prt_spnew(results,vnames,1)% Print out effects estimatesspat_model=0;direct_indirect_effects_estimates(results,W,spat_model);panel_effects_sar(results,vnames,W);3、时点固定效应(Time period fixed effects)T=30;N=46;W=normw(W1);y=A(:,[3]);x=A(:,[4,6]);for t=1:Tt1=(t-1)*N+1;t2=t*N;wx(t1:t2,:)=W*x(t1:t2,:);endxconstant=ones(N*T,1);[nobs K]=size(x);info.lflag=0; % required for exact resultsinfo.model=2;info.fe=0; % Do not print intercept and fixed effects; use info.fe=1 to turn onresults=sar_panel_FE(y,x,W,T,info);vnames=strvcat('logcit','logp','logy');prt_spnew(results,vnames,1)% Print out effects estimatesspat_model=0;direct_indirect_effects_estimates(results,W,spat_model);panel_effects_sar(results,vnames,W);4、双固定效应(Spatial and time period fixed effects)T=30;N=46;W=normw(W1);y=A(:,[3]);x=A(:,[4,6]);for t=1:Tt1=(t-1)*N+1;t2=t*N;wx(t1:t2,:)=W*x(t1:t2,:);endxconstant=ones(N*T,1);[nobs K]=size(x);info.lflag=0; % required for exact resultsinfo.model=3;info.fe=0; % Do not print intercept and fixed effects; use info.fe=1 to turn onresults=sar_panel_FE(y,x,W,T,info);vnames=strvcat('logcit','logp','logy');prt_spnew(results,vnames,1)% Print out effects estimatesspat_model=0;direct_indirect_effects_estimates(results,W,spat_model);panel_effects_sar(results,vnames,W);三、静态面板SDM模型1、无固定效应(No fixed effects)T=30;N=46;W=normw(W1);y=A(:,[3]);x=A(:,[4,6]);for t=1:Tt1=(t-1)*N+1;t2=t*N;wx(t1:t2,:)=W*x(t1:t2,:);endxconstant=ones(N*T,1);[nobs K]=size(x);info.lflag=0;info.model=0;info.fe=0;results=sar_panel_FE(y,[xconstant x wx],W,T,info);vnames=strvcat('logcit','intercept','logp','logy','W*logp','W*l ogy');prt_spnew(results,vnames,1)% Print out effects estimatesspat_model=1;direct_indirect_effects_estimates(results,W,spat_model);panel_effects_sdm(results,vnames,W);2、空间固定效应(Spatial fixed effects)T=30;N=46;W=normw(W1);y=A(:,[3]);x=A(:,[4,6]);for t=1:Tt1=(t-1)*N+1;t2=t*N;wx(t1:t2,:)=W*x(t1:t2,:);endxconstant=ones(N*T,1);[nobs K]=size(x);info.lflag=0; % required for exact resultsinfo.model=1;info.fe=0; % Do not print intercept and fixed effects; use info.fe=1 to turn onresults=sar_panel_FE(y,[x wx],W,T,info);vnames=strvcat('logcit','logp','logy','W*logp','W*logy');prt_spnew(results,vnames,1)% Print out effects estimatesspat_model=1;direct_indirect_effects_estimates(results,W,spat_model);panel_effects_sdm(results,vnames,W);3、时点固定效应(Time period fixed effects)T=30;N=46;W=norm(W1);y=A(:,[3]);x=A(:,[4,6]);for t=1:Tt1=(t-1)*N+1;t2=t*N;wx(t1:t2,:)=W*x(t1:t2,:);endxconstant=ones(N*T,1);[nobs K]=size(x);info.lflag=0; % required for exact resultsinfo.model=2;info.fe=0; % Do not print intercept and fixed effects; use info.fe=1 to turn on% New routines to calculate effects estimatesresults=sar_panel_FE(y,[x wx],W,T,info);vnames=strvcat('logcit','logp','logy','W*logp','W*logy');% Print out coefficient estimatesprt_spnew(results,vnames,1)% Print out effects estimatesspat_model=1;direct_indirect_effects_estimates(results,W,spat_model);panel_effects_sdm(results,vnames,W)4、双固定效应(Spatial and time period fixed effects)T=30;N=46;W=normw(W1);y=A(:,[3]);x=A(:,[4,6]);for t=1:Tt1=(t-1)*N+1;t2=t*N;wx(t1:t2,:)=W*x(t1:t2,:);endxconstant=ones(N*T,1);[nobs K]=size(x);info.bc=0;info.lflag=0; % required for exact resultsinfo.model=3;info.fe=0; % Do not print intercept and fixed effects; use info.fe=1 to turn onresults=sar_panel_FE(y,[x wx],W,T,info);vnames=strvcat('logcit','logp','logy','W*logp','W*logy');prt_spnew(results,vnames,1)% Print out effects estimatesspat_model=1;direct_indirect_effects_estimates(results,W,spat_model);panel_effects_sdm(results,vnames,W)wald test spatial lag% Wald test for spatial Durbin model against spatial lagmodelbtemp=results.parm;varcov=results.cov;Rafg=zeros(K,2*K+2);for k=1:KRafg(k,K+k)=1; % R(1,3)=0 and R(2,4)=0;endWald_spatial_lag=(Rafg*btemp)'*inv(Rafg*varcov*Rafg')*Raf g*btemp prob_spatial_lag=1-chis_cdf (Wald_spatial_lag, K) wald test spatial error% Wald test spatial Durbin model against spatial error model R=zeros(K,1);for k=1:KR(k)=btemp(2*K+1)*btemp(k)+btemp(K+k); % k changed in 1,7/12/2010% R(1)=btemp(5)*btemp(1)+btemp(3);% R(2)=btemp(5)*btemp(2)+btemp(4);endRafg=zeros(K,2*K+2);for k=1:KRafg(k,k) =btemp(2*K+1); % k changed in 1, 7/12/2010Rafg(k,K+k) =1;Rafg(k,2*K+1)=btemp(k);% Rafg(1,1)=btemp(5);Rafg(1,3)=1;Rafg(1,5)=btemp(1);% Rafg(2,2)=btemp(5);Rafg(2,4)=1;Rafg(2,5)=btemp(2);endWald_spatial_error=R'*inv(Rafg*varcov*Rafg')*Rprob_spatial_error=1-chis_cdf (Wald_spatial_error,K)LR test spatial lagresultssar=sar_panel_FE(y,x,W,T,info);LR_spatial_lag=-2*(resultssar.lik-results.lik)prob_spatial_lag=1-chis_cdf (LR_spatial_lag,K)LR test spatial errorresultssem=sem_panel_FE(y,x,W,T,info);LR_spatial_error=-2*(resultssem.lik-results.lik)prob_spatial_error=1-chis_cdf (LR_spatial_error,K)5、空间随机效应与时点固定效应模型T=30;N=46;W=normw(W1);y=A(:,[3]);x=A(:,[4,6]);for t=1:Tt1=(t-1)*N+1;t2=t*N;wx(t1:t2,:)=W*x(t1:t2,:);endxconstant=ones(N*T,1);[nobs K]=size(x);[ywith,xwith,meanny,meannx,meanty,meantx]=demean(y,[x wx],N,T,2); % 2=time dummiesinfo.model=1;results=sar_panel_RE(ywith,xwith,W,T,info);prt_spnew(results,vnames,1)spat_model=1;direct_indirect_effects_estimates(results,W,spat_model);panel_effects_sdm(results,vnames,W)wald test spatial lagbtemp=results.parm(1:2*K+2);varcov=results.cov(1:2*K+2,1:2*K+2);Rafg=zeros(K,2*K+2);for k=1:KRafg(k,K+k)=1; % R(1,3)=0 and R(2,4)=0;endWald_spatial_lag=(Rafg*btemp)'*inv(Rafg*varcov*Rafg')*Raf g*btempprob_spatial_lag= 1-chis_cdf (Wald_spatial_lag, K)wald test spatial errorR=zeros(K,1);for k=1:KR(k)=btemp(2*K+1)*btemp(k)+btemp(K+k); % k changed in 1,7/12/2010% R(1)=btemp(5)*btemp(1)+btemp(3);% R(2)=btemp(5)*btemp(2)+btemp(4);endRafg=zeros(K,2*K+2);for k=1:KRafg(k,k) =btemp(2*K+1); % k changed in 1, 7/12/2010 Rafg(k,K+k) =1;Rafg(k,2*K+1)=btemp(k);% Rafg(1,1)=btemp(5);Rafg(1,3)=1;Rafg(1,5)=btemp(1);% Rafg(2,2)=btemp(5);Rafg(2,4)=1;Rafg(2,5)=btemp(2);endWald_spatial_error=R'*inv(Rafg*varcov*Rafg')*Rprob_spatial_error= 1-chis_cdf (Wald_spatial_error,K)LR test spatial lagresultssar=sar_panel_RE(ywith,xwith(:,1:K),W,T,info);LR_spatial_lag=-2*(resultssar.lik-results.lik)prob_spatial_lag=1-chis_cdf (LR_spatial_lag,K)LR test spatial errorresultssem=sem_panel_RE(ywith,xwith(:,1:K),W,T,info);LR_spatial_error=-2*(resultssem.lik-results.lik)prob_spatial_error=1-chis_cdf (LR_spatial_error,K)四、静态面板SEM模型1、无固定效应(No fixed effects)T=30;N=46;W=normw(W1);y=A(:,[3]);x=A(:,[4,6]);for t=1:Tt1=(t-1)*N+1;t2=t*N;wx(t1:t2,:)=W*x(t1:t2,:);endxconstant=ones(N*T,1);[nobs K]=size(x);info.lflag=0;info.model=0;info.fe=0;results=sem_panel_FE(y,[xconstant x],W,T,info);vnames=strvcat('logcit','intercept','logp','logy');prt_spnew(results,vnames,1)% Print out effects estimatesspat_model=0;direct_indirect_effects_estimates(results,W,spat_model); panel_effects_sar(results,vnames,W);2、空间固定效应(Spatial fixed effects)T=30;N=46;W=normw(W1);y=A(:,[3]);x=A(:,[4,6]);for t=1:Tt1=(t-1)*N+1;t2=t*N;wx(t1:t2,:)=W*x(t1:t2,:);endxconstant=ones(N*T,1);[nobs K]=size(x);info.lflag=0;info.model=1;info.fe=0;results=sem_panel_FE(y,x,W,T,info);vnames=strvcat('logcit','logp','logy');prt_spnew(results,vnames,1)% Print out effects estimatesspat_model=0;direct_indirect_effects_estimates(results,W,spat_model); panel_effects_sar(results,vnames,W);3、时点固定效应(Time period fixed effects)T=30;N=46;W=normw(W1);y=A(:,[3]);x=A(:,[4,6]);for t=1:Tt1=(t-1)*N+1;t2=t*N;wx(t1:t2,:)=W*x(t1:t2,:);endxconstant=ones(N*T,1);[nobs K]=size(x);info.lflag=0; % required for exact resultsinfo.model=2;info.fe=0; % Do not print intercept and fixed effects; use info.fe=1 to turn onresults=sem_panel_FE(y,x,W,T,info);vnames=strvcat('logcit','logp','logy');prt_spnew(results,vnames,1)% Print out effects estimatesspat_model=0;direct_indirect_effects_estimates(results,W,spat_model);panel_effects_sar(results,vnames,W);4、双固定效应(Spatial and time period fixed effects)T=30;N=46;W=normw(W1);y=A(:,[3]);x=A(:,[4,6]);for t=1:Tt1=(t-1)*N+1;t2=t*N;wx(t1:t2,:)=W*x(t1:t2,:);endxconstant=ones(N*T,1);[nobs K]=size(x);info.lflag=0; % required for exact resultsinfo.model=3;info.fe=0; % Do not print intercept and fixed effects; use info.fe=1 to turn onresults=sem_panel_FE(y,x,W,T,info);vnames=strvcat('logcit','logp','logy');prt_spnew(results,vnames,1)% Print out effects estimatesspat_model=0;direct_indirect_effects_estimates(results,W,spat_model); panel_effects_sar(results,vnames,W);五、静态面板SDEM模型1、无固定效应(No fixed effects)T=30;N=46;W=normw(W1);y=A(:,[3]);x=A(:,[4,6]);。
详解使用MATLAB软件进行科学计算

详解使用MATLAB软件进行科学计算第一章:MATLAB软件的简介和安装1.1 MATLAB软件的定义和特点MATLAB(Matrix Laboratory)是一种基于数值分析包的软件,它采用高级编程语言进行科学计算和数据可视化。
与其他编程语言相比,MATLAB具有易于学习和使用的特点。
1.2 MATLAB软件的安装和配置首先,从MathWorks官方网站下载MATLAB软件的安装包。
运行安装程序,按照指导完成安装过程。
安装完成后,根据个人需求配置MATLAB的工作环境,包括设置工作目录、添加路径等。
第二章:MATLAB基本操作和基本语法2.1 MATLAB的运行界面和基本操作启动MATLAB软件后,会显示主界面,包括命令窗口、编辑窗口、工作区等。
在命令窗口中输入和执行MATLAB命令,可以直接进行计算和操作。
2.2 MATLAB的数据类型和基本运算MATLAB支持多种数据类型,包括数值型、逻辑型、字符型等。
数值型数据可以进行基本运算,如加减乘除、幂运算等。
此外,MATLAB还提供了各种数学函数和工具箱,方便进行高级运算和分析。
第三章:MATLAB的向量和矩阵操作3.1 向量和矩阵的定义和初始化在MATLAB中,可以使用一维数组定义向量,使用二维数组定义矩阵。
也可以使用特定命令生成特定类型的向量和矩阵,如单位矩阵、随机矩阵等。
3.2 向量和矩阵的运算MATLAB提供了丰富的向量和矩阵运算函数,包括加减乘除、转置、矩阵乘法、逆矩阵等。
这些函数可以大大简化矩阵运算的过程。
第四章:MATLAB的数据可视化4.1 绘制二维图形MATLAB提供了丰富的函数和工具箱用于绘制二维图形,如plot函数、bar函数、scatter函数等。
可以通过设置参数和添加标签等方式,使得图形更加清晰美观。
4.2 绘制三维图形除了二维图形,MATLAB也支持绘制三维图形。
可以使用mesh函数、surfc函数等进行三维曲面绘制,使用scatter3函数进行散点图绘制等。
(一)空间面板数据模型

中国经济增长与能源消费空间面板分析*王火根1沈利生 2(1. 华侨大学商学院;2. 华侨大学数量经济与技术经济研究所、中国社会科学院数量经济与技术经济研究所)【摘要】近年来面板数据广泛应用于各类统计分析,但变量的空间相关并没有引起足够的重视。
本文引入空间面板回归模型研究中国各省市经济增长和能源消费的关系。
利用matlab软件及其spatial econometric模块建立和比较传统面板回归模型与空间面板回归模型,研究结果表明空间面板回归模型较传统面板回归模型优越,我们的工作为空间面板数据分析提供了一个应用实例。
关键词经济增长;能源消费;空间面板自相关;空间面板回归中图分类号F224 文献标识码AA Spatial Panel Statistical Analysis on Chinese Economic Growthand Energy ConsumptionAbstract This article studies the spatial panel autocorrelation of the Chinese provincialeconomic growth and the energy consumption. We found there was statistically significant spatial panel autocorrelation for these three variables. Further, we established and compared the simple linear panel regression model and the spatial linear panel regression. Our results indicated that the spatial linear panel regression model was better than the simple linear panel regression.Key words Economic growth, Energy consumption, Spatial panel autocorrelation, Spatiallinear panel model一、前言经济增长与能源消费之间关系一直是经济领域学者热门研究的主题。
MATLAB模型构建与优化方法介绍

MATLAB模型构建与优化方法介绍一、引言MATLAB(Matrix Laboratory)是一种强大而灵活的数值计算与数据可视化软件,广泛应用于科学、工程、金融等各个领域。
在模型构建与优化方面,MATLAB提供了丰富的工具和函数,使得用户可以方便地进行模型构建和参数优化。
二、MATLAB模型构建在MATLAB中,模型构建是指通过定义变量、方程和约束条件,将实际问题转化为数学模型。
MATLAB提供了多种方式来构建模型,其中最常用的是使用符号运算工具箱。
符号运算工具箱提供了符号计算的功能,可以在MATLAB中创建符号变量、符号函数和符号表达式。
用户可以使用符号计算工具箱对数学公式进行展开、求导、积分等操作,从而方便地构建数学模型。
例如,我们可以使用符号计算工具箱来构建一个简单的线性回归模型。
首先,创建符号变量x和y,表示输入和输出变量。
然后,定义线性模型的表达式为y =a*x + b,其中a和b为待求参数。
最后,通过最小二乘法等方法,可以求解出最优的参数值。
除了符号运算工具箱外,MATLAB还提供了其他模型构建工具,如优化工具箱、神经网络工具箱等。
用户可以根据具体需求选择合适的工具进行模型构建。
三、MATLAB模型优化模型优化是指通过调整模型参数,使得模型能够更好地拟合实际数据或达到最优性能。
MATLAB提供了多种优化方法,包括数值优化、遗传算法、模拟退火等。
1. 数值优化数值优化是一类通过迭代求解数值问题的方法。
MATLAB中的数值优化工具箱提供了多种数值优化算法,包括最小二乘法、非线性规划、最大似然估计等。
用户可以根据具体情况选择合适的算法进行优化。
例如,我们可以使用最小二乘法来优化线性回归模型中的参数。
最小二乘法通过最小化实际输出与模型输出之间的误差平方和,来得到最优的参数估计。
MATLAB中的lsqcurvefit函数可以方便地进行最小二乘法优化,用户只需提供模型函数和初始参数值即可。
2. 遗传算法遗传算法是一种模拟生物进化过程的启发式优化算法。
学习使用MATLAB进行数据分析和可视化的技巧
学习使用MATLAB进行数据分析和可视化的技巧MATLAB是一款功能强大且广泛使用的科学计算软件。
它提供了丰富的数据分析和可视化工具,可以帮助研究人员和工程师更好地处理和解释数据。
本文将介绍几种学习使用MATLAB进行数据分析和可视化的技巧,帮助读者更好地利用这个工具进行数据处理和呈现。
1. 数据导入和预处理:在开始数据分析之前,首先需要将数据导入到MATLAB中。
MATLAB提供了多种方法来导入不同格式的数据,如Excel、CSV、文本文件等。
可以使用`readtable`函数导入表格数据,`readmatrix`函数导入数值矩阵数据,`fopen`和`fscanf`函数等方式导入文本文件。
一旦数据导入成功,可能需要进行一些预处理步骤,例如数据清洗、缺失值处理等。
MATLAB提供了丰富的函数和工具箱,如数据清洗工具箱和统计工具箱,可帮助进行数据预处理。
2. 数据分析:一旦数据导入和预处理完成,下一步是进行数据分析。
MATLAB提供了许多常用的数据分析函数和工具,可以满足不同需求的分析任务。
例如,使用`mean`、`std`、`median`等函数可以计算数据的均值、标准差和中位数。
使用`correlation`函数可以计算多个变量之间的相关性。
使用`anova`函数可以进行方差分析等。
此外,MATLAB还提供了各种统计模型的函数和工具箱,例如线性回归、逻辑回归、聚类分析、时间序列分析等。
通过学习和掌握这些函数和工具箱,可以进行更复杂和深入的数据分析工作。
3. 可视化工具:数据分析的结果最好通过图形化方式展示,以便更好地理解和解释数据。
MATLAB提供了丰富的可视化函数和工具,可以方便地创建各种类型的图表和图形。
例如,使用`plot`函数可以创建二维折线图、散点图、柱状图等。
使用`histogram`函数可以创建直方图,显示数据的分布情况。
使用`heatmap`函数可以创建热力图,展示数据的矩阵关系。
如何使用MATLAB进行数据处理和模拟实验
如何使用MATLAB进行数据处理和模拟实验第一章:MATLAB简介MATLAB是一种强大的数值计算软件,广泛应用于科学与工程领域。
它具备丰富的数学和统计函数库,可以进行各种数据处理和模拟实验。
在本章中,我们将简要介绍MATLAB的基本特点和使用方法。
1.1 MATLAB的特点MATLAB具备以下特点:(1)矩阵计算:MATLAB内置了矩阵运算功能,使得数据处理更加简便和高效。
(2)图形显示:MATLAB可以生成高质量的二维和三维图形,方便数据可视化。
(3)函数丰富:MATLAB内置了大量的数学和统计函数,能够满足各种数值计算需求。
(4)易于学习:MATLAB的语法简单易懂,上手较容易,适合初学者。
1.2 MATLAB的安装和启动要使用MATLAB进行数据处理和模拟实验,首先需要安装MATLAB软件。
(1)从MathWorks官方网站下载MATLAB安装程序。
(2)运行安装程序,并按照提示进行安装。
(3)安装完成后,通过启动菜单或桌面图标启动MATLAB。
1.3 MATLAB的基本语法MATLAB的语法类似于其他编程语言,主要包括变量定义、函数调用、循环和条件判断等基本操作。
(1)变量定义:使用等号将数值或表达式赋给变量,例如:x = 2.5。
(2)函数调用:通过函数名和参数调用函数,例如:y =sin(x)。
(3)循环:使用for或while循环重复执行一段代码,例如:for i = 1:10。
(4)条件判断:使用if语句根据条件执行不同的代码块,例如:if x > 0。
第二章:数据处理数据处理是指从原始数据中提取、转换和整理信息的过程。
在MATLAB中,通过使用各种数据处理函数和工具箱可以实现对数据的各种操作。
2.1 数据导入和导出MATLAB支持多种数据格式的导入和导出,包括文本文件、Excel文件、图像文件等。
通过导入数据,可以将数据加载到MATLAB工作空间中进行处理。
(1)导入文本文件:使用readtable函数可以将文本文件中的数据读取为一个表格变量。
第二章Matlab 基本功能
>> A=[1,2,3,4;5,6,7,8;9,10,11,12;13,14,15,16] A=
1234 5678 9 10 11 12 13 14 15 16
>> B=[1,sqrt(25),9,13 2,6,10,7*2 3+sin(pi),7,11,15 4,abs(-8),12,16]
B= 1 5 9 13 2 6 10 14 3 7 11 15 4 8 12 16
3.利用M文件建立矩阵
对于比较大且比较复杂的矩阵,可以为它专门建立一个M
文件。下面通过一个简单例子来说明如何利用M文件创建
矩阵。
A=[1,2,3,4,5 6,7,8,9,10 11,12,13,14,15 16,17,18,19,20 21,22,23,24,25]
(1)启动有关编辑程序或MATLAB文本 编辑器,并输入待建矩阵:
3.访问多个元素
操作符“:”可以用来表示矩阵的多个元素。 若A是二维矩阵,其主要用法如下: Ø A(:,:) 返回矩阵A的所有元素。 Ø A(i,:) 返回矩阵A第i行的所有元素。
Ø A(i,k1:k2) 返回矩阵A第i行的自k1到k2 列的所有元素。
Ø A(:,j) 返回矩阵A第j列的所有元素。 Ø A(k1:k2,j) 返回矩阵A第j列的自k1到k2
>> a= linspace(-6,6,4) a=
-6 -2 2 6
>> b=logspace(0,2,4) b=
1.0000 4.6416 21.5443 100.0000
2.2.2 矩阵下标引用
本小节将介绍通过矩阵 下标 来存取元素值 的方法,包括访问单个元素、线性引用元 素和访问多个元素等。
MATLAB空间面板数据模型操作简介
MATLAB空间面板数据模型操作简介MATLAB安装:在民主湖资源站上下载MA TLAB 2009a,或者2010a,按照其中的安装说明安装MATLAB。
(MATLAB较大,占用内存较大,安装的话可能也要花费一定的时间)一、数据布局:首先我们说一下MA TLAB处理空间面板数据时,数据文件是怎么布局的,熟悉eviews的同学可能知道,eviews中面板数据布局是:一个省份所有年份的数据作为一个单元(纵截面:一个时间序列),然后再排放另一个省份所有年份的数据,依次将所有省份的数据排放完,如下图,红框中“1-94”“1-95”“1-96”“1-97”中,1是省份的代号,94,95,96,97表示年份,eviews是将每个省份的数据放在一起,再将所有省份堆放在一起。
与eviews不同,MATLAB处理空间面板数据时,面板数据的布局是(在excel中说明):先排放一个横截面上的数据(即某年所有省份的数据),再将不同年份的横截面按时间顺序堆放在一起。
如图:这里需要说明的是,MA TLAB中省份的序号需要与空间权重矩阵中省份一一对应,我们一般就采用《中国统计年鉴》分地区数据中省份的排列顺序。
(二阶空间权重矩阵我会在附件中给出)。
二、数据的输入:MATLAB与excel链接:在excel中点击“工具→加载宏→浏览”,找到MA TLAB的安装目录,一般来说,如果安装时没有修改安装路径,此安装目录为:C:\Programfiles\MATLAB\R2009a\toolbox\exlink,点击excllink.xla即可完成excel与MATLAB的链接。
这样的话excel中的数据就可以直接导入MATLAB中形成MATLAB的数据文件。
操作完成后excel 的加载宏界面如图:选中“Spreadsheet Link EX3.0.3 for use with MATLAB”即表示我们希望excel 与MATLAB实现链接。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
MATLAB空间面板数据模型操作简介MATLAB安装:在民主湖资源站上下载MA TLAB 2009a,或者2010a,按照其中的安装说明安装MATLAB。
(MATLAB较大,占用内存较大,安装的话可能也要花费一定的时间)一、数据布局:首先我们说一下MA TLAB处理空间面板数据时,数据文件是怎么布局的,熟悉eviews的同学可能知道,eviews中面板数据布局是:一个省份所有年份的数据作为一个单元(纵截面:一个时间序列),然后再排放另一个省份所有年份的数据,依次将所有省份的数据排放完,如下图,红框中“1-94”“1-95”“1-96”“1-97”中,1是省份的代号,94,95,96,97表示年份,eviews是将每个省份的数据放在一起,再将所有省份堆放在一起。
与eviews不同,MATLAB处理空间面板数据时,面板数据的布局是(在excel中说明):先排放一个横截面上的数据(即某年所有省份的数据),再将不同年份的横截面按时间顺序堆放在一起。
如图:这里需要说明的是,MA TLAB中省份的序号需要与空间权重矩阵中省份一一对应,我们一般就采用《中国统计年鉴》分地区数据中省份的排列顺序。
(二阶空间权重矩阵我会在附件中给出)。
二、数据的输入:MATLAB与excel链接:在excel中点击“工具→加载宏→浏览”,找到MA TLAB的安装目录,一般来说,如果安装时没有修改安装路径,此安装目录为:C:\Programfiles\MATLAB\R2009a\toolbox\exlink,点击excllink.xla即可完成excel与MATLAB的链接。
这样的话excel中的数据就可以直接导入MATLAB中形成MATLAB的数据文件。
操作完成后excel 的加载宏界面如图:选中“Spreadsheet Link EX3.0.3 for use with MATLAB”即表示我们希望excel 与MATLAB实现链接。
点击确定后,excel窗口如图:红色框内选项为:startMATLAB:表示打开MATLAB,一般来说,如果excel实现了与MA TLAB的链接,当我们打开excel时,excel会自动启动MATLAB,所以excel的打开速度很慢。
Putmatrix:表示将excel中的数据输入MATLAB中,我们经常用的就是此项,选中需要导入到MA TLAB中的数据(就是一个矩阵),点击putmatrix即可。
如:下表是一个数据表格,那么红色框内的数据就是我们需要导入MATLAB中的数据。
选中数据矩阵,点击putmatrix,出现如下窗口:我们需要在弹出的窗口中输入变量名称,即我们选中并输入到MA TLAB中的数据矩阵在MA TLAB中是以一个变量的形式存在,我们之后在使用时,需要调用该矩阵的某一列(后面详解)。
如我们在此输入变量名为“pc”,点击确定。
三、MATLAB窗口此时原来已经打开的MA TLAB窗口如图:标题栏菜单栏工具栏工作空间控制窗口历史记录这里我们简单介绍一下MATLAB的窗口,与很多我们见过的很多软件,如excel,word,spss 一样,MA TLAB一样有标题栏、菜单栏、工具栏。
我们主要讲MA TLAB的工作窗口,如图,左侧是“控制窗口”,在此可输入很多命令,如打开某一个文件,查找函数,建立模型等等。
右侧上面是“工作空间”,一般是存储我们需要的数据文件(包括导入的原始数据,模型模拟过程中产生的数据文件等),如我们之前导入了变量名为“pc”的一个数据矩阵,就存放在这里,双击“pc”,就能查看该数据文件。
右侧下方是“历史记录”,你在控制窗口进行的任何一项操作都会在这里有显示,所以当你在此需要进行原来某项操作时,其实可以点击历史窗口中相应的记录就可。
控制窗口左侧隐藏了“current directory”,这个是“当前目录”,即我们现在所在的位置。
点击“当前目录”就会以浮动的形式出现当前目录,或方便我们查找我们需要的目录。
这是我习惯的一种桌面布局,你也可以根据需要调整,在菜单栏有一项“Desktop”(桌面),点击desktop→desktop layout(桌面布局),会有几种布局形式,大家自己去看吧。
四、与MATLAB相关的重要操作1、数据文件存储之前我们已经将模型需要的数据作为一个变量导入并存储在MATLAB的“工作空间”中,由于我们是处理空间面板数据,所以我们还需要导入空间权重矩阵(如命名为“w1”),方法一样。
这时我们需要将包含空间权重矩阵“w1”和所有数据的“pc”的数据文件进行存储,方便以后调用。
数据存储方法:“File→Save Workspace As”,找到存储的地址,输入文件名,就形成了后缀名为.mat的MATLAB能识别的数据文件。
2、设置路径MATLAB并没有自带空间计量软件包,这个需要在网上下载(我打包给你们),当然我们也需要将操作MATLAB过程中需要的数据文件、程序等保存在某个文件夹中。
MA TLAB通过调用软件包中已有的程序命令,以及自己保存的数据文件,来实现模型的模拟。
此时我们需要告诉MA TLAB它的权限在哪里,即它可以在哪里去查找这些程序、数据等(默认状况下,MA TLAB只承认安装目录下文件夹中已有的程序)。
所以我们需要为MA TLAB设置一条路径,让它能够使用这条路径下包含的程序,数据。
设置路径的方法:点击“File→Set Path”,出现“set path”窗口,如图:空间计量工具箱红框下按钮“Add with Subfolders”表示在添加路径时,在文件夹下的子目录也被MA TLAB承认,否则该文件夹下的子文件夹中的程序、数据将不能被MA TLAB识别,而不能使用。
点击此按钮,选择文件夹位置,然后点击该窗口的“Save”即可实现路径的设置。
如图:我将D盘下的MATLAB 文件夹及其子文件夹添加到了MATLAB能识别的路径中,那么此文件夹中的所有与MA TLAB相关的程序、数据等都能被MATLAB识别并使用。
五、MATLAB程序——空间计量工具箱一般来说,我们不会在MATLAB的控制窗口一个一个的输入命令,而是在MATLAB 的“Editor”(编辑器)中将一个完整的程序编辑完毕然后进行存储,方便以后使用。
当然我们更一般的是使用别人已经编辑好的程序,进行一定的组合和修改来进行自己的研究。
这里先讲MATLAB的空间计量工具箱。
在MATLAB官方网上下载的最新版的空间计量工具箱的名称为:“jplv7”。
如上图,我在设置路径时,该工具箱已经包含在D盘下的MA TLAB文件夹下。
这时,我们可以从红框所标识的按钮找到该工具箱,如图,左侧“current directory”(当前目录)即显示该目录下所有的文件夹,其中我们要使用的是“spatial”,该文件夹下包含我们需要的关于空间面数据模型相关的程序,而我们主要使用的完整程序是该文件夹下的“panel”(空间面板)。
我们可以先看一下以“demo ”开头的M 文件(MATLAB 程序),demo 即演示,如双击打开“demoLMsarsem_panel ”,就会弹出该程序文件的编辑器(editor ),点击红圈下的运行按钮,整个程序的运行结果就会显示在MATLAB 的“控制窗口”中。
六、空间面板数据模型解读空间计量模型帮助(一)空间面板数据模型建立的一般步骤是:1、空间相关性检验:Moran’s I检验,LM检验(这是我目前知道的两种检验方法,对于其他的一些检验如LR,Walds等本来就是用于截面空间数据空间相关性的检验,如何推广到空间面板数据上来,我也不是很清楚,我也没找到相关的程序,只是看到有些人做空间面板数据模型时也给出了这几种检验的结果)。
打包文件中有一个“作业”文件夹,里面有单独的LM与moran检验的M文件,对自己的数据进行空间相关性检验可以直接使用这个程序,当然需要修改某些东西(后面有详解)。
2、空间模型的选择:即选择用SAR模型,还是SEM模型,同时还涉及到固定效应和随机效应选择,以及在固定或随机效应模型中选择(地区固定、时期固定、双固定、还是混合面板)。
LM检验的结果可以为SAR与SEM的选择提供依据(查看相关文献)。
面板数据的固定效应SAR 模型直接调用“sar_panel_FE”程序,而固定效应SEM直接调用“sem_panel_FE”程序(这些程序已经作为程序文件存在于某个子目录下)。
对于固定效应(地区固定,时间固定,双向固定,混合)的选择,其实只需要在引用上述程序时,对某些指标进行设置。
如下图,是截取的一段面板SAR模型的程序,其实我们可以从百分号“%”后的文字去理解这段程序在做什么。
红框中是设定模型是那种固定效应:info.model=0:表示此模型为混合模型,即没有固定效应;info.model=1:表示此模型为地区固定效应模型;info.model=2:表示时间固定效应模型;info.model=3:表示双向固定效应模型。
关于如何使用已有的完整程序来做自己的研究将在后面详解。
(二)学会使用“帮助”自学空间面板数据关于“panel”文件夹下带有demo字样的M文件,一般都是一个完整的演示文件,可以运行,大家可以读一下。
一般等号后面的语句就是对等号左边的变量进行赋值之类的,对于任何命令,都可以在MA TLAB的控制窗口输入“which 命令名”进行查找,或者直接使用MA TLAB提供的帮助,看该命令是什么意思,该怎么使用(上上图给出了帮助的位置)。
下图是“帮助”窗口,在红框内输入如“wk1read”点回车即可获取“wk1read”的相关解释,用法,描述,实例等等。
目前关于MA TLAB 用于空间面板计量方面的中文操作书我没有在网上找到,所以也只能通过这种方法来学习“panel”下的每一个M文件到底是干什么用的。
(三)常见的命令:1、关于%:%后面可以输入中文,对已写程序进行描述和解释,%后的文字是不被运行的。
2、wk1read:读取后缀名为.wk1的数据文件。
(wk1数据文件是MA TLAB能识别的数据文件,但具体该文件怎么形成的,我也不清楚。
我一般使用的都是通过EXCEL链接导入到MATLAB中的数据,该数据存储后后缀名为.mat,该文件的读取,直接使用命令load,如读取名为“pc”的mat 文件,直接用load pc.mat)3、在任何一个空间面板数据模型的程序中,首先要做的,当然是读取数据,第二步就是对空间面板数据进行描述(也叫定义空间面板数据),同时指定被解释变量y和解释变量x:如下图:每一行分别表示:该面板数据的时期数为30(T=30),该面板数据有30个地区(N=30),将空间权重矩阵标准化(W=normw(w1)),将名为consume(以矩阵形式出现在MA TLABA中)的变量的第3列数据定义为被解释变量y,将名为consume的变量的第4、5、7、8、9、10、12列数据定义为解释变量矩阵x,定义一个有N*T行,1列的全1矩阵,该矩阵名为:xconstant,(ones即为全1矩阵)说明解释变量矩阵x的大小:有nobs行,K列。
