线段的垂直平分线及角平分线专题复习
线段的垂直平分线复习巩固、角平分线
线段的垂直平分线复习巩固【知识要点】线段垂直平分线的性质与判定： （1）垂直平分线．．．．．是垂直于一条线段．．并且平分这条线段的直线．．； （2）性质定理：线段垂直平分线上的点到这一条线段两个端点距离相等；（3）线段垂直平分线逆定理：到一条线段两端点距离相等的点，在这条线段的垂直平分线上； （4）三角形三条边的垂直平分线交于一点，并且这个点到三个顶点的距离相等。
专题一 线段的垂直平分线与等腰三角形等的综合应用1. 如图，在ABC ∆中，AB =AC ，36A ∠=︒，AB 的垂直平分线DE 交AC 于D ，交AB 于E ，下述结论错误的是（ ）A ．BD 平分ABC ∠ B. BCD ∆的周长等于AB +BC C. AD =BD =BC D. 点D 是线段AC 的中点2. 如图所示，已知在三角形纸片ABC 中，BC =3， AB =6，∠BCA =90°，在AC 上取一点E ，以BE 为折痕，使AB 的一部分与BC 重合，A 与BC 延长线上的点D 重合，求DE 的长度。
3. 如图1所示，在直角梯形ABCD 中，AD ∥BC ，AB ⊥BC ，∠DCB =75º，以CD 为一边的等边△DCE 的另一顶点E 在腰AB 上．（1）求∠AED 的度数；（2）求证：AB =BC ；（3）如图2所示，若F 为线段CD 上一点，∠FBC =30º．求 DFFC的值．ABCDE F图2A BCDE 图1角平分线复习巩固【知识要点】角平分线的性质与判定：（1）性质定理：角平分线上的点到角两边的距离相等；（2）角平分线逆定理：在一个角的内部，且到角的两边距离相等的点在这个角的平分线上；（3）三角形三条角平分线交于一点，并且这一点到三边的距离相等。
专题一角平分线性质及判定定理的应用1.（2011，岳阳）如图，AD∥BC，∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P，作PE⊥AB于点E．若PE＝2，则两平行线AD与BC间的距离为．2.如图，在Rt△ACB中，∠C=90°, BE平分∠ABC，ED垂直平分AB于D，若AC=9，则AE的值是（）A．B．C．6 D．43.如图，1l，2l，3l是三条公路线，且2l//3l，现在决定在区域内建立一个公路维修站，要求到三条公路的距离相等，请问维修站应该建立在何处，共有几处？请画出图形.4.如图，AD是△ABC的角平分线，DF⊥AB，垂足为F，DE=DG，△ADG和△AED的面积分别为50和39，求△EDF的面积。
角平分线、线段垂直平分线、三线合一练习复习
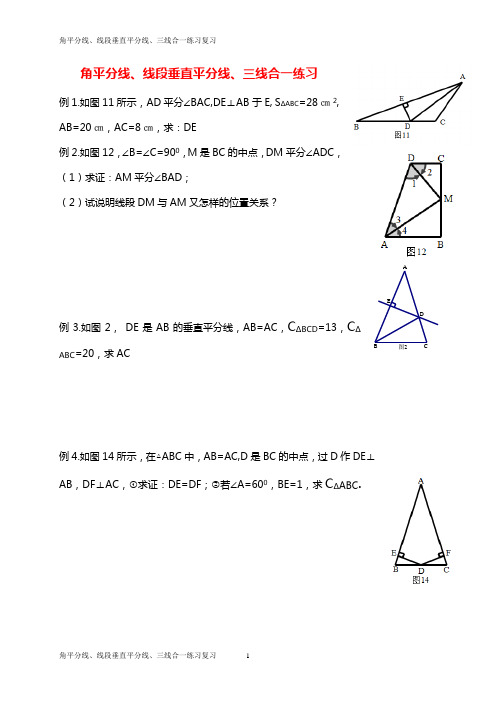
角平分线、线段垂直平分线、三线合一练习例1.如图11所示，AD平分∠BAC,DE⊥AB于E, S∆ABC=28㎝2, AB=20㎝，AC=8㎝，求：DE例2.如图12，∠B=∠C=900，M是BC的中点，DM平分∠ADC，（1）求证：AM平分∠BAD；（2）试说明线段DM与AM又怎样的位置关系？例3.如图2，DE是AB的垂直平分线，AB=AC，C∆BCD=13，C∆ABC=20，求AC例4.如图14所示，在△ABC中，AB=AC,D是BC的中点，过D作DE⊥AB，DF⊥AC，①求证：DE=DF；②若∠A=600，BE=1，求C∆ABC.图2EDCBA例5.如图15，等边三角形ABC中，D是AC的中点，延长BC到E使CE=CD，过D作DF⊥BC，求证：F是BE的中点。
练习：1. 如图3，∠C=900，AC=BC,AD是∠BAC的平分线，DE⊥AB，若AB=8㎝,求C∆DEB2.如图5，OB 、OC 分别平分∠ABC 、∠ACB ，OD ⊥BC ，OD=3，C ∆CAB =12, 求S ∆ABC3. 如图9，△ABC 中∠C=900，AD 平分∠BAC ，AB=10，AC=8，求S ∆ABD ：S ∆ADC 的值4.如图2， DE 是AB 的垂直平分线， AE=3，C ∆BCD =13，求C ∆ABC5.如图2， DE 是AB 的垂直平分线，BC=3，C ∆BCD =13，求ACOD 图5CBA图2EDCBA6.如图2，DE是AB的垂直平分线，AB=AC，C∆BCD=13，C∆ABC=20，求AB7.如图12，AB=AC，点D是BC的中点，AB平分∠DAE，AE⊥BE，求证：AD=AE。
角平分线与垂直平分线知识点
角平分线与垂直平分线知识点一、角平分线1.角平分线可以得到两个相等的角。
（角平分线的定义）∵AD是∠CAB的角平分线1∠CAB∴∠CAD=∠B AD=22.角平分线上的点到角两边的距离相等。
（角平分线的性质）∵AD是∠CAB的角平分线，DC⊥AC ，DB⊥AB∴DC=DB3.三角形的三条角平分线交于一点，称作三角形内心。
三角形的内心到三角形三边的距离相等。
4.到角两边的距离相等的点在角平分线上。
（角平分线的判定）∵DC⊥AC ，DB⊥AB，DC=DB∴点D在∠CAB的角平分线上。
二、角平分线图模（对称性）1、角平分线作垂线角平分线+垂直一边：“图中有角平分线，可向两边作垂线，作完垂线全等必出现”若PA⊥OM于点A，可以过P点作PB⊥ON于点B，则PB=PA。
利用角平分线的性质定理，可以得到∆OAP≌∆OBP（AAS）。
2、角平分线+垂线：“角分垂必延长”垂直角分线，等腰全等现。
若AP⊥OP于点P，可延长AP交ON于点B，构造△AOB是等腰三角形，P是底边AB的中点，三线合一，∆OAP≌∆OBP（ASA）。
3、角平分线+斜线：“截等长构造全等”若点A是射线OM上任意一点，可以在ON上截取OB=OA，连接PB，构造△OPB≌△OPA（SAS）。
4、角平分线+平行线：“角平分线+平行线，等腰三角形必出现”若过P点作PQ∥ON交OM于点Q，利用平行的内错角相等及等角对等边可以得到△POQ是等腰三角形。
5、角平分线+对角互补：“截长补短构造全等”6、夹角模型①双内角角平分线模型：BP、CP分别是∠ABC、∠ACE的角平分线，则：∠P=90°+12∠A．②内角和外交角平分线模型：BP、CP分别是∠ABC、∠ACE的角平分线，则：∠P=12∠A．③双外角角平分线模型：BP、CP分别是∠CBD、∠BCD的角平分线，则：∠D=90°-12∠B．在∠AOB中，画角平分线：1.以点O为圆心，以任意长为半径画弧，两弧交∠AOB两边于点M，N。
线段的垂直平分线和角平分线专题训练及答案
线段的垂直平分线和角平分线专题训练及答案一、选择题（本大题共7小题，共21.0分）1.如图是一块三角形草坪，现要在草坪上建一个凉亭供大家休息．若要使凉亭到草坪三条边的距离都相等，则凉亭应建在三角形草坪()A. 三条角平分线的交点处B. 三条中线的交点处C. 三条高的交点处D. 三条边的垂直平分线的交点处2.下列说法错误的是()A. 等腰三角形底边上的高所在的直线是它的对称轴B. 等腰三角形底边上的中线所在的直线是它的对称轴C. 等腰三角形顶角的平分线所在的直线是它的对称轴D. 等腰三角形一个内角的平分线所在的直线是它的对称轴3.如图，在Rt△ABC中，∠A=90°，BD是角平分线，DE垂直平分BC，AD=3，则AC的长为()A. 9B. 5C. 4D. 3√34.如图，在△ABC中，AB的垂直平分线交BC于D，AC的垂直平分线交BC于E，∠BAC=124°，则∠DAE的度数为()A. 68°B. 62°C. 66°D. 56°5.如图，在△ABC中，CD平分∠ACB，交AB于点D，DE⊥AC于点E，若BC=2m+6，DE=m+3，则△BCD的面积为()A. 2m2−18B. 2m2+12m+18C. m2+9D. m2+6m+96.如图，P是∠BAC平分线上的点，PM⊥AB于M，PN⊥AC于N，则下列结论：①PM=PN；②AM=AN；③△APM≌△APN；④∠PAN+∠APM=90°．其中正确结论的个数是()A. 4个B. 3个C. 2个D. 1个7.如图所示，在△ABC中，AB=AC，AD是BC边上的高线，E，F是AD的三等分点，若△ABC的面积为12，则图中△BEF的面积为()A. 2B. 3C. 4D. 6二、解答题（本大题共10小题，共80.0分）8.直线OA，OB表示两条相互交叉的公路，点M，N表示两个蔬菜种植基地．现要建一个蔬菜批发市场P，要求它到两条公路的距离相等，且到两个蔬菜基地的距离也相等，请用尺规作图说明市场的位置．9.如图，在△ABC中，∠C=90°，AC=BC，AD平分∠BAC，交BC于点D，DE⊥AB于点E.已知AB=10cm，求△DEB的周长．10.如图，已知AD是∠BAC的平分线，DE⊥AB于点E，DF⊥AC于点F，且BE=CF，试判断BD和CD的数量关系，并说明理由．11.如图，要在街道旁修建一个奶站，向居民区A，B提供牛奶．奶站应建在什么地方才能使A，B到它的距离相等？12.A，B，C这3个村庄的位置如图所示，每两个村庄之间有公路相连，村民希望共同投资建一个货运中转站，使中转站的位置到3个村庄的距离相等．请你利用尺规作图确定中转站的位置．13.如图，四边形ABCD为矩形台球桌面，现有一白球M和黑球N，应怎样去打白球M，才能使白球M撞击桌边AB后反弹击中黑球N？请你画出白球M经过的路线．14.如图，在△ABC中，AB=AC，M是BC的中点，D，E分别是AB，AC边上的点，且BD=CE.试说明MD=ME．15.如图，在Rt△ABC中，∠C=90°，BC=3.∠CAB的平分线交BC于点D，DE是AB的垂直平分线，垂足为E．(1)求∠B度数．(2)求DE的长．16.如图，已知∠ABC，射线BC上一点D.求作：等腰三角形PBD，使线段BD为等腰三角形PBD的底边，点P在∠ABC内部，且点P到∠ABC两边的距离相等(保留作图痕迹，但不要求写作法)．17.如图，在Rt△ABC中，∠ACB=90°．(1)请用直尺和圆规按下列步骤作图，保留作图痕迹：①作∠ACB的平分线，交斜边AB于点D；②过点D作AC的垂线，垂足为点E．(2)在(1)作出的图形中，若CB=4，CA=6，则DE=______．答案和解析1.【答案】A【解析】[分析]本题主要考查的是角平分线的性质在实际生活中的应用．由于凉亭到草坪三条边的距离相等，所以根据角平分线上的点到角两边的距离相等，可知是三角形三条角平分线的交点．由此即可确定凉亭位置．[详解]解：∵凉亭到草坪三条边的距离相等，∴凉亭应建在三角形草坪的三条角平分线的交点处．故选A．2.【答案】D【解析】[分析]本题考查了等腰三角形的性质，属于基础题，解题的关键是了解对称轴是一条直线，难度不大．根据等腰三角形性质分别判断后即可确定正确的选项．[详解]解：A.等腰三角形底边上的高所在的直线是对称轴，正确；B.等腰三角形底边上的中线所在的直线是对称轴，正确；C.等腰三角形顶角的平分线所在的直线是对称轴，正确；D.等腰三角形顶角的平分线所在的直线是对称轴，如果这个内角是底角，不一定是它的对称轴，错误．故选D．3.【答案】A【解析】[分析]根据角平分线性质得出AD=DE，证明Rt△ADB≌Rt△EDB(HL)，得BE=AB，由DE 是BC的垂直平分线，得BC=2AB，所以∠C=30°，可得CD的长，从而得AC的长．本题考查了直角三角形的性质，线段垂直平分线的性质，角平分线性质的应用，注意：角平分线上的点到角两边的距离相等．[详解]解：∵BD是角平分线，DE⊥BC，∠A=90°，∴DE=AD=3，在Rt△ADB和Rt△EDB中，∵{AD=DEBD=BD，∴Rt△ADB≌Rt△EDB(HL)，∴BE=AB，∵DE是BC的垂直平分线，∴CE=BE，∴BC=2AB，∴∠C=30°，∴CD=2DE=6，∴AC=CD+AD=6+3=9，故选：A．4.【答案】A【解析】[分析]根据三角形内角和定理求出∠B+∠C，根据线段垂直平分线的性质得到DA=DB，得到∠DAB=∠B，同理可得，∠EAC=∠C，结合图形计算，得到答案．本题考查的是线段的垂直平分线的性质、三角形内角和定理，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．[详解]解：∠B+∠C=180°−∠BAC=56°，∵AB的垂直平分线交BC于D，∴DA=DB，∴∠DAB=∠B，∵AC的垂直平分线交BC于E，∴EA=EC，∴∠EAC=∠C，∴∠DAE=∠BAC−(∠DAB+∠EAC)=124°−56°=68°．故选A．5.【答案】D【解析】[分析]过点D作DF⊥BC交CB的延长线于F，根据角平分线上的点到角的两边距离相等可得DE=DF，再根据三角形面积公式列式，然后根据多项式乘多项式法则进行计算即可得解．本题考查了角平分线上的点到角的两边距离相等的性质，熟记性质并作辅助线构造出BC边上的高线是解题的关键．[详解]解：如图，过点D作DF⊥BC交CB的延长线于F，∵CD平分∠ACB，DE⊥AC，∴DE=DF，∴△BCD的面积=12·BC·DF=12(2m+6)(m+3)=m2+6m+9．故选D．6.【答案】A【解析】[分析]利用角平分线的性质结合全等三角形的判定与性质分析得出答案．此题主要考查了角平分线的性质，全等三角形的判定与性质，正确得出△APM≌△APN 是解题关键．[详解]解：∵P是∠BAC平分线上的点，PM⊥AB于M，PN⊥AC于N，∴∠MAP=∠NAP，∠AMP=∠ANP=90°，PM=PN，故①正确在△APM和△APN中{∠MAP=∠NAP ∠AMP=∠ANP AP=AP,∴△APM≌△APN(AAS)，故③正确，∴AM=AN，故②正确，∠APM=∠APN，∵∠PAN+∠APN=90°，∴∠PAN+∠APM=90°，故④正确，综上所述：正确的有4个．故选A．7.【答案】A【解析】[分析]本题考查了等腰三角形的性质及轴对称性质；利用对称发现并利用△ABD和△ACD的面积相等是正确解答本题的关键．由图，根据等腰三角形是轴对称图形知，△ABD和△ACD的面积相等，再根据点E、F，依此即可求解．是AD的三等分点，可得△BEF的面积为△ACD的面积的13[详解]解：∵在△ABC中，AB=AC，AD是BC边上的高，S△ABC=12，BC，S△ABD=6，∴BD=CD=12∵点E、F是AD的三等分点，AD，∴EF=13S△BEF=1S△ABD=2．2故选A．8.【答案】解：如图：P为所求做的点．【解析】本题考查了基本作图，理解角的平分线以及线段的垂直平分线的作图是关键．连接MN，先画出∠AOB的角平分线，然后再画出线段MN的中垂线．这两条直线的交点即为所求．9.【答案】解：∵AD平分∠BAC交BC于D，DE⊥AB，∠C=90°，∴CD=DE．又∵AD=AD，∴Rt△ACD≌△RtAED．∴AE=AC，∴△DEB的周长=DE+DB+EB=CD+DB+BE=BC+BE=AC+BE=AE+BE=AB=10cm．【解析】本题主要考查的是全等三角形的判定及性质，角平分线的性质等有关知识，由题意根据AD平分∠BAC交BC于D，DE⊥AB，∠C=90°，得到CD=DE，然后利用全等三角形的判定及性质得到AE=AC，最后利用三角形的周长公式进行求解即可．10.【答案】解：∵AD平分∠BAC，DE⊥AB，DF⊥AC，∴DE=DF，∠E=∠DFC=90°．在△BED和△DFC中，DE=DF，∠E=∠DFC，BE=CF，∴△BED≌△DFC(SAS)，∴BD=CD．【解析】本题主要考查全等三角形的判定和性质，掌握全等三角形的判定方法(即SSS、SAS、ASA、AAS和HL)和全等三角形的性质(即对应边、对应角相等)是解题的关键．由角平分线的性质可得DE=DF，再结合条件可证明Rt△BED≌Rt△CFD，即可求得BE=CF.11.【答案】解：连接AB，作AB的垂直平分线，与街道的交点为P，点P即为所求作的点．【解析】本题考查线段垂直平分线的性质，根据线段垂直平分线上的点到线段两端点的距离相等，可知此点P在AB的垂直平分线上即可解答，12.【答案】解：如图，【解析】此题主要考查了应用设计与作图，正确掌握线段垂直平分线的性质是解题关键．利用线段垂直平分线的性质进而得出AB，AC的垂直平分线进而得出交点，得出M即可．13.【答案】解：如图所示，作点N于AB的对称点N′，连接N′M，与AB相交于点O，连接MO，NO，就是白球路线．【解析】此题考查了轴对称作图，作点N于AB的对称点N′，连接N′M，与AB相交于点O，连接MO，NO，就是白球路线．14.【答案】证明：△ABC中，∵AB=AC，∴∠DBM=∠ECM．∵M是BC的中点，∴BM=CM．在△BDM和△CEM中，，∴△BDM≌△CEM(SAS)，∴MD=ME．【解析】本题主要考察等腰三角形的性质和全等三角形的判定与性质.根据等腰三角形的性质可证∠DBM=∠ECM，可证△BDM≌△CEM，可得MD=ME，即可解题．15.【答案】解：(1)∵DE是AB的垂直平分线，∴DA=DB，∴∠B=∠DAB．∵AD平分∠CAB，∴∠CAD=∠DAB．∵∠C=90°，∴3∠CAD=90°，∴∠CAD=30°，∴∠B=30°；(2)∵AD平分∠CAB，DE⊥AB，CD⊥AC，BD，∴CD=DE=12∵BC=3，∴CD=DE=1．【解析】本题主要考查线段垂直平分线的性质，熟悉掌握是关键．(1)由角平分线和线段垂直平分线的性质可求得∠B=∠CAD=∠DAB=30°；(2)根据角平分线的性质即可得到结论．16.【答案】解：如图，△PBD即为所求作的三角形【解析】【分析】本题考查尺规作图.根据角平分线的性质及线段垂直平分线的性质作图即可.作∠ABC的平分线与线段BD的垂直平分线交于点P，则△PBD为所求作的等腰三角形．作∠ABC的平分线与线段BD的垂直平分线交于点P，则△PBD为所求作的等腰三角形．【解答】解：∵点P到∠ABC两边的距离相等，∴点P在∠ABC的平分线上，∵线段BD为等腰△PBD的底边，∴PB=PD，∴点P在线段BD的垂直平分线上，∴点P是∠ABC的平分线与线段BD的垂直平分线的交点．17.【答案】解：(1)如图所示；(2)解：∵DC是∠ACB的平分线，∴∠BCD=∠ACD，∵DE⊥AC，BC⊥AC，∴DE//BC，∴∠EDC=∠BCD，∴∠ECD=∠EDC，∴DE=CE，∵DE//BC，∴△ADE∽△ABC，∴DEBC =AEAC，设DE=CE=x，则AE=6−x，∴x4=6−x6，解得：x=125，即DE=125，故答案为：12．5【解析】本题考查了角的平分线的性质，平行线的性质，等腰三角形的性质，相似三角形的判定和性质，基本作图，解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．(1)以C为圆心，任意长为半径画弧，交BC，AC两点，再以这两点为圆心，大于这两点的线段的一半为半径画弧，过这两弧的交点与C在直线交AB于D即可，根据过直线外一点作已知直线的垂线的方法可作出垂线即可；(2)根据平行线的性质和角平分线的性质推出∠ECD=∠EDC，进而证得DE=CE，由DE//BC，推出△ADE∽△ABC，根据相似三角形的性质即可推得结论．。
专题训练(四) 有关线段的垂直平分线和角的平分线的四种解题方法-学习文档
专题训练(四) 有关线段的垂直平分线和角的平分线的四种解题方法►方法一直接根据相关性质定理解题1．如图4－ZT－1所示，在四边形ABCD中，AC，BD相交于点O，AB＝BC＝CD＝DA.求证：AC与BD互相垂直平分．图4－ZT－1►方法二连线构造全等三角形2．如图4－ZT－2，AB＝AC，BD＝CD，DE⊥AB于点E，DF⊥AC于点F.求证：DE＝DF.图4－ZT－23．如图4－ZT－3，在△ABC中，AB＝2AC，∠BAD＝∠CAD，AD＝DB.求证：CD⊥CA.图4－ZT－3►方法三作垂线段得距离4．如图4－ZT－4，在△ABC中，∠BAC的平分线AD平分底边BC.求证：AB＝AC.图4－ZT－45．如图4－ZT－5，在△ABC中，∠ABC与∠ACB的平分线相交于点O，OE⊥BC于点E，△ABC的周长为12，面积为6，求OE的长．图4－ZT－56.如图4－ZT－6所示，在△ABC中，AD是△ABC的角平分线，E，F分别是AB，AC上的点，并且有∠EDF＋∠EAF＝180°，DG⊥AB于点G.(1)试判断DE和DF的数量关系，并说明理由；(2)若△ADF和△AED的面积分别为50和39，求△EDG的面积．图4－ZT－67．如图4－ZT－7，DA⊥AB于点A，CB⊥AB于点B，P为AB边上一点，且DP平分∠ADC，CP平分∠DCB.求证：(1)P为AB的中点；(2)DC＝AD＋BC.图4－ZT－78．如图4－ZT －8，D 是△ABC 的边BC 的延长线上一点，BE 平分∠ABC，CE 平分∠ACD. 求证：(1)∠BAC＝2∠BEC；(2)∠CAE＋∠BEC＝90°.图4－ZT －8► 方法四 作线段的延长线构造全等三角形9．如图4－ZT －9，在△ABC 中，∠BAC ＝90°，AB ＝AC ，CD 垂直于∠ABC 的平分线BD 于点D ，BD 交AC 于点E.求证：BE ＝2CD.图4－ZT －9详解详析1．证明：∵AB ＝DA ，BC ＝CD ，∴点A ，C 在线段BD 的垂直平分线上，即AC 垂直平分BD ，同理可证得BD 垂直平分AC.∴AC 与BD 互相垂直平分．2．证明：连接AD.在△ABD 与△ACD 中，∵⎩⎨⎧AB ＝AC ，BD ＝CD ，AD ＝AD ，∴△ABD ≌△ACD ，∴∠BAD ＝∠CAD. 又∵DE ⊥AB ，DF ⊥AC ，∴DE ＝DF.3．[解析] 要证明CD ⊥CA ，只要使∠ACD ＝90°即可．由于AD ＝DB ，可在AB 边上取中点E ，连接DE ，由AB ＝2AC 及∠BAD ＝∠CAD ，得△ADE ≌△ADC ，从而得∠ACD ＝∠AED.由AD ＝DB 知DE 是AB 的垂直平分线，可得∠AED ＝90°.证明：在AB 边上取中点E ，连接DE.因为AD ＝DB ，E 为AB 的中点，所以ED ⊥AB.因为AB ＝2AC ，所以AE ＝12AB ＝AC. 在△ADE 和△ADC 中，⎩⎨⎧AE ＝AC ，∠DAE ＝∠DAC ，AD ＝AD ，所以△ADE ≌△ADC ， 所以∠ACD ＝∠AED ＝90°，所以CD ⊥CA.4．[解析] 根据题意可知AD 是∠BAC 的平分线，可过点D 作∠BAC 两边的垂线段，根据角平分线的性质，并结合三角形的面积进行证明．证明：如图，分别过点D 作DE ⊥AB ，DF ⊥AC ，垂足分别为E ，F.因为AD 为∠BAC 的平分线，所以DE ＝DF.又因为AD 平分BC ，所以BD ＝CD ，所以S △ABD ＝S △ACD .又S △ABD ＝12AB ·DE ，S △ACD ＝12AC ·DF ， 所以AB·DE ＝AC·DF ，所以AB ＝AC.5．[解析] 连接OA ，过点O 作OM ⊥AC 于点M ，OF ⊥AB 于点F ，则OE ＝OF ＝OM.由S △ABC ＝S △AOB ＋S △BOC ＋S △AOC 可求OE 的长．解：如图，连接OA ，过点O 作OM ⊥AC 于点M ，OF ⊥AB 于点F.∵BO 平分∠ABC ，OF ⊥AB ，OE ⊥BC ，∴OF ＝OE.同理OE ＝OM.∴OF ＝OE ＝OM.∵S △ABC ＝S △AOB ＋S △BOC ＋S △AOC ，∴12AB ·OF ＋12BC ·OE ＋12AC ·OM ＝6， ∴12OE ·(BC ＋AB ＋AC)＝6. 又∵△ABC 的周长为12，即BC ＋AB ＋AC ＝12，∴OE ＝1.6．解：(1)DE ＝DF.理由：过点D 作DN ⊥AC 于点N.∵DG ⊥AB 于点G ，∴∠EGD ＝∠FND ＝90°.∵AD 平分∠BAC ，DG ⊥AB ，DN ⊥AC ，∴DG ＝DN(角平分线的性质)．∵∠EAF ＋∠EDF ＝180°，∴∠AED ＋∠AFD ＝360°－180°＝180°.∵∠AED ＋∠DEG ＝180°，∴∠DEG ＝∠NFD.在△EGD 和△FND 中，⎩⎨⎧∠GED ＝∠DFN ，∠DGE ＝∠DNF ，DG ＝DN ，∴△EGD ≌△FND(AAS)，∴DE ＝DF.(2)由已知易证△ADG ≌△ADN.由(1)知△EGD ≌△FND ，∴S △ADG ＝S △ADN ，S △EGD ＝S △FND ，∴S △ADE ＋S △EGD ＝S △ADF －S △EGD ，即39＋S △EGD ＝50－S △EGD ，∴S △EGD ＝5.5.7．证明：(1)如图，过点P 作PE ⊥DC 于点E.∵DP 平分∠ADC ，PA ⊥AD ，PE ⊥DC ，∴PA ＝PE.同理PB ＝PE.∴PA ＝PB ，∴P 为AB 的中点．(2)在△ADP 与△EDP 中，∵DP 平分∠ADC ，∴∠ADP ＝∠EDP.又∵∠PAD ＝∠PED ＝90°，DP ＝DP ，∴△ADP ≌△EDP ，∴AD ＝ED.同理BC ＝EC.∵DC ＝DE ＋EC ，∴DC ＝AD ＋BC.8．证明：(1)∵∠ACD ＝∠BAC ＋∠ABC ，CE 平分∠ACD ，∴∠ECD ＝12∠ACD ＝12(∠BAC ＋∠ABC)． ∵BE 平分∠ABC ，∴∠EBC ＝12∠ABC. ∴∠ECD ＝∠BEC ＋∠EBC ＝∠BEC ＋12∠ABC ， ∴∠BEC ＋12∠ABC ＝12(∠BAC ＋∠ABC)， ∴∠BEC ＝12∠BAC ，即∠BAC ＝2∠BEC. (2)过点E 作EM ⊥BD 于点M ，EN ⊥BA 支BH 的延长线于点N ，EG ⊥AC 于点G. ∵CE 平分∠ACD ，EM ⊥BD ，EG ⊥AC ，∴EG ＝EM.∵BE 平分∠ABC ，EM ⊥BD ，EN ⊥BA ，∴EN ＝EM ，∴EG ＝EN ，∴AE 平分∠CAN ，∴∠CAE ＝12∠CAN ＝12(180°－∠BAC)， ∴∠CAE ＋∠BEC ＝12(180°－∠BAC)＋12∠BAC ＝90°. 9．[解析] 要证BE ＝2CD ，想到要构造等于2CD 的线段，结合角平分线， 利用轴对称的性质把△CBD 沿BD 翻折，使BC 重叠到BA 所在的直线上，构造全等三角形，然后证明BE 和CF(2CD)所在的三角形全等．证明：如图，延长BA ，CD 交于点F.∵BD ⊥CF(已知)，∴∠BDC ＝∠BDF ＝90°.∵BD 平分∠ABC(已知)，∴∠1＝∠2.在△BCD 和△BFD 中，⎩⎨⎧∠2＝∠1（已证），BD ＝BD （公共边），∠BDC ＝∠BDF （已证），∴△BCD ≌△BFD(ASA)，∴CD ＝FD ，即CF ＝2CD.∵∠5＝∠4＝90°，∠BDF ＝90°，∴∠3＋∠F ＝90°，∠1＋∠F ＝90°，∴∠1＝∠3.在△ABE 和△ACF 中，⎩⎨⎧∠4＝∠5，AB ＝AC ，∠1＝∠3（已证），∴△ABE ≌△ACF(ASA)，∴BE ＝CF ，∴BE ＝2CD.。
16章2复习线段的垂直平分线和角平分线
M
A
B
4 .如图，△ＡＢＣ的∠Ｂ的外角的平分线ＢＤ 与∠Ｃ的外角的平分线ＣＥ相交于点Ｐ． 求证：点Ｐ到三边ＡＢ，ＢＣ，ＣＡ所在直线 的距离相等．
Ｃ 更上一层楼！ F H
Ｄ Ｐ Ｅ
Ａ
Ｂ
G
5. 如图，△ABC的角平分线BM，CN相交于点P。 求证：(1)点P到三边AB、BC、CA的距离相等 A D (2)点P在∠A的平分线上 F
解： ∵AB=AC， ∴∠ABC=∠C=70°。 ∴∠A=180°-2∠C=40°， 又∵DE垂直平分AB， ∴AD=BD。 ∵∠DBA=∠A=40°。 ∴∠BDC=∠A+∠ABD =40°+40°=80°。
2、如图，在△ABC中， AB=AC， ∠BAC= 120°，AC的垂直平分线EF交AC 于点E，交BC于点F。求证：BF=2CF。
A
B
点P为校址
2.:如图,在直线 l 上求一点P,使PA=PB A
B l
P
点P为所求作的点
角平分线的性质与判定 角的平分线上的点到角的两 1:角平分线的性质： 边的距离相等。 2：角平分线性质的逆定理（角平分线的判定） 在角的内部到角的两边的距离相等的点在角的平 分线上。 A P到OA的距离
PA=PB
任何图形都是有点组成的。因 三、 此我们可以把图形看成点的集 线段的垂直平分线的集合定义： 合。由上述定理和逆定理，线 线段的垂直平分线可以看作是到线 段的垂直平分线可以看作符合 段两上端点距离相等的所有点的集合 什么条件的点组成的图形？
1：如图，已知：AB=AC，AB的垂直平分线交AC于D，垂 足是点E，∠C=70°，求∠BDC的度数。
D
C
复习课线段的垂直平分线和角平分线
A 在BC 的垂直平分线上 复习课——第十九章 线段的垂直平分线和角平分线
普陀区课题组
教学目标：
2．会灵活运用线段垂直平分线、角平分线的定理和逆定理解决相关问题，体会构造基本图形的重要性.
教学重点与难点：线段垂直平分线、角平分线的定理及逆定理的灵活应用. 教学过程：
教师活动
学生活动
设计意图 一、建立知识结构
问：今天主要复习线段的垂直平分线、角的平分线相关知识.
问1:几何证明的依据有哪些？
问2:定理和公理都是命题,由命题你想到了什么？
(师生共同完成回答)
教师帮助建立知识结构：
在建立知识结构的同时复习各知识点.PPT 显示线段垂直平分线的定理及逆定理，角平分线定理及逆定理的图形语言表示.
(1) ⇒
AB=AC (2) ⇒
（3） ⇒
PM=PN (4)
答1：定义、公理、定理
答2：逆命题、逆定理、线段垂直平分线的定理及逆定理、角平分线定理及逆定理，点的三种基本轨迹.
梳理知识，建立知识结构.
学生了解知识点，重点在于线段垂直平分线、角平分线定理及逆定理，点的三种轨迹.
复习线段的垂直平分线定理及逆定理、角平分线定理及逆定理运用的规范书写.
C D A B N M
C D
A
B N M
C A
B C D A B N M O P N
M B A
B M N O A P B
M
N
O
A P
2
1
O
M
B
A。
线段的垂直平分线和角平分线的复习
B
例 1已知：如图，AP、BP分别平分∠DAB和∠CBA，PE、PF 分别垂直于AD、BC，垂足为E、F. 求证：点P在EF的垂直平分线上. 添辅助线的目的 分析：（1）从已知条件你能想到什么定理？ 构造角平分线的 是什么？ 基本图形. （2）缺少了什么?怎么办？ D 角平分线上的点到另一边的垂线段. E 添加辅助线. A （3）能得到什么结论? G （4）用什么定理来证明结论?
8在△ABC中,D为BC 的点,DE⊥BC 交∠BAC的平分线AE于点,EF⊥AB A 于F点,EG⊥AC于G点
求证:BF=CG
F B
D
C G
E
当缺少运用角平分线、线段垂直平分线的定理及逆定理的 基本图形时，要添置辅助线构造运用它们的基本图形.
1、作图题： 已知：∠AOB和∠AOB内一点C. 求作：点P，使PC=PO， 且点P到∠AOB的两边OA、OB的距离相等.
D
2、在△ABC,PM,QN分别垂直 平分AB,AC，则: (1)若BC=10cm则△APQ的周长 10 =_____cm; (2)若∠BAC=100°则 200 ∠PAQ=______.
如图，在△ABC中， AB=AC=16cm，AB的垂直平分线 交AC于D，如果BC=10cm，那么 26 △BCD的周长是_______cm. A
4.如图4-4-5所示，在△ABC中，∠C=90°，∠B=15°， AB 的垂直平分线交 BC 于 D，交 AB 于 E，DB=10cm，则 AC=( C ) A.6 B.8 C.5 D.10
5.如图4-4-6所示，在Rt△ABC中，∠C=90°，AB的垂 直平分线交BC于D，∠CAD∶∠DAB=1∶2，则 36° ∠B= .
(完整版)中考数学尺规作图专题复习(含答案)
中考尺规作图专题复习（含答案）尺规作图定义：用无刻度的直尺和圆规画图，中考中常见画的图是线段的垂线，垂直平分线，角平分线、画等长的线段，画等角。
1.直线垂线的画法：【分析】：以点C为圆心，任意长为半径画弧交直线与A，B两点，再分别以点A，B为圆心，大于12AB的长为半径画圆弧，分别交直线l两侧于点M，N，连接MN，则MN即为所求的垂线2.线段垂直平分线的画法【分析】：作法如下：分别以点A，B为圆心，大于12AB的长为半径画圆弧，分别交直线AB两侧于点C，D，连接CD，则CD即为所求的线段AB的垂直平分线.3.角平分线的画法【分析】1.选角顶点O为圆心，任意长为半径画圆，分别交角两边A，B点，再分别以A，B为圆心，大于12AB的长为半径画圆弧，交H点，连接OH，并延长，则射线OH即为所求的角平分线.4.等长的线段的画法直接用圆规量取即可。
5.等角的画法【分析】以O为圆心，任意长为半径画圆，交原角的两边为A,B两点，连接AB；画一条射线l，以上面的那个半径为半径，l的顶点K为圆心画圆，交l与L，以L为圆心，AB 为半径画圆，交以K为圆心，KL为半径的圆与M点，连接KM，则角LKM即为所求.备注：1.尺规作图时，直尺主要用作画直线，射线，圆规主要用作截取相等线段和画弧；2.求作一个三角形，其实质是依据三角形全等的基本事实或判定定理来进行的；3.当作图要满足多个要求时，应逐个满足，取公共部分.例题讲解例题1.已知线段a，求作△ABC，使AB=BC=AC=a.解：作法如下:①作线段BC=a；（先作射线BD，BD截取BC=a）.②分别以B、C为圆心，以a半径画弧，两弧交于点A；③连接AB、AC.则△ABC 要求作三角形.例2.已知线段a 和∠α，求作△ABC ，使AB=AC=a ，∠A=∠α.解：作法如下：①作∠MAN=∠α；②以点A 为圆心，a 为半径画弧，分别交射线AM ，AN 于点B ，C. ③连接B ，C.△ABC 即为所求作三角形.例3.(深圳中考)如图，已知△ABC ，AB <BC ，用尺规作图的方法在BC 上取一点P ，使得PA ＋PC ＝BC ，则下列选项中，正确的是(D )【解析】由题意知，做出AB 的垂直平分线和BC 的交点即可。
第一章第04讲 线段的垂直平分线和角平分线(8类热点题型讲练)(解析版)
第04讲 线段的垂直平分线和角平分线(8类热点题型讲练)1.理解线段垂直平分线，角平分线的概念；2.掌握线段垂直平分线的性质定理及逆定理；3.能运用线段的垂直平分线的有关知识进行证明或计算；4.能够利用尺规作出三角形的垂直平分线和角平分线；5.会证明和运用“三角形的三条角平分线相交于一点，并且这一点到三条边的距离相等”.角平分线的性质定理和判定定理的灵活运用.知识点01 线段的垂直平分线ìíî线段垂直平分线的：线段垂直平分线上的任意一点到这条线段两端点的距离相等；线段垂直平分线的：和一条线段两个端点距离相等的点，在这条线段的垂直平分线上性质定理判.定定理知识点02 角的平分线ìïíïî角的平分线的：在角的平分线上的点到这个角两边的距离相等；角的平分线的：在一个角的内部（包括顶点）且到角两边距离相等的点，在这个角的平分线上.性质定理性质定理题型01 线段的垂直平分线的性质(1)求证：BE AC =(2)若35B Ð=°，则BAC Ð=【答案】(1)见解析(2)75°∵AD BC ^于点D ，且D 为线段∴AD 垂直平分CE ，∴AC AE =，∵EF 垂直平分AB ，∵AD BC ^，∴90ADB Ð=°，∴903555BAD Ð=°-°=°，∴553520EAD Ð=°-°=°，∵AC AE =，AD BC ^，∴20EAD CAD Ð=Ð=°，∴75BAC BAE EAD CAD Ð=Ð+Ð+Ð=°．故答案为：75°．【变式训练】1．（2023下·全国·八年级专题练习）如图，在ABC V 中，DM ，EN 分别垂直平分AC 和BC ，交AB 于M ，N 两点，DM 与EN 相交于点F ．(1)若CMN V 的周长为15cm ，求AB 的长；(2)若70MFN Ð=°，求MCN Ð的度数．【答案】(1)15cmAB =(2)40MCN Ð=°【分析】此题考查了线段垂直平分线上的点到线段两端点的距离相等的性质，等边对等角的性质，三角形的内角和定理，解题的关键是熟练掌握以上知识的应用及整体思想的应用．（1）根据线段垂直平分线上的点到线段两端点的距离相等可得AM CM =，BN CN =，然后求出CMN V 的周长AB =；（2）根据三角形的内角和定理列式求出 MNF NMF Ð+Ð，再求出A B ÐÐ+，根据等边对等角可得A ACM Ð=Ð，B BCN Ð=Ð，然后利用三角形的内角和定理列式计算即可得解；【详解】（1）解：∵DM 、EN 分别垂直平分AC 和BC ，∴AM CM =，BN CN =，∴CMN V 的周长CM MN CN AM MN BN AB =++=++=，∵CMN V 的周长为15cm ，∴15cm AB =；（2）解：∵70MFN Ð=°，∴18070110MNF NMF Ð+Ð=°-°=°，∵AMD NMF Ð=Ð， BNE MNF Ð=Ð，∴110AMD BNE MNF NMF Ð+Ð=Ð+Ð=°，∴909018011070A B AMD BNE Ð+Ð=°-Ð+°-Ð=°-°=°，∵AM CM =，BN CN =，∴A ACM Ð=Ð，B BCN Ð=Ð，∴()180218027040MCN A B Ð=°-Ð+Ð=°-´°=°．2．（2023上·全国·八年级专题练习）如图，在ABC V 中，EF 垂直平分AC ，交AC 于点F ，AD BC ^于点D ，BD DE =，连接AE ．(1)若AE 平分BAC Ð，求C Ð的度数；(2)若ABC V 的周长为13cm ，5cm AC =，求CD 的长．【答案】(1)36°(2)4cm【分析】本题主要考查了等腰三角形的性质、角平分线、线段垂直平分线、三角形内角和定理等，解答本题的关键在于熟练掌握垂直平分线上的点到线段两端的距离相等及等腰三角形的性质本题即可求解．【详解】（1）解：AD BC BD DE ^Q ，＝，EF 垂直平分AC ，∴AB AE EC ＝＝，C CAE \ÐÐ＝，∵AE 平分BAC Ð，∴BAE EAC ÐÐ＝，∵AD BC ^于点D ，B D ＝D E ，∴AB AE ＝，∴2B AEB C EAC C ÐÐÐ+ÐÐ＝＝＝，根据三角形内角和等于180°可得，180B AEB BAE Ð+Ð+а＝，22180C C C \Ð+Ð+а＝，36C \а＝．（2）ABC QV 周长13cm ，5cm AC =，∴8cm AB BC +＝，∴8cm AB BE EC ++＝，即，228cm DE EC +＝，∴4cm DE EC +＝，∴4cm DC DE EC +＝＝．题型02 线段的垂直平分线的判定(1)求证：AD (2)已知ABC Ð【详解】（1）证明：∴点A 在BC AD \垂直平分（2）解：V 【变式训练】1.如图，ABC V 为等边三角形，AD AB ^，4AD DC ==，AC BD ，相交于点E ．(1)求证：BD 垂直平分AC ；(2)求BE 的长；(3)若点F 为BC 的中点，点P 在BD 上，则PC PF +的最小值为______．（直接写出结果）．【详解】（1）证明：∵ABC V 是等边三角形，∴AB BC =；∵,,AB BC AD CD BD BD ===，∴()ABD CBD SSS V V ≌，∴ADB CDB Ð=Ð，∵,,AD DC ADB CDB DE DE =Ð=Ð=，∴()ADE CDE SAS V V ≌，∴,90AE EC AED DEC =Ð=Ð=°，∴BD 垂直平分AC ；（2）解：∵DB AC ^，∴BE 平分ABC Ð，∵60ABC BAC Ð=Ð=°，∴30ABD Ð=°，∵90BAD Ð=°，∴30DAE Ð=°，∵4=AD ，∴8,2BD DE ==，∴6BE BD DE =-=；（3）解：连接AF 交BD 于点P ，连接PC ，∵BD 是AC 的垂直平分线，∴A 、C 关于BD 对称，(1)求证：DB DE=；(2)过点A作AF BC∥，交ED延长线于点F，交①若12EM=，则BD= ．题型03 线段的垂直平分线的实际应用【例题】如图，地面上有三个洞口A 、B 、C ，老鼠可以从任意一个洞口跑出，猫为能同时最省力地顾及到三个洞口（到A 、B 、C 三个点的距离相等），尽快抓到老鼠，应该蹲守在( )A ．ABC V 三边垂直平分线的交点B ．ABC V 三条角平分线的交点C ．ABC V 三条高所在直线的交点D ．ABC V 三条中线的交点【答案】A 【详解】解：∵猫所在的位置到A 、B 、C 三个点的距离相等，∴猫应该蹲守在ABC V 三边垂直平分线的交点处；故选A ．【变式训练】1．如图，某一个城市在一块空地新建了三个居民小区，它们分别为、、A B C ，且三个小区不在同一直线上，要想规划一所中学，使这所中学到三个小区的距离相等．这所中学应建在（ ）A ．ABC V 的三条中线的交点B ．ABC V 三边的垂直平分线的交点C ．ABC V 三条角平分线的交点D ．ABC V 三条高所在直线的交点【答案】B 【详解】解：根据线段的垂直平分线的性质：线段的垂直平分线上的点到线段的两个端点的距离相等．则学校应建在ABC V 三条边的垂直平分线的交点处．故选：B ．题型04 线段的垂直平分线的尺规作图【例题】如图，已知在ABC V 中，7AC =．(1)用尺规作BC 边的垂直平分线；（保留作图痕迹，不写作法）(2)BC 边的垂直平分线分别交AC BC 、于点D 、E ，连接BD ，若ABD △的周长是10，求AB ．【详解】（1）解：如图，DE 即为所求；；（2）解：∵DE 是BC 边的垂直平分线，∴BD DC =，∵7AC =，∴7AD DC AD BD +=+=，∵ABD △的周长是10，∴10AB BD AD ++=．∴3AB =．【变式训练】1．某公司招收职工的试卷中有道题：如图，有三条两两相交的公路，为便于及时进行监控，防止违章，这个监控仪器应安装在什么位置可以使离三个路口的交叉点的距离相等你能找到这个监控安装的位置吗？（尺规作图，不写过程，保留作图痕迹）【详解】解：如图，点P 这个监控安装的位置．．2．如图，已知点A 、点B 以及直线L ．(1)用尺规作图的方法在直线L 上求作一点P ，使PA PB =．（保留作图痕迹，不要求写出作法）；(2)在（1）中所作的图中，连接AP BP ，，若90APB Ð=°，过点A 作AM L ^于点M ，过点B 作BN L ^于点N ．求证：MN AM BN=+【详解】（1）解：点P 如图所示，；（2）解：∵AM L ^，BN L ^，90APB Ð=°，∴90MAP APM NPB Ð=°-Ð=Ð，∵PA PB =，∴()AAS MAP NPB ≌△△，∴AM PN =，PM BN =，∴MN PN PM AM BN =+=+．题型05 角平分线的性质定理【例题】（2023上·江苏连云港·八年级校考阶段练习）已知：如图AC 平分BAD Ð，CE AB CF AD ^^，，垂足分别为E 、F ，且BC CD =．(1)求证：BCE DCF △≌△；(2)若106AD BE ==，，求AB 的长．【答案】(1)见解析(2)22【分析】本题考查了角平分线的性质，全等三角形的判定与性质，本题中求证BCE DCF △≌△和Rt Rt ACF ACE @△△是解题的关键．（1）先证明CE CF =，再根据HL 即可证明BCE DCF △≌△；（2）先求出6DF BE ==，再根据HL 即可证明Rt Rt ACF ACE ≌△△，进而可求出AB 的长．【详解】（1）AC Q 平分BAD Ð，CE AB ^于E ，CF AD ^于F ，90CFD \Ð=°，90CEB Ð=°，CE CF =，在Rt BCE V 和Rt DCF V 中，CE CF BC CD =ìí=î，Rt Rt (HL)BCE DCF \△≌△；（2）∵BCE DCF △≌△，6BE =，∴6DF BE ==．∵10AD =，∴10616AF =+=．在Rt ACF V 和Rt ACE V 中，CF CE AC AC=ìí=î，Rt Rt (HL)ACF ACE \△≌△，∴16AE AF ==，∴16622AB =+=．【变式训练】1)求证：AE 是DAB Ð2)已知4AE =，DE 【答案】(1)见解析2)12【分析】本题主要考查了三角形全等的判定和性质，角平分线的性质定理；（1）根据角平分线的性质得出∵90C Ð=°，∴EF AD ^，∵AE 是DAB Ð的平分线，∴EF EC =，(1)求证：BE CF =；(2)若67AF BC ==，，则ABC V 【答案】(1)证明见解析(2)19可．【详解】（1）证明：连接CD BD ，，∵D 在BC 的中垂线上，∴BD CD =，∵DE AB ^，DF AC ^，AD 平分BAC Ð，∴DE DF =，90BED CFD Ð=Ð=°，∴()Rt Rt HL BDE CDF V V ≌，∴BE CF =；（2）解：∵AD 平分BAC Ð，∴∠∠E A D FA D =，∵DE AB ^，DF AC ^，∴90AED AFD Ð=Ð=°，又∵AD AD =，∴()AAS AED AFD V V ≌，∴AE AF 6==，由（1）可知BE CF =，∴ABC V 的周长为：66719AC AB BC AF CF AE BE BC AF AE BC ++=-+++=++=++=，故答案为：19．题型06 角平分线的判定定理【例题】如图，A ，B 两点分别在射线OM ，ON 上，点C 在MON Ð的内部且CA CB =，CD OM ^，CE ON ^，垂足分别为D ，E ，且AD BE =．(1)求证：OC 平分MON Ð；(2)如果12AO =，4BO =，求OD 的长．【详解】（1）证明：由题意得：CD OM ^，CE ON ^，\90CDA CEB Ð=Ð=°，在Rt ACD △和Rt BCE V 中，AC BC AD BE=ìí=î，\()Rt Rt HL ACD BCE V V ≌，\CD CE =，Q CD OM ^，CE ON ^，\OC 平分MON Ð．（2）在Rt ODC △和Rt OEC △中，CD CE OC OC =ìí=î，\()L Rt Rt H ODC OEC ≌V V ，\OD OE =，设BE x =，Q 4BO =，\4OE OD x ==+，Q AD BE x ==，\4212AO OD AD x =+=+=，\4x =，\448OD =+=．【变式训练】1．如图，DE AB ^于E ，DF AC ^于F ，若,BD CD BE CF ==．(1)求证：AD 平分BAC Ð；(2)写出+AB AC 与AE 之间的等量关系，并说明理由．【详解】（1）证明：∵DE AB ^∴90E DFC Ð=Ð=°，(1)求证：OC 是AOB Ð的平分线；(2)若30AOB Ð=°，23PF =，PF 【详解】（1）证明：在Rt PDF V 和题型07 角平分线性质的实际应用【例题】三条公路将、、A B C 三个村庄连成一个如图的三角形区域，如果在这个区域内修建一个集贸市场，要使集贸市场到三条公路的距离相等，那么这个集贸市场应建的位置是（ ）A ．三条高的交点B ．三条中线的交点C ．三条角平分线的交点D ．三边垂直平分线的交点【答案】C 【详解】解：在这个区域内修建一个集贸市场，要使集贸市场到三条公路的距离相等，根据角平分线的性质，集贸市场应建在A B C ÐÐÐ、、的角平分线的交点处，故选：C ．【变式训练】1．如图是三条两两相交的笔直公路，某物流公司现要修建一个货物中转站，使它到三条公路的距离相等，这个货物中转站可选的位置有（ ）A ．3个B ．4个C ．5个D ．1个【答案】B 【详解】解：如图所示，分别作直线交点处的角平分线，根据角平分线的性质，可得点1234,,,P P P P 共4个点，故选：B ．题型08 作角平分线（尺规作图）【例题】已知：如图，在ABC V 中，AB AC =，2B A Ð=Ð．(1)求作ABC Ð的平分线，交AC 于点P ．（要求：尺规作图，不写作法，保留作图痕迹）；(2)在（1）的条件下，求ABP Ð的角度？【详解】（1）解：以点B 为圆心，适当长为半径画弧交BA ，BC 于两点，再分别以两点为圆心，适当长为半径画弧交于一点，连接点B 与该点所在直线交AC 于点P ，如图所示：BP 即为所求；（2）解：∵AB AC =，1．如图所示，某县计划在张村、李村之间建一座定点医疗站P，张、李两村坐落在两相交公路内（如图所示）．医疗站必须满足下列条件：①使其到两公路距离相等；②到张、李两村的距离也相等．请你通过作图确定点P的位置．【详解】解：如图所示，点P即为所要求作的点．一、单选题A．4cm B．5cm【答案】C【分析】本题考查的知识点是垂直平分线的性质、等腰三角形的性质、含Q是AB的垂直平分线，DEAD DB cm\==，12\Ð=Ð=°，15DAE BA ．3B ．4C ．5D ．6【答案】A 【分析】本题考查了角平分线上的点到角的两边距离相等的性质，垂线段最短的性质，熟记性质是解题的关键．过点D 作DE OB ^于E ，根据角平分线上的点到角的两边距离相等可得DP DE =，再根据垂线段最短解答．【详解】解：如图，过点D 作DE OB ^于E ，OC Q 是AOB Ð的角平分线，DP OA ^，DP DE \=，由垂线段最短可得DQ DE ³，4DP =Q ，4DQ \³．故选：A ．3．（2023上·江苏无锡·八年级校考阶段练习）在联合会上，有A 、B 、C 三名选手站在一个三角形的三个顶点位置上，他们在玩抢凳子游戏，要求在他们中间放一个木凳，谁先抢到凳子谁获胜，为使游戏公平，则凳子应放的最适当的位置是在ABC V 的（ ）A ．三边中线的交点B ．三条角平分线的交点C ．三边中垂线的交点D ．三边上高的交点【答案】C【分析】本题考查线段垂直平分线的性质定理的逆定理，熟练掌握垂直平分线的性质是解题的关键，利用要使游戏公平，凳子就需要放在到A 、B 、C 三名选手距离相等的位置即可得到答案．【详解】解：由题可得：要使游戏公平，凳子就需要放在到A 、B 、C 三名选手距离相等的位置，则凳子所在的位置是ABC V 的外接圆圆心，A ．16°B ．26【答案】B 【分析】本题考查了线段垂直平分线的性质，直角三角形斜边上的中线等于斜边的一半，三角形内角和定理， 根据90ACB Ð=°，直线116BDC Ð=°，结合CDE ÐA ．①②【答案】D∵DM 是BC 的垂直平分线，∴DB DC =，在Rt BED △和Rt CFD V DE DF BD DC=ìí=î，【答案】80°/80度【分析】本题主要考查了线段垂直平分线的性质，等腰三角形的性质．根据线段垂直平分线的性质可得CD BD =，从而得到BCD B Ð=Ð的性质可得50A ADC Ð=Ð=°，即可求解．【答案】3【分析】此题考查了角平分线的性质定理，作DH AB ^于点H ，先求出即可得到点D 到的距离．∵8BC =，5BD =，∴3CD BC BD =-=，∵90C Ð=°，∴DC AC ^，【答案】20【分析】本题考查垂直平分线画图及性质，三角形周长公式．根据题意可知利用垂直平分线可知AD 【详解】解：∵分别以点【答案】50【分析】本题考查了角的等分线计算，正确理解定义是解题的关键．设分线的性质，角的平分线的判定，三角形内角和定理计算即可．【详解】设3ABC x Ð=，Ð∵点M N 、是ABC Ð与Ð∵点M N 、是ABC Ð与ACB Ð∴BN 平分MBC Ð，CN 平分∴,NE NG NF NG ==，∴NE NF =，∴MN 平分BMC Ð，150BMN BMC Ð=Ð=°，【答案】 15° 6【分析】本题考查了角平分线的判定与性质、三角形全等的判定与性质、三角形内角和定理，熟练掌握以上知识点，证明三角形全等是解此题的关键．（1）先证明Rt Rt BDE △≌△11．（2023上·河南南阳·八年级校考阶段练习）如图，在ABC V 中，AC 边的垂直平分线分别交BC AC 、于点E 、F ，连接AE ，作AD BC ^于点D ，且D 为BE 的中点．(1)试说明：AB CE =；(2)若32C Ð=°，求BAC Ð的度数．【答案】(1)见解析(2)84°【分析】本题主要考查的是三角形内角和定理，三角形外角的性质，线段垂直平分线的性质．（1）根据等腰三角形的判定得出AB AE =，根据垂直平分线的性质得出AE CE =，等量代换即可得出结论；（2）根据等边对等角得出32C EAC Ð=Ð=°，再根据三角形的外角的性质得出64AEB C EAC Ð=Ð+Ð=°，再根据等边对等角得出64B AEB Ð=Ð=°，根据三角形内角和定理得出52BAE Ð=°，进而得出答案．【详解】（1）∵D 为BE 的中点，∴BD DE =，∵AD BC ^，∴AB AE =，∵EF 是AC 的垂直平分线，∴AE CE =，∴AB CE =；（2）∵32C AE CE Ð=°=，，∴32C EAC Ð=Ð=°，∴64AEB C EAC Ð=Ð+Ð=°，∵AB AE =，∴64B AEB Ð=Ð=°，∴180180646452BAE B AEB Ð=°-Ð-Ð=°-°-°=°，∴523284BAC BAE EAC Ð=Ð+Ð=°+°=°．12．（2023上·河南周口·八年级校联考阶段练习）如图，已知ABC V 中，90C Ð=°，按下列要求作图（尺规作图，保留作图痕迹，不必写作法）．(1)作AB 边的垂直平分线，交AC 于点E ，交AB 于点F ；(2)连接CF ；(3)作BFC Ð的平分线，交BC 于点G ．【答案】(1)见解析(2)见解析(3)见解析【分析】本题考查了作线段的垂直平分线，作角平分线，掌握基本作图是解题的关键．根据题意作AB 边的垂直平分线，交AC 于点E ，交AB 于点F ，连结CF ，作BFC Ð的平分线，交BC 于G ．【详解】（1）解：如图，（2）解：如图，（3）解：如图，13．（2023上·河南信阳·八年级统考期中）如图，在ABC V 中，D 是BC 上一点，DF AC ^于点F ，连接EF ，AD 垂直平分EF ．(1)求证：AD 是BAC Ð的平分线；(2)若ABC V 的周长为18，ABC V 的面积为24，6BC =，求DE 的长．【答案】(1)见解析(2)4【分析】本题主要考查了垂直平分线的性质，角平分线的判定定理，熟知垂直平分线的性质是解题的关键．（1）根据垂直平分线的性质得到DE DF =，然后利用角平分线的判定定理即可证明结论；（2）首先求出12AB AC +=，然后根据等面积法进行求解即可．【详解】（1）证明：∵AD 垂直平分EF ，(1)试问：BF 与CG 的大小如何？证明你的结论．(2)若104AB AC ==，，试求【答案】(1)BF CG =，证明见解析(2)7【分析】本题考查角平分线的性质，垂直平分线的性质，全等三角形的判定和性质：Q AE 平分BAC Ð，EF AB ^\EF EG =，Q D 为BC 的中点，DE BC ^\DE 垂直平分BC ，\EB EC =，在Rt BFE △和Rt CGE △中，∵AB AC =，∴()111809022B A A Ð=°-Ð=°-Ð∵MN 为AB 的垂直平分线，∴90BNM Ð=°，(1)若120ACB Ð=°，则MCN Ð的度数为 (2)若MCN a Ð=，则MFN Ð的度数为 ；（用含(3)连接FA FB FC 、、，CMN V 的周长为6cm 【答案】(1)60°(2)1902a °-Q DM EN ，分别垂直平分AC 和BC ，MA MC \=，NB NC =，Q CMN V 的周长为6cm ，6cm MC NC MN \++=，6cm MA NB MN \++=，即6cm AB =，Q FAB V 的周长为14cm ，14cm FA FB AB \++=，8cm FA FB \+=，Q DF EF ，分别垂直平分AC 和BC ，FA FC \=，FB FC =，28cm FC \=，4cm FC \=．17．（2023上·湖南衡阳·八年级校考期末）如图，90BAC Ð=°，CD 平分ACB Ð交AB 于D ，CM CD ^，点M 在AB 的垂直平分线上，AM 交BC 于O ，MG AC ^于点G ，MF BC ^于点F ．(1)求证：BCM GCM Ð=Ð；(2)若2CG =，求BC AG -的长；(3)若点D 在BC 的垂直平分线上，试判断ABM V 的形状，并说明理由．【答案】(1)见解析；(2)2；(3)ABM V 是等边三角形，理由见解析．【分析】（1）由角平分线的性质可得ACD BCD Ð=Ð，由余角的性质可得结论；（2）由“AAS ”可证FCM GCM ≌V V ，可得MF MG =，2CF CG ==，由“HL ”可证Rt Rt BFM AGM ≌V V ，可得BF AG =，即可求解；（3）由线段垂直平分线的性质可求30DBC DCB ACD Ð=Ð=Ð=°，由等腰三角形的性质可求30MAG Ð=°，由三角形内角和定理可求解．【详解】（1）证明：∵CD 平分ACB Ð，∴ACD BCD Ð=Ð，∵CM CD ^，∴90DCM Ð=°，∴90ACD MCG Ð+Ð=°，90DCB BCM Ð+Ð=°，∴BCM GCM Ð=Ð；（2）∵BCM GCM Ð=Ð，90MFC MGC Ð=Ð=°，CM CM =，∴()AAS FCM GCM ≌V V ，∴MF MG =，2CF CG ==，∵点M 在AB 的垂直平分线上，∴AM BM =，且FM MG =，∴()Rt Rt HL BFM AGM ≌V V ，∴BF AG =，CBM MAG Ð=Ð，∴2BC AG BC BF CF -=-==；（3）∵点D 在BC 的垂直平分线上，∴BD CD =，∴DBC DCB Ð=Ð，且ACD DCB Ð=Ð，90DBC DCB ACD Ð+Ð+Ð=°，∴30DBC DCB ACD Ð=Ð=Ð=°，∵AM BM =，∴30MAB MBA ABC CBM CBM Ð=Ð=Ð+Ð=°+Ð，∵CBM MAG Ð=Ð，∴30MAB MAG Ð=°+Ð，∵90MAB MAG BAC Ð+Ð=Ð=°，∴30MAG Ð=°，∴60MAB MBA Ð=Ð=°，∴60AMB Ð=°，∴ABM V 是等边三角形．【点睛】本题考查了全等三角形的判定和性质，等腰三角形的性质，角平分线的性质，线段垂直平分线的性质等知识，证明全等三角形是本题的关键．18．（2023上·新疆和田·八年级统考期末）数学活动：如图1，角的平分线的性质的几何模型，已知OP 平分AOB Ð，PA OA ^于点A ，PB OB ^于点B ．(1)探究：如图2，点M 是OP 上任意一点（不与O 、P 重合），连接MA 、MB ，问题：请判断MA 与MB 的数量关系，并证明你的结论．(2)如图3，连接AB ．问题：①OP 垂直平分AB 吗？请说明理由．②若30AOP Ð=°，6AB =，求AOB V 的周长．【答案】(1)MA MB =，证明见解析(2)①OP 垂直平分AB ，理由见解析；②18【分析】（1）证明()AAS OAP OBP V V ≌，则OA OB =，证明()SAS AOM BOM V V ≌，进而可得MA MB =．（2）①如图3，记AB 与OP 的交点为C ，由（1）可知()AAS OAP OBP V V ≌，则OA OB =，证明()AAS OAP OBP V V ≌，则AC BC =，90ACO BCO Ð=Ð=°，进而可得OP 垂直平分AB ；②由题意知60AOB Ð=°，可证AOB V 是等边三角形，则6OA OB AB ===，然后求AOB V 的周长即可．【详解】（1）解：MA MB =，证明如下：∵OP 平分AOB Ð，PA OA ^，PB OB ^，∴AOP BOP Ð=Ð，90OAP OBP Ð=Ð=°，又∵OP OP =，∴()AAS OAP OBP V V ≌，∴OA OB =，∵OM OM =，AOM BOM Ð=Ð，OA OB =，∴()SAS AOM BOM V V ≌，∴MA MB =．（2）①解：OP 垂直平分AB ，理由如下：如图3，记AB 与OP 的交点为C ，。
中考数学复习----《角的平分线与线段的垂直平分线》知识点总结与专项练习题(含答案解析)
中考数学复习----《角的平分线与线段的垂直平分线》知识点总结与专项练习题（含答案解析）知识点总结1.角平分线的定义：角的内部把角平均分成两个相等的角的射线叫做角的平分线。
2.角平分线的性质：①平分角。
②角平分线上任意一点到角两边的距离相等。
3.角平分线的判定：角的内部到角两边相等的点一定在角平分线上。
4.角平分线的尺规作图：具体步骤：①以角的顶点O为圆心，一定长度为半径画圆弧，圆弧与角的两边分别交于两点M、N。
如图①。
②分别以点M与点N为圆心，大于MN长度的一半为半径画圆弧，两圆弧交于点P。
如图②。
③连接OP，OP即为角的平分线。
5.线段的垂直平分线的定义：过线段的中点且与线段垂直的直线是这条线段的垂直平分线。
6.垂直平分线的性质：①垂直且平分线段。
②垂直平分线上任意一点到这条线段两个端点的距离相等。
7.垂直平分线的判定：到线段两端点距离相等的点一定在线段的垂直平分线上。
8.垂直平分线的吃规作图：具体步骤：①以线段两个端点为圆心，大于线段长度的一半为半径画圆弧，两圆弧在线段的两侧别分交于M、N。
如图①②连接MN，过MN的直线即为线段的垂直平分线。
如图②练习题1、（2022•鄂尔多斯）如图，∠AOE＝15°，OE平分∠AOB，DE∥OB交OA于点D，EC⊥OB，垂足为C．若EC＝2，则OD的长为（）A．2 B．2C．4 D．4+2【分析】过点E作EH⊥OA于点H，根据角平分线的性质可得EH＝EC，再根据平行线的性质可得∠ADE的度数，再根据含30°角的直角三角形的性质可得DE的长度，再证明OD＝DE，即可求出OD的长．【解答】解：过点E作EH⊥OA于点H，如图所示：∵OE平分∠AOB，EC⊥OB，∴EH＝EC，∵∠AOE＝15°，OE平分∠AOB，∴∠AOC＝2∠AOE＝30°，∵DE∥OB，∴∠ADE＝30°，∴DE＝2HE＝2EC，∵EC＝2，∴DE＝4，∵∠ADE＝30°，∠AOE＝15°，∴∠DEO＝15°，∴∠AOE＝∠DEO，∴OD＝DE＝4，故选：C．2、（2022•北京）如图，在△ABC中，AD平分∠BAC，DE⊥AB．若AC＝2，DE＝1，则S △ACD＝．【分析】过D点作DH⊥AC于H，如图，根据角平分线的性质得到DE＝DH＝1，然后根据三角形面积公式计算．【解答】解：过D点作DH⊥AC于H，如图，∵AD平分∠BAC，DE⊥AB，DH⊥AC，∴DE＝DH＝1，∴S△ACD＝×2×1＝1．故答案为：1．3、（2022•黑龙江）在Rt△ABC中，∠C＝90°，AD平分∠CAB，AC＝6，BC＝8，CD＝．【分析】过点D作DE⊥AB于E，利用勾股定理列式求出AB，再根据角平分线上的点到角的两边距离相等可得CD＝DE，然后根据△ABC的面积列式计算即可得解．【解答】解：如图，过点D作DE⊥AB于E，∵∠C＝90°，AC＝6，BC＝8，∴AB＝＝＝10，∵AD平分∠CAB，∴CD＝DE，∴S△ABC＝AC•CD+AB•DE＝AC•BC，即×6•CD+×10•CD＝×6×8，解得CD＝3．故答案为：3．4、（2022•宜昌）如图，在△ABC中，分别以点B和点C为圆心，大于BC长为半径画弧，两弧相交于点M，N．作直线MN，交AC于点D，交BC于点E，连接BD．若AB＝7，AC＝12，BC＝6，则△ABD的周长为（）A．25 B．22 C．19 D．18【分析】根据题意可知MN垂直平分BC，即可得到DB＝DC，然后即可得到AB+BD+AD ＝AB+DC+AD＝AB+AC，从而可以求得△ABD的周长．【解答】解：由题意可得，MN垂直平分BC，∴DB＝DC，∵△ABD的周长是AB+BD+AD，∴AB+BD+AD＝AB+DC+AD＝AB+AC，∵AB＝7，AC＝12，∴AB+AC＝19，∴△ABD的周长是19，故选：C．5、（2022•湖北）如图，在矩形ABCD中，AB＜BC，连接AC，分别以点A，C为圆心，大于AC的长为半径画弧，两弧交于点M，N，直线MN分别交AD，BC于点E，F．下列结论：①四边形AECF是菱形；②∠AFB＝2∠ACB；③AC•EF＝CF•CD；④若AF平分∠BAC，则CF＝2BF．其中正确结论的个数是（）A．4 B．3 C．2 D．1【分析】根据题意分别证明各个结论来判断即可．【解答】解：根据题意知，EF垂直平分AC，在△AOE和△COF中，，∴△AOE≌△COF（ASA），∴OE＝OF，∴AE＝AF＝CF＝CE，即四边形AECF是菱形，故①结论正确；∵∠AFB＝∠FAO+∠ACB，AF＝FC，∴∠FAO＝∠ACB，∴∠AFB＝2∠ACB，故②结论正确；∵S四边形AECF＝CF•CD＝AC•OE×2＝AC•EF，故③结论不正确；若AF平分∠BAC，则∠BAF＝∠FAC＝∠CAD＝90°＝30°，∴AF＝2BF，∵CF＝AF，∴CF＝2BF，故④结论正确；故选：B．33．（2022•鄂尔多斯）如图，在△ABC中，边BC的垂直平分线DE交AB于点D，连接DC，若AB＝3.7，AC＝2.3，则△ADC的周长是．【分析】根据线段垂直平分线的性质可得BD＝CD，进一步即可求出△ADC的周长．【解答】解：∵边BC的垂直平分线DE交AB于点D，∴BD＝CD，∵AB＝3.7，AC＝2.3，∴△ADC的周长为AD+CD+AC＝AB+AC＝6，故答案为：6．34．（2022•青海）如图，在Rt△ABC中，∠ABC＝90°，ED是AC的垂直平分线，交AC 于点D，交BC于点E，∠BAE＝10°，则∠C的度数是．【分析】根据线段垂直平分线的性质可得AE＝EC，从而可得∠EAC＝∠C，然后利用三角形内角和定理可得∠EAC+∠C＝80°，进行计算即可解答．【解答】解：∵ED是AC的垂直平分线，∴AE＝EC，∴∠EAC＝∠C，∵∠ABC＝90°，∠BAE＝10°，∴∠EAC+∠C＝180°﹣∠BAE﹣∠ABC＝80°，∴∠EAC＝∠C＝40°，故答案为：40°．。
线段的垂直平分线和角平分线的复习
https://
REPORTING
目录
• 垂直平分线与角平分线基本概念 • 垂直平分线相关定理与推论 • 角平分线相关定理与推论 • 垂直平分线与角平分线在几何图形中应用 • 解题技巧与策略总结 • 练习题与答案解析
PART 01
垂直平分线与角平分线基 本概念
对称性等。
角平分线在多边形中可用于求解 角度和线段长度，如利用角平分 线性质求解多边形中的角度和边
长。
垂直平分线和角平分线的交点在 多边形中可用于求解多边形的内 切圆和外接圆以及与这些圆相关
的性质。
PART 05
解题技巧与策略总结
REPORTING
WENKU DESIGN
观察图形特征，选择合适方法
03
2. 题目
在△ABC中，AD是∠BAC的平分 线，DE⊥AB于点E，DF⊥AC于 点F，交BC于点G，且 DE=DF． 求证：△ABC是等腰三 角形．
04
解析
根据角平分线的性质“角的平分 线上的点到角的两边的距离相等” 可得点D在∠BAC的平分线上，再 根据等腰三角形的性质“等边对 等角”以及平角的性质证明 ∠B=∠C即可。
练习题三：证明四边形性质
题目
四边形ABCD中，AB=CD，AD=BC， E、F分别是BD、AC的中点，求证： EF垂直平分AC。
解析
连接AE、CE，由于AB=CD，AD=BC， BD=BD，所以△ABD≌△CDB，从而 ∠ABD=∠CDB，又因为E是BD的中点，所以 AE=CE，又因为F是AC的中点，所以EF垂直平 分AC。
两者关系与区别
关系
垂直平分线和角平分线都是几何学中的基本概念，它们都与距离和角度有关。
线段的垂直平分线、角平分线经典习题及答案
线段的垂直平分线、角平分线经典习题及答案由于A、B都在CD的垂直平分线上，所以直线AB是CD的垂直平分线。
证毕。
例4：解：连接EF，由于AB=AC，所以∠BAC=60°，∴∠DEG=30°，∠GFC=60°，又因为DE⊥AB，FG⊥AC，所以DEGF是一个菱形，且DG=GF=7.5cm，所以EG=2DGsin30°=7.5cm。
例5：证明：因为BD=BC，所以∠XXX∠CBD，又因为BE⊥CD，CF⊥BD，所以∠BEC=∠BCF，所以BE平分∠XXX，CF平分∠CBD，又因为∠XXX∠CBD，所以BE和CF都平分∠BCD，即BE垂直平分CD。
证毕。
例6：证明：连接OF，OE，MN，∵MN∥BC，∴∠EOF=∠ACB，又∠XXX∠EOM+∠MOF，∠XXX∠EOM+∠EOF，∴∠MOF=∠ACB-∠EOF，又因为EF是AC的角平分线，∴∠XXX∠EAF，又因为EF是AC的外角平分线，∴∠XXX∠XXX，∴∠MOF=∠ACB-∠XXX，又因为OE⊥AC，OF⊥AC，所以OE=OF，证毕。
例7：证明：连接AD，因为AD是∠A的平分线，所以∠EAD=∠FAD，又因为BD=BC，所以∠XXX∠DCB，又因为AD⊥DE，所以∠EDB=90°-∠XXX，又因为DF⊥CF，所以∠XXX°-∠DCB，所以∠EDB=∠XXX，又因为∠EAD=∠FAD，所以三角形ADE与三角形ADF全等，所以DE=DF，又因为BE⊥DE，CF⊥DF，所以BE=DEsin∠EDB=DFsin∠FDC=CF，证毕。
例4：根据题意，作AH垂直BC于点H，可以得到HC 的长度为15/2.由于△ABC是等腰三角形，所以∠ACB=∠ABC=30°。
根据正弦定理，可以求得AC的长度为5√3.由于F是AC的中点，所以FC的长度为5/2√3.根据勾股定理，可以得到CG和BE的长度都为5.因此，EG的长度也为5.例5：由于DE垂直于AB，而∠ACB=90°，所以∠BDE=∠ACB=90°。
线段的垂直平分线和角平分线性质复习
(第8题）ED C BA线段的垂直平分线和角平分线性质复习学习目标：1．利用角平分线的性质解决问题2．利用线段垂直平分线的性质解决问题教学过程：一、基础练习：1、如图，△ABC 中，AD 垂直平分边BC ，AB ＝5，那么AC ＝_________.2、如图，AB 垂直平分CD ，若AC=1.6cm ，BC=2.3cm ，则四边形ABCD 的周长是（ ）cm.A.3.9B.7.8C.4D.4.63、如右图，△ABC 中，AB=AC=16cm ，AB 的垂直平分线ED 交AC 于D 点. （1）当AE=13cm 时，BE= cm ；（2）当△BEC 的周长为26cm 时，则BC= cm ； （3）当BC=15cm ，则△BEC 的周长是 cm.垂直平分线的性质：1．∠AOB 的平分线上一点M ，M 到 OA 的距离为1.5 cm ，则M 到OB 的距离为2．∠AOB =60°，CD ⊥OA 于D ，CE ⊥OB 于E ，且CD =CE ，则∠DOC =_________. 3．如图，在△ABC 中，∠C =90°，AD 是角平分线，DE ⊥AB 于E ，且DE =3cm ，BD =5 cm ，则BC =_____cm .(第1题)4、如图，CD 为Rt △ABC 斜边上的高，∠BAC 的平分线分别交CD 、CB 于点E 、F ，FG ⊥AB ，垂足为G ，则CF ______FG ，CE ________CF .角平分线上的点到______________距离相等；到一个角的两边距离相等的点都在_____________． 二、综合应用：1、已知如图，在△ABC 中，AB =AC ，O 是△ABC 内一点，且OB =OC ， 求证：AO ⊥B C ．2、如图，在△ABC 中，AB =AC ，∠A =120°，AB 的垂直平分线MN 分别交BC 、AB 于点M 、N ．求证：CM =2BM ．3、如图，AB=AC ，BD=CD ，DE ⊥AB 于E ，DF ⊥AC 于F. 求证：DE=DF.E F B C A D4、如图，已知∠1=∠2，试添加一个条件，使得PA=PC.并说明理由。
专题：线段垂直平分线与角平分线
1.已知△ABC的三边的垂直平分线交点在△ABC的边上，则△ABC的形状为2. 如图1，AD是△ABC中∠BAC的平分线，DE⊥AB交AB于点E，DF⊥AC交AC于点F．若S△ABC＝7，DE＝2，AB＝4，则AC＝图1 图2 图33.如图2，在△ABD中，AD=4，AB=3，AC平分∠BAD，则S△ABC:S△ACD=4.如图3，在△ABC中，BC=5cm，BP、CP分别是∠ABC和∠ACB的角平分线，且PD∥AB，PE ∥AC，则△PDE的周长是___________cm.5. 如图4，△ABC中，DE、FG分别为AB、AC的垂直平分线。
（1）如果BC=16cm，那么△AEG的周长为_______；（2）如果∠BAC=100°，那么∠EAG=_______．图46. ⑴如图5，若P点是∠ABC和∠ACB的角平分线的交点，∠A=α，则∠P= ；⑵如图6，若P点是∠ABC和外角∠ACE的角平分线的交点，∠A=α，则∠P= ；⑶如图7，若P点是外角∠CBF和∠BCE的角平分线的交点，∠A=α，则∠P= 。
图5 图6图77. 如图，EG、FG分别是∠MEF和∠NFE的角平分线，交点是G，BP、CP分别是∠MBC和∠NCB的角平分线，交点是P，若∠G＝68°，那么∠P＝。
8. 随着人们生活水平的不断提高，汽车逐步进入到千家万户，小红的爸爸想在本镇的三条相互交叉的公路（如图所示），建一个加油站，要求它到三条公路的距离相等，这样可供选择的地址有（）处。
A、1B、2C、3D、49. 如图，已知在△ABC中，AB=AC，∠BAC=120°，AC的垂直平分线EF交AC于点E，交BC 于点F．求证：BF=2CF．10. 如图所示，∠AOP=∠BOP=15°，PC∥OA，PD⊥OA，若PC=4，求PD的长．11. 在Rt△ABC中，∠C=90°，AD平分∠BAC，DE垂直平分AB。
专题06 线段的垂直平分线与角平分线综合压轴题五种模型全攻略(解析版)
专题06线段的垂直平分线与角平分线综合压轴题五种模型全攻略【考点导航】目录【典型例题】 (1)【考点一利用线段垂直平分线的性质求解】 (1)【考点二线段垂直平分线的判定】 (4)【考点三利用角平分线的性质求解】 (8)【考点四角平分线的判定】 (11)【考点五线段的垂直平分线与角平分线的综合问题】 (14)【过关检测】 (20)【典型例题】【考点一利用线段垂直平分线的性质求解】∴()SAS ADE CDE △△≌，∴36DCE A ==︒∠∠，∴72BEC A ACE ∠=∠+∠=︒，故答案为：72︒．【点睛】本题主要考查了三角形外角的性质，全等三角形的性质与判断，线段垂直平分线的定义，正确推出36DCE A ==︒∠∠是解题的关键．【变式训练】【答案】8【分析】根据垂直平分线的性质定理，得【详解】解：∵AB 的中垂线交【点睛】本题主要考查垂直平分线的性质定理，掌握垂直平分线的性质定理是解题的关键．线段的垂直平分线上的点到线段的两个端点的距离相等．3．（2023春·广东深圳·七年级校考期末）如图，在ABC 中，DM ，EN 分别垂直平分边AC 和边BC ，交边AB 于M ，N 两点，DM 与EN 相交于点F ．(1)若10cm AB =，求CMN 的周长；(2)若o 65MFN ∠=，则MCN ∠的度数为______°．【答案】(1)10cm(2)50【分析】（1）由线段垂直平分线的性质可得MA MC =，NB NC =，则CMN 的周长CM CN MN AM MN BN AB =++=++=；（2）根据等边对等角可得A MAC ∠=∠，B NCB ∠=∠，根据三角形内角和定理，列式求出FMN FNM ∠+∠，再求出A B ∠∠+，即可求解．【详解】（1）解：∵DM ，EN 分别是AC ，BC 的中垂线∴MA MC =，NB NC=∴CMN C CM MN CN AM MN BN =++=++ AB =10cm =；（2）由（1）得MA MC =，NB NC =，由DM ，EN 分别垂直平分AC 和BC ，可得90MDA NEB ∠=∠=︒，∴A MCA ∠=∠，B NCB ∠=∠，∵在MNF 中，65MFN ∠=︒，∴115FMN FNM ∠+∠=︒，根据对顶角的性质可得：FMN AMD ∠=∠，FNM BNE ∠=∠，在Rt ADM △中，9090A AMD FMN ∠=︒-∠=︒-∠，在Rt BNE 中，9090B BNE FNM ∠=︒-∠=︒-∠，∴909065A B FMN FNM ∠+∠=︒-∠+︒-∠=︒，∴65MCA NCB ∠+∠=︒，在ABC 中，65A B ∠+∠=︒∴115ACB ∠=︒，∴()50MCN ACB MCA NCB ∠=∠-∠+∠=︒．故答案为：50．【点睛】本题考查了线段垂直平分线的性质，等边对等角的性质，三角形内角和定理，解题的关键是熟练掌握相关基本性质和整体思想的利用．【考点二线段垂直平分线的判定】例题：（2023春·陕西西安·七年级校考阶段练习）如图，AD 为三角形ABC 的角平分线，DE AB ⊥于点E ，DF AC ⊥于点F ，连接EF 交AD 于点O ．(1)若BE DE =，60BAC ∠=︒，求CDF ∠的度数；(2)写出AD 与EF 的关系，并说明理由；【答案】(1)15︒(2)AD EF ⊥，AD 平分EF【分析】（1）根据三角形内角和可得C ∠，再利用内角和即可得出CDF ∠；（2）由角平分线的意义及两个垂直可证明ADE ADF V V ≌，从而有,AE AF DE DF ==，由线段垂直平分线的判定知，AD EF ⊥，AD 平分EF ．【详解】（1）解：∵DE AB⊥90BED ∴∠=︒∵BE DE=45B ∴∠=︒∵60BAC ∠=︒180456075C ∴∠=︒-︒-︒=︒∵DF AC⊥90DFC ∴∠=︒∴15CDF ∠=︒（2）解：AD EF ⊥，AD 平分EF ；理由如下：∵AD 平分BAC ∠，∴∠=∠DAB DAC ，∵DE AB ⊥，DF AC ⊥，∴90DEA DFA ∠=∠=︒，∵AD AD =，∴ADE ADF V V ≌，∴AE AF DE DF ==，，∴AD 是线段EF 的垂直平分线，即AD EF ⊥，AD 平分EF ．【点睛】本题考查了全等三角形的证明，等腰三角形的性质，三角形内角和，角平分线的性质．找到Rt AED △和Rt ADF ，通过两个三角形全等，找到各量之间的关系，完成证明是关键．【变式训练】1．（2023秋·广西河池·八年级统考期末）如图，在ABC 中，边AB ，BC 的垂直平分线交于点P ．(1)求证：PA PB PC ==；(2)求证：点P 在线段AC 的垂直平分线上．【答案】(1)见解析(2)见解析【分析】（1）根据垂直平分线的性质直接可得到答案；（2）根据到线段两个端点的距离相等的点在线段的垂直平分线上即可得到答案；【详解】（1）证明：∵边AB 、BC 的垂直平分线交于点P ，∴PA PB =，PB PC =，∴PA PB PC ==；（2）证明：∵边AB ，BC 的垂直平分线交于点P ，∴PA PB =，PB PC =，∴PA PC =，∴点P 在AC 的垂直平分线上．【点睛】本题考查垂直平分线的性质及判定，解题的关键是熟练掌握垂直平分线上的点到线段两个端点距离相等及到线段两个端点的距离相等的点在线段的垂直平分线上．2．（2023春·全国·八年级专题练习）如图，点D 是等边ABC 外一点，120BDC ∠=︒，DB DC =，点E ，F 分别在AB ，AC 上，连接AD 、DE 、DF 、EF ．(1)求证：AD 是BC 的垂直平分线；(2)若ED 平分BEF ∠，5BC =，求AEF △的周长．【答案】(1)见解析；(2)10．【分析】（1）根据到线段两端距离相等的点在垂直平分线上即可证明；（2）如图，过D 作DM EF ⊥于M ，结合已知易证90DBE ∠=︒即DB AB ⊥，同理可得DC AC ⊥，易证()Rt DBE Rt DME HL ≌得BE ME =，同理可得CF MF =，然后转换求周长即可．【详解】（1）证明：ABC 是等边三角形，AB AC ∴=，∴A 在BC 的垂直平分线上，又DB DC =，∴D 在BC 的垂直平分线上，AD ∴是BC 的垂直平分线；（2）如图，过D 作DM EF ⊥于M ，120BDC ∠=︒ ，DB DC=30DBC ∴∠=︒又ABC 是等边三角形，90DBE DBC ABC ∴∠=∠+∠=︒A DB B∴⊥同理可得DC AC∴⊥ED 平分BEF ∠，DM EF⊥DB DM DC∴==DF ∴平分CFE ∠，在Rt DBE 与Rt DME 中DE DE DB DM=⎧⎨=⎩()Rt DBE Rt DME HL ∴ ≌BE ME∴=同理可得CF MF=()AEF C AE AF EF AE AF EM MF =++=+++ ()AE AF EB CF =+++()()AE EB AF CF =+++AB AC=+210BC ==.【点睛】本题考查了垂直平分线的判定，角平分线的判定和性质，全等三角形的判定和性质；解题的关键是通过相关性质构造线段相等、进行转换．【考点三利用角平分线的性质求解】A ．14B ．26【答案】D 【分析】如图：作DF AC ⊥交∵AD 平分BAC ∠，DE AB ⊥∴4DF DE ==，∴12ABC ADC ADB S S S AC ==+ 【变式训练】1．（2023春·甘肃张掖·八年级校考期末）一块三角形的草坪，现要在草坪上建一个凉亭供大家休息，要使凉亭到草坪三边的距离相等，凉亭的位置应选在（）A ．三角形三条边的垂直平分线的交点B ．三角形三条角平分线的交点C ．三角形三条高所在直线的交点D ．三角形三条中线的交点【答案】B【答案】5【分析】根据垂线段最短确定点【详解】解： O是BA上任意一点，∴当PO BA⊥时，OP的值最小，∠，P是BD又 BD平分ABC(1)求PAD∠的度数；=．(2)试说明PD PC∵AP 平分DAB ∠，PD AD ⊥，PE ∴PE PD =．∵BP 平分ABC ∠，PC BC ⊥，PE ∴PE PC =，【考点四角平分线的判定】例题：（2023·全国·八年级假期作业）如图，ABC ∠的平分线与ACB ∠的外角平分线相交于点D ，连接AD ．求证：AD 是BAC ∠的外角平分线．【答案】证明见解析【分析】作DE BA ⊥交BA 的延长线于E ，DF AC ⊥于F ，DG BH ⊥于G ，根据角平分线的性质得到DE DF =，根据角平分线的判定定理证明结论．【详解】证明：作DE BA ⊥交BA 的延长线于E ，DF AC ⊥于F ，DG BH ⊥于G ，DB 平分ABC ∠、DC 平分ACH ∠，DE DG ∴=，DF DG =，DE DF ∴=，又DE BA ⊥，DF AC ⊥，∴AD 是BAC ∠的外角平分线．【点睛】本题考查的是角平分线的性质和判定，掌握角的平分线上的点到角的两边的距离相等、到角的两边的距离相等的点在角的平分线上是解题的关键．【变式训练】1．（2023·广东惠州·校联考二模）如图，CB CD =，180D ABC ∠+∠=︒，CE AD ⊥于E ．(1)求证：AC 平分DAB ∠；(2)若10AE =，4DE =，求AB 的长．【答案】(1)见解析(2)6【分析】（1）过C 点作CF AB ⊥，交AB 的延长线于点F ．由AAS 证明CDE CBF ≌，可得CE CF =，结论得证；（2）证明Rt ACE Rt ACF ≌，可得AE AF =，可求出AB ．【详解】（1）证明：过C 点作CF AB ⊥，交AB 的延长线于点F ．∵CE AD ⊥，∴90DEC CFB ∠=∠=︒，∵180D ABC ∠+∠=︒，180CBF ABC ∠+∠=︒，∴D CBF ∠=∠，又∵CB CD =，∴CDE CBF ≌，∴CE CF =，∴AC 平分DAB ∠；（2）解：由（1）可得4BF DE ==，在Rt ACE 和Rt ACF 中，CE CF AC AC=⎧⎨=⎩，∴Rt ACE Rt ACF ≌，∴10==AE AF ，∴6AB AF BF =-=．【点睛】本题考查了角平分线的判定与性质，全等三角形的判定与性质，关键是作出辅助线构造全等三角形．2．（2023·江苏·八年级假期作业）如图，DE AB ⊥于点E ，DF AC ⊥于点F ，若,BD CD BE CF ==．(1)求证：AD 平分BAC ∠；(2)请猜想+AB AC 与AE 之间的数量关系，并给予证明．【答案】(1)见解析(2)2AB AC AE +=，证明见解析【分析】（1）根据HL 证明Rt Rt DBE DCF ≌ ，得到DE DF =，再根据角平分线的判定定理，求证即可；（2）通过HL 证明Rt Rt ADE ADF ≌△△，得到AE AF =，利用线段之间的关系，求解即可．【详解】（1）证明：∵DE AB ⊥，DF AC ⊥，∴90E DFC ∠=∠=︒，在Rt DBE 和Rt DCF 中，BD CD BE CF =⎧⎨=⎩，∴()Rt Rt HL DBE DCF ≌△△，∴DE DF =，∵DE AB ⊥，DF AC ⊥，∴AD 平分BAC ∠．（2）解：2AB AC AE +=，证明如下：在Rt ADE △和Rt ADF 中，AD AD DE DF=⎧⎨=⎩，∴()Rt Rt HL ADE ADF ≌△△，∴AE AF =，∴2AB AC AB AF CF AB AE BE AE +=++=++=．【点睛】此题考查了全等三角形的判定与性质，以及角平分线的判定定理，解题的关键是灵活利用相关性质进行求解．【考点五线段的垂直平分线与角平分线的综合问题】例题：（2023秋·河北保定·八年级统考期末）如图，在ABC 中，AD 平分BAC ∠，90C = ∠，DE AB ⊥于点E ，点F 在AC 上，BD DF =．(1)求证：CF EB =．(2)连接CE ，求证AD 垂直平分CE ．(3)若10AB =，6AF =，求CF 的长．【答案】(1)证明见解析(2)证明见解析(3)2CF =【分析】（1）利用角平分线的性质可得DC DE =，再利用“HL ”证明t R DCF Rt DEB △≌△，即可证明CF EB =；（2）利用“HL ”证明Rt ACD Rt AED ≌，可得AC AE =，所以点A 在CE 的垂直平分线上，根据DC DE =，可得点D 在CE 的垂直平分线上，进而可以解决问题；（3）设CF BE x ==，则AE AB BE x AC AF FC x 106=-=-==+=+，即可建立方程求解．【详解】（1）证明：∵DE AB ⊥于点E ，∴90DEB ∠= ，又AD 平分BAC ∠，90C = ∠，∴DC DE =，在t R DCF △和Rt DEB 中，DF DB DC DE =⎧⎨=⎩，∴()t R DCF Rt DEB HL ≌，∴CF EB =．（2）证明：连接CE ，如图在Rt ACD 和Rt AED △中，AD AD DC DE =⎧⎨=⎩，∴()Rt ACD Rt AED HL ≌，∴AC AE =∴点A 在CE 的垂直平分线上，∵DC DE =，∴点D 在CE 的垂直平分线上，∴AD 垂直平分CE （3）解：设CF BE x ==，∵10AB =，6AF =，∴AE AB BE x 10=-=-，AC AF FC x 6=+=+，∵AE AC =，∴106x x -=+，解得：2x =∴2CF =【点睛】本题考查了直角三角形全等的判定与性质，角平分线的性质，解题关键是在图形中找到正确的全等三角形以及熟悉以上性质与判定．【变式训练】1．（2023秋·河南洛阳·八年级统考期末）如图，AD 是ABC 的角平分线，DE AB ⊥于点E ，DF AC ⊥于点F ，连接EF ．(1)求证：AD 为CAB ∠的角平分线；(2)若8AB =，6AC =，求AE 的长．【答案】(1)见解析(2)7AE =DG 为BC 的垂直平分线，CD BD ∴=，DE AB ∵⊥，DF AC ⊥，90DEB DFC ∴∠=∠=︒，在Rt DEB △和Rt DFC △中，(1)求证：BD平分∠ABC；(2)如图2，AC的垂直平分线交BD于点Q，交AC于点G，QM 【答案】(1)见解析(2)MC=1.5【分析】（1）由∠ACF=∠A+∠ABF，∠ECF=∠BPC+∠DBF，得∠【详解】（1）证明：∵∠ACF=∠A+∠ABF，∠ECF=∠BPC+∠DBF，∴∠ABF=∠ACF-78°，∠DBF=∠ECF-39°，∵CE平分∠ACF，∴∠ACF=2∠ECF，∴∠ABF=2∠ECF-78°=2（∠ECF-39°）=2∠DBF，∴BD平分∠ABC；（2）解：连接AQ，CQ，过点Q作BA的垂线交BA的延长线于N，∵QG垂直平分AC，∴AQ=CQ，∵BD平分∠ABC，QM⊥BC，QN⊥BA，∴QM=QN，∴Rt△QNA≌Rt△QMC（HL），∴NA=MC，∵QM=QN，BQ=BQ，∴Rt△QNB≌Rt△QMB（HL），∴NB=MB，∴BC=BM+MC=BN+MC=AB+AN+MC，∴7=4+2MC，∴MC=1.5．【点睛】本题主要考查了角平分线的定义和性质，三角形外角的性质，线段垂直平分线的性质，全等三角形的判定与性质等知识，作辅助线构造全等三角形是解题的关键．【过关检测】一、选择题1．（2023春·四川成都·八年级统考期末）如图，在ABC 中，DE 是AC 边的垂直平分线，分别交BC AC 、于D 、E 两点，连接AD ，25BAD ∠=︒，35C ∠=︒，则B ∠的度数为（）A ．70︒B ．75︒C ．80︒D ．85︒【答案】D 【分析】利用垂直平分线的性质，可得35DAC C ∠=∠=︒，根据三角形内角和定理，可得B ∠的度数．【详解】解：DE 是AC 边的垂直平分线，35DAC C ∴∠=∠=︒，根据三角形内角和定理，可得18085B BAD DAC C ∠=︒-∠-∠-∠=︒，故选：D ．【点睛】本题考查了垂直平分线的性质，三角形内角和定理，熟练利用垂直平分线的性质是解题的关键．2．（2023春·四川达州·八年级统考期末）如图，点P 为定角AOB ∠平分线上的一个定点，且MPN ∠与AOB ∠互补．若MPN ∠在绕点P 旋转的过程中，其两边分别与OA 、OB 相交于M 、N 两点，则以下结论中，不正确的是（）A ．OM ON +的值不变C ．MN 的长不变【答案】C 【分析】如图作PE OA ⊥于E ∠∠EPM FPN =，由OP 平分∵∠∠90PEO PFO ==︒，∴∠∠180EPF AOB +=︒，∵∠∠180MPN AOB +=︒，∴∠∠MPN EPF =，∴∠∠EPM FPN =，∠故选：C【点睛】本题主要考查角平线的性质定理、全等三角形的判定和性质；能够结合角平分线的性质定理作出角平分线上点到两边的垂线段，构建全等三角形是解题的关键．二、填空题【答案】6【分析】过点C 作CP AB ⊥再根据三角形的面积公式求出【详解】解：过点C 作CP ∵BD 平分ABC ∠，PE AB ⊥∴PE EF =，∴CP CE PE CE EF =+=+的最小值．∵ABC 的面积为18，AB =性，是一道比较好的题目．三、解答题(1)如图1，若DE OB ∥．①DEO ∠的度数是︒，当DP OE ⊥时，x =②若EDF EFD ∠=∠，求x 的值；(2)如图2，若DE OA ⊥，是否存在这样的x 的值，使得说明理由．②∵20DEO ∠=︒，EDF EFD ∠=∠，∴80EDF ∠=︒，又∵140ODE ∠=︒，∴1408060ODP ∠=︒-︒=︒，∴60x =；（2）存在这样的x 的值，使得4EFD EDF ∠=∠．分两种情况：①如图2，若DP 在DE 左侧，∵DE OA ⊥，∴90EDF x ∠=︒-︒，∵20AOC ∠=︒，∴20EFD x ∠=︒+︒，当4EFD EDF ∠=∠时，()20490x x ︒+︒=︒︒﹣，解得68x =；②如图3，若DP 在DE 右侧，∵90EDF x ∠=︒-︒，18020160EFD x x ∠=︒-︒-︒=︒-︒，∴当4EFD EDF ∠=∠时，()160490x x ︒-︒=︒-︒，解得104x =；综上所述，当68x =或104时，4EFD EDF ∠=∠．(1)如图1，求BGC ∠的度数；(2)如图2，求证：EG FG =；(3)如图3，过点C 作CD EC ⊥交BF 延长线于点D ，连接AD ，点N 在BA 延长线上，连接NG 交AC 于点M 使DAC NGD ∠=∠，若:1:2EB FC =，10CG =，求线段MN 的长．【答案】(1)120︒(2)见解析∴60BGH CGH ∠=∠=︒，∵60BGE CGF GBC GCB ∠=∠=∠+∠=∴G BGH C CG GH B E F ∠∠=∠=∠=，∵GBC GBE ∠=∠，BG BG=∴BGE BGH ≌△△，∴EG GH =，∵CE 平分ACB ∠，∴2ACB ACE ∠=∠，∵CD EC ⊥，∴90ECD ∠=︒，∴90ACE ACD ∠+∠=︒，∵180ACB ACP ∠+∠=︒，∴2ACP ACD ∠=∠，∴CD 平分ACP ∠，∵DR AC ⊥，DP BC ⊥，∴DR DP =，∵BF 平分ABC ∠，DR AC ⊥，DQ AB ⊥，∴DP DQ =，∴DR DQ =，∴AD 平分QAC ∠，∵60BAC ∠=︒，∴60DAQ DAC ∠=∠=︒，∴60NGD DAC ∠=∠=︒，由（1）得120BGC ∠=︒，∴18060BEG FGC BGC ∠=∠=︒-∠=︒，∵60MGF ABF BNG ∠=∠+∠=︒，60FGC FBC ECB ∠=∠+∠=︒，(1)如图1，请指出AB 与PB 的数量关系，并说明理由．(2)如图2，当P ，Q 两点都在射线ON 的反向延长线上时，线段AB ，PB 是否还存在（1）中的数量关系？若存在，请写出证明过程；若不存在，请说明理由．【答案】(1)AB PB =，理由见解析(2)存在，理由见解析【分析】（1）连接BQ ，根据BC 垂直平分OQ ，可知BO BQ =，则BOQ BQO ∠=∠，根据OF 平分MON ∠，则AOB BOQ ∠=∠，即AOB BQO ∠=∠，根据OA QP =，可知AOB PQB △≌△，则可知AB PB =；（2）如图，连接BQ ，根据BC 垂直平分OQ ，可知BQ BO =，CQ CO =结合条件可证BQC BOC △≌△，则BQO BOQ ∠=∠，根据OF 平分MON ∠，BOQ FON =∠∠，可知AOF FON BOQ ∠=∠=∠，则AOF BQO =∠∠，进而可知AOB PQB =∠∠，由此可证AOB PQB △≌△（SAS ），则AB PB =．【详解】（1）解：AB PB=理由如下：连接BQ∵BC 垂直平分OQ∴BO BQ=∴BOQ BQO∠=∠∵OF 平分MON∠∴AOB BOQ∠=∠∴AOB BQO∠=∠∵OA QP=∴AOB PQB△≌△∴AB PB =；（2）存在，理由：如图，连接BQ ，∵BC 垂直平分OQ ，∴BQ BO =，CQ CO=在BQC 和BOC 中，BC BC CQ CO BQ BO =⎧⎪=⎨⎪=⎩∴BQC BOC △≌△（SSS ）∴BQO BOQ ∠=∠，∵OF 平分MON ∠，BOQ FON =∠∠，∴AOF FON BOQ ∠=∠=∠，∴AOF BQO =∠∠，∴AOB PQB =∠∠，在△AOB 和△PQB 中，OA PQ AOB PQB BO BQ =⎧⎪∠=∠⎨⎪=⎩【知识回顾】（1）如图1，P 是BOA ∠的平分线上的一点，PE OB ⊥于点E ，作PD OA ⊥于点D ，试证：【深入探究】（2）如图2，在ABC 中，BD 为ABC ∠的角平分线交于AC 于D 点，其中10,AB BC AD +=BD Q 平分BAC ∠，DM DN ∴=，11,22ABD CBD S AB DM S BC =⋅= ABD S AB S BC∴= ，∴BC∥EF由①知：∠CBP＝90°∴BP⊥EF∵EB＝EP∴EF是线段BP的垂直平分线∴PF＝BF∴∠PFE＝∠BFE＝30°（2）如图2，延长DE到Q，使EQ＝DE，连接CD，PQ，FQ∵EC＝EP，∠DEC＝∠QEP∴△QEP≌△DEC（SAS）则PQ＝DC＝DB∵QE＝DE，∠DEF＝90°∴EF是DQ的垂直平分线∴QF＝DF∵CD＝AD∴∠CDA＝∠A＝60°∴∠CDB＝120°∴∠FDB＝120°﹣∠FDC＝120°﹣（60°+∠EDC）＝60°﹣∠EDC＝60°﹣∠EQP＝∠FQP ∴△FQP≌△FDB（SAS）∴∠QFP＝∠BFD∵EF是DQ的垂直平分线∴∠QFE＝∠EFD＝30°(1)【理解运用】如图2，在ABC 中，D 为BC 上一点，点D ，E 关于直线AB 对称，连接判断点B 是否为点D ，F 关于直线AB 的“等角点”，并说明理由；(2)【拓展提升】如图2，在（1）的条件下，若70A ∠=︒，AB AC =，点Q 是射线EF 上一点，且点D ，Q 角点”为点C ，请利用尺规在图2中确定点Q 的位置，并求出BQC ∠的度数；(3)【拓展提升】∵D 、E 关于AB 对称，∴BE BD =，AB DE ⊥，∴ABE ABC ∠=∠，∵ABE MBF Ð=Ð，∴ABC MBF Ð=Ð，∴点B 是点D ，F 关于直线AB 的“等角点”；（2）如图2，∵70A ∠=︒，AB AC =，∴55ABC ACB ∠=∠=︒．∵点D ，Q 关于直线AB ，AC 的“等角点”分别为点B 和点C ，∴55MBQ NCQ ∠=∠=︒，∴70CBQ BCQ ∠=∠=︒，∴40BQC ∠=︒；（3）如图3，。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
线段的垂直平分线与角平分线专题复习
知识点复习：
1、线段垂直平分线的性质
（1）垂直平分线性质定理：线段垂直平分线上的点到这条线段两个端点
的距离相等.
定理的数学表示：如图1，∵ CD ⊥AB ，且AD ＝BD
∴ AC ＝BC.
定理的作用：证明两条线段相等 （2）线段关于它的垂直平分线对称.
2、线段垂直平分线的判定定理：
到一条线段两个端点距离相等的点在这条线段的垂直平分线上. 定理的数学表示：如图2，∵ AC ＝BC
∴ 点C 在线段AB 的垂直平分线m 上.
定理的作用：证明一个点在某线段的垂直平分线上.
3、关于线段垂直平分线性质定理的推论
（1）关于三角形三边垂直平分线的性质：
三角形三边的垂直平分线相交于一点，并且这一点到三个顶点．．．．．的距离相等.
性质的作用：证明三角形内的线段相等.
（2）三角形三边垂直平分线的交点位置与三角形形状的关系：
若三角形是锐角三角形，则它三边垂直平分线的交点在三角形内部； 若三角形是直角三角形，则它三边垂直平分线的交点是其斜边的中点；
若三角形是钝角三角形，则它三边垂直平分线的交点在三角形外部. 反之，也
图1
图2
成立。
4、角平分线的性质定理：
角平分线的性质定理：角平分线上的点到这个角的两边的距离相等. 定理的数学表示：如图4，
∵ OE 是∠AOB 的平分线，F 是OE 上一点，且CF ⊥OA 于点C ，DF ⊥OB 于点D ， ∴ CF ＝DF.
定理的作用：①证明两条线段相等；②用于几何作图问题；
角是一个轴对称图形，它的对称轴是角平分线所在的直线.
5、角平分线性质定理的逆定理：
角平分线的判定定理：在角的内部到角的两边距离相等的点在这个角的角平分线上. 定理的数学表示：如图5，
∵点P 在∠AOB 的内部，且PC ⊥OA 于C ，PD ⊥OB 于D ，且PC ＝PD ，
∴点P 在∠AOB 的平分线上.
定理的作用：用于证明两个角相等或证明一条射线是一个角的角平分线
6、关于三角形三条角平分线的定理：
（1）关于三角形三条角平分线交点的定理：
三角形三条角平分线相交于一点，并且这一点到三边的距离相等.
定理的数学表示：如图6，如果AP 、BQ 、CR 分别是△ABC 的内角∠BAC 、 ∠ABC 、∠ACB 的平分线，那么：
① AP 、BQ 、CR 相交于一点I ；
② 若ID 、IE 、IF 分别垂直于BC 、CA 、AB 于点D 、E 、F ，则DI ＝EI ＝FI.
图4
定理的作用：①用于证明三角形内的线段相等；②用于实际中的几何作图问题. （2）三角形三条角平分线的交点位置与三角形形状的关系：
三角形三个内角角平分线的交点一定在三角形的内部.这个交点叫做三角形的内心（即内切圆的圆心）.
7、关于线段的垂直平分线和角平分线的作图：
（1）会作已知线段的垂直平分线； （2）会作已知角的角平分线； （3）会作与线段垂直平分线和角平分线有关的简单综合问题的图形.
精品习题：
1．在△ABC 中，∠C=90º，BD 是∠ABC 的平分线.已知，AC=32，且AD ：DC=5：3，则点D 到AB 的距离为_______.
2．如图，在△ABD 中，AD=4，AB=3，AC 平分∠BAD ，则:ABC ACD S S ∆∆= （ ） A ．3:4 B ．4:3 C ．16:19 D ．不能确定
3．如图，ΔABC 的三边AB 、BC 、CA 的长分别是20、30、40、其中三条角平分线将ΔABD 分为三个三角形，则S ABO ∆：S BCO ∆：S CAO ∆等于______.
4．如图所示，∠BAC ＝105°，若MP 和NQ 分别垂直平分AB 和AC ．则∠PAQ 的度数为 ．
5．AD∥BC，∠D=90 ，AP平分∠DAB，PB平分∠ABC，点P恰好在CD上，则PD与PC的
关系是（）
A．PD>PC B．PD<PC C．PD=PC D．无法判断
6．如图，有A、B、C三个居民小区的位置成三角形，现决定在三个小区之间修一个超市，使超市到三个小区的距离相等，则超市应建在( )
A．在AC、BC两边高线的交点处
B.在AC、BC两边中线的交点处
C．在AC、BC两边垂直平分线的交点处
D.在∠A、∠B的角平分线的交点处
7．如图，CD是Rt△ABC斜边AB上的高，将△BCD沿CD折叠，B点恰好落在AB的中点E 处，则∠A等于( )
A．25º B.30º C.45º D.60º
8．AC=AD，BC=BD，则有（）
A．AB垂直平分CD B．CD垂直平分AB
C．AB与CD互相垂直平分D．CD平分∠ACB
9．如图，OP平分∠AOB，PA⊥OA，PB⊥OB，垂足分别为A，B．下列结论中不一定成立的是（）
A．PA=PB B．PO平分∠APB C．OA=OB D．AB垂直平分OP
10．随着人们生活水平的不断提高，汽车逐步进入到千家万户，小红的爸爸想在本镇的三条相互交叉的公路（如图所示），建一个加油站，要求它到三条公路的距离相等，这样可供选择的地址有（）处。
A、1
B、2
C、3
D、4
11．在Rt△ABC中，∠A=90°，AB=3，AC=4，∠ABC，∠ACB的平分线交于P点，PE⊥BC于E点，求PE的长．
12．如图，△BDA、△HDC都是等腰直角三角形，且D在BC上，BH的延长线与AC交于点E，请你判断线段AC与BH有什么关系？并说明理由.
13．如图，∠C=90°，AC=BC，AD是∠BAC的角平分线．求证：AC+CD=AB．
14．如图，AD为△ABC的角平分线，AD的中垂线交AB于点E、交BC的延长线于点F，AC 于EF交于点O．
（1）求证：∠3=∠B；
（2）连接OD，求证：∠B+∠ODB=180°．
15．已知：∠DAB=120°，AC平分∠DAB，∠B+∠D=180°．
（1）如图1，当∠B=∠D时，求证：AB+AD=AC；
（2）如图2，当∠B≠∠D时，猜想（1）中的结论是否发生改变？说明理由．
16．小明做了一个如图所示的“风筝”骨架，其中AB=AD，CB=CD．
（1）小芳同学观察了这个“风筝”骨架后，他认为AC⊥BD，垂足为点E，并且BE=ED，你同意小德的判断吗？为什么？
（2）设AC=a，BD=b，请用含a，b的式子表示四边形ABCD的面积．
17．如图，AB∥CD，AE、DE分别平分∠BAD和∠ADE，求证：AD=AB+CD。
18．如图，AC 平分∠BAD ，CE ⊥AB ，且∠B+∠D=180°，求证：AE=AD+BE 。
D
A
E C
B
A
B
E
C
D
19．已知：如图在△ABC中，∠A=90°，AB=AC，BD是∠ABC的平分线，求证：BC=AB+AD
A
D
B C。